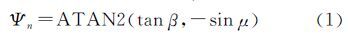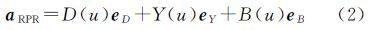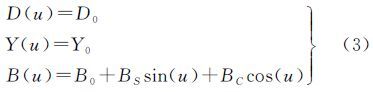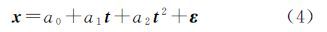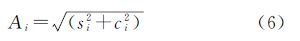准天顶星系统(quasi-zenith satellite system,QZSS)是日本在2000年提出的一套兼具导航定位、移动通信和广播功能的GPS辅助增强系统,其计划以4颗IGSO卫星保持任意时段都有一颗卫星处于日本上空顶点位置,其第1颗卫星QZS-1(Michibiki)已于2010年9月发射[1, 2, 3]。QZSS能够实现与GPS高度的兼容互操作,因此它既是对GPS的增强,也是一种补充。
根据文献[4, 5, 6, 7, 8, 9],QZS-1采用的卫星姿态控制模型与现行的北斗IGSO和MEO卫星类似,QZS-1在太阳与轨道面夹角|β|约为20°并且卫星偏航姿态最为接近于零偏置或动态偏置名义姿态时开始姿态转换,偏航姿态由动态偏置转为零偏置,而北斗IGSO和MEO相应的动转零条件|β|约为4°。
卫星姿态变化对于精密定轨解算得到的轨道和钟差产品有较大影响。相较北斗IGSO和MEO卫星而言,QZS-1在|β|约为20°时开始姿态切换,其姿态切换的|β|阈值大于北斗IGSO和MEO卫星,对于轨道和钟差的影响更为明显,因此也更容易发现卫星姿态与卫星轨道和钟差产品相关性的规律。此外,由于QZSS与GPS很好的互操作性,国际上对于QZSS的数据处理更为成熟,为研究这一规律提供了较好的数据产品。因此,分析QZSS卫星姿态变化对轨道和钟差特性的影响对于研究我国BDS姿控模型有一定参考价值。目前,文献[10, 11, 12]等对GPS和GLONASS的姿态变化做了大量研究,构建了导航卫星姿态模型的理论基础。文献[4]对GNSS的姿态切换模型及其影响做了深入研究,得出了很多有意义的结论,但并未直接给出姿态切换对QZSS精密定轨产品影响的分析,且未考虑姿态切换对卫星钟差特性的影响。
基于IGS组织(International GNSS Service)的MGEX(Multi-GNSS Experiment)和欧洲CONGO(Cooperative Network for GLOVE Observation)等地基观测网[13],慕尼黑工业大学(TUM)利用CODE五参数光压模型对QZS-1光压进行建模,开展了基于非差处理的“两步法”GPS和QZSS精密轨道和钟差解算,并发布QZSS事后精密星历,详细解算策略参考文献[14]。本文首先从理论上分析了QZSS卫星姿态模型切换及其影响,而后通过卫星激光测距(SLR)进行了轨道精度检核并分析了SLR残差与太阳角的相关性,最后从卫星钟差拟合精度和周期特性两个方面分析了卫星姿态模式切换对钟差产品的影响。结果表明,目前精密定轨所使用的非保守力模型在卫星零偏置时期的建模存在缺陷,导致零偏置期的轨道以及钟差精度显著降低,需要在数据处理中予以慎重考虑。
1 QZSS卫星偏航姿态模式切换导航卫星在轨运行期间,为了确保地面用户能够有效接收卫星信号并且保证卫星有充足的能量供给[15],姿态控制系统需要根据太阳、地球和卫星位置计算和调动态整导航卫星偏航姿态。
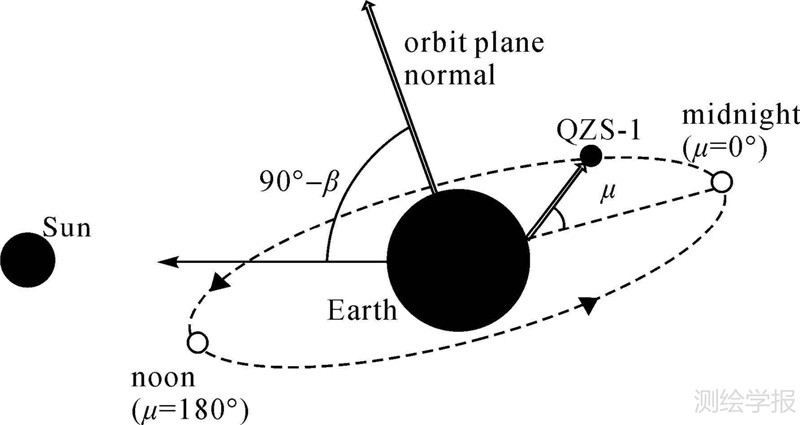
QZS-1卫星的星固系定义如下:z轴沿卫星信号发射天线方向指向地心,y轴为太阳帆板旋转轴并垂直于太阳、地球和卫星所构成的平面,x轴垂直于y轴和z轴构成右手坐标系并背离太阳光入射方向。从而卫星偏航角ψn的名义值为[10]
式中,β为太阳与导航卫星轨道面的夹角(太阳角)。μ为轨道面内卫星与地心连线和“远日点”夹角(轨道角)。太阳、地球和卫星三者空间关系如图 1所示。
|
| 图 1 太阳、地球和卫星空间关系 Fig. 1 Sun,Earth and satellite in space |
卫星在轨期间受到多种因素的影响,实际姿态常常会偏离式(1)所确定的名义姿态。这种非名义偏航姿态主要有3种情况:①低太阳角下卫星动量轮速率过大并超过硬件限值而导致的卫星正午机动和午夜机动;②地影期内由于星敏感器无法正常工作导致的地影机动;③由于卫星本身设计所致的低太阳角下的动偏-零偏-动偏模式切换。
显然,太阳角是卫星姿态控制系统计算和调整偏航姿态的关键参数。对于QZS-1卫星而言,其本身设计具有动偏和零偏两种姿态模式,在太阳角|β|约为20°且卫星动态偏置或零偏置姿态最为接近于名义姿态时开始姿态切换。由于动偏-零偏-动偏切换的太阳角临界值大于地影期太阳角临界值,地影期包含在零偏期内,因此该卫星不会发生地影机动;当|β|≤20°时,卫星偏航姿态固定为零偏置模式,卫星不会出现低太阳角条件下动量轮速率超过硬件限值的情况,不需要正午机动和午夜机动。因此,QZS-1卫星一年中大部分时间处于动态偏航模式(即保持名义姿态),短期处于零偏模式(一年两次)。
目前来说,并不是所有的精密定轨数据处理流程都考虑了非名义姿态。通常是针对动偏期间的卫星偏航姿态和受力情况进行建模。以TUM精密定轨中所采用的CODE光压模型为例,分析姿态模式切换对精密定轨的影响。若定义D为卫星指向太阳方向,Y为卫星星固系y轴方向,B垂直于D和Y构成右手坐标系,则精密定轨解算采用的CODE五参数光压模型可以表示为[16]
式中,aRPR为光压导致的加速度;eD、eY、eB分别为三轴方向的单位向量;u为卫星在轨道面上与升交点间角度。且有从式(3)可以看出,CODE模型中的B轴并非固定于卫星星体某一方向,而是在+z、+x和-z向变化,并且B方向力的级数展开式为卫星相对于升交点角度的函数,因此该值并不具有清晰的物理意义,仅能表示光压摄动力呈周期变化,而没有考虑不同姿态模式下光压受力的差异。因此,姿态切换对太阳光压建模的影响主要表现为CODE光压模型无法满足零偏置期对光压的建模要求,即:
(1) 当卫星处于动偏模式时,CODE光压模型中的Y轴定义为星固系y轴且与太阳入射方向即D轴方向垂直,卫星星体-x板持续受照而+z和-z板轮流受照,此种模式下CODE模型能很好地对卫星的光压进行建模。
(2) 在其他姿态模式下,星固系y轴并不一定垂直于太阳入射方向,卫星星体受照面发生变化,除卫星±x和±z板轮流受照外,±y板也将分别受照。由于在太阳入射光线并不与太阳面板垂直而存在小角度夹角,该角度随太阳与轨道面夹角β变化而变化,此时CODE光压模型存在显著的误差。
由于卫星会随着太阳角的周年变化进行一年两次的动偏-零偏-动偏模式切换,若在定轨中全部采用动偏期间的受力模型则必然会导致零偏期间定轨精度的显著下降。需要指出的是,导航卫星定轨精度受到多种因素影响,本文仅从太阳光压建模误差出发对零偏置期间的卫星定轨精度进行了分析。除此之外,零偏期间的卫星天线相位中心改正误差也会对定轨精度造成一定影响。限于篇幅,本文不再展开探讨。
2 卫星轨道和钟差精度分析方法 2.1 卫星激光测距卫星激光测距(satellite laser ranging,SLR)是一种独立的轨道径向精度检核方法[16, 17, 18]。通过安置在地面上的卫星激光测距系统所发射的激光脉冲,跟踪装有激光反射棱镜(laser retro-reflector array,LRA)的人造地球卫星,以测定测站到卫星之间的距离。利用ILRS组织(International Laser Ranging Service)提供的QZS-1的SLR标准点数据,可以对TUM的QZS-1卫星轨道产品进行精度检核。
2014年内进行QZS-1观测的激光站主要有6个,分别为Yarragadee(7090)、Changchun(7237)、Beijing(7249)、Koganei(7308)、Shanghai(7821)、Mount Stromlo(7825)。
在对轨道进行SLR检核前,需要对激光观测值进行潮汐改正、大气折射改正、对流层改正等。此外,还需要利用ILRS提供的SLR反射棱镜相对于卫星质心的仪器偏差进行改正。在改正时假定卫星具有标称的偏航姿态,QZS-1卫星的LRA偏差参数如表 1所示[16]。
| mm | |||
| 卫星 | x | y | z |
| QZS-1 | -1 149.1 | -552.9 | +2 685.4 |
由于卫星轨道与钟差相互耦合等原因,通过精密定轨解算的卫星钟差精度与轨道视向精度强相关,从而也含有周期性波动变化[19]。卫星钟差的周期项一方面反映了卫星轨道特性,另一方面也对导航卫星原子钟预报和性能评价有较大影响。基于快速傅里叶变换(FFT)的谱分析方法可以用于提取和分析卫星钟差的主周期项,谱分析方法的步骤如下:
(1) 卫星钟差数据预处理。主要进行数据提取以及粗差剔除等。
(2) 计算逐日拟合残差。考虑到铷钟的频漂特性,以二次多项式拟合每天的卫星钟差,得到拟合残差。
(3) 傅里叶变换。将逐日拟合残差进行拼接,进行傅里叶变换,分析和提取卫星钟差的主周期。
使用谱分析方法提取卫星钟差主周期后,为了进一步的研究卫星姿态切换对周期特性的影响,采用附加周期项改正的多项式模型对卫星钟差进行拟合[20, 21],分析周期项振幅与β角的相关性。
针对卫星钟差序列{x},其卫星钟差二次多项式模型为
式中,a0、a1、a2分别为钟差、钟速以及钟加速;ε为残差。对于卫星钟差序列{x},其附加周期项改正的多项式模型为
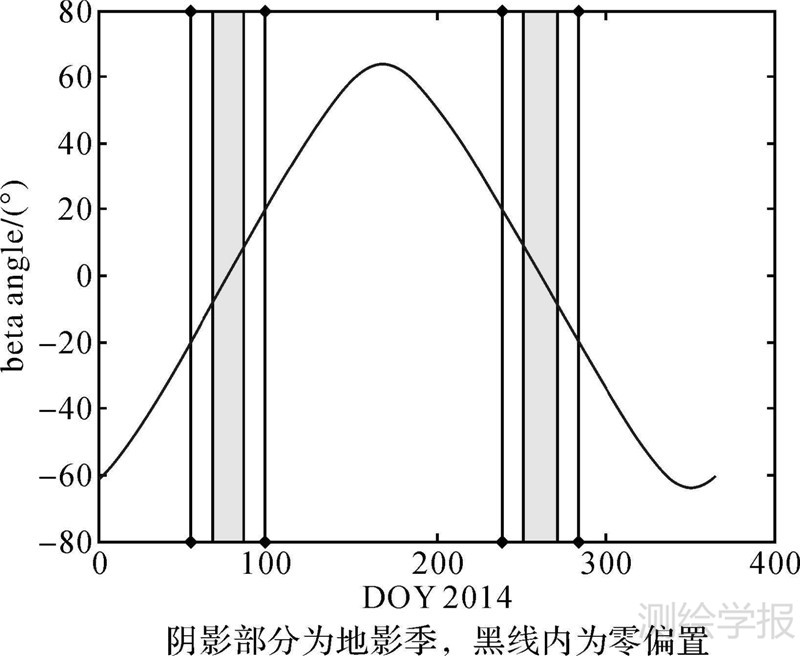
式中,fi为卫星钟差序列的第i主频项;si和ci为该主频项所对应的系数;Ai为周期项fi对应的振幅。 3 结果与分析 3.1 太阳角变化与地影季本文使用德国TUM发布的2014年全年的QZSS卫星精密轨道和钟差产品,数据采样间隔为5 min。首先进行坐标系转换并采用数值差分的方法计算出卫星速度,然后计算出2014年内QZS-1卫星太阳角β的变化情况及地影季,如图 2所示,图中阴影部分为地影季,直线内为零偏期。
|
| 图 2 2014年QZS-1太阳角变化及地影季 Fig. 2 Beta angle and eclipse seasons of QZS-1 in 2014 |
由图 2可知,卫星太阳角β呈现以半年为周期的正弦波动,变化范围约为[-60°,+60°],而卫星进出地影的临界角为±8.6°左右。2014年内QZS-1有两次地影季,分别为DOY 67—DOY 87和DOY 251—DOY 271,每次长约为20 d;而其零偏置分别为DOY 54—DOY 100和DOY 238—DOY 284,每次长约47 d。可以发现,QZS-1卫星具有较长的零偏置和地影季,有利于分析姿态切换对卫星定轨产品的影响。
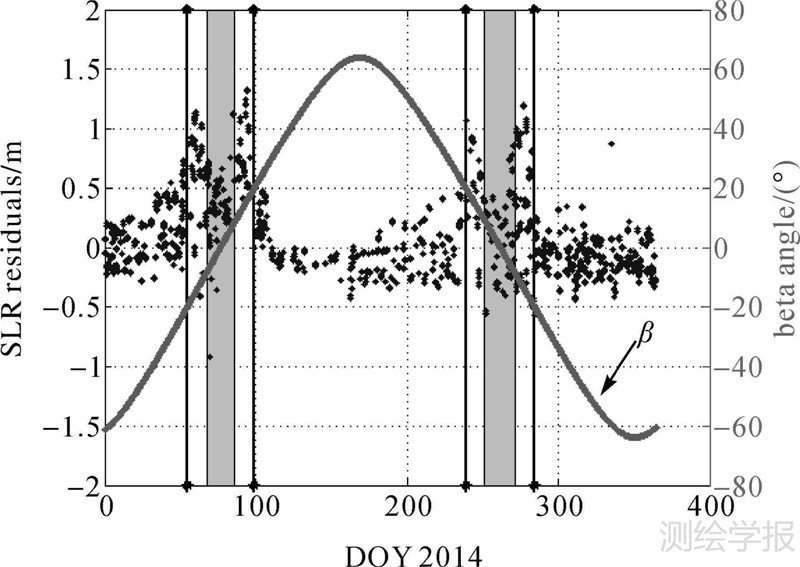
3.2 卫星轨道SLR检核残差采用SLR作为独立检核手段,可以对卫星轨道的外符精度进行评价。2014年内总共有6个站进行QZS-1的卫星激光测距,共计1650个标准点,可见激光观测的数据十分稀少。利用ILRS提供的标准点数据对TUM提供的卫星轨道产品进行了精度检核,对SLR残差进行了粗差剔除,结果如图 3所示。从图中可以看出:
|
| 图 3 TUM卫星轨道产品的SLR检核残差(6站) Fig. 3 SLR residuals derived from TUM satellite orbits(six stations) |
(1) SLR残差存在一定的均值偏差,其大小为-0.10 m左右。这种偏差的出现与其他导航卫星(GPS、GLONASS)等出现的偏差现象类似,可能的原因有星上LRA的坐标不准确以及卫星轨道产品中系统误差等。
(2) SLR残差存在半年周期的变化规律,且与太阳角β变化有很大的相关性。这说明由于太阳光压等非保守力模型的不完善,导致QZS-1卫星轨道产品精度与太阳角β有明显的相关性。由于QZS-1卫星姿态调整导致定轨精度降低,零偏置状态下卫星轨道中仍有较大的未被充分建模的误差项。此外,SLR测站坐标的建模也可能导致SLR残差序列中半年周期的变化。需要说明的是,本文中所使用的SLR仪器偏差改正为标称偏航姿态下进行的改正,并未随卫星姿态的变化进行调整,因此可能也会引入部分误差,下一步将探讨建立文献[22]所提出的卫星质心概率模型以进一步提高SLR轨道检核的精度。
此外,注意到在QZS-1卫星零偏置期内,地影季内的SLR残差反而小于地影季外的SLR残差,其原因可能为地影季期间光压摄动力为零,因而不受光压模型误差的影响。
3.3 卫星钟差拟合残差
由非差处理法进行精密定轨解算的卫星钟差与定轨误差存在一定程度的耦合,因此卫星钟差的精度也能部分反映出轨道模型的精度。由于缺乏独立的外部精度评价手段,且在卫星钟差中二次项占主导,因此一般以二次多项式拟合残差作为钟差精度的评价标准。在解算过程中,经常会出现数据缺失、粗差等异常情况,需要对钟差数据进行预处理。对经过数据预处理后的卫星钟差进行逐日二次多项式拟合,对其每日拟合残差进行统计,结果如图 4所示。
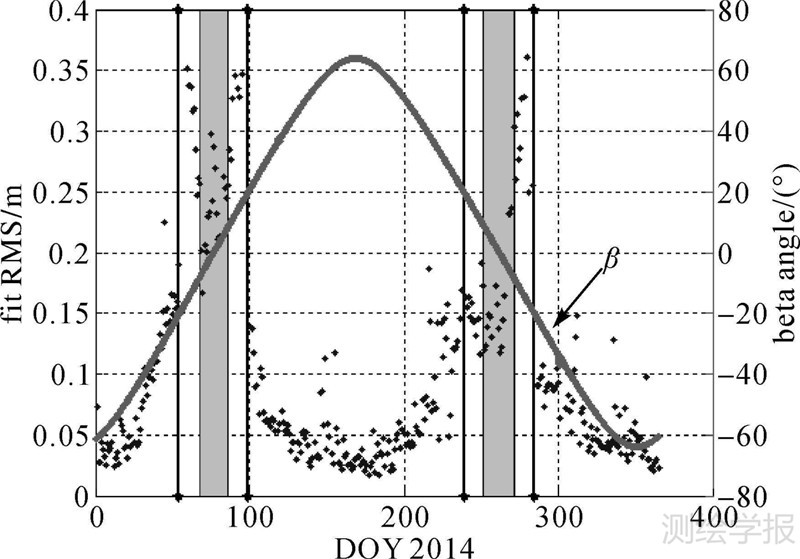
|
| 图 4 2014年QZS-1卫星钟差拟合精度 Fig. 4 Fit RMS of QZS-1 satellite clock offset in 2014 |
由图 4可以看出:
(1) TUM的QZS-1卫星钟差的精度在0.3 m以内,在动态偏置期(即|β|≥20°),钟差精度基本上在0.1 m以内。从图中可以看出,零偏置期间的卫星钟差拟合精度要低于地影季内的钟差精度,这与轨道SLR残差的分布相似,需要进一步研究其原因。
(2) 卫星钟差的精度变化情况与轨道精度相似,都随着|β|的变化而波动,且与太阳角|β|呈负相关。2014年QZS-1的拟合均方根误差(RMS)随着太阳角|β|有明显的波动变化,当|β|开始满足|β|≤20°的条件时,卫星钟差拟合精度开始逐渐降低,进入地影期后精度最低,在0.3 m左右。卫星拟合精度与太阳角|β|有显著的相关性,卫星拟合精度也存在半年周期的波动规律,这进一步验证了精密定轨过程中姿态误差对轨道和钟差产品的误差影响有一定程度的耦合。
3.4 卫星钟差周期特性周期性变化是卫星钟差的重要特性,可以反映卫星定轨过程中的力模型精度。由于卫星姿态模型切换和地影期间,卫星受力发生变化,将对卫星钟差的周期特性产生影响。采用谱分析方法对卫星钟差24 h以内的周期项进行提取并分析其振幅随β的变化情况。利用2014年TUM提供的卫星钟差进行二次多项式逐日拟合,将其拟合残差进行拼接,结果如图 5所示。从图中可以看出,其残差均值基本上为0,且在零偏置期的拟合残差明显增大,随着β的变化有明显波动。图 6为对2014年QZS-1卫星钟差进行谱分析的结果。

|
| 图 5 2014年QZS-1卫星钟差拟合残差 Fig. 5 Fit residuals of QZS-1 satellite clock offset in 2014 |
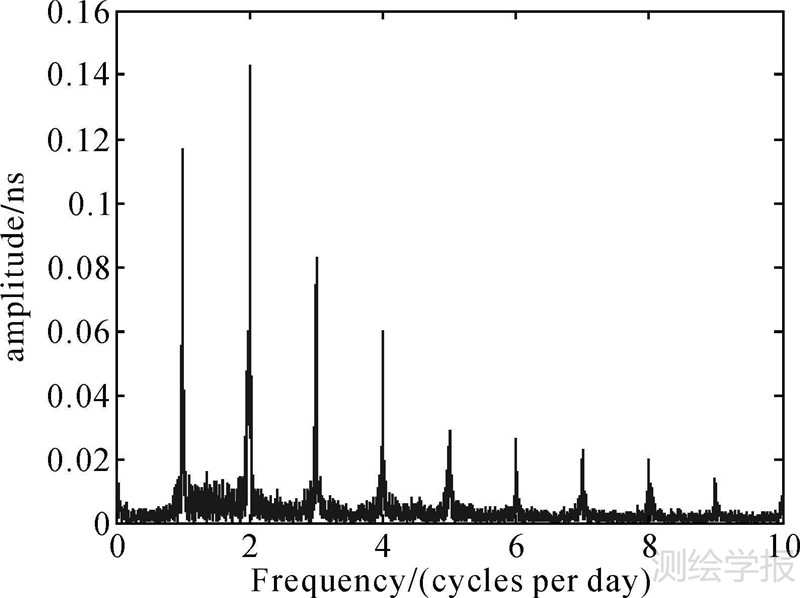
|
| 图 6 QZS-1卫星钟差谱分析结果 Fig. 6 Spectral analysis of QZS-1 satellite clock offsets |
从图 6可以看出,QZS-1卫星钟差的前4个主周期分别为:T1=23 h 54 min、T2=11 h 58 min、T3=7 h 59 min、T4=5 h 59 min。卫星钟差中存在着与轨道周期相近或者呈倍数关系的周期项,这表明QZS-1卫星钟差误差与轨道误差相耦合。QZS-1卫星钟差周期性波动的原因可能为:①卫星受力建模不准确,尤其是光压摄动力;②精密定轨解算过程中,卫星轨道与钟差部分误差耦合在一起,两者的周期性误差无法全部分离。
为了进一步研究卫星钟差周期特性与卫星姿态切换的关系,选取谱分析得出的4个主周期,建立周期模型。考虑到卫星钟差的天跳变以及消除单天拟合的误差,采用了连续3 d的卫星钟差多项式残差进行周期模型拟合,依次分析4个主周期项的振幅变化情况,如图 7所示。
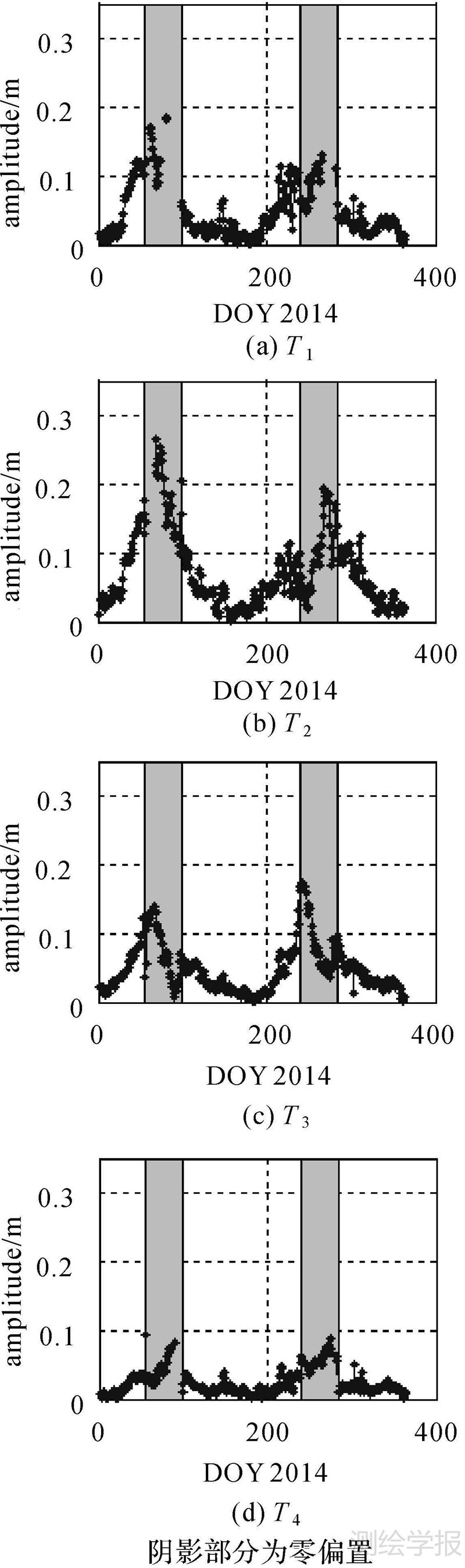
|
| 图 7 周期项振幅的变化规律 Fig. 7 Variations of amplitudes of periodic terms |
从图 7中可以看出:
(1) 卫星钟差各周期的振幅随时间变化,且与太阳角|β|具有明显的相关性。卫星进入零偏置期间(|β|≤20°)后,各个周期项的振幅明显增大,而主周期项T2振幅的增大尤为明显。推断可能的原因一方面为零偏期间,轨道建模较差导致定轨误差增大,且反映在拟合残差的周期项振幅上;另一方面为姿态转换后天线相位中心建模精度降低,部分误差表现出周期性且被卫星钟差吸收,导致钟差周期项振幅增大。
(2) 周期项T4的振幅明显小于前3个主周期项。这说明在对卫星钟差进行建模时,除了在零偏置期间必须考虑其影响外,其他情况下可以不用考虑。
需要说明的是,通过对比图 6和图 7中卫星钟差周期项的振幅发现,周期项振幅的大小关系并不完全一致,这说明拟合天数长度对周期项振幅的相对大小会有一定影响,需要做进一步的研究。
为了验证谱分析的结果并进一步评价非差定轨方法的轨道误差对钟差周期特性的影响,采用改进阿伦方差[20]对姿态模式切换前47 d、零偏期间47 d以及切换后47 d共计3个时段内的原子钟稳定度及其噪声变化情况进行了分析。图 8给出了计算的改进阿伦方差及其噪声变化情况,统计结果分别对应2014年内的DOY 191—DOY 237、DOY 238—DOY 284以及DOY 285—DOY 331共3个时间段。
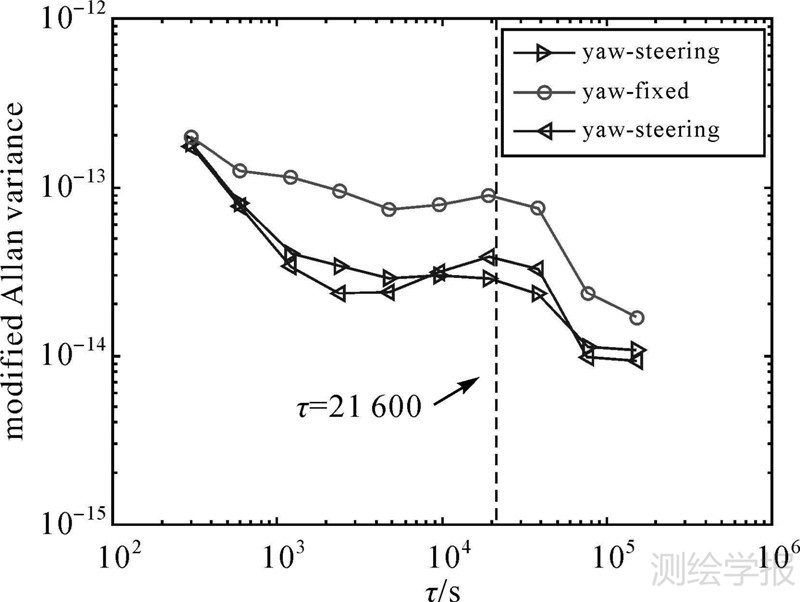
|
| 图 8 零偏与动偏期间的改进阿伦方差比较 Fig. 8 Comparison of modified Allan variance in yaw-fixed and yaw-steering period |
由图 8可知:
(1) 3个时段内的卫星钟差均有以0.5 d为周期的显著周期项。从图中曲线可以看出,3条曲线在采用间隔τ≈21 600 s附近达到最大值。根据时频域的转换关系[23],可知该“鼓包”对应的卫星钟差周期为T=2τ≈43 200 s,这与谱分析的结果一致,且该周期项对应为谱分析中的周期项T2。说明该周期性变化与姿态调整没有关系,而是与精密定轨本身所采用的策略有关,因此定轨解算策略仍有待优化。
(2) 3个时段的噪声类型基本一致,但是零偏期间噪声的量级显著增大。由于改进阿伦方差的斜率可以用来大致表征卫星钟差的噪声类型,因此可以通过图 8对卫星钟差的噪声类型及其大小进行分析。从图 8可以看出,3个时间段内的主要噪声类型均为调频闪变噪声、调频白噪声和调频随机游走噪声(对应斜率分别为0,-1和1),但是噪声的量级显著增大,这说明零偏期间的定轨误差增大对卫星钟差的噪声特性也会有所影响。
4 结束语(1) 以光压模型为例,从理论上分析了偏航姿态切换对精密定轨的影响,并以实测数据分析了卫星姿态切换至零偏置模式后轨道和钟差精度的变化。结果表明光压建模误差在精密定轨的过程中会被卫星轨道和钟差吸收,零偏置期的轨道和钟差精度显著降低。卫星轨道和钟差精度呈现半年周期的波动变化且与太阳角β有明显的相关性,现有的卫星非保守力建模仍需改善。
(2) 以谱分析方法提取了QZS-1卫星钟差中的主要周期项并分析了一年内其振幅的变化情况,并采用改进阿伦方差对谱分析的结果进行了验证。卫星钟差中存在与轨道周期耦合的周期项,这些周期项的振幅与太阳角β也有明显相关性。在高太阳角β的情况下,仅考虑前3个主周期项即可,但是在低太阳角β的情况下,前4个周期项都不能忽略。
本文研究的QZS-1卫星与我国BDS星座中的IGSO/MEO卫星姿态控制模型基本一致,因此该结论对提高BDS IGSO/MEO轨道和钟差精度也有一定的参考价值。当然,卫星姿态与很多因素有关,本文仅考虑了卫星轨道和钟差与地影季及太阳角β的相关性,下一步将重点研究优化导航卫星姿态建模以提高零偏期间精密定轨精度。
致谢:感谢TUM分析中心提供的数据支持。特别感谢武汉大学郭靖博士和王彬博士提供的指导与帮助。
| [1] | KISHIMOTO M, HASE H, MATSUMOTO A, et al. QZSS System Design and Its Performance[C]//Proceedings of the 2007 National Technical Meeting of the Institute of Navigation. San Diego, California:NTM, 2007:405-410. |
| [2] | SAWAMURA T, TAKAHASHI T, MORIGUCHI T, et al. Performance of QZSS(Quasi-zenith Satellite System) & L-band Navigation Payload[C]//Proceedings of the 2012 International Technical Meeting of the Institute of Navigation. Newport Beach, CA:[s.n.], 2012:1228-1254. |
| [3] | 孙宏伟, 李玉莉, 袁海波. 日本准天顶卫星系统概要[J]. 武汉大学学报(信息科学版), 2010, 35(8):1004-1007. SUN Hongwei, LI Yuli, YUAN Haibo. Outline of the Quasi-zenith Satellite System of Japan[J]. Geomatics and Information Science of Wuhan University, 2010, 35(8):1004-1007. |
| [4] | 郭靖. 姿态、光压和函数模型对导航卫星精密定轨影响的研究[D]. 武汉:武汉大学, 2014. GUO Jing. The Impacts of Attitude, Solar Radiation and Function Model on Precise Orbit Determination for GNSS Satellites[D]. Wuhan:Wuhan University, 2014. |
| [5] | GUO Jing, ZHAO Qile, GENG Tao, et al. Precise Orbit Determination for COMPASS IGSO Satellites during Yaw Maneuvers[C]//China Satellite Navigation Conference(CSNC) 2013 Proceedings. Berlin:Springer, 2013:41-53. |
| [6] | HAUSCHILD A, STEIGENBERGER P, RODRIGUEZ-SOLANO C. Signal, Orbit and Attitude Analysis of Japan's First QZSS Satellite Michibiki[J]. GPS Solutions, 2012, 16(1):127-133. |
| [7] | HAUSCHILD A, STEIGENBERGER P, RODRIGUEZ-SOLANO C. QZS-1 Yaw Attitude Estimation Based on Measurements from the CONGO Network[J]. Navigation, 2012, 59(3):237-248. |
| [8] | DAI Xiaolei,GE Maorong,LOU Yidong,et al. Estimating the Yaw-attitude of BDS IGSO and MEO Satellites[J]. Journal of Geodesy, 2015, 89(10):1005-1018. |
| [9] | 毛悦, 宋小勇, 王维, 等. IGSO姿态控制模式切换期间定轨策略研究[J]. 武汉大学学报(信息科学版), 2014, 39(11):1352-1356. MAO Yue, SONG Xiaoyong, WANG Wei, et al. IGSO Satellite Orbit Determining Strategy Analysis with the Yaw-steering and Orbit Normal Attitude Control Mode Switching[J]. Geomatics and Information Science of Wuhan University, 2014, 39(11):1352-1356. |
| [10] | BAR-SEVER Y E. A New Model for GPS Yaw Attitude[J]. Journal of Geodesy, 1996, 70(11):714-723. |
| [11] | KOUBA J. A Simplified Yaw-attitude Model for Eclipsing GPS Satellites[J]. GPS Solutions, 2009, 13(1):1-12. |
| [12] | DILSSNER F, SPRINGER T, GIENGER G, et al. The GLONASS-M Satellite Yaw-attitude Model[J]. Advances in Space Research, 2011, 47(1):160-171. |
| [13] | MONTENBRUCK O,STEIGENBERGER P,KHACHIKYAN R, et al. IGS-MGEX:Preparing the Ground for Multi-constellation GNSS Science[J]. Inside GNSS, 2014, 9(1):42-49. |
| [14] | STEIGENBERGER P,HAUSCHILD A,MONTENBRUCK O, et al. Orbit and Clock Determination of QZS-1 Based on the CONGO Network[J]. Navigation, 2013, 60(1):31-40. |
| [15] | 毛悦, 宋小勇, 贾小林, 等. 北斗导航卫星地影状态分析[J]. 测绘学报, 2014, 43(4):353-359. DOI:10.13485/j.cnki.11-2089.2014.0053. MAO Yue, SONG Xiaoyong, JIA Xiaolin, et al. Earth Eclipse Status Analysis of BeiDou Navigation Satellite[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(4):353-359. DOI:10.13485/j.cnki.11-2089.2014.0053. |
| [16] | ARNOLD D, MEINDL M, BEUTLER G, et al. CODE's New Solar Radiation Pressure Model for GNSS Orbit Determination[J]. Journal of Geodesy, 2015, 89(8):775-791. |
| [17] | PEARLMAN M R, DEGNAN J J, BOSWORTH J M. The International Laser Ranging Service[J]. Advances in Space Research, 2002, 30(2):135-143. |
| [18] | URSCHL C, GURTNER W, HUGENTOBLER U, et al. Validation of GNSS Orbits Using SLR Observations[J]. Advances in Space Research, 2005, 36(3):412-417. |
| [19] | SENIOR K L, RAY J R, BEARD R L. Characterization of Periodic Variations in the GPS Satellite Clocks[J]. GPS Solutions, 2008, 12(3):211-225. |
| [20] | 郭海荣. 导航卫星原子钟时频特性分析理论与方法研究[D]. 郑州:信息工程大学, 2006. GUO Hairong. Study on the Analysis Theories and Algorithms of the Time and Frequency Characterization for Atomic Clocks of Navigation Satellites[D]. Zhengzhou:The PLA Information Engineering University, 2006. |
| [21] | 黄观文, 张勤, 许国昌, 等. 基于频谱分析的IGS精密星历卫星钟差精度分析研究[J]. 武汉大学学报(信息科学版), 2008, 33(5):496-499. HUANG Guanwen, ZHANG Qin, XU Guochang, et al. IGS Precise Satellite Clock Model Fitting and Its Precision by Using Spectral Analysis Method[J]. Geomatics and Information Science of Wuhan University, 2008, 33(5):496-499. |
| [22] | 赵群河, 王小亚, 何冰, 等. 卫星激光反射器质心改正的概率模型[J]. 测绘学报, 2015, 44(4):370-376. DOI:10.11947/j.AGCS.2015.20130338. ZHAO Qunhe,WANG Xiaoya,HE Bing, et al. Probability Model of Center-of-mass Calibration of Satellites' Retro-reflectors Used for Laser Ranging[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(4):370-376. DOI:10.11947/j.AGCS.2015.20130338. |
| [23] | RILEY W J. User Manual:Stable32 Frequency Stability Analysis Version 1.5.0[M].Beaufort, SC:Hamilton Technical Services, 2007. |