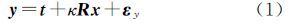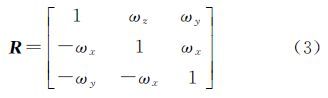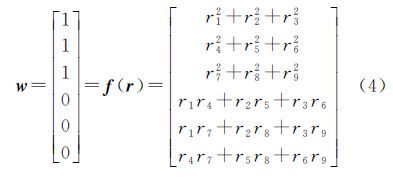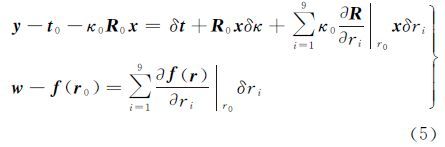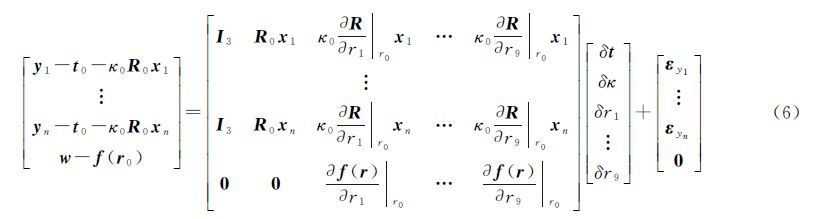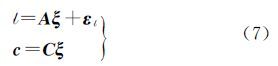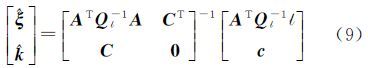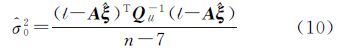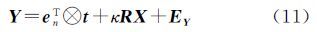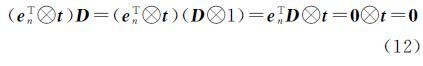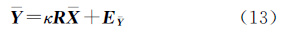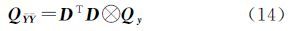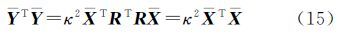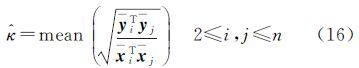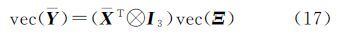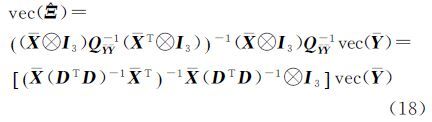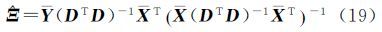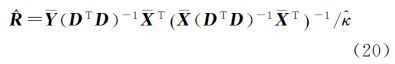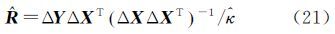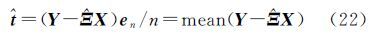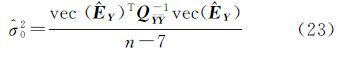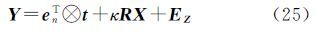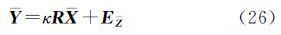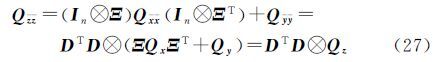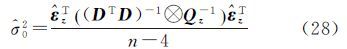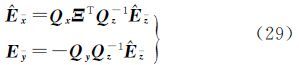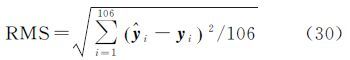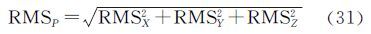采用基准转换理论将传感器测量基准下的成果转换至应用基准下的成果才能满足实际应用的需求[1, 2],基准转换的核心是利用公共点的两套坐标求解转换参数,从而实现非公共点的成果转换[3]。根据测量传感器与实际应用基准的维度、尺度和旋转的差异,可采用不同的基准转换模型,例如相似变换和仿射变换,以及不同数量参数的转换模型[1, 2]。
传统大地测量应用中的基准转换往往涉及小角度旋转,且只考虑公共点的一套坐标误差,忽略了构成系数阵的另一套坐标误差,因此可只考虑旋转角的一阶量,忽略二阶及以上小量得到简单的线性基准转换模型[1, 2, 3, 4, 5, 6]。当观测误差服从正态分布时,采用最小二乘求解最优估值。针对该线性基准转换模型,提出高崩溃率的转换参数抗差解法[4]以及用于局部区域三维基准转换的病态方法[5];考虑到实际应用中平面与高程系统分离,提出了采用过渡坐标系的三维基准转换模型[6];为了补偿地面变形等因素所引起的点位系统性变化,提出了附加信号参数的基准变换模型并采用拟合推估法求解[6, 7, 8],且当信号与观测值的权重不匹配时,还可采用方差分量估计确定合理的权比[9, 10]。
现代空间观测技术对基准转换提出新需求:首先,由于自由式多传感器的引入(例如无人机、LiDAR等),使得传感器直接测量成果与实际应用基准之间难免存在大旋转角度(可达数十秒甚至几度);其次,由于多传感器海量观测数据和对测量成果的实时应用,需要更高计算效率的基准转换方法。针对该问题,需要发展适用于大旋转角的高计算效率基准转换模型。对于大旋转角的基准转换已有大量研究,文献[2]提出将旋转矩阵所有元素作为未知数(并非将旋转角作为参数)并利用旋转矩阵的正交条件,采用附约束条件平差法迭代求解,该方法已成功应用于摄影测量等领域[11];文献[12]采用四元素理论导出了任意旋转角度的三维基准解析方法,但该方法只适用于等精度观测模型。
以解决现代空间观测技术对基准转换的新需求为初衷,本文以空间三维基准转换为例,研究大角度三维基准转换的解析解,实现高计算效率基准转换。
1 大旋转角三维基准转换的迭代法三维基准转换通常采用七参数(3个平移参数、3个旋转参数和1个尺度参数)相似变换,根据旋转与尺度参数参考点的定义不同,常用的三维基准转换模型有布尔沙模型、Molodensky模型和Vaniček-Wells模型等[2]。以布尔沙模型为例,基准转换方程为
式中,x和y分别为第1套和第2套基准下的三维坐标向量,εy为y的误差;t、κ和R分别为平移参数、尺度参数和旋转矩阵。由绕3个坐标轴以旋转角ωx、ωy和ωz旋转构成传统测量三维基准转换中,旋转角为小角度(通常几秒的旋转角度)以至于旋转矩阵可近似为
因此,可通过线性化迭代求解7个转换参数[1, 2]。然而,在近景摄影测量等工业测量应用中,旋转角并非总是小角度,经常涉及大角度,因此采用传统的小角度数学模型处理需要对R矩阵中的3个旋转角求偏导数线性化,公式比较复杂。文献[2]提出了直接将旋转矩阵中的9个元素作为未知参数,并附加旋转矩阵正交约束条件RRT=I3,即对旋转矩阵9个未知参数附加6个约束方程 式中,r=[r1,r2,…,r9]T。将式(2)代入式(1)并顾及约束条件式(4),对t、κ和r共13个参数附加6个约束条件,得到附约束条件的线性化观测模型联合n个公共点的附约束条件大角度三维基准转换误差方程为
简记为 式中,第1个方程为公共点构成的基准转换误差方程,第2个方程为约束方程。在实际坐标转换计算中通常采用等权模型,本文假设公共点相互独立且点位等精度,故协方差矩阵为 式中,Qy为点位协方差阵;⊗表示Kronecker积算子,其运算准则参考文献[13]。每次迭代得到转换参数附约束条件的最小二乘估值为 式中,$\hat \xi $和$\hat k$分别为转换参数和约束方程联系数的估值。验后单位权方差为显然,大角度三维基准转换附约束条件平差法需要迭代计算,直到前后两次计算的转换参数满足条件$\hat \xi $TQ$\hat \xi $$\hat \xi $-1$\hat \xi $<δ,其中δ是一足够小量;Q$\hat \xi $$\hat \xi $为转换参数的方差-协方差矩阵。
2 大旋转角三维基准转换解析封闭解为了提高大旋转角三维基准转换的计算效率,本节研究大旋转角三维基准转换的解析封闭解,其关键是采用多元模型的矩阵形式将n个公共点构成矩阵处理。先通过等价差分变换消除平移参数并利用旋转矩阵的正交条件计算尺度参数,再利用最小二乘求解旋转矩阵,最后计算平移参数。
将n个公共点坐标表示为矩阵形式X=[x1x2…xn]、Y=[y1y2…yn],则坐标转换模型的矩阵形式为
首先定义差分矩阵DT=-en-1In-1,则
式(11)两端右乘差分矩阵D,消去平移参数得到等价坐标转换模型为
式中,差分坐标矩阵为$\bar X$=XD=[x2-x1…xn-x1]=[$\bar x$2…$\bar x$n];$\bar Y$和E与其形式相同。对应的差分坐标的协方差矩阵因为旋转矩阵满足RTR=I3,则
理论上可采用方程两端矩阵的任意元素计算尺度参数,因此采用所有元素计算尺度参数的均值作为尺度参数的估值,则尺度参数的解析公式为
令Ξ=κR,坐标转换矩阵模型(13)对应的向量形式为
式中,vec为矩阵向量化算子[13]。最小二乘解为[14]根据Kronecker积和向量化算子的性质[13]vec(ABC)=(CT⊗A)vec(B),得
将尺度参数估值式(16)代入,则旋转矩阵解析解为
又因为(DTD)-1是幂等阵,即(DTD)-1=(DTD)-2,则
式中,ΔX=[x2-$\bar x$…xn-$\bar x$],为n个点坐标均值;ΔY与其类似。将式(19)代入式(11)并采用最小二乘准则求解平移参数验后单位权方差为
3 基准转换扩展模型的解析封闭解从以上推导可以看出,传统的基准转换模型只考虑了公共点的一套坐标,即Y的误差,忽略了作为系数矩阵的公共点坐标X的误差。近年来,诸多学者深入研究了同时考虑公共点两套坐标误差的基准变换,提出了整体最小二乘方法[15, 16, 17, 18]。若能充分考虑非公共点与公共点的相关关系,可进一步提高坐标转换的精度[3, 19]。本节推导同时顾及两套坐标误差的大角度基准转换扩展模型的解析解。
对坐标X也引入误差EX,则顾及两套坐标误差的坐标转换模型为
令综合误差项为EZ=κREX-EY,式(24)重整为 式中,综合误差的协方差阵为QZZ=In⊗(ΞQxΞT+Qy)=In⊗Qz。两边右乘差分矩阵D消去平移参数 相应的,令综合误差项为E=κRE-E$\bar Y$,则协方差矩阵 式中,Q${\bar x}$${\bar x}$=DTD⊗Qx、Q=DTD⊗Qy、Qz=ΞQxΞT+Qy。类似于第2节的推导,先根据旋转矩阵的正交条件求解尺度参数,得到与式(16)相同的解析式。同理可导出与式(21)和式(22)相同的旋转矩阵和平移参数解析解。然而,与传统模型不同,单位权方差的估值为 式中,${\hat E}$${\bar z}$=${\bar Y}$-$\hat \Xi \bar X$=${\bar Y}$R${\bar X}$为综合误差EZ的估值;R${\bar X}$=I-(DTD)-1${\bar X}$T(${\bar X}$(DTD)-1${\bar X}$T)-1${\bar X}$为投影矩阵。值得注意的是,由于采用等价消去3个平移参数的模型(26)计算单位权方差,因此自由度为n-4。由于QZZ的计算需已知参数Ξ,因此严格意义上需要迭代计算,给出的解析解只是每步迭代过程中计算转换参数的解析解。事实上,由于转换参数解析解较传统迭代解具有较高计算效率,且该迭代没有引入多余的求逆运算,也较传统方法具有较高计算效率。此外,还可采用拟合推估方法求解X和Y的各自误差[3]
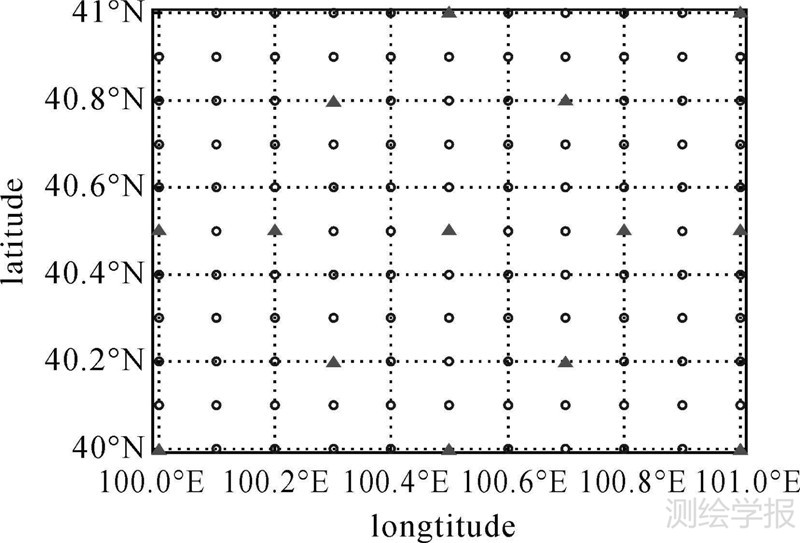
该误差的求解可用于分析两套坐标各自的误差特性,例如两套坐标的方差分量估计[10]和粗差探测[20]等。 4 算例与分析采用WGS-84参考椭球参数,在区域40°N—41°N、100°E—101°E模拟坐标转换试验,沿纬度和经度方向均每隔0.1°选取一个点,共121个点,如图 1所示。取大地高为0,计算得到所有点的三维空间坐标作为第1套坐标。给定一组转换参数t=[10 50 20]T、κ=1+10×10-6D、3个旋转角ωx=1°、ωy=0.5°和ωy=2.5°,转换所有点第1套坐标得到第2套坐标。试验中,均匀地选取15个点作为公共点,如图 1三角点所示,其余106个点为非公共点,如图 1圆点所示。
|
| 图 1 模拟试验的公共点和非公共点分布 Fig. 1 The layout of common and uncommon points in simulation experiment |
首先分析本文给出的大角度三维基准转换解析解在基准变换中的应用效果,只给第1套坐标模拟期望为零、精度为5 cm的正态分布随机误差,得到传统应用中只假设第1套坐标含有误差的基准转换模型。分别采用第2节的传统附约束条件迭代解法(迭代终止条件中取δ=10-8)和第3节的解析解法,模拟计算500次,比较两种方法的坐标转换效果。令计算得到的非公共点转换后的第Ⅱ套坐标为${\hat y}$i,对应的已知坐标yi,统计3个坐标分量的转换精度
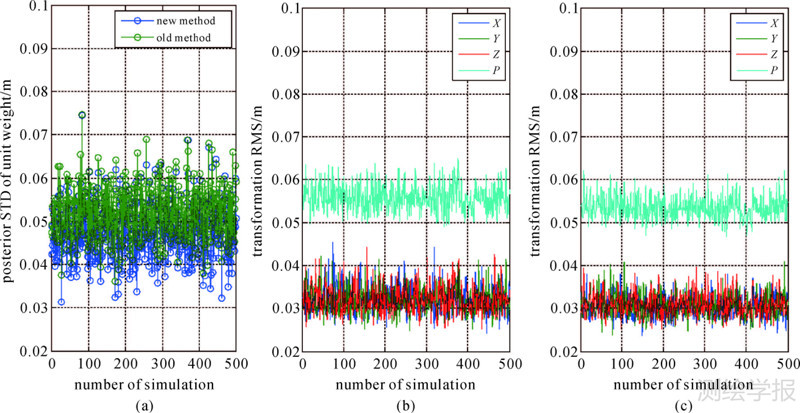
以及基准转换的点位精度为图 2给出了附约束条件迭代解和解析解的坐标转换500次试验结果,图 2(a)为两种方法计算的验后单位权精度,图 2(b)和图 2(c)分别为两种方法的3个坐标分量和点位转换精度。表 1给出了两种方法500次试验转换精度平均值。显然,两种方法得到的验后单位权精度和3个坐标分量及点位转换精度相当,即两种方法的转换效果等效。
|
| 图 2 大角度基准转换的迭代解(旧方法)与解析解(新方法)转换精度比较 Fig. 2 Comparison of transformation accuracies between iteration method (old method) and analytical method (new method) for datum transformation with big angles |
| cm | |||||
| 方法 | 验后精度σ0 | 转换点检核精度 | |||
| X | Y | Z | P | ||
| 迭代法 | 5.18 | 3.05 | 3.08 | 3.09 | 5.34 |
| 新方法 | 4.80 | 3.22 | 3.20 | 3.22 | 5.58 |
分析本文给出的大角度三维基准转换扩展模型解析解在基准变换中的应用,给两套坐标模拟期望为零、精度为5 cm的正态分布随机误差,得到含有误差的两套坐标。分别采用第2节的传统附约束条件迭代解法和第3节的解析解法,同样模拟计算500次,采用式(30)和式(31)统计转换精度,结果如图 3所示,500次试验的转换精度平均值如表 2所示。同样,两种方法的3个坐标分量及点位转换精度相当,但验后单位权精度差异较大,新方法得到的验后单位权精度4.69 cm与先验精度5 cm更为接近,而传统迭代解的验后单位权精度达到7.22 cm。其原因是无论第2套坐标受误差影响与否,传统迭代法只顾及第1套坐标误差,基于此理论估计的单位权精度必然不能反映实际观测精度,而新的解析解法在一定程度上考虑了两套坐标误差的影响,得到的验后精度更客观。这一优势在实际应用中是很关键的,因为通常先验精度是未知的,只有求解正确的验后精度才能客观地评定转换参数精度,实现有效的粗差探测和假设检验等。

|
| 图 3 大角度基准转换扩展模型的迭代解(旧方法)与解析解(新方法)转换精度比较 Fig. 3 Comparison of transformation accuracies between iteration method (old method) and analytical method (new method) for extended datum transformation with big angles |
| cm | |||||
| 方法 | 验后精度σ0 | 转换点检核精度 | |||
| X | Y | Z | P | ||
| 迭代法 | 7.22 | 4.31 | 4.37 | 4.35 | 7.54 |
| 新方法 | 4.69 | 4.55 | 4.54 | 4.54 | 7.90 |
如文中引言所述,为满足现代测量技术的实时应用需求,需要高计算效率的基准转换方法,这也是本文研究基准转换解析解的初衷之一,因此分析本文大角度三维基准转换模型解析解的计算效率。
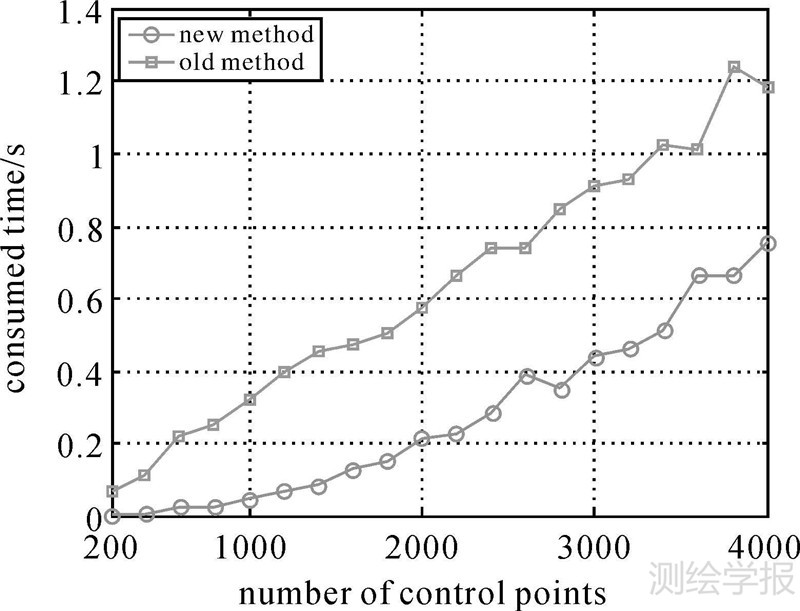
以大角度三维基准转换模型为例,在该试验区域加密采样,得到从200至4000个公共点,分别采用迭代法和解析法计算转换参数,分析采用不同数量公共点的两种方法计算转换参数所需时间。结果如图 4所示,显然迭代法所需时间远超过解析法,即解析法能得到与迭代法等效基准转换精度的同时,有效提高基准转换效率。
|
| 图 4 大角度基准转换模型迭代解(旧方法)与解析解(新方法)的计算效率比较 Fig. 4 Comparison of computation efficiency between iteration method (old method) and analytical method (new method) for datum transformation with big angles |
值得说明的是,尽管本文算例中给出的大角度为2.5°,但从理论推导可看出,新方法不涉及大角度的线性化处理,因此可适用于任意角度旋转的基准转换。
5 结 论本文围绕解决现代空间观测技术对基准转换提出大旋转角和高计算效率的需求,开展了大角度三维基准转换模型及其扩展模型的解析解研究,得出以下结论:
(1) 大角度基准转换解析解能得到与传统附约束条件迭代解等效的转换精度和验后单位权精度。
(2) 大角度基准转换扩展模型的解析解能得到与传统附约束条件迭代解等效的转换精度,且能计算可靠的验后单位权精度,而迭代解的验后单位权精度与实际精度相差较大。
(3) 本文给出的解析法在实现与迭代法等效转换精度的同时,有效提高基准转换效率,为海量数据应用提供理论基础。
| [1] | 朱华统, 杨元喜, 吕志平. GPS坐标系统的变换[M]. 北京:测绘出版社, 1994. ZHU Huatong, YANG Yuanxi, LV Zhiping. GPS Coordinate System Transformation[M]. Beijing:Surveying and Mapping Press, 1994. |
| [2] | RAPP R H. Geometric Geodesy Part Ⅱ[M]. Ohio:Ohio State University, 1993. |
| [3] | LI Bofeng, SHEN Yunzhong, LI Weixiao. The Seamless Model for Three-dimensional Datum Transformation[J]. Science China Earth Sciences, 2012, 55(12):2099-2108. |
| [4] | YANG Yuanxi. Robust Estimation of Geodetic Datum Transformation[J]. Journal of Geodesy, 1999, 73(5):268-274. |
| [5] | 沈云中, 胡雷鸣, 李博峰. Bursa模型用于局部区域坐标变换的病态问题及其解法[J]. 测绘学报, 2006, 35(2):95-98.DOI:10.3321/j.issn:1001-1595.2006.02.001. SHEN Yunzhong, HU Leiming, LI Bofeng. Ill-posed Problem in Determination of Coordinate Transformation Parameters with Small Area's Data Based on Bursa Model[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(2):95-98. DOI:10.3321/j.issn:1001-1595.2006.02.001. |
| [6] | 沈云中, 卫刚. 利用过渡坐标系改进3维坐标变换模型[J].测绘学报, 1998, 27(2):161-165. SHEN Yunzhong, WEI Gang. Improvement of Three Dimensional Coordinate Transformation Model by Use of Interim Coordinate System[J]. Acta Geodaetica et Cartographica Sinica, 1998, 27(2):161-165. |
| [7] | 杨元喜, 徐天河. 不同坐标系综合变换法[J]. 武汉大学学报(信息科学版),2001, 26(6):509-513. YANG Yuanxi, XU Tianhe. The Combined Method of Datum Transformation between Different Coordinate Systems[J]. Geomatics and Information Science of Wuhan University, 2001, 26(6):509-513. |
| [8] | YOU R, HWANG H.Coordinate Transformation between Two Geodetic Datums of Taiwan by Least-squares Collocation[J]. Journal of Surveying Engineering, 2006, 132(2):64-70. |
| [9] | 杨元喜, 张菊清, 张亮. 基于方差分量估计的拟合推估及其在GIS误差纠正的应用[J]. 测绘学报, 2008, 37(2):152-157. YANG Yuanxi,ZHANG Juqing,ZHANG Liang.Variance Component Estimation Based Collocation and Its Application in GIS Error Fitting[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(2):152-157. |
| [10] | 李博峰, 沈云中, 楼立志. 基于等效残差的方差-协方差分量估计[J]. 测绘学报, 2010, 39(4):349-354. LI Bofeng,SHEN Yunzhong,LOU Lizhi.Variance-covariance Component Estimation Based on the Equivalent Residuals[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(4):349-354. |
| [11] | 陈义, 陆珏, 郑波. 近景摄影测量中大角度问题的探讨[J]. 测绘学报, 2008, 37(4):458-463. CHEN Yi, LU Jue, ZHENG Bo. Research on Close-range Photogrammetry with Big Rotation Angle[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(4):458-463. |
| [12] | SHEN Yunzhong, CHEN Yi, ZHENG Dehua. A Quaternion-Based Geodetic Datum Transformation Algorithm[J]. Journal of Geodesy, 2006,80(5):233-239. |
| [13] | KOCH K R. Parameter Estimation and Hypothesis Testing in Linear Models[M]. 2nd ed.Berlin:Springer,1999. |
| [14] | 张尧庭, 方开泰. 多元统计分析引论[M]. 武汉:武汉大学出版社, 2013. ZHANG Yaoting, FANG Kaitai. Multivariate Statistics Analysis[M]. Wuhan:Wuhan University Press, 2013. |
| [15] | SCHAFFRIN B, WIESER A. On Weighted Total Least-squares Adjustment for Linear Regression[J]. Journal of Geodesy,2008, 82(7):415-421. |
| [16] | SHEN Yunzhong, LI Bofeng, CHEN Yi. An Iterative Solution of Weighted Total Least-squares Adjustment[J]. Journal of Geodesy, 2011,85(4):229-238. |
| [17] | FANG Xing. Weighted Total Least Squares:Necessary and Sufficient Conditions, Fixed and Random Parameters[J]. Journal of Geodesy,2013, 87(8):733-749. |
| [18] | XU Peiliang, LIU Jingnan, SHI Chuang. Total Least Squares Adjustment in Partial Errors-in-variables Models:Algorithm and Statistical Analysis[J]. Journal of Geodesy, 2012, 86(8):661-675. |
| [19] | 李微晓, 沈云中, 李博峰. 顾及2套坐标误差的三维坐标变换方法[J]. 同济大学学报(自然科学版), 2011, 39(8):1243-1246. LI Weixiao, SHEN Yunzhong, LI Bofeng. Three-dimensional Coordinate Transformation with Consideration of Coordinate Errors in Two Coordinate Systems[J].Journal of Tongji University(Natural Science), 2011, 39(8):1243-1246. |
| [20] | 李博峰, 沈云中. 基于等效残差积探测粗差的方差-协方差分量估计[J]. 测绘学报, 2011, 40(1):10-14. LI Bofeng, SHEN Yunzhong. Equivalent Residual Product Based Outlier Detection for Variance and Covariance Component Estimation[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(1):10-14. |