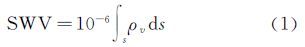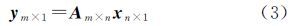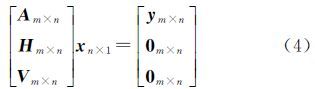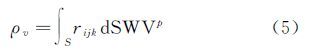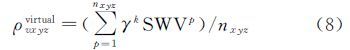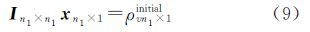2. 武汉大学地球空间环境与大地测量教育部重点实验室, 湖北 武汉 430079;
3. 中国电建西北勘测设计研究院有限公司, 陕西 西安 710065
2. Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, Wuhan University, Wuhan 430079, China;
3. Power China Xibei Engineering Corporation Limited, Xi'an 710065, China
水汽是大气中重要的组成部分之一,虽然在大气中的含量非常少[1],但对天气的变化具有重要作用。传统水汽探测方法有无线电探空技术、地基微波辐射计、激光雷达和太阳光谱分析仪等,但这些方法受精度低、成本高、天气条件等多方面的限制。利用地基GNSS层析技术探测大气水汽具有全天候、高精度、高时空分辨率的特点[2],获得的水汽分布信息对暴雨等降水天气的研究具有重要意义。
文献[3]首先提出利用GNSS反演大气水汽信息,并证明了其可行性。此后,地基GNSS反演大气水汽的方法日益成熟[4, 5, 6, 7, 8, 9, 10, 11, 12]。但目前在大多数研究中,针对观测值的选取都是利用穿过整个研究区域的射线,这大大限制了已有观测数据的使用。文献[13]利用降低层析区域高度和移动整体层析网格的方法来尽可能多地利用已有数据,但受网格边长的影响,对已有数据的利用有很大的限制。
针对水汽层析中观测数据利用率低的局限性,本文提出一种基于水汽密度比例因子的三维水汽层析算法,该方法不仅可以使用穿过整个研究区域的观测值,还可以利用从研究区域侧面穿出的信号,大大提高了观测数据的利用率。
1 基于水汽密度比例因子的三维水汽层析算法 1.1 层析方程建立利用GAMIT数据处理软件[14],结合GNSS观测站相应的气象文件进行解算,得到卫星和测站所在连线上的SWV(slant water vapor),其表达式为
式中,s表示卫星信号的射线路径;ρv表示水汽密度,单位为g/m3。将式(1)离散化后可得到线性方程
式中,SWVp表示完整穿过层析区域的第p条射线路径上的水汽含量;dijkp为射线p在网格(i,j,k)内的截距,单位为km;Xijk为(i,j,k)网格内的水汽密度。将线性方程(2)写成矩阵形式 式中,y表示观测值,通常指SWV;m表示SWV的个数;A表示信号穿过每个网格的截距组成的系数矩阵;n表示研究区域内网格的个数;x是要求的未知量,这里指水汽密度ρv。 1.2 约束条件对层析方程求解实质就是求反问题的研究。由于卫星星座和测站几何位置分布的影响,观测方程在多数情况下是不适定的。矩阵A是维数较大的稀疏矩阵,直接求逆会导致严重的数值问题[15]。通常,需要加入额外约束解决该问题[16, 17, 18, 19]。本文附加两种约束条件,在水平方向上,利用高斯加权函数方法进行约束[10],垂直方向上则利用指数分布建立网格间的函数关系进行约束[20]。因此,可以得到传统方法的层析模型
式中,H和V分别表示水平约束和垂直约束的系数矩阵。对于式(4),可利用奇异值分解法(singular value decomposition,SVD)计算矩阵的广义逆[21]。 1.3 基于水汽密度比例因子的三维水汽层析算法针对传统水汽层析方法的缺点,本文提出一种基于水汽密度比例因子的三维水汽层析算法,该方法的优点是可充分利用所有穿过研究区域的射线,即传统层析方法中被剔除的在研究区域侧面穿出的射线也可以被利用。假定每条射线在所穿过的网格内都有一个水汽密度比例因子,定义为网格内倾斜路径上的单位水汽密度,用于反映网格内水汽密度的大小,计算公式为
式中,rijk表示(i,j,k)网格内的水汽密度比例因子;dSWVp表示SWVp对距离的导数。本文层析算法的具体计算过程如下:
(1) 建立水汽密度比例因子模型。水汽密度比例因子计算公式为
式中,ρvijkactual表示利用试验前3 d的探空数据估计出的(i,j,k)网格内的水汽密度。由式(6)可知,水汽密度比例因子与SWV成反比,而SWV的大小受高度角的影响。此外,射线在不同网格内的截距也不同,因此,通过分析可以建立以下经验模型
式中,ele表示卫星高度角;dijkp表示第p条射线在(i,j,k)网格内的截距;a1k、a2k、a3k和a4k表示第k层水汽密度比例因子模型对应的系数,k表示第几层。通过式(6)可以计算出有地面实测探空资料的网格内每条射线所对应的水汽密度比例因子,然后利用这些水汽密度比例因子根据式(7)通过最小二乘方法即可求出经验模型所对应的各个系数。
(2) 计算虚拟水汽密度。利用所建立的水汽密度比例因子模型以及观测到的所有SWV即可求出有射线穿过的网格内的虚拟水汽密度值,计算公式为
式中,ρvxyzvirtual表示利用穿过网格的SWV虚拟出的该网格内的水汽密度;nxyz表示穿过(x,y,z)网格的SWV条数。将式(8)计算的虚拟水汽密度作为初始约束值,写成矩阵的形式为
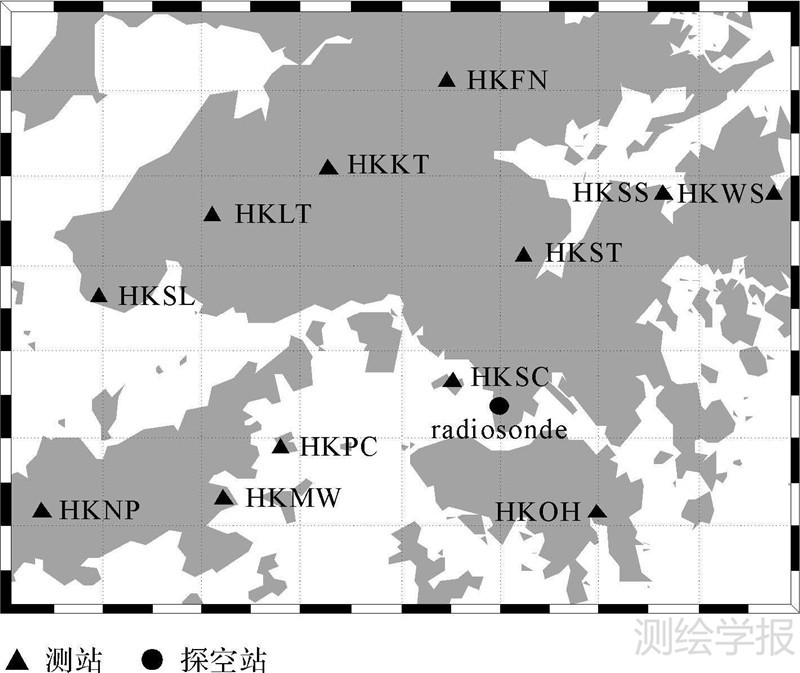
式中,n1表示层析区域内有射线穿过的网格个数。此时联立方程(4)和方程(9),即可得到本文提出方法的层析模型。 2 层析策略 2.1 试验数据选取选取香港卫星定位参考站网12个测站(图 1)2014-03-25—04-25共32 d的数据进行层析试验,研究区域范围:22.19°N—22.54°N,113.87°E—114.35°E;网格划分:水平分辨率经度方向为0.06°(约6.6 km),纬度方向为0.05°(约5.9 km),垂直分辨率为0.8 km,研究区域共有8×7×13个网格。其中,试验区域在King’s Park有一个无线电探空仪站(图 1)。探空气球每天在UTC 00:00和UTC 12:00发射,本文将探空数据作为检核层析结果的标准。
|
| 图 1 测站分布图 Fig. 1 The distribution of stations |
试验中采用两种层析方法获得水汽密度信息,分别为:方法1,利用传统层析方法,即利用方程(4)建立的层析模型;方法2采用本文提出的层析方法,将方程(4)和(9)联合作为层析模型。
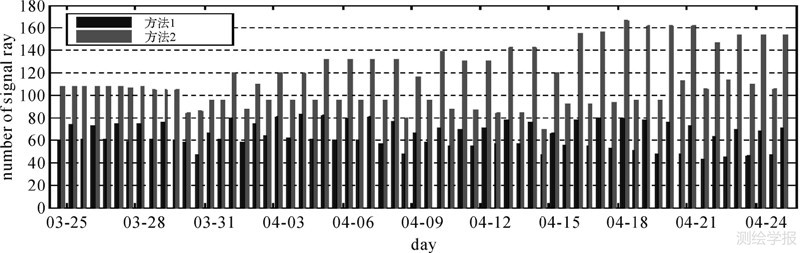
2.2 研究区域射线穿过条数分析本文首先统计了2014-03-25—2014-04-25共32 d每天在UTC 00:00和12:00时刻,两种方法在研究区域内信号条数的使用情况,如图 2所示。此外,表 1给出32 d内两种方法射线条数使用情况的具体统计结果。
|
| 图 2 两种方法信号使用条数对比图 Fig. 2 The number of signal rays used for different methods |
| 方法 | mean | max | min |
| 方法1 | 65 | 83 | 43 |
| 方法2 | 114 | 167 | 70 |
由图 2和表 1可以看出,方法2通过利用从研究区域侧面穿出的射线后,使用的射线条数远大于方法1。通过对32 d的信号使用情况计算得出,方法2将观测数据的利用率由传统方法的51%左右提高到91%左右,大大提高了已有数据的利用率。
2.3 水汽密度比例因子模型可靠性检验为检验建立的水汽密度比例因子模型的可靠性,利用2014-03-25—2014-04-25共32 d的探空数据计算每天UTC00:00和12:00时刻的水汽密度比例因子,并与模型计算的结果进行对比。表 2给出了利用模型和探空数据计算结果的具体误差统计。
| g/m4 | |||
| 参数 | mean | max | min |
| RMS | 0.004 0 | 0.006 3 | 0.002 1 |
由表 2可以看出,利用模型计算的水汽密度比例因子的平均RMS为0.004 kg/m4,假设SWV为200 mm,则利用该模型计算水汽密度的误差在0.8 g/m3左右,这说明建立的模型具有很高的精度。
3 算例分析
本文利用2014-03-25—2014-04-25共32 d的数据进行层析水汽精度检验,并选取2014年3月25日和3月30日King’s Park探空站对水汽层析结果进行评估。King’s Park探空站位于层析区域内,因此,将该探空站所在网格对应的层析垂直廓线与探空数据进行对比。由香港天文台提供的天气信息可知:3月25日为无雨天气,3月30日为大到暴雨天气。因此,单独选取3月25日和3月30日两天的数据分析不同天气对层析结果的影响。
3.1 层析结果精度检验无线电探空仪能够提供垂直方向上精确的水汽密度廓线图,通常将其作为检验其他方法得到水汽密度廓线信息的一个标准[22, 23, 24]。本文采用平均绝对偏差(MAE)和均方根误差(RMS)作为评定该方法的指标。
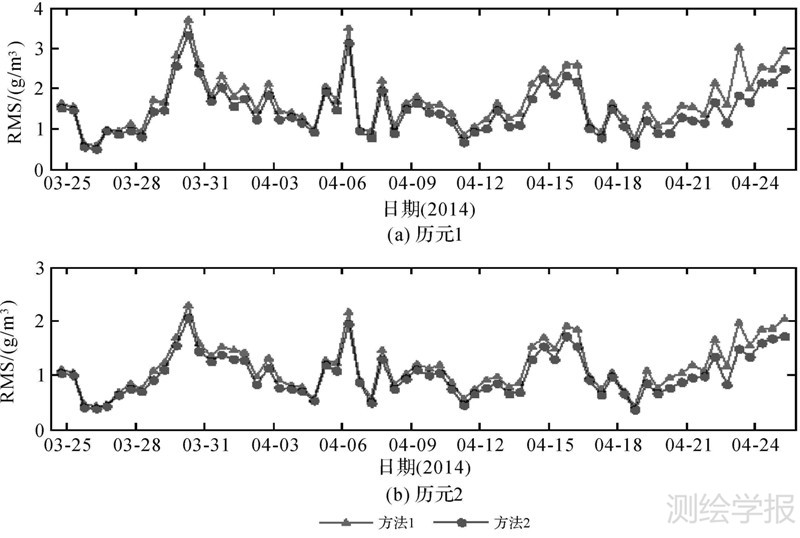
为了对层析重构结果和探空数据计算结果做一个直接对比,本文分别统计了2014-03-25—2014-04-25共32 d每天两个历元时刻(UTC 00:00和12:00)两种方法的层析结果。首先利用每个历元层析重构的结果计算出无线电探空站所在位置的水汽密度,再分别与无线电探空仪数据计算的结果进行对比。表 3给出了两种方法与探空数据对比的统计结果,图 3给出了两种方法统计的每天的RMS和MAE。
| g/m3 | |||||||
| 方法 | RMS | MAE | |||||
| mean | max | min | mean | max | min | ||
| 方法1 | 1.69 | 3.70 | 0.57 | 1.16 | 2.29 | 0.43 | |
| 方法2 | 1.45 | 3.32 | 0.51 | 1.02 | 2.05 | 0.36 | |
|
| 图 3 两种方法的统计结果 Fig. 3 The statistical result of different methods |
由表 3可以看出,方法2的平均RMS和MAE比方法1的要小。由图 3可以看出,方法2每天层析结果的RMS和MAE也均小于方法1的层析结果。这说明,本文提出的基于水汽密度比例因子的三维水汽层析算法比传统层析方法精度要高。
3.2 不同天气影响分析 3.2.1 与探空数据对比2014年3月25日和3月30日对应两种不同的天气状况,为了检验层析方法在不同天气下的层析精度,表 4和表 5分别给出了2014年3月25日和3月30日每天两个历元时刻(UTC 00:00和12:00)两种方法的RMS和MAE。
| g/m3 | ||||
| 方法 | RMS | |||
| 25日 | 30日 | |||
| 方法1 | 1.02 | 0.98 | 2.83 | 3.69 |
| 方法2 | 0.72 | 0.58 | 2.56 | 3.32 |
| g/m3 | |||||
| 方法 | MAE | ||||
| 25日 | 30日 | ||||
| 方法1 | 1.10 | 1.05 | 1.71 | 2.29 | |
| 方法2 | 1.04 | 1.00 | 1.55 | 2.05 | |
由表 4和表 5可以看出,方法2的RMS和MAE比方法1的小。这说明,与传统的层析方法相比,本文提出的层析方法其结果与探空数据结果具有更好的一致性,层析重构质量得到了很大的改善。两种方法在3月30日的RMS和MAE均比3月25日的大,其可能的原因是3月25日对应无雨天气,水汽的空间结构较稳定,而3月30日为大到暴雨天气,水汽的空间分布变化较大、空间结构不稳定,故其RMS和MAE较大。
3.2.2 层析水汽廓线对比
为了更加直观地对比两种方法的层析效果,进行以下对比:分别统计了3月25日和3月30日两天两种方法在UTC 00:00不同高度上的水汽密度,并分别与无线电探空仪计算的水汽密度对比。图 4、图 5分别给出了两种方法与无线电探空仪对比的廓线结果。
|
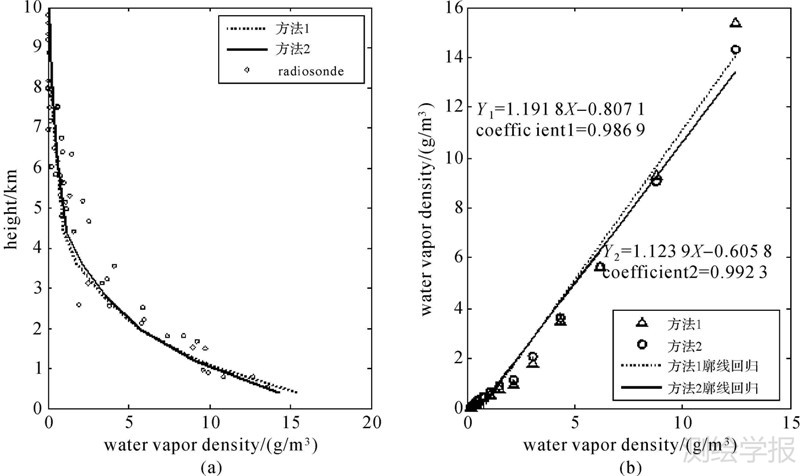
| 图 4 3月25日00:00时廓线对比结果 Fig. 4 The profile comparison of different methods at UTC 00:00,March 25 |
|
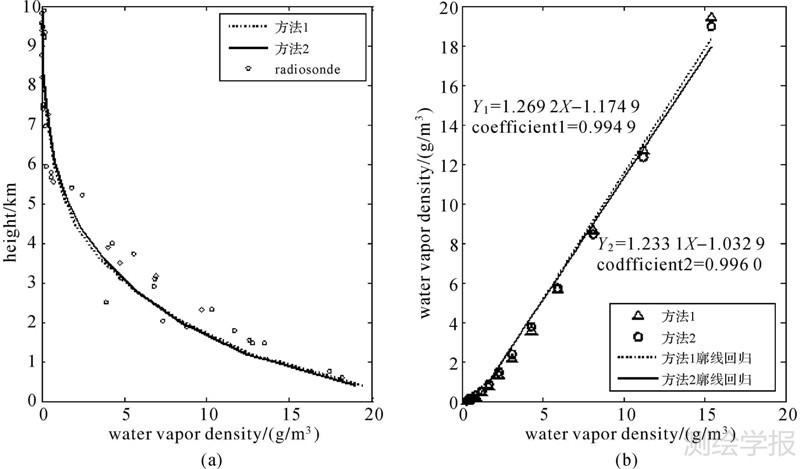
| 图 5 3月30日00时廓线对比结果 Fig. 5 The profile comparison of different methods at UTC 00:00,March 30 |
由图 4(a)、图 5(a)可以看出,整体上两种方法层析廓线与探空数据廓线都具有很好的一致性。图 4(b)为3月25日不同方法层析廓线对探空廓线的回归,由该图可以看出,方法1的回归相关系数达到了0.986 9,利用本文提出的层析算法后,方法2将其提高到0.992 3。同时,方法2将截距由初始的0.807 1降至0.605 8。根据图 5(b)回归结果,3月30日方法1的回归相关系数为0.994 9,但截距达到了1.174 9;通过方法改进,方法2的回归系数增加至0.996 0,同时截距下降至1.032 9。
综合图 4、图 5可以得出,两种方法对探空廓线的回归均具有很高的相关系数,说明本文水汽层析结果的精度很高,可用于天气研究。通过对比两次廓线发现,考虑了在研究区域侧面穿出的射线后,层析结果精度得到了不同程度的提高,也证明了本文建立和使用该层析方法的有效性。
3.3 误差分布统计以层析时段(2014-03-25—2014-04-25)内每天2次(UTC 00:00和12:00)共64次探空结果为真值,统计两种层析方法的误差分布情况。图 6给出了32 d两种方法误差分布统计结果。由图 6可以看出,两种方法层析结果的误差在-3~2 g/m3之间分布最为集中。通过计算可得,方法1和方法2分别有91.11%和91.95%的误差在此范围内,由此可以得出,基于水汽密度比例因子的层析算法的层析结果在误差分布上也优于传统方法的层析结果。

|
| 图 6 2014-03-25—2014-04-25共32 d误差统计分布图 Fig. 6 The error statistical distribution for 32 days from 25 March to 25 April 2014 |
利用香港CORS网2014-03-25—2014-04-25共32 d的实测GPS和气象数据,验证本文提出的三维水汽层析算法的有效性及精度。
试验结果表明:本文提出的算法大大提高了观测数据的利用率,能够充分利用已有观测信息;以探空数据为基准通过计算发现,该算法计算的结果在RMS、相关系数和误差分布等方面均优于传统方法。此外,降水天气对层析结果的影响要比无降水天气影响大,但无论在何种天气下,本文提出的算法均优于传统方法。
致谢:感谢IGRA提供的无线电探空数据,感谢香港天文台提供的试验数据及降水量信息。
| [1] | 万蓉. 我国暴雨研究中新型探测资料反演技术及其应用[J]. 气象科技进展, 2014, 4(2):24-35. WAN Rong. Research Progress of the Unconventional Observing Technology and the Data Used in the Study of Rainstorm in China[J]. Advances in Meteorological Science and Technology, 2014, 4(2):24-35. |
| [2] | 王久珂, 韩素芹,边海, 等. 一次暴雨过程中GPS三维层析水汽场的变化特征[J]. 北京大学学报(自然科学版), 2014, 50(6):1053-1064. WANG Jiuke, HAN Suqin, BIAN Hai, et al. Characteristics of the Three-dimensional GPS Tomography Water Vapor Field during the Rainstorm[J]. Acta Scientiarum Naturalium UniversitatisPekinensis, 2014, 50(6):1053-1064. |
| [3] | BEVIS M, BUSINGER S, HERRING T A, et al. GPS Meteorology:Remote Sensing of Atmospheric Water Vapor Using the Global Positioning System[J]. Journal of Geophysical Research,1992, 97(D14):15787-15801. |
| [4] | ROCKEN C, WARE R, HOVE T V, et al. Sensing Atmospheric Water Vapor with the Global Positioning System[J]. Geophysical Research Letters, 1993, 20(23):2631-2634. |
| [5] | DUAN Jingping, BEVIS M, FANG Peng, et al. GPS Meteorology:Direct Estimation of the Absolute Value of Precipitable Water[J]. Journal of Applied Meteorology,1996, 35(6):830-838. |
| [6] | 毛节泰. GPS的气象应用[J]. 气象科技, 1993, 21(4):45-49. MAO Jietai.The Application of GPS Meteorological Science and Technology[J]. 1993, 21(4):45-49. |
| [7] | 陈洪滨, 吕达仁. GPS测量中的大气路径延迟订正[J]. 测绘学报, 1996, 25(2):127-132. CHEN Hongbin, LV Daren. Atmospheric Path Delay Correction in the GPS Measurements[J]. Acta Geodaetica et Cartographica Sinica, 1996, 25(2):127-132. |
| [8] | 陈俊勇. 地基GPS遥感大气水汽含量的误差分析[J]. 测绘学报, 1998, 27(2):113-118. CHEN Junyong. On the Error Analysis for the Remote Sensing of Atmospheric Water Vapor by Ground Based GPS[J]. Acta Geodaetica et Cartographica Sinica, 1998, 27(2):113-118. |
| [9] | 李成才, 毛节泰. GPS地基遥感大气水汽总量分析[J]. 应用气象学报, 1998, 9(4):470-477. LI Chengcai, MAO Jietai. Analysis for Remote Sensing of Atmospheric Precipitable Water Using Ground Based GPS Receiver[J]. Quarterly Journal of Applied Meteorology, 1998, 9(4):470-477. |
| [10] | 于胜杰, 柳林涛, 梁星辉. 约束条件对GPS水汽层析解算的影响分析[J]. 测绘学报, 2010, 39(5):491-496. YU Shengjie, LIU Lintao, LIANG Xinghui. Influence Analysis of Constraint Conditions on GPS Water Vapor Tomography[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(5):491-496. |
| [11] | 叶世榕, 江鹏, 刘炎炎. 地基GPS网层析水汽三维分布数值积分方法[J]. 测绘学报, 2013, 42(5):654-660. YE Shirong, JIANG Peng, LIU Yanyan. A Water Vapor Tomographic Numerical Quadrature Approach with Ground-based GPS Network[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(5):654-660. |
| [12] | 何林, 柳林涛, 苏晓庆, 等. 水汽层析代数重构算法[J]. 测绘学报, 2015, 44(1):32-38. HE Lin, LIU Lintao, SU Xiaoqing, et al. Algebraic Reconstruction Algorithm of Vapor Tomography[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(1):32-38. |
| [13] | CHEN Biyan, LIU Zhizhao. Voxel-optimized Regional Water Vapor Tomography and Comparison with Radiosonde and Numerical Weather Model[J]. Journal of Geodesy, 2014, 88(7):691-703. |
| [14] | HERRING T A, KING R W, FLOYD M A, et al. Introduction to GAMIT/GLOBK[EB/OL]. Release 10.4.Boston:Department of Earth, Atmospheric, and Planetary Science.(2010-10-04)[2013-05-15].http://www-gpsg.mit.edu/-simon/gtgk/Intro_GG.pdf. |
| [15] | BENDER M, STOSIUS R, ZUS F, et al. GNSS Water Vapour Tomography-expected Improvements by Combining GPS, GLONASS and Galileo Observations[J]. Advances in Space Research, 2011, 47(5):886-897. |
| [16] | FLORES A, RUFFINI G, RIUS A. 4D Tropospheric Tomography Using GPS Slant Wet Delays[J]. Annales Geophysicae, 2000, 18(2):223-234. |
| [17] | TROLLER M, BVRKI B, COCARD M, et al.3-D Refractivity Field from GPS Double Difference Tomography[J]. Geophysical Research Letters, 2002, 29(24):2-1-2-4. |
| [18] | ROHM W, BOSY J. Local Tomography Troposphere Model over Mountains Area[J]. Atmospheric Research, 2009, 93(4):777-783. |
| [19] | BENDER M, DICK G, GE M R, et al. Development of a GNSS Water Vapour Tomography System Using Algebraic Reconstruction Techniques[J]. Advances in Space Research, 2011, 47(10):1704-1720. |
| [20] | ELÓSEGUI P, RUIS A, DAVIS J L, et al. An Experiment for Estimation of the Spatial and Temporal Variations of Water Vapor Using GPS Data[J]. Physics and Chemistry of the Earth, 1998, 23(1):125-130. |
| [21] | RUAN Baiyao, GE Weizhong.Singular Value Decomposition Method Compared with Damping Least Square Method[J]. Computing Techniques for Giophysical and Geochenical Exploration, 1997, 19(1):46-49. |
| [22] | NIELLA E, COSTER A J, SOLHEIM F S, et al. Comparison of Measurements of Atmospheric Wet Delay by Radiosonde, Water Vapor Rdiometer, GPS, and VLBI[J]. Journal of Atmospheric and Oceanic Technology, 200118(6):830-850. |
| [23] | ADEYEMI B, JOERG S. Analysis of Water Vapor over Nigeria Using Radiosonde and Satellite Data[J]. Journal of Applied Meteorology and Climatology, 2012, 51(10):1855-1866. |
| [24] | LIU Z Z, WONG M S, NICHOL J, et al. A Multi-sensor Study of Water Vapour from Radiosonde, MODIS and AERONET:A Case Study of Hong Kong[J]. International Journal of Climatology, 2013, 33(1):109-120. |