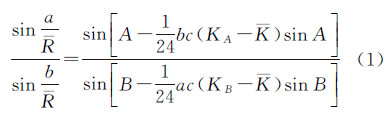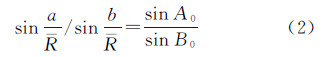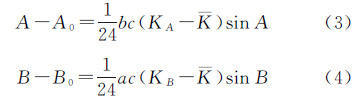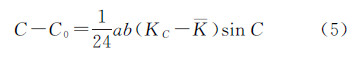2. 国家海洋信息中心,天津 300171;
3. 中国科学院地理科学与资源研究所资源与环境信息系统国家重点实验室,北京 100101;
4. 中国科学院大学,北京 100049
2. National Marine Data and Information Service, Tianjin 300171, China;
3. State Key Laboratory of Resources and Environmental Information System, Institute of Geographic Sciences and Natural Resources Research, CAS, Beijing 100101, China;
4. University of Chinese Academy of Sciences, Beijing 100049, China
从计算几何[1]的观点来看,椭球面三角形外心就是与3个相邻顶点所对应的椭球面Voronoi图的公共顶点,而Voronoi图具有许多优秀的性质,研究椭球面Voronoi图对于全球数据的管理和空间关系的动态维护具有重要意义[2]。根据Voronoi图和Delaunay三角网的对偶关系,采用间接Delaunay三角剖分算法由椭球面Voronoi图能够比较容易地构造椭球面Delaunay三角网,而Delaunay三角网被广泛应用于数字高程模型(DEM)构建、空中三角测量、大地控制网评估和连续运行参考系统(CORS)网布站优化[3]。因此作为生成椭球面Voronoi图并构造相应的Delaunay三角网的关键步骤,研究椭球面三角形外心的求解具有重要的理论和应用价值。
在平面上由3个相邻顶点计算三角形外心的坐标可采用确定的公式和成熟的算法[4],然而大地线距离是由在椭球面某范围内足够精确且不产生二义的大地线尺度函数所定义的,直接在椭球面上计算三角形外心大地坐标异常复杂[5]。因此在传统的地理信息系统中大多数采用球面或投影平面对椭球面进行高或低精度的近似以降低实现难度[6, 7],例如在球面上103km跨度内误差达到了35m,而在投影平面上103km跨度内误差竟达到了8km[7],可见两者的误差控制情况都不是很理想。
文献[4]以构建区域性椭球面数字地面模型(DTM)为目的,提出了一种在测地坐标系[8]中由椭球面三角形3个相邻顶点求解其外心测地坐标的方法。对于平均边长在1~2km的椭球面三角形,计算所得外心到该三角形各顶点的大地线距离偏差小于0.1mm[4]。因为测地坐标系是基于区域性椭球面建立起来的,适用范围仅限于较大的局部区域[5],所以该方法对于跨度远远超过2km甚至达到103~104km的很多实际问题,如无人机航迹规划[9]、巡航导弹突防路径规划[10]以及海域划界中间线及其三接点的求解[11]等,无法保证其结果的高精度。
文献[12]以求解海域划界中间线上的转折点位置为目的,提出了一种在球面和椭球面上求解三角形外心大地坐标的初步思路,但是未见该方法的有效试验结果。对于椭球面三角形外心大地坐标的求解,首先要计算得到相应的球面三角形外心的经纬度坐标,然后采用求解线性方程组的一般迭代方法逼近外心的精确大地坐标,然而迭代过程中产生的向量序列并不一定逐步逼近线性方程组的解,且不同迭代方法的收敛效率差别较大[13]。
为了能够在全球范围内高效计算椭球面三角形外心的精确大地坐标,解决上述方法各自存在的问题,本文基于地图代数[14]中的测地变换[15],提出了一种求解椭球面三角形外心的矢栅结合方法。算法可以直接在椭球面上快速计算大量离散点集的高精度Voronoi顶点,对于椭球面Voronoi图的生成和椭球面Delaunay三角网的构造具有重要作用,从而为建设动态全球性地理信息系统[16, 17](Global GIS)并实现精确椭球几何计算[18]与空间分析[19]打下基础。
1 方法原理本文方法基于地图代数理论,利用“矢栅结合使用长处”[20]的思想,通过栅格大地线尺度距离变换——测地变换,先精确求解椭球面空间中各栅格中心点到其最近地理实体上来源点的距离,后在临界相邻栅格范围内,以栅格中心点作为控制点,通过数值计算内插初始等距点大地坐标并最终逼近椭球面三角形外心的精确位置。算法的误差主要来自于在椭球面3~4个临界相邻栅格范围内由初始等距点逼近三角形外心所导致的精度损失,下面从椭球大地测量学[21]和球面三角学[22]的角度论证:在满足一定条件下上述逼近过程与大地主题解算的精度[23]能够保持一致。
设KA、KB和KC分别表示椭球面三角形ABC各顶点的高斯曲率,RA、RB和RC分别表示对应顶点纬度处的曲率半径,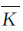 是3个顶点的平均高斯曲率,
是3个顶点的平均高斯曲率,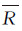 是3个顶点平均纬度处的平均曲率半径,如图 1所示,以
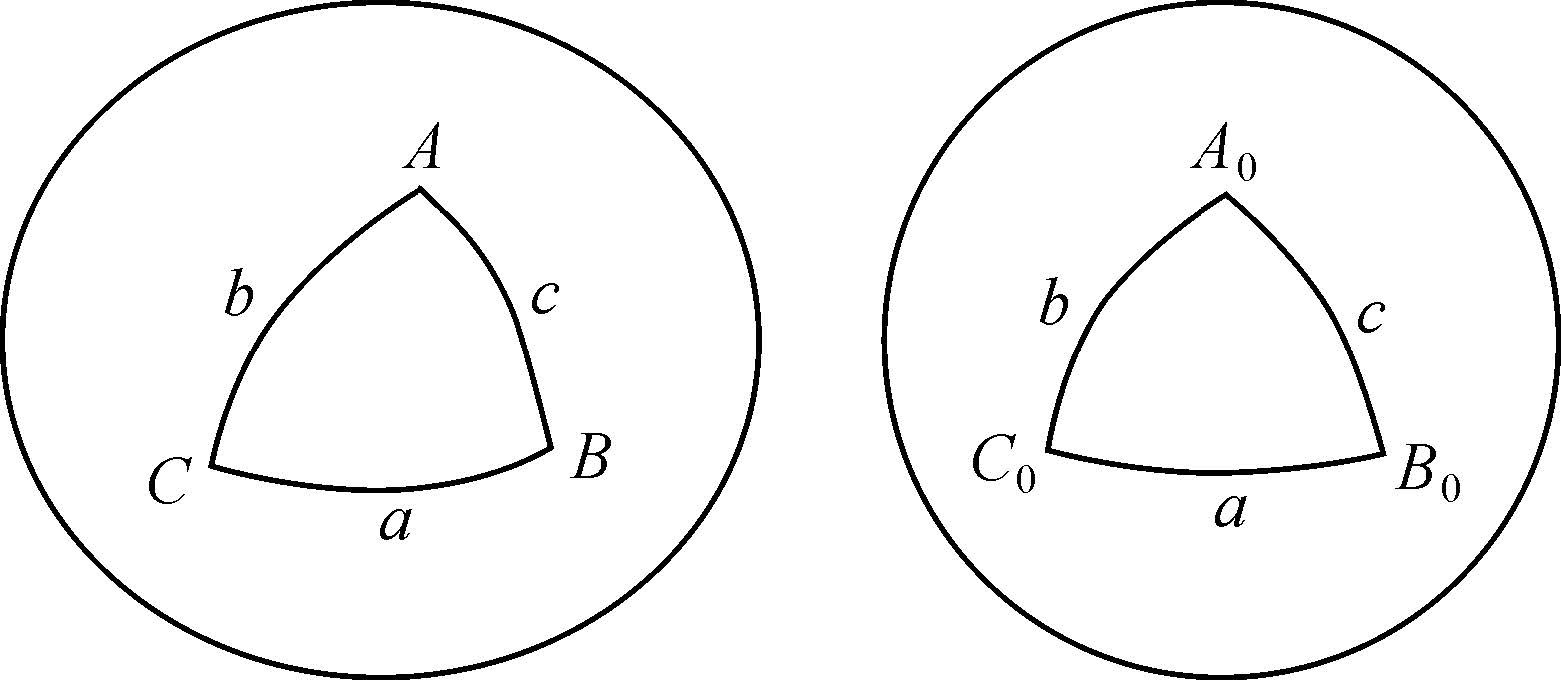
是3个顶点平均纬度处的平均曲率半径,如图 1所示,以 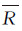 为半径作密切球[21],在球面上做与三角形ABC对应边长度相等的三角形A0B0C0。
为半径作密切球[21],在球面上做与三角形ABC对应边长度相等的三角形A0B0C0。
|
| 图 1 椭球面三角形ABC与球面三角形A0B0C0 Fig. 1 Triangle ABC on ellipsoidal surface and triangle A0B0C0 on spherical surface |
对于椭球面三角形ABC,由椭球面正弦定理[21]可得
对于球面三角形A0B0C0,由球面正弦定理[28]可得
比较式(1)和式(2)可得
同理可得
因为式(3)、式(4)和式(5)中 
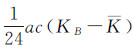 和
和 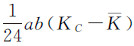 都是微小量,所以
都是微小量,所以 
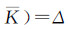 ,且
,且 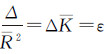 ,其中ε是球面角超,以同样的精度得出
,其中ε是球面角超,以同样的精度得出
式(6)为椭球面改正数公式,当椭球面三角形ABC的平均边长小于200 km时,椭球面改正数小于0.001″,而当200km线长的方向变化0.001″时,端点的位移小于0.001m。因此在平均边长小于200km的条件下可直接把椭球面三角形当作球面三角形,而对于平均边长在200~400km 之间的椭球面三角形需要经过适当改正转化为球面三角形[21]。
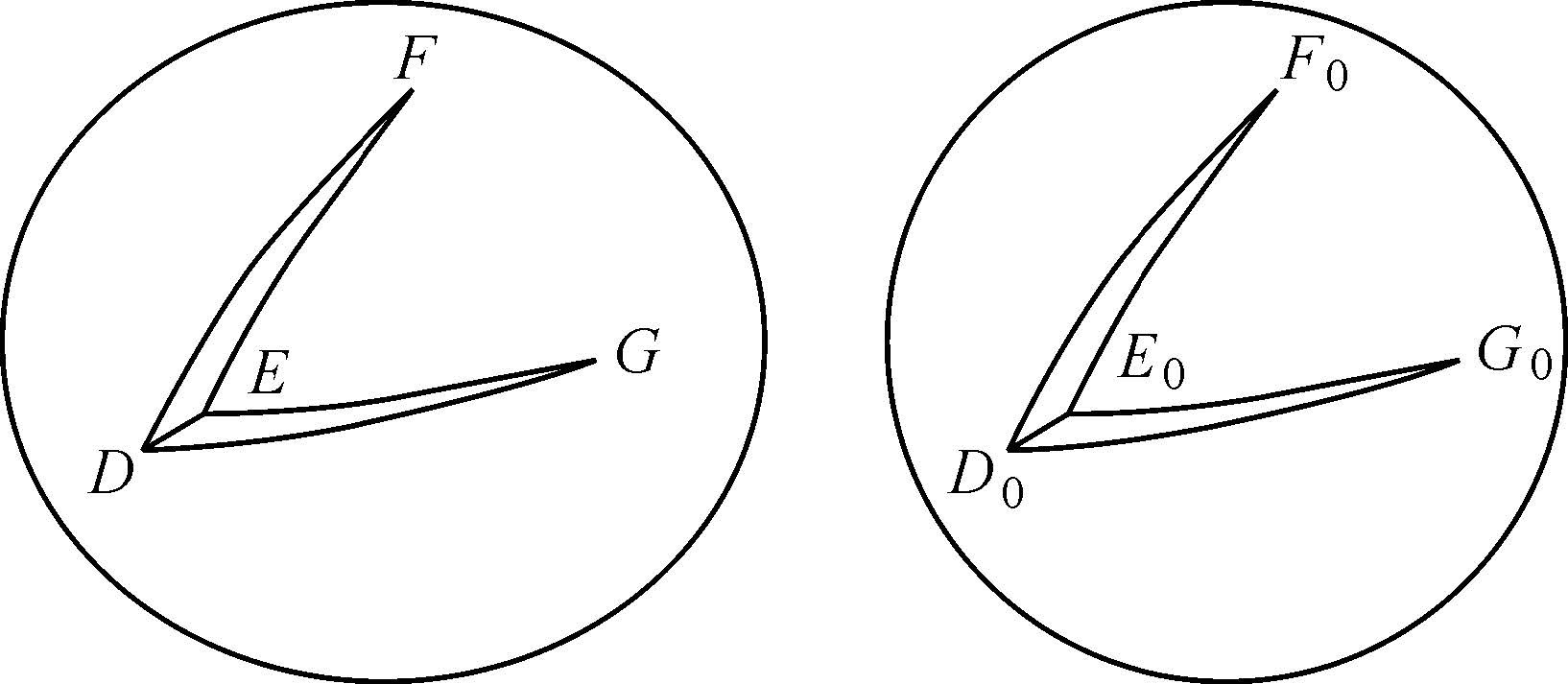
如图 2所示,椭球面三角形DEF和DEG共用同一边DE,且大地线DF和DG长度相等,∠EDF和∠EDG也相等。对应到本文方法中,D表示初始等距点,F和G分别表示相邻两个栅格中心点的来源点,E表示∠FDG平分线(大地线)上的一点。当DF和DG的长度不超过104km且DE的长度不大于1km时,如果能够论证EF和EG的长度偏差小于0.001m,由初始等距点逼近三角形外心与大地主题解算的精度[23]相当的结论就是成立的。在密切球上做与椭球面三角形DEF和DEG对应边长度相等的三角形D0E0F0和D0E0G0,已知大圆弧D0F0和D0G0长度相等,假设∠E0D0F0和∠E0D0G0也相等,即两边及其夹角彼此相等。根据球面三角形全等定理[22],球面三角形D0E0F0和D0E0G0全等,由全等球面三角形的性质可知大圆弧E0F0和E0G0的长度也相等。实际上,将椭球面三角形转化到对应球面上以后,∠E0D0F0和∠E0D0G0并不相等,因此大圆弧E0F0和E0G0的长度不相等。
|
| 图 2 椭球面三角形DEF和DEG与球面三角形D0E0F0和D0E0G0 Fig. 2 Triangle DEF and DEG on ellipsoidal surface and triangle D0E0F0 and D0E0G0 on spherical surface |
由式(3)可知,椭球面上的∠EDF与对应球面上的∠E0D0F0仅相差一个椭球面改正数,其大小主要与椭球面上大地线DE和DF长度的乘积有关。因为大地线DF的长度不超过104km,且大地线DE的长度不大于1km,所以椭球面改正数小于0.001″,由球面余弦公式[22]可知对应球面上大圆弧E0F0端点的位移小于0.001m,同理可知大圆弧E0G0端点的位移也小于0.001m,即大地线EF与EG的长度偏差在0.001m以内可控,也即逼近过程与大地主题解算的精度[23]保持一致。
一般情况下大地线DF、DG和DE的长度越短,大地线EF与EG的长度偏差就越小,逼近的精度也就越高。在本文方法中DF、DG的大地线长度对应于外心到椭球面三角形顶点的大地线距离,DE的大地线长度对应于栅格单元的跨度。因此理论上算法的精度与大地线距离的长短呈负相关,与栅格分辨率的高低呈正相关。
2 关键技术本文方法基于地图代数测地变换,充分发挥了矢栅紧密结合数据结构的优势,在保证栅格计算效率的条件下,能够计算定位误差小于0.001m的大跨度(103~104km范围)内椭球面三角形外心大地坐标。按照算法流程的先后顺序,主要涉及以下几个关键技术:测地变换、边界跟踪配对和求解外心大地坐标,其中边界跟踪配对用来确定外心所在的临界相邻栅格范围。
2.1 测地变换所谓测地变换是指在椭球面上进行的栅格大地线尺度距离变换,其目的是建立椭球面空间的高精度距离场。地图代数测地变换的时间复杂度为O(m),其中m为计算规模,是全空间的栅格单元总数[15],等于横向分辨率(地理网格阵列的列数)与纵向分辨率(地理网格阵列的行数)的乘积。与利用穷举算法进行距离变换相比,地图代数测地变换完全不受生成元个数和生成元复杂程度的影响,不但能够适用于复杂的自然图形,而且可以大大提高计算效率,适用于本文问题的解决。作为大地线尺度下的空间度量,测地变换的精度最终取决于大地主题解算公式的精度,在20000km的范围内误差小于数厘米[23],因此可以认为栅格中心间的大地线距离是没有偏差的,在全球范围内可用。
文献[15]规定测地变换必须满足3个基础定义,其中定义3明确指出两定点a、b间的栅格距离等同于a、b所属栅格中心间的距离,顾及整个栅格和舍入误差,有不大于0.5个栅格单元的长度[15]。虽然该算法的精度可以由栅格分辨率来控制,理论上能够达到很高的精度,但是对于某些实际应用,例如要在103~104km范围内计算误差小于0.001m的椭球面三角形外心,各栅格单元的跨度都不能超过0.001m,相应的横向和纵向分辨率将达到109~1010,全空间的栅格单元总数就增加到了1018~1020,现阶段普通的计算机显然无法处理规模如此庞大的地理网格阵列。
2.2 边界跟踪配对文献[24]提出了一种基于八邻域边界跟踪的物体标号算法,一次扫描即可同时获得物体的边界点序列以及边界链码,为后续处理提供数据准备。在此基础上,本文通过以下方法对测地变换所得分配场进行边界跟踪配对:首先找到最左上角的一个边界栅格作为搜索起点,按顺时针方向,自上而下、从左至右,搜索其八邻域,并将搜索路径上的四邻域栅格作为上一个边界栅格的配对栅格,直到找到下一个边界栅格;然后以此边界栅格为新的起点继续搜索,这一搜索过程不断重复下去,直至回到搜索起点。经过边界跟踪配对以后,所有边界栅格的邻接匹配关系都可以被确定。遍历所得边界栅格对序列,按顺序从前往后每两对一组进行判别扫描,过滤出匹配关系发生变化的相邻两对边界栅格对,即为椭球面三角形外心所在的栅格范围。
2.3 求解外心大地坐标经过边界跟踪配对确定椭球面三角形外心所在的栅格范围以后,最终求解足够精确的结果又可分为两个步骤:初始等距点的内插以及外心大地坐标的逼近,它们分别如图 3和图 4所示。其中O1和O2分别表示上述相邻两对边界栅格对中的配对栅格中心点,B1和B2分别表示O1和O2的来源点,B1到O1的大地线距离和B2到O2的大地线距离分别等于S1和S2,O3和O4分别表示与O1和O2相互对应的边界栅格中心点,B3表示O3和O4的同一个来源点,B3到O3的大地线距离和B3到O4的大地线距离分别等于S3和S4。

|
| 图 3 内插初始等距点 Fig. 3 Interpolation of the initial equidistant point |
|
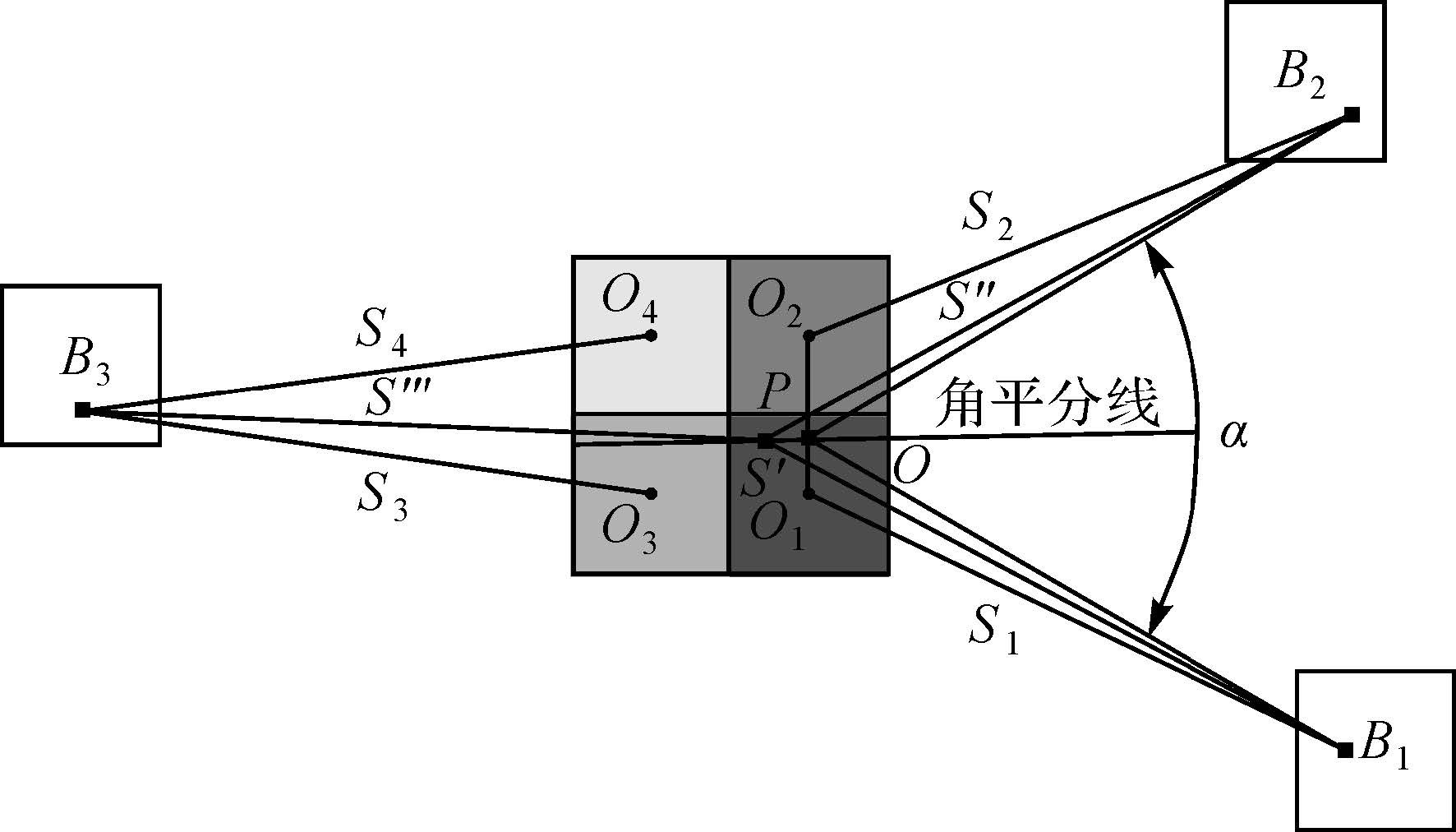
| 图 4 逼近椭球面三角形外心 Fig. 4 Approximation of the circumcenter of triangle on ellipsoidal surface |
经过大地线尺度下的地图代数测地距离变换,可以确保O1距离B1比B2更近,O2距离B2比B1更近。由大地线长度变化的连续性容易证明,在如图 3所示的O1与O2连接成的大地线段上必然存在一点O到B1和B2的大地线距离都等于S,即得到初始等距点O。
2.3.2 逼近椭球面三角形外心在103~104km范围内,当栅格单元的跨度不大于1km时,在如图 4所示的3~4个临界相邻栅格范围内,∠α的平分线(大地线)上任意一点P到B1和B2的大地线距离偏差都小于0.001m。由大地线长度变化的连续性同理可证,在该角平分线上必然存在一个到B1和B3的大地线距离相等或到B2和B3的大地线距离相等的点,不妨假设该点为P,则P到B1、B2和B3的大地线距离S′、S″和S’’’的偏差都小于0.001m,即求解得到由B1、B2和B3构成的椭球面三角形外心的精确位置。
3 具体实现及试验结果分析 3.1 具体实现充分利用测地变换所生成的高精度距离场,通过数值计算先内插初始等距点,再以同样的方式不断逼近椭球面三角形外心是本文方法的关键。原则上在103~104km范围内要使得各栅格单元的跨度都不超过1km,因此一般情况下将横向分辨率范围设定为103~104,纵向分辨率范围也随之确定,相应的计算规模(全空间的栅格单元总数)控制在106~108之间。本文方法的具体实现步骤如图 5所示,其中源点坐标场记录的是各控制点的最近来源点经纬度坐标信息,距离场记录的是每个控制点到对应来源点的大地线距离信息,分配场则记录了所有控制点与其最近地理实体之间的对应关系。

|
| 图 5 椭球面三角形外心的求解流程 Fig. 5 Flow chart of determination of circumcenter of triangle on ellipsoidal surface |
为了保证方法在全球范围内的普遍适用性,本文采用了WGS-84坐标中的椭球基本参数:椭球长半轴a= 6378137.0m,椭球扁率f= 1.0/298.257223563,且采用了解算精度与距离无关的贝塞尔大地主题解算公式[25]。
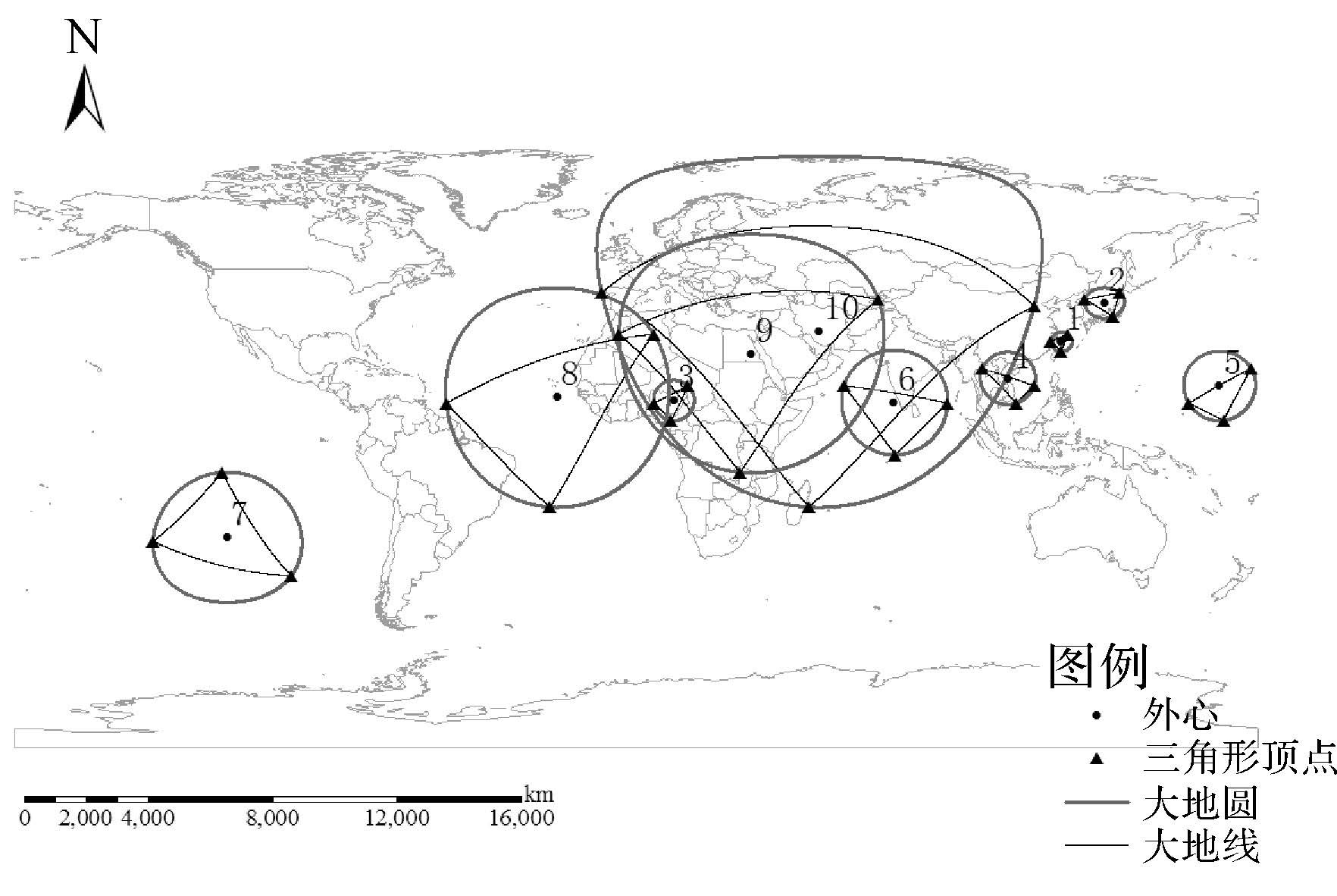
3.2.1 验证方法精度与大地线距离的关系进行以下10组数据的计算,其中横向分辨率都设定在5000以内,各椭球面三角形3个顶点及其外心的位置如图 6所示,具体的大地坐标见表 1。为了验证所得结果的正确性,分别计算各外心到对应椭球面三角形3个顶点的大地线距离及其标准差,详细结果见表 2。在表 1和表 2中,λ都表示经度,Φ则表示纬度。
|
| 图 6 椭球面上各三角形及其外心与外接大地圆 Fig. 6 Triangles on ellipsoidal surface and their geodetic circumcenters and circumcircles |
| 三角形编号 | A点坐标 | B点坐标 | C点坐标 | 外心坐标 | ||||
| λ | φ | λ | φ | λ | φ | λ | φ | |
| 1 | 120.0 | 28.0 | 123.0 | 25.0 | 125.0 | 30.0 | 123.1142794726 | 27.7748547075 |
| 2 | 130.0 | 40.0 | 138.0 | 35.0 | 140.0 | 42.0 | 135.6265884294 | 39.0382336461 |
| 3 | 5.0 | 10.0 | 10.0 | 5.0 | 15.0 | 15.0 | 10.8570804343 | 10.7900421494 |
| 4 | 100.0 | 20.0 | 110.0 | 10.0 | 115.0 | 15.0 | 107.4462816976 | 17.2105435562 |
| 5 | 160.0 | 10.0 | 178.0 | 20.0 | 170.0 | 5.0 | 168.8910018210 | 15.0077255698 |
| 6 | 60.0 | 15.0 | 75.0 | -5.0 | 90.0 | 10.0 | 74.6720699858 | 10.1889295085 |
| 7 | -100.0 | -40.0 | -120.0 | -10.0 | -140.0 | -30.0 | -118.4478776900 | -28.8430204215 |
| 8 | -55.0 | 10.0 | -25.0 | -20.0 | 5.0 | 30.0 | -22.8597957047 | 11.7306785997 |
| 9 | -5.0 | 30.0 | 30.0 | -10.0 | 70.0 | 40.0 | 33.3180534375 | 24.4455028190 |
| 10 | -10.0 | 42.0 | 50.0 | -20.0 | 115.0 | 38.0 | 52.9791232254 | 30.9507307310 |
由表 2可知,随着外心到对应椭球面三角形各顶点的大地线距离变得越来越远,标准差呈现不断增大的趋势,说明本文方法的计算精度与大地线距离的长短呈负相关。1—9号椭球面三角形外心到对应各三角形3个顶点的大地线距离之差都小于0.001m,其中外心到对应三角形顶点的最短大地线距离为307648.8577m,标准差不超过0.00006m;最长大地线距离达到3827513.4529m,标准差也不超过0.0005m。10号椭球面三角形外心到对应各三角形3个顶点的大地线距离分别是5646875.7513m、5646875.7518m和5646875.7539m,虽然两两之差不都小于0.001m,但是标准差不超过0.002m。因此在中、长距离情况下,本文方法对于椭球面三角形外心的求解精度非常高。在超长距离情况下,计算精度虽有所降低,但仍然保持在0.001m左右。
| 三角形编号 | 外心到3顶点的大地线距离 | 标准差/m | ||
| 到A的距离 | 到B的距离 | 到C的距离 | ||
| 1 | 307648.8577 | 307648.8578 | 307648.8577 | 0.0000577350 |
| 2 | 495378.7581 | 495378.7583 | 495378.7580 | 0.0001527525 |
| 3 | 647287.1030 | 647287.1031 | 647287.1033 | 0.0001527525 |
| 4 | 844193.3370 | 844193.3370 | 844193.3366 | 0.0002309401 |
| 5 | 1113598.2098 | 1113598.2098 | 1113598.2102 | 0.0002309401 |
| 6 | 1680030.9983 | 1680030.9983 | 1680030.9991 | 0.0004618801 |
| 7 | 2092296.4951 | 2092296.4942 | 2092296.4946 | 0.0004509249 |
| 8 | 3517485.3194 | 3517485.3199 | 3517485.3201 | 0.0003605552 |
| 9 | 3827513.4529 | 3827513.4520 | 3827513.4526 | 0.0004582575 |
| 10 | 5646875.7513 | 5646875.7518 | 5646875.7539 | 0.0013796136 |
进行以下5组数据的计算,其中构成椭球面三角形ABC各顶点的大地坐标分别是A(88.1314°,55.2526°)、B(100.3333°,40.5152°)和C(111.6666 °,66.3738 °),分别计算不同分辨率下外心的大地坐标和相应外心到各顶点的大地线距离及其标准差,详细结果见表 3,在表 3中λ和φ分别表示经度和纬度。
| 横向分辨率 | 外心坐标/(°) | 外心到各顶点的大地线距离/m | 标准差/m | |||
| λ | φ | 到A的距离 | 到B的距离 | 到C的距离 | ||
| 1000 | 111.4698754413 | 52.3338478473 | 1564069.0623 | 1564069.0610 | 1564069.0592 | 0.0015567060 |
| 2000 | 111.4698754074 | 52.3338478412 | 1564069.0604 | 1564069.0591 | 1564069.0599 | 0.0006557439 |
| 3000 | 111.4698753782 | 52.3338478472 | 1564069.0583 | 1564069.0584 | 1564069.0592 | 0.0004932883 |
| 4000 | 111.4698753881 | 52.3338478473 | 1564069.0589 | 1564069.0588 | 1564069.0592 | 0.0002081666 |
| 5000 | 111.4698753859 | 52.3338478465 | 1564069.0588 | 1564069.0587 | 1564069.0593 | 0.0003214551 |
由表 3可知,随着分辨率变得越来越高,标准差呈现不断减小的趋势,说明本文方法的计算精度与分辨率的高低呈正相关。当横向分辨率从1000逐渐增大到4000时,标准差从0.0015567060m逐渐减小到0.0002081666m,计算结果的精度在不断提高。当横向分辨率继续增大到5000时,标准差反而增加到0.0003214551m,说明当分辨率增加到一定程度后,对于算法精度的提高作用是有限的,由于大地主题解算的精度限制[23],此时大地主题解算的误差对结果的影响超过逼近误差,精度发生异常波动属于正常现象。因此本文方法能够在可计算的栅格分辨率范围内(横向分辨率在103~104之间,全空间的栅格单元总数在106~108之间)高效计算定位误差小于0.001m的大跨度(103~104km范围内)椭球面三角形外心大地坐标。
3.2.3 分析椭球面三角形各顶点所处纬度的高低对算法精度的影响由于本文方法在划分网格单元的步骤中采用的是基于大地坐标系统的传统平面格网系统构建方法,不可避免地存在面积变形、形状变形以及由赤道向南北极递增的问题[26],因此分析方法精度与椭球面三角形各顶点所处纬度的关系也很有必要。观察表 2中的6号和7号椭球面三角形,两者的横向分辨率都设定为4000,前者的外心到各顶点的大地线距离分别是1680030.9983m、1680030.9983m和1680030.9991m,标准差是0.0004618801m,后者的外心到各顶点的大地线距离分别是2092296.4951m、2092296.4942m和2092296.4946m,标准差是0.0004509249m,同属中长距离情况,计算精度基本相当。由表 1可知,6号椭球面三角形各顶点处于低纬度地区,而7号椭球面三角形各顶点处于中高纬度地区。因此在正确划分网格单元的条件下,本文方法的精度与所处纬度无关。
3.2.4 分析地理数据的复杂程度对算法效率的影响选取如图 7所示的位于大西洋两岸的100个城市结点进行试验。在横向分辨率设定为4000的条件下,采用配置为Intel Core 2 Duo E7500处理器和2GB内存的台式电脑,本文方法计算100个城市的所有167个Voronoi顶点的整个过程耗时不超过20s(包括测地变换过程在内),与相同条件下计算单个椭球面三角形外心速度相当,说明算法效率基本不受对象个数的影响。作为一种面向椭球面空间且内容无关的算法,本文方法更适合于海量空间数据的高精度快速计算。

|
| 图 7 大西洋两岸100个城市及其Voronoi顶点 Fig. 7 The hundred cities on both sides of the Atlantic and their Voronoi vertexes |
综上所述,本文方法精度与外心到对应椭球面三角形各顶点的大地线距离的长短呈负相关,与栅格分辨率的高低呈正相关,与椭球面三角形各顶点所处纬度无关,能够满足在全球范围内以可计算的栅格分辨率(全空间的栅格单元总数在106~108之间)快速求解外心精确大地坐标(定位误差小于0.001m)的需求。
4 结 论本文方法采用矢栅紧密结合的数据结构,基于地图代数测地变换建立了椭球面空间的高精度距离场,在对分配场进行边界跟踪、配对、遍历和过滤操作之后,通过数值计算内插逼近的方法,最终计算出精确的大跨度椭球面三角形外心大地坐标。算法充分发挥了矢栅结合的优势,具有面向椭球面空间且内容无关的特性,能够同时兼顾计算精度和效率。该方法可以用来生成椭球面Voronoi图和构造椭球面Delaunay三角网,且已经成功应用于海域划界三接点的高精度快速求解。后续工作将研究如何将本文方法拓展到椭球面缓冲区和等比例线的求解问题[27],从而提高海域划界相关计算的精度和效率。
| [1] | 周培德. 计算几何[M]. 北京: 清华大学出版社, 2000. ZHOU Peide. Computational Geometry[M]. Beijing: Tsinghua University Press, 2000. |
| [2] | GOLD C M. The Global GIS[C]//Proceeding of the International Workshop on Dynamic and Multi-Dimension GIS. Hong-Kong, China: [s.n.], 1997: 80-91. |
| [3] | 刘广军, 郭晶, 刘旭东. 基于椭球面大地线三角网的CORS布站研究与仿真[C]//第13届中国系统仿真技术及其应用学术年会论文集. 黄山: 中国自动化学会系统仿真专业委员会, 2011. LIU Guangjun, GUO Jing, LIU Xudong. Research and Simulation on CORS Station Distribution Based on Ellipsoid Geodetic-line Triangulation Network[C]//Proceedings of 13th Chinese Conference on System Simulation Technology & Application. Huangshan: Professional Committee of China Automation Society System Simulation, 2011. |
| [4] | 施一民, 朱紫阳. 椭球面上Delaunay三角形的外接大地圆圆心的求解[J]. 同济大学学报, 2004, 32(1): 78-81. SHI Yimin, ZHU Ziyang. Determination of Center for Geodetic Circle Which Passes through Three Top Points of Triangle on Ellipsoidal Surface[J]. Journal of Tongji University, 2004, 32(1): 78-81. |
| [5] | 冯琰, 施一民. 基于区域性椭球面数字地面模型的研究[J]. 同济大学学报, 2003, 31(8): 964-967. FENG Yan, SHI Yimin. New DTM Based on Surface of Regional Ellipsoid[J]. Journal of Tongji University, 2003, 31(8): 964-967. |
| [6] | 赵学胜, 陈军, 王金庄. 基于O-QTM的球面Voronoi图的生成算法[J]. 测绘学报, 2002, 31(2): 157-163. ZHAO Xuesheng, CHEN Jun, WANG Jinzhuang. QTM-based Algorithm for the Generating of Voronoi Diagram for Spherical Objects[J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(2): 157-163. |
| [7] | HOREMUZ M. Error Calculation in Maritime Delimitation between States with Opposite or Adjacent Coasts[J]. Marine Geodesy, 1999, 22(1): 1-17. |
| [8] | 施一民, 冯琰. 地球椭球面上另一种形式的测地坐标系的建立[J]. 同济大学学报, 2001, 29(11): 1282-1285. SHI Yimin, FENG Yan. Establishment of Another Form of Geodesic Coordinate System on Earth Ellipsoid[J]. Journal of Tongji University, 2001, 29(11): 1282-1285. |
| [9] | 赵文婷, 彭俊毅. 基于Voronoi图的无人机航迹规划[J]. 系统仿真学报, 2008(z2): 159-162, 165. ZHAO Wenting, PENG Junyi. Voronoi Diagram-based Path Planning for UAVs[J]. Journal of System Simulation, 2008(z2): 159-162, 165. |
| [10] | 阎代维, 谷良贤, 王兴治. 基于Voronoi图的巡航导弹突防路径规划研究[J]. 弹箭与制导学报, 2005, 25(2): 11-13. YAN Daiwei, GU Liangxian, WANG Xingzhi. The Study of Cruise Missile Path Planning with Voronoi Diagram[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2005, 25(2): 11-13. |
| [11] | FERRERO S, PIEROZZI M, REPETTI L, et al. An Algorithm for the Unambiguous Determination of the Equidistant Boundary Line between Two (or More) Coastlines[J]. Applied Geomatics, 2009, 1(3): 49-58. |
| [12] | SJÖBERG L E. The Three-point Problem of The Median Line Turning Point: on the Solutions for the Sphere and Ellipsoid[J]. International Hydrographic Review, 2002, 3(1): 81-87. |
| [13] | 李庆扬, 王能超, 易大义. 数值分析[M]. 第5版. 北京: 清华大学出版社, 2008. LI Qingyang, WANG Nengchao, YI Dayi. Numerical Analysis[M]. 5th ed. Beijing: Tsinghua University Press, 2008. |
| [14] | 胡鹏, 游涟, 胡海. 地图代数概论[M]. 北京: 测绘出版社, 2008. HU Peng, YOU Lian, HU Hai. Introduction to Map Algebra[M]. Beijing: Publishing House of Surveying and Mapping, 2008. |
| [15] | 胡鹏, 范青松, 胡海. 椭球上的测地变换和Voronoi图的生成--地理空间度量[J]. 武汉大学学报(信息科学版), 2007, 32(9): 825-828. HU Peng, FAN Qingsong, HU Hai. Distance Transformation and Voronoi Generation on Earth Ellipsoid--Metrics of Geographic Space[J]. Geomatics and Information Science of Wuhan University, 2007, 32(9): 825-828. |
| [16] | GOLD C, MOSTAFAVI M A. Towards the Global GIS[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2000, 55(3): 150-163. |
| [17] | 胡鹏, 刘沛兰, 胡海, 等. 地球信息的度量空间和Global GIS[J]. 武汉大学学报(信息科学版), 2005, 30(4): 317-321. HU Peng, LIU Peilan, HU Hai, et al. Metric Space of Earth Information and Global GIS[J]. Geomatics and Information Science of Wuhan University, 2005, 30(4): 317-321. |
| [18] | KJENSTAD K. Construction and Computation of Geometries on the Ellipsoid[J]. International Journal of Geographical Information Science, 2011, 25(9): 1413-1437. |
| [19] | HU Hai, LIU Xiaohang, HU Peng. Voronoi Diagram Generation on the Ellipsoidal Earth[J]. Computers & Geosciences, 2014, 73: 81-87. |
| [20] | 胡鹏, 杨传勇, 胡海, 等. GIS的基本理论问题--地图代数的空间观[J]. 武汉大学学报(信息科学版), 2002, 27(6): 616-621. HU Peng, YANG Chuanyong, HU Hai,et al. Space View of Map Algebra[J]. Geomatics and Information Science of Wuhan University, 2002, 27(6): 616-621. |
| [21] | 熊介. 椭球大地测量学[M]. 北京: 解放军出版社, 1988. XIONG Jie. Ellipsoidal Geodesy[M]. Beijing: Publishing House of Liberation Army, 1988. |
| [22] | 张楚宾. 球面三角学[M]. 北京: 高等教育出版社, 1959. ZHANG Chubin. Spherical Trigonometry[M]. Beijing: Higher Education Press, 1959. |
| [23] | 陈健, 晁定波. 椭球大地测量学[M]. 北京: 测绘出版社, 1992. CHEN Jian, CHAO Dingbo. Ellipsoidal Geodesy[M]. Beijing: Publishing House of Surveying and Mapping, 1992. |
| [24] | 刘相滨, 向坚持, 阳波. 基于八邻域边界跟踪的标号算法[J]. 计算机工程与应用, 2001, 37(23): 125-126, 132. LIU Xiangbin, XIANG Jianchi, YANG Bo. A Labeling Algorithm Based on 8-Connected Boundary Tracking[J]. Computer Engineering and Applications, 2001, 37(23): 125-126, 132. |
| [25] | 孔祥元, 郭际明, 刘宗泉. 大地测量学基础[M]. 武汉: 武汉大学出版社, 2005. KONG Xiangyuan, GUO Jiming, LIU Zongquan. Foundation of Geodesy[M]. Wuhan: Wuhan University Press, 2005. |
| [26] | 宋树华, 程承旗, 关丽, 等. 全球空间数据剖分模型分析[J]. 地理与地理信息科学, 2008, 24(4): 11-15. SONG Shuhua, CHENG Chengqi, GUAN Li, et al. Analysis on Global Geodata Partitioning Models[J]. Geography and Geo-Information Science, 2008, 24(4): 11-15. |
| [27] | 胡海, 吴艳兰. 椭球面上混合基线图形的缓冲区和等比例线问题[J]. 测绘工程, 2011, 20(3): 1-4, 8. HU Hai, WU Yanlan. Problems of Graphics Buffers and the Proportion Line of Ellipsoid Mixed Baseline (or Normal Curve)[J]. Engineering of Surveying and Mapping, 2011, 20(3): 1-4, 8. |