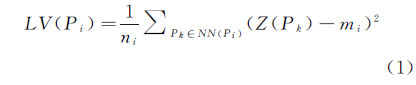空间聚类是一种重要的空间数据探索性分析手段,能够有效挖掘地理现象的空间分布模式[1, 2, 3]。根据空间聚类是否顾及实体的专题属性,可以将空间聚类大致分为两种类型[4]:一种是只依据实体间空间位置的接近程度进行聚类,另一种是同时考虑实体间空间位置毗邻和专题属性相近。前一类空间聚类问题最先得到关注,并已经提出了一些较为成熟的空间聚类模型,如基于邻近图的方法[5]、局部密度自适应的方法[6, 7]及基于神经网络的方法[8]等。然而,相比前一种聚类任务,顾及专题属性的空间聚类方法在挖掘空间分布模式时更具实际意义,且更为复杂,已经成为当前空间聚类分析研究中的一个重点[9, 10, 11]。
空间层次聚类是目前使用最为广泛的一种顾及专题属性的空间聚类方法[12, 13],可以获得多层次的聚集结构,但聚类结果显著性(或层次合并截止条件)的统计判别依然是一个尚未解决的难题。针对层次聚类结果显著性的统计判别问题,一些学者进行了初步的探索研究。如文献[14]借助多尺度Bootstrap方法,通过比较原始数据与随机样本的聚类结果判断层次聚类结果的显著性;文献[13]以误差平方和(SSE)作为簇的均质性度量指标,通过比较簇内实体专题属性随机重排前后SSE的大小变化定义簇的显著性;文献[15]依据层次聚类中两个簇的合并距离判断聚类的显著性。这些方法都是针对单纯的多维属性数据(如时间序列、基因和微阵列数据)层次聚类结果显著性的判别,未考虑空间位置与专题属性耦合的问题,无法直接应用于顾及专题属性的空间层次聚类的显著性判别。同时,文献[14—15]提出的方法隐含的前提假设是层次聚类的合并距离是单调的,但是由于空间层次聚类在聚合的过程中受空间邻近约束的影响无法保证合并距离的单调性。文献[13]可以通过进一步的扩展,对空间层次聚类结果的显著性进行检验,但是其容易受噪声的影响,对于实体间的微小差异过于敏感而难以获得全局最优的划分结果。为此,本文针对同时顾及空间邻近与专题属性相似的层次聚类结果显著性检验问题,提出了一种空间层次聚类显著性判别的重排检验方法。
1 研究策略空间簇的显著性判别实际上是对空间簇的均质性进行度量和评价。空间簇的均质性度量需要同时满足两方面条件:一方面每个空间实体与其空间邻近实体的专题属性相似,另一方面同一空间簇内实体的专题属性相似。度量一个空间实体与其邻近实体专题属性相似性的显著程度,可以借鉴局部空间自相关指数(如局部Moran’s I)显著性判别的策略[16]。本文对空间簇内实体的专题属性相似性度量提出如下假设:①若一个空间簇是均质的,则簇内实体的专题属性随机重排(即随机分配簇内实体的专题属性值)后每个空间实体与其空间邻近实体的专题属性应仍是相似的;②若重排后出现实体与其空间邻近实体的专题属性不相似的情况,则说明空间簇内实体专题属性间不满足簇内相似性约束,即簇内实体的专题属性值之间存在着较大的差异。
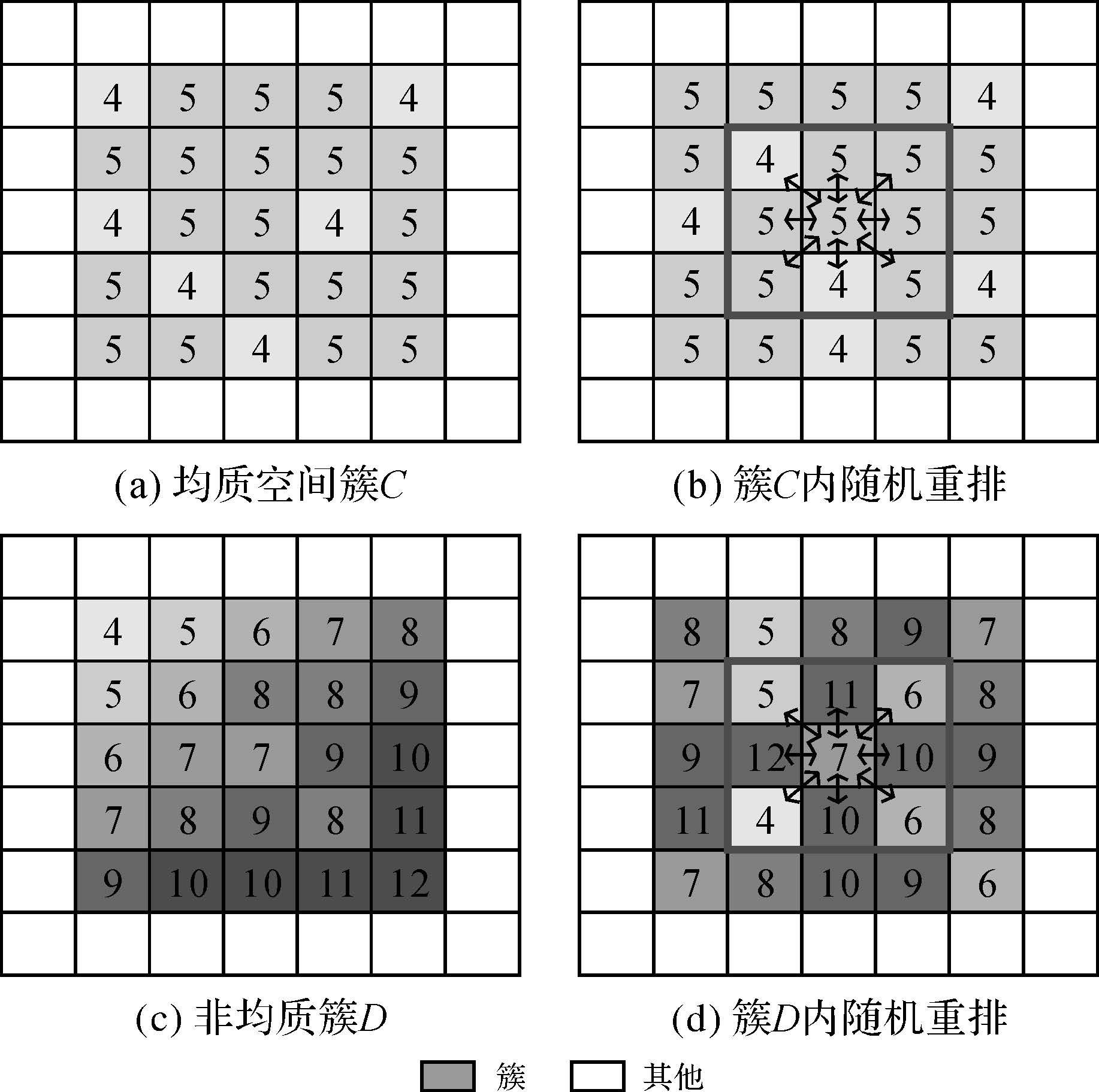
因此,度量簇的均质性可转化为度量簇内随机重排后每个空间实体与其邻近实体的专题属性相似性的保持情况:如果重排后空间簇内实体与其邻近实体的专题属性依然是显著相似的,说明该空间簇满足均质性度量的两个约束条件,则定义该空间簇是显著的。下面给出一个简单的示例对本文的研究策略进行说明。如图 1(a)所示,每个单元格表示一个空间实体,数字表示实体的专题属性,C表示一个均质的空间簇。对C内实体专题属性进行随机重排后(如图 1(b)所示),位于簇C中心的实体与其空间邻近实体(箭头表示邻近关系)的专题属性仍然是相似的。图 1(c)显示了一个非均质的空间簇D,位于簇D中心的空间实体虽然也满足与其空间邻近实体专题属性相似,然而簇内重排后可以发现(如图 1(d)所示),如位于中心位置的实体与其空间邻近实体的专题属性具有较大的差异,簇内实体间专题属性不相似。
|
| 图 1 示例数据和簇内随机重排 Fig. 1 An example of the random permutation within a cluster |
基于上述思想,本文方法主要包括3方面内容:首先识别空间数据中与其空间邻近实体专题属性显著相似的空间实体(本文称之为核点),核点及其空间邻近实体是构成均质簇的基本要素;其次,在方差增量最小约束下,将核点及其空间邻近实体凝聚成簇;最后,空间簇内进行随机重排,对簇内实体的专题属性相似性进行统计判别。与当前研究策略相比,本文的研究思路一方面可以对空间数据中有无聚集结构进行统计检验,另一方面可以对空间层次聚类的停止准则进行判别,减少聚类过程对参数设置的依赖。基于上述策略,下面介绍本文方法的具体步骤。
2 空间层次聚类显著性判别的重排检验方法 2.1 基于全局随机重排的核点检测空间层次聚类显著性判别的首要步骤为识别空间实体中的核点。受局部空间自相关探测的启发,首先需要对实体的空间邻域进行定义;进一步,需要定义核点显著性判别的零假设及统计量;最后,依据零假设通过随机模拟计算统计量的经验概率密度分布,识别空间实体中的核点。
对于空间数据集SD={P1,P2,…,Pn},与实体Pi在空间上相邻的实体的集合称为Pi的空间邻居,Pi与其空间邻居的集合称为Pi的空间邻域,记为NN(Pi)。对于格网或面状数据,可以直接依据拓扑邻接关系定义实体的空间邻域;针对不规则点数据,由于约束Delaunay三角网法[17]具有良好的自适应性,且不需要参数设置,因此本文采用约束Delaunay三角网法构建不规则点的空间邻域。
在此基础上,采用方差度量空间实体Pi与其空间邻域NN(Pi)内实体间专题属性的相似性,称为Pi的局部方差,记为LV(Pi),具体表达为
式中,mi表示NN(Pi)内实体专题属性均值;ni为NN(Pi)内实体数目;Z(Pk)表示空间实体Pk的专题属性值。需要注意的是,局部方差的计算实际上附加了空间邻近关系的约束(即仅计算空间实体与其空间邻近实体的专题属性的方差),因而同时考虑了空间与专题属性相似两方面的因素。进而,本文从空间随机性的角度定义零假设,即任意空间位置上的专题属性值不依赖于空间邻近位置上的专题属性值[18]。基于该假设,采用随机重排的方法构造空间随机数据,计算实体局部方差的经验概率密度分布,并对核点的显著性进行统计判别,具体步骤如下:(1) 给定空间数据集SD={P1,P2,…,Pn},依据式(1)计算实体Pk(k=1,2,…,n)的局部方差LV(P1)、LV(P2)、…、LV(Pn)。
(2) 保持实体的空间位置不变,将所有实体的专题属性值进行一次随机重排。计算重排后每个实体的局部方差,记为Dk=[LV(Pk1)LV(Pk2)…LV(Pkn)]T,其中k表示第k次随机重排,LV(Pki)表示第k次重排后实体Pi的局部方差。空间约束依然在局部方差的经验概率密度分布构造过程中得以体现,即在空间随机数据中计算局部方差时依然仅计算空间实体与其空间邻近实体间的方差。如图 2所示,显示了方框内中心实体(记为Pi)局部方差的经验概率密度分布的计算步骤(箭头表示空间邻域)。

|
| 图 2 随机重排构造实体局部方差经验概率密度分布示例 Fig. 2 Construction of the empirical probability density distribution of local variance |
(3) 重复步骤(2)m次,可以得到实体局部方差的样本矩阵W = [D1D2…Dm](W矩阵即为通过全局随机重排构造的显著性检验统计量的零假设概率密度分布),由此可以计算出每个空间实体局部方差的显著性p-value(·)
式中,Wik表示矩阵W的第i行第k列的元素值;I(·)表示指示函数。在给定的显著性水平α下,如果实体局部方差的显著性p-value(·)小于α,则将该实体标记为核点。需要注意的是,由于对局部方差显著性的假设检验是一种多重假设检验问题,当要求严格时需要进一步对其校正。本文试验中采用FDR方法[19]进行多重假设检验的校正。如上所述,核点是构成均质空间簇的基本要素,为了避免聚类过程中噪声干扰,进一步的聚类过程将只针对核点及其空间邻域内实体(称为边界点)进行凝聚式的合并聚类。如果在全局随机重排步骤中未检测到核点,则聚类过程结束,即数据近似随机分布不存在聚集模式。
2.2 方差约束下的凝聚合并空间数据中的核点识别后,需要进一步将核点及边界点凝聚成簇。本文采用空间约束的Ward法[11]进行凝聚聚类,首先从局部方差最小的核点出发,在凝聚合并时每个空间簇只与其空间邻近的簇计算专题属性相似性,这样保证了在空间相邻的前提下将专题属性相似的实体聚合到一起。聚类开始首先将每一个实体视为一个簇,分别计算每个簇与其空间邻接的簇合并前后的方差增量,将方差增量最小且通过簇内均质性检验的两个簇进行合并,更新各空间簇的邻接关系;重复以上过程,直到所有实体聚合为一个类或没有可以合并的簇时停止。本文提出的重排检验方法与空间层次聚类紧密结合,下面介绍簇内均质性判别方法。
2.3 簇内均质性统计判别在空间层次聚类过程中,需要对每次合并获得的空间簇的均质性进行统计判别,以确定合并的停止条件。若经过大量簇内随机重排操作后,簇内核点与邻近实体专题属性仍是显著相似的(即核点稳定),则称该空间簇是显著的或均质的。具体计算步骤如下:
(1) 假设空间层次聚类过程中簇A和簇B将要合并为一个新的空间簇S,为了判别其显著性(或能否合并的条件),首先计算位于S内的核点Pi(i=1,2,…,g)的局部方差LV(Pi)。
(2) 保持簇内实体的空间位置不变,对空间簇S内实体的专题属性进行一次随机重排,计算重排后簇内核点的p-value(Pi)(i=1,2,…,g);利用局部方差样本矩阵W中核点Pi对应的局部方差经验概率密度分布,即[LV(Pi1)LV(Pi2)…LV(Pmi)],依据式(2)计算重排后核点Pi的p-value(·),经过多重假设检验校正后,判别其是否依然显著(即p-value(·)小于显著性阈值α)。用Ik进行标记,若簇内核点Pi(i=1,2,…,g)都依然是显著的,则Ik取1,否则为0。
(3) 重复步骤(2)r次,空间簇S的显著性可通过下式计算
在给定的统计显著性水平β下,如果p-value(S)≤β,则称空间簇S是显著的或均质的。
经过上述步骤计算后,若空间簇S是显著的,则簇A和簇B满足合并条件,合并A和B,更新当前所有空间簇的空间邻接关系并进行下一次的凝聚合并,直到数据集中没有满足合并条件或所有实体聚为一个类时停止,并返回最后一次的合并结果作为最终的聚类结果。由于该方法聚类过程中不需要人为指定簇的数目或聚类停止条件,更具实用性,且簇合并时可根据空间邻接关系向任意方向进行扩展,因此可以识别复杂形状的空间簇。
3 试验分析与应用为了验证本文方法的有效性,分别采用模拟数据与实际数据进行试验分析,并与文献[13]和ST-DBSCAN[20]、Mean shift[21]进行比较。试验中随机重排次数(m和r)的选择,需从效率和精度两个方面进行折中考虑,本文对重排次数的设置进行了试验分析:所采用的测试数据集SD1如图 3(a)所示,包含324个核点;测试环境为Windows 8 系统,CPU 2.0GHz,内存8GB,每种重排次数都试验20次,取其运行时间的平均值。如表 1所示,运行时间与重排次数呈线性增长的关系,当重排次数大于5000时检测结果趋于稳定。现有研究亦发现,当重排次数为9999次时,p-value(·)可以取得的最小值为0.0001,在显著性水平为0.05时,可以满足绝大多数应用的精度需求[22]。试验中全局和簇内随机重排次数(m和r)均设为9999,核点和簇的显著性水平(α和β)均取0.05。
| 参数 | 随机重排次数 | ||||||
| 100 | 500 | 1000 | 5000 | 10000 | 50000 | 100000 | |
| 运行时间/s | 2.486 | 12.427 | 24.502 | 123.365 | 246.017 | 1236.681 | 2480.534 |
| 核点个数 | 323(1) 324(11) 325(6) 326(2) | 324(20) | 324(18) 325(2) | 324(20) | 324(20) | 324(20) | 324(20) |
| 注:运行时间是取20次重复试验的平均值;核点个数括号内的数字表示20次试验出现该结果的次数。 | |||||||

|
| 图 3 模拟数据SD1以及试验结果对比 Fig. 3 Experiments on simulated dataset SD1 |
为了说明本文方法在挖掘随机数据中均质簇的能力,设计模拟数据集SD1如图 3(a)所示,在中心位置设置了一个由两个专题属性差异很小的矩形区域构成的空间簇(区域A和B大小均为20×10,区域A内实体专题属性值都为1,区域B内实体专题属性值都为1.1),其余实体的专题属性值设置为1到100之间的随机整数。文献[13]的聚类结果如图 3(c)所示。由于区域A和B合并前误差平方和为0,而将这两个簇的专题属性进行随机重排后误差平方和必然变大,文献[13]判断其不能合并,故两个专题属性值差异很小的区域被错误割裂。本文方法的核点检测结果如图 3(b)所示,聚类结果如图 3(d)所示,与人眼的识别结果相吻合,发现了被随机噪声包围的均质簇(图 3(a)中蓝色区域)。由此可见,文献[13]针对简单的空间数据依然过于保守,为此在接下来的试验中将不与文献[13]作进一步的比较。
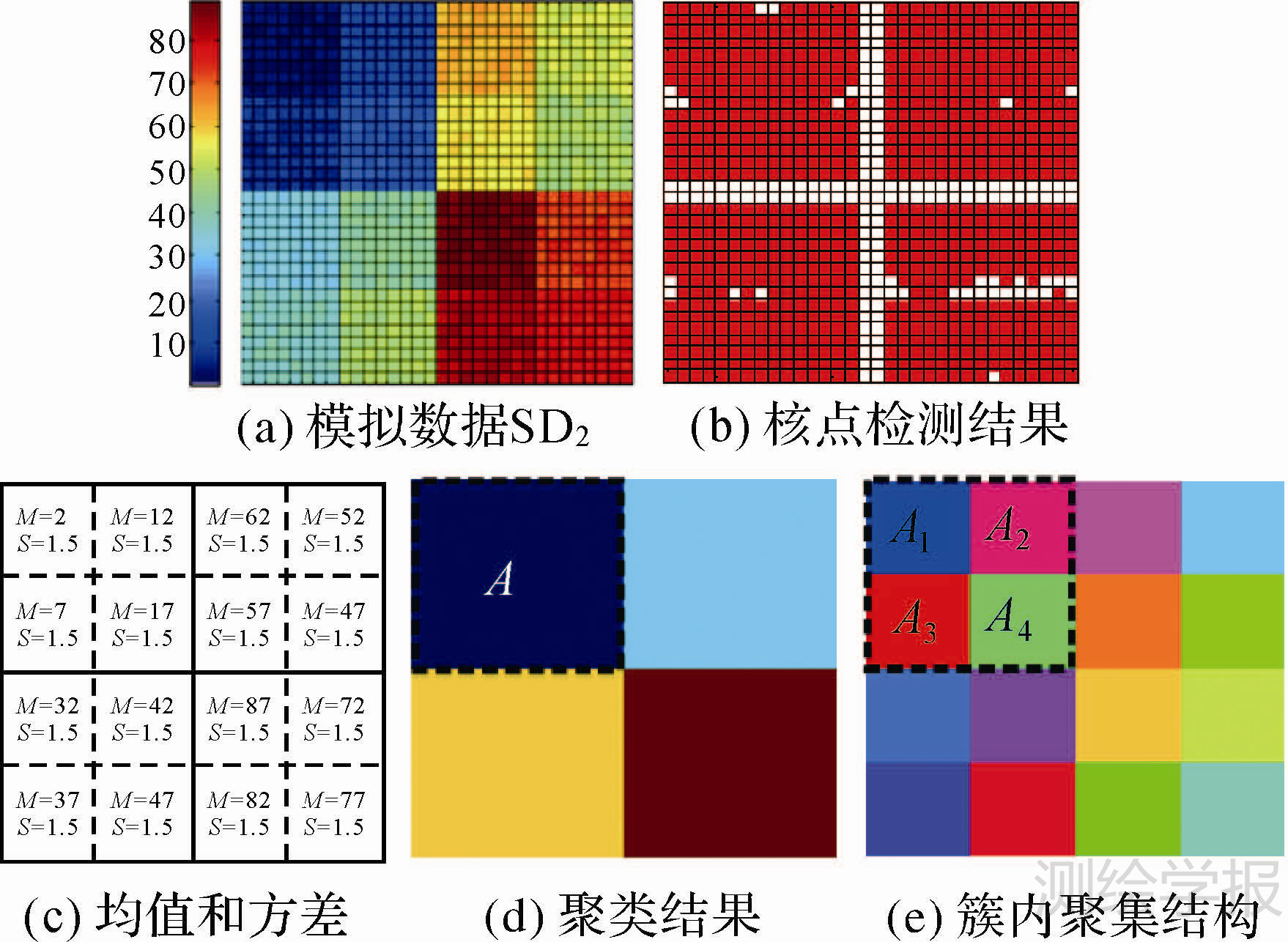
模拟数据SD2(32×32)包含4个大簇,每个大簇包含4个小簇,如图 4(a)所示。模拟数据的方差矩阵如图 4(c)(M表示专题属性均值,S表示专题属性标准方差)所示。本文方法聚类结果如图 4(d)所示,准确地识别了数据中预设的4个大簇。对于每个整体上显著的大簇,可以进一步通过迭代求解的方式识别局部的小簇,即将聚类结果中的每个大簇作为新的数据集再进行聚类。例如,对左上角的大簇A进行分析,可获得其中的4个小簇A1—A4,如图 4(e)。如此重复迭代,即可识别数据局部所有显著的聚集结构(共16个簇)。这一从整体到局部的聚类过程亦符合人类视觉多尺度认知由整体到局部,由粗到细的识别过程。
|
| 图 4 模拟数据SD2以及聚类结果 Fig. 4 Experiments on simulated dataset SD2 |
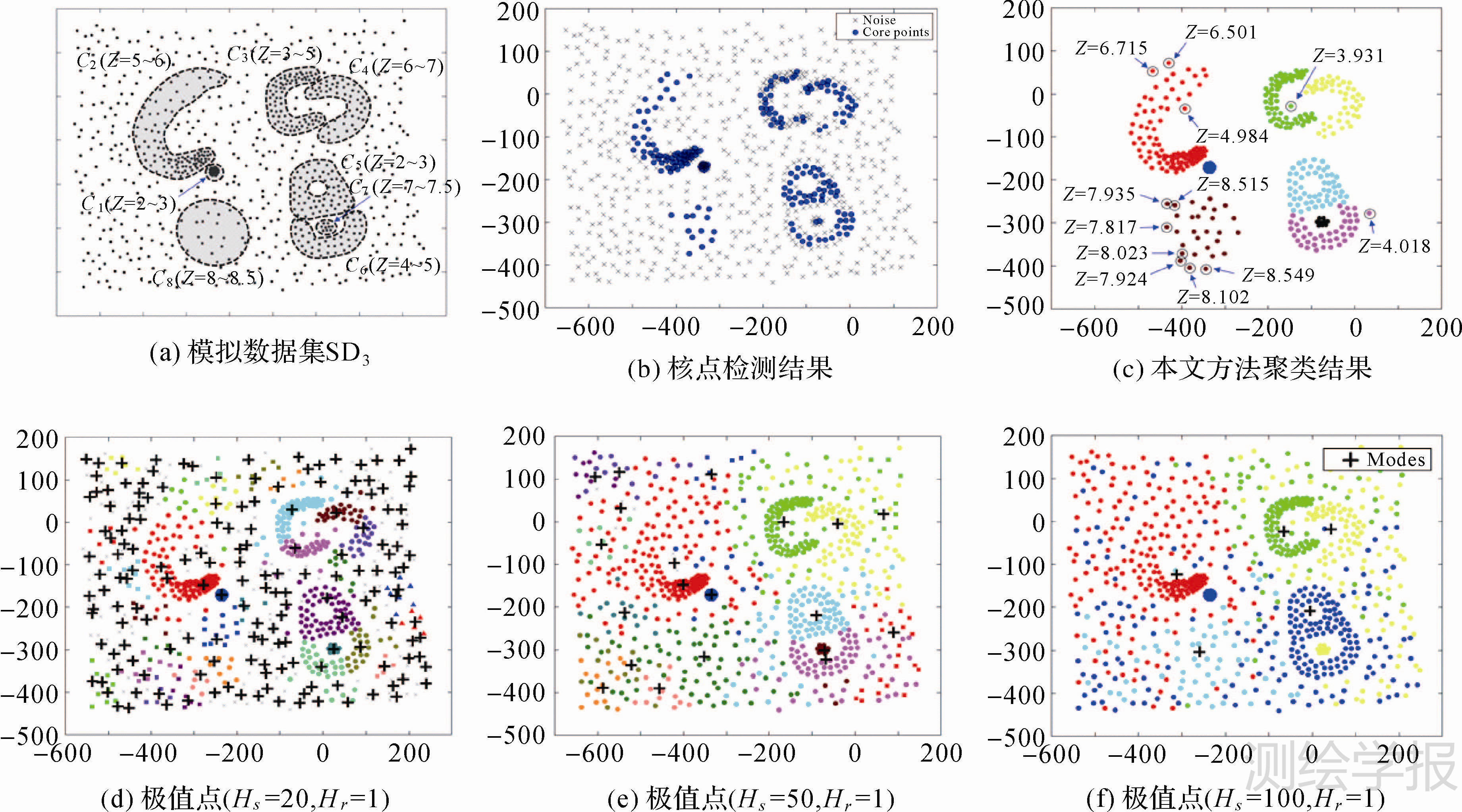
模拟数据SD3包含了8个空间簇,如图 5(a)所示,图中Z表示簇内实体专题属性的取值范围,噪声点的专题属性值设置为0~10之间的任意随机数。其中,C1为高密度的空间簇,C2表示了变密度的空间簇,C3、C4以及C5和C6表示了任意形状且相邻的空间簇,C7表示了面积较小的空间簇,C8表示了低密度的空间簇。本文方法核点检测结果和最终聚类结果如图 5(b)和5(c)所示,可以发现本文方法很好地识别出数据中预设的各类空间簇。在一些空间簇的周围包含了个别的“噪声点”(图 5(c)中带圆圈的点),但通过进一步的观察发现,这些点的专题属性值与空间簇的专题属性值分布一致,这进一步验证了本文方法探测均匀簇的能力。核点检测是本文的关键步骤,为了显示本文策略探测核点的有效性,与经典的Meanshift算法进行比较,图 5(d)—(f)显示了Meanshift算法在不同带宽下局部极值点(modes)检测结果和聚类结果,可以发现Meanshift算法难以准确的识别预设的聚集结构,簇内包含了大量的随机噪声。此外,Meanshift算法两个带宽(即空间带宽Hs和属性带宽Hr)的设置缺乏严密的依据,因而增加了用户实际使用的难度。
|
| 图 5 模拟数据SD3聚类结果及Meanshift聚类结果 Fig. 5 Clustering result of SD3 and modes detected by Meanshift with different band widthparamters |
为了进一步验证本文方法的有效性,与经典ST-DBSCAN聚类方法进行对比试验分析。ST-DBSCAN算法的参数采用文章作者推荐的启发式方法进行设置,扫描半径Eps和最小包含点数MinPts,聚类结果如图 6所示,可以发现:ST-DBSCAN算法仅正确识别了SD1中最简单的空间簇;对于SD2聚类效果较差,未能识别主要聚类结构;对于SD3未能识别空间簇的完整结构,类别面积较小的空间簇(C7)亦未能正确识别。

|
| 图 6 模拟数据集SD1、SD2和SD3的ST-DBSCAN聚类结果 Fig. 6 Clustering results of ST-DBSCAN on dataset SD1, SD2 and SD3 |
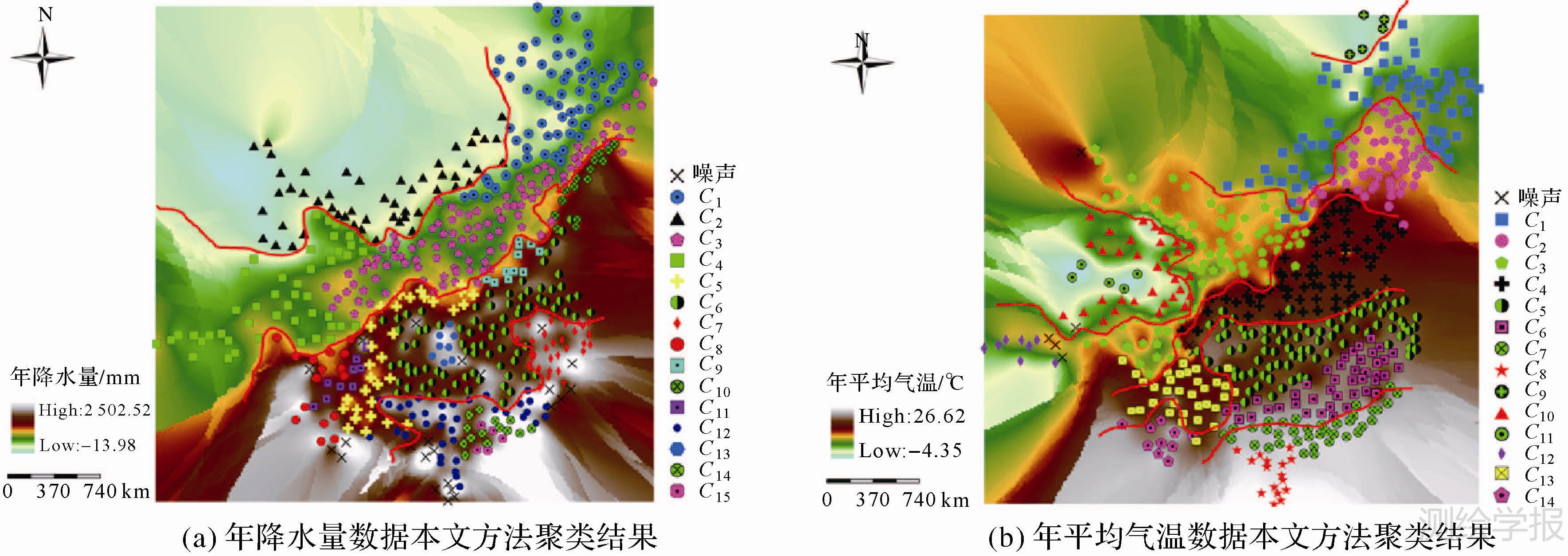
降水和气温的空间分布模式是地理学的研究热点,我国具有复杂的气候条件,降水和气温都具有明显的空间分异性,提取其中的均质区域,对于研究降水、气温分布规律和特征具有重要作用,亦可为进一步的深入研究提供有益的参考。此外,对于我国降水和气温分布具备一定的先验知识,可以为检验聚类结果的有效性提供一定的依据。本文方法对2009年我国554个陆地气象观测站的年降水量和年平均气温数据进行分析,聚类结果如图 7所示,在表 2显示了各个簇内专题属性的标准方差(其中,Std.Dev表示数据总体的标准方差)。
| 参数 | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 | C11 | C12 | C13 | C14 | C15 | Std.Dev |
| 降水/mm | 79.9 | 84.6 | 108.7 | 92.7 | 107.3 | 129.8 | 100.3 | 160.8 | 86.9 | 129.4 | 153.2 | 177.2 | 138.5 | 176.3 | 123.4 | 475.5 |
| 气温/℃ | 1.67 | 1.57 | 1.81 | 1.47 | 1.46 | 1.36 | 0.97 | 1.06 | 0.99 | 2.18 | 1.18 | 2.71 | 2.02 | 1.80 | — | 6.57 |
从图 7可以发现,不同空间簇间均具有比较明显的分界线。对于降水数据的聚类结果(图 7(a)),较好反映了我国降水空间分布的基本特征,图中标记的红色线由北向南分别代表我国年降水量400mm、800mm和1600mm等值线,如簇C2与簇(C1、C3和C4)的边界构成了我国400mm年降水量等值线;簇C3、C4与簇C5、C8、C9、C10的边界构成了我国800mm降水等值线;簇C5、C6与簇C7、C12、C14的边界构成了我国1600mm降水等值线。对于气温数据的聚类结果(图 7(b)),充分反映了我国气温分布的空间分异特征,由北到南发现的空间簇与相关气象资料[23]中我国主要气温带十分吻合,如簇C9对应了寒温带,簇C1、C2、C3表示了中温带、簇C4表示了暖温带、簇C5、C13对应了北亚热带、簇C6表示了中亚热带、簇C7代表了南亚热带、簇C8、C14表示了边缘热带、簇C10、C12表示了高原温带、簇C11代表了高原寒带。此外,进一步结合克里金插值结果亦可以发现同一空间簇内各站点的气温和降水相似,说明了空间聚类结果保证了簇内部的均质性,且与气象领域的分区结果相吻合。
|
| 图 7 本文方法对2009年年降水量和气温数据聚类结果 Fig. 7 Clustering results obtained by the proposed method |
为了进行比较分析,图 8给出了ST-DBSCAN的聚类结果,可以发现,针对降水数据绝大部分站点都被识别为噪声,并没有发现降水的空间分布模式;针对气温数据仅仅发现了东部和中部地区几个小簇,我国气温分异特征难以从聚类结果中得到反映。

|
| 图 8 年降水量和年平均气温的ST-DBSCAN算法聚类结果 Fig. 8 Clustering results obtained by ST-DBSCAN |
本文提出的统计检验方法,能克服空间层次聚类方法合并截止条件判别困难的缺陷。通过试验分析与比较发现,本文方法能够有效判别空间层次聚类结果的显著性,提取数据中显著的结构模式,避免随机结构的干扰。
重排检验要进行大量的数据模拟,运行效率较低,在海量数据的分析应用中可能会有一定的局限性,进一步工作将研究采用并行计算、数据分块或采样等技术手段提升算法的运行效率,使其可以适用于海量数据的分析处理。对于高维专题属性聚类依然是当前研究的一个难点,本文提出的方法针对高维专题属性聚类问题的应用效果及扩展亦将是未来的一个重要研究方向。本文方法在其他领域中具有一定的应用前景,如地图综合、遥感图像的分割和分类等。
| [1] | 李德仁, 王树良, 李德毅. 空间数据挖掘理论与应用[M]. 北京: 科学出版社, 2006. LI Deren, WANG Shuliang, LI Deyi. Spatial Data Mining Theories and Applications[M]. Beijing: Science Press, 2006. |
| [2] | 艾廷华, 郭仁忠. 基于格式塔识别原则挖掘空间分布模式[J]. 测绘学报, 2007, 36(3): 302-308. AI Tinghua, GUO Renzhong. Polygon Cluster Pattern Mining Based on Gestalt Principles[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(3): 302-308. |
| [3] | 汪闽, 周成虎, 裴韬, 等. MSCMO: 基于数学形态学算子的尺度空间聚类方法[J]. 遥感学报, 2004, 8(1): 45-50. WANG Min, ZHOU Chenghu, PEI Tao, et al. MSCMO: A Scale Space Clustering Algorithm Based on Mathematical Morphology Operators[J]. Journal of Remote Sensing, 2004, 8(1): 45-50. |
| [4] | 李光强, 邓敏, 程涛, 等. 一种基于双重距离的空间聚类方法[J]. 测绘学报, 2008, 37(4): 482-488. LI Guangqiang, DENG Min, CHENG Tao, et al. A Dual Distance Based Spatial Clustering Method[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(4): 482-488. |
| [5] | 郭庆胜, 郑春燕, 胡华科. 基于邻近图的点群层次聚类方法的研究[J]. 测绘学报, 2008, 37(2): 256-261. GUO Qingsheng, ZHENG Chunyun, HU Huake. Hierarchical Clustering Method of Group of Points Based on the Neighborhood Graph[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(2): 256-261. |
| [6] | 李光强, 邓敏, 刘启亮, 等. 一种适应局部密度变化的空间聚类方法[J]. 测绘学报, 2009, 38(3): 255-263. LI Guangqiang, DENG Min, LIU Qiliang, et al. A Spatial Clustering Method Adaptive to Local Density Change[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(3): 255-263. |
| [7] | PEI Tao, ZHU Axing, ZHOU Chenghu, et al. A New Approach to the Nearest-Neighbour Method to Discover Cluster Features in Overlaid Spatial Point Processes[J]. International Journal of Geographical Information Science, 2006, 20(2): 153-168. |
| [8] | 程博艳, 刘强, 李小文. 一种建筑物群智能聚类法[J]. 测绘学报, 2013, 42(2): 290-294. CHENG Boyan, LIU Qiang, LI Xiaowen. Intelligent Building Grouping Using Selft-organizing Map[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(2): 290-294. |
| [9] | 李新运, 郑新奇, 闫弘文. 坐标与属性一体化的空间聚类方法研究[J]. 地理与地理信息科学, 2004, 20(2): 38-40. LI Xinyun, ZHENG Xinqi, YAN Hongwen. On Sptial Clustering Combination of Coordinate and Attribute[J]. Geography and Geo-Information Science, 2004, 20(2): 38-40. |
| [10] | 宋晓眉, 程昌秀, 周成虎, 等. 利用k阶空间邻近图的空间层次聚类方法[J]. 武汉大学学报(信息科学版), 2010, 35(12): 1496-1499. SONG Xiaomei, CHENG Changxiu, ZHOU Chenghu, et al. Spatial Hierarchical Clustering Method Based on k-order Spatial Neighbouring Map[J]. Geomatics and Information Science of Wuhan University, 2010, 35(12): 1496-1499. |
| [11] | 焦利民, 洪晓峰, 刘耀林. 空间和属性双重约束下的自组织空间聚类研究[J]. 武汉大学学报(信息科学版), 2011, 36(7): 862-866. JIAO Limin, HONG Xiaofeng, LIU Yaolin. Self-organizing Spatial Clustering under Spatial and Attribute Constraints[J]. Geomatics and Information Science of Wuhan University, 2011, 36(7): 862-866. |
| [12] | GUO Diansheng. Greedy Optimization for Contiguity-Constrained Hierarchical Clustering[C]//Proceedings of IEEE International Conference on Data Mining Workshops.Miami, FL: IEEE, 2009: 591-596. |
| [13] | PARK P J, MANJOURIDES J, BONETTIM, et al. A Permutation Test for Determining Significance of Clusters with Applications to Spatial and Gene Expression Data[J]. Computational Statistics and Data Analysis, 2009, 53(12): 4290-4300. |
| [14] | SUZUKI R, SHIMODAIRA H. Pvclust: An R Package for Assessing the Uncertainty in Hierarchical Clustering[J]. Bioinformatics, 2006, 22(12): 1540-1542. |
| [15] | GREENACRE M, PRIMICERIO R. Multivariate Analysis of Ecological Data[M]. Bilbao: Fundación BBVA, 2013. |
| [16] | ANSELIN L. Local Indicators of Spatial Association-LISA[J]. Geographical Analysis, 1995, 27(2): 93-115. |
| [17] | 刘启亮, 邓敏, 石岩, 等. 一种基于多约束的空间聚类方法[J]. 测绘学报, 2011, 40(4): 509-516.LIU Qiliang, DENG Min, SHI Yan, et al. A Novel Spatial Clustering Method Based on Multi-Constraints[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(4): 509-516. |
| [18] | 王远飞, 何洪林. 空间数据分析方法[M]. 北京: 科学出版社, 2007.WANG Yuanfei, HE Honglin. Spatial Data Analysis Method[M]. Beijing: Science Press, 2007. |
| [19] | BENJAMINI Y, YEKUTIELI D. The Control of the False Discovery Rate in Multiple Testing under Dependency[J]. The Annals of Statistics, 2001, 29(4): 1165-1188. |
| [20] | BIRANT D, KUT A. ST-DBSCAN: An Algorithm for Clustering Spatial-temporal Data[J]. Data & Knowledge Engineering, 2007, 60(1): 208-221. |
| [21] | COMANICIU D, MEER P. Mean Shift: A Robust Approach Toward Feature Space Analysis[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24(5): 603-619. |
| [22] | OJALA M, GARRIGA G C. Permutation Tests for Studying Classifier Performance[J]. The Journal of Machine Learning Research, 2010, 11(1): 1833-1863. |
| [23] | 《中华人民共和国气候图集》编委会. 中华人民共和国气候图集[M]. 北京: 气象出版社, 2002.The Editorial Board of Climatic Atlas of the People's Republic of China. Climatological Atlas of the People's Republic of China[M]. Beijing: China Meteorological Press, 2002. |