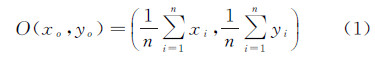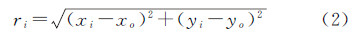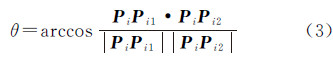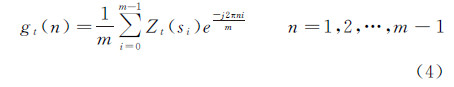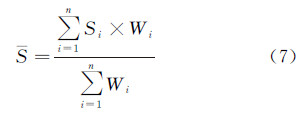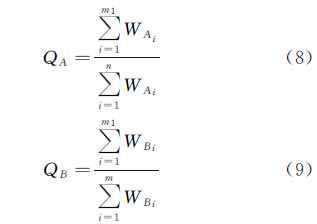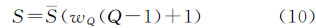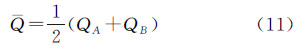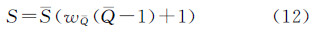2. 地理信息工程国家重点实验室, 陕西 西安 710054
2. State Key Laboratory of Geography Information Engineering, Xi'an 710054, China
同一地物在不同的数据来源中通常存在着差异,如何快速而准确地进行同名实体的识别对于空间数据的更新以及对多源、多类型、多尺度空间数据的有效集成和融合都有着重要意义[1, 2, 3]。近年来,关于同名实体识别的研究越来越多,也越来越深入,但是大多集中于对相同或相近比例尺中单个实体间的识别,例如文献 [4, 5, 6, 7, 8],通过实体图形的空间位置、形状、大小等特征构建综合度量模型来对相近比例尺中的实体进行识别和匹配,但是对于复杂结构的空间数据匹配并不适用,且在全局检索中相较于复杂面实体的匹配效率较低。
鉴于实体匹配方法中拓扑匹配和语义匹配的局限性[9, 10],常用几何匹配的方法来对同名实体进行识别。如今已使用的方法有正切空间形状描述法、傅里叶变换描述法[11, 12]、基于曲率的形状描述法、矩描述法[13]、小波描述法等,这些方法都取得了较好的效果。然而,正切空间形状描述法[14, 15]在对复杂面实体进行匹配时需要对其提取的特征点进行简化,可能会导致某些重要局部特征的缺失;基于曲率的形状描述法只能较好地反映局部特征[16];小波描述法对起始点具有过度依赖性[17]。而复杂带洞多边形相似性度量的关键在于要对几何图形的整体和局部特征都能较好地进行描述,且要满足稳健性以及起始点的独立性。
为此,本文采用一种基于多级弦长弯曲度复函数的傅里叶形状描述算子来对实体之间的几何形状相似性进行度量。面实体在边界线上某点两侧割线的夹角可以很好地反映边界线在该点的弯曲度,从而达到描述实体外形特征的目的,而多级弦长的引入可以通过调节相关参数刻画图形的整体和局部特征,而转化成向量进行相似性度量可以满足起始点的独立性。同时根据场景完整度和相似性度量模型计算复杂带洞多边形中每个场景的匹配度,利用多级特征完成复杂面实体间的几何相似性度量,对不同空间复杂度的面实体的几何相似性进行度量。
1 复杂面实体从应用的观点出发,空间应用处理更多的是复合的几何结构,而不是当前空间数据库系统,空间查询语言和GIS中常见的简单点、线、面。开放地理信息联盟(OGC)在OGC抽象规范及地理标记语言GML中提出了简单要素的几何结构,对这些被称为MultiPoint、MultiLineString和MultiPolygon的几何结构进行了非正式的描述。
复合面状对象A是由n(n≥1)个区域组成,这些区域或分离,或相交于一个或多个边界点,或带洞,即A={A1∪A2∪…∪An},如图 1所示。

|
| 图 2 复杂面状实体A Fig. 2 Complex geometric objects A |
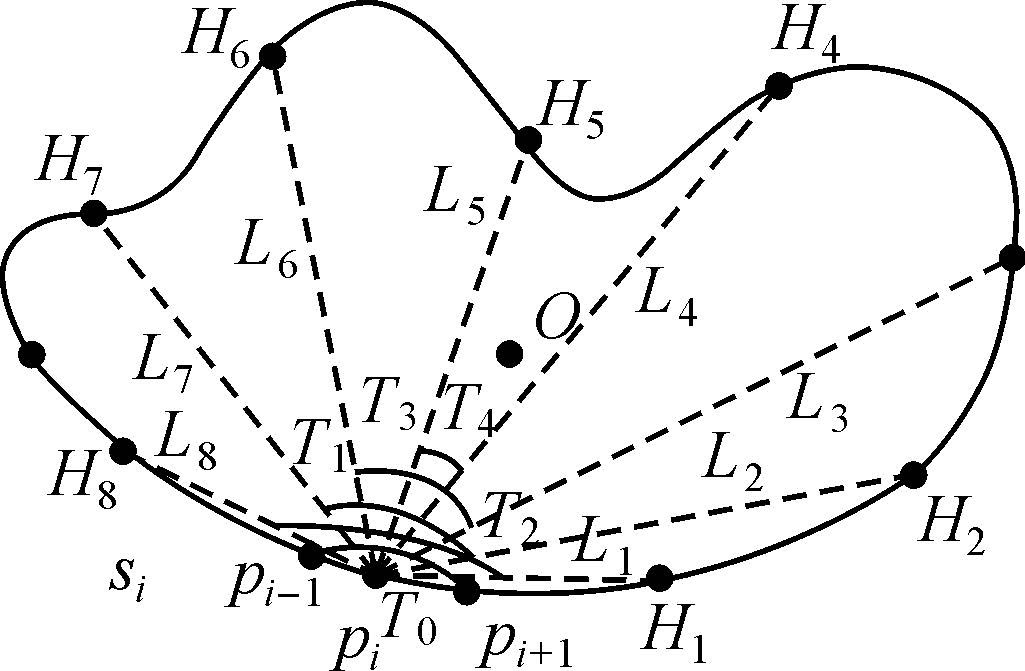
本文采用文献[5]中提出的多级弦长的概念,将面实体的轮廓表示为一组有序点集:C={Pi=(xi,yi)|i=1,2,…,N},如图 2所示,选取点P0为起始点,则沿轮廓线逆时针方向所得到的弧P0Pi的长度si可以表示为以Pi为自变量的函数,从Pi出发,沿逆时针将C按弧长等分为M个弧段(M>1)。Ht(t=1,2,…,M-1)是对应的等分点。连接Pi和Ht可以得到M-1条弦PiH1,PiH2,…,PiHM-1,用Lt(Pi)表示Pi对应的第t条弦PiHt的弦长。又由于Pi和si一一对应,所以可以将si作为因变量,得到M-1个弦长函数L1(si),L2(si),…,LM-1(si),这里si∈[0,S],其中S为轮廓线周长。由此,轮廓线可以由自变量si和因变量Lt(si)来描述。对于轮廓线的凸凹性在3.1节中会详细描述。

|
| 图 2 多级弦长 Fig. 2 Multilevel chord length |
将有序集合A={L1(si),L2(si),…,LM-1(si)}称之为si的多级弦长函数,函数Lt(si)为多级弦长函数A中的第t级函数。由于t越小,Lt(si)越能更好地描述轮廓的局部特征,故引入零级弦长的概念,用来更好地描述轮廓线的局部特征。零级弦长的定义如下:将有序点集C={Pi=(xi,yi)|i=0,1,2,…,N}和Pi对应的等分点集D={Ht=(xt,yt)|t=1,2,…,M-1}合并为有序点集F={Rj=(xj,yj)|j=1,2,…,M+N-1},顺时针方向、逆时针方向离Pi最邻近的两点为Rj1和Rj2,则弦长Rj1Pi、Rj2Pi均记为Pi的零级弦长。
因为平移和旋转并不改变等分点在轮廓线上的相对位置,所以多级弦长函数满足旋转和平移的不变性,但是并不满足缩放不变性,因此用轮廓线的周长S对弧长进行归一化,用各级弦长的平均值对函数值进行归一化,得到的M个弦长函数满足平移、旋转和缩放不变的特性。
2.2 多边形轮廓弯曲度轮廓线的表示方法同3.1节,此处不再赘述,设点O为几何图形轮廓线的几何中心点,则
式中,(xi,yi)为轮廓线上点的坐标。将轮廓线上任意一点Pi到几何中心点O的距离称为轮廓线在该点的中心距离,记为ri,则有
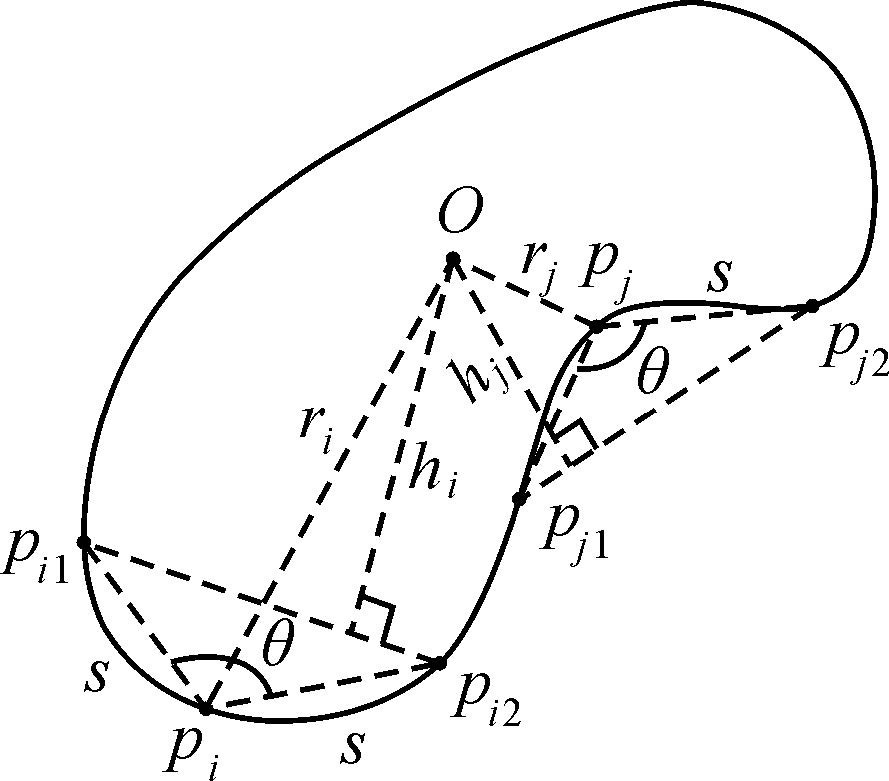
将Pi沿轮廓线顺时针方向和逆时针方向分别扫描弧长为s(s∈[0,S]),其中S为轮廓线周长,得到轮廓线上两点Pi1、Pi2,记向量PiPi1和向量PiPi2的夹角为θi、θi即称为轮廓线在Pi处的弯曲度[4],如图 2所示。θi的计算公式为
由于仅凭θi的值无法判断轮廓线在该点的凹凸性,因此,需计算几何中心点到向量Pi1Pi2的距离h,若ri>h,则轮廓线在该点是外凸的;若ri<h,则轮廓线在该点是内凹的。从图 4中可以看出,轮廓线在Pi点处是凸的,而在Pj点处是凹的。
|
| 图 3 多级弯曲度 Fig. 3 Multilevel bending degree |
|
| 图 4 面实体轮廓线弯曲度 Fig. 4 The bending degree of geometric objects’ boundary line at one point |
弧长s取值的不同会导致弦长|PiPi1||PiPi2|的变化,从而影响弯曲度θi的大小,运用2.1节多级弦长的概念,|PiPi1|、|PiPi2|分别对应点Pi的第t级和第(M-t-1)级弦长,若M为奇数则可以得到任意一点Pi的M/2个弯曲度函数θ1(Pi),θ2(Pi),…,θM/2(Pi),由零级弦长可得到Pi的零级弯曲度函数θ0(Pi),图 2中的面实体轮廓线的多级弯曲度见图 3。θt(Pi)(t=0,1,2,…,M/2)同样可表示为关于si的函数θt(si)(t=0,1,2,…,M/2)。将有序集合B={θ0(si),θ1(si),θ2(si),…,θM/2(si)}称之为si对应的多级弦长弯曲度函数。
复数的几何形式为z=a+bi,指数形式为z=reiθ。轮廓线在Pi处的中心距离为ri,第t级弯曲度为θt(t=0,1,2,…,M/2),由此可得复数zi=rieiθt。当si改变时,Pi的位置也随之发生改变,从而zi也发生改变,因此,可以设以si为自变量,以zi为因变量的复函数Z(si)为多级弦长弯曲度复函数,为方便理解,将其记为Zt(si)(t=0,1,2,…,M/2)。
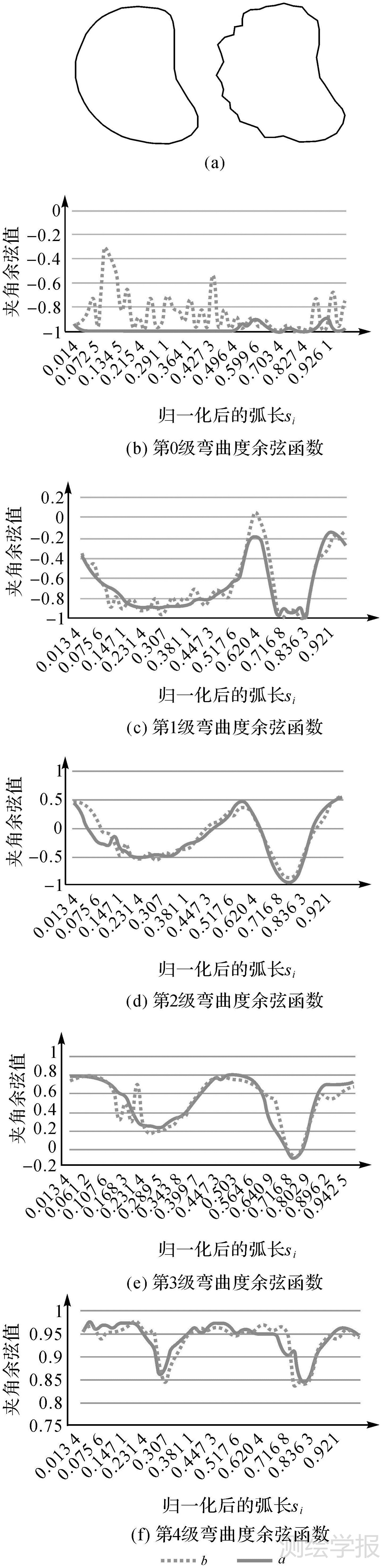
2.3 多级弯曲度函数描述能力由多级弯曲度半径复函数的定义可知,该函数满足旋转和平移不变性,用半径的最大值rmax,弯曲度绝对值最大值|θmax|(|θmax|=π/2),轮廓线周长S分别对中心距离ri,多级弯曲度θt和弧长si进行归一化处理,使函数满足缩放不变性。下面通过试验对多级弯曲度函数的描述能力进行测试分析。图 5(a)为整体相似而局部有较大差别的两个面实体,计算当M=9时的零级到四级弦长弯曲度的余弦函数,并绘制曲线进行对比。两条曲线的差距越大,说明两形状越不相似。经第0级弯曲度描述的两形状最不相似,表明其能对形状的局部特征进行较好的刻画,第1、2、3级曲线的相似程度逐渐增加,到第4级函数已非常接近,说明其描述的形状非常相似,能有效地描述形状的整体特征。由此,多级弯曲度函数随着级数的不同,可以较好地度量不同尺度空间形状的局部和整体特征。
|
| 图 5 多级弯曲度半径复函数描述能力测试 Fig. 5 The descriptive power test of the multilevel bending radius complex function |
上述方法只是对曲线进行大致比较,并没有对两面实体的相似程度进行精确计算,为使相似度的度量满足起始点的独立性以及采样点个数的不一致性,并对面实体间的相似程度进行定量计算,对轮廓线上的点进行等间隔重采样m个点(近似表达轮廓线,其中m=2j,j是满足2j>n的最小值)。对每一个Zt(si)进行快速傅里叶变换,公式为
以gt(n)描述第t级弦长弯曲度复函数,|gt(0)|=1,为了使每一级函数的个数一致方便比较,取m个系数的前k个,构造成向量u=[|gt(1)||gt(2)||gt(3)|…|gt(k)|],即向量u为基于第t级弦长弯曲度复函数的形状描述子。可证u满足边界起始点的独立性。至此,得到了满足平移、旋转、缩放不变性,独立于轮廓线起始点且满足紧致性的形状描述子u。设待匹配的两个面实体为A和B,则它们所对应的形状描述子为uA和uB,用向量间的欧氏距离来定义A和B之间的形状差异度,即
式中,D(A,B)∈[0,1],S(A,B)∈[0,1]。 3 复杂面实体形状相似度综合度量模型 3.1 复杂面实体的平均相似度由于复杂面实体由n(n≥1)个区域组成,为了更加有效地计算复杂面实体的匹配度,引入了几何特征向量的平均相似度。单个实体间的相似度Si(Ai,Bi)(i=1,2,…,n),设Si的权重为Wi,则可得复杂面实体的平均相似度为
3.2 复杂面实体形状完整度当待匹配的两个复杂面实体An和Bm所包含的实体数目不相同(即n≠m)时,通过复杂面实体形状完整度QA和QB来分别表示An和Bm的完整度,则
式中,n表示复杂面实体An中的实体数目;m表示复杂面实体Bm中的实体数目;m1表示复杂面实体Bm中与An匹配的实体数目;WAi表示复杂面实体An中的第i个实体在An中的权重;WBi表示复杂面实体Bm中第i个实体在Bm中的权重;QA,QB∈0,1。 3.3 形状相似性综合度量模型由于复杂面实体所包含的单个实体数目较多,一般为n:m(n≠m)型,并不能一对一进行完全匹配,设能够匹配的单个实体数目为m1,即m1≤min{m,n}。文献[19]利用模糊拓扑关系来处理面实体集非一对一的情况,而本文引入匹配完整度的概念来寻找最佳的匹配。通过计算出的向量平均相似度以及复杂面实体的完整度,用式(10)来计算复杂面实体的完整匹配度
式中,wQ表示完整度所占的权重;S∈0,1。
然而,由式(8)和式(9)可以看出当n≠m时,QA,QB的值并不相等,这样便会导致SAB≠SBA,即An和Bm的相似度与Bm和An的相似度不相等,不满足对称性,显然是不合理的,因此,引入了平均完整度 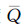 ,用来解决该问题,则
,用来解决该问题,则
至此,式(10)可以改进为式(12),即
4 试验与分析 4.1 复杂面实体形状匹配步骤设待匹配的两个复杂面实体分别为A={A1,A2,…,An}和B={B1,B2,…,Bm},在整体的匹配过程中,采用双向匹配法,即首先在B中查找和A中每一个复杂面实体匹配的目标,然后对B中未被匹配的复杂面实体,在A中查找与其匹配的目标[18]。复杂面实体的匹配采用三原则:先外后内,先上后下,先左后右。其中,先外后内是指对于带洞的面实体,首先对外圈的相似性进行度量,若相似度高于一定值再比较内圈的相似度,否则即可与下一个候选实体进行匹配,这样可以节省大量的时间,提高匹配效率。复杂面实体的匹配是以单个实体间的匹配为基础的,单个实体间的匹配步骤如下:
(1) 对数据的坐标系进行统一;
(2) 提取待匹配实体a和b的轮廓线,并对轮廓线上的点进行等间隔重采样;
(3) 计算各个点的多级弦长弯曲度,并对弧长,各个点半径和弯曲度进行归一化处理;
(4) 得到实体的多级弯曲度复函数,对其进行快速傅里叶变换,并取傅里叶变换系数的模组成向量,计算两个实体特征向量的欧氏距离,获取两个实体的形状相似度S(A,B)。
在得到复杂面实体中单个实体之间的相似度后,则需要:
(1) 确定各个权值及平均完整度的权重;
(2) 计算出复杂面实体的平均相似度和平均完整度;
(3) 根据公式求出复杂面实体的完整匹配度S,并与阈值进行比较,看其是否为最佳匹配。
4.2 面状水系和岛屿的形状相似性度量及影响分析
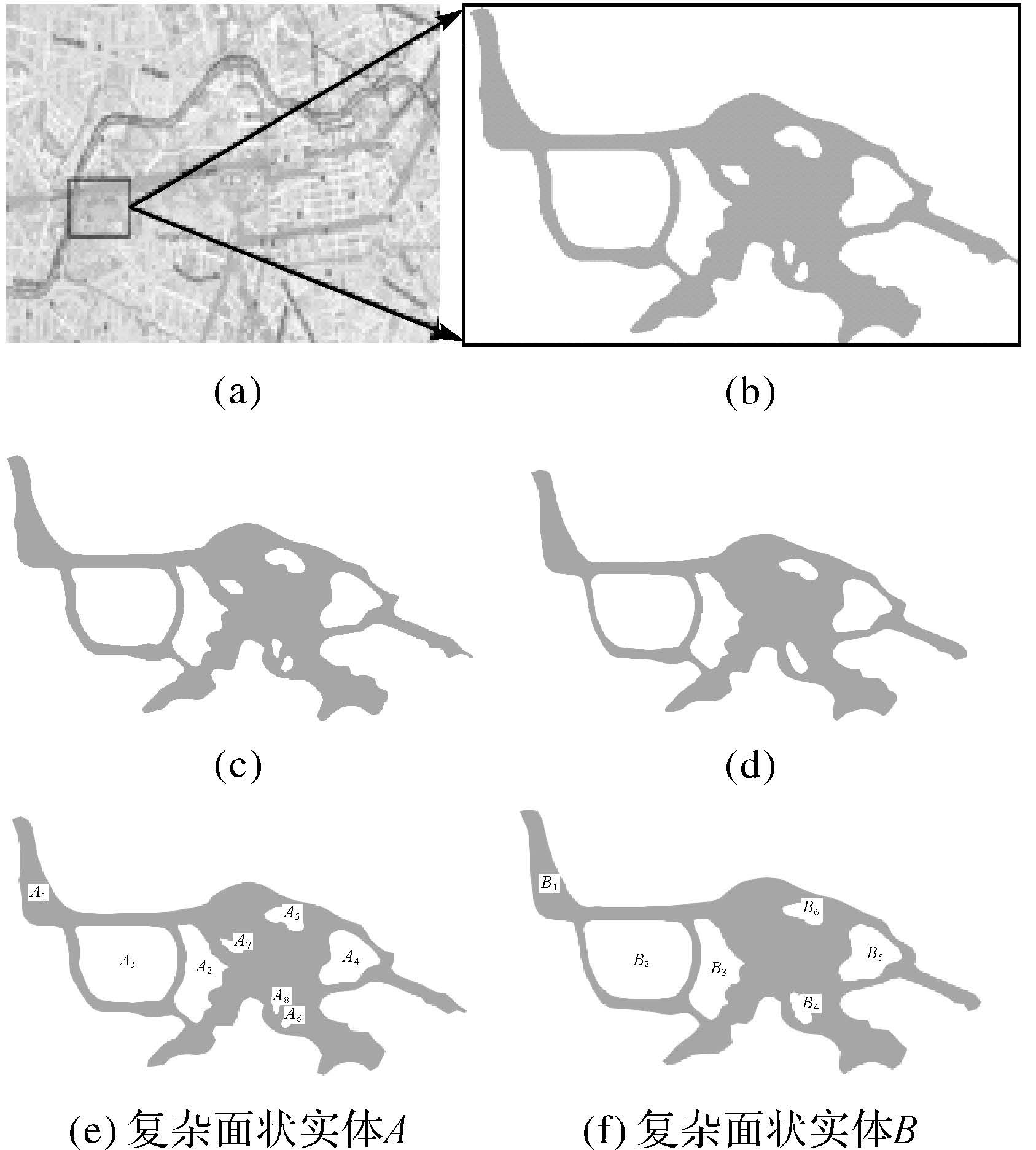
本文采用德国柏林新湖的矢量化数据进行试验。利用GIS软件提取新湖及其岛屿的几何轮廓作为数据源,如图 6(c)所示。将原数据进行处理,得到与原数据总体相似而局部有较大区别的数据图 6(d)。为使实体间的相似性度量满足起始点的独立性以及轮廓线点的个数的不一致性,对图 6(c)、图 6(d)轮廓线上的点分别进行等间隔重采样,得到图 6(e)、图 6(f),利用图 6(e)、图 6(f)进行复杂面实体的相似性度量试验。
|
| 图 6 相似性度量实例 Fig. 6 Similarity measurement examples |
对图 6中的两个复杂面实体A、B进行综合相似性度量。根据复杂面实体匹配三原则之一的先外后内原则,先对A、B的最外圈面实体A1、B1进行相似性度量,设定阈值为0.75,即当A1和B1的相似度小于0.75时,则两个复杂面实体不匹配,不需要对内圈进行相似性度量,提高匹配效率;若A1和B1的相似度大于或等于0.75,则需要对内圈进行进一步的相似性度量来确定两个复杂面实体是否匹配。在匹配过程中,由于傅里叶级数越高,则越不稳定,容易受噪声干扰[20],取傅里叶描述子阶数为20,弦长级数为8,即弯曲度级数为4,后文会对弯曲度级数的取值进行讨论。
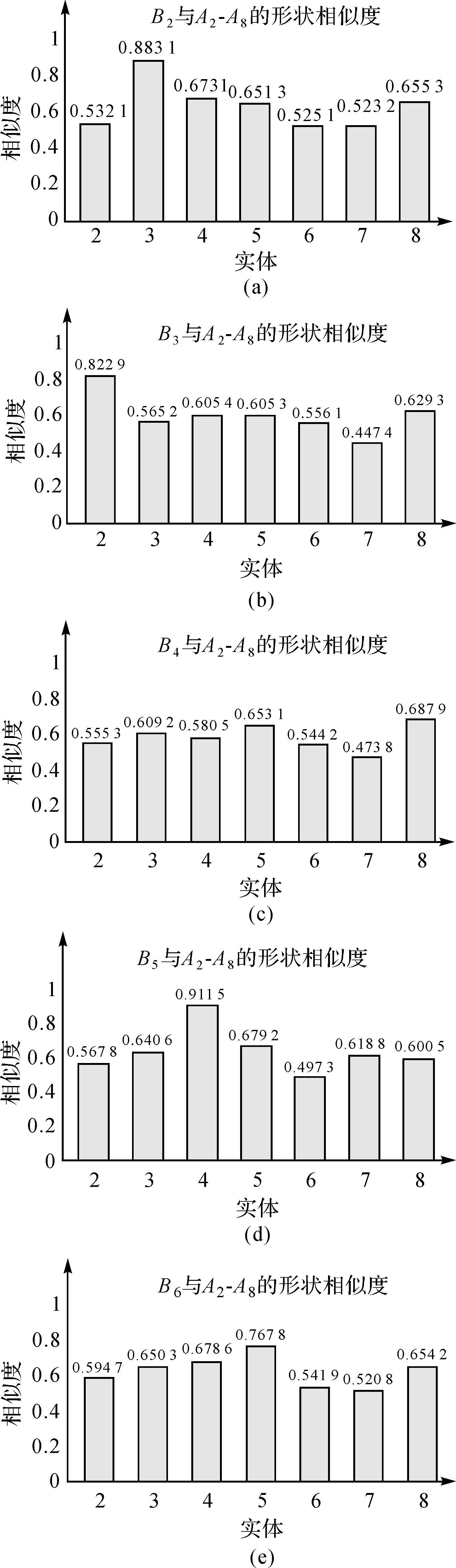
由表 1可看出,A1和B1的形状相似度为0.8087,大于阈值0.75,故A1和B1是匹配的,因此,需要对复杂面实体A、B进行进一步的相似性度量。对于内圈的匹配,方式与外圈类似。由于无法根据位置推测哪两个面实体更可能相互匹配,所以需对A、B中的内圈进行两两相似性度量,形状相似度最高且超过阈值的则相互匹配。结果见图 7。由图 7可以得出,B2与A3相匹配,B3与A2相匹配,B5与A4相匹配,B6与A5相匹配,而B4、A6、A7、A8都没有可以匹配的面实体。
| 0级 | 1级 | 2级 | 3级 | 4级 | 形状相似度S | 是否匹配 | |
| A1-B1 | 0.5736 | 0.9716 | 0.9853 | 0.9953 | 0.9901 | 0.8087 | 是 |
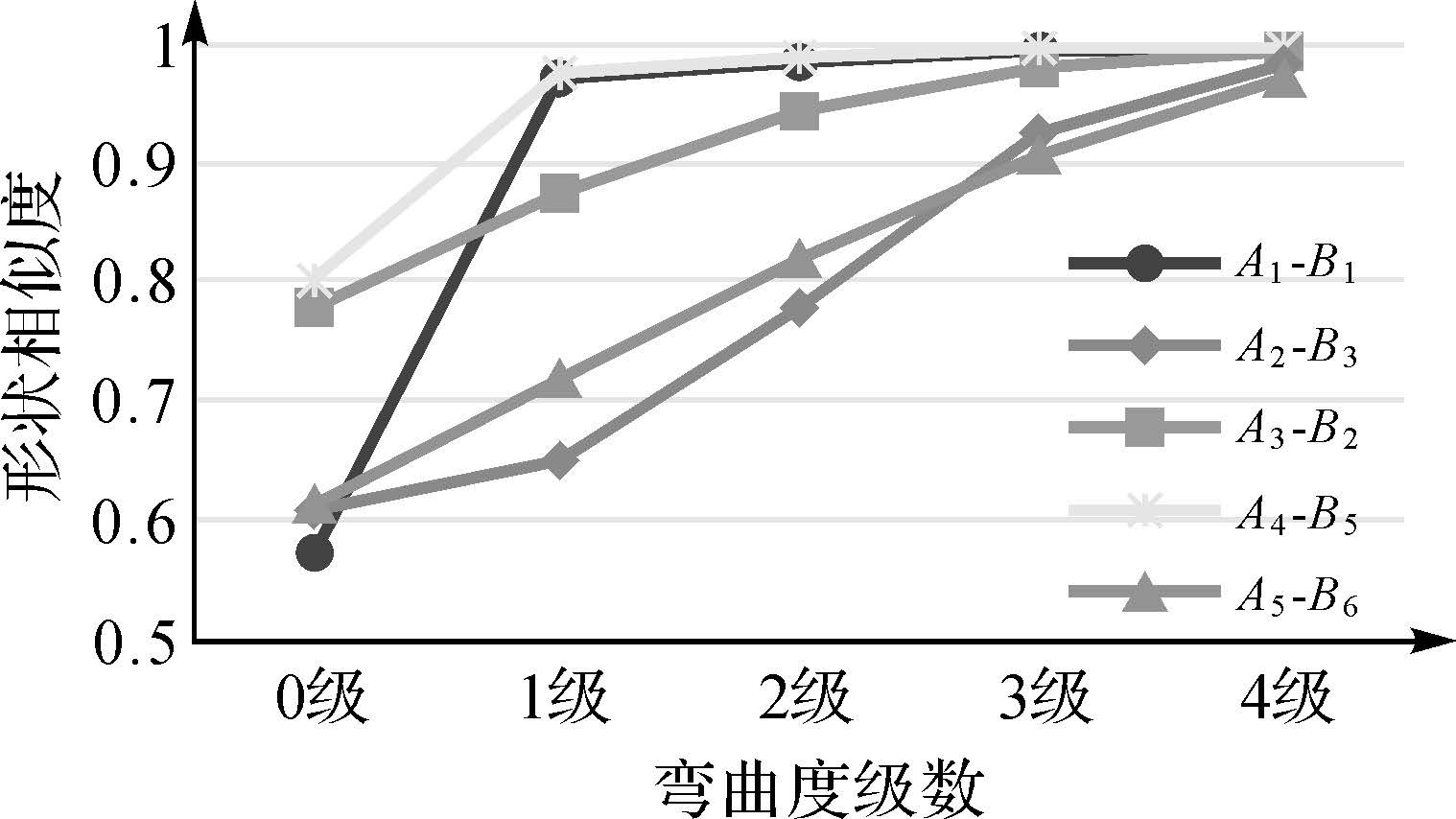
由于图 7所利用的是实体间的总的形状相似度,并不能体现出多级弯曲度对实体轮廓局部和整体良好的描述能力,为进一步验证多级弯曲度级数越低越能刻画轮廓的局部特征,越高越适于描述轮廓的整体特征的性质,对上述相互匹配的实体对A1-B1、A2-B3、A3-B2、A4-B5、A5-A6分别利用0~4级弯曲度进行形状相似性度量,结果如图 8。从图 8中可以看出,当弯曲度级数为0时,实体对的形状相似程度最小,说明相匹配的实体对之间的局部差异较大,而随着级数的增大,实体对的形状相似程度也逐渐增加,当为四级弯曲度时,实体对的形状相似程度达到最大,均接近于1,表明实体对的整体形状非常相似。验证结果与2.3节描述一致。
|
| 图 7 复杂面实体A和B内圈形状相似性度量结果 Fig. 7 Shape similarity measurement results of holes of A and B |
|
| 图 8 t为4时0~4级弯曲度分别对应的形状相似度 Fig. 8 Shape similarities of 0~4 levels of bending level 4 |
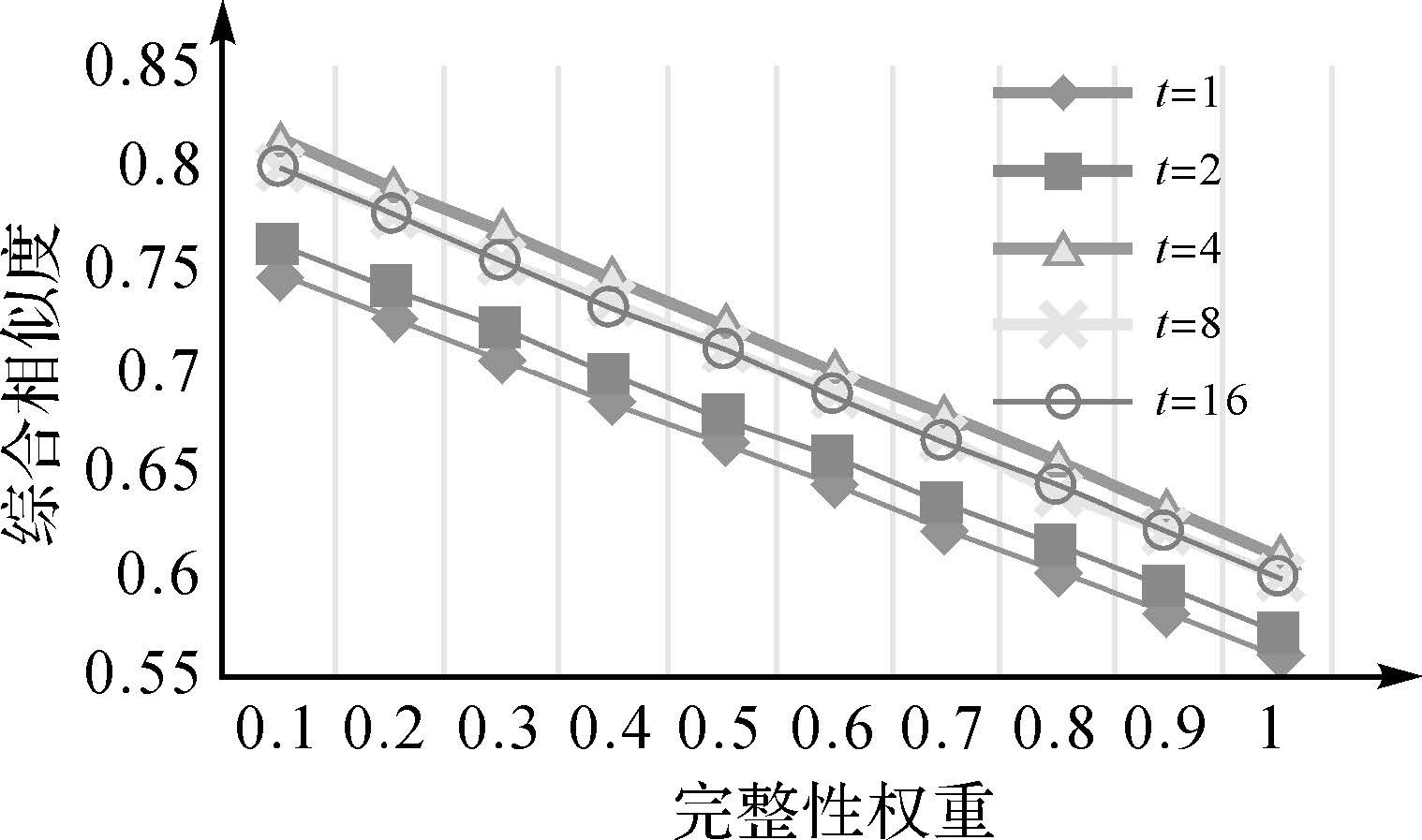
在上述形状相似性度量过程中是以弯曲度级数t=4为例进行的详细说明,由于并未确定最佳t的取值,所以在随后对t=1、2、8、16分别进行了试验,得到了5组形状相似度。考虑到复杂面实体A、B所包含的单个实体并非一一对应,存在一些单个实体没有匹配项的情况,故引入完整度对复杂面实体的相似性度量进行更加详细的描述。由于完整度的权重对复杂面实体的综合相似性度量产生较大的影响,采用不同权重计算复杂面实体的综合相似度得到结果如图 9所示。当完整度的权重越大时,即对复杂面实体的完整性越重视,综合相似度越低。
|
| 图 9 不同完整度权重时复杂面实体的综合相似度 Fig. 9 General similarities of different weight |
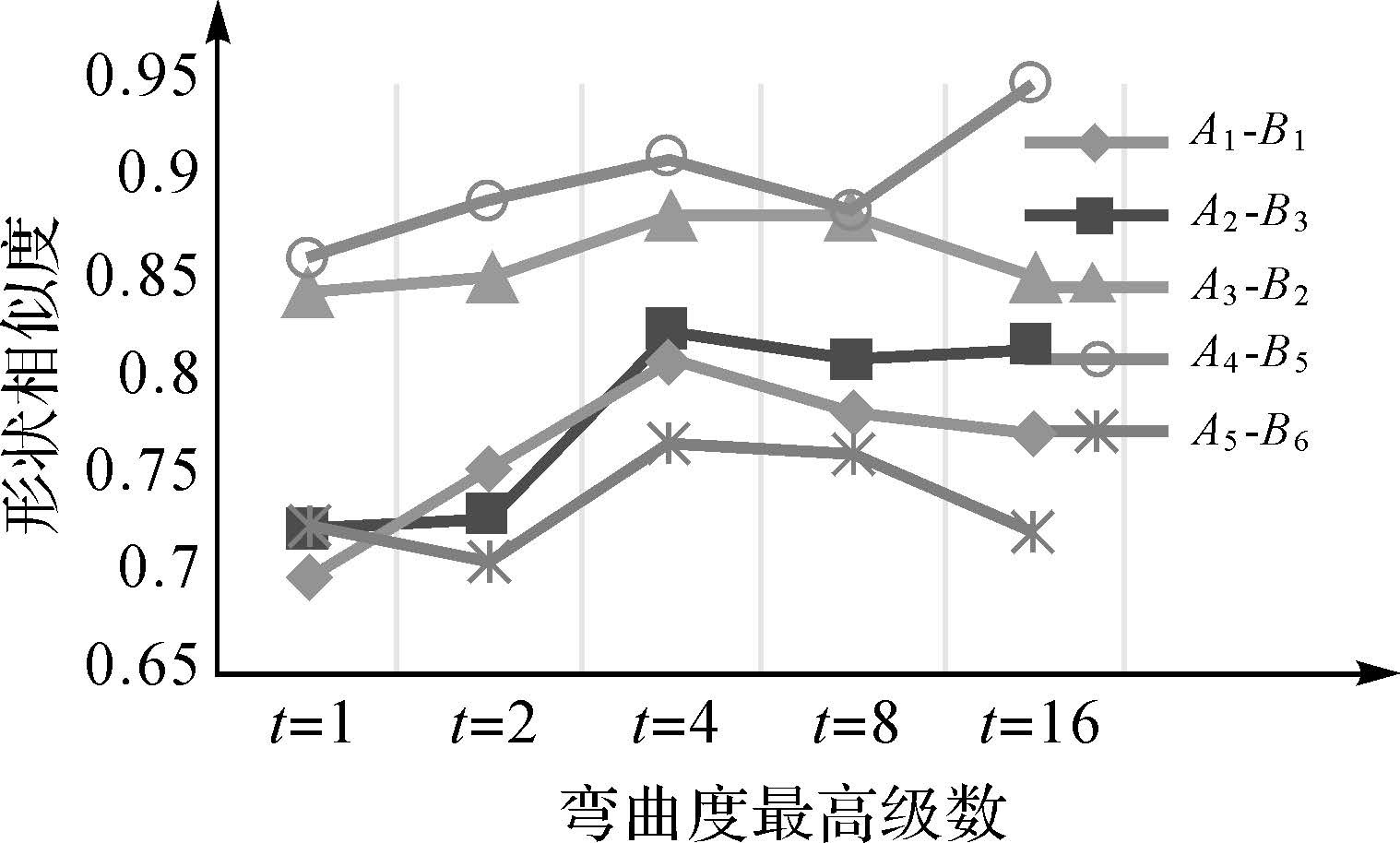
仍以上述数据作为试验数据,比较当t分别取1、2、4、8、16时实体对的形状相似程度,得到如图 10所示的结果。从图 10中可以看出,当t=1、2时,实体对的相似程度较低,且A2-B3与A5-B6当t=1时的相似程度比t=2时大,而A1-B1、A3-B2、A4-B5比t=2时相似程度小,没有特殊规律,而当t=4时,相似程度达到最大。当t继续增长至8、16时,除了A4-B5在t=16时相似程度达到顶峰,其余的都较t=4时有所减小。在面实体的匹配中,既要保证匹配的正确性,也要使t尽量小以提高匹配的速率,故选择弯曲度级数t=4最为合适。
|
| 图 10 取不同弯曲度级数时实体对的形状相似度 Fig. 10 Shape similarities of different bending levels of completeness |
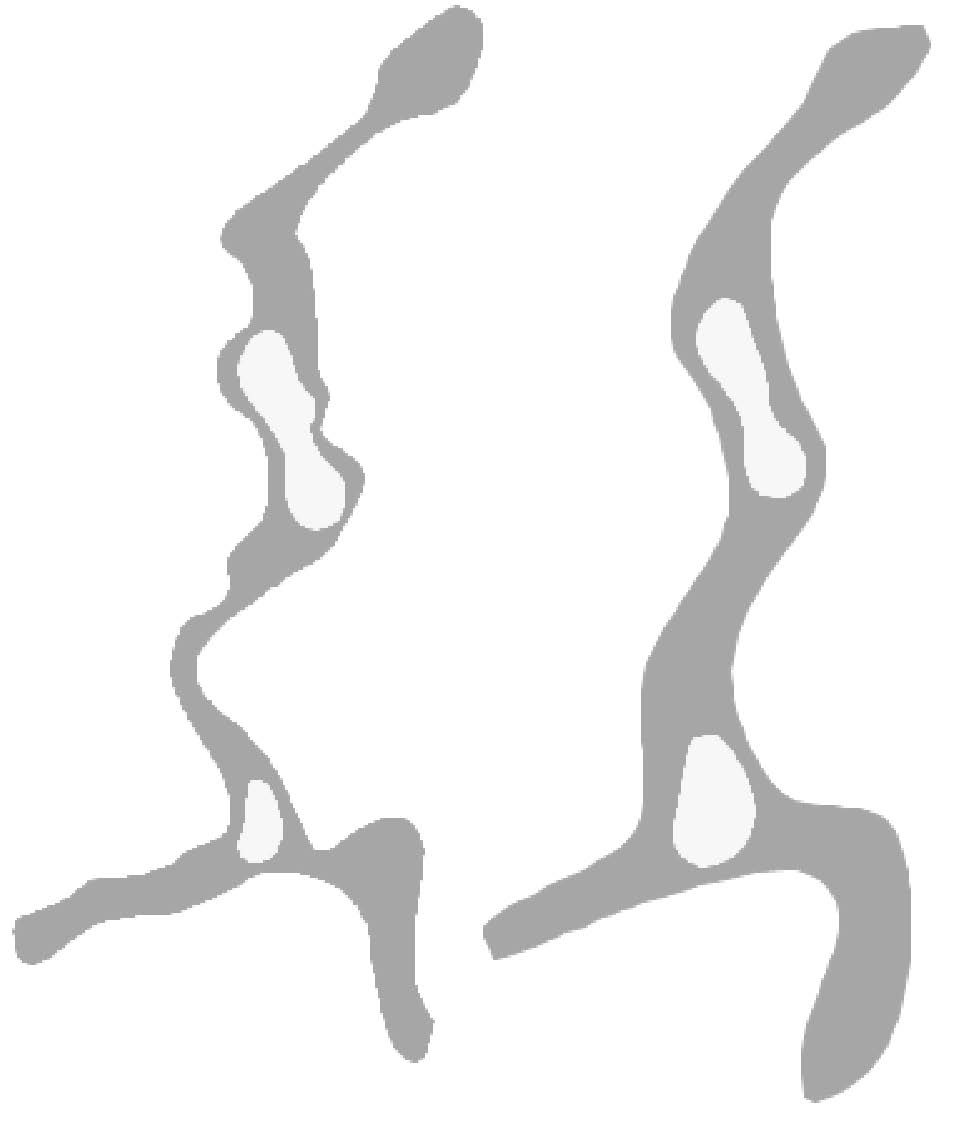
|
| 图 11 1∶5万和1∶25万水系数据 Fig. 11 The 1∶50000 and 1∶250000 data |
采用重庆市某地区1∶50000和1∶250000的水系数据进行多尺度形状相似性度量。重采样后的数据如图 12。由4.2节可知,当t=4时既能满足试验的正确性又能满足试验对效率的要求,故试验过程中弯曲度级数t确定为4。

|
| 图 12 重采样后的水系数据 Fig. 12 The data after resampling |
首先对外圈面实体S1和S2进行形状相似性度量,结果为0.7691>0.75,继续进行内圈相似性度量,度量结果见表 2。
| Q1 | W1 | |
| Q2 | 0.9101 | 0.6763 |
| W2 | 0.6719 | 0.7779 |
由表 2可以看出,Q1与Q2相互匹配,W1与W2相互匹配,所以两复杂面实体的完整度均为1。从而两个实体的相似度即为平均形状相似度。若单个面实体的权重相同,则
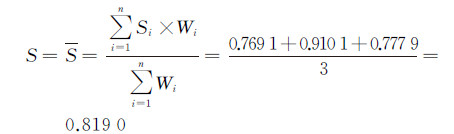
复杂面实体的匹配是空间数据库的更新和融合的核心问题,复杂面实体的几何相似性度量是决定匹配的关键。本文结合多级、弯曲度、中心距离要素,构建多级弯曲度半径复函数对空间面实体的几何形状进行描述,其中,通过级数t的变化,可以从整体到局部逐级描述形状,达到了对形状描述的唯一性。对多级弯曲度半径复函数进行快速傅里叶变换,取前20项归一化后的系数作为傅里叶描述子,不仅解决了起始点和轮廓点数不一致的问题,同时也满足了平移、缩放、旋转等不变性。本文将“多级弦长”和“轮廓弯曲度”两个概念相结合,通过“多级弯曲度”来描述面实体的几何性状。对复杂面实体进行综合相似性度量时引入了完整度的概念,以区分复杂面实体完全匹配和不完全匹配的情况。经试验验证,本文所构建的形状相似性综合度量模型能够很好地实现同名复杂面实体间的匹配,相较于其他研究中单个实体间的匹配更具实用价值。
由于利用多级弯曲度复函数对面实体的轮廓进行描述,使得归一化后的系数作为傅里叶描述子时忽略了面实体的空间位置关系,为多尺度面实体的相似性度量提供可能,但同时也可能将位于不同地区但形状较为相似的面实体进行匹配,增大了误匹配的可能性。在后续的研究中将着重于研究复杂面实体中单个实体的相对位置对匹配的影响,提高匹配的正确性和唯一性。
| [1] | 翟仁健. 基于全局一致性评价的多尺度矢量空间数据匹配方法研究[D]. 郑州:信息工程大学, 2011. ZHAI Renjian. Research on Automated Matching Methods for Multi-scale Vector Spatial Data Based on Global Consistency Evaluation[D]. Zhengzhou: Information Engineering University, 2011. |
| [2] | 付仲良, 逯跃锋. 一种基于拱高半径复变函数的面实体匹配算法[J]. 计算机应用研究, 2012, 29(9): 3303-3306. FU Zhongliang, LU Yuefeng. Polygon Entity Matching Algorithm Based on Arc-height Radius Complex Function[J]. Application Research of Computers, 2012, 29(9): 3303-3306. |
| [3] | 安晓亚. 空间数据几何相似性度量理论方法与应用研究[J]. 测绘学报, 2013, 42(1): 157. AN Xiaoya. Research on Theory, Methods and Applications of Geometry Similarity Measurement for Spatial Data[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(1): 157. |
| [4] | 付仲良, 逯跃锋. 利用弯曲度半径复函数构建综合面实体相似度模型[J]. 测绘学报, 2013, 42(1): 145-151. FU Zhongliang, LU Yuefeng. Establishment of the Comprehensive Model for Similarity of Polygon Entity by Using the Bending Radius Complex Function[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(1): 145-151. |
| [5] | 安晓亚, 孙群, 肖强, 等. 一种形状多级描述方法及在多尺度空间数据几何相似性度量中的应用[J]. 测绘学报, 2011, 40(4): 495-501, 508. AN Xiaoya, SUN Qun, XIAO Qiang, et al. A Shape Multilevel Description Method and Application in Measuring Geometry Similarity of Multi-scale Spatial Data[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(4): 495-501, 508. |
| [6] | 郝燕玲, 唐文静, 赵玉新, 等. 基于空间相似性的面实体匹配算法研究[J]. 测绘学报, 2008, 37(4): 501-506. HAO Yanling, TANG Wenjing, ZHAO Yuxin, et al. Areal Feature Matching Algorithm Based on Spatial Similarity[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(4): 501-506. |
| [7] | 郑宇志, 张青年. 基于拓扑及空间相似性的面实体匹配方法研究[J]. 测绘科学技术学报, 2013, 30(5): 510-514. ZHENG Yuzhi, ZHANG Qingnian. An Approach to Identical Areal Entity Matching Based on Topology and Spatial Similarity[J]. Journal of Geomatics Science and Technology, 2013, 30(5): 510-514. |
| [8] | MASUYAMA A. Methods for Detecting Apparent Differences between Spatial Tessellations at Different Time Points[J]. International Journal of Geographical Information Science, 2006, 20(6): 633-648. |
| [9] | LYNCH M P, SAALFELD A J. Conflation: Automated Map Compilation-A Video Game Approach[C]//Proceedings of Auto-Carto. Falls Church, VA: [s.n.], 1985, 7. |
| [10] | 徐枫, 邓敏, 赵彬彬, 等. 空间目标匹配方法的应用分析[J]. 地球信息科学学报, 2009, 11(5): 657-663. XU Feng, DENG Min, ZHAO Binbin, et al. A Detailed Investigation on the Methods of Object Matching[J]. Journal of Geo-Information Science, 2009, 11(5): 657-663. |
| [11] | ZHANG Dengsheng, LU Guojun. A Comparative Study on Shape Retrieval Using Fourier Descriptors with Different Shape Signatures[C]//Proceedings of International Conference on Intelligent Multimedia and Distance Education (ICIMADE01). Fargo, ND: [s.n.], 2001. |
| [12] | 艾廷华, 帅赟, 李精忠. 基于形状相似性识别的空间查询[J]. 测绘学报, 2009, 38(4): 356-362. AI Tinghua, SHUAI Yun, LI Jingzhong. A Spatial Query Based on Shape Similarity Cognition[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(4): 356-362. |
| [13] | LI Z, YAN H, AI T, et al. Automated Building Generalization Based on Urban Morphology and Gestalt Theory[J]. International Journal of Geographical Information Science, 2004, 18(5): 513-534. |
| [14] | 付仲良, 邵世维. 复杂面状矢量要素快速形状匹配方法[J]. 测绘通报, 2011(3): 26-28. FU Zhongliang, SHAO Shiwei. Methods of Complex Polygon Element Fast Shape Matching[J]. Bulletin of Surveying and Mapping, 2011(3): 26-28. |
| [15] | 付仲良, 邵世维, 童春芽. 基于正切空间的多尺度面实体形状匹配[J]. 计算机工程, 2010, 36(17): 216-217, 220. FU Zhongliang, SHAO Shixiong, TONG Chunya. Multi-scale Area Entity Shape Matching Based on Tangent Space[J]. Computer Engineering, 2010, 36(17): 216-217, 220. |
| [16] | 魏怡, 何一伟, 倪海峰, 等. 形状描述法在图像检索中的应用综述[J]. 系统工程与电子技术, 2009, 31(7): 1755-1762. WEI Yi, HE Yiwei, NI Haifeng, et al. Review on Shape Representation Techniques and Their Applications in Image Retrieval[J]. Systems Engineering and Electronics, 2009, 31(7): 1755-1762. |
| [17] | 夏敏, 刘宏申. 基于小波描述子和神经网络的形状识别[J]. 计算机技术与发展, 2007, 17(3): 106-108. XIA Min, LIU Hongshen. The Shape Recognition System Based on Wavelet Descriptors and Neural Networks[J]. Computer Technology and Development, 2007, 17(3): 106-108. |
| [18] | 童小华, 邓愫愫, 史文中. 基于概率的地图实体匹配方法[J]. 测绘学报, 2007, 36(2): 210-217. TONG Xiaohua, DENG Susu, SHI Wenzhong. A Probabilistic Theory-based Matching Method[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(2): 210-217. |
| [19] | 张桥平, 李德仁, 龚健雅. 城市地图数据库面实体匹配技术[J]. 遥感学报, 2004, 8(2): 107-112. ZHANG Qiaoping, LI Deren, GONG Jianya. Areal Feature Matching among Urban Geographic Databases[J]. Journal of Remote Sensing, 2004, 8(2): 107-112. |
| [20] | ZHANG Dengsheng, LU Guojun. Study and Evaluation of Different Fourier Methods for Image Retrieval[J]. Image and Vision Computing, 2005, 23(1): 33-49. |