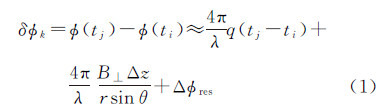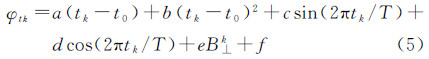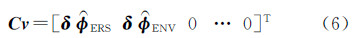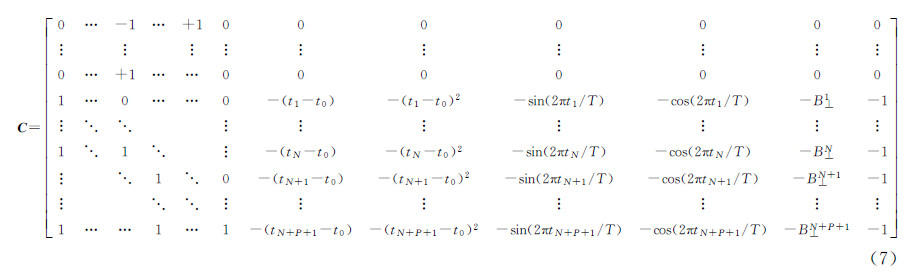2. 高速铁路运营安全空间信息技术国家地方联合工程实验室， 四川 成都 610031
2. State-Province Joint Engineering Laboratory of Spatial Information Technology for High-speed Railway Safety, Chengdu 610031, China
由自然地质活动或人为因素(如地震、火山、矿产开采、地下水抽取、地下施工等)引起的地表形变，对人类社会的生存和生产具有很大的威胁[1, 2, 3, 4]。利用大地测量手段对区域地表形变进行长期监测，对减灾、防灾以及灾害治理等均具有重要的指导意义。20世纪90年代以来，合成孔径雷达干涉技术(InSAR)以其高空间分辨率、广覆盖范围和高精度测量的优势[5]，在区域地表形变监测中展现出了极好的应用潜力。特别是近年来，随着SAR卫星数目的增多和SAR数据的不断获取，基于大量数据中某些高质量的点目标进行建模分析的时序差分雷达干涉技术[6]，受到越来越多研究者的重视。其中，通过自由组合并选取空间基线和时间基线都较小的干涉对进行地表形变信息提取的短基线集(small baseline subset,SBAS)技术[7]，能够有效地减缓由于时空基线过长而导致的失相干影响和提高形变监测的时间分辨率，已经在众多研究领域得到成功应用[8, 9, 10]。
然而，受到当前SAR卫星寿命、重访周期及卫星姿态等因素的制约[11]，仅利用单一平台SAR影像为某一特定地区提供长时间跨度(5~10年)的数据源进行时序形变计算和分析仍然较为困难。此外，针对时空演化规律较为复杂的地表形变，时域差分干涉建模技术对SAR影像成像的时间分布、频度以及数量都有严格的要求。但SBAS方法对干涉配对的时/空基线的限定，容易导致部分时段的观测量间断和不连续，即减少了时序建模过程中可用的影像数目和时域观测量，从而引起最终形变参数估计的偏差。
针对上述SBAS方法存在的缺陷，学者们提出了多种思路来改进SBAS技术。为了提高SBAS观测量的连续性，文献[12]提出引入不满足基线限制的干涉对参与分析，将单一平台下不同的小基线集进行连接，然后采用加权解算方法获取形变序列，但是所引入干涉对质量的好坏将直接影响最终解算结果的可靠性。文献[13]将三阶形变模型引入到时序InSAR处理过程，并应用于非线性形变明显的城市地表沉降监测，但未考虑长时序过程中的周期性形变信号，并且高阶模型易导致长时序形变探测不稳定。文献[14]提出使用约束条件连接单一平台所获取的具有时序间断性的影像，并提取墨西哥地区的时序形变，但该约束模型较为简单，难以描述线性、非线性与周期性等地表形变演变过程。文献[15]采用附加Tikhonov正则化约束方程解决SBAS解算过程中观测方程秩亏问题，并求得数学意义上的最优约束模型参数，显然这种附加约束模型并没有考虑地表形变特征。文献[16]联合多平台数据，采用波长补偿归一化方式提取了1993—2007年间Napoli海湾的地表形变时间序列，但并未考虑到不同小基线集间的连接问题，因而可能导致形变序列解算结果存在偏差。
为了有效扩展区域地表形变监测的时间跨度和增强形变时间序列的连续性，本文提出基于多平台SAR影像且融入非线性形变模型约束条件的短基线集(model-constrained small baseline subset,MC-SBAS)长时序形变提取模型与方法。其核心思想是：首先将不同平台SAR影像按照SBAS方法分别生成干涉对子集，并将不同平台的干涉解缠结果经投影转换至同一地理空间，然后构建附加约束条件(含非线性和周期性形变分量)的多平台时序观测方程，以解算形变速率和恢复形变时间序列。
1 MC-SBAS理论模型与方法假设有N+1幅时间跨度为t0到tN的SAR影像，按照“基线集内时空基线距小，基线集间时空基线距大”的原则生成M幅差分干涉图，并逐一进行相位解缠[7]。对于干涉图中某一像素(设对应于地面点P)，设t0时刻未发生形变，即d(t0)≡0，(t0)≈4πd(t0)/λ=0，则差分相位(解缠后)向量δϕT=[δϕ1…δϕM]与SAR影像相位(解缠后)向量δT[ϕ(t1)…ϕ(tN)]之间的关系可由式(1)来体现
式中，∀i,j=0,…,N，j＞i；k=1,2,…，M；qti和qtj分别表示ti到tj时刻相对于t0时刻沿雷达视线方向(line of sight,LOS)的累积形变量，q为低频线性形变系数；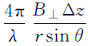
表示因外部数字高程模型(DEM)引起的地形误差，B⊥、r和θ分别为干涉对的垂直基线、卫星到目标的斜距和雷达入射角；Δϕres表示ti到tj时刻大气变化、失相关及系统噪声等引起的残差。
为了获得准确的形变量，需将地形、大气及失相关等误差剔除，以校正差分相位观测向量。利用全部差分干涉对依据方程(1)可建立方程(2)
式中，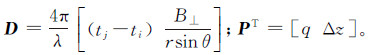
。式(2)中有M个观测方程和2个未知数，M>2时可获得向量P的最小二乘解，实现低频形变信号、地形误差和残差信号的分离。此外由于残差信号中存在高频形变信号，并且大气及高频形变在时空域特征各异[17]，可采用时域高通滤波和空间域低通滤波分离大气和高频形变信号。利用分离出的四部分信号校正差分相位观测向量，扣除地形误差及大气误差，保留低频形变和高频形变信号，即可获得仅包含形变信号的校正后差分相位观测向量。
为求解对应每个时刻的形变时间序列，依据地表形变的差分相位观测向量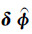 
(校正后)与未知形变相位向量ϕ(相对于t0时刻)之间的函数关系，即
理论上，若A为满秩矩阵，根据式(3)即可得到最小二乘意义上的形变相位序列估计值，即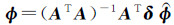 
。然而SAR影像一般会被分割在不同的独立数据集里，从而可能导致A矩阵秩亏，方程组有无穷解。针对该问题，文献[7]采用奇异值分解(singular value decomposition,SVD)的方法来求解，即对矩阵A进行奇异值分解运算获得A矩阵的穆尔-彭罗斯广义逆矩阵[18]，然后再求得方程组(3)的最小范数最小二乘解，获取覆盖t0到tN时间段的形变信息。通常，SBAS方法求解的是两个时间点间的平均速率，通过积分获得累积形变量，但这依然存在矩阵秩亏问题，只能求得平均速率的最小范数最小二乘解[7]。
从上文分析可以看出，SBAS一般是针对单一平台的SAR数据进行建模，并利用SVD方法进行求解。根据矩阵理论，虽然SVD方法能够求得秩亏方程的最小范数最小二乘解，但其在一定程度上对待求的速率做了线性假设[14, 19]。显然，这种假设并不完全符合长时间地表形变(高阶及周期性等)的复杂规律[20]。因此，当利用SBAS获取长时间跨度(超过5年)地表形变信号时，两个相邻时刻跨度过大时，形变传递可能会出现偏差。
为了解决SBAS解算方程组时秩亏的问题，并实现长时间跨度区域地表形变的有效监测，本文在文献[7]和文献[14]的理论基础上，提出利用多平台SAR影像，采用非线性形变模型(通过试验验证二阶多项式和周期性组合模型解算结果更优)对秩亏方程组(3)约束求解的时序干涉方法(MC-SBAS)。
现假设ERS和ASAR影像分别有N+1和P+1景，在(N+P+1)个时刻建立非线性形变约束方程，其中非线性形变模型为(N+P+1)个由一阶线性、二阶非线性、周期性形变和高程误差项4部分组成的约束方程，则得到
式中，a、 b、 c、d、e、 f是最优模型系数；T是周期形变的变化周期；k=1,2,…,N+P+1。那么，将两个平台的约束方程组与SBAS的系统方程组联立，可得到(M+N+P+1)阶的联合观测方程组[14] 式中，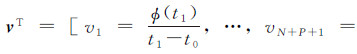
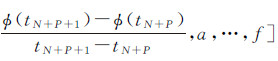，是包含(N+P+1)个形变速率和6个最优模型参数的未知数列向量； 
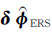和 
为多平台校正后的差分相位观测量；C是(M+N+P+1)×(N+P+7)阶系数矩阵，即
显然，当M>6时，式(6)所示方程组存在唯一解。因此，加入非线性形变模型后的观测方程可达到满秩的条件，进而可以根据最小二乘方法进行解算，得到可靠的地表形变序列估计值。
将覆盖同一研究区的多平台SAR数据分别按照上述MC-SBAS方法进行处理，是一种扩展地表形变监测时间跨度的思路。由于不同卫星平台的观测几何不同，一般应将LOS向形变统一投影至地理坐标方向(东西、垂直、南北)后才能联合解算。本文所选研究区的地表形变一般被认为其表现形式主要是垂直向的位移[21]，因此在忽略了水平形变后，可将各个数据集观测结果统一转换至垂直向。在经过投影转换至同一地理坐标框架后，按照式(6)联立方程组则可解算得到长时间跨度的地表形变序列，具体的MC-SBAS数据处理流程如图 1所示。
|
| 图 1 MC-SBAS数据处理流程 Fig. 1 The flowchart of MC-SBAS data processing |
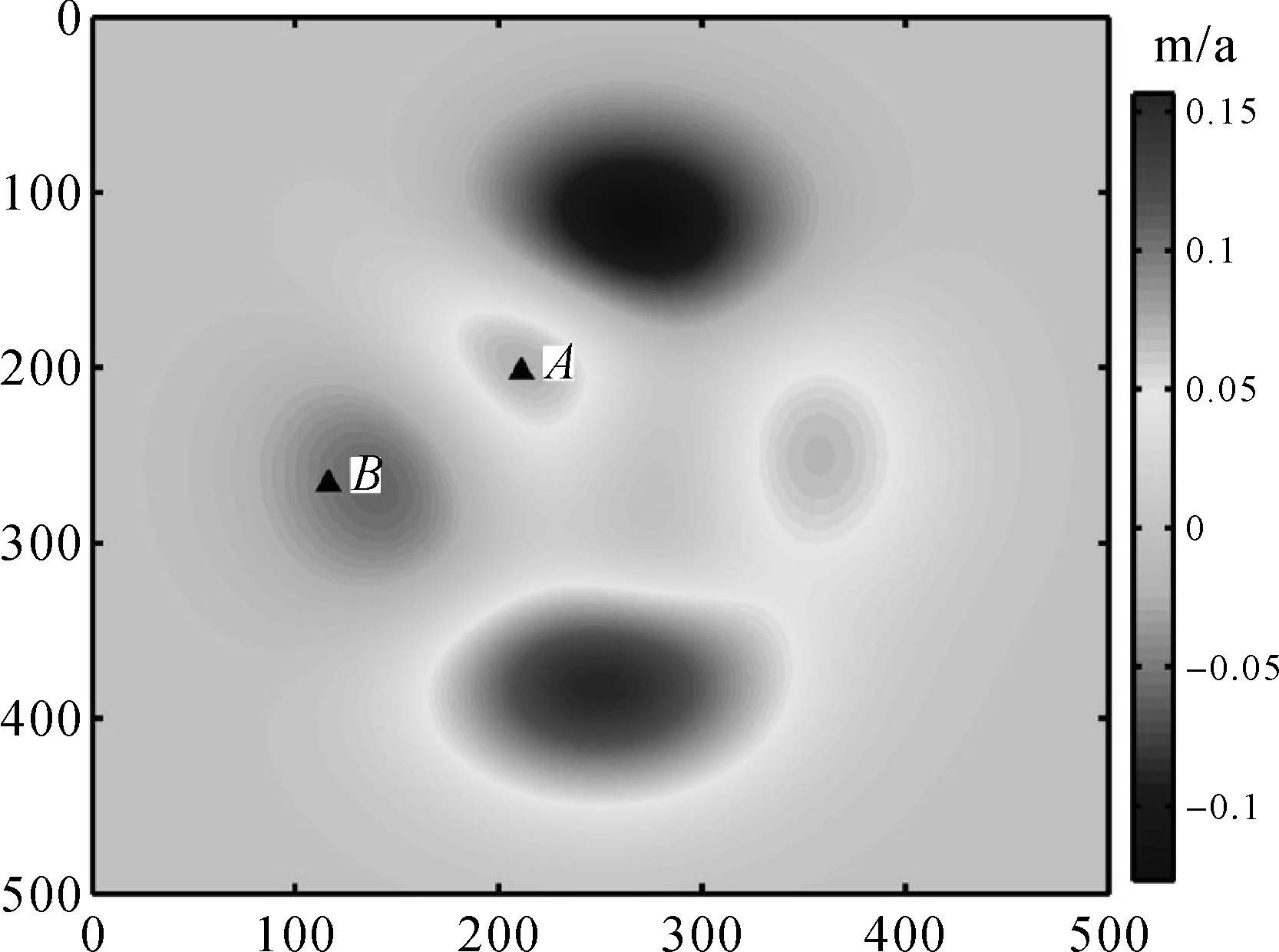
为验证MC-SBAS方法的有效性，笔者利用Peaks函数[22]模拟产生地表形变速率场，如图 2所示。为保证模拟形变的真实性，采用一组时间跨度为5869d的影像信息做为模拟数据参数，具体参数见表 1。以形变速率场和干涉对基线信息模拟线性形变、二次形变信号、20mm的地形误差信号和周期为365d的正余弦形变信号，最终共生成263个干涉对数据集。
|
| 图 2 模拟形变速率场 Fig. 2 Simulation of deformation velocity field |
| 影像系统 | 影像数量 | 干涉对数量 | 垂直基线限制/m | 时间基线限制/d | 波长/cm | 入射角/(°) |
| ERS | 57 | 180 | 420 | 2415 | 5.656 | 23.2 |
| EnviSat | 28 | 83 | 400 | 1470 | 5.624 | 22.8 |
利用两种方法分别对模拟数据集进行时序形变的恢复，并将解算得到的形变时间序列与模拟产生的形变序列进行对比。图 3分别展示了模拟形变场中两种不同的形变特征。由图 3可以看出，解算出的地表形变在整个时序上以线性形变为主，并伴随着周期性形变。在第3000d之前两种方法(SBAS和MC-SBAS)计算的时序形变结果基本一致，且与模拟形变值差异很小，而在第3000d之后两种方法计算结果就出现较大差异，且SBAS方法与模拟时序形变差异较大。究其原因，在3000d的时间间隔前，数据集影像分布均匀，并没有出现较大的时序影像的缺失，所以SBAS方法能够有效恢复时序形变结果。在此之后，时序影像有664d的影像缺失，SBAS方法采用SVD分解方法恢复时序形变，对于时间间隔过长的区域无法准确计算其形变，导致后续时序形变的整体偏移。然而，MC-SBAS则能够在非线性模型的约束下恢复时间间隔过长区域的时序形变，使得计算结果与模拟形变结果较为一致，由此证明了MC-SBAS方法的有效性。
|
| 图 3 特征点A和B的垂直向形变时间序列 Fig. 3 The vertical deformation time series at the selected points (A and B) |
|
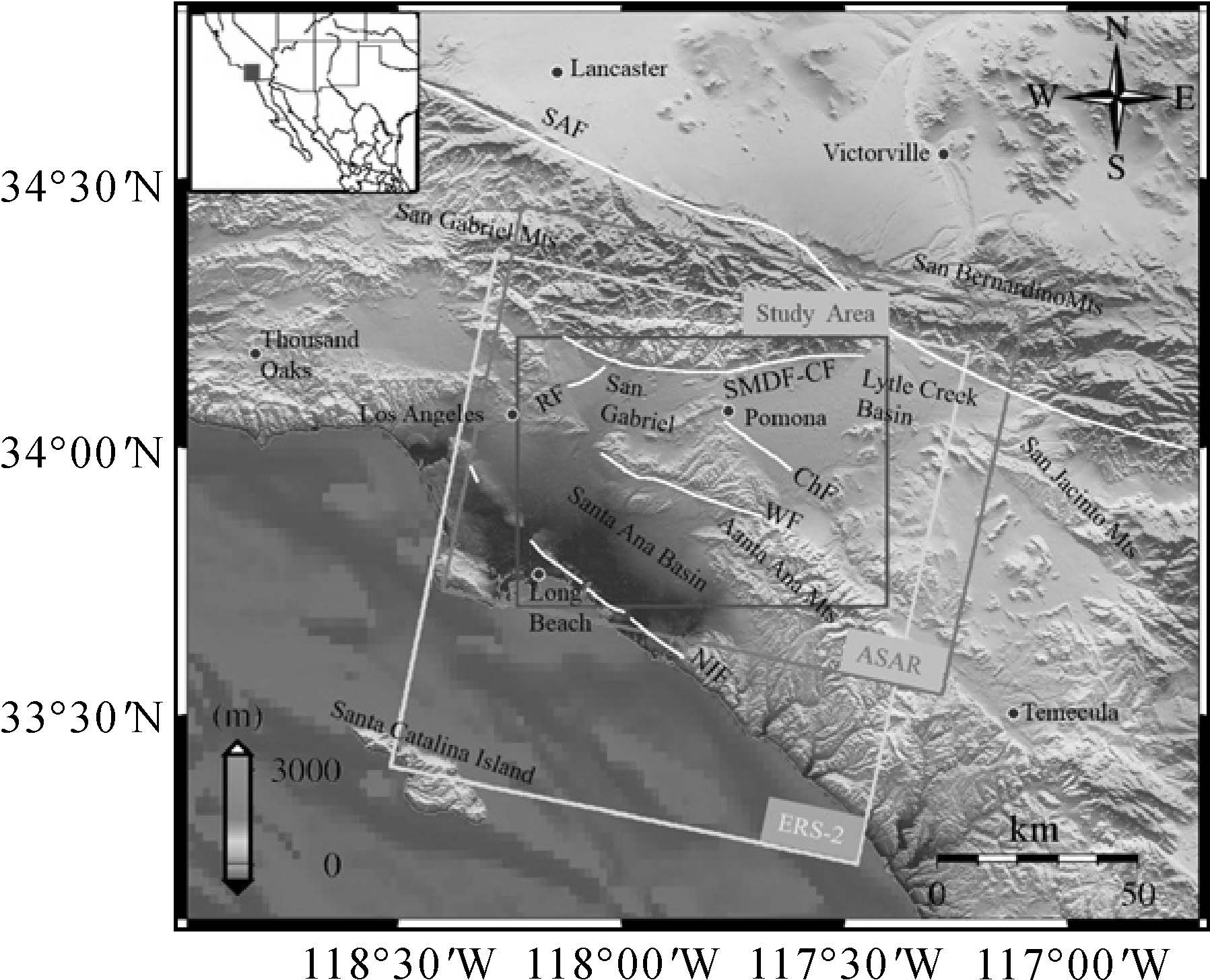
| 图 4 研究区域 Fig. 4 The study area of South California |
通过计算A点和B点的均方根误差，MC-SBAS方法的均方根误差比SBAS方法的提高近一倍，这也证明了MC-SBAS方法的可靠性。但是，由于模型约束算法需要将多平台数据投影至垂直向，因此该方法主要适用于水平位移不够明显的长时序地表形变监测，对于水平和垂直位移均为明显的情况适用性不强。
3 研究区域地表形变提取与分析 3.1 研究区域与数据介绍美国南加州地区受到太平洋板块和北美洲板块的南北向挤压，地质构造复杂，是世界上构造运动最为活跃的区域之一[23]。该地区最大的断层是位于洛杉矶西北方向50km处的San Andreas断层，此外还有一些小型断层分布在洛杉矶、San Gabriel流域及长滩附近(见图 4白色实线)。1994年发生的Mw 6.8级Northridge地震[24]和1999年发生的Mw 7.1级Hector Mine地震[25]给洛杉矶带来重大损失。该地区拥有加州2/3的人口，气候干燥，年降雨量少，地下水资源采伐活动频繁；另外该地区拥有丰富的石油、天然气及石绵等矿产资源，资源钻探工业发达；再加上大城市发展所伴随的大型地下工程建设活动剧烈，该地区在这些因素的综合影响下地表形变情况显著[12, 21]。
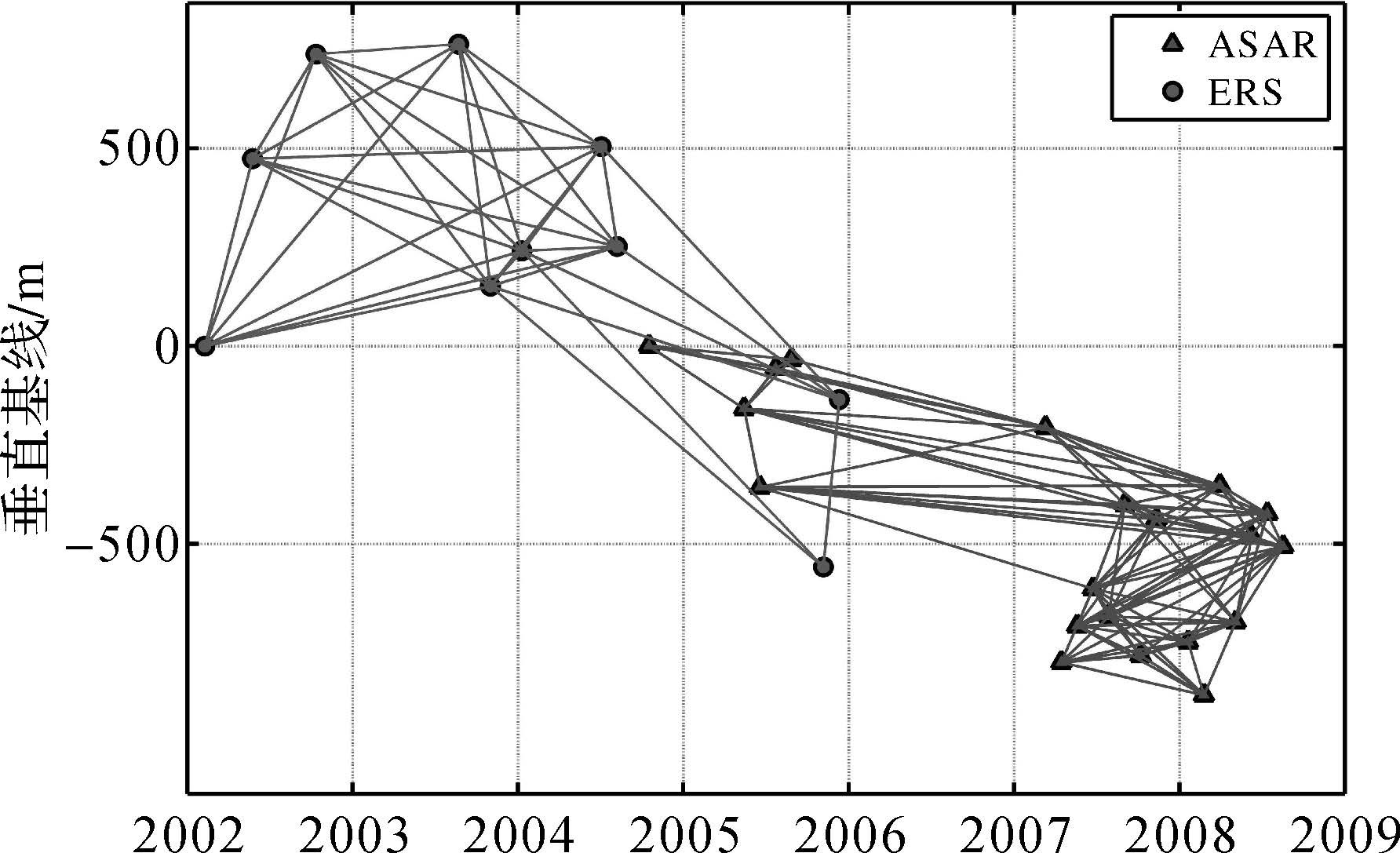
试验选取覆盖该地区2002—2005年获取的10幅ERS和2004—2008年获取的20幅ASAR降轨影像(图 4)，两类影像重叠区域面积约为79km×48km。根据SBAS原理，分别限制ERS和ASAR的时间基线为1000d和1600d，垂直基线为800和300m，共形成131个干涉对(ERS 35对，ASAR 96对)。图 5显示了干涉基线组合情况，显然，这里选取的ERS和ASAR数据虽然增加了时间跨度及影像数量，受到卫星重访周期等因素的影响，数据时域不连续现象依然存在。即由于2006—2007年缺乏SAR影像采样，这一间断可能导致SBAS方法难以准确估计地表时序形变。
|
| 图 5 干涉对基线组合情况 Fig. 5 The spatiotemporal baselines of the interferograms |
图 6(a)显示了按照MC-SBAS方法解算的2002-02—2008-06期间，南加州地区地表垂直向平均位移速率结果，而图 6(b)显示了按照SBAS方法解算的垂直向平均位移速率。图中黑色三角符号为GPS观测站的位置，白色虚线圆表示形变显著的区域，白色方块为后续进行形变时序分析而选择的特征点分布位置。
|
| 图 6 MC-SBAS和SBAS垂直向形变速率图 Fig. 6 The vertical deformation rate maps derived by MC-SBAS and SBAS |
从图 6可以看出，MC-SBAS和SBAS的解算的垂直向地表形变在空间分布上具有高度的一致性。两者均显示该研究区域共存在有5处显著形变区(白色虚线圆内)，它们分别位于San Gabriel流域、Pasadena盆地、Santa Ana盆地、Pomona-Ontario盆地和Santa Fe Springs地区。分析表明，采用MC-SBAS方法计算的垂直向最大抬升速率为12.5mm/a，位于Santa Fe Springs地区；最大沉降速率为-19.1mm/a，位于Pomona-Ontario盆地；而SBAS结果的最大抬升速率与最大沉降速率分别为6.7和-12.9mm/a。已有研究结果揭示[12, 21]，该地区2003—2009年沉降速率为-10~-40mm/a，由于参考基准点和时域分布不同，无法从沉降量上进行直接对比，就沉降量变化范围而言，MC-SBAS的测量结果具有更好的一致性。
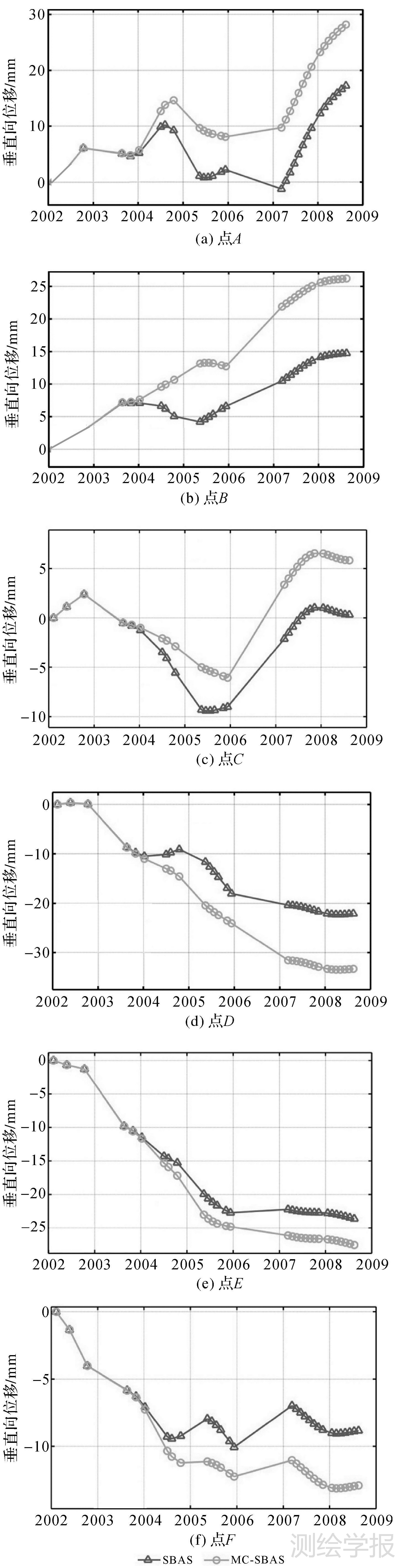
为了展示该地区在2002—2008年间地表形变的演变过程，笔者选取并绘制了6个特征点A—F(图 6中白色方框所示)的时序形变图(图 7)。观察点A—F的形变时间序列，可以看出在长达6.5年的时间内，采用MC-SBAS方法计算的形变结果在整体上要比SBAS的计算结果更加平滑连续，特别是在成像时间不连续的时间内段更为显著。例如，在2004—2005年间，利用SBAS解算的点B和点D的累积垂直向位移量增量近似为0，这与该地区的活跃形变事实不符；在2006—2007年间，利用SBAS解算的点A、D和F的形变序列存在不合理的跳跃，结合影像获取的时间分布情况，可以断定这是由于SAR影像数据在某些时域上采样稀疏，基于SVD解算的SBAS方法产生了较大的解算误差。
|
| 图 7 特征点A—F的垂直向形变时间序列 Fig. 7 The vertical deformation time series at the selected points (A—F) |
从图 6和图 7中可以看出，受自然地质条件和人为因素复合作用的影响，研究区域的地表形变演化机理复杂。在监测时间段内，该地区在垂直向同时存在下沉、抬升和周期性形变等多种形变演变特征。其中，地表沉陷区域主要位于Pasadena盆地和Pomona-Ontario盆地周边，具体代表为特征点D和点E所处区域。在这两个区域可以观察到一个有趣的现象，即显著的地表形变仅存在于逆冲断层RF(Raymond fault)和ChF (Chino fault)的一侧，而断层另一侧的地表则几乎没有形变特征。RF和ChF断层分别是左旋和右旋的大倾角(约为75°)走滑型断层，走滑速率分别约为0.2和1mm/a，并伴随有极小的逆冲分量(http://www.data.scec.org/significant/)。因此，RF和ChF断层在观测时间段内滑动引起的地表形变可以忽略，文献[26]认为很可能是由于断层阻碍了地下水的自由流动，导致这两条断层两侧展现出截然不同的形变特征，表明了区域地质构造在地表形变分析中同样是非常值得考虑的因素；点B所在区域的地表形变序列整体展现出抬升趋势，这是由于其位于Santa Fe Springs油田附近，由于当地采取了对采油区进行气体回灌措施导致[21]。特别是在2006年后，为控制石油开采引起过大的沉降，当地加大了气体回灌导致该区域地表在2006—2007年中旬出现约1cm的相对抬升；点F位于Santa Ana盆地，已有研究[12, 21, 27]表明，该盆地是主要含水层，受地下水过度采伐和政府的回灌措施的影响，该区域的地表有显著地均匀沉降，并伴随有周期性沉降特征。
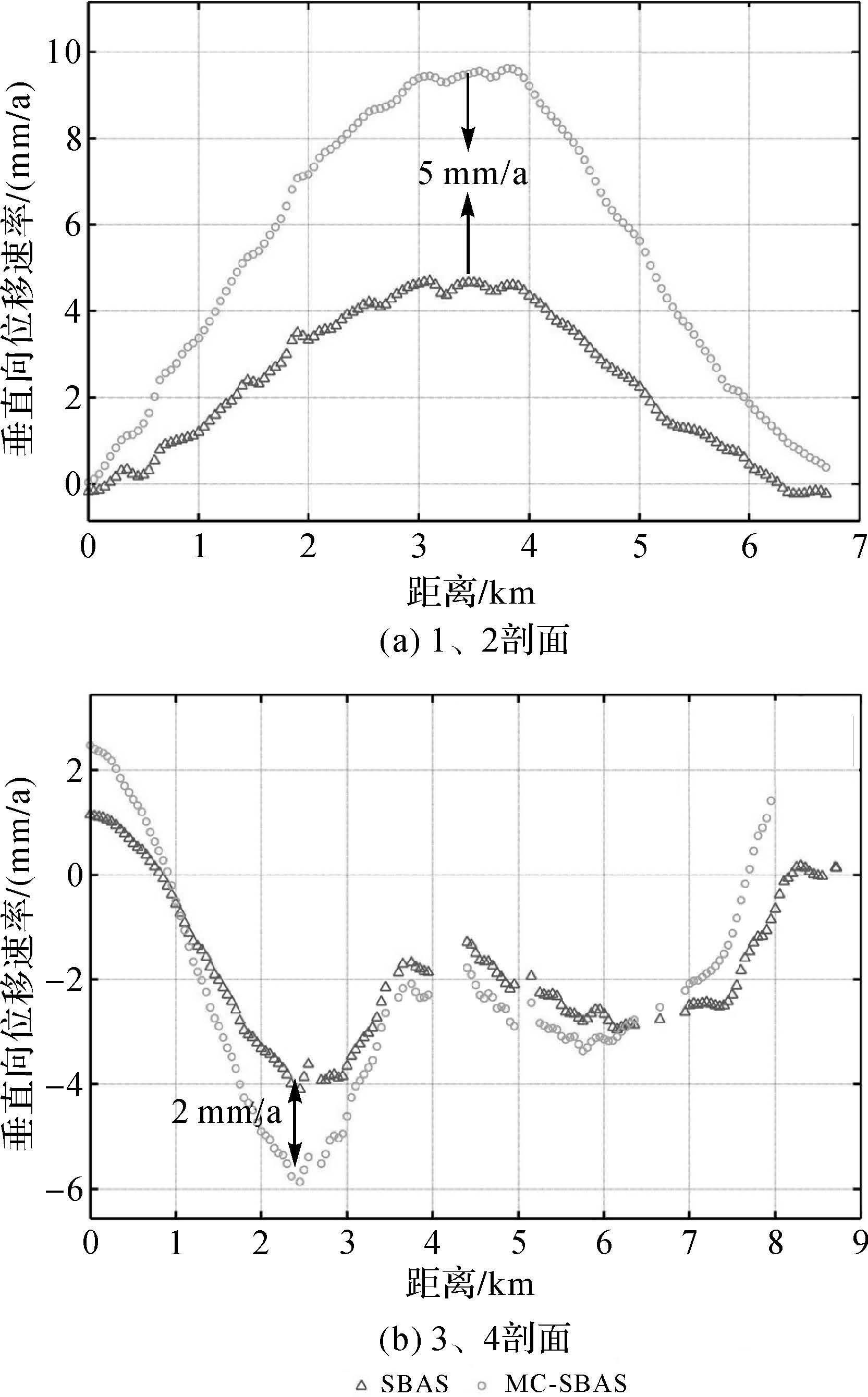
为了进一步说明并详细比较MC-SBAS和SBAS的解算结果的差异，笔者截取了两条分别位于Santa Fe Springs地区和Pomona-Ontario盆地的两个剖面线(图 6中的剖面线1、2和3、4)，并比较它们的垂直向位移速率(图 8)。显然，两种方法获取的垂直向位移速率最大有5mm/a的差异，并且SABS解算结果在幅度上要比MC-SBAS小，这很可能是由于SBAS忽略了高阶和周期性形变分量，从而出现时序形变幅度较小的现象。
|
| 图 8 垂直向位移速率剖面图 Fig. 8 The vertical deformation rates along the profiles 1、2 and 3、4 |
为了验证MC-SBAS解算结果的可靠性，本文选取了6个(点位分布如图 6中黑三角所示)位于研究区的连续GPS观测站作为检校点，并与MC-SBAS和SBAS测量结果对比。为了方便对比，需要先将GPS记录的三维形变投影到LOS向(即雷达视线方向)，再依据雷达入射角将该LOS向形变量转换至垂直向[28]。图 9显示了6个GPS站测量结果与SAR数据测量的累计形变的对比图。
|
| 图 9 GPS与SBAS和MC-SBAS垂直向位移结果对比 Fig. 9 Comparisons of the vertical deformation results among GPS, SBAS and MC-SBAS |
在长达6.5年的时间跨度上，BKMS、LBC2和LBCH 3个GPS监测站发生明显的抬升形变，最大累积抬升量分别为42mm、70mm和69mm，其余3个GPS站(CVHS、CCCO和ELSC)的垂直向形变则相对平稳，形变幅度约在50mm以内。其中，BKMS站点靠近Santa Fe Springs地区的油田开采区，2006年时该地区由于气体回灌，有10mm左右的抬升；CCCO和ELSC站点靠近Santa Ana盆地，该盆地随着地下水的开采及回灌具有周期性形变特征；LBC2位于靠近海边的长滩市附近，其时序累积形变量最大，CVHS站点位于San Gabriel流域附近，其时序累积形变量最小。
针对形变各异的GPS观测数据，从形变趋势上看，虽然MC-SBAS和SBAS方法所测量的形变时间序列整体较为一致，但MC-SBAS获取的形变结果明显与GPS测量结果更为接近。比较MC-SBAS和SBAS与GPS观测值之间的均方根误差，发现MC-SABS方法对应的RMSE值均小于SBAS方法，说明MC-SBAS明显改善了地表形变的估计精度。这种改善效应在累计形变量比较大的观测站处显得更为明显，如在LBC2站点处两者的RMSE最大差异值达到了8.83mm。将这6个GPS观测站处RMSE求均值发现，MC-SBAS测量结果与GPS测量结果的平均RMSE为8.7mm，而SBAS测量结果与GPS测量结果之间的均值为11.7mm。上述分析表明，MC-SBAS相对于SBAS能够明显提升地表形变时间序列的估计精度。
4 结 论石油开采、地下水抽取、矿产开发及大型地下工程等人为因素导致的地表形变具有一定的规律性，基于长时序差分雷达干涉监测地表形变能够为灾害预警和控制提供重要的观测数据。为克服单一卫星平台SAR数据源固有的时域观测量间断和不连续等局限性，并拓展地表形变监测的时间跨度，本文提出了联合多平台SAR影像且在时域建模过程中融入非线性和周期性形变约束模型的MC-SBAS模型与方法，以获取准确可靠的长时序地表形变演化结果。
为验证MC-SBAS方法的有效性，本研究选取ERS和EnviSat卫星平台在美国南加州地区获取的两类SAR影像序列(2002—2008年)，得到该研究区域(范围约为79km×48km)长达6.5年的垂直向平均形变速率和时序形变演化结果。分析结果显示，该地区在地质活动和人为因素的综合作用下具有显著性不均匀复合地表形变，其中最大的地表沉降位于Pomona盆地(沉降速率约为-19.1mm/a，累积沉降量约为-113mm)；而位于Santa Fe Springs的地表抬升同样显著(抬升速率约为12.5mm/a，累积抬升量约为70mm)。与6个GPS观测站记录的形变数据对比分析发现，MC-SBAS和SBAS与GPS测量结果的均方根误差分别为8.7mm和11.7mm。对于垂直向形变主导的地区，本文提出的方法能够有效提高长时序地表形变监测的连续性和可靠性，但对于水平位移同样较为明显的地区，利用多平台MC-SBAS方法恢复地表多维长时序形变仍将是今后值得研究的内容。此外，相比SBAS，多平台MC-SBAS方法势必增加了数据处理的时间，因此，如何优化MC-SBAS处理大范围SAR数据的计算效率也将是未来需要关注的问题。
致谢：特别感谢美国地质调查局提供的数字高程模型(SRTM DEM)，欧洲空间局提供的ERS-2和EnviSat ASAR影像数据及DORIS轨道数据，美国南加州综合GPS网(SCIGN)提供的GPS数据。
| [1] | AMELUNG F, JóNSSON S, ZEBKER H, et al. Wides Pread Uplift and “Trapdoor” Faulting on Galápagos Volcanoes Observed with Radar Interferometry[J]. Nature, 2000, 407(6807): 993-996. |
| [2] | 伍吉仓, 许厚泽, 丁晓利, 等. 台湾集集大地震断层非均匀滑动分布的反演[J]. 测绘学报, 2009, 31(z1): 34-38. WU Jicang, XU Houze, DING Xiaoli, et al. Inversion of Variable Fault Slip of Taiwan Chi-Chi Earthquake[J]. Acta Geodaetica et Cartographica Sinica, 2009, 31(z1): 34-38. |
| [3] | COLESANTI C, FERRETTI A, NOVALI F, et al. SAR Monitoring of Progressive and Seasonal Ground Deformation Using the Permanent Scatterers Technique[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(7): 1685-1701. |
| [4] | 刘国祥, 张瑞, 李陶, 等. 基于多卫星平台永久散射体雷达干涉提取三维地表形变速度场[J]. 地球物理学报, 2012, 55(8): 2598-2610. LIU Guoxiang, ZHANG Rui, LI Tao, et al.Extracting 3D Ground Deformation Velocity Field by Multi-platform Persistent Scatterer SAR Interferometry[J]. Chinese Journal of Geophysics, 2012, 55(8): 2598-2610. |
| [5] | LIU G X, DING X L, LI Z L, et al. Pre-and Co-seismic Ground Deformations of the 1999 Chi-Chi, Taiwan Earthquake, Measured with SAR Interferometry[J]. Computers & Geosciences, 2004, 30(4): 333-343. |
| [6] | FERRETTI A, PRATI C, ROCCA F. Nonlinear Subsidence Rate Estimation Using Permanent Scatterers in Differential SAR Interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(5): 2202-2212. |
| [7] | BERARDINO P, FORNARO G,LANARI R,et al.A New Algorithm for Surface Deformation Monitoring Based on Small Baseline Differential SAR Interferograms[J]. IEEE Transactions on Geoscience and Rmote Sensing, 2002, 40(11): 2375-2383. |
| [8] | 尹宏杰, 朱建军, 李志伟, 等. 基于SBAS的矿区形变监测研究[J]. 测绘学报, 2011, 40(1): 52-58. YIN Hongjie, ZHU Jianjun, LI Zhiwei, et al. Ground Subsidence Monitoring in Mining Area Using DInSAR SBAS Algorithm[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(1): 52-58. |
| [9] | MORA O, MALLORQUI J J, BROQUETAS A. Linear and Nonlinear Terrain Deformation Maps from a Reduced Set of Interferometric SAR Images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(10): 2243-2253. |
| [10] | 程海琴, 陈强, 刘国祥, 等. 短基线InSAR探测龙门山主断裂带两侧震后雨期的滑坡空间分布特征[J]. 测绘学报, 2014, 43(9): 931-938. CHENG Haiqin, CHEN Qiang, LIU Guoxiang, et al. Post-earthquake Landslides Distribution along Longmenshan Major Fault during Rainy Season with Short-baseline InSAR[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(9): 931-938. |
| [11] | 黄世奇, 刘代志. 星载SAR成像与SAR图像中一些不确定性因素分析[J]. 测绘学报, 2007, 36(2): 152-157. HUANG Shiqi, LIU Daizhi. Analysis of Some Uncertain Factors in Spaceborne SAR Imaging and SAR Image[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(2): 152-157. |
| [12] | HU Jun, LI Zhiwei, DING Xiaoli, et al. Spatial Temporal Surface Deformation of Los Angeles over 2003-2007 from Weighted Least Squares DInSAR[J]. International Journal of Applied Earth Observation and Geoinformation, 2013, 21: 484-492. |
| [13] | 张永红, 吴宏安, 孙广通. 时间序列InSAR技术中的形变模型研究[J]. 测绘学报, 2012, 41(6): 864-869. ZHANG Yonghong, WU Hong'an, SUN Guangtong. Deformation Model of Time Series Interferometric SAR Techniques[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(6): 864-869. |
| [14] | LÓPEZ-QUIROZ P, DOIN M P, TUPIN F, et al. Time Series Analysis of Mexico City Subsidence Constrained by Radar Interferometry[J]. Journal of Applied Geophysics, 2009, 69(1): 1-15. |
| [15] | SAMSONOV S, D'OREYE N. Multidimensional Time-series Analysis of Ground Deformation from Multiple InSAR Data Sets Applied to Virunga Volcanic Province[J]. Geophysical Journal International, 2012, 191(3): 1095-1108. |
| [16] | BONANO M, MANUNTA M, MARSELLA M, et al. Long-term ERS/EnviSat Deformation Time-series Generation at Full Spatial Resolution via the Extended SBAS Technique[J]. International Journal of Remote Sensing, 2012, 33(15): 4756-4783. |
| [17] | 李珊珊, 李志伟, 胡俊, 等. SBAS-InSAR 技术监测青藏高原季节性冻土形变[J]. 地球物理学报, 2013, 56(5): 1476-1486. LI Shanshan, LI Zhiwei, HU Jun, et al. Investigation of the Seasonal Oscillation of the Permafrost over Qinghai-Tibet Plateau with SBAS-InSAR Algorithm[J]. Chinese Journal of Geophysics, 2013, 56(5): 1476-1486. |
| [18] | 鲁铁定, 陶本藻, 周世健. 矩阵的 SVD 分解性质及其在秩亏网平差中的应用[J]. 大地测量与地球动力学, 2007, 27(5): 63-67. LU Tieding, TAO Benzao, ZHOU Shijian. Characteristics of Matrix SVD and Its Applications to Rank Deficiency Free Network Adjustment[J]. Journal of Geodesy and Geodynamics, 2007, 27(5): 63-67. |
| [19] | 李永生, 张景发, 李振洪, 等. 利用短基线集干涉测量时序分析方法监测北京市地面沉降[J]. 武汉大学学报(信息科学版), 2013, 38(11): 1374-1377. LI Yongsheng, ZHANG Jingfa, LI Zhenhong, et al. Land Subsidence in Beijing City from InSAR Time Series Analysis with Small Baseline Subset[J]. Geomatics and Information Science of Wuhan University, 2013, 38(11): 1374-1377. |
| [20] | ZHANG Rui,LIU Guoxiang,LI Tao,et al. An Integrated Model for Extracting Surface Deformation Components by PSI Time Series[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(2): 544-548. |
| [21] | 许文斌, 李志伟, 丁晓利, 等. 利用InSAR短基线技术估计洛杉矶地区的地表时序形变和含水层参数[J]. 地球物理学报, 2012, 55(2): 452-461. XU Wenbin, LI Zhiwei, DING Xiaoli, et al. Application of Small Baseline Subsets D-InSAR Technology to Estimate the Time Series Land Deformation and Aquifer Storage Coefficients of Los Angeles Area[J]. Chinese Journal of Geophysics, 2012, 55(2): 452-461. |
| [22] | 徐飞, 施晓红. Matlab应用图像处理[M]. 西安: 西安电子科技大学出版社, 2002. XU Fei, SHI Xiaohong. Matlab Image Processing[M]. Xi'an: Xi'an Electronic and Technology University Press, 2002. |
| [23] | ARGUS D F, HEFLIN M B, PELTZER G, et al. Interseismic Strain Accumulation and Anthropogenic Motion in Metropolitan Los Angeles[J]. Journal of Geophysical Research, 2005, 110(B4): B04401. |
| [24] | MURAKAMI M, TOBITA M, FUJIWARA S, et al. Coseismic Crustal Deformations of 1994 Northridge, California, Earthquake Detected by Interferometric JERS-1 Synthetic Aperture Radar[J]. Journal of Geophysical Research, 1996, 101(B4): 8605-8614. |
| [25] | SANDWELL D T, SICHOIX L, AGNEW D, et al. Near Real-time Radar Interferometry of the Mw 7.1 Hector Mine Earthquake[J]. Geophysical Research Letters, 2000, 27(19): 3101-3104. |
| [26] | KING N E, ARGUS D, LANGBEIN J, et al. Space Geodetic Observation of Expansion of the San Gabriel Valley, California, Aquifer System, during Heavy Rainfall in Winter 2004-2005[J]. Journal of Geophysical Research, 2007, 112(B3): B03409. |
| [27] | ZHANG Lei, LU Zhong, DING Xiaoli, et al. Mapping Ground Surface Deformation Using Temporarily Coherent Point SAR Interferometry: Application to Los Angeles Basin[J]. Remote Sensing of Environment, 2012, 117: 429-439. |
| [28] | ELGHARBAWI T, TAMURA M. Measuring Deformations Using SAR Interferometry and GPS Observables with Geodetic Accuracy: Application to Tokyo, Japan[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2014, 88: 156-165. |