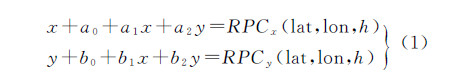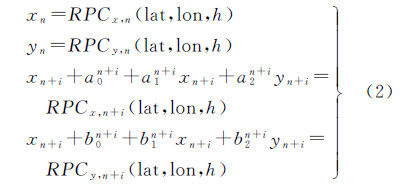2. 武汉大学测绘遥感信息工程国家重点实验室,湖北 武汉 430079;
3. 地球空间信息技术协同创新中心,湖北 武汉 430079;
4. 武汉大学资源与环境科学学院,湖北 武汉 430079;
5. 长光卫星技术有限公司,吉林 长春 130033;
6. 武汉大学遥感信息工程学院,湖北 武汉 430079
2. State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan 430079, China;
3. Collaborative Innovation Center of Geospatial Technology, Wuhan 430079, China;
4. School of Resource and Environmental Sciences, Wuhan University, Wuhan 430079, China;
5. Chang Guang Satellite Technology Co. Ltd, Changchun 130033, China;
6. School of Remote Sensing and Information Engineering, Wuhan University, Wuhan 430079, China
21世纪初,第一颗高分辨率光学卫星IKONOS发射,开启了高分辨率商业卫星发展新篇章;2013年,Skybox Imaging公司发射了首颗SkySat视频卫星,视频卫星对地观测记录了运动目标信息[1],开创了动态遥感的新纪元。
视频稳像是视频应用的前提,其主要消除视频各帧影像之间的相对变形,建立同名像元之间正确的映射关系。典视频稳像过程主要是由图像预处理[2]、运动估计和运动补偿3部分组成[3],其中运动估计就是通过块匹配法、特征点匹配法[4, 5]、灰度投影法、位平面匹配法提取帧间的同名点,利用平移模型、仿射模型、相似模型或投影变换模型[5]估计帧间的由于载体运动引起的帧间变形。运动补偿主要是利用运动估计步骤的计算的变换模型将当前帧校正使视频显示稳定的位置上,常见的运动补偿算法主要有固定帧补偿法[5]、逐帧补偿算法和运动滤波补偿法。
针对类SkySat的面阵“凝视”视频,视频每帧影像外方位元素数值的差异是引起帧间运动的主要原因,但是相邻帧影像间的同名点在不同帧影像上的像面位置不同,且每帧影像均存在几何畸变,因此经典帧间的变换模型不能精确描述相邻帧之间的同名点关系。针对该问题,本文提出基于主帧的卫星视频运动估计模型,同时顾及帧间外方位元素差异引起的变形和由帧内几何畸变引起的同名点在像面不同位置引起的变形。
1 卫星视频帧间运动估计和补偿 1.1 顾及像面畸变的卫星视频稳像技术流程针对SkySat的面阵“凝视”视频,由于每帧影像的覆盖范围基本一致,可采用固定帧补偿法进行运动补偿[5],需直接估计基于固定帧的帧间运动模型进而进行运动补偿,其主要流程如下:①主帧和辅帧同名点匹配,选取连续视频影像若干帧,选择中间帧为主帧,把辅帧和主帧采用分块模式进行SIFT[6]同名点匹配,同名点匹配过程中利用投影变换模型[5]和RANSAC 算法[7]进行匹配粗差剔除。②基于固定帧的卫星视频运动估计,利用匹配获取的同名点计算主帧与辅帧之间的运动估计参数,补偿计算辅帧的RPC模型。③基于固定帧的卫星视频运动补偿,利用步骤②求解的辅帧的RPC模型参数,将辅帧向主帧进行影像重采样,完成视频运动补偿。
1.2 基于固定帧的卫星视频运动估计 1.2.1 卫星视频单帧定向模型由于严密几何模型改正的复杂性和稳定性不高,在IKONOS-2上天后,卫星影像的几何处理基本采用RPC模型[5, 8, 9, 10, 11],由于RPC参数一般采用与地形无关方式求解[12],RPC模型参数都存在系统误差,针对单帧影像,采用像方改正模型补偿此类误差,补偿模型如下式所示[13]
式中,(lat,lon,h)为地面点经纬度高程;(x,y)为像点坐标;在窄视场条件下,a0、b0用来吸收轨道中沿轨误差、垂轨误差、径向误差以及姿态中滚动误差、俯仰误差引起的平移误差;a1、b1、a2、b2用来吸收轨道中径向误差引起的缩放误差以及姿态中偏航误差引起的旋转误差[13, 14, 15, 16, 17]。 1.2.2 基于固定帧的帧间运动估计模型针对面阵“凝视”视频,固定帧一般选择视频时间段内中间帧(主帧),其余所有帧(辅帧)都和主帧影像进行运动估计,然后辅帧都采样到主帧,该过程同时完成了相邻帧之间的运动估计,实现卫星视频稳像。由于主帧为固定帧,主帧影像不采样,因此主帧RPC模型参数系统误差不补偿,采用像面仿射模型补偿辅帧的RPC模型参数,完成帧间的运动估计。依据辅帧的仿射变换参数,重算采样后辅帧的RPC模型参数,获得稳像后每帧的RPC参数。基于固定帧的帧间运动估计模型如下
式中,n表示主帧,n+i(i≠0)表示辅帧,该运动估计模型实际上把主帧姿态轨道误差引起的平移误差、比例误差和旋转误差直接叠加到辅帧的像面仿射变换系数中,由于利用视频每帧严密几何模型求解RPC模型采用与地形无关模式[12],且在求解RPC模型时候顾及像面畸变,因此该运动估计模型在考虑姿态轨道误差引起的帧间运动外同时顾及像面畸变对帧间变换模型影响。在该运动模型估计中,部分辅帧和主帧之间的交会角比较小(如小于10°),利用公式(2)进行立体平差,该运动模型估计可能不收敛,因此针对主帧和辅帧交会角小于10°情况,采用主帧和辅帧匹配同名点,采用主帧的RPC模型投影到SRTM-DEM高程面求解地面点坐标,辅帧的配准点作为像点坐标,求解辅帧的像面仿射参数,完成主帧和辅帧运动模型估计;针对主帧和辅帧交会角大于10°情况,采用主帧和辅帧匹配同名点,进行利用公式(2)进行立体平差,求解辅帧的像面仿射参数,完成主帧和辅帧运动模型估计。
1.3 基于固定帧的卫星视频运动补偿利用帧间运动估计后的辅帧的RPC模型参数和主帧的RPC模型参数,直接可实现卫星视频辅帧和主帧的像点的点点对应,简化的主帧和辅帧正反算公式如下,可表达两个影像像面对应坐标关系

在该坐标关系中,辅帧和主帧的RPC模型参数采用严密几何模型参数求解中顾及影像的几何畸变(Δx,Δy),主帧和辅帧运动估计中考虑了主帧和辅帧外方位元素误差引起的帧间变形,因此该模型可精确描述帧间的同名点关系。
利用主帧的RPC模型对像点坐标(x,y)正算到相应的SRTM-DEM高程面,可以得到对应的物方坐标(X,Y,Z);利用基于辅帧的补偿后的RPC模型参数对物方坐标(X,Y,Z)进行模型反算可以得到辅帧上像点坐标(x1,y1),然后采用高精度重采样算法,获得(x1,y1)处在辅帧的亮度值,完成基于固定帧的卫星视频运动补偿。
2 试验和分析 2.1 试验数据由于在国内未经稳像的类SkySat面阵“凝视”视频到2015年10月吉林一号视频星发射才能获得,因此本文试验所用卫星视频采用仿真手段获得。
采用吉林一号视频星的技术指标,该卫星运行在656 km太阳同步轨道,采用4000×3000像素的CMOS成像器件,视频的帧频为25,采集最长为120 s的凝视面阵视频,该视频的地面分辨率为1.13 m。利用登封地区的1∶5000的DEM和DOM,采用唐新明等研制的卫星影像仿真系统[18]仿真获得8 s的视频,共200帧视频影像。在仿真中为轨道加上±5 m的随机误差,姿态加±5″的随机误差,畸变模型考虑k1、k2的径向畸变和p1、p2的偏心畸变[19]。
2.2 原始视频几何模型试验采用与地形无关的方式[12]求解面阵视频每帧RPC参数,获得RPC模型替代面阵影像严密几何模型的精度。取第70帧、第100帧和第130帧的拟合精度如表 1所示。由于面阵数据外方位元素是定值,畸变模型采用不超过5阶的模型,因此沿轨向和垂轨向RPC模型替代严密几何模型的精度较高[20],优于5×10-6像素,满足5%像素的RPC拟合精度要求。
| 像素 | ||||||
| 帧数 | 沿轨向 | 垂轨向 | ||||
| 最大值/ ×10 -6 | 最小值/ ×10 -7 | 中误差/ ×10 -6 | 最大值/ ×10 -6 | 最小值/ ×10 -8 | 中误差/ ×10 -6 | |
| 70 | 7.076 8 | 8.814 | 2.744 | 3.723 6 | 2.26 | 1.229 4 |
| 90 | 6.974 9 | 8.78 | 2.709 7 | 3.641 5 | 2.35 | 1.203 8 |
| 130 | 6.757 7 | 8.409 | 2.614 5 | 3.493 7 | 2.64 | 1.152 5 |
利用SIFT算子获取辅帧和主帧之间的同名点,利用投影变换模型[5]和RANSAC 算法[7]进匹配粗差剔除,利用基于固定帧的帧间运动估计模型,采用SRTM-DEM投影或立体平差方式获取辅帧的像方仿射变换参数,选取任意相邻帧之间的定向残差,计算运动估计残差,如表 2所示。
| 帧对 | 沿轨向 | 垂轨向 | ||||
| 最大值 | 最小值 | 中误差 | 最大值 | 最小值 | 中误差 | |
| 99-100 | 0.671 297 | 0 | 0.138 547 | 0.656 555 | 10 -6 | 0.136 552 |
| 100-101 | 0.710 788 | 0 | 0.135 972 | 0.624 698 | 10 -6 | 0.133 845 |
由表 2所示,帧间运动估计中误差在0.15个像素之内,验证了本文提出的运动估计模型的精度。
为了保证稳像后视频三维重建和目标运动轨迹计算,进一步对比了采样后辅帧有理函数模型拟合精度,如表 3所示,采样后辅帧的RPC拟合精度优于万分之一像素。
| 像素 | ||||||
| 帧数 | 沿轨向 | 垂轨向 | ||||
| 最大值 | 最小值 | 中误差 | 最大值 | 最小值 | 中误差 | |
| 70 | 4×10 -6 | 0 | 2×10 -6 | 2.6×10 -5 | 0 | 9×10 -6 |
| 90 | 4×10 -6 | 0 | 1×10 -6 | 2.4×10 -5 | 0 | 8×10 -6 |
| 130 | 4×10 -6 | 0 | 1×10 -6 | 2.5×10 -5 | 0 | 9×10 -6 |
为了验证卫星视频稳像精度,利用基于ENVI开发的Corr-Cosi插件[21]对稳像后相邻帧视频图像进行相关匹配运算。配准窗为32×32像素,步长为32像素,最大迭代两次。表 4为任意抽取的3个相邻帧对之间配准精度的统计结果。
| 像素 | ||||||||
| 帧对 | 沿轨向 | 垂轨向 | ||||||
| 最大值 | 最小值 | 均值 | 中误差 | 最大值 | 最小值 | 均值 | 中误差 | |
| 19-20 | 0.126 79 | -0.261 48 | -0.027 12 | 0.057 70 | 0.159 15 | -0.331 09 | 0.020 01 | 0.063 90 |
| 100-101 | 0.319 61 | -0.312 57 | 0.008 87 | 0.102 24 | 0.272 16 | -0.367 36 | -0.004 71 | 0.105 01 |
| 121-122 | 0.202 09 | -0.297 27 | 0.028 20 | 0.207 76 | 0.585 76 | -0.314 65 | -0.025 80 | 0.113 66 |
从表 4卫星视频稳像后的精度可以看出,相邻帧配准精度优于0.25像素,优于SkySat稳像[5],满足卫星视频稳像的目的。
3 结 论针对面阵“凝视”卫星视频,本文分析了影响帧间不能一一对应的原因,提出了面阵“凝视”视频运动估计和运动补偿方法,通过仿真数据验证了算法的精度,得到如下结论:
(1) 基于固定帧的帧间运动估计模型严密,充分顾及了临近帧之间外方位元素数值的差异引起的平移旋转和缩放误差,同时顾及临近帧同名点在不同像面位置位置引起的几何畸变误差。
(2) 利用仿真数据验证,稳像后视频配准精度优于0.25像素,满足流畅视频要求。
(3) 稳像后的卫星视频每帧图像带几何模型,可以进一步满足三维重建、运动目标检测跟踪后地面轨迹计算要求。
| [1] | Skybox Imaging[EB/OL]. [2015-04-23]. http://www.skyboximaging.com/. |
| [2] | 刘祥磊, 童小华, 马静. 视频测量影像序列椭圆形人工目标点快速识别和跟踪方法[J]. 测绘学报, 2015, 44(6): 663-669. LIU Xianglei, TONG Xiaohua, MA Jing. A Systemic Algorithm of Elliptical Artificial Targets Identification and Tracking for Image Sequences from Videogrammetry[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(6): 663-669. |
| [3] | 吉淑娇, 朱明, 胡汉平. 基于特征点匹配的电子稳像技术[J]. 中国光学, 2013, 6(6): 841-849. JI Shujiao, ZHU Ming, HU Hanping. Aero-borne Electronic Image Stabilization Based on Feature Point Matching[J]. Chinese Optics, 2013, 6(6): 841-849. |
| [4] | KIM T, LEE S, PAIK J. Combined Shape and Feature-based Video Analysis and Its Application to Non-rigid Object Tracking[J]. IET Image Processing, 2011, 5(1): 87-100. |
| [5] | MURTHY K, KIRANM M, SMILEY B D, et al. SkySat-1: Very High-resolution Imagery from a Small Satellite[C]//Proceedings of SPIE 9241, Sensors, Systems, and Next-generation Satellites XVIII, 92411E. Amsterdam: [s.n.], 2014. |
| [6] | LOWE D G. Distinctive Image Features from Scale-invariant Keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91-110. |
| [7] | FISCHLER M A, BOLLES R C. Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography[J]. Communications of the ACM, 1981, 24(6): 381-395. |
| [8] | HASHIMOTO T. RPC Model for ALOS/PRISM Images[C]// Proceedings of 2003 IEEE International Geoscience and Remote Sensing Symposium, IGARSS'03.Toulouse: IEEE, 2003, 3: 1861-1863. |
| [9] | LUTES J. Accuracy Analysis of Rational Polynomial Coefficients for IKONOS Imagery[C]//Proceedings of ASPRS 2004 Conference. Denver, Colorado: [s.n.], 2004: 23-28. |
| [10] | NAGASUBRAMANIAN V, RADHADEVI P, RAMACHANDRAN V, et al. Rational Function Model for Sensor Orientation of IRS-P6 LISS-4 Imagery[J]. The Photogrammetric Record, 2007, 22 (120): 309-320. |
| [11] | ZHANG Guo, LI Zhen, PAN Hongbo, et al. Orientation of Spaceborne SAR Stereo Pairs Employing the RPC Adjustment Model[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(7): 2782-2792. |
| [12] | 张过, 李德仁. 卫星遥感影像RPC参数求解算法研究[J]. 中国图象图形学报, 2007, 12(12): 2080-2088. ZHANG Guo, LI Deren. The Algorithm of Computation RPC Model's Parameters for Satellite Imagery[J]. Journal of Image and Graphics, 2007, 12(12): 2080-2088. |
| [13] | FRASER C S, BALTSAVIAS E, GRUEN A. Processing of IKONOS Imagery for Submetre 3D Positioning and Building Extraction[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2002, 56(3): 177-194. |
| [14] | GRODECKI J. IKONOS Stereo Feature Extraction-RPC Approach[C]//Proceedings of the ASPRS Annual Conference. St. Louis: [s.n.], 2001. |
| [15] | GRODECKI J, DIAL G. Block Adjustment of High-resolution Satellite Images Described by Rational Polynomials[J]. Photogrammetric Engineering & Remote Sensing, 2003, 69(1): 59-68. |
| [16] | 蒋永华, 张过, 唐新明, 等. 资源三号测绘卫星三线阵影像高精度几何检校[J]. 测绘学报, 2013, 42(4): 523-529, 553. JINAG Yonghua, ZHANG Guo, TANG Xinming, et al. High Accuracy Geometric Calibration of ZY-3 Three-line Image [J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(4): 523-529, 553. |
| [17] | 蒋永华. 国产线阵推扫光学卫星高频误差消除方法研究[D]. 武汉: 武汉大学, 2015. JIANG Yonghua. Research on Elimination of High-frequency Errors for Homemade Linear Pushbroom Optical Satellite[D]. Wuhan: Wuhan University, 2015. |
| [18] | 唐新明, 张过, 黄文超, 等. 低轨卫星平面和立体精度预估方法: 中国, 201410134689.7[P]. 2014-04-04. TANG Xinming, ZHANG Guo,HUANG Wenchao, et al. A Method to Estimate Low Orbiter Imagery's Plane and Stereo Precision: China, CN 201410134689.7 [P]. 2014-04-04. |
| [19] | 詹总谦. 基于纯平液晶显示器的相机标定方法与应用研究[D]. 武汉: 武汉大学, 2006. ZHAN Zongqian. Research on Camera Calibration Based on Completely Flat Liquid Crystal Display[D]. Wuhan: Wuhan University, 2006. |
| [20] | TAO C V, HU Yong. A Comprehensive Study on the Rational Function Model for Photogrammetric Processing[J]. Photogrammetric Engineering & Remote Sensing, 2001, 67(12): 1347-1357. |
| [21] | LEPRINCE S, BARBOT S, AYOUB F, et al. Automatic and Precise Orthorectification, Coregistration, and Subpixel Correlation of Satellite Images, Application to Ground Deformation Measurements[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(6): 1529-1558. |