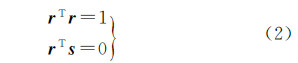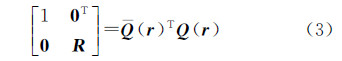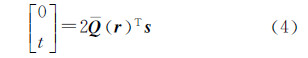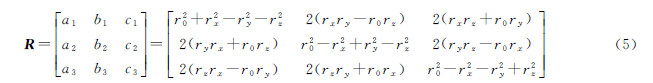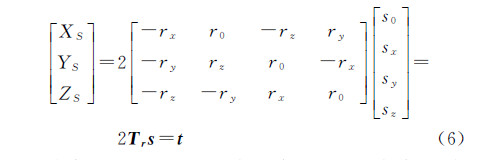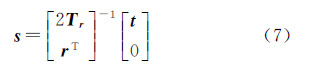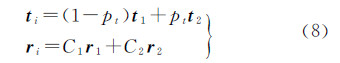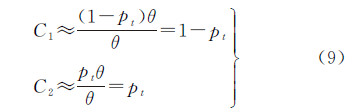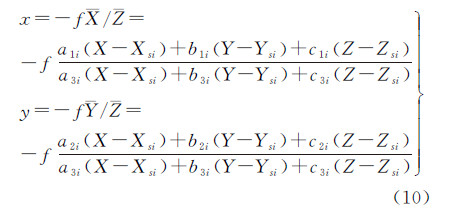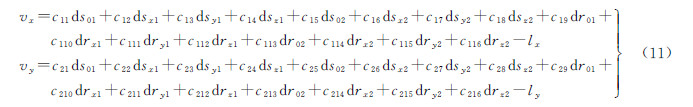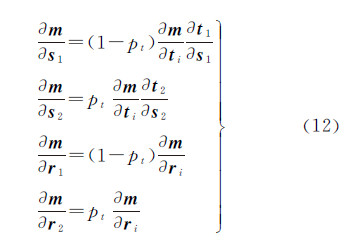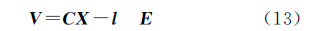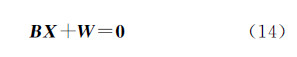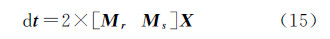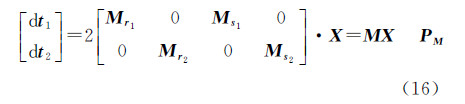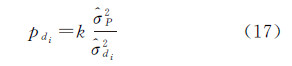Download PDF  
文章快速检索  
  高级检索
引用本文
余岸竹，姜挺，龚辉，等。线阵卫星遥感影像外方位元素对偶四元数求解法[J]. 测绘学报，2016，45(2)：186-193. DOI:10.11947/j.AGCS.2016.20140643
YU Anzhu, JIANG Ting, GONG Hui, et al. Dual Quaternion Method to Solve Exterior Orientation Parameters for Satellite Linear Array Images[J]. Acta Geodaeticaet Cartographica Sinica, 2016, 45(2): 186-193. DOI:10.11947/j.AGCS.2016.20140643
线阵卫星遥感影像外方位元素对偶四元数求解法
余岸竹1, 姜挺1, 龚辉2, 郭文月1, 江刚武1     
1. 信息工程大学地理空间信息学院，河南 郑州 450052;
2. 西安测绘研究所，陕西 西安 710054
收稿日期：2014-12-10；修回日期：2015-08-28
基金项目：国家自然科学基金(41201477；41471387；41301526)。
第一作者简介：余岸竹(1989-)，男，博士生，研究方向为航空航天高精度目标定位理论与方法。E-mail： anzhu_yu@126.com
摘要：基于对偶四元数可统一描述位置与姿态的特点，提出了利用对偶四元数求解线阵卫星遥感影像外方位元素的方法。该方法使用对偶四元数的实部描述传感器的姿态，并利用对偶部和实部共同描述成像传感器的位置。通过对位置和姿态的内插建立了基于对偶四元数的外方位元素模型。为减少运算，将球面线性插值进行化简，进而建立了基于线性插值的成像几何模型。为求解外方位元素，首先对共线条件方程进行了线性化，然后通过矩阵微分运算推导了线元素的虚拟观测方程，并根据误差传播定律确定其权值，最终采用具有约束条件的参数平差法求解外方位元素。试验结果表明本文方法正确可靠，与采用欧拉角和单位四元数的外方位元素求解方法相比，有更高的参数解算精度，同时也表明了准确的初值和虚拟观测方程对外方位元素求解的必要性。
关键词： 对偶四元数     线阵遥感影像     虚拟观测方程     外方位元素     单位四元数    
Dual Quaternion Method to Solve Exterior Orientation Parameters for Satellite Linear Array Images
YU Anzhu1 , JIANG Ting1, GONG Hui2, GUO Wenyue1, JIANG Gangwu1    
1. Institute of Surveying and Mapping, Information Engineering University, Zhengzhou 450052, China;
2. Xi'an Research Institute of Surveying and Mapping, Xi'an 710054, China
Foundation support:The National Natural Science Foundation of China (Nos.41201477;41471387;41301526)
First author: YU Anzhu(1989—), male, PhD candidate, majors in high precision photogrammetric point determination theory and method.E-mail: anzhu_yu@126.com
Abstract: According to the characteristics that dual quaternion can describe the position and orientation simultaneously, a method using dual quaternion to calculate the exterior orientation parameters for satellite linear array images is proposed. In this method the real part of dual quaternion is used to represent attitude of the sensor, and both the real part and the dual part are used to represent the position of the sensor.The model describing exterior parameters is established by interpolating the position and attitude. To reduce calculation, the simplified spherical linear interpolation algorithm is proposed, and the geometric model is established.In order to calculate the exterior parameters, the collinear equation is linearized at first. Then the virtual observation equations for position parameters are deduced according to the theory of matrix derivative, and the weight of the equation is calculated using error propagation principle. The exterior orientation parameters are calculated iteratively using parameter adjustment with constraints at last. Experimental results indicate that the proposed method is reliable and correct, and the precision of parameter estimation is higher than traditional methods using Euler angles or unit quaternion. The necessity of accuracy initial values and virtual observation equations for calculating exterior parameters is also revealed.
Key words: dual quaternion     linear array images     virtual observation equation     exterior orientation parameters     unit quaternion    

空间后方交会是卫星摄影测量几何处理中的重要环节，是卫星遥感影像几何定位、区域网平差和自检校光束法平差等计算的关键步骤，其基本思想是利用合适的外方位元素模型描述成像传感器的位置与姿态，建立线阵影像的成像几何模型，对共线条件方程进行线性化后迭代求解外方位元素。当前，大多数卫星采用线阵CCD传感器成像，传感器在一定时间内的外方位元素通常被描述为某一成像行关于时间的多项式函数形式[1, 2, 3]，或者若干离散成像时刻外方位元素的插值形式[4, 5, 6]。对于运行比较平稳的卫星，这两类模型均可较好地描述成像传感器的成像位置与姿态，参数之间的相关性成为影响后方交会精度的主要因素，其成因是线阵传感器的焦距较大、CCD线阵较短，使得成像时刻传感器的瞬时视场角较小，共线条件方程经线性化后产生了线元素和角元素的相关。

为了解决此类问题，学者们试图从方程解算方法和外方位元素建模这两个方面来提高外方位元素的求解精度与稳定性。在方程解算方面，文献[7]使用广义岭估计法求解外方位元素；文献[8] 采用岭-压缩组合估计的方法进行了参数解算；文献[9,10]对虚拟观测方程中权值的确定进行了改进。以上文献中均利用欧拉角描述角元素，因而这些算法仅能提高参数解算的精度，却无法消除或者降低参数之间的相关性。在外方位元素建模方面，文献[11]使用姿态四元数代替了欧拉角，建立了基于四元数球面线性(spherical linear interpolation,SLERP)的线阵影像外方位元素模型，实现了外方位元素的高精度解算；文献[12]利用四元数微分理论，提出了一种基于四元数微分方程(quaternion differential equation,QDE)的外方位元素模型，使用Tikhonov正则化法进一步提高了外方位元素求解的精度；文献[13]利用信噪比定量比较了各种四元数外方位元素模型在参数求解中的差异。虽然利用四元数可以有效降低参数之间的相关性，但仍是将平移与旋转分开考虑，位置与姿态之间没有严格的约束条件。

近些年，部分学者引入对偶四元数对外方位元素进行描述，利用其同时描述平移与旋转的特性，已在遥感影像几何处理中取得了初步的成果：文献[14]利用对偶四元数实现了面阵影像的空间后方交会；文献[15]验证了对偶四元数在区域网平差求解中的优势；文献[16]利用对偶四元数进行了面阵影像的直接定向；文献[17]利用线性蒙皮混合算法进行外方位元素建模，提高了GeoEye-1卫星遥感影像的立体定位结果，但是该卫星隐藏了定轨和定姿数据，因而该文献未研究定轨、定姿数据在后方交会中的应用，难以保证迭代在真值附近进行。

实际上，线阵卫星遥感影像的后方交会计算依赖于未知数的初值[18]，应当在外方位元素准确建模的基础上，充分利用卫星定轨、定姿设备的观测结果，准确给定各类观测方程的权值[19]，才能确保外方位元素的正确求解。本文试图利用对偶四元数同时描述成像传感器的位置和姿态，引入虚拟观测方程，进一步提高外方位元素的求解精度。

1 对偶四元数

对偶四元数由单位四元数和对偶数理论发展起来，其定义为

式中，r=[r0 rx ry rz]T和s=[s0 sx sy sz]T分别称为对偶四元数的实部和对偶部；ε为对偶运算符，满足关系：ε≠0且ε2=0。r和s虽有8个参数，但是二者满足关系

因此对偶四元数中仅有6个自由度，与平移和旋转未知数的数量相同。利用对偶四元数的性质[20]，旋转矩阵R与平移矢量t可利用对偶四元数的实部与对偶部分别表示为[16]

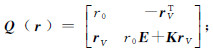
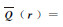
式中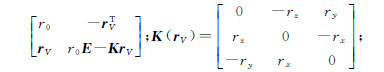，rV=[rx ry rz]T；E为单位阵。将式(3)右侧进行矩阵乘法运算，可得到对偶四元数组成的旋转矩阵R的具体表达式为

式(5)与单位四元数[11]所构成的旋转矩阵是一样的。同理可知，平移矢量t的具体表达式为

式中，(XS,YS,ZS)T为平移矢量的3个分量，在传统摄影测量中表示线元素。当线元素和姿态欧拉角已知时，对偶四元数实部r可按欧拉角计算单位四元数的方法确定[21]，对偶部s可由利用矢量t和r计算为

由式(5)和式(6)可知，两个坐标系之间的旋转矩阵R可以用由对偶四元数的实部r计算得到，坐标系原点之间的平移矢量t可由实部r与对偶s共同计算得到，因而利用对偶四元数建立线阵影像的外方位元素模型是可行的。

2 基于对偶四元数的外方位元素求解 2.1 基于对偶四元数的成像几何模型

设q1=r1+εs1和q2=r2+εs2分别为影像首行和末行外方位元素所对应的对偶四元数，rk=[r0krxk ryk rzk]T与sk=[s0k sxk syk szk]T( =1,2)分别表示影像首行和末行外方位元素的实部和对偶部。在卫星成像过程中，卫星的位置和姿态变化比较平稳，可利用低阶插值计算第i个成像行的外方位元素为

式中，pt=i/n，n为首末两行之间成像行的数量；t1与t2分别表示首末两行的外方位线元素；C1和C2为四元数的插值系数。为了实现四元数在插值时角度匀速变化[6, 11]，通常采用四元数球面线性插值，即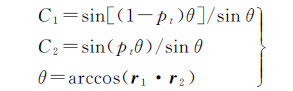

显然球面插值会导致C1和C2中包含三角函数与反三角函数的复合运算，使得线性化求解外方位元素的表达式过于复杂。由于卫星平台运行较为平稳，首末两行的姿态四元数差异很小，因而θ→0+，sinθ与θ是等价无穷小，此时插值系数可化简为

式(9)表明，当卫星运行比较平稳，两成像行的成像间隔不太长时，可利用线性插值代替球面线性插值计算任意成像行的姿态。本文将利用式(9)所示的线性表达式构建的外方位元素模型称为线性插值的对偶四元数模型(linear interpolation based dual quaternion model,LDQ)，将利用球面线性插值构建的外方位元素模型称为球面线性插值的对偶四元数模型(SLERP based dual quaternion model,SDQ)。

本文以LDQ模型为例推导求解外方位元素的误差方程式。不考虑主点偏移与焦距变化时，第个成像行的瞬时构像方程可以写成

式中，f为相机焦距；(X,Y)为像点坐标，可利用传感器沿轨道方向的指向角ψX和垂直于轨道方向的指向角ψY表示为(-ftan ψY,f tan ψX)；系数aji、bij、cji(j=1,2,3)为该行对应的旋转矩阵中的元素，可内插计算ri后，由式(5)计算旋转矩阵得到；ti=[Xsi Ysi Zsi]T是成像行摄影中心在物方坐标系内的坐标，可由式(6)和式(8)联立计算得到。式(10)即为利用LDQ模型构建的线阵影像成像几何方程。

为求解外方位元素，将式(10)在初值处展开至一次项，可得误差方程为

式中，lx=x-xc；ly=y-yc；xc=-fX/Z；yc=-fY/Z；cij(i=1,2;j=1,2,…,16)为线性化系数，可对m=[x y]T求ri和ti的偏导数，并依据复合函数微分法则计算s1、s2、r1和r2的偏导数为

则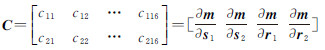中不包含三角函数运算。式中，əm/əti(i=1,2)为线元素的偏导数，与航空摄影测量中的结果一致；əti/əsi可由对式(6)求偏导数计算得到；əm/əri的具体表达式在文献[14]和文献[15] 中有详细描述，在此不再赘述。

误差方程(11)的矩阵形式为

式中，X=[ds1T ds2T drT1 dr2T]T为未知数改正数向量；V=[vx vy]T；l=[lx ly]T。

此外，影像首行和末行对应的对偶四元数均满足式(2)，对该式进行线性化并写成矩阵形式可得

式中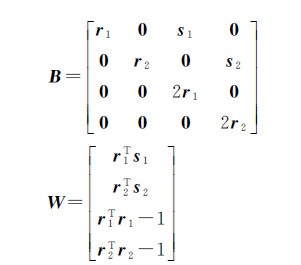

误差方程(13)与条件方程(14)构成了外方位元素计算的基本平差模型。

2.2 对偶四元数虚拟观测方程的建立

虚拟观测方程在摄影测量中有很高的实际应用价值，在线阵影像的后方交会和光束法平差中被广泛采用。由于该方法可以将外方位元素的改正数限制在一个合理的范围内，因而于有偏估计这种方法更为严密[18]。当前大多数卫星可以提供高精度的定轨数据，而定姿数据通常含有系统误差，且误差的构成较为复杂[22]。本文仅对线元素设置虚拟观测方程，适当放宽姿态改正数的限制。

对式(6)求微分可得

式中，Mr和Ms的表达式分别为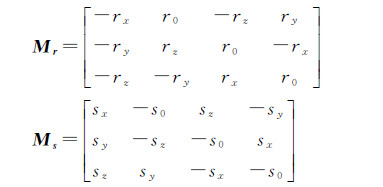

对线元素增设的虚拟观测方程可表示为

式中，PM为虚拟观测方程的权矩阵。本文在迭代过程中动态调整权值[18]，即先利用验前权值进行预平差，并进行方差分量估计值，然后计算第次迭代中参数di在虚拟观测方程中的权值为

式中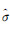，p2为像点观测值的方差估计值；k为正常数，通常取k=1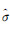；di2为未知数di第n-1次迭代时计算得到的方差估计值，可由X各分量的方差估计值按误差传播定律得到。将误差方程(13)、条件方程(14)以及虚拟观测方程(16)联立构成总误差方程式

利用nG个地面控制点，按照式(18)总共可以列出2nG+6个误差方程和4个条件方程，应有nG≥3。当nG＜6时，式(18)实质上是将定轨数据作为控制条件参与方程的求解，仅在精确给定初值时正确收敛，通常情况下应有nG≥6。利用约束条件的参数平差方法可求得改正数X，通过迭代即可求得利用对偶四元数描述的外方位元素值。

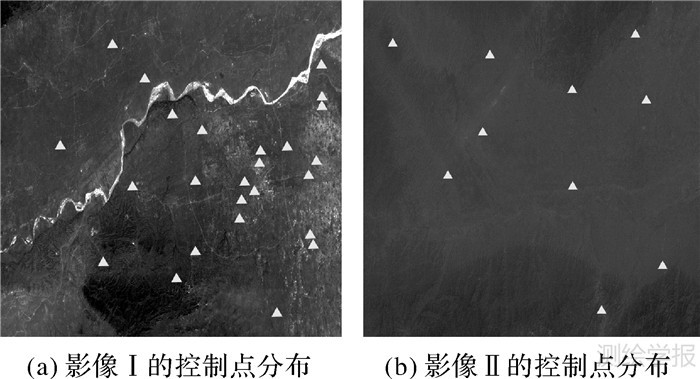
3 试验与分析

为验证提出方法的正确性与有效性，本文将使用两组高分辨率卫星遥感影像进行对比试验验证。第1组试验数据(影像Ⅰ)为河南某地SPOT-5 HRS立体影像，共有13 376条扫描行，每个扫描行有12 000个像元，影像内包含25个平面高程控制点(图 1(a))。第2组试验数据(影像Ⅱ)为中国西部某地丘陵地区的SPOT-5 HRS立体影像，影像内共有12 000条扫描行，共包含10个平高控制点(图 1(b))。

图 1 SPOT-5 HRS影像控制点分布示意图 Fig. 1 Distribution of ground control points for SPOT-5 HRS images
图选项
3.1 试验1——影像I的外方位元素求解

本试验用于比较对偶四元数外方位元素模型、欧拉角外方位模型和单位四元数外方位元素模型在外方位元素求解中的差异。为了验证式(9)的合理性，本试验还将比较SDQ模型和LDQ模型在后方交会计算中的区别。试验评价指标有两种：一是利用求解出的外方位元素反算地面点的像点坐标，并计算像点重投影误差的中误差；二是利用两张影像的外方位元素进行空间前方交会，计算三维坐标残差的中误差。试验中分别采用6、7、14和20个控制点求解外方位元素。表 1和表 2为不同控制点数量时检查点的像点坐标重投影的中误差及单位权方差统计结果；表 3和表 4为求解外方位元素值按空间前方交会计算地面点的三维坐标，计算检查点坐标残差的误差统计结果。

表 1 影像Ⅰ中不同控制点数量下像方重投影误差统计结果 Tab. 1 Statistics result of root mean square error for re-projection in image space with different numbers of GCPs for image Ⅰ
影像 控制 点数 检查 点数 x/像素 y /像素
Euler SLERP QDE SDQ LDQ Euler SLERP QDE SDQ LDQ
前视影像 6 19 2.712 1.799 1.766 1.735 1.722 1.529 1.526 1.447 1.530 1.531
7 18 1.734 1.856 1.847 1.793 1.776 1.418 1.317 1.481 1.322 1.326
14 11 2.202 1.667 1.598 1.518 1.469 1.256 1.257 1.452 1.261 1.262
20 5 1.196 1.303 1.276 1.207 1.195 0.789 0.754 0.767 0.753 0.752
后视影像 6 19 不收敛 1.582 1.414 1.554 1.538 不收敛 1.261 1.439 1.261 1.261
7 18 1.576 1.517 1.536 1.495 1.481 1.768 1.238 1.335 1.238 1.238
14 11 1.676 1.656 1.485 1.614 1.585 1.554 1.444 1.487 1.444 1.444
20 5 0.929 1.210 0.997 1.142 1.092 1.436 1.193 1.183 1.191 1.191
注：Euler为利用欧拉角求解外方位元素的算法，SLERP为文献[11]中利用四元数球面线性插值求解外方位元素算法，QDE为文献[12]中的四元数微分方程算法，下同。
表选项
表 2 影像Ⅰ中不同控制点数量下平面重投影误差与单位权方差统计结果 Tab. 2 Statistics result of plane root mean square error for re-projection and unit weight variance with different numbers of GCPs for image Ⅰ
影像 控制 点数 检查 点数 平面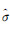/像素 0/像素
Euler SLERP QDE SDQ LDQ Euler SLERP QDE SDQ LDQ
前视影像 6 19 3.114 2.359 2.283 2.313 2.304 0.391 2.573 2.007 0.994 0.965
7 18 2.240 2.276 2.370 2.227 2.216 0.476 1.889 1.566 1.155 1.131
14 11 2.536 2.087 2.159 1.973 1.937 0.677 1.635 1.480 1.304 1.299
20 5 1.433 1.505 1.489 1.423 1.412 0.877 1.762 1.565 1.374 1.358
后视影像 6 19 不收敛 2.023 2.018 2.002 1.989 不收敛 0.916 0.839 0.517 0.509
7 18 2.368 1.958 2.035 1.941 1.931 0.224 0.998 0.668 0.739 0.736
14 11 2.285 2.197 2.101 2.165 2.144 0.441 1.051 0.920 0.871 0.860
20 5 1.710 1.699 1.548 1.651 1.616 0.436 1.672 1.279 1.182 1.163
表选项
表 3 影像Ⅰ中不同控制点数量下求解地面三维坐标水平方向误差统计 Tab. 3 Statistics result of horizontal root mean square error for orientation with different numbers of GCPs for image Ⅰ
控制 点数 检查 点数 平面/m 高程/m
Euler SLERP QDE SDQ LDQ Euler SLERP QDE SDQ LDQ
6 19 — 16.283 15.292 15.676 15.507 — 19.164 20.212 19.237 19.283
7 18 17.845 16.001 15.782 15.292 15.058 20.077 16.222 19.687 16.352 16.444
14 11 25.356 16.308 16.415 14.986 14.551 16.042 15.726 19.123 15.772 15.797
20 5 11.505 11.208 10.534 9.916 9.588 5.777 7.133 8.314 7.506 7.723
表选项
表 4 影像Ⅰ中不同控制点数量下求解地面三维坐标平面和高程误差统计 Tab. 4 Statistics result of plane and height root mean square error for orientation with different numbers of GCPs for image Ⅰ
控制 点数 检查 点数 平面/m 高程/m
Euler SLERP QDE SDQ LDQ Euler SLERP QDE SDQ LDQ
6 19 — 25.148 25.345 24.816 24.745 — 13.234 16.045 13.252 13.257
7 18 26.861 22.785 25.232 22.388 22.296 19.883 12.669 14.877 12.695 12.708
14 11 30.005 22.655 25.202 21.756 21.477 15.920 14.661 15.906 14.673 14.678
20 5 12.874 13.285 13.419 12.437 12.312 13.837 11.763 11.974 11.777 11.778
表选项

从试验1的结果可知：

(1) 引入了虚拟观测方程后，除6个点时Euler算法在后视影像上未能收敛，其余情况下所有算法均可正确收敛。当7个和14个控制点参与平差时，Euler算法的立体定位精度较低。主要因为传统外方位元素描述中，角元素、线元素之间的相关性很强，误差方程系数矩阵呈现严重病态。当控制点数量较少时，方程不能稳定求解，使得第1次迭代的改正数比较大，求解过程未能在初值附近收敛，反而得到临近区间的局部最优值。这也从侧面表明了合理的初值和虚拟观测方程的必要性。

(2) SDQ算法和LDQ算法的立体定位平面精度略高于SLERP算法，三者的高程精度相当，仅有厘米级的差别；在6个、7个和14个控制点参与运算时，三者的立体定位精度均优于QDE算法，像点重投影的中误差相当，这表明利用对偶四元数描述外方位元素模型正确可靠，且在外方位元素求解中具有一定优势，主要是因为对偶四元数的实部与对偶部满足正交关系，使得r与s之间的相关性很低，对参数求解较为有利。值得注意的是，试验中QDE的计算精度略低于SLERP算法，这与文献[13]中结果有出入，原因是为确保试验变量唯一，本文试验中未使用Tikhonov正则化求解参数，因而平差结果有所差异。

(3) SDQ算法和LDQ算法的计算结果基本一样，立体定位的结果仅有厘米级的差别，说明利用式(9)简化球面线性插值是正确可靠的。同时，LDQ算法中共线条件方程经线性化后的系数矩阵中不包括三角函数运算，在保证精度的同时提高了运算效率和参数求解精度，这对实际应用有重要意义。但是这种近似是有条件的，应针对不同的卫星影像和不同成像条件区分对待。

(4) 当6、7和14个控制点参与平差解算时，5种算法立体定位的精度并无明显提高，直到20个点参与平差后精度才达到1个像元左右。这主要因为试验所用控制点均在立体环境下人工量测得到，存在一定的辨识误差和量测误差，并且试验中未针对系统误差进行处理，欲进一步提高立体定位的精度，需要顾及控制点的误差，引入自检校参数进行自检校光束法平差计算。

3.2 试验2——影像Ⅱ外方位元素求解

本试验用于比较本文外方位元素模型和文献[17]中基于线性蒙皮混合的对偶四元数外方位元素模型(linear blending dual quaternion model,BDQ)在后方交会中的区别。由于文献[17]在求解外方位元素时没有准确给定初值，且未增设虚拟观测方程，试验中将对本文方法与原始BDQ算法、赋初值的BDQ算法和赋初值并增设虚拟观测方程的BDQ算法在求解外方位元素时的差异。分别使用6、7和8个控制点求解影像Ⅱ的外方位元素并统计重投影误差和立体定位精度，结果见表 5。

表 5 影像Ⅱ求解外方位元素的重投影误差和立体定位精度统计 Tab. 5 Statistics result of root mean square error for re-projection and orientation for image Ⅱ
试验方案 外方位元素模型 控制点数 检查点数 重投影误差/像素 立体定位精度/m
前视 后视 平面 高程
1 BDQ 不收敛 不收敛 — —
BDQ+初值 不收敛 不收敛 — —
BDQ+初值+虚拟观测 6 4 1.334 1.628 26.675 15.475
SDQ 1.227 1.712 26.307 14.049
LDQ 1.227 1.712 26.308 14.048
2 BDQ 不收敛 不收敛 — —
BDQ+初值 2.359 不收敛 — —
BDQ+初值+虚拟观测 7 3 1.755 1.112 14.227 12.940
SDQ 1.566 0.988 13.549 12.041
LDQ 1.566 0.988 13.549 12.040
3 BDQ 不收敛 不收敛 — —
BDQ+初值 2.159 1.404 14.746 16.563
BDQ+初值+虚拟观测 8 2 2.079 1.256 12.817 15.445
SDQ 1.563 1.105 12.356 12.385
LDQ 1.562 1.105 12.356 12.384
表选项

由试验2的结果可知：

(1) 当没有准确给定初值时，BDQ算法在3次试验中均不能正确收敛。这是因为线阵卫星遥感影像定向参数的求解过程中通常使用地心地固坐标系作为物方坐标系[9]，像方坐标系和物方坐标系之间的旋转矩阵不再近似为单位阵。同时，传感器的成像姿态会随着星下点经度和纬度的不同而变化，应由定轨、定姿数据给定外方位元素初值。

(2) 加入初值后，BDQ算法在8个控制点参与运算时可以收敛，但是重投影误差较大，立体定位的精度较低。在此基础上引入虚拟观测方程后，BDQ算法在各次试验中均正确收敛，重投影误差和立体定位结果也有一定的改善，这表明了求解线阵影像外方位元素时增设虚拟观测方程的必要性。

(3) 准确给定初值并加入虚拟观测方程之后，BDQ算法与本文方法的精度相近，但是本文方法的精度更高，这种精度的差异是由外方位元素模型的区别引起的。BDQ算法中的使用插值算法是一种近似算法[23]，对外方位元素的对偶部进行插值，物理意义并不明确；本文方法依据卫星成像时运动平稳的特性，对线元素进行插值来构建外方位元素模型，具有明确的物理意义，因而在3组试验中重投影和立体定位的精度更高。

4 结 论

本文利用对偶四元数构建的SDQ模型和LDQ模型可实现线阵卫星遥感影像的外方位元素求解。试验结果表明，相比于利用欧拉角和利用单位四元数的外方位元素求解方法，本文方法更具优势；与已有的对偶四元数外方位元素求解方法相比，本文的外方位元素模型与平差手段更为合理，是线阵卫星遥感影像外方位元素求解的一条新途径。然而在试验过程中也发现了本文方法的局限性，控制点的精度和权初值会影响平差计算的结果，应引入抗差估计等手段进一步提高算法的性能。当然，欲将对偶四元数实际应用到卫星遥感影像的几何处理当中，需要进行更为深入和系统的研究，如何利用对偶四元数进行自检校区域网平差计算和构建定向片模型等问题，都是今后研究的重点内容。

参考文献
[1] 张永生, 巩丹超, 刘军, 等. 高分辨率遥感卫星应用[M]. 北京: 科学出版社, 2004. ZHANG Yongsheng, GONG Danchao, LIU Jun, et al. Application of High-resolution Remote Sensing Satellites[M]. Beijing: Science Press, 2004.
[2] 袁修孝, 余翔. 高分辨率卫星遥感影像姿态角系统误差检校[J]. 测绘学报, 2012, 41(3): 385-392. YUAN Xiuxiao, YU Xiang. Calibration of Angular Systematic Errors for High Resolution Satellite Imagery[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 385-392.
[3] POLI D. Modelling of Spaceborne Linear Array Sensors[D]. Zurich: Swiss Federal Institute of Technology, 2005.
[4] HOFMANN O, NAVE P, EBNER H. DPS-A Digital Photogrammetric System for Producing Digital Elevation Models and Orthophotos by Means of Linear Array Scanner Imagery[J]. Photogrammetric Engineering and Remote Sensing, 1984, 50(8): 1135-1142.
[5] 刘军, 王冬红, 刘敬贤, 等. IMU/DGPS 系统辅助ADS40三线阵影像的区域网平差[J]. 测绘学报, 2009, 38(1): 55-60. LIU Jun, WANG Donghong, LIU Jingxian, et al. IMU/DGPS Supported Block Adjustment of ADS40 Three Line Imagery Data[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(1): 55-60.
[6] 刘军, 王冬红, 张永生, 等. 基于单位四元数的机载三线阵影像光束法平差[J]. 测绘学报, 2008, 37(4): 451-457. LIU Jun, WANG Donghong, ZHANG Yongsheng, et al. Bundle Adjustment of Airborne Three Line Array Imagery Based on Unit Quaternion[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(4): 451-457.
[7] 郭海涛, 张保明, 归庆明. 广义岭估计在解算单线阵CCD卫星影像外方位元素中的应用[J]. 武汉大学学报(信息科学版), 2003, 28(4): 444-447. GUO Haitao, ZHANG Baoming, GUI Qingming. Application of Generalized Ridge Estimate to Computing the Exterior Orientation Elements of Satellite Linear Array Scanner Imagery[J]. Geomatics and Information Science of Wuhan University, 2003, 28(4): 444-447.
[8] 张艳, 王涛, 朱述龙, 等. 岭-压缩组合估计在线阵推扫式影像外定向中的应用[J]. 武汉大学学报(信息科学版), 2004, 29(10): 893-896. ZHANG Yan, WANG Tao, ZHU Shulong, et al. Application of Combined Ridge-stein Estimator to Linear Pushbroom Imagery Exterior Orientation[J]. Geomatics and Information Science of Wuhan University, 2004, 29(10): 893-896.
[9] 余岸竹. 遥感卫星摄影测量参数动态检测关键技术研究[D]. 郑州: 信息工程大学, 2014. YU Anzhu. Research on the Key Technology of Dynamic Calibration of Photogrammetric Parameters for Spaceborne Sensors[D]. Zhengzhou: Information Engineering University, 2014.
[10] 余俊鹏. 基于先验求权的虚拟观测值法及其在线阵影像定向中的应用[J]. 测绘科学, 2009, 34(3): 124-126. YU Junpeng. The Virtual Observation Method with Weight Prior-determined and Its Application in Orientation of the Linear Array Imagery[J]. Science of Surveying and Mapping, 2009, 34(3): 124-126.
[11] JIANG Gangwu, JIANG Ting, GONG Hui, et al. Exterior Orientation of Line-array CCD Images Based on Quaternion Spherical Linear Interpolation[C]//ISPRS TC VII Symposium-100 Years ISPRS. Vienna: [s.n.], 2010, 38: 71-76.
[12] 龚辉, 姜挺, 江刚武, 等. 四元数微分方程的高分辨率卫星遥感影像外方位元素求解[J]. 测绘学报, 2012, 41(3): 409-416. GONG Hui,JIANG Ting,JIANG Gangwu, et al. Solution of Exterior Orientation Parameters for High-resolution Satellite Imagery Based on Quaternion Differential Equation[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 409-416.
[13] 龚辉. 基于四元数的高分辨率卫星遥感影像定位理论与方法研究[D]. 郑州: 信息工程大学, 2011. GONG Hui. Study on Theory and Method of Geopositioning for High-resolution Satellite Imagery Based on Quaternion[D]. Zhengzhou: Information Engineering University, 2011.
[14] 姬亭, 盛庆红, 王惠南, 等. 对偶四元数单片空间后方交会算法[J]. 中国图象图形学报, 2012, 17(4): 494-503. JI Ting, SHENG Qinghong, WANG Huinan, et al. Dual Quaternion of Space Resection with Single-image[J]. Journal of Image and Graphics, 2012, 17(4): 494-503.
[15] 龚辉, 姜挺, 江刚武, 等. 利用单位对偶四元数进行航空影像区域网平差解算[J]. 武汉大学学报(信息科学版), 2012, 37(2): 154-159. GONG Hui, JIANG Ting, JIANG Gangwu, et al. Bundle Block Adjustment of Aerial Imagery Based on Unit Dual Quaternion[J]. Geomatics and Information Science of Wuhan University, 2012, 37(2): 154-159.
[16] 龚辉, 江刚武, 姜挺, 等. 基于对偶四元数的绝对定向直接解法[J]. 测绘科学技术学报, 2009, 26(6): 434-438. GONG Hui, JIANG Gangwu, JIANG Ting, et al. Close-form Solution of Absolute Orientation Based on Dual Quaternion[J]. Journal of Geomatics Science and Technology, 2009, 26(6): 434-438.
[17] 盛庆红, 姬亭, 刘微微, 等. 对偶四元数线阵遥感影像几何定位[J]. 中国图象图形学报, 2012, 17(10): 1319-1326. SHENG Qinghong, JI Ting, LIU Weiwei, et al. Geo-positioning Line-array CCD Images with Dual Quaternion[J]. Journal of Image and Graphics, 2012, 17(10): 1319-1326.
[18] 袁修孝, 曹金山. 高分辨率卫星遥感精确对地目标定位理论与方法[M]. 北京: 科学出版社, 2012.YUAN Xiuxiao,CAO Jinshan. Theory and Method of High Resolution Satellite Remote Sensing for Precise Orientation[M]. Science Press, 2012.
[19] 隋立芬, 宋力杰, 柴洪洲. 误差理论与测量平差基础[M]. 北京: 测绘出版社, 2010.SUI Lifen, SONG Lijie, CHAI Hongzhou. Error Theory and Foundation of Surveying Adjustment[M]. Beijing: Surveying and Mapping Press, 2010.
[20] WALKER M W, SHAO Lejun, VOLZ R A. Estimating 3-D Location Parameters Using Dual Number Quaternions[J]. CVGIP: Image Understanding, 1991, 54(3): 358-367.
[21] 江刚武. 空间目标相对位置和姿态的抗差四元数估计[D]. 郑州: 信息工程大学, 2009.JIANG Gangwu. A Robust Estimation Using Quaternions for Relative Position of Space Object[D]. Zhengzhou: Information Engineering University, 2009.
[22] 王任享. 三线阵CCD影像卫星摄影测量原理[M]. 北京: 测绘出版社, 2006.WANG Renxiang. Satellite Photogrammetric Principle for Three-line-array CCD Imagery[M]. Beijing: Surveying and Mapping Press, 2006.
[23] KAVAN L, ŽÁRA J. Spherical Blend Skinning: A Real-time[JP] Deformation of Articulated Models[C].//Proceedings of the 2005 Symposium on Interactive 3D Graphics and Games. New York, NY: ACM, 2005: 9-16.
http://dx.doi.org/10.11947/j.AGCS.2016.20140643
中国科学技术协会主管、中国测绘地理信息学会主办。
0

文章信息

余岸竹，姜挺，龚辉，郭文月，江刚武
YU Anzhu, JIANG Ting, GONG Hui, GUO Wenyue, JIANG Gangwu
线阵卫星遥感影像外方位元素对偶四元数求解法
Dual Quaternion Method to Solve Exterior Orientation Parameters for Satellite Linear Array Images
测绘学报，2016，45(2)：186-193
Acta Geodaeticaet Cartographica Sinica, 2016, 45(2): 186-193.
http://dx.doi.org/10.11947/j.AGCS.2016.20140643

文章历史

收稿日期：2014-12-10
修回日期：2015-08-28

相关文章

工作空间