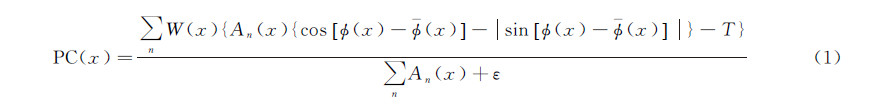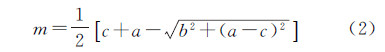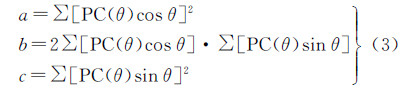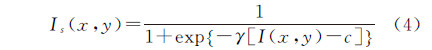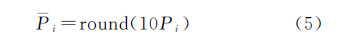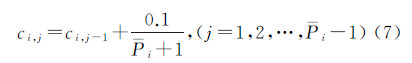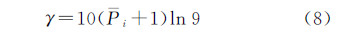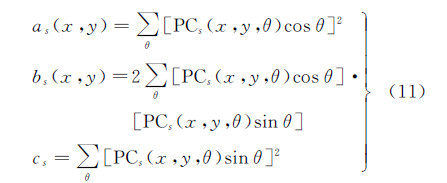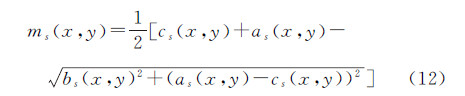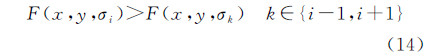2. 四川省应急测绘与防灾减灾工程技术研究中心,四川 成都 610041;
3. 教育部轨道交通安全协同创新中心,四川 成都 610031;
4. 高速铁路运营安全空间信息技术国家地方联合工程实验室,四川 成都 610031
2. Sichuan Engineering Research Center for Emergency Mapping & Disaster Reduction, Chengdu 610041, China;
3. Collaborative Innovation Center for Rail Transport Safety, Chengdu 610031, China;
4. State-Province Joint Engineering Laboratory of Spatial Information Technology for High-speed Railway Safety, Chengdu 610031, China
特征点检测是遥感影像处理的一个关键问题。对于多光谱遥感影像,影像之间较大程度的非线性辐射差异导致特征点检测结果不稳定。因此,多光谱遥感影像特征点检测是目前研究的难点之一。
经过数十年的发展,研究人员提出了许多著名的特征点检测算子,包括基于影像灰度梯度的方法[1, 2, 3]、基于影像灰度强度对比的方法[4, 5, 6]和基于尺度空间理论的方法[7, 8, 9]等,其中应用最广泛的是基于尺度空间理论的SIFT方法[7](scale invariant feature transform)。研究人员利用该方法进行多光谱遥感影像的特征点检测[10, 11, 12, 13, 14, 15]。但是,这些方法存在一个共同的问题:特征点响应值与影像对比度相关,导致特征点检测算子对影像对比度变化敏感。因此,这些方法在多光谱遥感影像上往往不能获得稳定的特征检测结果。为了提高算法对影像对比度变化的稳健性,研究人员提出了一类基于相位一致性的特征点检测方法[16, 17],这类方法能够更好地适应影像之间的辐射变化,因此也被用于多光谱遥感影像特征点检测[18, 19, 20]。相位一致性方法在一定程度上改善了多光谱影像特征点检测效果,但仍然存在以下问题:①相位一致性方法在理论上对影像对比度变化具有不变性,但在实际应用中该方法对多光谱遥感影像辐射变化的稳健性不足;②相位一致性方法只是在单一影像层上进行特征点检测,获得的特征点没有特征尺度信息。
针对以上问题,本文在相位一致性方法的基础上提出一种对多光谱遥感影像辐射和尺度变化稳健的特征点检测方法:首先对输入影像建立影像亮度空间,然后在亮度空间计算像素点相位一致性特征响应值并进行特征点判别,最后在尺度空间计算特征点的尺度值。
1 相位一致性特征点检测方法相位一致性特征点检测方法通过假设影像信号的傅里叶分量相位最一致的点为特征点进行特征检测。文献[16, 17] 定义的相位一致性度量函数为
式中,An为信号上点x处第n个傅里叶分量的幅值;φ(x)为相位角;φ(x)为整体平均相位角;W(x)为频率传播权重;ε是常数,其目的是避免分母为0;T为影像噪声估计量;符号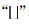 表示当其内部计算结果大于0时,输出结果为计算值本身,否则输出结果为0。文献[16, 17]采用矩分析的方法实现二维影像的相位一致性特征检测:根据式(1)独立地计算每个方向上的相位一致性度量值,然后计算相位一致性最小矩。如果像素点的相位一致性最小矩大于一定的阈值,则认为该像素点为特征点。相位一致性最小矩为
式中
式中,PC(θ)表示在方向θ 上的相位一致性度量值,求和运算是计算各个方向(6个方向)上的相位一致性累加值。本文将文献[16, 17]提出的相位一致性特征点检测算子标记为PC算子(phase congruency)。
2 本文方法
表示当其内部计算结果大于0时,输出结果为计算值本身,否则输出结果为0。文献[16, 17]采用矩分析的方法实现二维影像的相位一致性特征检测:根据式(1)独立地计算每个方向上的相位一致性度量值,然后计算相位一致性最小矩。如果像素点的相位一致性最小矩大于一定的阈值,则认为该像素点为特征点。相位一致性最小矩为
式中
式中,PC(θ)表示在方向θ 上的相位一致性度量值,求和运算是计算各个方向(6个方向)上的相位一致性累加值。本文将文献[16, 17]提出的相位一致性特征点检测算子标记为PC算子(phase congruency)。
2 本文方法
多光谱遥感影像之间的辐射差异体现在影像对比度和亮度两方面。因此,特征检测方法需要对影像对比度和亮度变化具有较强的稳健性。本文基于相位一致性原理,提出一种多光谱遥感影像特征点检测方法,算法整体流程如图 1所示。
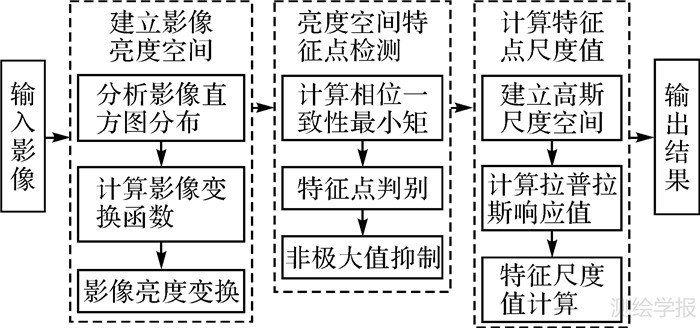
|
| 图 1 本文方法流程图 Fig. 1 Flow chart of the proposed point feature detection method |
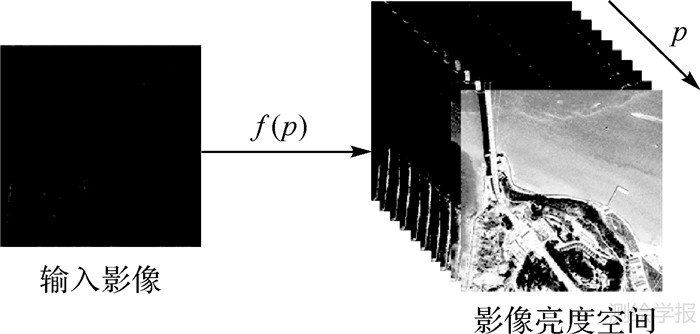
借鉴尺度空间的思想,通过建立影像亮度空间并在亮度空间进行特征检测来提高算法对影像亮度变化的稳健性。利用不同参数的灰度变换函数对影像进行亮度变换,构建影像亮度空间,如图 2所示。
|
| 图 2 影像亮度空间示意图 Fig. 2 Image illumination-space |
图 2中,f(p)为建立影像亮度空间时所采用的灰度变换函数,p 为灰度变换函数中的变量集合。建立影像亮度空间时,如果对于任意的输入影像都采用同一组参数的灰度变换函数进行处理,那么对于不同的影像,其处理后的效果可能会存在很大的差异。因此,在设计灰度变换函数时,函数参数值应根据具体的输入影像动态确定。本文以输入影像的直方图分布作为参数设置依据。对于每幅输入影像,根据其直方图分布特性确定灰度变换函数的参数值,再利用灰度变换函数对输入影像进行变换建立影像亮度空间,具体过程如下。
2.1.1 分析影像灰度直方图
对灰度值区间进行子区间划分,具体划分规则为:将[0,244]区间等间隔划分为9个子区间,将[225,255]作为第10个子区间。计算各个子区间内像素个数占影像像素总数的比例。假设第 i个子区间像素个数所占比例为Pi(i=1,2,…,10),则 。
。
本文选择对比拉伸函数作为变换函数
式中,I(x,y)为归一化的输入影像,取值范围为[0,1];Is(x,y)为变换后影像,取值范围为[0,1];γ和c为函数参数,γ决定函数曲线的倾斜程度,c表示函数曲线的横坐标中心值,取值范围为[0,1]。本文根据影像直方图分布确定参数值。对每个子区间内灰度级出现频次所占的比例Pi进行如下处理
式中,round( )为四舍五入函数。从第一个子区间开始逐区间遍历,只在P不为0的子区间内计算参数c,即P为0的子区间内不进行灰度变换。对于P不为0的子区间i 式中,当j=1时,ci,0=ci。如果子区间i对应的Pi等于1,则在该子区间内只需做一次灰度变换,生成一幅变换影像,此时只需计算式(6);否则,在该区间内需要进行多次灰度变换,生成多幅变换影像,此时在式(6)的基础上还需要计算式(7)。确定了参数c的值以后,变换函数曲线的中心点位置以及分布稀疏程度也相应地确定了。本文在参数c的基础上按下述方法计算参数γ的值:本文规定在每个Pi不为0的子区间,子区间左端点在子区间内第一条变换函数曲线上的取值为0.1,右端点在子区间内最后一条变换函数曲线上的取值为0.9。因此,子区间i左端点对应的输入值为I(x,y)=0.1(i-1),输出值为Is(x,y)=0.1,子区间内第一条变换函数曲线的参数c=0.1(i-1)+0.1/(Pi+1)。将I(x,y)、Is(x,y)以及c值代入式(4)可得
2.1.3 建立影像亮度空间确定了影像变换函数以后,利用变换函数对输入影像进行处理,对应不同的函数参数获得一系列亮度变换影像,构成输入影像的亮度空间。
2.2 影像亮度空间特征点检测本文在影像亮度空间采用PC算子进行特征点检测,结合影像亮度空间的亮度稳健性和PC算子的对比度不变性实现对多光谱遥感影像辐射变化稳健的特征检测,具体步骤如下。
(1) 计算亮度空间每层亮度影像上所有像素各个方向的相位一致性度量值
式中(2) 计算每层亮度空间影像上各个像素点所有方向的相位一致性累加值as(x,y)、bs(x,y)和cs(x,y)
(3) 计算每层亮度空间影像上各个像素点的相位一致性最小矩
(4) 设置最小矩阈值t,保存相位一致性最小矩大于阈值t 的像素点,将其作为候选特征点。
(5) 将整个亮度空间各层影像上的所有候选特征点反算回原始输入影像。如果在原始影像上同一个位置存在多个不同亮度层上检测到的候选特征点,则保留相位一致性最小矩值最大的一个候选特征点。在3×3的邻域内根据相位一致性最小矩对候选特征点进行非极大值抑制,局部极大值点为最终的特征点。
2.3 计算特征尺度值得到特征点影像坐标以后,为了便于影像匹配等后续应用,需要对每个特征点确定一个特征区域。由于影像之间可能存在尺度缩放,因此在确定特征区域时,需要考虑影像尺度变化问题。本文基于尺度空间理论计算特征的尺度值,具体计算步骤如下。
(1) 对原始影像计算高斯平滑影像,并建立高斯尺度空间
式中,I(x,y)为输入影像;L(x,y,σ)为经过标准差为σ的高斯函数平滑后的影像;G(x,y,σ)为标准差为σ的高斯函数。(2) 设高斯尺度空间层数为n+1,对于每个候选特征,在各层高斯尺度空间影像上计算同一个空间位置的拉普拉斯响应值F(x,y,σi),i=0,1,2,…,n。
(3) 将各层高斯尺度空间影像的拉普拉斯响应值与其上下两层高斯尺度空间影像的拉普拉斯响应值进行比较,如果满足式(14),则该拉普拉斯极值所对应的高斯尺度空间尺度值为该特征点的尺度值
由于高斯尺度空间尺度值为离散值,获得的拉普拉斯极值往往并不是真实的连续尺度空间极值。因此,需要对获得的拉普拉斯极值及特征尺度值进行二次函数插值来逼近连续尺度空间极值点。
(4) 如果对于某个特征点p(x,y),在步骤(3)中没有找到拉普拉斯极值点,则将拉普拉斯响应值最大值点对应的尺度值作为该特征点的尺度值。
3 试验及结果分析 3.1 试验数据采用如图 3-图 5中所示的遥感影像测试本文方法的性能,并与一些经典特征检测算子进行对比试验和分析。鉴于DoG算子综合性能较好,试验选择DoG算子作为传统特征检测方法的代表。另外,由于本文方法是基于相位一致性理论提出的,因此将本文方法与经典的相位一致性PC算子进行对比分析。

|
| 图 3 试验数据1(Landsat 8影像) Fig. 3 Dataset 1(Landsat 8 images) |

|
| 图 4 试验数据2(Pleiades-1旋转影像) Fig. 4 Dataset 2( Pleiades-1 images with rotation) |

|
| 图 5 试验数据3(Pleiades-1尺度缩放影像) Fig. 5 Dataset 3(Pleiades-1 images with scale change) |
图 3所示为Landsat8影像,试验选择波段2蓝波段影像为参考影像,影像分辨率为30 m。波段3、4、5依次为绿、红、近红外影像,分辨率均为30 m。波段6和波段7为短波红外影像,分辨率为30 m。波段10和波段11为长波红外影像,分辨率为100 m。
图 4所示为2 m分辨率的Pleiades-1多光谱影像。试验选择图 4(a)中所示的波段3红波段影像为参考影像。图 4(b)中所示为波段4近红外波段影像,图 4(c)-(h)中影像为图 4(b)中波段4影像的模拟影像,与图 4(b)中所示影像分别存在30°至180°的逆时针旋转变化。
图 5中所示为2 m分辨率的Pleiades-1多光谱影像。图 5(a)中所示为波段3红波段影像,图 5(b)中所示为波段4近红外波段影像,图 5(c)-(j)中影像为图 5(b)中波段4影像的模拟影像,与图 5(b)中影像分别存在1.1至2.15倍的尺度缩放。
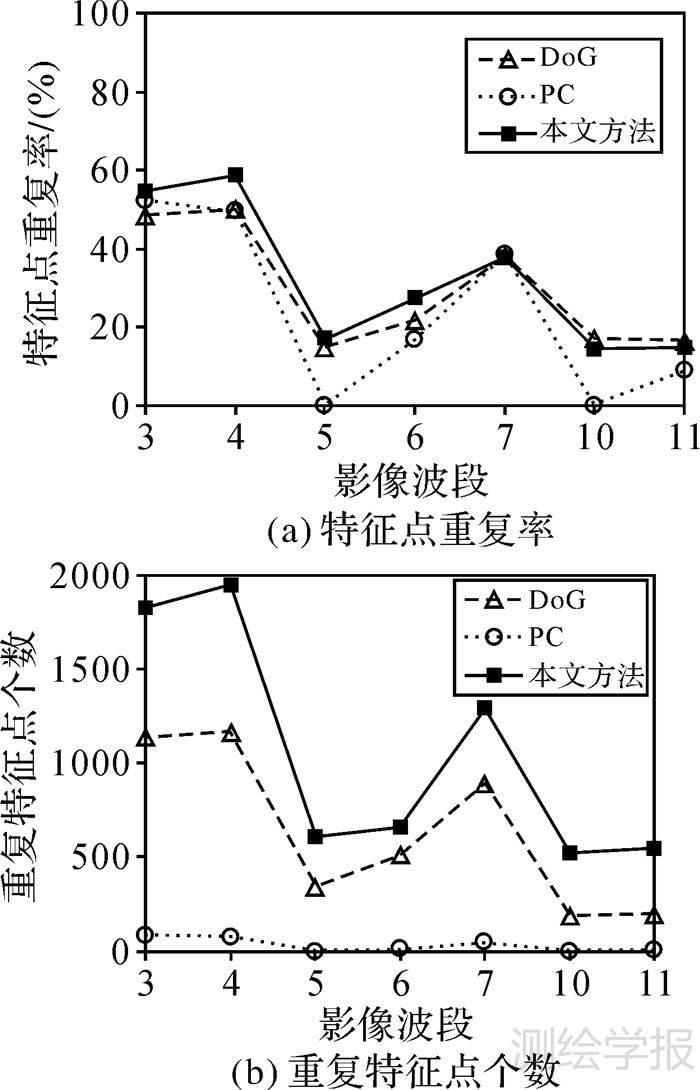
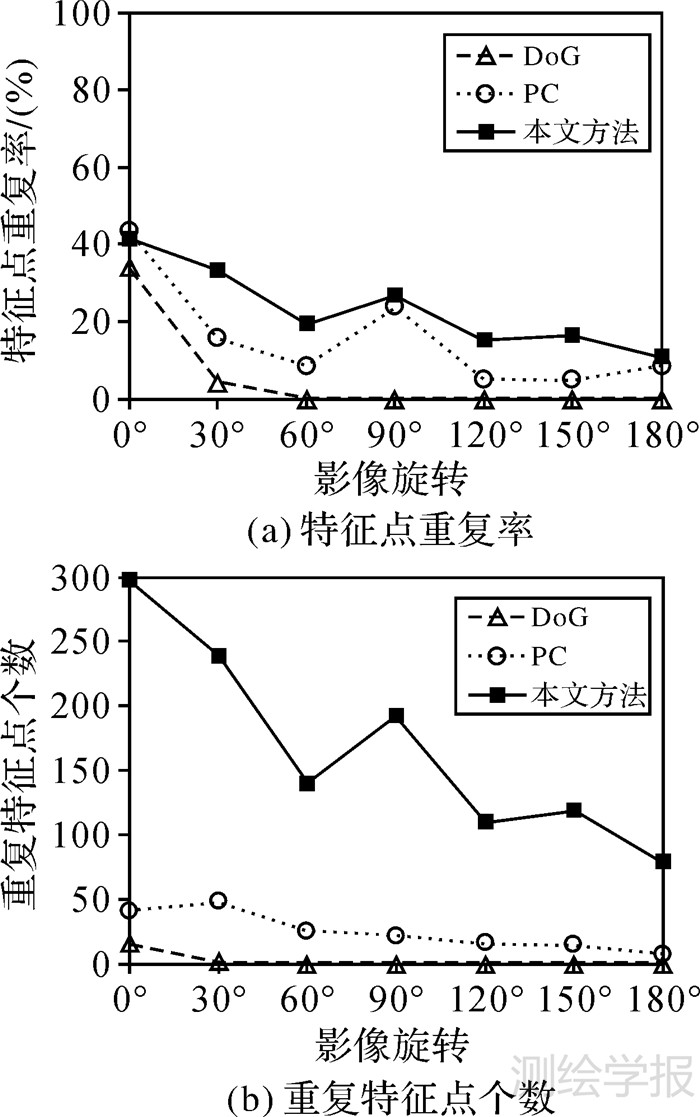
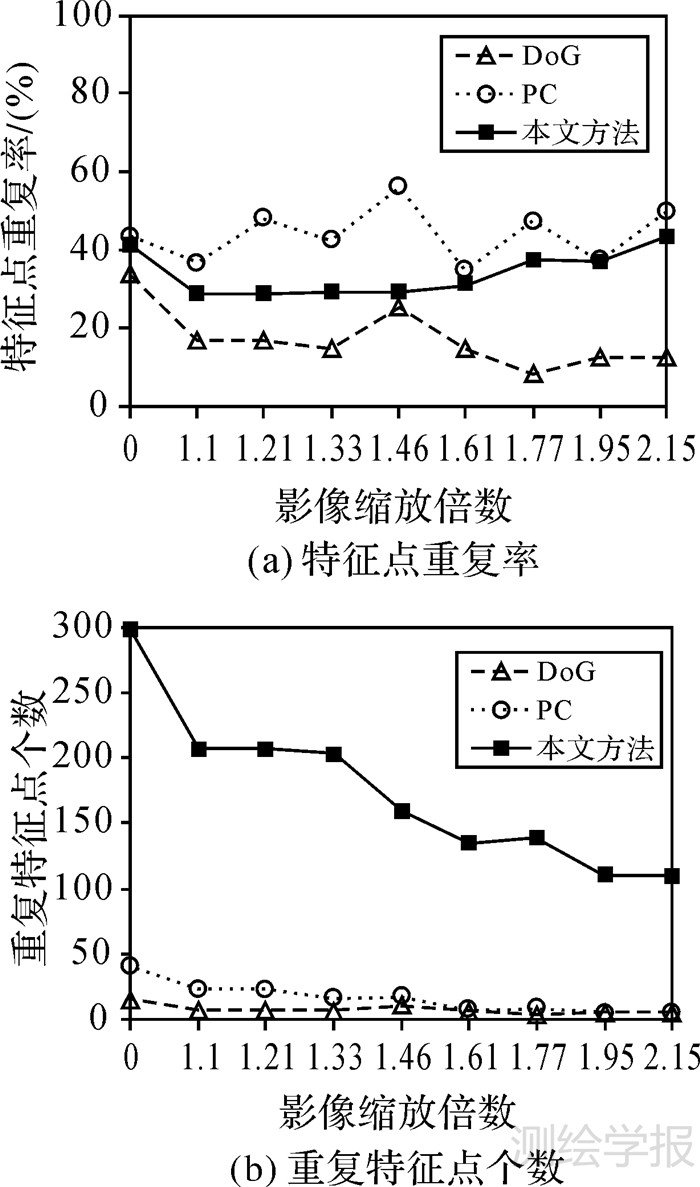
3.2 试验结果分析对比本文方法与PC算子以及DoG算子的特征点重复率和重复特征点个数,验证本文方法对影像辐射、旋转和尺度变化的稳健性。试验中统计重复特征点数量时,如果左右两幅影像上特征点位置欧氏距离小于1个像素,则认为这两个特征点为一对重复特征。特征点重复率为重复特征的个数与两幅影像上检测到的特征个数中较少的一个特征数的比值。特征点重复率及重复特征点个数试验结果分别如图 6-图 8所示。
|
| 图 6 Landsat 8影像特征点检测结果 Fig. 6 Point feature detection results of Landsat 8 images in dataset 1 |
|
| 图 7 Pleiades-1旋转影像特征点检测结果 Fig. 7 Point feature detection results of rotated Pleiades-1 images in dataset 2 |
|
| 图 8 Pleiades-1尺度变化影像特征点检测结果 Fig. 8 Point feature detection results of Pleiades-1 images with scale change in dataset 3 |
从图 6所示结果可以看出,对于Landsat 8影像,本文方法无论是特征点重复率还是重复特征点个数都表现出了最优的性能。其中,由于波段3影像、波段4影像与参考影像都是可见光波段影像,影像间灰度值差异较小,因此在这两个波段影像上特征检测重复率最高,重复特征数量最多。对于其他影像,由于处于近红外、短波红外和长波红外波段,与参考影像之间在亮度和对比度方面存在严重的差异,因此特征检测效果有所下降,但是本文方法在特征检测过程中通过亮度空间和相位一致性模型分别处理了影像的亮度和对比度变化问题,其检测效果优于PC算子和DoG算子。虽然PC算子中相位一致性模型本身能够在一定程度上适应影像之间的非线性畸变,但是对于可见光波段与红外波段这类对比度和整体亮度变化都比较大的影像,单独依靠相位一致性模型难以获得较好的结果。因此,PC算子在这类影像上的检测效果不佳。对比本文方法和PC算子,从本文方法检测特征的步骤可知,在计算特征尺度时并不会增加特征点的数量,因此本文方法相对于PC算子性能的提高完全得益于影像亮度空间的建立。同时,本文方法在建立影像亮度空间时,通过影像灰度直方图分布自适应地计算亮度变换函数的参数值,进一步提高了本文方法对影像非线性辐射畸变的稳健性。从图 7所示结果可以看出,在3种方法中,仍然是本文方法表现出了最优的性能,可见本文方法对影像旋转变化具有较强的稳健性。相比而言,当影像发生旋转时,DoG算子无论是特征重复率还是重复特征点个数都发生了急剧的下降。另外,由于试验选择的Pleiades-1影像整体亮度较低,PC算子和DoG算子受影像亮度影响较大,检测效果不理想。本文方法通过建立亮度空间使其对影像亮度变化具有较强的稳健性,因此能够获得较好的特征检测效果,特征重复率和重复特征数量都明显优于PC算子和DoG算子。在图 8所示结果中,对于影像尺度缩放,PC算子的特征点重复率高于本文方法。但是,其重复特征点个数远远少于本文方法。本文方法在保证较高特征重复率的同时能够获得更多的重复特征,更有利于后续的特征应用。
以上3组试验结果表明:本文方法在影像辐射、旋转以及尺度变化情况下均表现出很好的检测性能。在重复特征点判别阈值设置为1个像素时,本文方法依然能够获得非常多的重复特征,说明本文方法检测到的特征点定位精度非常高。接下来,对本文方法特征区域的计算性能进行试验分析。将本文方法与DoG算子进行对比试验,通过对比两种算子检测到的特征区域重复率来验证本文方法的有效性。计算特征区域重复率时,通过计算特征区域之间的区域误差来判别重复特征[21],具体试验结果如图 9所示。
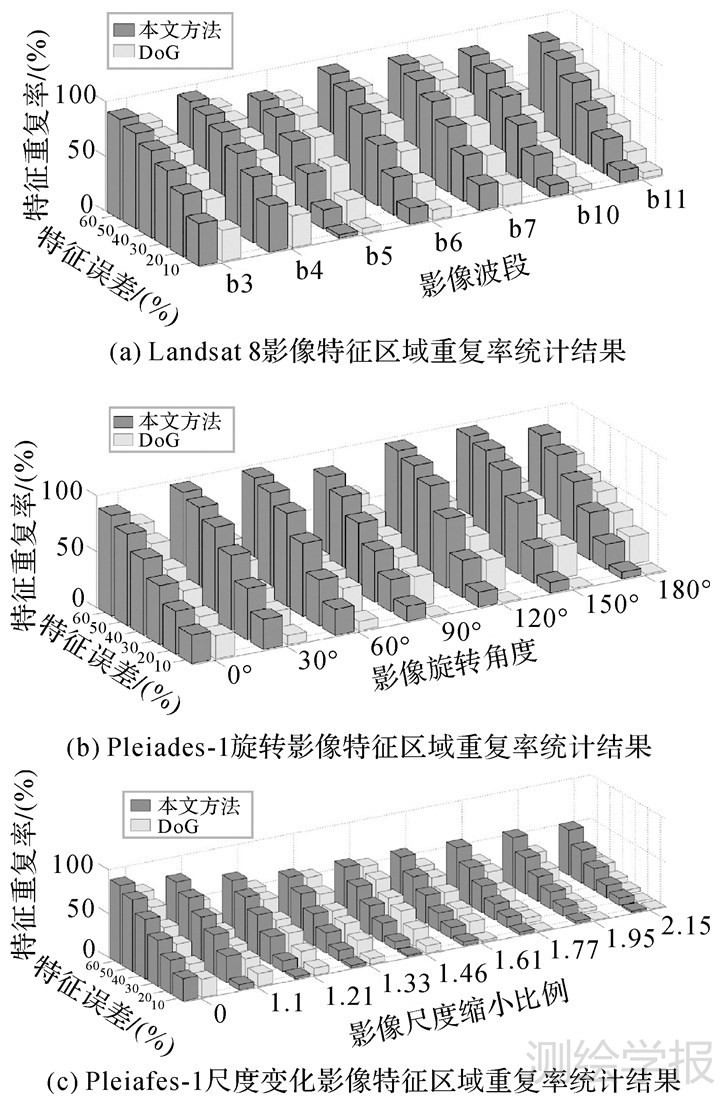
|
| 图 9 特征区域重复率统计结果 Fig. 9 Results of feature area repeatability rate |
从图 9中试验结果可以看出,在同等特征区域误差阈值下,本文方法的特征区域重复率高于DoG算子,说明本文方法在保证特征点重复的同时能够获得较准确的特征尺度值,有利于将本文方法获得的特征用于影像匹配、目标识别等其他应用。
需要指出的是,本文方法的时间效率较低。本文方法建立n层影像亮度空间,并在n层亮度空间影像上分别计算相位一致性度量值,因此本文方法的时间复杂度大约是PC算子的n倍。本文以图 3中的Landsat 8影像为试验数据,将本文方法与PC算子的时间效率进行对比,试验结果见表 1。
| 特征检测算法 | Band 2 | Band 3 | Band 4 | Band 5 | Band 6 | Band 7 | Band 10 | Band 11 |
| PC算子 | 1.198 | 1.187 | 1.196 | 1.208 | 1.190 | 1.199 | 1.216 | 1.229 |
| 本文方法 | 13.125 | 13.017 | 13.119 | 14.112 | 13.109 | 13.124 | 14.223 | 14.317 |
表 1中的数据是在Intel Core 2 2.1 GHz的 Windows XP 系统中,利用Matlab程序运行的结果。从表 1中的试验结果可以看出,由于在本文方法中影像亮度空间的层数设置为10,同时在建立亮度空间时会占用一些时间开销,因此总时间开销略大于10倍PC算子。但是,由于本文方法n层亮度影像上特征检测过程是相互独立的,可以进行并行处理。如果采用并行处理,本文方法的时间效率将大幅提升。
4 结 论本文基于相位一致性原理提出了一种对多光谱遥感影像辐射、旋转和尺度变化稳健的特征检测方法。该方法通过建立影像亮度空间提高了算法对影像亮度变化的稳健性,同时在亮度空间利用相位一致性模型进行特征点检测,有效利用了相位一致性模型对影像对比度变化的稳健性。将亮度空间与相位一致性模型有机结合,使得特征检测能够较好地克服多源遥感影像之间的辐射差异问题。大量的试验结果表明,本文方法对影像辐射变化和几何变化都具有较强的稳健性。本文方法的不足在于时间效率较低,但是由于在每层亮度影像上计算相位一致性度量值是相互独立的,因此可以进行并行运算。本文的后续工作将尝试实现特征检测的并行处理。
| [1] | HARRIS C, STEPHENS M. A Combined Corner and Edge Detector[C]//Proceedings of the 4th Alvey Vision Conference. Plessey Research Roke Manor: The Plessey Company, 1988: 147-152. |
| [2] | REISFELD D, WOLFSON H, YESHURUN Y. Context-free Attentional Operators: The Generalized Symmetry Transform[J]. International Journal of Computer Vision, 1995, 14(2): 119-130. |
| [3] | 王青松, 赵西安, 吕京国, 等. 基于高斯差分的改进Harris特征点提取算法[J]. 测绘科学, 2014, 39(4): 119-122, 134. WANG Qingsong, ZHAO Xi'an, LV Jingguo, et al. Feature Points Extraction with Improved Harris Algorithm Based on Difference of Gaussian[J]. Science of Surveying and Mapping, 2014, 39(4): 119-122, 134. |
| [4] | SMITH S, BRADT J M. SUSAN: A New Approach to Low Level Image Processing[J]. International Journal of Computer Vision, 1997, 23(1): 45-78. |
| [5] | 王巍, 赵红蕊. 面向影像匹配的SUSAN角点检测[J]. 遥感学报, 2011, 15(5): 940-956. WANG Wei, ZHAO Hongrui. The Improvement of SUSAN for Image Matching[J]. Journal of Remote Sensing, 2011, 15(5): 940-956. |
| [6] | 陈敏, 邵振峰. 一种稳健的高效角点特征检测方法提取变换[J]. 武汉大学学报(信息科学版), 2013, 38(10): 1142-1147. CHEN Min, SHAO Zhenfeng. A Robust and Efficient Feature Extract Transform[J]. Geomatics and Information Science of Wuhan University, 2013, 38(10): 1142-1147. |
| [7] | LOWE D G. Distinctive Image Features from Scale-invariant Keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91-110. |
| [8] | BAY H, ESS A, TUYTELAARS T, et al. Speeded-up Robust Features (SURF)[J]. Computer Vision and Image Understanding, 2008, 110(3): 346-359. |
| [9] | ALAHI A, ORTIZ R, VANDERGHEYNST P. FREAK: Fast Retina Keypoint[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition. Providence, RI: IEEE, 2012: 510-517. |
| [10] | HASAN M, JIA Xiuping, ROBLES-KELLY A, et al. Multi-spectral Remote Sensing Image Registration via Spatial Relationship Analysis on SIFT Keypoints[C]//Proceedings of IEEE International Geoscience and Remote Sensing Symposium. Honolulu, HI: IEEE, 2010: 1011-1014. |
| [11] | VURAL M, YARDIMCI Y, TEMIZEL A. Registration of multispectral Satellite Images with Orientation-restricted SIFT[C]//Proceedings of IEEE International, IGARSS 2009, Geoscience and Remote Sensing Symposium. Cape Town: IEEE, 2009, 3: III-243-III-246. |
| [12] | 戴激光, 宋伟东, 贾永红, 等. 一种新的异源高分辨率光学卫星遥感影像自动匹配算法[J]. 测绘学报, 2013, 42(1): 80-86. DAI Jiguang, SONG Weidong, JIA Yonghong, et al. A New Automatically Matching Algorithm for Multi-source High Resolution Optical Satellite Images[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(1): 80-86. |
| [13] | 戴激光, 宋伟东, 李玉. 渐进式异源光学卫星影像SIFT匹配方法[J]. 测绘学报, 2014, 43(7): 746-752. DAI Jiguang, SONG Weidong, LI Yu. Progressive SIFT Matching Algorithm for Multi-source Optical Satellite Images[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(7): 746-752. |
| [14] | 张谦, 贾永红, 胡忠文. 多源遥感影像配准中的SIFT特征匹配改进[J]. 武汉大学学报(信息科学版), 2013, 38(4): 455-459. ZHANG Qian, JIA Yonghong, HU Zhongwen. An Improved SIFT Algorithm for Multi-source Remote Sensing Image Registration[J]. Geomatics and Information Science of Wuhan University, 2013, 38(4): 455-459. |
| [15] | 袁修孝, 李然. 带匹配支持度的多源遥感影像SIFT匹配方法[J]. 武汉大学学报(信息科学版), 2012, 37(12): 1438-1442. YUAN Xiuxiao, LI Ran. A SIFT Image Match Method with Match-support Measure for Multi-source Remotely Sensed Images[J]. Geomatics and Information Science of Wuhan University, 2012, 37(12): 1438-1442. |
| [16] | KOVESI P. Image Features from Phase Congruency[J]. Journal of Computer Vision Research, 1999, 1(3): 2-27. |
| [17] | KOVESI P. Phase Congruency Detects Corners and Edges[C]//Proceedings of the 7th Digital Image Computing: Techniques and Applications. Sydney: [s.n.], 2003: 309-318. |
| [18] | 叶沅鑫, 单杰, 熊金鑫, 等. 一种结合SIFT和边缘信息的多源遥感影像匹配方法[J]. 武汉大学学报(信息科学版), 2013, 38(10): 1148-1151, 1260. YE Yuanxin, SHAN Jie, XIONG Jinxin, et al. A Matching Method Combining SIFT and Edge Information for Multi-source Remote Sensing Images[J]. Geomatics and Information Science of Wuhan University, 2013, 38(10): 1148-1151, 1260. |
| [19] | 叶沅鑫, 单杰, 彭剑威, 等. 利用局部自相似进行多光谱遥感图像自动配准[J]. 测绘学报, 2014, 43(3): 268-275. YE Yuanxin, SHAN Jie, PENG Jianwei, et al. Automated Multispectral Remote Sensing Image Registration Using Local Self-similarity[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(3): 268-275. |
| [20] | 李明, 李德仁, 范登科, 等. 利用PC-SIFT的多源光学卫星影像自动配准方法[J]. 武汉大学学报(信息科学版), 2015, 40(1): 64-70. LI Ming, LI Deren, FAN Dengke, et al. An Automatic PC-SIFT-based Registration of Multi-source Images from Optical Satellites[J]. Geomatics and Information Science of Wuhan University, 2015, 40(1): 64-70. |
| [21] | MIKOLAJCZYK K, TUYTELAARS T, SCHMID C, et al. A Comparison of Affine Region Detectors[J]. International Journal of Computer Vision, 2005, 65(1-2): 43-72. |