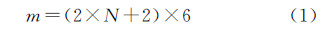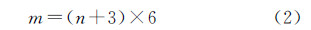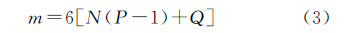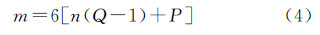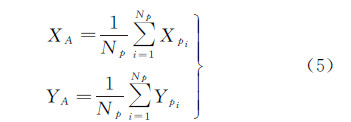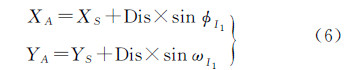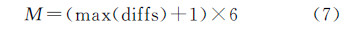传统摄影测量中,摄影交会角大小的选择和影像匹配处于一个相互矛盾的局面。在一定范围内,交会角越大,深度量测精度越高,而越大的交会角会带来更大的影像变形和地物遮挡,给影像匹配造成困难,导致匹配正确率和可靠性降低,甚至是匹配失败。针对上述问题,[文献1]提出了一种新的理论方法,即近景旋转多基线摄影技术。
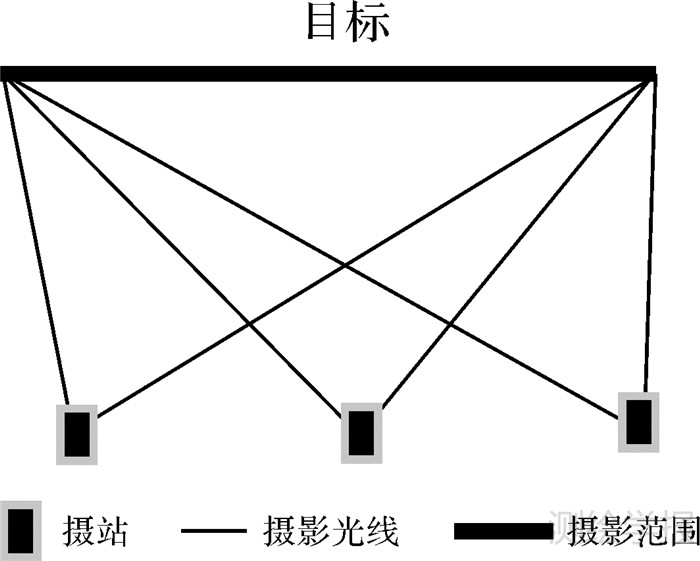
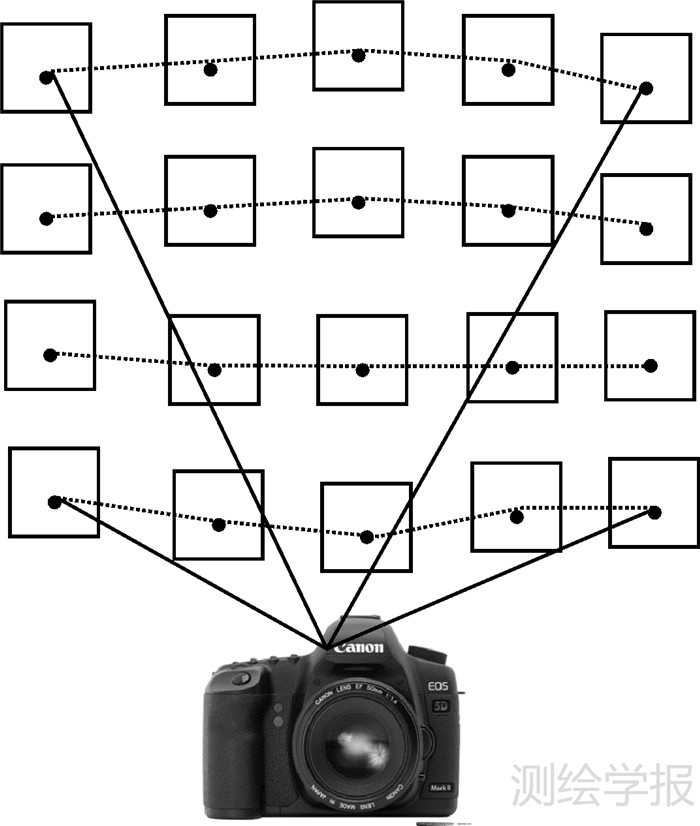
近景旋转多基线摄影,又称为旋转相机摄影,按图 1所示的方式获取数据,每个摄站上相机绕水平轴和垂直轴旋转,每旋转一个角度拍摄一张影像(同一摄站的影像分布矩阵见图 2,该摄站共拍摄了20张影像)。每个摄站上相机旋转的角度需保证相邻影像间具有足够的重叠度,并且多个摄站拍摄的相同编号的影像应尽量对应目标的同一区域,从而有利于不同摄站间匹配影像对的搜索。
|
| 图 1 旋转多基线摄影 Fig. 1 Multi-baseline rotational photography |
|
| 图 2 同一摄站影像分布矩阵 Fig. 2 Image matrix of an exposure station |
多基线摄影中,相邻的影像基线短,交会角小,首尾影像基线长,交会角大,如此结合就能较好地解决影像匹配和交会二者精度相互影响的问题[2, 3],借之能得到更高精度的物方点坐标信息,可以更好地应用到目标三维重建等研究生产当中[4];与借助多拼相机(如TOPDC-4相机,由4个指向不同方向的相机拼装组合而成)获取大范围地面覆盖度的拼接影像类似[5],通过相机旋转,也可以达到增大摄站摄影视场角,提高摄站影像地面覆盖范围的目的,借之可改善近景摄影测量中因非量测相机像幅小而产生的影响[6]。基于以上种种优点,旋转相机摄影技术已经在许多工程项目中崭露头角,如在三峡工程尾水边坡项目、部分地区水电站建设中都有所应用,并帮助解决了许多实际问题[7, 8]。
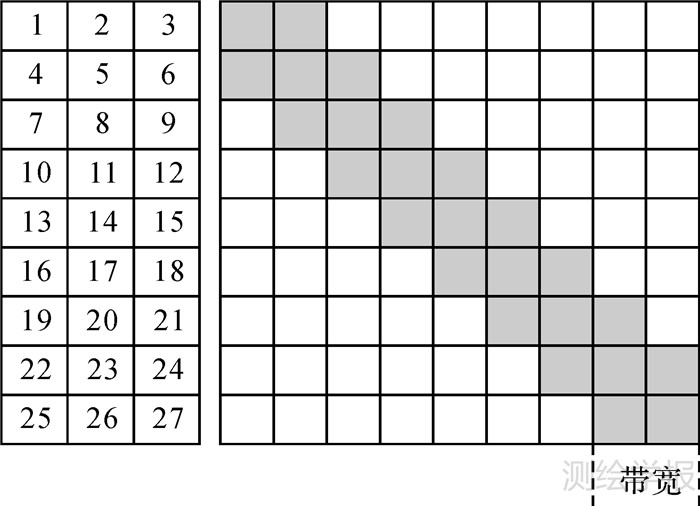
在区域网空中三角测量平差解算中,对于不同的构网形式,其法方程结构具有相同之处。如图 3所示,改化法方程系数矩阵作为对称带状稀疏矩阵,其带宽定义为矩阵主对角线到任一行最远处的非零元素间所包含的未知数个数[9]。同时,方程运算所占用的计算机存储量与带宽值大小关系密切,带宽越小,解方程的计算量和所需的计算机内存就越小[10]。由于影像编号顺序是决定带宽大小的因素之一,因而在影像数量及其他条件一定的情况下,对影像进行合适的编号,组成最小带宽的改化方程系数矩阵是空中三角测量解算中节省计算机存储量,提升平差计算速度的重要途径。
|
| 图 3 垂直于航带方向编号的带宽 Fig. 3 Bandwidth of sorting in perpendicular to strip direction |
在计算机和数学等专业领域,一些学者就减小稀疏矩阵运算带宽这一问题进行了研究,其中包含的一个概念就是通过互换矩阵中间隔排列的任何两个节点,来达到带宽值缩减的目的[11, 12]。
文献[13] 从无向图的角度出发,提出了一种根据节点间的相连情况构造图的分层,然后按照节点在分层中出现的顺序对之进行编号的方法(CM方法),该方法有助于矩阵带宽的缩减。文献[14] 指出了CM方法的不足,CM方法带宽优化的结果很大程度上依赖于根节点的选择,稳定性不好,对于许多特殊的图形也很难有较好的处理效果。文献[15] 针对CM方法的不足,提出了新的算法,对图的分层结构中的节点进行重分布,要求各层节点数尽量相同,如此能进一步减小矩阵带宽,也能适应更多的网格系统。此外,文献[16] 提出了通过计算节点商来进行编号的AD算法,该方法实现起来更为方便,但是在网格加密时对节点编号优化速度较慢。文献[17] 从最典型的最佳二维网格节点编号的特性及规律出发,对原有的AD法进行改进,提出了一种新的编号方法,在数据适用性以及优化速度上都有所提升。
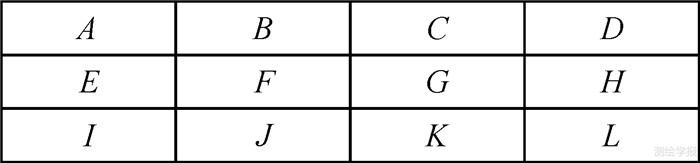
在航空摄影测量生产中面临大型稀疏矩阵的计算问题时,通常采用的是最典型、最简单的二维网格节点编号的方法来缩减带宽。如图 4所示,航带规则分布的情况下,可以在垂直于航带方向编号(图 3)和沿航带方向编号二者中选择一种更为合适的方式来求解最小带宽(目前已有成熟的计算公式可以使用[8, 9])。
|
| 图 4 以A—L为影像中心的规则航带 Fig. 4 Regular strips with A—L as image centers |
在不规则分布的航摄成果下,使用理论公式计算出的带宽值只是预计的带宽最小值,并不一定能代表实际的数值。因此,需要采用合适的方式对影像进行重新编号,得到影像逻辑顺序,进而使其实际带宽接近于预期最小值。在传统摄影测量中,可以借助摄站位置的平面坐标来完成影像的排序编号,进而求解最优带宽[8]。与航拍中一个摄站拍摄一张影像不同,在旋转相机摄影中,每个摄站都拍摄多张影像,即存在一系列影像具有相同的摄站坐标。摄站重叠分布、航带信息特殊等特点都使得在旋转相机摄影测量中无法使用上述传统的对影像排序编号并求解最小带宽的方法。
本文提出的针对旋转相机摄影数据优化光束法区域网平差法方程系数矩阵带宽的方法,充分结合数据的自身特点,利用影像间的相互联系及影像地面覆盖范围,为每张影像计算出一个近似的等效摄站位置,然后按等效摄站间的位置关系,根据其X、Y坐标值,分别在水平和垂直两个方向上对之进行编号并求解带宽,取两个方向中较小带宽值及其对应的编号形式作为最终结果。
1 影像编号及带宽求解 1.1 传统规则航带光束法区域网平差最小带宽计算光束法区域网平差是以一张影像所组成的一束光线作为平差的基本单元,以中心投影共线方程作为平差的基本方程,以每张影像的6个外方位元素及待定点的物方坐标作为未知数来进行解算(自检校光束法区域网平差[18, 19]中,还引入了包含若干附加参数的系统误差模型,因此待求解的未知数更多)。对于航带分布规则的摄影成果,在消除待定点坐标未知数之后,构成的改化法方程系数矩阵的最小带宽可按以下方式计算[8, 9]。
垂直于航带方向编号的带宽计算公式为
沿着航带方向编号的带宽计算公式为
式中,N为航带数;n为一条航带中的影像数;m为带宽。上述公式默认航带为航向3°重叠,旁向2°重叠,借之可推导得出以下一般公式。
垂直于航带方向编号的带宽计算一般公式为
沿着航带方向编号的带宽计算一般公式为
式中,P为航向重叠数;Q为旁向重叠数(80%重叠度对应重叠数为5)。上述公式适用于规则分布的航摄成果,可以得到带宽的理论最小值。本文提出的旋转多基线摄影光束法平差法方程矩阵带宽优化方法,其解算过程包括等效摄站计算、影像编号以及带宽计算等步骤。
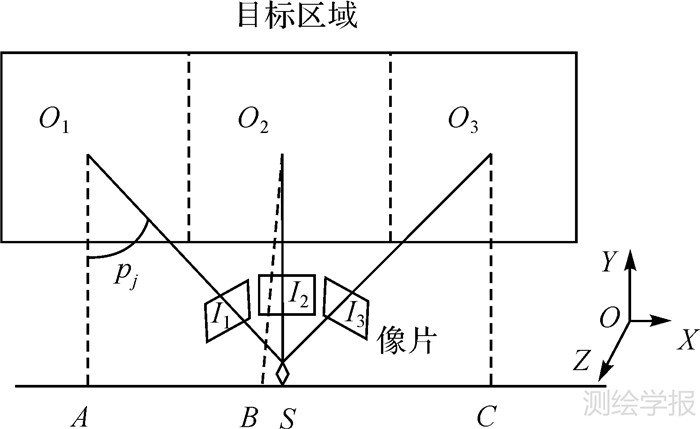
1.2 等效摄站坐标计算如图 5所示,在摄站S处相机旋转到不同的角度拍摄得到3张影像I1、I2、I3,它们对应的实际地面范围分别为O1、O2、O3区域(3个区域有一定重叠)。图中A、B、C 3点分别与O1、O2、O3区域的中心在XOY平面上具有相同的位置。这里,将A、B、C称为对应影像的等效摄站,文中使用两种方法来求解其平面坐标X、Y。
|
| 图 5 等效摄站示意图 Fig. 5 Illustration of equivalent exposure stations |
方法1: 物方范围中心作为等效摄站平面位置。对于影像I1,其等效摄站A与区域O1的中心在XOY平面上重合,因此A的平面坐标可近似为O1范围内所有物方点平面坐标的平均值,计算公式为
式中,Np为O1区域内物方点个数;Xpi、Ypi 为各物方点的平面坐标;XA 、YA为等效摄站A的物方平面坐标。方法2:根据几何关系确定等效摄站平面位置。 由图 5可知,对于影像I1,相机位置S、影像覆盖地面范围中心O1及其等效摄站A构成直角三角形O1AS,线段AS为点A相对于点S在X方向上的偏量,借助这一偏量和S的坐标值XS,即可求出XA值。三角形O1AS中,pj角大小为相机绕垂轴Y旋转的角度,近似于影像外方位角元素φ,在已知摄距O1S的情况下,可以计算出偏移量AS的值。同样,相机绕水平轴X旋转的角度近似为外方位角元素ω,借之可以求出Y方向的偏量,从而得到等效摄站坐标YA。上述过程计算公式为
式中,Dis 为当前摄站对于目标区域O1的摄距,即相机位置S到O1内所有物方点重心的距离; XS、YS、XA、YA分别为摄站S和等效摄站A的平面坐标;φI1、ωI1 为影像I1的两个外方位角元素。上述两种方法确定等效摄站位置都依赖于交会求出的每张影像覆盖范围内的物方点坐标,数据中难免会存在未能成功匹配出同名点的影像(后文称之为匹配无效的影像),它们将无法被正常纳入等效摄站系统。考虑匹配无效的影像与其他数据邻接情况较差,可以人为将其等效摄站平面坐标设为较大值(不在整个测区物方坐标范围之内),等效视其覆盖范围处于较为偏远的位置,这也与匹配结果情况相符。试验时也对匹配无效的影像的等效摄站坐标进行了调整(较大值、较小值或测区范围内的随机值),以验证其位置对编号及带宽的具体影响,从而指导获得最佳的编号方式,进而使平差过程中的矩阵运算带宽达到最优。
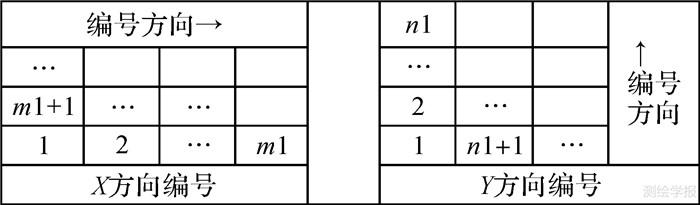
1.3 影像排序编号以将匹配无效的影像等效摄站坐标设为较大值为例,求出各影像等效摄站平面坐标后,分别在X和Y两个方向上对之进行编号,得到影像的逻辑序号。如顺着Y方向编号,首先建立一组平行于Y轴的直线,平行线间隔为XOY平面内等效摄站间的最短距离。除匹配无效的影像外,平行线在X方向的覆盖范围需将其他所有影像的等效摄站的X坐标全部包含在内。如此,摄站点就分布于平行线组成的区间之中。
如图 6所示,按区间顺序从左到右,所有落在同一区间的摄站点自下而上进行编号。将区间内所有影像编号完毕后,再继续对匹配无效的影像进行编号。由于匹配无效的影像排在最后,不会影响其他影像的编号顺序,而且它们内部之间并无邻接,相互独立,所以这一过程中不必考虑匹配无效的影像之间的先后顺序关系。
|
| 图 6 不同方向影像排序示意图 Fig. 6 Illustration of image sorting by different directions |
空中三角测量平差解算改化法方程系数矩阵中,对角线外的某单元处是否有非零元素,确定于其相应两个摄站间是否有共同的连接点。光束法区域网平差中,改化法方程以影像的6个外方位元素作为未知数,若某个加密点落在带有逻辑序号i和j的摄站点对应的影像中,就要在法方程式第i行第j列中加入一个6×6子矩阵。求出所有的连接点各自所在摄站的最大最小序号之差,将最大的差值加1就是该编号形式下的最大带宽子块数,带宽计算公式如下
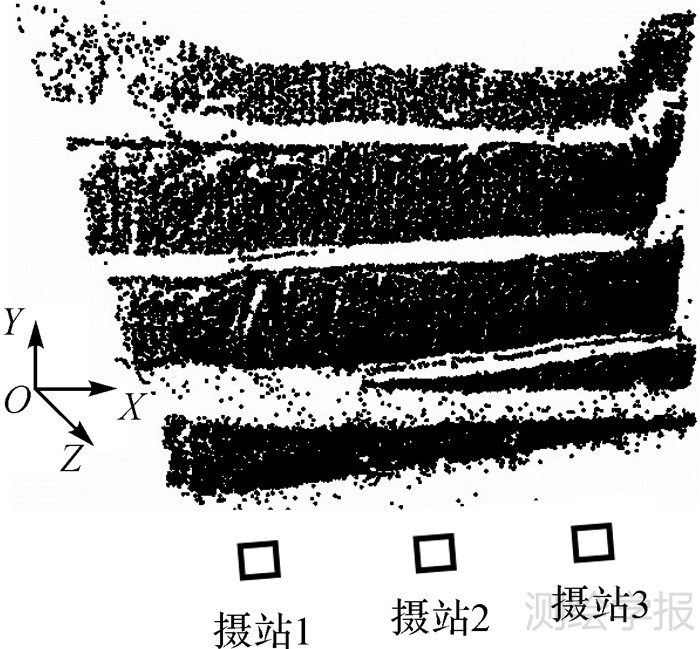
式中,M为带宽值;max(diffs)表示连接点所在影像的最大最小序号之差的最大值。 2 试验与分析 2.1 数据说明为了验证本文算法的有效性,使用3组三峡船闸边坡影像数据(图 7)进行试验。由于船闸立于长江之上,地理位置特殊,这给野外监测架站带来困难,旋转相机摄影可减少实地摄站数的优势在这里也得到体现。试验所用3组旋转相机摄影数据基本情况见表 1,每组数据都分3个摄站完成拍摄 ,摄站与被摄目标的位置关系如图 8所示,其中摄站1、2、3为架站位置,-Z为拍摄方向,X、Y 为相机水平、垂直旋转扫描方向。

|
| 图 7 拍摄目标:三峡船闸边坡 Fig. 7 Photogrammetric object: Three Gorges ship lock slope |
| 组别 | 场景宽 /m | 场景高 /m | 摄站数 | 摄影距离 /m | 影像数 |
| 1 | 150 | 60 | 3 | 270 | 1325 |
| 2 | 150 | 60 | 3 | 270 | 602 |
| 3 | 80 | 40 | 3 | 130 | 407 |
|
| 图 8 摄站与被摄目标关系示意图 Fig. 8 Illustration of relationship among exposure stations and photogrammetric object |
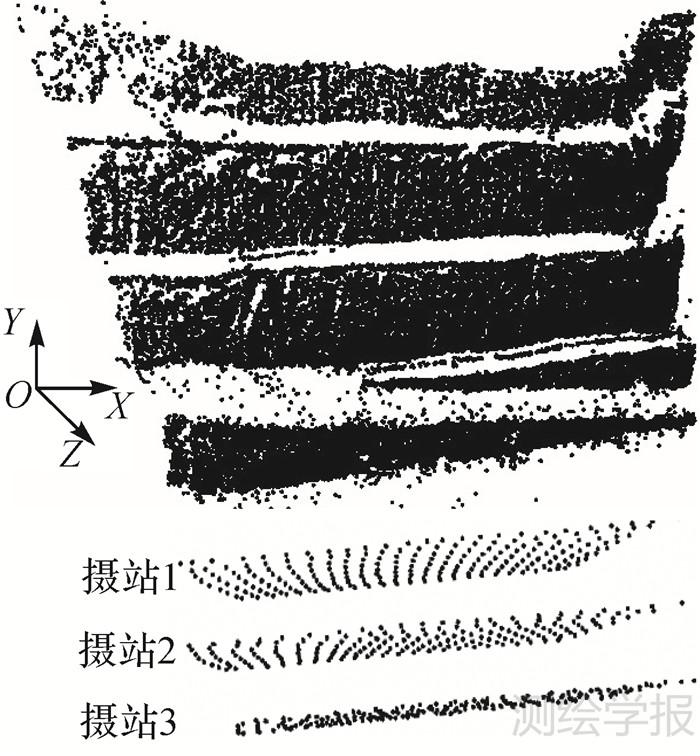
图 9所示为使用方法1求出的等效摄站分布情况(方法2结果与之相近),其中摄站1、2、3对应的3块点云分别为原始3个摄站所拍摄影像的等效摄站位置。由于等效摄站的坐标Z值等于影像原始摄站的Z坐标,因此所有的等效摄站形成3个相互平行且与Z轴垂直的区域,每一个区域表示了原始同一个摄站处所有影像实际地面范围中心的分布。3个区域分布相近,这与旋转相机摄影中,每一个摄站上拍摄的对应顺序的影像对准目标同一区域的情况相符。将所有等效摄站投影到同一个垂直于Z轴的平面上,就形成了待编号的影像资料。
|
| 图 9 等效摄站分布 Fig. 9 Distribution of equivalent exposure stations |
由图 2可以看出,同一摄站上相机在水平方向的旋转具有一定重复性,即若将水平旋转角作为 X轴,垂直旋转角作为Y轴,对于同一摄站的影像,相机旋转角度分布近似为一组朝X 方向延伸,且相互平行的直线(由于旋转角度分布并非严格意义的平行直线,为避免混淆,后文称之为扫描线)。有别于航空摄影,旋转相机摄影中并没有“航带”的定义,然而,考虑与航摄中非规则航带影像的排序编号相联系,为便于说明,这里将上述每一条扫描线所代表的一组影像视作一条“航带”,3个摄站的“航带”数之和被认为是本组影像数据的“航带”数估计值。由此估计值,应用航摄中规则航带求解最小带宽的公式进行带宽计算,取二者结果中的较小值作为本文方法结果的理论参考。
在旋转相机摄影中,不同摄站中对应顺序的影像拍摄目标的同一区域,它们之间具有很大的重叠。试验所用数据,各“航带”航向以及旁向重叠度均达到80%以上,因此具有5°甚至7°重叠。
为了便于比较分析,试验时以5°重叠和7°重叠计算理论带宽,并与所提出的两种方法的带宽优化结果进行对比。同时,为表达本文方法在保障处理精度的情况下对矩阵带宽进行缩减,进而减少运算占用内存方面具有的优化效果,进一步按照文献[8] 介绍的区域网平差法方程运算占用内存估算方法(字节数=影像数×带宽×6×8)计算各组试验优化前后所需内存,并且使用同一套软件对优化前后的数据进行平差,做更为直观的比较分析。另外,试验使用的数据中并不包括匹配无效的影像,操作中人为额外添加几张影像(与其他所有影像无匹配点)来进行模拟试验,借之探究匹配无效的影像对编号及带宽的影响。上述试验结果如表 2—表 5所示。
| 组别 (影像数) | 航带数 航带影 像数 | 带宽 初始值 | 带宽参考值 | 方法1 带宽 | 方法2 带宽 | |
| 5°重叠 | 7°重叠 | |||||
| 1(1325) | 36 37 | 5718 | 894 | 1338 | 1656 | 1632 |
| 2(602) | 25 25 | 2952 | 630 | 942 | 1236 | 1254 |
| 3(407) | 23 18 | 1824 | 462 | 690 | 750 | 702 |
| 组别 | 影像数 | 初始值/MB | 方法1/MB | 差值/MB | 优化率/(%) |
| 1 | 1325 | 346.8 | 100.4 | 246.4 | 71.0 |
| 2 | 602 | 81.3 | 34.1 | 46.8 | 57.6 |
| 3 | 407 | 34.0 | 14.0 | 20.0 | 58.8 |
| 组别 | 原始平差结果/m | 方法1平差结果/m | 方法2平差结果/m | ||||||
| RMSx | RMSy | RMSz | RMSx | RMSy | RMSz | RMSx | RMSy | RMSz | |
| 1 | 0.003 9 | 0.003 2 | 0.002 7 | 0.003 9 | 0.003 3 | 0.002 8 | 0.004 0 | 0.003 2 | 0.002 7 |
| 2 | 0.003 3 | 0.003 3 | 0.003 9 | 0.003 4 | 0.003 5 | 0.003 9 | 0.003 2 | 0.003 3 | 0.003 9 |
| 3 | 0.003 0 | 0.001 0 | 0.003 0 | 0.003 1 | 0.001 0 | 0.003 1 | 0.003 1 | 0.000 1 | 0.003 1 |
| 组 别 | 影像 数 | 初始优 化带宽 (方法1) | 匹配 无效 影像数 | 匹配无效影像处于不同等 效摄站位置下的优化带宽 | ||
| 较小值 | 较大值 | 随机值 | ||||
| 1 | 1325 | 1656 | 5 | 1656 | 1656 | 1674 |
| 2 | 407 | 750 | 5 | 750 | 750 | 774 |
| 3 | 407 | 750 | 10 | 750 | 750 | 774 |
表 2中,带宽初始值为按影像原始拍摄顺序进行编号,使用式(7)求出的带宽;参考值作为理论估值,是使用式(3)、式(4)求出的最小带宽,但是受实际数据获取方式、目标起伏情况等现实因素的影响,理论估值不是实际最小带宽;本文提出的方法最终结果与7°重叠情况下的理论带宽比较接近,相对初始值有了很大改进。此外,3组试验中分别使用文中的两种方法求出的带宽值差别很小,证明了借助等效摄站对影像重新编号从而优化带宽这一方法的可行性。
表 3中,3组试验内存优化率都大于50%。第1组1325张影像,数据量最大,其平差矩阵运算占用内存优化率最高,超过70%。以上结果表明,在近景旋转多基线摄影测量中,使用本文方法进行带宽优化,进而减少运算内存开销,这是切实有效的。
表 4中,3组试验数据各自带宽优化前后,使用同一套软件平差处理的结果基本保持不变,这直接说明了在近景旋转多基线摄影测量光束法区域网平差中,使用本文方法进行法方程矩阵带宽优化,进而提升平差运算效率,对最终平差结果的精度不会产生负面影响。
表 5是辅助性验证的结果,基于匹配结果所反映的影像间的邻接关系,将匹配无效的影像的等效摄站坐标值设为较大值或较小值时,其他影像间的相对顺序关系并不会发生改变,最终带宽优化结果也不会受到任何影响;当匹配无效的影像的编号介于其他影像之间时,最终带宽优化结果将受到不同程度的影响。因此,在影像排序操作中,可让匹配无效的影像独立于其他影像之外,排在最前或是最后,在不影响平差结果精度的同时,也能使带宽优化效果达到最佳,进而最大程度地提升平差处理效率。
3 结 论本文在传统的对不规则航摄成果进行影像编号求解平差法方程矩阵带宽的理论基础上,提出了一种借助等效摄站对近景旋转多基线摄影影像进行排序编号,进而优化光束法区域网平差法方程矩阵带宽的方法。该方法考虑了旋转多基线摄影获取数据时摄站内部和摄站之间的邻接联系,充分利用了目标空间位置信息这一物方稳定量,带宽优化效果明显,能在不影响平差解算结果精度的情况下,一定程度上节省平差矩阵运算过程对计算机内存的消耗。同时,使用不同的等效摄站求解方法最终都能得到较为稳定的结果,这说明该思路用于解决近景旋转多基线摄影测量中平差法方程矩阵带宽优化问题是可行有效的。
此外,由于旋转多基线摄影系统提供了每张影像的姿态角近似值,是否能够使用相机角度关系进行影像重新编号,进而对带宽进行优化,这是后期研究的主要目标。
| [1] | 张祖勋,吴百川. 一种数字近景摄影测量方法: CN101226057[P]. 2010-10-27. ZHANG Zuxun, WU Baichuan. A Method of Digital Close Range Photogrammetry: CN101226057[P]. 2010-10-27. |
| [2] | 张军, 刘安伟. 旋转多基线摄影测量浅析[J]. 矿山测量, 2013(2): 53-56. ZHNAG Jun, LIU Anwei. Analysis of Multi-baseline Rotational Photogrammetry[J]. Mine Surveying, 2013(2): 53-56). |
| [3] | 张剑清, 胡安文. 多基线摄影测量前方交会方法及精度分析[J]. 武汉大学学报(信息科学版), 2007, 32(10): 847-851. ZHANG Jianqing, HU Anwen. Method and Precision Analysis of Multi-baseline Photogrammetry[J]. Geomatics and Information Science of Wuhan University, 2007, 32(10): 847-851. |
| [4] | 郑顺义, 张祖勋, 翟瑞芳. 基于非量测相机的复杂物体三维重建[J]. 武汉大学学报(信息科学版), 2008, 33(5): 446-449. ZHENG Shunyi, ZHANG Zuxun, ZHAI Ruifang. 3D Reconstruction of Complex Objects Based on Non-metric Image[J]. Geomatics and Information Science of Wuhan University, 2008, 33(5): 446-449. |
| [5] | 徐斌, 李英成, 刘晓龙, 等. 附加约束条件的光束法区域网平差在四拼数码航空相机平台检校中的应用[J]. 测绘学报, 2014, 43(1): 66-73, 82. XU Bin,LI Yingcheng,LIU Xiaolong,et al.The Application of Bundle Block Adjustment with Constraint Conditions in Platform of Four-head Aerial Digital Camera[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(1): 66-73, 82. |
| [6] | 柯涛, 张祖勋, 张剑清. 旋转多基线数字近景摄影测量[J]. 武汉大学学报(信息科学版), 2009, 34(1): 44-47, 51. KE Tao, ZHANG Zuxun, ZHANG Jianqing. Panning and Multi-baseline Digital Close-range Photogrammetry[J]. Geomatics and Information Science of Wuhan University, 2009, 34(1): 44-47, 51. |
| [7] | 张祖勋, 杨生春, 张剑清, 等. 多基线-数字近景摄影测量[J]. 地理空间信息, 2007, 5(1): 1-4. ZHANG Zuxun, YANG Shengchun, ZHANG Jianqing, et al. Multi-baseline Digital Close-range Photogrammetry[J]. Geospatial Information, 2007, 5(1): 1-4. |
| [8] | 赵文峰, 王斌, 关泽群. 多基线近景摄影测量在边坡位移监测中的应用研究[J]. 工程勘察, 2014, 42(5): 68-71. ZHAO Wenfeng, WANG Bin, GUAN Zequn. Multi-baseline Digital Close Range Photogrammetry in the Slope Displacement Monitoring[J]. Geotechnical Investigation & Surveying, 2014, 42(5): 68-71. |
| [9] | 王之卓. 摄影测量原理[J]. 测绘通报, 1979(4): 48. WANG Zhizhuo. The Principle of Photogrammetry[J]. Bulletin of Surveying and Mapping, 1979(4): 48. |
| [10] | 李德仁, 郑肇葆. 解析摄影测量学[M]. 北京: 测绘出版社, 1992. LI Deren, ZHENG Zhaobao. Analytical Photogrammetry[M]. Beijing: Surveying and Mapping Press, 1992. |
| [11] | 李波. 矩阵带宽的最小化[J]. 科技资讯, 2007(17): 152-153. LI Bo. Bandwidth Minimization of Matrix[J]. Science & Technology Information, 2007(17): 152-153. |
| [12] | 林诒勋. 稀疏矩阵计算中的带宽最小化问题[J]. 运筹学学报, 1983, 2(1): 20-27. LIN Yixun. Bandwidth Minimization Problem in Sparse Matrix Computations[J]. Chinese Journal of Operations Research, 1983, 2(1): 20-27. |
| [13] | CUTHILL E, MCKEE J. Reducing the Bandwidth of Sparse Symmetric Matrices[C]//Proceedings of the 1969 24th National Conference. New York, NY: ACM, 1969: 157-172. |
| [14] | GIBBS N E, POOLE JR W G, STOCKMEYER P K. An Algorithm for Reducing the Bandwidth and Profile of a Sparse Matrix[J]. SIAM Journal on Numerical Analysis, 1976, 13(2): 236-250. |
| [15] | 郑志镇, 李尚健, 李志刚. 稀疏矩阵带宽减小的一种算法[J]. 华中理工大学学报, 1998, 26(12): 43-45. ZHENG Zhizhen, LI Shangjian, LI Zhigang. A New Algorithm for Reducing Bandwidth of Sparse Matrix[J]. Journal of Huazhong University of Science & Technology, 1998, 26(12): 43-45. |
| [16] | AKHRAS G, DHATT G.An Automatic Node Relabelling Scheme for Minimizing a Matrix or Network Bandwidth[J]. International Journal for Numerical Methods in Engineering, 1976, 10(4): 787-797. |
| [17] | 黄志超, 包忠诩, 周天瑞. 有限元节点编号优化[J]. 南昌大学学报(理科版), 2004, 28(3): 281-284. HUANG Zhichao, BAO Zhongxu, ZHOU Tianrui. Automatic Node Reordering for Finite Element Analysis[J]. Journal of Nanchang University(Natural Science), 2004, 28(3): 281-284. |
| [18] | 王建梅, 朱紫阳. 利用已有像控点的多期航空影像光束法区域网联合平差[J]. 测绘学报, 2010, 39(1): 22-27. WANG Jianmei, ZHU Ziyang. Combined Bundle Block Adjustment Based on Existing Ground Control Points and Multi-period Aerial Imagery[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 22-27. () |
| [19] | 李德仁. 论自检校区域网平差中的信噪比[J]. 测绘学报, 1982, 11(3): 170-184. LI Deren. On the Signal-to-noise Ratio in Self-calibrating Block Adjustment[J]. Acta Geodaetica et Cartographica Sinica, 1982, 11(3): 170-184. |