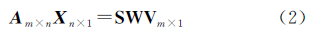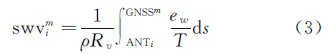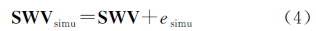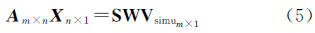2. 中国科学院上海天文台,上海 200030;
3. 同济大学测绘与地理信息学院,上海 200092
2. Shanghai Astronomical Observatory, Chinese Academy of Sciences, Shanghai 200030, China;
3. College of Surveying and Geo-informatics, Tongji University, Shanghai 200092, China
随着GNSS气象学的发展,GNSS对空间大气的探测逐步从一维的可降水量[1, 2]发展到三维的空间水汽分布[3, 4, 5]。卫星到测站的每一个观测值对应着一条观测路径方向上的水汽延迟量(slant water vapor,SWV),包含了该路径方向上水汽的分布信息。层析技术可以将SWV还原为空间水汽并重构水汽的分布情况,其主要计算方法为最小二乘求逆。对稀松矩阵求逆容易出现欠定和病态的情况,微小的变动都可能引起整体结果不稳定甚至出现完全不同的结果[6]。很多研究人员尝试了一些改进方案以解决求逆困难的问题,最常见的是为观测方程增加约束条件。文献[7]在中纬度地区采用标准大气资料作为先验分布;文献[8]利用地面气象站的数据对没有观测数据的空格网进行内插以获得初始信息;文献[9, 10]采用Kalman滤波的方法既解决病态方程问题又避免了借助其他传感器附加约束条件的限制。代数重构技术[11, 12, 13, 14]具有解算稳定及迭代次数较少的优点,被用来代替法方程求逆过程;拟合插值法[15, 16, 17]等从本质上说都属于附加约束条件的方法,但是都有明确的准则来确定参数。目前存在的研究方法均从现有观测条件出发,采用其他物理观测手段和数学处理方法在空格网和有观测数据的格网间建立函数关系,通过这种方式获得稳定性的水汽空间分布。但是从另一个方面考虑,如果能获得数量多、覆盖广、几何分布较好的斜路径观测值,也可以改善观测方程中的系数矩阵。而这种方式是直接通过卫星导航系统的观测值求解水汽分布,较少地使用数学模型干预。
本文分析了在长三角地区现有监测网条件下,采用多模GNSS观测进行水汽层析试验的效果。首先介绍水汽层析基本原理和本文采用的仿真试验方法,然后对长三角地区GNSS监测网现状以及多模GNSS观测值的质量进行分析描述,最后用模拟仿真的方式进行多系统层析试验,并比较单一的GNSS和多模GNSS层析结果。
1 水汽层析原理和仿真试验水汽层析的思想是将GNSS区域上空的对流层大气离散化,即在水平和垂直方向上等间距地划分成许多立体单元格,每个格网具有相同体积。假设在指定观测时间段内每个格网包含的水汽密度是均匀的,在解算时设为一个未知参数xi,j,k,GNSS信号穿过大气时在格网内截取的长度ai,j,k作为系数,对于一条观测路径可以列出观测方程为
式中,swv为某一时刻一颗卫星到一个测站观测路径方向上的水汽延迟量。对于一个区域,在某一时间段内,所有观测方程可以用矩阵形式表达 式中,Am×n为系数阵,表示全部有效信号在格网内截取的长度,m为观测值数量,n为格网数量;Xn×1为参数向量表示格网水汽值;SWVm×1为所有观测路径的水汽延迟量。对于现有的GNSS观测网络而言,测站的几何结构较差,观测值分布不均匀给层析解算带来一定困难。研究显示,通过加密GNSS观测网能够从整体上提高层析的精度,主要是改善了底层格网内水汽的垂直结构[18]。在区域观测站数量不变的情况下,采用多个卫星导航系统在任意时刻都可以接收15颗以上的卫星信号,比单一的GNSS增加了3倍以上的观测值。另外,多模GNSS融合具有减弱系统相关误差,数据冗余特性好以及显著提高时空分辨率等优势[19],在水汽层析解算过程中能够改善观测网络几何结构差带来的问题。
由于目前GNSS观测网络接收机还不具备同时接收四大导航系统卫星信号的功能,因此本文采用模拟仿真的方法进行试验研究。这里的模拟仿真主要指对流层大气中湿大气成分在卫星到接收机路径上的水汽密度值。根据ECMWF资料提供的气压(P)、温度(T)和比湿(h)可以计算湿折射率,进而能够积分出一条观测路径上的斜方向水汽值。用公式可以表达为
式中,Rv=461.5 J/(kg·K);ρ=103g/m3;水汽压ew=h×P/0.622。积分路径为第m颗GNSS卫星到第i个接收机ANT的观测路径。顾及实际观测中观测噪声和离散误差的存在,为模拟观测值加入一定量的随机误差esimu,则观测值向量为
按照式(2)的形式可以形成观测方程,即
经过层析计算以后的网格水汽值越接近模拟值,说明层析效果越好。文中试验所采用的水汽模拟值和模拟斜路径观测值均根据ECMWF资料中的气象参数通过模型计算获取。欧洲数值天气预报资料(ECMWF)提供了较高分辨率的气象参数,数据的时间分辨率为6 h,每天0、6、12、18时有气象参数值,平面分辨率为0.5°×0.5°的格网。分层数据每个格网点上有60层的数据,包括海拔高度、温度、比湿和气压等;地面数据有地面气压、2 m露点温度、2 m温度[20];数据文件为.nc格式,需要用程序读取转换。
2 长三角GPS监测网现状本文所研究的长三角地区包括江苏、上海、浙江北部以及安徽大部,范围在29°N—35°N,116°E—122°E之间。目前研究区域内已经获得连续观测数据的测站70个,相邻基准站之间的距离为3到200 km,平均距离约为57 km。测站分布不均匀,区域东北角海域无基准站,安徽和浙江基准站较少,上海和江苏地区站点相对比较密集,平均站间距约为50 km,距离在30 km以内的测站约7个,主要集中在上海地区。从现有测站分布情况来看,上海测站密度相对较大,安徽省内和浙江大部分地区测站稀疏,存在大片的无测站区域。测站的不均匀分布会对层析计算造成困难[18]。
由于长三角地区现有GPS测站几何分布不均匀,其观测值在空间就会产生分布过密和分布稀疏的区域,造成观测信息的不平衡。在水平分辨率为0.3°和垂直分辨率500 m的条件下,空间格网空格率高于50%,即超过一半的格网不能被观测信息覆盖,而同时有部分格网因测站密集积累了过剩观测信息。对于观测方程来说,系数阵呈现病态,微小的扰动都会对层析结果产生很大影响。所以单一的导航观测在长三角区域存在观测分布不均的现象,对层析解算不利。
3 多模GNSS用于水汽层析的分析 3.1 GNSS简介GNSS是指全球卫星导航系统,包括美国的全球定位系统(GPS)、俄罗斯的卫星导航系统(GLONASS)、欧盟的伽利略定位系统(Galileo)和我国的北斗卫星导航系统(BDS)。
3.2 多系统观测值质量分析单一导航系统提供的观测值在空间分布上呈现出不均匀的状态,并且随观测时段的变化观测值分布会发生转移[21]。对于GPS来说,一个测站最多同时观测到12颗卫星,最少可以同时观测到6颗。在测站数量一定的情况下有限的卫星数很难提供充足的观测值,更难以满足均匀覆盖大气的要求。目前地面GPS监测网测站数量很难实现对空间格网的全面覆盖,在分辨率为0.3°×0.3°×500 m的时候,1 h观测时段内格网平均空格率高于60%。增加GPS监测网基准站数量可以改善观测值在空间分布的质量,降低格网空格率。除此以外,通过接收GLONASS、Galileo和BDS的卫星信号,也可以增加斜路径观测值[22],较之单系统增加观测时间来提高观测数量,多系统观测值的组合在空间分布上更加均匀,可以在更多方向上覆盖空间格网。图 1表示一个历元内测站的多系统观测值在天顶方向的分布情况。图 1的中心点为测站天顶方向,顺时针方向0~360°表示测站到卫星的方位角范围,箭头所指位置为观测值方位角的大小,箭头长度表示高度角的余弦值,该值越大,箭头越长,则表示高度角越低。可以看出,多系统观测值角度变化范围大,在空间分布更均匀。
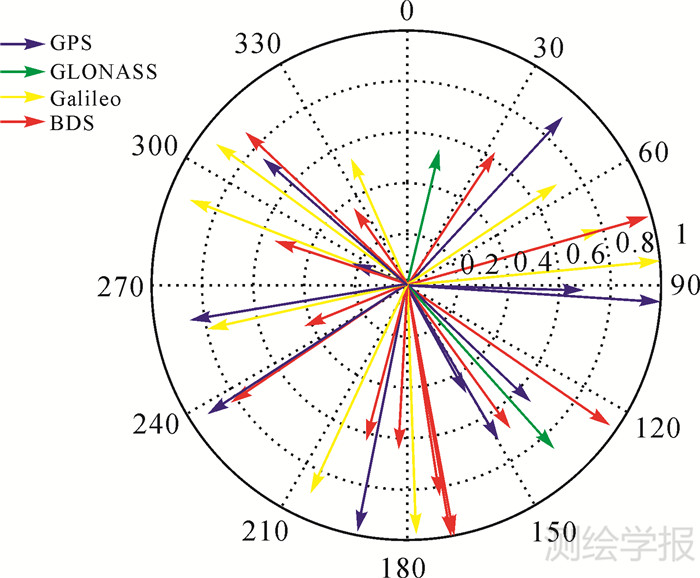
|
| 图 1 测站在一个历元内接收的多系统观测值 Fig. 1 The distribution of GNSS slant delays at one epoch |
格网的空格率从侧面反映了观测值的空间分布情况。空间分辨率发生变化时,相同的观测值在空间内的分布情况也会发生改变,穿过格网的观测值数量和覆盖面随着空间分辨率的提高而降低。
可靠的层析解算需要角度变化范围广、能够覆盖研究区域大气全部格网的观测值。对于同一种空间分辨率,导航系统的增加为研究区域提供了更多种高度和方位的观测值,但是仍有大量格网不能被观测值覆盖。随着导航系统的增加,观测值数量也成倍增长。
当只采用一个导航系统的观测值时,约有一半数量的格网没有观测信息,其中GPS的平均空格率约为47%,BDS的平均空格率约为52%,GLONASS的平均空格率约为51%,Galileo的空格率约为50%。采用两个系统或者更多系统的组合观测值则可以改善这种情况。GPS与BDS、GLONASS、Galileo组合观测值覆盖下,格网6 h内(1 h为观测时段)的平均空格率分别为44%、43%和44%。同时采用4个导航系统的观测数据,格网平均空格率可以下降到39%(图 2)。
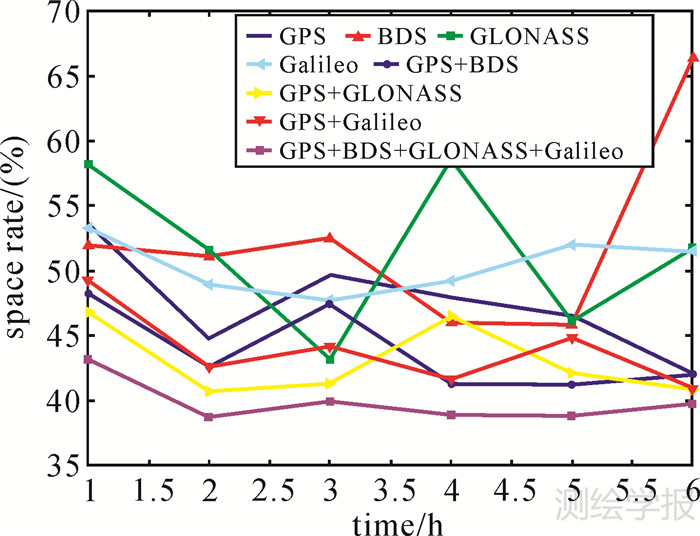
|
| 图 2 多系统观测值在连续6h内的格网空格率变化情况 Fig. 2 The space rate of GNSS slant delays in six hours |
在一个观测时段内(UTC 0:00—1:00时段),GPS和其他3个系统的组合观测值对不同层格网的影响也不一样。如图 3所示,GNSS的组合观测值未能在大气底层改善格网的覆盖情况,但是随着高度的增加,空格率下降很快。可以看出多系统组合观测值对中高层大气覆盖较好,对于改善中高层大气的格网空格率具有良好效果。改善底层格网的覆盖情况只有通过加密测站才能实现。图中分析了UTC 0:00—1:00时段内各层格网的平均空格率,其中GPS+BDS平均空格率47%;GPS+GLONASS平均空格率47%;GPS+Galileo平均空格率49%;4个系统组合观测值平均空格率42%。可以看出,4个导航系统的组合观测值可以改善有限时段内观测值在空间分布的状况,有利于提高层析结果的质量。
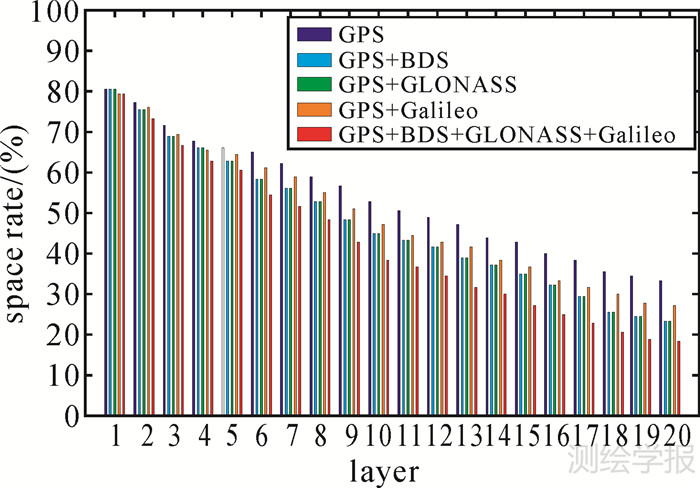
|
| 图 3 GPS与BDS、GLONASS、Galileo系统组合观测值下的各层空格率 Fig. 3 The space rate of combination observations by two or four satellite systems in each layer |
图 4反映了单系统(GPS)观测值和多系统(GNSS)组合观测值在相同观测条件下分别在顶层格网的分布情况。图上蓝色由深到浅逐渐变为红色表示了格网内观测值数量的从少到多。可以看出,多系统组合观测值可以增强原被覆盖区域,同时增加了覆盖的范围,将一部分空格网纳入被观测值覆盖的区域。
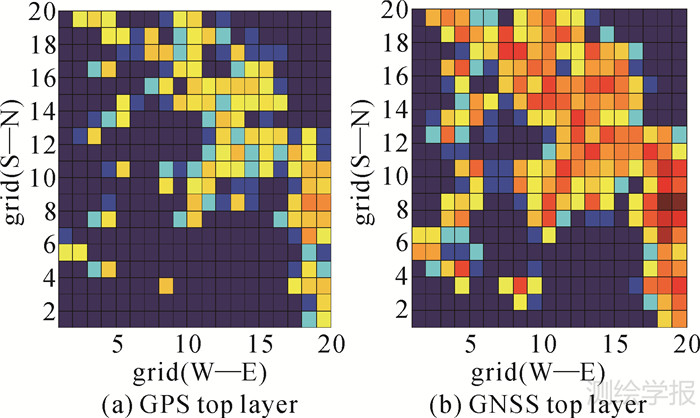
|
| 图 4 不同导航系统观测值在格网顶层的覆盖情况 Fig. 4 Grid coverage at top layer by GPS and GNSS observations respectively |
以长三角地区GNSS观测网络为例进行试验研究。假设长三角观测网络内所有测站接收机可以接收四大导航系统信号,选择2009年9月2日UTC 0:00—0:30作为研究时段,GPS和GLONASS采用IGS网站公布的精密星历,BDS和Galileo则分别模拟了全部卫星轨道。每个测站的观测路径均由测站位置坐标和卫星轨道确定,观测值根据气象资料在观测路径上积分得出。具体仿真步骤为:
(1) 选取研究区域大气格网水平分辨率0.3°和垂直分辨率500 m进行层析计算。
(2) 假设采样率30 s,确定观测时段内所有观测路径方向上观测值与相应格网的截距,并形成系数矩阵A。
(3) 根据式(3)和式(4)仿真每一历元卫星到测站间斜向观测路径的观测值并形成观测方程。
(4) 水平方向采用高斯加权函数进行约束,垂直方向用处理后的数值预报资料(ECMWF)作为背景场,处理方法为内插计算格网内平均水汽值,为每个格网水汽增加合理的随机误差。另外再为观测方程增加边界约束。
(5) 层析常采用的求逆以及奇异值分解法已经无法满足当前解算的需要,因此采用联合迭代重构算法[11, 12, 13, 14]对参数x 进行迭代。
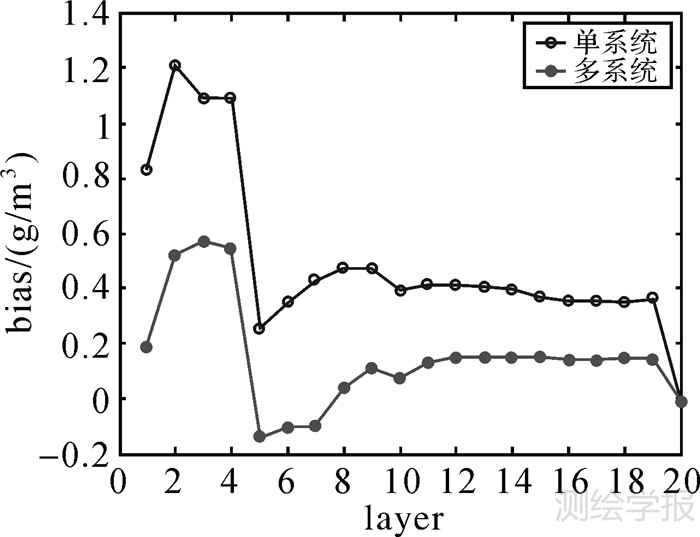
3.4 试验结果分析本文采用均方根误差和平均偏差作为层析质量的判别标准,以数值预报资料内插的格网水汽作为比较的标准值,分析单系统和多系统的层析质量。层析解算后,单系统和多系统层析解算的均方根误差和平均偏差见表 1。可以看出,多系统整体层析精度无论是均方根误差还是平均偏差,均高于单系统层析精度。图 5中可以看出多系统层析在每一层的平均偏差都小于单系统,多系统层析结果在2.5 km以上更接近标准值。
| g/m3 | ||
| 参数 | 单系统(GPS) | 多系统(GNSS) |
| rms | 0.82 | 0.69 |
| bias | 0.50 | 0.15 |
|
| 图 5 单系统和多系统层析后各层平均偏差 Fig. 5 Compared the mean bias of GPS tomography with GNSS tomography in each layer |
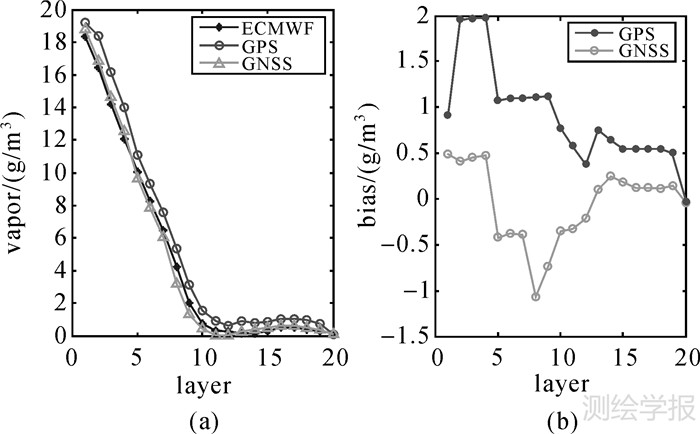
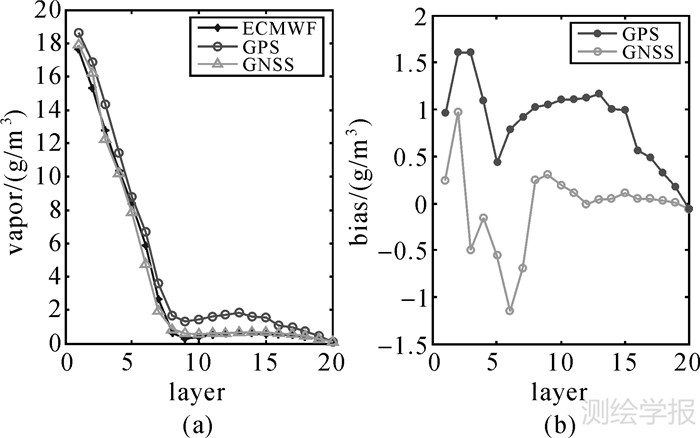
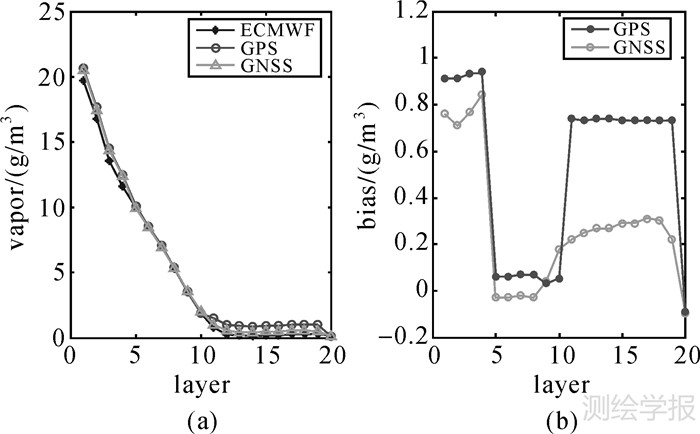
图 6—图 8给出了单系统(GPS)和多系统(GNSS)层析的水汽垂直轮廓线。试验采用了相同的GNSS监测网,不同的是观测值对周围格网的覆盖情况,为了比较两个系统的层析结果,按照测站在格网平面中的位置从所有格网中选取了3列格网进行对比分析,分别代表了3种情况:①测站在格网中心(30°N—31°N,116°E—117°E);②测站靠近格网的边缘(30°N—31°N,118°E—119°E);③测站在格网外(在相邻格网内,30°N—31°N,119°E—120°E)。图 6(a)、图 7(a)、图 8(a)比较了单系统、多系统与ECMWF资料在同一列格网内的水汽垂直轮廓线。图 6(b)、图 7(b)与图 8(b)为单系统与标准值的偏差量以及多系统与标准值的偏差量。3种情况下,多系统层析结果均优于单系统。对于图 6,单系统层析结果与ECMWF之间的偏差随高度增加整体呈下降趋势,偏差最大值出现在2 km高度上,多系统层析结果的偏差在0附近上下摆动,大气6 km以上偏差接近0。图 7中,单系统层析结果整体大于ECMWF资料,最大偏差量为1.6 g/m3,多系统层析结果在近地面4 km范围内波动较大,4 km以上的格网水汽偏差逐渐降为0。由图 8可以看出,多系统层析结果优于单系统,使用多系统进行层析,5 km以上区域的水汽层析精度明显提高。
|
| 图 6 测站处于格网水平面中心时水汽轮廓线的比较和各层平均偏差 Fig. 6 The water vapor profiles and mean bias in each layer when station at the middle of the grid |
|
| 图 7 测站处于格网水平面边缘时水汽轮廓线的比较和各层平均偏差 Fig. 7 The water vapor profiles and mean bias in each layer when station at the edge of the grid |
|
| 图 8 格网内无测站时水汽轮廓线的比较和各层平均偏差 Fig. 8 The water vapor profiles and mean bias in each layer when no station at the grid |
可以说,多模GNSS观测值的使用弥补了单系统观测值分布不均的状况,在空间方位和数量上提供了完整的观测信息,也为空间格网提供了更为丰富的水汽信息,对层析结果的改善具有十分明显的作用,尤其能够改善地面3 km以上的格网水汽的精度。但是大气底层水汽的垂直分布不均匀无法通过增加卫星的方法弥补,而应该采用加密GNSS网测站的方式进行改善。
4 结 论本文针对现有GPS监测网测站分布不均的状况,采用多模GNSS观测值进行改善,并对多模GNSS观测值进行了质量分析。可以从格网空格率和观测值在格网中的分布情况看出多系统观测值角度变化范围大,在空间分布更均匀,能够弥补单系统观测值分布不均的状况,为空间格网提供更为丰富的水汽信息。相同观测条件下,多模GNSS可以降低空间格网的空格率,尤其可以改善大气中上层格网的观测值覆盖情况。
根据数值预报资料(ECMWF)仿真出高度角10°以上的斜路径观测值,对GPS单系统和多模GNSS进行水汽层析的仿真试验,给出了部分格网的垂直轮廓线并进行精度分析和比较。多系统层析结果的均方根误差和平均偏差均优于单系统层析结果。从水汽垂直轮廓线来看,多系统层析在改善中高层大气的垂直结构方面具有优势。
总的来说,使用多系统组合观测值(GPS+BDS+GLONASS+Galileo)进行层析很大程度上提高了层析结果的精度,组合观测值在空间分布上更加均匀,即使是1个历元测站也可以获得在360°范围内分布较为均匀的观测值。由于观测数量的增加和观测质量的提高,为提高格网时间和空间分辨率创造了良好的条件。但是多系统观测值在近地面的大气范围内分布较差,增加卫星数量不能解决底层格网的观测问题,应该通过加密GNSS监测网的方法进行改善。
致谢:感谢IGS、ECMWF以及iGMAS提供数据。
| [1] | BEVIS M, BUSINGER S, HERRING T A, et al. GPS Meteorology: Remote Sensing of Atmospheric Water Vapor Using the Global Positioning System[J]. Journal of Geophysical Research, 1992, 97(D14): 15787-15801. |
| [2] | BEVIS M, BUSINGER S, CHISWELL S, et al. GPS Meteorology: Mapping Zenith Wet Delays onto Precipitable Water[J]. Journal of Applied Meteorology, 1994, 33(3): 379-386. |
| [3] | FLORES A, RUFFINI G, RIUS A. 4D Tropospheric Tomography Using GPS Slant Wet Delays[J]. Annales Geophysicae, 2000, 18: 223-234. |
| [4] | SEKO H, SHIMADA S, NAKAMURA H, et al. Three-dimensional Distribution of Water Vapor Estimated from Tropospheric Delay of GPS Data in a Mesoscale Precipitation System of the Baiu Front[J]. Earth, Planets Space, 2000, 52(11): 927-933. |
| [5] | MACDONALD A E, XIE Yuanfu, WARE R. Diagnosis of Three Dimensional Water Vapor Using Slant Observations from a GPS Network[J]. Monthly Weather Review, 2002, 130 (2): 386-397. |
| [6] | NOTARPIETRO R, CUCCA M, GABELLA M. Tomographic Reconstruction of Wet and Total Refractivity Fields from GNSS Receiver Networks[J]. Advances in Space Research, 2011, 47(5): 898-912. |
| [7] | CHAMPOLLION C, MASSON F, BOUIN M N, et al. GPS Water Vapour Tomography: Preliminary Results from the ESCOMPTE Field Experiment[J]. Atmospheric Research, 2005, 74(1-4): 253-274. |
| [8] | TROLLER M, GEIGER A, BROCKMANN E, et al. Tomographic Determination of the Spatial Distribution of Water Vapor Using GPS Observations[J]. Advances in Space Research, 2006, 37(12): 2211-2217. |
| [9] | CHAMPOLLION C, FLAMANT C, BOCK O, et al. Mesoscale GPS Tomography Applied to the 12 June, 2002 Convective Initiation Event of IHOP_2002[J]. Quarterly Journal of the Royal Meteorological Society, 2009, 135(640): 645-662. |
| [10] | 张双成, 叶世榕, 万蓉, 等. 基于Kalman滤波的断层扫描初步层析水汽湿折射率分布[J]. 武汉大学学报(信息科学版), 2008, 33(8): 796-799, 809. ZHANG Shuangcheng, YE Shirong, WAN Rong, et al. Preliminary Tomography Spatial Wet Refractivity Distribution Based on Kalman Filter[J]. Geomatics and Information Science of Wuhan University, 2008, 33(8): 796-799, 809. |
| [11] | JIN Shuanggen, LUO O F, PARK P. GPS Observations of the Ionospheric F2-layer Behavior during the 20th November, 2003 Geomagnetic Storm over South Korea[J]. Journal of Geodesy, 2008, 82(12): 883-892. |
| [12] | STOLLE C, SCHLVTER S, HEISE S, et al. A GPS Based Three-dimensional Ionospheric Imaging Tool Process and Assessment[J]. Advances in Space Research, 2006, 38(11): 2313-2317. |
| [13] | 王维, 王解先. 联合迭代重构算法在对流层水汽三维重构中的应用研究[J]. 大地测量与地球动力学, 2011, 31(6): 100-103, 120.WANG Wei, WANG Jiexian. Application of Simultaneous Iterations Reconstruction Technique for 3D Water Vapor Tomography System[J]. Journal of Geodesy and Geodynamics, 2011, 31(6): 100-103, 120. |
| [14] | WANG Wei, YE Biwen, WANG Jiexian. Application of a Simultaneous Iterations Reconstruction Technique for a 3-D Water Vapor Tomography System[J]. Geodesy and Geodynamics, 2013, 4(1): 41-45. |
| [15] | 叶世榕, 江鹏, 刘炎炎. 地基GPS网层析水汽三维分布数值积分方法[J]. 测绘学报, 2013, 42(5): 654-660. YE Shirong, JIANG Peng, LIU Yanyan. A Water Vapor Tomographic Numerical Quadrature Approach with Ground-based GPS Network[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(5): 654-660. |
| [16] | 夏朋飞, 蔡昌盛, 戴吾蛟, 等. 地基GPS联合COSMIC掩星数据的水汽三维层析研究[J]. 武汉大学学报(信息科学版), 2013, 38(8): 892-896. XIA Pengfei,CAI Changsheng, DAI Wujiao, et al. Three-dimensional Water Vapor Tomography Using Ground-based GPS and COSMIC Occultation Observations[J]. Geomatics and Information Science of Wuhan University, 2013, 38(8): 892-896. |
| [17] | 于胜杰, 柳林涛. 利用选权拟合法进行GPS水汽层析解算[J]. 武汉大学学报(信息科学版), 2012, 37(2): 183-186. YU Shengjie, LIU Lintao. Application of Fitting Method by Selection of the Parameter Weights on GPS Water Vapor Tomography[J]. Geomatics and Information Science of Wuhan University, 2012, 37(2): 183-186. |
| [18] | 王维, 宋淑丽, 王解先, 等. 长三角地区GPS斜路径观测值分布分析[J]. 大地测量与地球动力学, 2013, 33(2): 151-154, 159. WANG Wei,SONG Shuli,WANG Jiexian,et al.Distribution of GPS Slant Delay for Water Vapor Tomography in Yangtze River Delta[J]. Journal of Geodesy and Geodynamics, 2013, 33(2): 151-154, 159. |
| [19] | 何丽娜. 多系统GNSS卫星精密轨道确定的研究[D]. 上海: 同济大学, 2013. HE Lina. The Research of Multi-GNSS Satellite Precise Orbit Determination[D]. Shanghai: Tongji University, 2013. |
| [20] | 陈钦明, 宋淑丽, 朱文耀, 等. 利用GPS ZTD检验ECMWF-NCEP分析和预报资料在中国地区的适用性[C]//第一届中国卫星导航学术年会论文集. 北京: [s.n.], 2010. CHEN Qinming, SONG Shuli, ZHU Wenyao, et al. Assessment of ECMWF-NCEP Analysis and Forecast Data with GPS ZTD in China[C]//Proceedings of the 1st symposium of CNSC. Beijing: [s.n.], 2010. |
| [21] | BENDER M, DICK G, WICKERT J. Estimates of the Information Provided by GPS Slant Data Observed in Germany Regarding Tomographic Applications[J]. Journal of Geophysical Research, 2009, 114(D6): D06303. |
| [22] | BENDER M, STOSIUS R, ZUS F, et al. GNSS Water Vapour Tomography-expected Improvements by Combining GPS, GLONASS and Galileo Observations[J]. Advances in Space Research, 2011, 47(5): 886-897. |