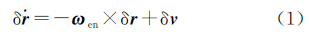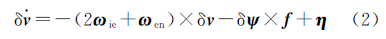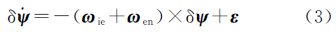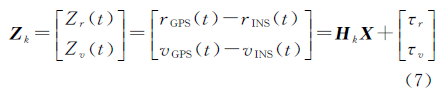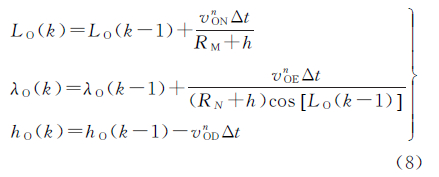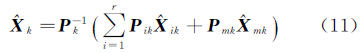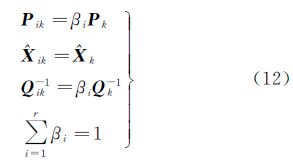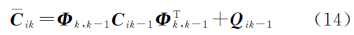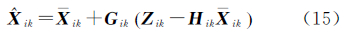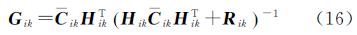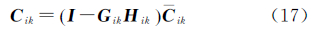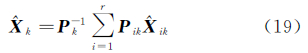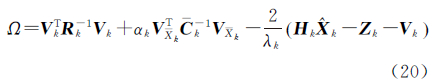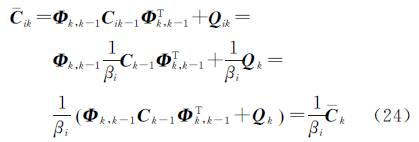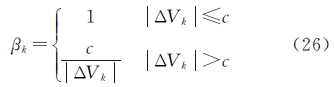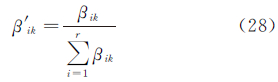2. 中国矿业大学环境与测绘学院，江苏 徐州 221116
2. School of Environment Science and Spatial Informatics, China University of Mining and Technology, Xuzhou 221116, China
全球定位系统(GPS)和惯性导航系统(INS)的测量值具有互补特性[1]，GPS-INS组合导航可以利用两个系统的优点，通过信息融合减小各系统对组合导航总体精度的影响。GPS需要接受卫星信号才能实现观测的目的，因此具有一定的局限性[2]。GPS-INS组合导航过程中，引入更多的传感器[3](里程计、磁力计)可以较好地提高系统的可观测性。Odometer无需外部信号输入，不存在信号遮挡的问题，因此，其被较多地引入GPS-INS组合导航系统中。
在GPS-INS-Odometer组合导航系统中，Odometer与INS系统的数据融合误差状态方程多引入Odometer的刻度因子[4]，尤其是对于低精度Odometer，以实现对Odometer误差的修正。与此同时，里程计的安装偏差对里程计的位置速度解算影响较大，需要对其精确估计并实时更新[5]。在Odometer航位推算算法中，微路程增量变换算法被提出并应用[6]，能够充分利用里程增量信息以提高航位推算精度。杆臂效应是影响GPS-INS-Odometer组合系统导航的精度的一个重要因素，通过补偿算法能够消除由于杆臂效应引起的坐标转换等方面的误差[3]。组合导航的信息融合一般采用Kalman滤波技术，一些改进的滤波方法也被应用于GPS-INS-Odometer组合系统[7, 8]。
当组合传感器的个数大于等于3个的时候，滤波解算的状态向量参数较多，而且滤波输入中包括多传感器的观测信息，因此计算效率较低，联邦滤波器在不失估计无偏性[9, 10]的情况下可以将滤波器拆分[11]，大幅度提高计算效率[12]，在多传感器数据融合计算时具有较大的优势。在利用GPS、INS、伪卫星[13]和天文导航[14]等方法进行组合的过程中，联邦滤波器均实现了较好的应用效果。
在运用联邦滤波器进行GPS-INS-Odometer组合系统等多传感器数据融合的过程中，往往只注重计算效率的提高，信息分配因子只是起到了分配计算量的作用，并没有充分发挥联邦滤波器对不同传感器的信息调节能力。联邦滤波器的信息分配因子直接作用于权矩阵，因此还可以起到状态参数权值调节的作用，从而可以削弱动力学模型误差对于状态参数的影响。本文在GPS-INS-Odometer组合导航的基础上，分析了联邦滤波器和自适应滤波器的等价性，推导了等价性成立的条件，构建了自适应联邦滤波器，并应用于GPS-INS-Odometer组合导航系统。
1 GPS-INS-Odometer组合导航 1.1 动力学模型组合导航动力学模型的构建基于INS误差方程，在线性化的过程中非重要的项被忽略了[15]
式中，δr、δv和δψ分别是位置、速度和方向误差向量；ωen是地理坐标系相对于地球坐标系的旋转角速度矢量；ωie是地球坐标系相对于惯性坐标系的旋转角速度矢量；f是加速度计测量的比力矢量。加速度误差向量η和陀螺误差向量ε近似于随机游走过程模型，其模型表达式为[16] 式中，uη和uε是高斯白噪声向量。
综合上述各式，动力学模型用矩阵形式表达[17]
式中，X为误差状态向量；F为系统状态转移矩阵；u为状态过程噪声向量，其协方差矩阵为Qk。 1.2 GPS-INS观测模型
取GPS和INS输出的位置和速度之差作为观测值，构造观测量[18]，则Kalman滤波的量测方程为
式中，Zr(t)是t时刻滤波位置观测量；Zv(t)是滤波速度观测量；rGPS(t)是GPS的位置观测值；rINS(t)是INS的位置计算值；vGPS(t)是GPS的速度观测值；vINS(t)是INS的速度计算值；Hk为观测矩阵；τ为观测噪声，满足高斯白噪声特性，其协方差矩阵为Rik。 1.3 INS-Odometer观测模型
Odometer的位置计算是通过速度积分得到的，Odometer的速度信息采集属于离散采样，可以推导出Odometer的位置计算方法
式中，LO、λO和hO为Odometer计算得到的经度、纬度和高度；RM和RN分别为载体所在地点地球子午圈和卯酉圈曲率半径；vONn、vOEn和vODn为导航坐标系下北东地3个方向的速度值；(k-1)表示里程计k-1时刻的信息；(k)表示里程计k时刻信息；Δt为里程计采样时间间隔。GPS和Odometer传感器都可以测量出载体的位置和速度，所以Odometer-INS观测模型类似于GPS-INS观测模型，只需将式(7)中GPS测量的位置和速度替换为里程计测量的位置和速度。 2 联邦滤波器与自适应滤波器的等价性 2.1 联邦滤波器
将联邦滤波器应用于GPS-INS-Odometer组合导航系统中，可以分解为GPS-INS组合子滤波器和Odometer-INS组合子滤波器，GPS和Odometer传感器的观测值相互独立，而且两个子滤波器的状态方程均与主系统的状态方程一致。GPS-INS-Odometer组合导航系统的动力学模型如式(6)，第i个子系统的观测方程可以统一表示为
设子滤波器的滤波估计值、主滤波器滤波估计值和全局融合导航解分别为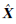
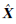ik、mk和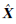k，相应的权矩阵为Pik、Pmk和Pk，协方差矩阵分别为Cik、Cmk和Ck，下标ik表示k时刻第i个子滤波器的信息，下标mk表示k时刻主滤波器的信息，下标k表示k时刻全局滤波器的信息。
设传感器的数量为r，在传感器独立的基础上，联邦滤波器的融合解为[12]
在GPS-INS-Odometer组合导航系统中，各子滤波器的状态向量相同，因此设计主滤波器中无信息分配，在主滤波器中执行误差状态变量及其协方差阵的时间更新，即Pmk=0。
假设全局状态估计值为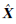k，权矩阵为Pk，根据信息守恒原理，通过分配因子βi把权矩阵分配到子传感器，分配原则为[19]
各子滤波器时间更新过程相互独立
子滤波器的观测更新方程为
式中，Gik为子滤波器的增益矩阵。
子滤波器的估计状态值按照式(12)融合得到新的全局状态估计值和协方差矩阵
2.2 自适应滤波器
自适应滤波通过引入自适应因子，对动力学模型的异常误差进行调节修正，通过求条件极值的方法可以推导出Kalman自适应滤波解，极值函数为
式中，VXk和Vk分别为状态预测信息和观测向量的误差向量，相应的协方差矩阵分别为Ck和Rk；αk为自适应因子；λk为拉格朗日乘数。求取式(20)的极小值，可以推导出自适应滤波解为[20] 式中，Gk为自适应滤波器的增益矩阵。 2.3 等价性证明
通过对比可以看出，联邦滤波器的子滤波是对状态估计值的权矩阵调整，而自适应滤波是对状态估计值的协方差阵调整，修正的参数具有等价性。
由于Pk=C-1k，所以对式(12)中的Pik=βiPk两边求逆，可以得到
所以 代入等式(14)右边，可以得到 所以，式(16)的增益矩阵可以写成
如果αk=βi，则Gik和式(21)中的Gk等价，说明联邦滤波器的子滤波器和自适应滤波在形式上是等价的。
3 自适应联邦滤波器通过上述论证已经得出了联邦滤波器的子滤波器和自适应滤波在形式上是等价，因此联邦滤波器分配因子可以通过自适应因子的计算方法选取，构成自适应联邦滤波器，在原有联邦滤波的基础上提高了子滤波器的自适应能力。
联邦滤波器分配因子取值基于预报残差[21]
式中，c为常量，可以取c=0.85~1.0。
ΔVk为基于预报残差Vk构造的统计量，其表达式为
与此同时，为确保信息分配因子满足信息守恒定理，对利用式(26)计算的分配因子进行归一化 式中，β′ik即为归一化后的k时刻的i子滤波器的分配因子。
通过对自适应联邦滤波器观察分析可知：①本文提出的自适应联邦滤波器很好地保留了联邦滤波器计算效率高的特性，局部滤波器可以并行、单独运算；②利用自适应算法计算分配因子能够根据不同传感器的观测值精度进行信息调节，使全局滤波具备自适应能力，而且自适应信息分配因子计算简易，因此在整体计算效率方面不会带来负担。
4 实例分析试验数据采集于2011年北京大兴区(图 1)，试验采用两台Laica-GPS接收机、1台惯性测量系统和1台里程计。1台GPS接收机作为静止参考基站，另1台GPS接收机和惯性测量系统、里程计一起安置在运动车辆内(GPS天线安装在车顶)。惯性测量单元为导航级别，采样频率为100 Hz，GPS接收机选用NovAtel OEM2板卡，采样频率为1 Hz，里程计为非接触车速传感器，测量精度为±0.5%(距离≥100 m)，数据更新频率为1 Hz，非接触车速传感器的输出信号为不规则的小信号，所以需要安装跟踪滤波器将信号变为与车速成正比的基波信号并转换为计算机能够接受的TTL电平的脉冲信号。表 1是IMU技术参数。为验证自适应联邦滤波器对于模型误差的消除效果，人为在GPS和Odometer动力学模型加入误差。表 2为人为加入动力学模型误差的时间、位置和量级。除此之外，在第900 s引入系统模型偏差，将状态转移矩阵F扩大两倍，加入动力学模型误差的位置在图 1中标出。
|
| 图 1 车辆测试轨迹 Fig. 1 Vehicular test trajectory |
| 参数 | 陀螺 | 加速度计 |
| 偏心 | 0.2 deg/h | 0.1 mg |
| 尺度因子 | 1×10-4 | 5×10-5 |
| 随机游走 | 0.035 deg/sqrt(h) | 20 ug/sqrt(h) |
| 历元/s | GPS | Odometer | ||
| 位置/m | 速度/(m/s) | 位置/m | 速度/(m/s) | |
| 378 | 30 | 3 | 10 | 1 |
| 580 | 30 | 3 | 0 | 0 |
| 787 | 0 | 0 | 30 | 3 |
组合导航Kalman滤波参数通过分析及经验确定。NED 3个方向的位置初始方差分别为1.0 m2、1.0 m2、5 m2；速度初始方差为0.02 m2/s2、0.02 m2/s2、0.1 m2/s2；姿态的初始方差为0.05 deg2、0.05 deg2、0.2 deg2；加速度计的初始方差为500 mg；陀螺仪初始方差为10 deg/h；采用GPS的位置和速度观测值进行组合导航时，初始方差取10 m2和0.02 m2/s2。为了说明新的滤波方法的有效性，分别采用3种方案进行导航解算[18]，非自适应联邦卡尔曼滤波器通过GPS和Odometer的位置和速度初始方差计算信息分配因子，整个导航过程中保持不变：
方案1。非自适应联邦卡尔曼滤波器(不加模型误差)。
方案2。非自适应联邦卡尔曼滤波器(加入模型误差)。
方案3。自适应联邦卡尔曼滤波器(加入模型误差)。
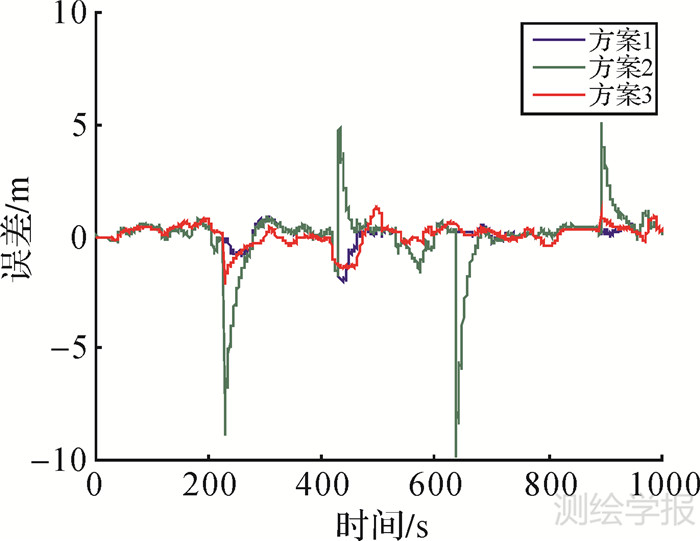
一般情况下，对于导航应用，仅需要平面位置信息，而且GPS和INS的垂直通道观测信息均存在较大的不稳定性(尤其是对于GPS单点定位)，因此位置和速度误差的对比只列出了北和东两个方向。图 2—5为3个解算方案在NED 3个方向的位置和速度误差序列图，由于位置误差较小，从经纬度误差角度不便于观察，因此，把位置误差转换到NED坐标系中。对比方案1和方案2，非自适应联邦滤波器算法可以提高计算效率，但其对动力学模型误差的稳键效果较差，没有充分利用信息分配因子调节滤波器的自适应能力。人为加入的动力学模型误差均导致了较大的位置和速度扰动。
|
| 图 2 北方向位置误差 Fig. 2 Position error in N direction |
|
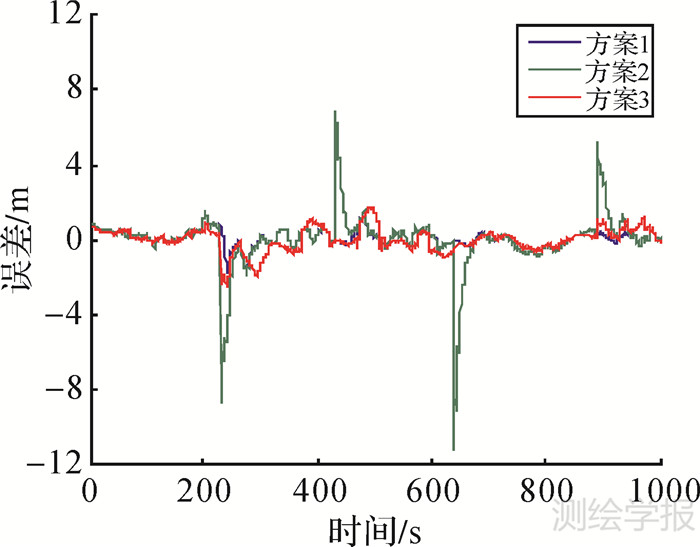
| 图 3 东方向位置误差 Fig. 3 Position error in E direction |
|
| 图 4 北方向速度误差 Fig. 4 Velocity error in N direction |
|
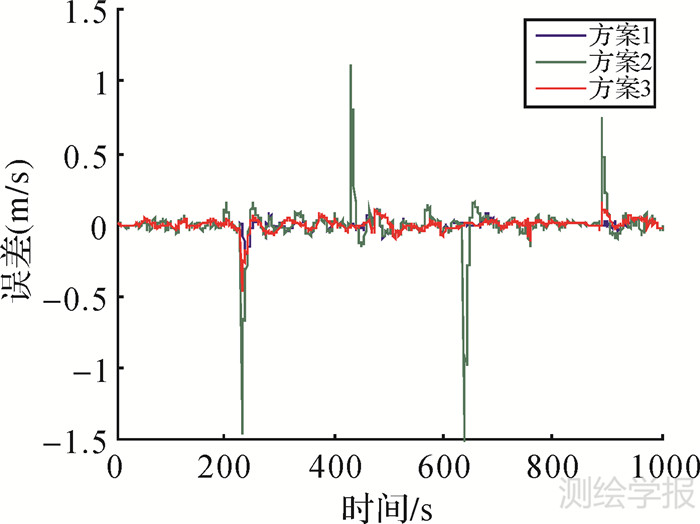
| 图 5 东方向速度误差 Fig. 5 Velocity Error in E direction |
对比方案2和方案3，当GPS和Odometer某一个传感器动力学模型存在误差时(580 s和787 s)，自适应联邦滤波器能够较好地消除误差的影响，在提高滤波计算效率的同时，增强了对于动力学模型的抗差性。对于GPS和Odometer动力学模型均存在误差的情况(378 s)，方案3仍具有一定的抵抗动力学模型误差的性能，但效果稍逊于单传感器动力学模型存在误差的情况。这是由于联邦滤波器只是对信息进行了重新分配，而没有降低观测信息的整体权重，当GPS和Odometer动力学模型均存在误差的情况下，联邦滤波器放大了动力学模型误差较小的传感器的信息分配因子。当动力学模型存在整体偏差时(900 s)，方案3同样表现出了很好的稳键特性，有效消除了动力学模型偏差的影响。
图 6—8给出了3种解算方案下俯仰角、横滚角和航向角误差。可以看出，虽然人为加入的动力学模型误差是位置和速度信息，但是在滤波融合过程中，位置和速度的动力学模型误差会导致错误的姿态误差修正值，因此对姿态角也会产生较大的影响。自适应联邦滤波器提高了直接可测参数的估计精度(位置和速度)，从而提高了间接可测参数(姿态角)的估计精度，有效避免了姿态角错误修正。
|
| 图 6 俯仰角误差 Fig. 6 Error of pitch |
|
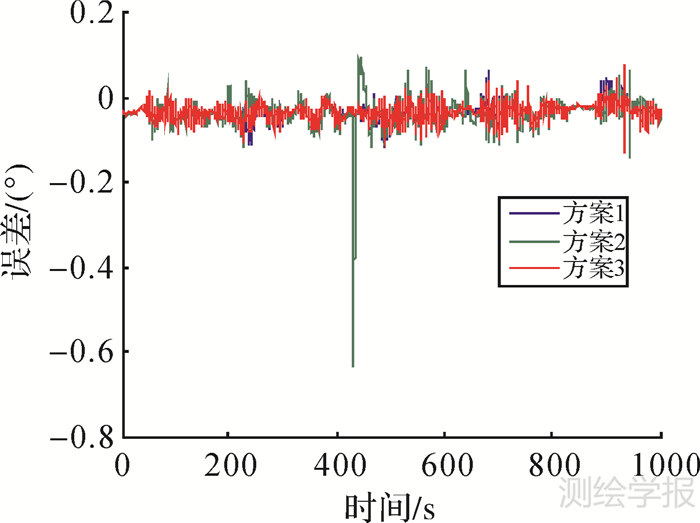
| 图 7 翻滚角误差 Fig. 7 Error of roll |
|
| 图 8 航向角误差 Fig. 8 Error of yaw |
对3种解算方案的位置、速度和姿态误差的最大值和均方根进行统计(表 3)。方案2的误差最大值和均方根均远大于方案1，说明方案2的联邦滤波方法不具有削弱动力学模型误差的能力，方案3通过自适应联邦滤波器对加入模型误差的数据进行处理，取得了较好的自适应效果，解算结果精度与方案1相当，说明了自适应联邦滤波器具备良好的对于动力学模型的抗差性能，方案3的误差最大值要略大于方案1(尤其是速度统计量)，主要是由于自适应联邦滤波器对于多传感器动力学模型误差的抑制能力稍弱导致的。
| 方案 | max | RMS | |||||
| N/roll | E/pitch | 平面/yaw | N/roll | E/pitch | 平面/yaw | ||
| 位置/m | 1 | 2.043 | 1.925 | 2.807 | 0.490 | 0.443 | 0.661 |
| 2 | 9.866 | 11.247 | 14.961 | 1.363 | 1.435 | 1.979 | |
| 3 | 2.198 | 2.581 | 3.390 | 0.500 | 0.627 | 0.802 | |
| 速度/(m/s) | 1 | 0.156 | 0.252 | 0.296 | 0.031 | 0.039 | 0.050 |
| 2 | 1.402 | 1.515 | 2.064 | 0.135 | 0.146 | 0.199 | |
| 3 | 0.462 | 0.469 | 0.658 | 0.039 | 0.043 | 0.058 | |
| 姿态/(°) | 1 | 0.228 | 0.321 | 0.598 | 0.038 | 0.042 | 0.119 |
| 2 | 0.866 | 0.631 | 1.212 | 0.070 | 0.049 | 0.139 | |
| 3 | 0.353 | 0.148 | 0.375 | 0.034 | 0.038 | 0.092 | |
GPS-INS-Odometer组合导航系统的观测信息较多，因此通过联邦滤波器能够有效提高数据融合的计算效率。联邦滤波器和自适应滤波器分别通过信息分配因子和自适应因子调节增益矩阵，两者具有等价特性，因此，本文提出了自适应联邦滤波器并应用于GPS-INS-Odometer组合导航，构建了自适应联邦滤波器的信息分配因子的计算方法。车载试验证明，自适应联邦滤波器能够有效消除单传感器的动力学模型扰动的影响，而且对多传感器动力学模型误差具有较好的抑制效果。相较于非自适应联邦滤波器，本文算法不但能够提高计算效率，而且具备了良好的控制动力学模型误差的性能，对于多滤波器的多系统融合有很好的实用价值。需要指出的是，滤波器在工程应用过程中，遇到的问题会更加复杂，探求滤波器的稳定性能以及组合系统的模型优化是下一步研究的重点。
| [1] | HASAN A M, SAMSUDIN K, RAMLI A R, et al. A Review of Navigation Systems (Integration and Algorithms)[J]. Australian Journal of Basic and Applied Sciences, 2009, 3(2): 943-959. |
| [2] | HONG S, LEE M H, CHUN H H, et al. Observability of Error States in GPS-INS Integration[J]. IEEE Transactions on Vehicular Technology, 2005, 54(2): 731-743. |
| [3] | SEO J, LEE H K, LEE J G, et al. Lever Arm Compensation for GPS-INS-Odometer Integrated System[J]. International Journal of Control, Automation, and Systems, 2006, 4(2): 247-254. |
| [4] | 肖烜, 王清哲, 程远, 等. 捷联惯导系统-里程计高精度紧组合导航算法[J]. 兵工学报, 2012, 33(4): 395-400. XIAO Xuan, WANG Qingzhe, CHENG Yuan, et al. High Accuracy Navigation Algorithm for Tightly Coupled INS-Odometer[J]. Acta Armamentarii, 2012, 33(4): 395-400. |
| [5] | 张小跃, 杨功流, 张春熹. 捷联惯导-里程计组合导航方法[J]. 北京航空航天大学学报, 2013, 39(7): 922-926. ZHANG Xiaoyue, YANG Gongliu, ZHANG Chunxi. Integrated Navigation Method for SINS and Odometer[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(7): 922-926. |
| [6] | 严恭敏. 车载自主定位定向系统研究[D]. 西安: 西北工业大学, 2006. YAN Gongmin. Research on Vehicle Autonomous Position and Azimuth Determining System[D]. Xi'an: Northwestern Polytechnical University, 2006. |
| [7] | GEORGY J, KARAMAT T, IQBAL U, et al. Enhanced MEMS-IMU-Odometer-GPS Integration Using Mixture Particle Filter[J]. GPS Solutions, 2011, 15(3): 239-252. |
| [8] | HU Haidong, HUANG Xianlin, LI Mingming, et al. Federated Unscented Particle Filtering Algorithm for SINS-CNS-GPS System[J]. Journal of Central South University of Technology, 2010, 17(4): 778-785. |
| [9] | MAIER A, KIESEL S, TROMMER G F. Performance Analysis of Federated Filter for SAR-TRN-GPS-INS Integration[J]. Gyroscopy and Navigation, 2011, 2(4): 293-300. |
| [10] | GAO Y, KRAKIWSKY E J, ABOUSALEM M A, et al. Comparison and Analysis of Centralized, Decentralized, and Federated Filters[J]. Navigation(Journal of the Institute of Navigation), 1993, 40(1): 69-86. |
| [11] | 顾启泰, 王颂. 联邦滤波器信息分配系数的优选算法[J]. 中国惯性技术学报, 2003, 11(6): 1-6. GU Qitai, WANG Song. Optimized Algorithm for Information-sharing Coefficients of Federated Filter[J]. Journal of Chinese Inertial Technology, 2003, 11(6): 1-6. |
| [12] | YANG Yuanxi, CUI Xianqiang, GAO Weiguang. Adaptive Integrated Navigation for Multi-sensor Adjustment Outputs[J]. Journal of Navigation, 2004, 57(2): 287-295. |
| [13] | LI D, WANG J, BABU S. Enhancing the Performance of Ultra-tight Integration of GPS-PL-INS: A Federated Filter Approach[J]. Journal of Global Positioning Systems, 2006, 5(1-2): 96-104. |
| [14] | 张科, 刘海鹏, 李恒年, 等. SINS-GPS-CNS组合导航联邦滤波算法[J]. 中国惯性技术学报, 2013, 21(2): 226-230. ZHANG Ke, LIU Haipeng, Li Hengnian, et al. SINS-GPS-CNS Integrated Navigation Federal Filtering Algorithm[J]. Journal of Chinese Inertial Technology, 2013, 21(2): 226-230. |
| [15] | TITTERTON H D, WESTON L J. Strapdown Inertial Navigation Technology[M]. 2nd ed. Lexington, Massachusetts: MIT Lincoln Laboratory, 2004. |
| [16] | HAN Songlai, WANG Jinling. Integrated GPS-INS Navigation System with Dual-rate Kalman Filter[J]. GPS Solutions, 2012, 16(3): 389-404. |
| [17] | GODHA S. Performance Evaluation of Low Cost MEMS-based IMU Integrated with GPS for Land Vehicle Navigation Application[D]. Calgary: University of Calgary, 2006. |
| [18] | 吴富梅, 杨元喜. 基于小波阈值消噪自适应滤波的GPS-INS组合导航[J]. 测绘学报, 2007, 36(2): 124-128. WU Fumei, YANG Yuanxi. GPS-INS Integrated Navigation by Adaptive Filtering Based on Wavelet Threshold Denoising[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(2): 124-128. |
| [19] | 杨元喜. 自适应动态导航定位[M]. 北京: 测绘出版社, 2006. YANG Yuanxi. Adaptive Navigation and Kinematic Positioning[M]. Beijing: Surveying and Mapping Press, 2006. |
| [20] | YANG Yuanxi, GAO Weiguang. An Optimal Adaptive Kalman Filter[J]. Journal of Geodesy, 2006, 80(4): 177-183. |
| [21] | 吴富梅, 杨元喜. 一种两步自适应抗差Kalman滤波在GPS-INS组合导航中的应用[J]. 测绘学报, 2010, 39(5): 522-527. WU Fumei, YANG Yuanxi. A New Two-step Adaptive Robust Kalman Filtering in GPS-INS Integrated Navigation System[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(5): 522-527. |