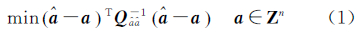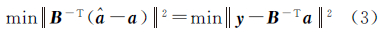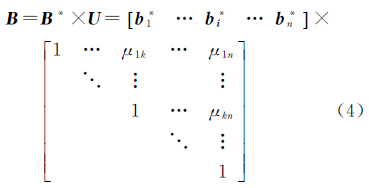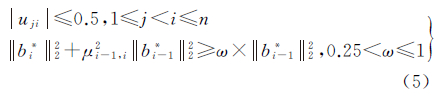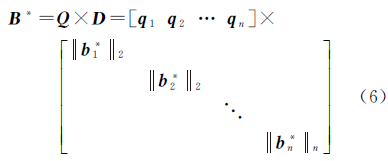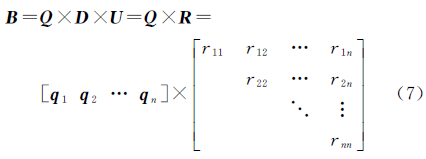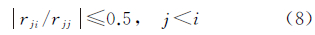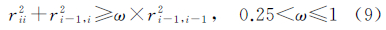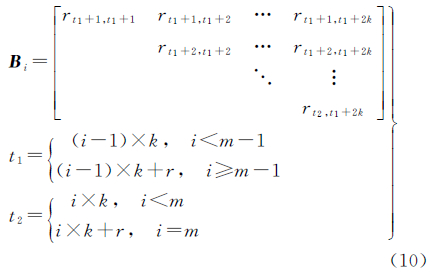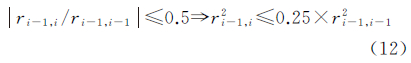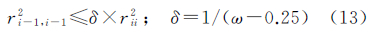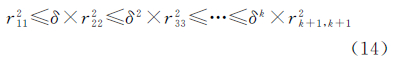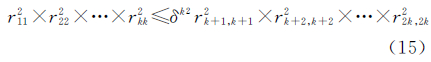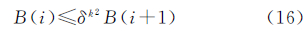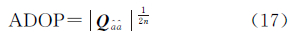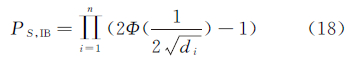2. 地球空间信息技术协同创新中心， 湖北 武汉 430079
2. Collaborative Innovation Center of Geospatial Technology, Wuhan 430079, China
为快速、准确求解载波相位观测值中的整周模糊度，最常用的处理方法为模糊度域内基于整数变换的整数最小二乘模糊度降相关平差(least-squares ambiguity decorrelation adjustment,LAMBDA)算法[1]，其核心思想是通过对模糊度方差协方差阵进行降相关来减小搜索空间，以提高搜索效率。随后，许多学者基于这个准则提出了各自的降相关方法[2, 3, 4, 5, 6, 7]。从格理论的角度来讲，整数最小二乘模糊度解算可以看作是格上最近向量问题[8, 9, 10]，通常采用格基规约的方式获得一组长度较短的基向量以快速寻找出一组最优整数解，其中文献 [11, 12, 13, 14]共同提出的LLL规约算法在模糊度解算中得到广泛应用。近来，通过对LLL与LAMBDA之间的关联性分析可知格基规约与降相关是同一处理过程的不同表达[15, 16, 17, 18]，而一般却对降相关片面理解为“降低模糊度方差分量间的相关性”，文献 [19, 20]分别采用理论和算法对比验证的方法得出降相关的实质在于通过降低方差分量的相关性实现条件方差(规约基)最大程度的交换，也即是规约性能(降相关)的好坏体现在最终获得的一组规约基的长度上。为表述方便，本文将所有基于整数变换的过程统称为“格基规约”(简称规约)。
目前的规约算法，除文献[19, 20, 21]分别采用部分元素尺度规约算法和贪心选择算法在一定程度上降低了规约算法复杂度(与规约耗时成正相关关系)外，多是侧重于提高规约性能以实现模糊度的快速搜索。由于规约性能的提高通常会增大计算复杂度，增加规约耗时，降低规约效率[8]，而模糊度解算过程是由规约和搜索两个部分组成的，因此为获得较小的整体解算耗时，需要实现规约复杂度和规约性能在解算效率上的均衡，如果单一地追求规约性能的提高，可能极大地消耗规约时间，不利于提高整体解算效率，反之亦然。
就多频多模GNSS观测数据处理来说，卫星冗余观测数据的增多，不仅增大了模糊度解算维数而且提高了模糊度的解算精度[22]。由于规约耗时不受模糊度解算精度的影响而只与解算维数成正相关关系，搜索耗时在很大程度上取决于解算精度[8]。因此，在高维整周模糊度解算中规约耗时通常远大于搜索耗时，此时规约耗时成为限制模糊度解算计算效率的主要因素。如前所述，规约耗时取决于模糊度解算的维数，如果对模糊度方差协方差阵进行分块处理降低单个规约矩阵维数，是否可以提高规约效率，实现快速规约进而减少模糊度解算的整体耗时呢？文献 [23, 24]首次提出了分块思想并给出了分块处理方法，但因为满足基向量交换的限制条件较多导致规约过程相对复杂致使该方法较难应用。近来，文献[25]提出了分块正交化算法，其基本思路是通过分块策略对基向量进行内外规约变换改变基向量间的规约次序，且在每次内外变换后再整体变换，因此该分块正交算法主要用以提高基向量的规约性能，而不是降低规约复杂度提高规约效率。
针对高维模糊度的解算特点，本文将研究LLL分块处理算法，即通过对LLL算法进行分块处理，降低单个规约矩阵的维数，并适当弱化分块基向量的交换条件，减少规约耗时，提高高维模糊度解算计算效率。因此，本文在阐述基本的理论方法基础之上，将重点讨论什么时候需要分块，如何分块处理，并对分块处理算法和效果进行研究分析。
1 数学模型 1.1 整数最小二乘原理假定、Qââ分别为最小二乘解算的实数模糊度和模糊度的方差协方差阵，对其进行整数最小二乘模糊度估计，估计准则为[1]
对Qââ进行Cholesky分解
式中，B为上三角矩阵。
将式(2)代入式(1)，可得
式中，y=B-Tâ是一个常数。
式(3)在格理论上也被称为最近向量问题，因此通常采用LLL等算法进行规约处理[9, 10]。
1.2 基于QR分解的LLL算法假定b1、b2、…、bn是上述矩阵B的一组基，采用施密特正交化(Gram-Schimidt orthogonaliza-tion，GSO)
式中，B*=[b*1…b*i…b*n]，且b*i=bi－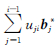
,i>j；U=[uji]为单位上三角矩阵，且满足uji=bi,b*j/b*j22。
经典的LLL算法满足如下两个规约条件[26]
式中，第1式称为尺度规约；第2式为基向量交换。
为提高规约基向量解算的浮点精度，通常采用基于QR分解的LLL规约算法。令
式中，Q=[q1q2…qn]为正交矩阵，且qi=b*i/b*i2；D=diag([b*12,b*22,…,b*n2])，b*i2为b*i的模长。
将式(6)代入式(4)，可得QR分解的表达式
式中，R=rji是上三角矩阵，且满足rji=b*j2×uji。 根据式(6)和式(7)，式(5)可以进一步写为 式(8)和式(9)即为基于QR分解的LLL算法的规约条件[27, 28]，具体实现可以参照文献[16]。当对高维模糊度规约解算时，为满足LLL算法的两个规约条件通常需要多次相邻基向量间的迭代交换和元素尺度规约过程，造成规约效率低下，因此为实现高维模糊度方差协方差阵的快速规约，本文提出了分块规约的处理方法。 2 分块LLL算法
分块LLL算法是通过将规约矩阵均匀分割成一定数目的子矩阵块，利用LLL算法对每个子矩阵块进行规约，并通过相邻分块间的交换条件实现所有基向量交换的一种快速规约算法。以下对分块LLL算法的解算原理和实现流程给予详细介绍。
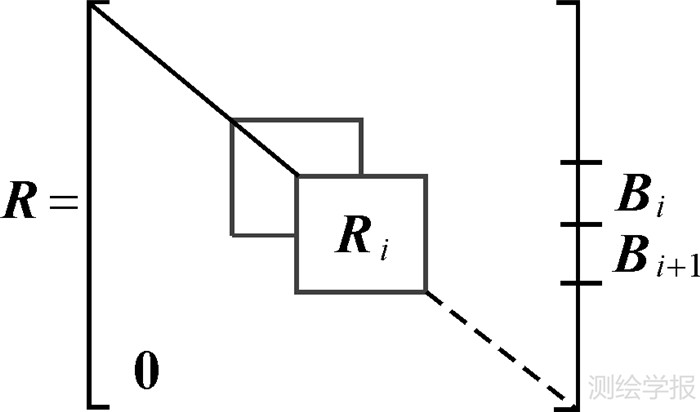
如图 1所示，将R阵分为m块(B1,B2,…,Bm)，每块大小为k，且满足n=mk+r，其中r为不足分块大小的部分。则任一分块大小Bi,1≤i≤m可以表示为
|
| 图 1 LLL算法分块示意图 Fig. 1 The schematic of Block LLL algorithm |
由于每个分块之间是相互独立的，如果单纯地对各个分块进行规约，不能实现各分块间的基向量交换。为确保各分块间的基向量能够进行交换，则需要对相邻分块进行叠加，构成公共交叉块实现基向量长度的传递，即对分块B1、B2、…、Bm进行组合形成新的传递块R1、R2、…、Rm-1，其中每个传递块大小Ri(1≤i≤m－1)可以表示为
从式(11)可以看到Ri是一个方阵且相邻传递块(Ri,Ri+1)包含分块Bi+1，因此当分别对Ri和Ri+1内部进行LLL规约时，通过Bi+1实现了(Ri,Ri+1)基向量间长度的传递。但如果依次对传递块进行规约，仅能满足分块之间一次性的传递，基向量交换效果较差，因而仍需给出分块之间的交换条件，下面对分块之间满足的交换条件进行简要推导。
由于采用LLL算法每次进行基向量交换前，需首先对次对角线元素进行尺度规约。因此，当对ri－1,i进行规约后，即满足
将式(12)代入式(9)，可得弱化的交换条件 由式(13)可得 因此 则相邻传递块(Ri,Ri+1)之间的一般交换条件为 式中，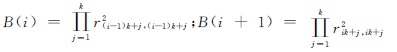
。
基于以上分析，分块LLL的处理流程可概括为：
(1) 给定分块数m(考虑(Ri,Ri+1)间的交换，一般m≥3)，获得分块大小k及余数r，并设置i=1。
(2) 对传递块Ri按照LLL算法进行解算，获得整数转换矩阵Zi、正交阵Qi和B(i)，同时对Ri块对应的R中剩余列向量Ric和行向量Rir按照Ric=RicZi和Rir=QiRir进行更新。其中
(3) 当i≥2时，判断B(i－1)≤δk2B(i)是否成立。如果不等式成立令i=i+1，直到i=m时退出规约过程；否则令i=i－1。
(4) 返回过程(2)。
以上即为分块LLL算法(block LLL,BLLL)的解算原理及具体处理步骤。根据上述过程可以看出，BLLL算法分块间的基向量交换强度要弱于相邻基向量间的交换强度，同时对传递块Ri进行处理时有效地避免了对Ric中元素的尺度规约过程。
3 试验数据分析为验证前文提出的BLLL算法的有效性，并探讨不同块数对解算效率的影响，笔者采用LLL算法和文献[25]提出的IBGS(针对高维数据选择性能最优的B-2策略)解算结果作为对比。分别采用规约耗时、搜索耗时和整体解算耗时评价3种方法的解算效率。其中，搜索算法采用当前效率最高的SE-VB算法[21](是由Schnorr和Euchner两位学者提出的SE算法与Viterbo和Boutros两位学者提出的VB算法相结合的一种搜索算法)。整体解算耗时为规约耗时与搜索耗时二者之和。
本文所有的计算都是在笔者的PC机上基于Matlab 2012b软件进行的，其软硬件配置为Intel Core i7-3520 CPU，2.90 GHz，4 GB内存，win7系统(64位)。
3.1 模糊度方差阵与规约和搜索耗时的关系为说明采用分块处理的合理性，本节首先分析模糊度方差阵与规约和搜索耗时之间的关系。其中，模糊度方差阵的特性主要体现在模糊度维数、精度以及解算成功率3个方面。
为衡量载波相位模糊度解算的精度，通常采用模糊度精度因子(ambiguity dilution of precision，ADOP)作为评价指标[29]，其定义如下[30]
式中，n为模糊度的维数。
当模糊度的方差协方差阵确定时，其整数最小二乘成功率(integer least square success rate,PS,ILS)是一个定值，而PS,ILS无法从理论上精确给出，通常采用序贯取整的成功率(bootstrapping success rate,PS,IB)作为其最优下边界[31, 32, 33]，其定义如下[34]
式中，di为Q规约后的条件方差。
由PS,IB计算公式可知其数值取决于条件方差(规约基)的大小。当采用的算法规约性能较优时，可以获得一组相对较短的规约基，此时解算的PS,IB数值较大从而更接近PS,ILS。因此，为较精确地衡量PS,ILS，通常采用规约性能较强的算法(比如LAMBDA或者LLL算法)计算PS,IB。由于PS,IB可以反映基向量的规约程度，因而PS,IB又被用作评价不同规约算法规约性能的指标[15, 20]。
为在普遍意义下阐述不同模糊度维数、精度和PS,IB对规约耗时和搜索耗时的影响。笔者按照文献[3]采用的模拟方法随机生成高维模糊度下的方差协方差阵Qââ及浮点解并计算分析。
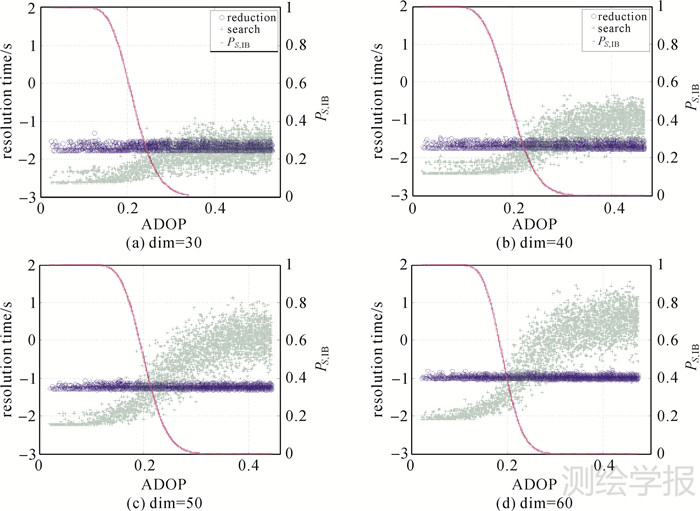
图 2给出了不同维数下采用LLL算法解算的规约耗时、搜索耗时和PS,IB与模糊度精度的关系。其中，PS,IB用来近似替代最小二乘的成功率。从图中可以看出：PS,IB值随着ADOP的增大而减小，说明模糊度解算的精度越高此时模糊度固定成功的概率越大；规约耗时随着维数的增大而增大(比如，维数等于30时规约时间约为0.02 s，而当维数增大为60时规约时间相应地增大为0.11 s左右)但并不受精度的影响；搜索耗时的大小取决于模糊度解算的维数和精度，其大小随着维数的增大或精度的降低而增大。同时，对比规约耗时和搜索耗时与精度之间的相互关系可以发现：当精度较高(尤其是ADOP小于0.2)时，搜索耗时明显小于规约耗时，反之亦然。
|
| 图 2 不同维数和精度下的Bootstrapping成功率、规约耗时和搜索耗时的变化趋势图 Fig. 2 The trend chart of Bootstrapping success rate, reduction time and search time under different dimensions and ADOP |
由于多频多系统下卫星冗余观测数据的增多，不仅可以提高模糊度解算的精度而且增大了模糊度解算维数。根据图 2结果可知，此时采用LLL算法的规约耗时较大且远大于搜索耗时。因此，规约耗时成为制约高维模糊度快速解算的主要因素，则有必要通过降低规约复杂度，减少规约耗时。本文在前面所提出的分块处理算法即是通过适当地降低规约耗时在总解算时间中的比重，提高模糊度解算整个过程的计算效率。因此，下文采取两组高维实测数据对其效果进行分析验证，其中为减少计算环境变化对解算时间造成的影响，每组试验中分别对每种处理算法重复进行3次试验，并以重复试验结果的平均值作为评估依据。
3.2 试验1本试验采用在武汉市某科技园楼顶观测的一组静态基线数据，按照表 1进行基线解算获得模糊度的浮点解â和方差-协方差阵Qââ。
| 参数 | 指标 |
| 接收机型号 | 司南M300-II |
| 系统和频率 | GPS(L1，L2) BDS(B1，B2，B3) GLONASS(G1，G2) |
| 起始时间 | 2014-11-20 03:13:00 |
| 历元数 | 2834 |
| 采样间隔/s | 5 |
| 截止高度角/(°) | 10 |
| 基线长/m | 0.5 |
| 处理模式 | 单历元 |
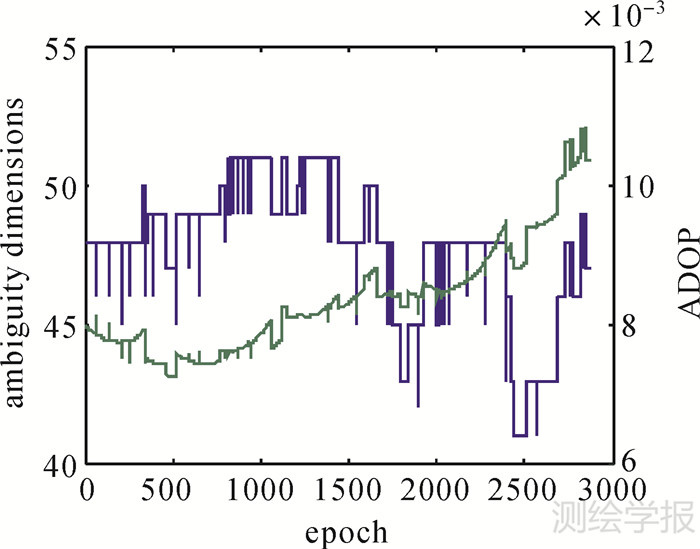
图 3是模糊度维数和ADOP随历元的变化趋势图。从图中可以看到，模糊度维数变化范围为41~51，ADOP数值维持在0.012以下。依据图 2的结果分析可知，此时模糊度的解算精度较高且维数较大，模糊度的规约耗时明显大于搜索耗时，有必要采用分块
|
| 图 3 不同历元下的模糊度维数与ADOP值 Fig. 3 Ambiguity dimensions and the value of ADOP under different epoches |
处理策略。从ADOP和维数的变化趋势上可以看出两者并没有呈现非常明确的相关性，主要是由于ADOP值取决于3个卫星系统的模糊度维数、站星几何关系和载波相位观测值精度等原因，导致ADOP并不严格和维数是一一对应关系。
表 2统计了分别采用LLL、IBGS和不同分块数的BLLL算法进行处理时规约耗时、搜索耗时和整体解算耗时的历元平均值和最大值，其中m=3~14代表BLLL的分块数分别为3~14。从表中可以看到LLL和IBGS解算耗时差异较小；BLLL规约耗时随着分块数的增大而逐次降低，搜索耗时除在分块数为14(个别历元出现了跃变)外，增长趋势缓慢，因此整体解算耗时也基本呈现随分块数增大而递减的趋势，尤其是在分块数达到13时，采用BLLL的模糊度解算计算效率相对于LLL算法提高了约65.2%。
| s | ||||||
| 方法 | reduction | search | total | |||
| mean | max | mean | max | mean | max | |
| LLL | 0.080 7 | 0.150 0 | 0.010 3 | 0.060 0 | 0.091 0 | 0.186 3 |
| IBGS | 0.077 6 | 0.195 7 | 0.010 5 | 0.029 6 | 0.088 1 | 0.208 8 |
| m=3 | 0.069 3 | 0.131 5 | 0.010 4 | 0.045 8 | 0.079 7 | 0.147 3 |
| m=4 | 0.058 7 | 0.100 8 | 0.010 6 | 0.042 0 | 0.069 3 | 0.119 5 |
| m=5 | 0.050 4 | 0.089 2 | 0.010 6 | 0.042 8 | 0.060 9 | 0.102 2 |
| m=6 | 0.044 6 | 0.103 7 | 0.010 7 | 0.049 2 | 0.055 3 | 0.117 7 |
| m=7 | 0.039 8 | 0.084 1 | 0.011 7 | 0.056 0 | 0.051 6 | 0.100 2 |
| m=8 | 0.034 2 | 0.080 0 | 0.011 6 | 0.044 0 | 0.045 8 | 0.093 5 |
| m=9 | 0.029 7 | 0.081 7 | 0.011 8 | 0.036 5 | 0.041 4 | 0.095 0 |
| m=10 | 0.025 7 | 0.075 1 | 0.012 0 | 0.051 3 | 0.037 7 | 0.090 6 |
| m=11 | 0.023 9 | 0.079 5 | 0.012 4 | 0.044 2 | 0.036 4 | 0.109 2 |
| m=12 | 0.020 5 | 0.069 2 | 0.011 9 | 0.050 9 | 0.032 4 | 0.087 2 |
| m=13 | 0.019 7 | 0.068 0 | 0.012 0 | 0.052 3 | 0.031 7 | 0.082 2 |
| m=14 | 0.017 9 | 0.042 9 | 0.013 8 | 3.737 8 | 0.031 7 | 3.752 9 |
由表 2结果可知，分块数并非越多越好，因此下文分别对块数为13和14两种情形下的解算结果进行分析。
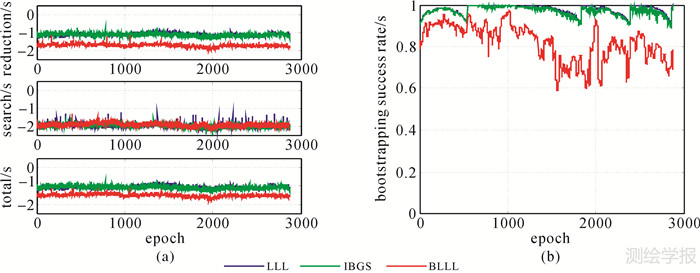
图 4给出了LLL、IBGS和BLLL(m=13)不同历元下的解算结果。图 4(a)是3种方法的解算时间变化图；图 4(b)是三者的PS,IB的变化图。
|
| 图 4 m=13时不同规约方法的模糊度解算耗时和PS,IB Fig. 4 Ambiguity resolution time and PS,IB in different methods under m=13 |
从LLL和IBGS解算结果对比可知，两者解算耗时差异较小，但是IBGS的PS,IB小于LLL算法，说明IBGS的规约性能要弱于LLL算法，与文献[25]结论不符，其主要原因在于该文献中比较的“LLL算法”更侧重于降低基向量间的相关性，有别于本文的LLL算法。从BLLL与LLL的结果对比可以看到，BLLL由于采用式(11)和式(16)进行分块处理时减少了分块矩阵外的元素尺度规约个数和分块矩阵间的基向量交换强度，因此较为显著地减小了规约耗时和PS,IB数值，故而规约复杂度和规约性能较低，导致规约耗时和PS,IB均减小。需要说明的是此处PS,IB仅用来反映规约性能的好坏，并不改变实际解算的整数最小二乘成功率PS,ILS的数值大小。从两者搜索耗时的差异较小来看，当在满足一定规约强度时已经可以获得较小的模糊度搜索空间，此时提高规约性能对搜索空间的改善效果不太明显。因此，在进行模糊度解算时适当地分块以降低PS,IB，可以获得相对较优的解算效果。
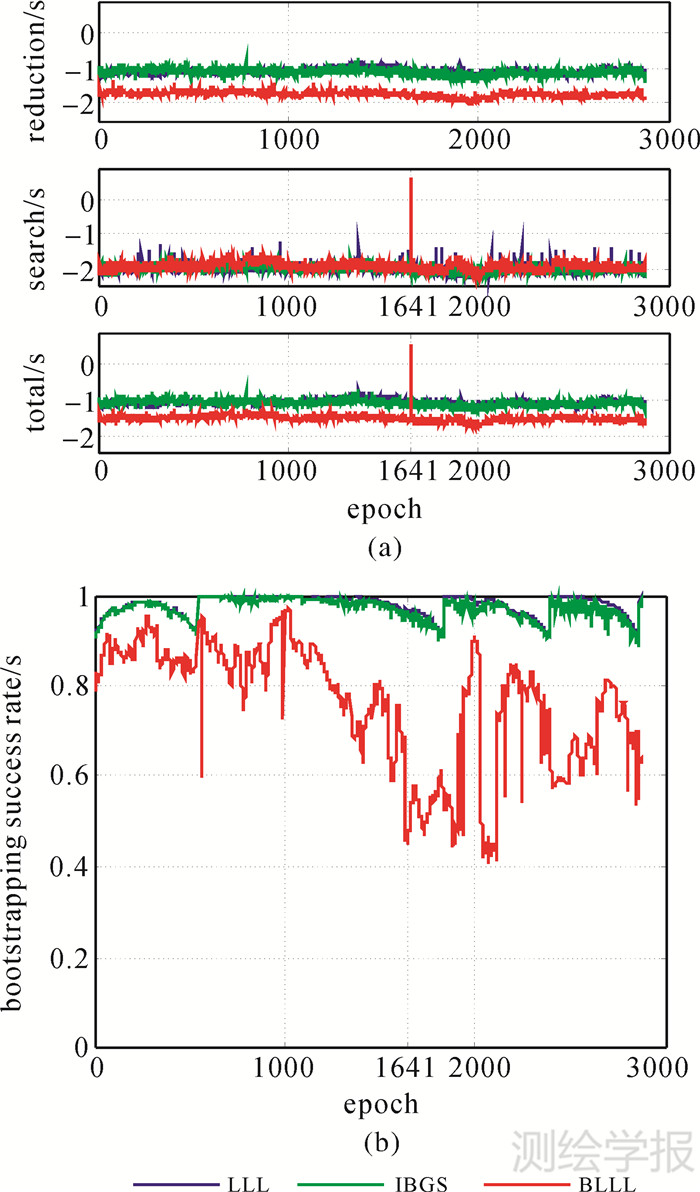
图 5给出了LLL、IBGS和BLLL(m=14)不同历元下的解算结果。其中，图 5(a)是3种方法的解算时间变化图；图 5(b)是三者的PS,IB的变化图。对比图 5和图 4可以看出，尽管分块数的增加可以获得更小的规约耗时，但是在历元1641处的搜索耗时相对于LLL和IBGS出现了跃变，此时BLLL的PS,IB大小为0.46且低于LLL和IBGS，说明当采用算法的规约性能较差且获得的PS,IB相对较小时有可能导致部分历元处解算的搜索耗时出现不稳定的现象。同时，可以发现BLLL算法在其他历元处的PS,IB普遍较小且存在部分历元处的PS,IB要小于跃变点处的PS,IB，但是搜索耗时均较稳定。笔者分析其原因主要是由不同历元处的模糊度信息(包括维数和精度等因素)不一致导致的。因为当对不同历元处的模糊度进行搜索时，除考虑模糊度的规约性能，还需顾及每个历元处的模糊度信息，此时即使各个历元间的PS,IB差异不大，也会因模糊度信息的差异而导致搜索耗时的不同。在模糊度实际解算中，会发现有些模糊度可能对规约强度要求较低，即使PS,IB很小也能快速搜索出整数模糊度；反之，则对模糊度的规约性能要求较高。因此，跃变点处的模糊度对规约性能可能要求较高，此时对BLLL进行较多的分块导致性能较差，超出了对规约性能的允许程度，导致耗时较大。
|
| 图 5 m=14时不同规约方法的模糊度解算耗时和PS,IB Fig. 5 Ambiguity resolution time and PS,IB in different methods under m=14 |
因此，如何选择合适的分块数以满足一定的规约性能并保证搜索耗时的稳定也是分块时要考虑的问题。
3.3 试验2本试验采用Curtin大学两个CORS站(CUT0、CUTA)提供的一组静态基线数据，按照表 3进行基线解算获得模糊度的浮点解和方差-协方差阵Qââ。
| 参数 | 指标 |
| 接收机型号 | Trimble NetR9 |
| 系统和频率 | GPS(L1，L2) BDS(B1，B2，B3) GLONASS(G1，G2) |
| 起始时间 | 2015-04-10 00:00:00 |
| 历元数 | 2872 |
| 采样间隔/s | 30 |
| 截止高度角/(°) | 10 |
| 基线长/m | 8.4 |
| 处理模式 | 单历元 |
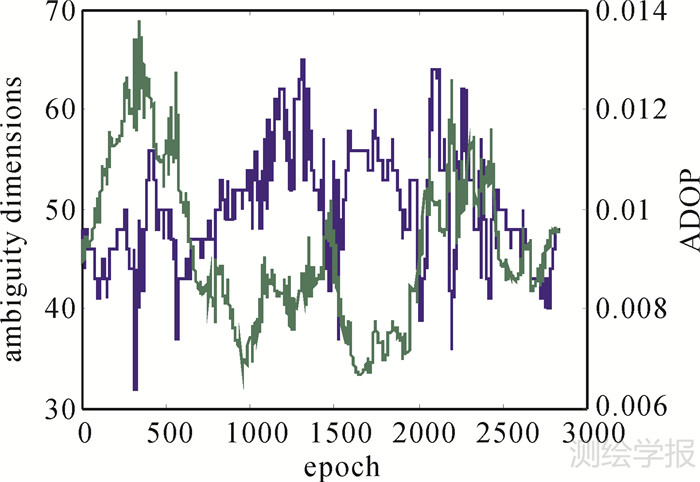
图 6是模糊度维数和ADOP随历元的变化趋势图。从图中可以看到模糊度维数在30~70维之间变化；ADOP值小于0.014。
|
| 图 6 不同历元下的模糊度维数与ADOP值 Fig. 6 Ambiguity dimensions and the value of ADOP under different epoches |
表 4统计了分别采用LLL、IBGS和不同分块数的BLLL算法进行处理时的规约耗时、搜索耗时和整体解算耗时的历元平均值和最大值，其中m=3~10代表BLLL的分块数分别为3~10。从表中可以看到IBGS相对于LLL算法的解算效率略有提高；BLLL随着分块数的增大平均规约耗时逐次降低，搜索耗时除在分块数为10(个别历元出现了跃变)外，增长趋势缓慢，因此整体解算耗时也基本呈现逐次递减趋势；当分块数为9时，采用BLLL的模糊度解算计算效率相对于LLL算法提高了约60.2%。
| S | ||||||
| 方法 | reduction | search | total | |||
| mean | max | mean | max | mean | max | |
| LLL | 0.074 4 | 0.148 6 | 0.008 3 | 0.061 4 | 0.082 7 | 0.163 7 |
| IBGS | 0.065 9 | 0.168 6 | 0.008 8 | 0.021 1 | 0.074 7 | 0.183 8 |
| m=3 | 0.060 3 | 0.136 4 | 0.008 7 | 0.041 6 | 0.069 0 | 0.156 2 |
| m=4 | 0.048 2 | 0.110 3 | 0.008 4 | 0.055 8 | 0.056 6 | 0.132 2 |
| m=5 | 0.042 9 | 0.106 8 | 0.009 1 | 0.046 1 | 0.052 0 | 0.117 9 |
| m=6 | 0.035 7 | 0.094 4 | 0.008 7 | 0.047 4 | 0.044 4 | 0.105 8 |
| m=7 | 0.030 1 | 0.084 2 | 0.008 8 | 0.048 3 | 0.039 0 | 0.101 4 |
| m=8 | 0.026 5 | 0.067 5 | 0.009 4 | 0.034 3 | 0.035 9 | 0.086 4 |
| m=9 | 0.023 1 | 0.070 4 | 0.009 8 | 0.134 5 | 0.032 9 | 0.146 0 |
| m=10 | 0.020 7 | 0.059 9 | 0.011 2 | 1.789 3 | 0.031 9 | 1.804 4 |
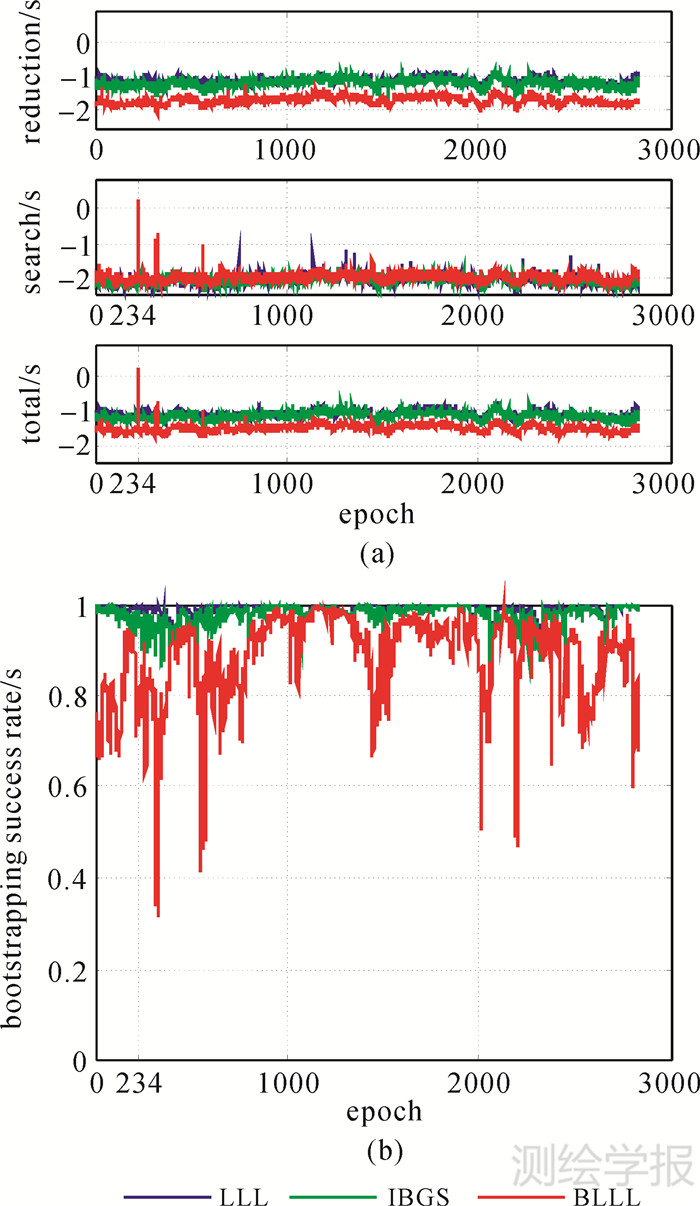
同理，为分析BLLL算法在分块等于10时，搜索耗时不稳定的原因，图 7给出了LLL、IBGS和BLLL(m=10)不同历元下的解算结果。图 7(a)是3种方法的解算时间变化图；右图是三者的PS,IB的变化图。从图中黑色虚线部分可以看出在历元234处BLLL的搜索耗时为1.789 3 s时，对应的PS,IB等于0.73。对于图中的结果与分析可以参考图 5。
|
| 图 7 m=10时不同规约方法的模糊度解算耗时和PS,IB Fig. 7 Ambiguity resolution time and PS,IB in different methods under m=10 |
本文针对多频多模情况下GNSS模糊度维数和精度较高、规约耗时明显大于搜索耗时的特点，提出了LLL分块处理算法(BLLL)，可减少矩阵尺度规约的个数和弱化分块矩阵间基向量交换的强度，降低规约计算复杂度，以达到减小规约耗时的目的。通过两组实测高维数据，对BLLL算法进行了效果验证与分析，并与LLL和IBGS算法的计算结果进行了对比，可以得出以下几点结论：
(1) 当模糊度的维数较高且精度因子ADOP较小时，基于经典的LLL算法进行模糊度解算的规约耗时明显大于搜索耗时，此时可以采用分块处理的方法减少规约耗时，以提高模糊度解算整个过程的计算效率。
(2) 分块数与规约耗时呈现负相关关系，即在一定的块数范围内，当分块数越多，规约强度越低(PS,IB越小)，规约耗时越小。因此，当分块选择合理时，此时搜索耗时相对稳定，可以获得较高的模糊度解算计算效率。
(3) 对于本文的两组实测高维数据而言，IBGS相对于LLL算法的解算效率略有提高，而本文提出的BLLL算法在分块数分别为13和9时相对于LLL算法的解算效率可以提高65.2%和60.2%。
此外，从本文的计算分析也可以看到，分块数的增加会造成规约性能变差(PS,IB减小)，有可能导致极个别历元搜索耗时增大，出现解算不稳定现象，因此后续有必要进一步分析ADOP和PS,IB的取值与搜索效率的关系进而来选择合适的分块数。初步思路为：首先根据模糊度维数和ADOP值确定分块数大小，当完成规约后采用合适的PS,IB阈值判断分块是否合理，以保障模糊度解算计算效率的稳定性。
| [1] | TEUNISSEN P J G. The Least-squares Ambiguity Decorrelation Adjustment: A Method for Fast GPS Integer Ambiguity Estimation[J]. Journal of Geodesy, 1995, 70(1-2): 65-82. |
| [2] | LIU L T, HSU H T, ZHU Y Z, et al. A New Approach to GPS Ambiguity Decorrelation[J]. Journal of Geodesy, 1999, 73(9): 478-490. |
| [3] | XU Peiliang. Random Simulation and GPS Decorrelation[J]. Journal of Geodesy, 2001, 75(7-8): 408-423. |
| [4] | XU Peiliang. Parallel Cholesky-based Reduction for the Weighted Integer Least Squares Problem[J]. Journal of Geodesy, 2012, 86(1): 35-52. |
| [5] | ZHOU Yangmei. A New Practical Approach to GNSS High-dimensional Ambiguity Decorrelation[J]. GPS Solutions, 2011, 15(4): 325-331. |
| [6] | 周扬眉, 刘经南, 刘基余. 回代解算的LAMBDA方法及其搜索空间[J]. 测绘学报, 2005, 34(4): 300-304. ZHOU Yangmei, LIU Jingnan, LIU Jiyu. Return-calculating LAMBDA Approach and Its Search Space[J]. Acta Geodaetica et Cartographica Sinica, 2005, 34(4): 300-304. |
| [7] | 刘宁, 熊永良, 冯威, 等. 单频GPS动态定位中整周模糊度的一种快速解算方法[J]. 测绘学报, 2013, 42(2): 211-217. LIU Ning, XIONG Yongliang, FENG Wei, et al. An Algorithm for Rapid Integer Ambiguity Resolution in Single Frequency GPS Kinematical Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(2): 211-217. |
| [8] | 卢立果, 刘万科, 于兴旺. 基于交叉排序算法解算模糊度的新规约方法[C]//第五届中国卫星导航学术年会电子文集. 南京: [s.n.], 2014. LU Liguo, LIU Wanke, YU Xingwang. A New Reduction Method for Ambiguity Resolution Based on Cross Sorting Algorithm[C]//The Fifth China Satellite Navigation Conference (CSNC). Nanjing: [s.n.], 2014. |
| [9] | 于兴旺. 多频GNSS精密定位理论与方法研究[D]. 武汉: 武汉大学, 2011. YU Xingwang. Multi-frequency GNSS Precise Positioning Theory and Method Research[D]. Wuhan: Wuhan University, 2011. |
| [10] | JAZAERI S, AMIRI-SIMKOOEI A R, SHARIFI M A. Fast Integer Least-squares Estimation for GNSS High Dimensional Ambiguity Resolution Using the Lattice Theory[J]. Journal of Geodesy, 2012, 86(2): 123-136. |
| [11] | HASSIBI A, BOYD S. Integer Parameter Estimation in Linear Models with Applications to GPS[J]. IEEE Transactions on Signal Processing, 1998, 46(11): 2938-2952. |
| [12] | 刘志平, 何秀凤. 改进的GPS模糊度降相关LLL算法[J]. 测绘学报, 2007, 36(3): 286-289. LIU Zhiping, HE Xiufeng. An Improved LLL Algorithm for GPS Ambiguity Solution[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(3): 286-289. |
| [13] | 杨荣华, 花向红, 李昭, 等. GPS模糊度降相关LLL算法的一种改进[J]. 武汉大学学报(信息科学版), 2010, 35(1): 21-24. YANG Ronghua, HUA Xianghong, LI Zhao, et al. An Improved LLL Algorithm for GPS Ambiguity Solution[J]. Geomatics and Information Science of Wuhan University, 2010, 35(1): 21-24. |
| [14] | 谢恺, 柴洪洲, 范龙, 等. 一种改进的LLL模糊度降相关算法[J]. 武汉大学学报(信息科学版), 2014, 39(11): 1363-1368. XIE Kai, CHAI Hongzhou, FAN Long, et al. An Improved LLL Ambiguity Decorrelation Algorithm[J]. Geomatics and Information Science of Wuhan University, 2014, 39(11): 1363-1368. |
| [15] | 刘经南, 于兴旺, 张小红. 基于格论的GNSS模糊度解算[J]. 测绘学报, 2012, 41(5): 636-645. LIU Jingnan, YU Xingwang, ZHANG Xiaohong. GNSS Ambiguity Resolution Using Lattice Theory[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 636-645. |
| [16] | 卢立果. 基于球形搜索的模糊度格基规约方法研究与分析[D]. 武汉: 武汉大学, 2013. LU Liguo. The Research and Analysis Based on Sphere Search for Ambiguity on Reduction[D]. Wuhan: Wuhan University, 2013. |
| [17] | LANNES A. On the Theoretical Link between LLL-reduction and LAMBDA-decorrelation[J]. Journal of Geodesy, 2013, 87(4): 323-335. |
| [18] | LEICA A, RAPOPORT L, TATARNIKOV D. GPS Satellite Surveying[M]. 4th ed. New York: Wiley, 2015: 324-356. |
| [19] | BORNO M A, CHANG X W, XIE X H. On “Decorrelation” in Solving Integer Least-squares Problems for Ambiguity Determination[J]. Survey Review, 2014, 46(334): 37-49. |
| [20] | 卢立果, 刘万科, 李江卫. 降相关对模糊度解算中搜索效率的影响分析[J]. 测绘学报, 2015, 44(5): 481-487. DOI: 10.11947/j.AGCS.2015.20140311. LU Liguo, LIU Wanke, LI Jiangwei. Impact of Decorrelation on Search Efficiency of Ambiguity Resolution[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(5): 481-487. DOI: 10.11947/j.AGCS.2015.20140311. |
| [21] | CHANG X W, YANG X, ZHOU T. MLAMBDA: A Modified LAMBDA Method for Integer Least-squares Estimation[J]. Journal of Geodesy, 2005, 79(9): 552-565. |
| [22] | TEUNISSEN P J G, ODOLINSKI R, ODIJK D. Instantaneous BeiDou+GPS RTK Positioning with High Cut-off Elevation Angles[J]. Journal of Geodesy, 2014, 88(4): 335-350. |
| [23] | KOY H, SCHNORR C P. Segment LLL-reduction of Lattice Bases[M]//SILVERMAN J H. Cryptography and Lattices, Lecture Notes in Computer Sciences. Berlin: Springer, 2001, 2146: 67-80. |
| [24] | KOY H, SCHNORR C P. Segment LLL-reduction with Floating Point Orthogonalization[M]//SILVERMAN J H. Cryptography and Lattices, Lecture Notes in Computer Sciences. Berlin: Springer, 2001, 2146: 81-96. |
| [25] | 范龙, 翟国君, 柴洪洲. 模糊度降相关的整数分块正交化算法[J]. 测绘学报, 2014, 43(8): 818-826. DOI: 10.13485/j.cnki.11-2089.2014.0094. FAN Long, ZHAI Guojun, CHAI Hongzhou. Ambiguity Decorrelation Algorithm with Integer Block Orthogonalization Algorithm[J]. .Acta Geodaetica et Cartographica Sinica, 2014, 43(8): 818-826. DOI: 10.13485/j.cnki.11-2089.20140094. |
| [26] | LENSTRA A K, LENSTRA H W, LOVASZ L. Factoring Polynomials with Rational Coefficients[J]. Mathematische Annalen, 1982, 261(4): 515-534. |
| [27] | LUK F T, TRACY D M. An Improved LLL Algorithm[J]. Linear Algebra and Its Applications, 2007, 428(2-3): 441-452. |
| [28] | NGUYEN P Q, VALLEE B. The LLL Algorithm: Survey and Applications (Information Security and Cryptography) [M]. Paris: Springer, 2010: 145-178. |
| [29] | ODIJK D, TEUNISSEN P J G. ADOP in Closed form for a Hierarchy of Multi-frequency Single-Baseline GNSS Models[J]. Journal of Geodesy, 2008, 82(8): 473-492. |
| [30] | TEUNISSEN P J G, ODIJK D. Ambiguity Dilution of Precision: Definition, Properties and Application[C]//Proceedings of ION GPS-97. Kansas City: [s.n.], 1997: 891-899. |
| [31] | VERHAGEN S. On the Approximation of the Integer Least-squares Success Rate: Which Lower or Upper Bound to Use?[J]. Journal of Global Positioning Systems, 2003, 2(2): 117-124. |
| [32] | FENG Yanming, WANG Jun. Computed Success Rates of Various Carrier Phase Integer Estimation Solutions and Their Comparison with Statistical Success Rates[J]. Journal of Geodesy, 2011, 85(2): 93-103. |
| [33] | VERHAGEN S, LI Bofeng, TEUNISSEN P J G. Ps-LAMBDA: Ambiguity Success Rate Evaluation Software for Interferometric Applications[J]. Computers & Geosciences, 2013, 54: 361-376. |
| [34] | TEUNISSEN P J G. Success Probability of Integer GPS Ambiguity Rounding and Bootstrapping[J]. Journal of Geodesy, 1998, 72(10): 606-612. |