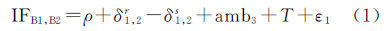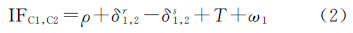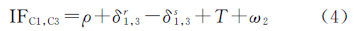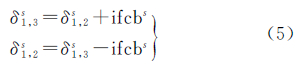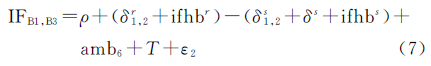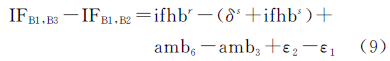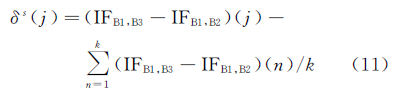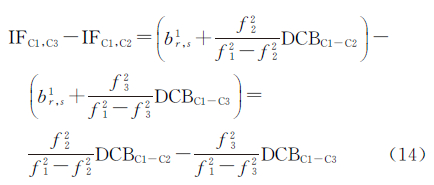2. 地理信息工程国家重点实验室, 陕西 西安 710054;
3. 西安测绘研究所, 陕西 西安 710054
2. State Key Laboratory of Geo-information Engineering, Xi'an 710054, China;
3. Xi'an Research Institute of Surveying and Mapping, Xi'an 710054, China
随着GNSS的发展,现代化之后的GPS系统、北斗卫星导航系统[1]等已经开始三频信号的发射,其中北斗是目前唯一全星座提供三频信号的卫星导航系统。研究表明,受卫星、接收机硬件延迟、太空环境等影响,采用不同频率观测、观测组合解算得到的卫星钟差间存在一定的差异[2, 3, 4, 5]。在基于双差观测的相对定位中,与卫星、接收机相关的偏差可以完全抵消,从而不影响现有研究成果的应用[6, 7]。然而,在采用非差观测的数据处理中,需要严格、细致地考虑各个偏差的特性、补偿措施。通常,采用无电离层延迟伪距、相位组合联合解算得到卫星钟差[8, 9, 10]。数据处理中,伪距、相位观测分别采用不同的权以减弱伪距观测噪声对解算参数的影响。虽然伪距观测对应的权与相位观测相比较小[11, 12],但其对卫星钟差的贡献不容忽视。伪距观测数据的参与保证了卫星钟差产品中卫星硬件偏差的存在,以使解算得到的钟差产品不影响伪距定位的精度和模糊度的解算[13]。对实测的GPS、北斗三频相位观测研究表明:不同的无电离层延迟相位组合间存在偏差,使得以无电离层延迟相位组合L1/L2、B1/B2解算得到的卫星钟差不能直接应用于无电离层延迟组合L1/L5、B1/B3的高精度定位中[2, 3, 4, 5, 14]。基于这一发现,文献[2, 3, 4, 5, 14]对三频观测频间钟差偏差的解算方法与结果分析进行了大量研究。研究成果表明,三频信号频间钟差偏差在 (-18,18)厘米范围内以正、余弦函数的特性变化。显然,只采用相位观测解算得到的频间卫星钟差偏差中缺少了卫星硬件偏差常数部分的存在。尽管这一结果不会影响采用相位观测进行的定位,但会影响模糊度的特性与解算策略以及仅采用伪距信号定位的精度[13]。
三频信号的发射与对应服务,将逐步成为各GNSS系统工作的常规模式。针对三频观测的研究,主要有周跳探测与修复[15, 16],三频观测组合方法[17, 19]、基于双差观测模型的相对定位及其模糊度的固定[6, 7, 20, 21]等。对于多频观测信号卫星钟差的解算与服务将逐步展开。基于传统方法进行卫星钟差计算时,两组无电离层延迟相位、伪距组合(B1/B2、C1/C2 和 B1/B3、C1/C3)会被采用。数据处理中,解算参数会成倍增加,如模糊度、卫星钟差等。为了提高计算效率,简化三频观测卫星钟差的解算内容、步骤,本文提出一种进行北斗系统三频信号卫星钟差的估计方法,并给出对应的服务策略。利用实测的观测数据,验证了本文所提方法的有效性。
1 数学方法一般情况下,卫星钟差采用无电离层延迟相位、伪距组合求解。
1.1 目前频间卫星钟差偏差解算方法三频观测可形成两组无电离层延迟相位(B1/B2 和 B1/B3)、伪距组合(C1/C2和C1/C3)。两组无电离层延迟相位、伪距组合如下
式中,IFB1,B2为B1/B2对应的观测值;IFC1,C2为C1/C2对应的观测值;IFB1,B3为B1/B3对应的观测值;IFC1,C3为C1/C3对应的观测值;ρ为站星间距离;δ1,2r、δ1,3r分别为观测B1/B2、C1/C2和B1/B3、C1/C3对应的接收机钟差;δ1,2s为采用观测B1/B2、C1/C2解算得到的卫星钟差;amb3、amb6分别为B1/B2、B1/B3观测对应的模糊度;T为对流层延迟;ε1、ε2分别为B1/B2、B1/B3观测对应的噪声;δ1,3s为采用观测B1/B3、C1/C3解算得到的卫星钟差;ω1、ω2分别为C1/C2、C1/C3观测对应的噪声。当应用传统的卫星钟差解算策略时,需要进行两套卫星钟差δ1,2s和δs1,3的估计,也需要进行两套模糊度参数的估计。与双频观测卫星钟差的解算相比较,当应用传统策略进行卫星钟差的估计时,会增加解算的负担与效率[3]。针对传统策略对应的缺陷,本文提出一种多频观测卫星钟差的估计策略。该方法基于两套卫星钟差(δ1,2s和δ1,3s)差异的解算和其中任意一套卫星钟差(δ1,2s或δ1,3s)的估计,另外一套卫星钟差通过这两结果值进行恢复。对应的公式如下式中,ifcbs为两套卫星钟差之间的差异,定义为频间卫星钟差偏差[2, 3, 4, 5]。式(5)表明,新方法的关键在于两套卫星钟差差异的求解。在频间卫星钟差偏差的估计研究中,文献[2, 14]率先采用式(1)和式(3)的差值进行了频间卫星钟差偏差的分析和估计。仅仅采用了相位观测值,使得频间卫星钟差偏差中常数部分被模糊度参数所吸收。采用缺失了常数部分的频间卫星钟差偏差进行另外一套卫星钟差的恢复时,会影响恢复得到的卫星钟差的精度,也影响对应产品的应用和定位精度[13]。
1.2 频间卫星钟差偏差估计新方法与模型化研究表明[2, 4],频间接收机钟差偏差为一常数,频间卫星钟差偏差除了常数部分之外还有对应的变化部分。频间接收机钟差偏差的常数特性,使得采用传统方法进行钟差估计时,可采用一个参数进行接收机钟差的求解,对应的频间接收机钟差偏差常数部分会被模糊度参数所吸收。设频间钟差偏差如下
式中,ifhbs为频间卫星钟差偏差的常数部分;δs为频间卫星钟差偏差的变化部分;ifhbr为频间接收机钟差偏差的常数部分。把频间钟差偏差代入式(3)和式(4)中,得到 式(1)减式(7),式(2)减式(8)得到式(9)表明,高精度频间卫星钟差偏差对应的变化部分可以采用单站观测解算得到。设对卫星s观测了k个历元,则每个历元对应频间卫星钟差偏差的变化部分为
当采用式(9)进行频间卫星钟差偏差估计时,常数部分(接收机和卫星)会被模糊度参数所吸收,因此,采用式(10)进行频间钟差偏差常数部分估计
式中,ifhbr,s为频间钟差偏差(卫星与接收机部分的和)。式(12)表明,采用其只能求解得到频间卫星钟差偏差和频间接收机钟差偏差的和。为了获得卫星部分,消除接收机部分的影响,可以选择一参考卫星,进行频间卫星钟差偏差的求解 当采用式(13)求解得到频间卫星钟差偏差的常数部分和采用式(11)求解得到频间卫星钟差偏差的变化部分之后,就可获得频间卫星钟差偏差。式(10)也可以写为式中,br,s1为伪距C1对应的接收机、卫星硬件偏差之和;fi(i=1,2,3)为第i频点观测值对应的频率;DCB为伪距观测对应的频间偏差。式(13)、式(14)表明,卫星钟差频间偏差可表示为DCBC1-C2和DCBC1-C3的代数和。虽然多频观测中卫星钟差频间偏差是DCB的表达式,但目前DCB产品难以替代频间钟差偏差的估计:①目前DCB是以常数参数解算得到并进行产品发布,而卫星钟差频间偏差包括常数和变化两个部分;②目前DCB结果是电离层延迟模型化的副产品,精度受预设电离层延迟模型的影响。数据处理中,不仅要进行DCB的估计,也要进行电离层延迟模型参数的解算,解算过程复杂且繁琐。研究表明[3, 4, 14]频间卫星钟差偏差具有明显的规律性和周期变化性,针对频间卫星钟差偏差特性,其可以模型化为
式中,d 为常数项;e为线性项;i为谐函数的阶次;Ti 为谐函数对应周期;θi为谐函数对应的初始相位;λi为谐函数对应的振幅。
2 数据处理与分析为了验证本文提出的北斗频间卫星钟差偏差估计方法,研究频间卫星钟差偏差的特性,对10个北斗观测站40 d(DOY 205—244,2012)的观测数据进行了处理。采样间隔为30 s,截止卫星高度角为10°。
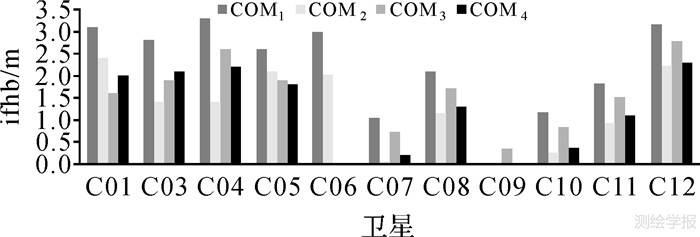
2.1 频间钟差偏差常数部分式(12)、式(13)表明,采用单站观测可以进行频间钟差偏差常数部分的估计。当采用式(12)时,解算得到的频间钟差偏差常数部分为卫星部分与接收机部分的和,采用10个站的观测数据分别进行频间钟差偏差(卫星和接收机部分的和)常数部分的求解,部分卫星对应的结果如图 1所示。
|
| 图 1 频间钟差偏差常数部分(卫星和接收机部分的和) Fig. 1 The constant part of inter-frequency clock bias (sum of the receiver and satellite parts) |
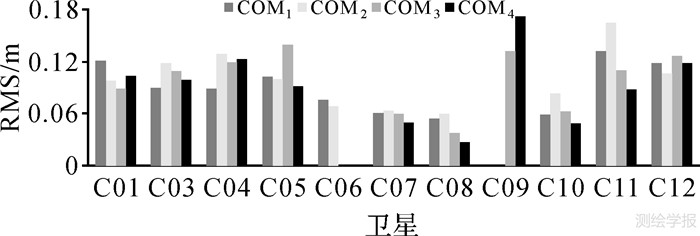
图 1表明,采用不同观测站解算得到的频间钟差偏差常数部分结果不同,这表明频间接收机钟差偏差常数部分与接收机有关,接收机不同对应的值不同。在频间钟差偏差(卫星和接收机部分的和)常数部分解算时,每天解算一个值,对40个结果序列进行统计,部分卫星对应RMS如图 2所示。
|
| 图 2 频间钟差偏差常数部分(卫星和接收机部分的和)对应的RMS Fig. 2 RMS of the constant part of inter-frequency clock bias (sum of the receiver and satellite parts) |
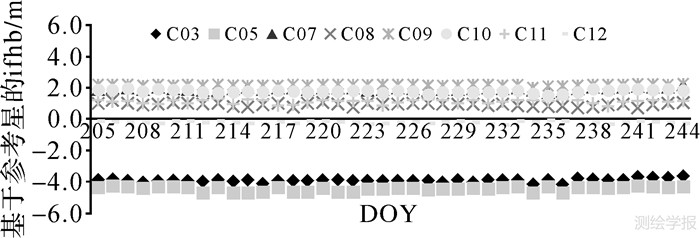
图 2表明,频间钟差偏差常数部分(卫星和接收机部分的和)基本保持稳定,对应的RMS值优于18 cm。为了研究频间卫星钟差偏差常数部分的特性,采用式(13)进行频间卫星钟差偏差常数部分的计算,选择参考卫星为C06,得到每颗卫星对应的结果如图 3所示。
|
| 图 3 频间卫星钟差偏差 Fig. 3 Inter-frequency satellite clock bias |
图 3表明,基于参考卫星的频间卫星钟差偏差常数部分在一定的时间里面也比较稳定。图 3也说明,每颗卫星对应的频间卫星钟差常数部分不同,不同的卫星间存在一定的差异,并且常数部分有的达到了米级。频间卫星钟差偏差常数部分的稳定性对于其短时间高精度预报具有重要的意义。
2.2 高精度频间卫星钟差偏差的模型化当采用式(11)计算得到频间卫星钟差偏差的变化部分和采用式(13)计算得到频间卫星钟差偏差的常数部分之后,就可获得频间卫星钟差偏差。对解算得到的频间卫星钟差偏差进行模型化时,目前采用了式(15)来实现。采用式(15)进行频间卫星钟差偏差模型化时,关键是频间卫星钟差偏差周期的确定。本文采用不同的周期组[4]进行频间卫星钟差偏差的模型化。针对GEO卫星与非GEO卫星的不同运动状态,采用了不同的周期组。模型化中,统计了模型的改正效果[4]和模型化值与估计值之间的RMS。对应的模型化精度如表 1、表 2所示。
| 周期组/h | 改正效果/(%) | RMS/cm | ||||||
| C01 | C03 | C04 | C05 | C01 | C03 | C04 | C05 | |
| T1=12,T2=6 | 48.1 | 49.2 | 51.4 | 52.2 | 2.3 | 3.0 | 3.1 | 3.9 |
| T1=24,T2=12 | 69.2 | 74.1 | 72.1 | 70.9 | 2.3 | 2.4 | 1.7 | 2.4 |
| T1=12,T2=6,T3=8 | 53.7 | 52.9 | 59.1 | 64.2 | 3.9 | 4.7 | 3.1 | 4.6 |
| T1=24,T2=12,T3=6 | 71.1 | 75.6 | 76.6 | 73.1 | 2.3 | 2.1 | 1.6 | 2.3 |
| T1=24,T2=12,T3=8 | 71.8 | 76.5 | 77.1 | 75.8 | 2.2 | 2.0 | 1.5 | 2.0 |
| T1=24,T2=12,T3=8,T4=4 | 73.4 | 78.1 | 78.4 | 77.9 | 2.1 | 1.9 | 1.4 | 1.9 |
| T1=24,T2=12,T3=8,T4=6 | 74.7 | 79.8 | 80.8 | 78.6 | 1.9 | 1.7 | 1.3 | 1.9 |
| 周期组/h | 改正效果/(%) | RMS/cm | ||||||||||||
| C06 | C07 | C08 | C09 | C10 | C11 | C12 | C06 | C07 | C08 | C09 | C10 | C11 | C12 | |
| T1=12,T2=6,T3=8,T4=3 | 97.1 | 96.3 | 98.2 | 98.0 | 95.1 | 94.3 | 95.7 | 1.4 | 1.7 | 1.9 | 1.6 | 2.0 | 1.8 | 1.7 |
| T1=12,T2=6,T3=8,T4=4 | 98.2 | 97.3 | 99.2 | 98.9 | 94.7 | 95.2 | 96.3 | 1.2 | 1.5 | 1.4 | 1.3 | 1.7 | 1.2 | 1.3 |
| T1=12,T2=6,T3=4,T4=3 | 97.2 | 95.9 | 97.9 | 97.9 | 93.9 | 94.9 | 94.9 | 1.3 | 1.6 | 1.5 | 1.4 | 1.8 | 1.6 | 1.5 |
| T1=12,T2=6,T3=8 | 96.1 | 95.8 | 97.6 | 97.7 | 92.9 | 94.1 | 94.2 | 1.7 | 1.9 | 2.1 | 1.8 | 2.2 | 1.9 | 1.9 |
| T1=12,T2=6,T3=4 | 96.2 | 95.3 | 97.3 | 97.4 | 91.9 | 93.9 | 93.4 | 1.9 | 2.1 | 2.3 | 2.0 | 2.3 | 2.1 | 2.2 |
表 1、表 2表明,采用基于谐函数的混合函数进行北斗频间卫星钟差偏差的模型化时,对应精度可以实现厘米级。表 1表明,当采用周期组T1=24、T2=12、T3=8、T3=4时,GEO卫星对应的频间卫星钟差偏差模型的精度最高;表 2表明,当采用周期组T1=12、T2=6、T3=8、T4=4时,非GEO卫星对应的频间卫星钟差偏差模型化的精度最高。这与对频间卫星钟差偏差变化部分模型化的结果是一致的。
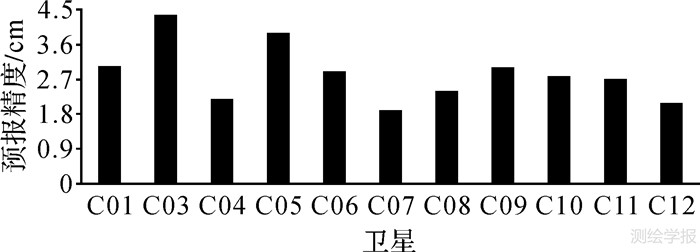
2.3 北斗频间卫星钟差偏差预报为了研究北斗频间卫星钟差偏差的稳定性和预报效果,采用2012年第244天每颗卫星对应的模型系数进行第245天每颗频间卫星钟差偏差的计算,统计预报结果与估计结果之间的差异和RMS,其中RMS结果如图 4所示。
|
| 图 4 频间卫星钟差偏差预报精度 Fig. 4 Accuracy of the prediction for the inter-frequency satellite clock bias |
图 4表明,采用前一天的北斗频间卫星钟差偏差模型系数进行第2天对应频间卫星钟差偏差的预报,可以实现厘米级结果。这也说明北斗频间卫星钟差偏差具有较好的稳定性。
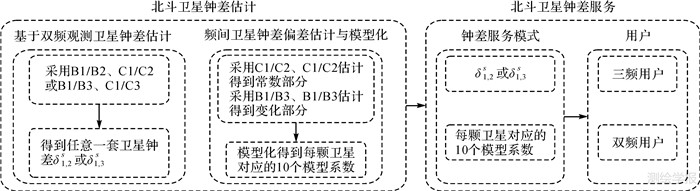
2.4 高精度北斗卫星钟差服务策略北斗频间卫星钟差偏差包括常数和变化部分,虽然对应变化部分一般为分米级[4],但对应常数部分可以达到米级。变化部分具有规律性变化特性,也具有一定的稳定性[4],对应常数部分在一定时间内也具有一定的稳定性。稳定变化的特性对于北斗频间卫星钟差偏差的模型化具有重要的意义,模型化结果也验证了这一特性。高精度的模型化结果表明,北斗卫星钟差偏差可以采用10个参数表示,对应精度可达到厘米级。北斗卫星导航系统是目前唯一全星座进行三频信号发射的导航系统,对应于三频观测进行的卫星钟差服务策略研究是非常必要的。针对三频观测以及北斗频间卫星钟差偏差的特性,对应的卫星钟差服务策略如图 5所示。
图 5为北斗卫星钟差估计和服务流程。流程中,首先估计得到任意一套双频卫星钟差δ1,2s或δ1,3s,同时采用本文提出的新方法进行频间卫星钟差偏差的估计。频间卫星钟差偏差估计中,包括常数部分和变化部分的估计。变化部分与常数部分求和获得每颗卫星对应的高精度频间卫星钟差偏差结果序列。然后,对每颗卫星对应的频间卫星钟差偏差序列进行模型化以获取每颗卫星对应模型的10个系数。基于双频卫星钟差δ1,2s或δ1,3s和每颗卫星对应的10个模型系数,就可以实现三频、双频用户的高精度卫星钟差需求。三频高精度非差定位中,可以采用式(1)—式(4)进行数据处理。双频定位中,可以采用式(1)和式(2)或式(3)和式(4)进行数据处理。
|
| 图 5 北斗卫星钟差服务策略 Fig. 5 Strategy for BeiDou satellite clock service |
北斗卫星导航系统是目前唯一一个全星座实现三频信号发射的导航系统。研究表明,三频信号间的不一致性,使得采用不同观测组合求解得到的卫星钟差偏差间存在显著的差异,且这一差异具有变化性,定义为频间卫星钟差偏差。目前对于频间卫星钟差偏差的求解方法中,仅仅采用了相位观测,其中的常数部分被模糊度参数所吸收,使之缺失于估计得到的频间卫星钟差偏差结果中。本文提出了一种北斗频间卫星钟差偏差估计方法,弥补了现有方法的不足。笔者采用本文方法与观测站数据,分析了频间卫星钟差偏差常数部分的特性。结果表明,频间卫星钟差偏差常数部分短期内是稳定的。对采用新方法估计得到的北斗频间卫星钟差偏差进行了模型化。模型化结果表明,10个模型参数可以高精度表示北斗频间卫星钟差偏差,精度优于2 cm。除此之外,本文也研究了北斗频间卫星钟差偏差的预报算法。采用第1天的模型化参数,进行第2天对应卫星频间卫星钟差偏差值的计算,可实现厘米级精度。针对北斗频间卫星钟差偏差的稳定性和可以模型化特性,提出了高精度北斗卫星钟差服务策略,为我国北斗高精度卫星钟差服务提供依据。
| [1] | 杨元喜, 李金龙, 徐君毅, 等. 中国北斗卫星导航系统对全球PNT用户的贡献[J]. 科学通报, 2011, 56(21): 1734-1740. YANG Yuanxi, LI Jinlong, XU Junyi, et al. Contribution of the Compass Satellite Navigation System to Global PNT Users[J]. Chinese Science Bulletin, 2011, 56(26): 2813-2819. |
| [2] | LI Haojun, ZHOU Xuhua, WU Bin, et al. Estimation of the Inter-frequency Clock Bias for the Satellites of PRN25 and PRN01[J]. Science China Physics, Mechanics and Astronomy, 2012, 55(11): 2186-2193. |
| [3] | LI Haojun, ZHOU Xuhua, WU Bin. Fast Estimation and Analysis of the Inter-frequency Clock Bias for Block IIF Satellites[J]. GPS Solutions, 2013, 17(3): 347-355. |
| [4] | LI Haojun, CHEN Yanling, WU Bin, et al. Modeling and Initial Assessment of the Inter-frequency Clock Bias for COMPASS GEO Satellites[J]. Advances in Space Research, 2013, 51(12): 2277-2284. |
| [5] | 李浩军, 朱卫东. 北斗导航系统卫星频间钟差偏差[J]. 测绘学报, 2014, 43(11): 1127-1131. LI Haojun, ZHU Weidong. Inter-frequency Clock Bias of BeiDou[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(11): 1127-1131. |
| [6] | FENG Yanming, LI Bofeng. Wide Area Real Time Kinematic Decimetre Positioning with Multiple Carrier GNSS Signals[J]. Science China(Earth Sciences), 2010, 53(5): 731-740. |
| [7] | LI Bofeng, FENG Yanming, SHEN Yunzhong. Three Carrier Ambiguity Resolution: Distance-independent Performance Demonstrated Using Semi-generated Triple Frequency GPS Signals[J]. GPS Solutions, 2010, 14(2): 177-184. |
| [8] | LI Haojun,CHEN Junping,WANG Jiexian,et al.Network Based Real-time Precise Point Positioning[J]. Advances in Space Research, 2010, 46(9): 1218-1224. |
| [9] | 李浩军, 王解先, 陈俊平, 等. 基于GNSS网络的实时精密单点定位及精度分析[J]. 地球物理学报, 2010, 53(6): 1302-1307. LI Haojun, WANG Jiexian, CHEN Junping, et al. The Realization and Analysis of GNSS Network Based Real-time Precise Point Positioning[J]. Chinese Journal of Geophysics, 2010, 53(6): 1302-1307. |
| [10] | 张小红, 李星星, 郭斐, 等. 基于服务系统的实时精密单点定位技术及应用研究[J]. 地球物理学报, 2010, 53(6): 1308-1314. ZHANG Xiaohong, LI Xingxing, GUO Fei, et al. Server-based Real-time Precise Point Positioning and Its Application[J]. Chinese Journal of Geophysics, 2010, 53(6): 1308-1314. |
| [11] | HAUSCHILD A, MONTENBRUCK O. Kalman-filter-based GPS Clock Estimation for Near Real-time Positioning[J]. GPS Solutions, 2009, 13(3): 173-182. |
| [12] | ZHANG Xiaohong, LI Xingxing,GUO Fei. Satellite Clock Estimation at 1 Hz for Realtime Kinematic PPP Applications[J]. GPS Solutions, 2011, 15(4): 315-324. |
| [13] | LI Haojun, XU Tianhe, LI Baofeng, et al. A New Differential Code Bias (C1-P1) Estimation Method and Its Performance Evaluation[J]. GPS Solutions, 2015: 1-9, doi: 10.1007/s10291-015-0438-4. |
| [14] | MONTENBRUCK O, HUGENTOBLER U, DACH R, et al. Apparent Clock Variations of the Block IIF-1 (SVN62) GPS Satellite[J]. GPS Solution, 2012, 16 (3): 303-313. |
| [15] | 李金龙, 杨元喜, 徐君毅, 等. 基于伪距相位组合实时探测与修复GNSS三频非差观测数据周跳[J]. 测绘学报, 2011, 40(6): 717-722, 729. LI Jinlong, YANG Yuanxi, XU Junyi, et al. Real-time Cycle-slip Detection and Repair Based on Code-phase Combinations for GNSS Triple-frequency Un-differenced Observations[J]. Acta Geodaetica et Cartographica Sinica, 2012, 40(6): 717-722, 729. |
| [16] | 黄令勇, 宋力杰, 王琰, 等. 北斗三频无几何相位组合周跳探测与修复[J]. 测绘学报, 2012, 41(5): 763-768. HUANG Lingyong,SONG Lijie,WANG Yan,et al.BeiDou Triple-frequency Geometry-free Phase Combination for Cycle-slip Detection and Correction[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 763-768. |
| [17] | HATCH R, JUNG J, ENGE P, et al. Civilian GPS: The Benefits of Three Frequencies[J]. GPS Solution, 2010, 3(4): 1-9. |
| [18] | ODIJK D. Ionosphere-free Phase Combinations for Modernized GPS[J]. Journal of Surveying Engineering, 2003, 129(4): 165-173. |
| [19] | COCARD M, BOURGON S, KAMALI O, et al. A Systematic Investigation of Optimal Carrier-phase Combinations for Modernized Triple-frequency GPS[J]. Journal of Geodesy, 2008, 82(9): 555-564. |
| [20] | TANG Weiming, DENG Chenlong, SHI Chuang, et al. Triple-frequency Carrier Ambiguity Resolution for BeiDou Navigation Satellite System[J]. GPS Solutions, 2014, 18(4): 335-344. |
| [21] | ZHAO Qile, DAI Zhiqiang, HU Zhigang, et al. Three-Carrier Ambiguity Resolution Using the Modified TCAR Method[J]. GPS Solutions, 2014, 19(4): 589-599, doi: 10.1007/s10291-014-0421-5. |