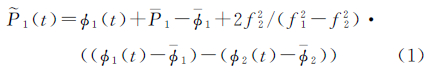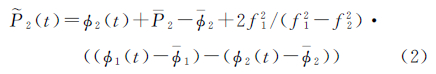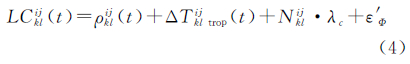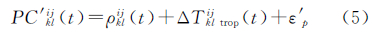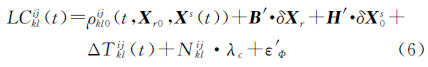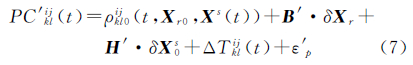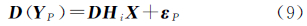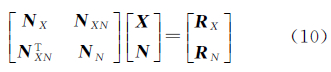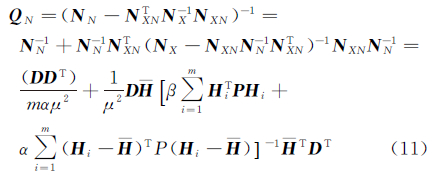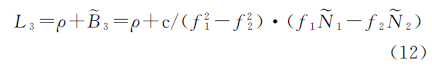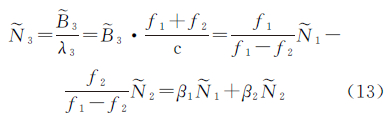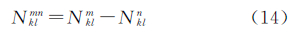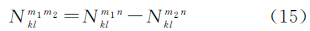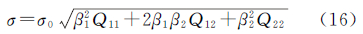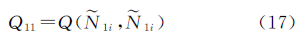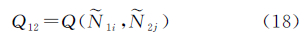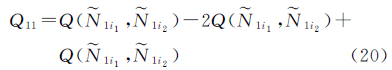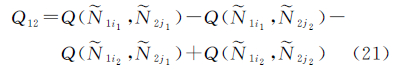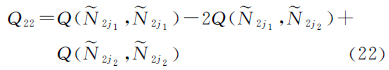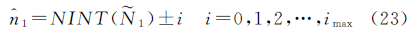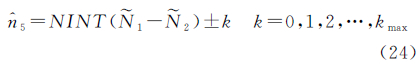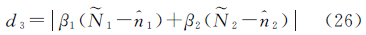导航卫星精密定轨是进行精密定位的基础,在卫星精密数据处理中占有重要地位。根据观测量组差方式的不同,导航卫星精密定轨方法可分为非差动力法和双差动力法[1]。2012年底,北斗卫星导航系统(BeiDou Navigation Satellite System,BDS)开通运行以来[2,3],已有多篇文献对北斗卫星非差动力法精密定轨进行了研究。文献[4]研究了北斗单系统非差精密定轨方法,GEO和IGSO卫星三维定轨精度分别达到3.3 m和0.5 m;文献[5, 6, 7, 8]借鉴Galileo、QZSS试验卫星的精密定轨方法,利用非差动力法对BDS精密定轨策略进行了深入分析;文献[9, 10, 11, 12]基于Panda软件,利用BDS/GPS双系统非差观测数据,实现了径向精度优于10 cm的北斗卫星精密定轨;文献[13]分析了观测几何构形、模糊度固定等对BDS非差精密定轨精度的影响作用;文献[14, 15]研究了BDS与GPS的融合非差精密定轨方法。然而,目前对基于双差模式的北斗卫星精密定轨方法研究相对还不多,其中,文献[16]重点讨论了基于双差伪距的北斗卫星精密定轨方法,并利用仿真数据初步验证了方法的可行性;文献[17]利用国内测站及部分IGS多系统测站的实测数据,对北斗卫星双差法精密定轨进行了初步探讨,但定轨精度偏低,且未涉及双差法中的核心问题--模糊度固定。
不同于GPS等导航系统,北斗系统是由GEO、IGSO和MEO 3类卫星构成的异构星座,特别是GEO卫星具有“高轨、静地”等特性[18],给北斗系统的精密定轨带来了新的问题。鉴于此,本文在对双差动力法精密定轨进行深入研究的基础上,针对北斗系统的特殊性,对经典的双差动力法进行了适当改进,给出了北斗系统的双差动力法精密定轨方法,并对其中的双差模糊度固定方法进行了分析讨论。
1 北斗卫星双差动力法精密定轨文献[19]分析认为,北斗GEO卫星模糊度参数与轨道参数中的近升角距ω、升交点赤经Ω、升交角距u0和半长轴a存在强相关性,造成模糊度与轨道切向分量不易分离。因此,如果采用与GPS相同的处理策略,仅依靠载波相位观测量进行北斗卫星双差动力法精密定轨,将造成GEO卫星轨道切向精度急剧降低。
针对以上问题,本文对传统双差动力法作如下改进:考虑伪距观测量中不包含模糊度参数,在精密定轨中引入双差伪距以加强GEO卫星轨道切向分量的观测约束,从而在一定程度上降低双差模糊度与轨道切向分量的相关性;同时,考虑伪距观测量精度较低,在组双差之前,还对伪距进行了相位平滑处理,以进一步改善定轨精度。平滑公式如下
式中,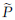 1(t)、
1(t)、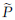 2(t)表示平滑之后的伪距;P1、P2分别表示B1、B2两个频率信号上平滑弧段内所有伪距的平均值; Φ1、Φ2表示相应的相位平均值;f1、f2表示载波频率。
2(t)表示平滑之后的伪距;P1、P2分别表示B1、B2两个频率信号上平滑弧段内所有伪距的平均值; Φ1、Φ2表示相应的相位平均值;f1、f2表示载波频率。
由于伪距与载波相位观测精度不同,为了合理利用两类观测量,这里采取了加权处理的方式。鉴于北斗实测数据质量情况[7, 8, 9, 10],经试验,采用如下加权方法
式中,σc表示伪距观测噪声;σp表示相位观测噪声。需要说明的是,平滑伪距的处理对相位模糊度的解算也是有益的,关于这一点,将在下节进行分析讨论。处理中采用了相位和伪距的消电离层组合,其双差观测方程可表示为
式中,t表示观测历元;LCklij(t)、PC′klij(t)表示测站k、l与卫星i、j形成的双差消电离层组合相位和相位平滑伪距观测量;ΔTijkl trop(t)为对应的对流程延迟双差形式;Nklij表示双差模糊度;λc表示消电离层组合相位观测量的波长;ε′Φ、ε′P分别为双差相位和伪距的观测噪声。组建双差之后,可以消除卫星钟差和测站钟差参数,并能获得具有整数特性的双差模糊度Nklij。对式(4)和式(5)进行线性化,可得
式中,B= ρklij(t)/ Xr;Xr0、δXr分别为测站近似坐标及其改正量,定轨中可对已知的高精度测站坐标进行固定或强约束;H′= ρklij(t)/ Xs(t)·ψ(t,t0),ψ(t,t0)为转移矩阵,通过求解变分方程获得;Xs(t)为卫星在t时刻的状态,通过求解卫星运动微分方程获得;ρkl0ij(t,X(t))为t时刻双差星地几何距离近似值;δX0s为参考时刻卫星状态改正量,包含力学参数(如光压参数);其他符号意义与式(4)和式(5)相同。以观测方程式(6)和式(7)为基础,利用最小二乘参数估计方法,即可进行北斗卫星的双差动力法精密轨道确定,具体的数据处理流程与传统双差动力法[20, 21]类似,这里不再赘述。
2 双差模糊度固定采用文献[16, 22]的推导方法,以N表示双差模糊度参数,X表示模糊度以外的其他参数,Hi表示ti历元的设计矩阵,D表示对应的双差算子,则双差消电离层组合相位和伪距观测方程可表示为
式中,YΦ、YP分别表示消电离层组合相位和伪距观测量;μ表示消电离层组合相位的波长;εΦ、εP表示相应的观测误差。以α和β分别表示相位和伪距的加权因子,假定共有m历元的观测量,则相应的法方程可表示为
式中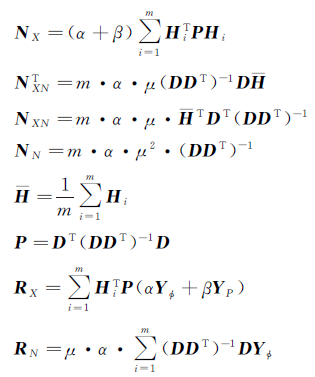
对(10)式中的X进行预消除,可获得双差模糊度的协方差阵为
结合(11)式,进行如下讨论:
(1) 若仅使用载波相位进行北斗卫星精密定轨,即相当于取α=1和β=0。此时,如果双差观测量均由GEO-GEO构成,则由于星地几何结构几乎不变,即Hi≈ H,造成QN趋于无穷大,模糊度参数无法正确解算;如果形成双差观测量时包含IGSO或MEO,由于观测几何结构的变化,QN为有限值,才有可能对模糊度参数进行正确解算,事实上,此时可以通过延长观测时间(相当于增大m),以加大观测几何结构的变化及增加相位数据的累积,来改善模糊度参数的解算精度。
(2) 若联合使用载波相位和伪距进行北斗卫星精密定轨,即α≠0且β≠0。此时,QN的取值主要由伪距观测条件决定,在这种情况下,即使双差观测量均由GEO-GEO构成,也可以解算模糊度参数,但是,受限于伪距的观测条件,无法再通过相位数据的累积来改善模糊度参数的解算精度。在观测结构一定的条件下,通过提高伪距精度(如相位平滑伪距),有助于模糊度参数的解算。
以上分析的启示是:①实际解算中,在同等条件下,应该减少由两颗GEO卫星形成双差观测量;②通过相位平滑伪距,提高伪距精度,有助于模糊度参数的解算。
具体解算中,针对长基线、长时间观测的数据处理特点,这里选用QIF(quasi ionosphere-free)方法进行北斗精密定轨中双差模糊度的固定,其处理方法如下所述。
首先,将消电离层组合观测量的观测方程表示为
式中,L3为消电离层组合观测量;ρ为包含各项误差影响的星地距离;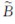 3为消电离层组合观测量对应的模糊度偏差;f1、f2为B1、B2载波的频率值;Ñ1、Ñ2为B1、B2载波的实数模糊度;c为光速。
3为消电离层组合观测量对应的模糊度偏差;f1、f2为B1、B2载波的频率值;Ñ1、Ñ2为B1、B2载波的实数模糊度;c为光速。
将式(12)中的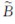 3表示成窄巷周的形式,有
3表示成窄巷周的形式,有
在组建双差观测量时,通常会涉及两类双差模糊度:①直接由两个测站和两颗卫星形成的双差模糊度,如式(14);②由具有相同参考星的两个双差模糊度之差形成的双差模糊度,如式(15)
式中,k、l为测站编号;m、n及m1、m2均为卫星编号。略去测站和卫星编号,以Ñ1i、Ñ1i1、Ñ1i2表示3个独立的B1载波双差模糊度的实数值,以Ñ2j、Ñ2j1、Ñ2j2表示3个独立的B2载波双差模糊度的实数值。消电离层组合观测量模糊度偏差3的均方根误差可表示为
式中,σ0为单位权均方根误差。对于Ñ1i、Ñ2j的情况,有
对于Ñ1i1-Ñ1i2、Ñ2j1-Ñ2j2的情况,有按照σ由小到大的顺序对双差模糊度进行固定。固定方法以搜索的形式进行,其搜索区间定义为
式中,imax、kmax按照经验给定。对于搜索区间中的每对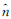 1、
1、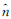 2,计算检测量
2,计算检测量
将与最小的d3值对应的模糊度对接收为模糊度固定值,记为Ñ=[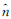 1
1 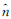 2]T,其中,
2]T,其中,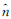 1、
1、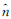 2分别为B1、B2载波的模糊度固定值。
2分别为B1、B2载波的模糊度固定值。
如果
则认为模糊度固定失败,开始进行下一个模糊度的固定。式(27)中dmax为检测量门限值,可依据经验事先给定。每当有模糊度被固定,则将其固定值代入,重新进行最小二乘估计,迭代进行上述模糊度固定过程,直到没有新的模糊度被固定。
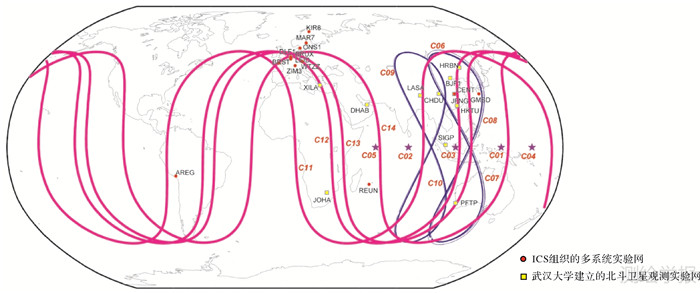
3 算例分析 3.1 改进方法的效果为了说明本文方法的有效性,采用全球24个测站2013年年积日165-168共4 d北斗观测数据进行精密定轨试验,其中,12个测站来自IGS组织的多系统实验网,12个测站来自武汉大学建立的北斗卫星观测实验网,见图 1。
|
| 图 1 测站分布图 Fig. 1 Monitor stations deployment |
处理中分别以165_166_167和166_167_168两个3 d弧段进行北斗卫星双差动力法精密定轨,以两者定轨结果的重叠弧段差值来统计定轨精度。采用如下3种方案进行定轨解算,基本处理策略相同(见表 1),区别如下:
| 类别 | 模型与参数 |
| 观测量组合模式 | 双差消电离层组合 |
| 卫星高度截止角/(°) | 3 |
| 数据处理采样间隔/s | 180 |
| 地球重力场 | JGM3 12阶×12阶 |
| N体引力 | JPL DE200(日、月) |
| 固体潮 | TIDE2000 |
| 海潮 | CSR30 |
| 相对论效应 | IERS 2003 |
| 太阳光压 | ECOM模型 |
| 测站坐标 | IGS08先验坐标,紧约束 |
| 对流层误差改正 | SAAS+NIELL干分量改正;每4 h估计一组天顶湿分量 |
| 电离层误差改正 | 消电离组合消除 |
| 潮汐改正 | IERS2003;FES2004 |
| 接收机钟差 | 双差消除 |
| 卫星钟差 | 双差消除 |
| 模糊度参数 | 浮点解 |
| 轨道动力学参数 | 6个卫星状态参数+5个光压参数 |
方案1(S1):仅使用载波相位数据;
方案2(S2):仅使用相位平滑伪距数据;
方案3(S3):按照本文方法,联合使用载波相位和相位平滑伪距数据。
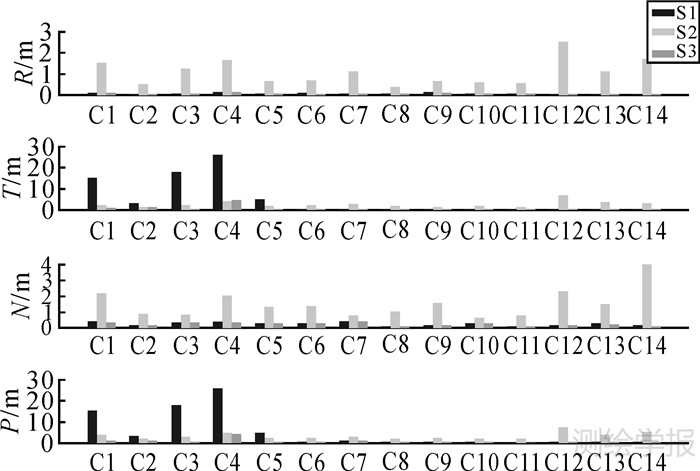
需要说明的是,为便于对比分析,本算例中涉及的双差模糊度均取浮点解。表 2给出了3种方案中各颗卫星径向(R)、切向(T)、法向(N)和三维方向(P)重叠弧段轨道差值的均方根误差(root mean square,RMS),图 2以图示的形式对其进行了对比。
| m | |||||||||||||
| 方案 | PRN | R | T | N | P | ||||||||
| S1 | S2 | S3 | S1 | S2 | S3 | S1 | S2 | S3 | S1 | S2 | S3 | ||
| GEO | C1 | 0.095 | 1.512 | 0.091 | 15.192 | 1.955 | 0.801 | 0.411 | 2.162 | 0.337 | 15.197 | 3.284 | 0.874 |
| C2 | 0.063 | 0.482 | 0.059 | 3.115 | 1.301 | 1.229 | 0.192 | 0.854 | 0.164 | 3.122 | 1.629 | 1.242 | |
| C3 | 0.060 | 1.235 | 0.059 | 17.827 | 2.050 | 0.163 | 0.346 | 0.800 | 0.324 | 17.830 | 2.524 | 0.367 | |
| C4 | 0.164 | 1.651 | 0.157 | 26.020 | 3.678 | 4.235 | 0.382 | 2.003 | 0.315 | 26.023 | 4.502 | 4.249 | |
| C5 | 0.061 | 0.654 | 0.058 | 4.683 | 1.483 | 0.484 | 0.251 | 1.306 | 0.246 | 4.690 | 2.081 | 0.546 | |
| MEAN | 0.089 | 1.107 | 0.085 | 13.367 | 2.094 | 1.382 | 0.316 | 1.425 | 0.277 | 13.372 | 2.804 | 1.456 | |
| IGSO | C6 | 0.114 | 0.685 | 0.076 | 0.298 | 1.719 | 0.225 | 0.248 | 1.375 | 0.259 | 0.404 | 2.305 | 0.351 |
| C7 | 0.031 | 1.111 | 0.041 | 0.657 | 2.288 | 0.608 | 0.368 | 0.717 | 0.355 | 0.753 | 2.642 | 0.706 | |
| C8 | 0.076 | 0.367 | 0.054 | 0.472 | 1.450 | 0.381 | 0.072 | 0.970 | 0.049 | 0.484 | 1.783 | 0.388 | |
| C9 | 0.122 | 0.617 | 0.088 | 0.360 | 0.838 | 0.351 | 0.142 | 1.561 | 0.182 | 0.406 | 1.876 | 0.405 | |
| C10 | 0.036 | 0.594 | 0.039 | 0.450 | 1.418 | 0.420 | 0.273 | 0.628 | 0.282 | 0.528 | 1.661 | 0.508 | |
| MEAN | 0.076 | 0.675 | 0.059 | 0.448 | 1.543 | 0.397 | 0.220 | 1.050 | 0.225 | 0.515 | 2.053 | 0.471 | |
| MEO | C11 | 0.029 | 0.521 | 0.027 | 0.142 | 1.235 | 0.159 | 0.058 | 0.751 | 0.050 | 0.156 | 1.536 | 0.169 |
| C12 | 0.066 | 2.530 | 0.061 | 0.329 | 6.312 | 0.335 | 0.177 | 2.295 | 0.161 | 0.380 | 7.177 | 0.377 | |
| C13 | 0.033 | 1.118 | 0.041 | 0.341 | 3.270 | 0.363 | 0.272 | 1.472 | 0.207 | 0.437 | 3.757 | 0.420 | |
| C14 | 0.062 | 1.694 | 0.070 | 0.298 | 2.739 | 0.235 | 0.124 | 3.968 | 0.083 | 0.329 | 5.110 | 0.259 | |
| MEAN | 0.048 | 1.466 | 0.050 | 0.278 | 3.389 | 0.273 | 0.158 | 2.121 | 0.125 | 0.326 | 4.395 | 0.306 | |
|
| 图 2 定轨精度对比图 Fig. 2 Comparison of orbit precision |
由表 2和图 2的结果可见:
(1) MEO和IGSO卫星在方案1和方案3中定轨精度相当,方案3中由于利用的观测信息更多,结果略优于方案1;但GEO卫星在方案1中的定轨精度明显低于方案3,进一步分析发现,GEO卫星R、N方向的精度在两种方案中基本相当,但方案1中T方向的精度明显较差,主要原因是GEO卫星模糊度参数与轨道切向分量具有强相关性,如果仅使用载波相位进行轨道确定,无法正确分离模糊度参数与切向分量,造成GEO卫星切向定轨精度变差,方案3联合使用载波相位和相位平滑伪距数据能够改善这种相关性,从而有效地提高了GEO卫星的切向定轨精度。
(2) 从方案2的结果可见,仅使用相位平滑伪距,平均来讲,GEO、IGSO和MEO卫星三维定轨精度分别达到2.804 m、2.053 m、4.395 m,均优于5 m,各类卫星的定轨精度基本相当,MEO定轨精度略低于GEO和IGSO主要是由于MEO在轨卫星仅有4颗且全球运行,地面测站的区域分布使其双差观测量数目明显少于其他两类卫星所致。由以上结果可见,虽然GEO卫星观测几何结构较差,但是如果仅依靠伪距而不引入载波相位数据,其定轨精度能够通过长弧段数据的累积达到与IGSO和MEO卫星相当的水平。载波相位数据的引入,导致GEO卫星切向轨道分量与模糊度参数无法完全分离,这是造成方案1和方案3中GEO卫星定轨精度明显低于IGSO和MEO卫星的主要原因。不幸的是,相位平滑伪距虽然能够显著改善伪距精度,但是其精度水平相比载波相位还要差1~2个数量级,从而造成方案2的定轨精度水平明显低于方案3。因此,从以上分析可得,与仅依靠伪距(或相位平滑伪距)数据或仅依靠载波相位数据相比,联合载波相位和相位平滑伪距数据实现北斗卫星双差动力法精密定轨效果更优。
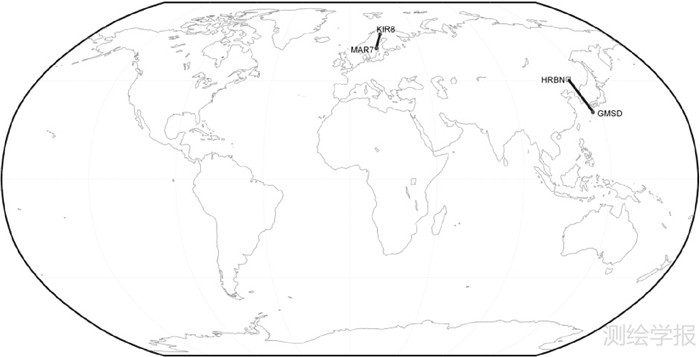
3.2 双差模糊度固定为了考察双差模糊度固定效果,采用2013年年积日161-171共11 d数据进行精密定轨试验,测站分布与上节算例相同。试验中以每3 d数据为一个定轨弧段,共形成9个定轨弧段,这里主要对GMHR和KIMA两条基线在9个定轨弧段(以N1、N2、…、N9标识)内双差模糊度的固定情况进行了统计分析。其中,GMHR的基线长度为1 724.5 km,处于亚太地区,由GMSD与HRBN两个测站形成,其对北斗卫星的观测条件较好,形成的双差模糊度基本上涵盖了所有类型的卫星配对情况(包括GEO-GEO、GEO-MEO、GEO-IGSO、MEO-MEO、IGSO-IGSO和MEO-IGSO等6种情况);KIMA的基线长度为831.6 km,处于北欧地区,由KIR8与MAR7两个测站形成,其对北斗卫星的观测条件较差,仅能观测到一颗GEO卫星(C05),因此无法形成GEO-GEO类型的双差模糊度,此外,其对IGSO卫星的可见弧段较短,但对MEO卫星的观测条件与GMHR相当。图 3给出了两条基线的位置示意图。
|
| 图 3 GMHR和KIMA基线位置示意图 Fig. 3 Sketch map of GMHR and KIMA |
由图 4可见,基线GMHR的双差模糊度固定成功率明显优于基线KIMA。原因是:虽然GMHR的基线长度比KIMA长了一倍有余,理论上,越短的基线,模糊度固定成功率应该越高。但是,有鉴于北斗系统的异构星座特点,位于亚太地区的GMHR基线观测条件要明显优于KIMA,从而使其双差模糊度能够得到更为有效的固定。

|
| 图 4 各弧段内双差模糊度的固定成功率 Fig. 4 Ambiguity fixing success rate in every arc |
由表 3可见,在长弧段的北斗卫星精密定轨处理中,对于观测条件较好的GMHR基线,MEO-MEO、IGSO-IGSO和IGSO-MEO 3类双差模糊度基本能够全部固定;GEO-IGSO类型的双差模糊度能以较高的比例得到固定;GEO-GEO类型的双差模糊度固定成功率虽然不高,但是在本文联合使用载波相位和相位平滑伪距的处理策略下,也获得了不错的固定效果,但其固定成功率在所有类型的模糊度中仍然最低。值得注意的是,GEO-MEO类型的双差模糊度固定成功率明显低于GEO-IGSO类型的双差模糊度,这主要是因为虽然MEO与IGSO卫星具有相似的运动特性,但是,相比IGSO卫星的区域运行特点,MEO卫星的地面运行轨迹遍布全球,每个GEO-MEO类型的双差模糊度对应的有效观测数据弧段较短,造成模糊度固定成功率受限。
| 弧段 | GEO-GEO | GEO-MEO | GEO-IGSO | ||||||
| 模糊度数 | 固定数 | 固定率/(%) | 模糊度数 | 固定数 | 固定率/(%) | 模糊度数 | 固定数 | 固定率/(%) | |
| N1 | 0 | 0 | — | 22 | 7 | 31.8 | 15 | 9 | 60.0 |
| N2 | 32 | 6 | 18.8 | 48 | 8 | 16.7 | 14 | 14 | 100.0 |
| N3 | 30 | 4 | 13.3 | 32 | 6 | 18.8 | 12 | 6 | 50.0 |
| N4 | 36 | 4 | 11.1 | 28 | 6 | 21.4 | 12 | 6 | 50.0 |
| N5 | 46 | 2 | 4.3 | 46 | 6 | 13.0 | 6 | 6 | 100.0 |
| N6 | 0 | 0 | — | 66 | 14 | 21.2 | 12 | 12 | 100.0 |
| N7 | 0 | 0 | — | 56 | 4 | 7.1 | 12 | 10 | 83.3 |
| N8 | 0 | 0 | — | 54 | 4 | 7.4 | 4 | 2 | 50.0 |
| N9 | 48 | 4 | 8.3 | 46 | 4 | 8.7 | 0 | 0 | — |
| SUM | 192 | 20 | 10.4 | 398 | 59 | 14.8 | 87 | 65 | 74.7 |
| 弧段 | MEO-MEO | IGSO-IGSO | IGSO-MEO | ||||||
| 模糊度数 | 固定数 | 固定率/(%) | 模糊度数 | 固定数 | 固定率/(%) | 模糊度数 | 固定数 | 固定率/(%) | |
| N1 | 13 | 12 | 92.3 | 23 | 23 | 100.0 | 7 | 7 | 100.0 |
| N2 | 4 | 4 | 100.0 | 18 | 18 | 100.0 | 12 | 12 | 100.0 |
| N3 | 8 | 8 | 100.0 | 26 | 26 | 100.0 | 14 | 14 | 100.0 |
| N4 | 10 | 10 | 100.0 | 26 | 26 | 100.0 | 16 | 16 | 100.0 |
| N5 | 23 | 23 | 100.0 | 21 | 21 | 100.0 | 14 | 14 | 100.0 |
| N6 | 10 | 10 | 100.0 | 20 | 20 | 100.0 | 10 | 10 | 100.0 |
| N7 | 18 | 18 | 100.0 | 22 | 22 | 100.0 | 8 | 8 | 100.0 |
| N8 | 20 | 20 | 100.0 | 26 | 26 | 100.0 | 10 | 10 | 100.0 |
| N9 | 12 | 12 | 100.0 | 26 | 26 | 100.0 | 12 | 12 | 100.0 |
| SUM | 118 | 117 | 99.2 | 208 | 208 | 100.0 | 103 | 103 | 100.0 |
由表 4可见,在基线KIMA较差的观测条件下,IGSO-IGSO和IGSO-MEO类型的双差模糊度固定成功率明显降低,GEO-MEO和GEO-IGSO类型的双差模糊度几乎无法固定,但由于基线KIMA对MEO卫星观测条件较好,MEO-MEO类型的双差模糊度固定成功率仍然较高。
| 弧段 | GEO-GEO | GEO-MEO | GEO-IGSO | ||||||
| 模糊度数 | 固定数 | 固定率/(%) | 模糊度数 | 固定数 | 固定率/(%) | 模糊度数 | 固定数 | 固定率/(%) | |
| N1 | 0 | 0 | — | 4 | 0 | 0.0 | 12 | 0 | 0.0 |
| N2 | 0 | 0 | — | 16 | 0 | 0.0 | 46 | 0 | 0.0 |
| N3 | 0 | 0 | — | 10 | 0 | 0.0 | 48 | 2 | 4.2 |
| N4 | 0 | 0 | — | 8 | 0 | 0.0 | 52 | 0 | 0.0 |
| N5 | 0 | 0 | — | 0 | 0 | — | 43 | 0 | 0.0 |
| N6 | 0 | 0 | — | 0 | 0 | — | 58 | 0 | 0.0 |
| N7 | 0 | 0 | — | 2 | 0 | 0.0 | 74 | 0 | 0.0 |
| N8 | 0 | 0 | — | 4 | 0 | 0.0 | 70 | 0 | 0.0 |
| N9 | 0 | 0 | — | 0 | 0 | — | 16 | 0 | 0.0 |
| SUM | 0 | 0 | — | 44 | 0 | 0.0 | 419 | 2 | 0.5 |
| 弧段 | MEO-MEO | IGSO-IGSO | IGSO-MEO | ||||||
| 模糊度数 | 固定数 | 固定率/(%) | 模糊度数 | 固定数 | 固定率/(%) | 模糊度数 | 固定数 | 固定率/(%) | |
| N1 | 10 | 6 | 60.0 | 16 | 2 | 12.5 | 22 | 6 | 27.3 |
| N2 | 8 | 6 | 75.0 | 18 | 8 | 44.4 | 18 | 8 | 44.4 |
| N3 | 6 | 6 | 100.0 | 20 | 6 | 30.0 | 20 | 4 | 20.0 |
| N4 | 4 | 4 | 100.0 | 22 | 8 | 36.4 | 20 | 8 | 40.0 |
| N5 | 2 | 2 | 100.0 | 21 | 6 | 28.6 | 28 | 8 | 28.6 |
| N6 | 4 | 4 | 100.0 | 20 | 6 | 30.0 | 22 | 10 | 45.5 |
| N7 | 6 | 6 | 100.0 | 22 | 6 | 27.3 | 20 | 10 | 50.0 |
| N8 | 4 | 4 | 100.0 | 24 | 6 | 25.0 | 24 | 14 | 58.3 |
| N9 | 6 | 6 | 100.0 | 20 | 6 | 30.0 | 22 | 2 | 9.1 |
| SUM | 50 | 44 | 88.0 | 183 | 54 | 29.5 | 196 | 70 | 35.7 |
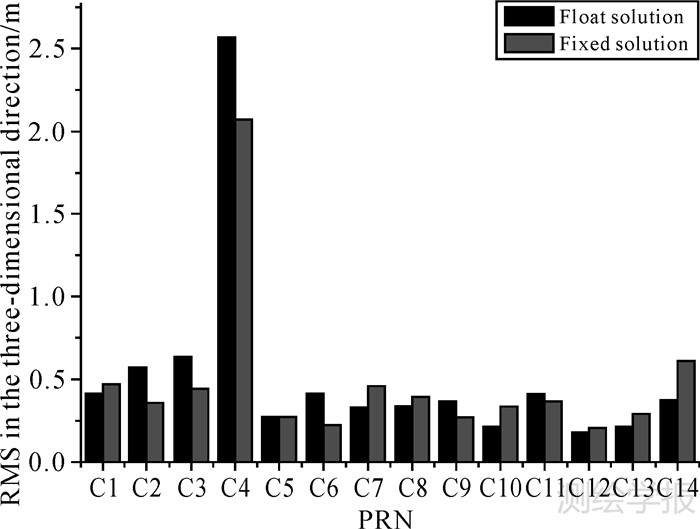
综上可见,在北斗卫星双差动力法精密定轨中,以相位平滑伪距达到提高伪距精度的目的,而后联合使用载波相位和平滑之后的伪距数据,能够取得较高精度的精密定轨结果,并有助于双差模糊度的解算。但是,需要指出的是,受观测条件限制,部分基线虽然长度较短,模糊度固定成功率反而较低。此外,由于目前北斗地面测站分布不均,会形成一些超长基线,其模糊度固定成功率更低,如本算例中CEWT基线,由CENT和WTZZ两个测站组成,基线长度近8000 km,模糊度固定成功仅有2%左右。受以上问题的影响,本文在进行北斗卫星双差动力法精密定轨时,所有基线的模糊度固定成功率平均仅达到20%~30%,因此,模糊度固定之后,对轨道精度的改善作用非常有限。以167_168_169与168_169_170两个定轨弧段为例,图 5对比了模糊度固定前后,重叠弧段轨道差值的RMS情况。由图 5可见,模糊度固定后,轨道精度稍有提高,但不明显,模糊度固定前所有卫星三维定轨精度星间平均为0.522 m,固定后为0.485 m。
|
| 图 5 双差模糊度固定前后北斗卫星定轨精度对比图 Fig. 5 Comparison of BeiDou satellite orbit precision before and after ambiguity fixing |
本文针对GEO卫星切向轨道分量与双差模糊度强相关的问题,对经典双差动力法进行了改进,提出联合使用双差相位及相位平滑伪距实现北斗卫星精密轨道的确定,实测数据分析表明:如果按照经典方法,仅依靠载波相位数据,GEO切向定轨精度急剧变差;如果仅依靠伪距(相位平滑伪距)数据,3类卫星整体精度水平偏低;联合载波相位和相位平滑伪距,既可以降低相关性,又可以兼顾精度,定轨效果最优。
对联合使用载波相位和伪距时,北斗卫星双差模糊度解算的影响因素进行了理论分析,指出:同等条件下,应减少由两颗GEO卫星形成双差观测量;通过相位平滑改善伪距精度,有助于双差模糊度参数的解算。推导给出了利用QIF方法实现北斗卫星双差模糊度固定的基本原理,实测数据分析表明:在本文给出的北斗卫星双差动力法精密定轨中,利用QIF方法能够取得一定的模糊度固定效果,但受观测条件限制,北斗卫星双差模糊度固定成功率整体不高,双差模糊度固定之后对轨道的改进作用有限,特别是由两颗GEO卫星形成的双差模糊度的固定方法尚需进一步分析研究。需要说明的是,有文献研究指出,由于GEO卫星轨道浮点解精度较差,可以取消对GEO-GEO类型模糊度的固定,仅通过其他类型模糊度的固定来改善北斗卫星定轨精度[4, 13, 15],具体效果尚需进一步分析研究。总之,北斗卫星精密定轨中双差模糊度的固定问题还有待进一步深入研究。
致谢:感谢全球连续监测评估系统(iGMAS)信息工程大学分析中心对本文工作的帮助和支持。
| [1] | 刘伟平. 北斗卫星导航系统精密轨道确定方法研究[D]. 郑州: 信息工程大学, 2014: 36-56. LIU Weiping. Research on Precise Orbit Determination of BeiDou Navigation Satellite System[D]. Zhengzhou: The PLA Information Engineering University, 2014. |
| [2] | 杨元喜. 北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报, 2010, 39(1): 1-6. YANG Yuanxi. Progress, Contribution and Challenges of Compass/Beidou Satellite Navigation System[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 1-6. |
| [3] | 中国卫星导航系统管理办公室. 北斗卫星导航系统发展报告2.2[S]. 北京: [s.n.], 2013: 1-10. China Satellite Navigation Office. Report on the Development of Beidou Navigation Satellite System V2.2[S]. Beijing: [s.n.], 2013: 1-10. |
| [4] | GE Maorong, ZHANG Hongping,JIA Xiaolin, et al. What is Achievable with the Current Compass Constellation?[J]. GPS World, 2012, 23(1): 29-34. |
| [5] | STEIGENBERGER P, HUGENTOBLER U, MONTENBRUCK O, et al. Precise Orbit Determination of GIOVE-B Based on the CONGO Network[J]. Journal of Geodesy, 2011, 85(6): 357-365. |
| [6] | STEIGENBERGER P, HAUSCHILD A, MONTENBRUCK O, et al. Orbit and Clock Determination of QZS-1 Based on the CONGO Network[J]. Navigation, 2013, 60(1): 31-40. |
| [7] | MONTENBRUCK O,HAUSCHILD A, STEIGENBERGER P, et al. Initial Assessment of the COMPASS/BeiDou-2 Regional Navigation Satellite System[J]. GPS Solutions, 2013, 17(2): 211-222. |
| [8] | STEIGENBERGER P, HUGENTOBLER U, HAUSCHILD A, et al. Orbit and Clock Analysis of Compass GEO and IGSO Satellites[J]. Journal of Geodesy, 2013, 87(6): 515-525. |
| [9] | 施闯, 赵齐乐, 李敏, 等. 北斗卫星导航系统的精密定轨与定位研究[J]. 中国科学: 地球科学, 2012, 42(6): 854-861. SHI Chuang, ZHAO Qile, LI Min, et al. Precise Orbit Determination of Beidou Satellites with Precise Positioning[J]. Science China: Earth Sciences, 2012, 55(7): 1079-1086. |
| [10] | ZHAO Qile, GUO Jing, LI Min, et al. Initial Results of Precise Orbit and Clock Determination for COMPASS Navigation Satellite System[J]. Journal of Geodesy, 2013, 87(5): 475-486. |
| [11] | LI M, ZHAO Q, SHI C, et al. Precise Orbit Determination of BeiDou Satellites by BeiDou/GPS Data[R]. Guangzhou: CSNC2012, 2012. |
| [12] | 刘伟平, 郝金明, 李建文, 等. 一种北斗卫星精密定轨方法[J]. 测绘科学技术学报, 2013, 30(3): 247-250. LIU Weiping, HAO Jinming, LI Jianwen,et al.A Method of Precise Orbit Determination of BeiDou Navigation Satellite[J]. Journal of Geomatics Science and Technology, 2013, 30(3): 247-250. |
| [13] | HE Lina,GE Maorong,WANG Jiexian,et al.Experimental Study on the Precise Orbit Determination of the BeiDou Navigation Satellite System[J]. Sensors, 2013, 13(3): 2911-2928. |
| [14] | 刘伟平, 郝金明, 李建文, 等. 多GNSS融合的北斗卫星精密定轨[J]. 测绘学报, 2014, 43(11): 1132-1138.DOI:10.13485/j.cnki.11-2089.2014.0186. LIU Weiping, HAO Jinming, LI Jianwen, et al. Multi-GNSS Joint Precise Orbit Determination of BeiDou Navigation Satellite System[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(11): 1132-1138. DOI:10.13485/j.cnki.11-2089.2014.0186. |
| [15] | LIU Yang, LOU Yidong, SHI Chuang, et al. Beidou Regional Navigation System Network Solution and Precision Analysis[M]//SUN Jiadong, JIAO Wenhai, WU Haitao, et al. China Satellite Navigation Conference (CSNC) 2013 Proceedings. Berlin Heidelberg: Springer, 2013: 173-186. |
| [16] | 宋小勇. COMPASS导航卫星定轨研究[D]. 西安: 长安大学, 2009. SONG Xiaoyong. Study on the Orbit Determination of COMPASS Navigation Satellites[D]. Xi'an: Chang'an University, 2009. |
| [17] | ZHU Jun, WANG Jiasong, ZENG Guang, et al. Precise Orbit Determination of BeiDou Regional Navigation Satellite System via Double-difference Observations[M]//SUN Jiadong, JIAO Wenhai, WU Haitao, et al. China Satellite Navigation Conference (CSNC) 2013 Proceedings. Berlin Heidelberg: Springer, 2013: 77-88. |
| [18] | 杜兰. GEO卫星精密定轨技术研究[D]. 郑州: 信息工程大学, 2006: 1-4. DU Lan. A Study on the Precise Orbit Dertermination of Geostationary Satellites[D]. Zhengzhou: The PLA Information Engineering University, 2006: 1-4. |
| [19] | 孙保琪. 基于三频数据的Compass卫星精密定轨[D]. 武汉: 中国科学院测量与地球物理研究院, 2010: 100-106. SUN Baoqi. Precise Orbit Determination of Compass Satellites Based on Triple-frequency Data[D]. Wuhan: Institute of Geodesy and Geophysics Chinese Academy of Sciences, 2010: 100-106. |
| [20] | 葛茂荣. GPS卫星精密定轨理论及软件研究[D]. 武汉: 武汉测绘科技大学, 1995: 37-55. GE Maorong. Study on Theory and Software of Precise Orbit Determination for GPS Satellite[D]. Wuhan: Wuhan Technical University of Surveying and Mapping, 1995: 37-55. |
| [21] | 刘伟平, 郝金明, 于合理, 等. 导航卫星精密轨道与钟差确定方法研究及精度分析[J]. 测绘通报, 2014(5): 5-7, 49.DOI:10.13474/j.cnki.11-2246.2014.0145. LIU Weiping, HAO Jinming, YU Heli, et al. Study on the Method of Precise Navigation Satellite Orbit and Clock Determination and Accuracy Analysis[J]. Bulletin of Surveying and Mapping, 2014(5): 5-7, 49. DOI:10.13474/j.cnki.11-2246.2014.0145. |
| [22] | TEUNISSEN P J G. A Canonical Theory for Short GPS Baselines. Part III: The Geometry of the Ambiguity Search Space[J]. Journal of Geodesy, 1997, 71(8): 486-501. |