2. 深圳大学 土木工程学院 空间信息智能感知与服务深圳市重点实验室, 广东 深圳 518060
2. Shenzhen Key Laboratory of Spatial Smart Sensing and Services, College of Civil Engineering, Shenzhen University, Shenzhen 518060, China
随着GPS装置的不断普及和无线通信、网络技术的飞速发展,人们不仅成为城市地理信息的感知者,同样也成为城市地理数据的采集者。这些由非专业地理数据采集人员提供的众源车载轨迹大数据逐渐成为数据挖掘的重要数据源。面对不同的研究需求,对原始轨迹数据集的数据质量要求也有所不同。例如:对于城市群体、个人行为模式挖掘[1-2],人们一般采用来自手机终端的轨迹数据,其定位精度大约在100 m左右;对于道路级城市交通动态、静态信息提取[2-6],一般采用来自城市出租车系统的车载GPS轨迹,其定位精度大约在15 m左右。对于车道级城市交通动态、静态信息挖掘[7-9],则需要原始轨迹数据的定位精度在3~5 m左右。然而,众源车载轨迹大数据因采集源、采集环境等因素导致数据整体质量参差不齐,尽管数据量丰富但有价值数据比例较低。未经滤选的原始数据,不仅加剧了信息提取结果的不确定性,同时海量数据也为数据操作和分析带来困难。因此,如何从众源轨迹数据中自适应地滤选出符合精度需求的有效数据是研究的重点。
目前,国内外有关众源车载轨迹大数据自适应滤选的相关研究仍然处于起步阶段。现有研究依然停留于对明显的GPS噪音或异常值剔除。例如:基于滤波方法剔除GPS轨迹数据中的明显噪音数据[10-12]和利用空间聚类方法去除GPS轨迹数据内大量的漂移点[7-8, 13-14]。滤波方法一般根据前一个轨迹点的位置、航向、速度等运动特征计算获取下一个轨迹点的空间位置预测值,并与其真实测量值进行对比,实现对异常数据的判别;空间聚类方法则主要利用密度聚类方法剔除轨迹数据中的漂移点。采用滤波方法修正GPS轨迹数据中的明显噪音点存在以下局限性:①依赖于数据采样频率;②只能修正明显噪音。
采用空间聚类方法优化轨迹数据的基本原理有两条:①低密度点等同于异常值,也等同于质量差的轨迹点;②高精度轨迹点一般会聚类于每一条车道中心线。第1种方式虽然不用考虑数据采样间隔,但是无法对夹杂在高密度点中的低质数据进行去除。第2种方式同样不需要考虑数据采样频率,然而却需要先验知识支持且算法复杂。这些方法从应用角度分析,一定程度上改善了原始数据的质量问题,但是仍然没有深入到轨迹数据自适应滤选。
本文提出一种众源车载轨迹大数据自适应滤选方法。利用观测信息和动力学模型信息的自适应平衡滤波已有充分研究[11-14, 18],本文侧重通过分析高精度GPS轨迹数据的空间特征和GPS误差分布,构建一种分割-滤选模型。该模型首先通过角度、距离约束将完整的浮动车轨迹数据进行分割,将轨迹分割段作为基本滤选单元;然后采用RANSAC[17]算法(随机抽样一致)构建每一个轨迹分割段的参考基线,并将其作为位置参考,计算GPS轨迹向量与其参考基线间的相似度,按照相似度阈值进行滤选。试验结果表明,该方法可以实现众源轨迹大数据按精度需求滤选,降低数据冗余度,为未来不同精度需求的信息提取提供可靠的数据源。
1 众源车载GPS轨迹数据质量分析众源车载GPS轨迹数据一般由居民或者团体自发采集,数据量大、来源广,其数据质量因GPS接收器性能、采集环境、采集行为而参差不齐。目前,按照GPS轨迹数据的定位精度可以将其粗略分为高精度GPS轨迹数据(如:定位精度分米级)和低精度GPS轨迹数据(定位精度米级,如10 m)。例如,由城市出租车采集的GPS轨迹数据一般是一种低精度的GPS轨迹数据,其定位精度是10~15 m。由于其采集环境较为复杂、采集过程非专业性,原始车载GPS轨迹数据内存在大量异常值及定位精度极差的轨迹点(图 1(a))。装有IMU的专业测量车利用差分GPS方法采集的高精度DGPS轨迹数据[18-19],定位精度往往可以达到厘米级或者分米级,异常值较少(如图 1(b))。

|
| 图 1 同步高低精度的GPS轨迹数据 Fig. 1 High-precision and low-precision synchronous GPS traces |
通过对比同步高低精度GPS轨迹数据的空间特征发现:低精度GPS数据集的某个轨迹点与其邻近的其他轨迹点之间的角度经常突然变大且漂移较远,该轨迹点的定位精度一般较低。另外,根据GPS数据误差分布原理[20],假设GPS位置数据的整体精度是5 m,则原始GPS数据集中,既存在一部分高精度定位GPS定位轨迹点,也存在一部分低于整体精度的GPS轨迹点。通常根据道路的线性特征和车辆运动过程的运动惯性,在相对平直的道路段内,车辆行驶状态的高精度GPS定位轨迹的线性特征往往比较平滑,其平滑度在一定程度上反映了GPS轨迹数据的定位精度。如何从原始轨迹数据中滤选出可以满足信息提取精度需求的轨迹数据,关键在于如何设定平滑度评价方法及参考,然后通过对滤选数据构成轨迹线的线性平滑度的控制,使得滤选数据的质量尽可能达到需求精度指标。
2 众源GPS车载轨迹大数据自适应滤选通过以上分析,本文提出了一种基于分割-滤选模型的众源车载轨迹大数据自适应滤选方法。分割阶段可以实现对轨迹数据自适应分割,将处于相同线性规律的子轨迹段作为滤选单元;滤选阶段则通过构建子轨迹段的参考基线,计算轨迹点向量与参考基线的相似度,制定可以控制子轨迹段整体线性平滑度的滤选阈值,对轨迹数据进行分阈值滤选。
2.1 轨迹分割轨迹分割是轨迹数据挖掘分析的前提[21]。目前大部分轨迹分割方法主要从轨迹位置、采样间隔、速度及其他移动特征出发,制定相应的分割约束因子及约束阈值对完整轨迹进行分割[22-23]。本文提出的轨迹分割主要服务于高精度轨迹数据滤选,因此,轨迹分割约束因子主要由可以反映GPS轨迹数据定位精度的轨迹向量角度和距离构成。本文从轨迹数据的图形复杂度及用户需求角度出发,提出了一种轨迹分割因子阈值自适应方法。
2.1.1 顾忌角度和距离的轨迹分割算法分割约束因子是轨迹分割的关键。一般情况下,车载轨迹数据体现了移动目标直行、转弯、掉头行驶等行为,通过角度约束可以很好地将这些表现不同行驶行为的轨迹进行分割,得到保持同一驾驶行为的子轨迹段,而距离约束则可以将车辆在同一行驶方向不同位置行驶时记录的轨迹进行区分。于是,采用GPS轨迹向量与整体轨迹行驶方向的夹角以及GPS轨迹点偏离整体轨迹行驶航线的距离,可以度量GPS轨迹点定位精度高低。因此本文从轨迹点的角度和距离出发,对整体轨迹进行分割。假设轨迹T={p1,p2,…,pn},ak和dj分别为分割约束因子,其中ak表示轨迹向量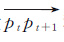
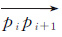
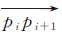
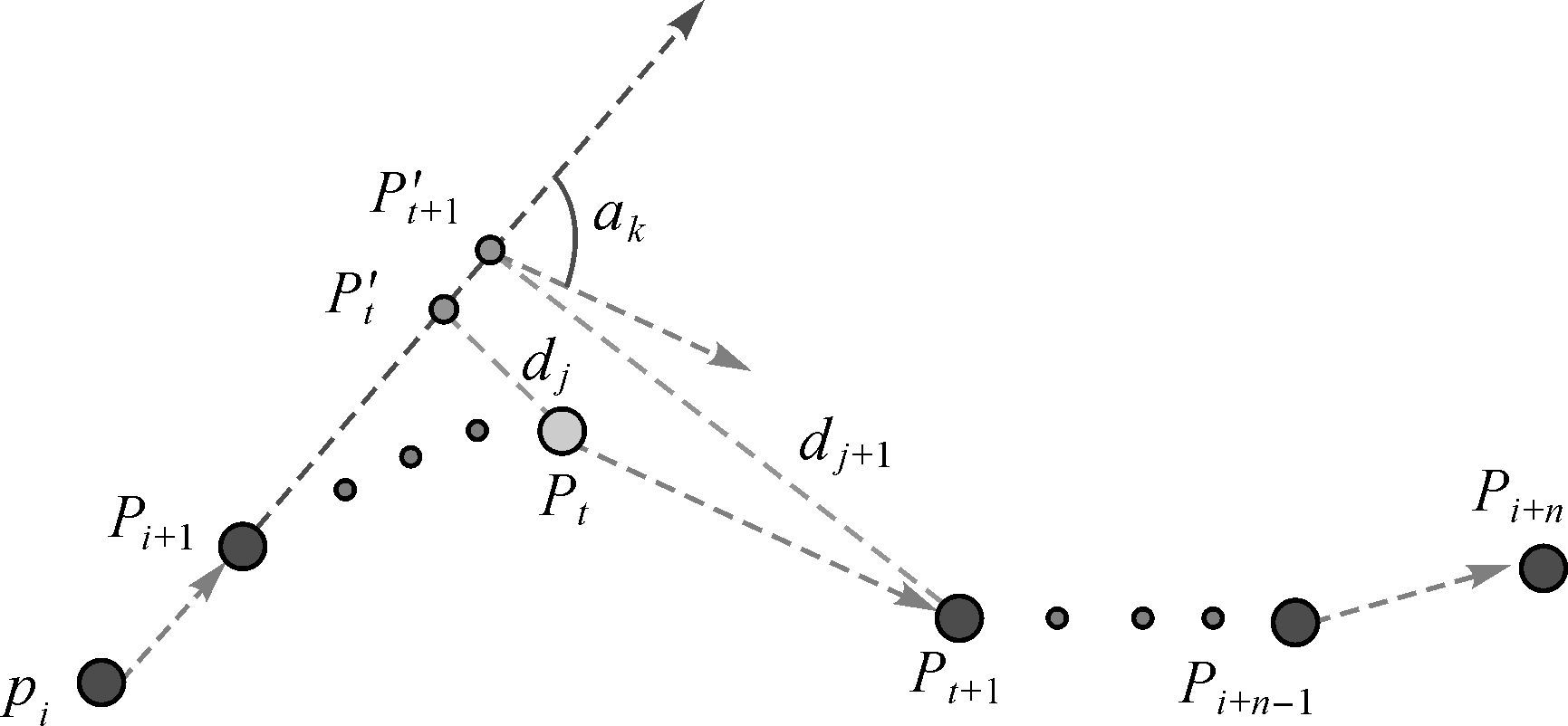
|
| 图 2 轨迹分割算法 Fig. 2 Algorithm to partition traces |
设A和D分别为角度阈值和距离阈值,则轨迹分割算法的具体步骤为:
第1步:将轨迹T的起点p1作为起点,连接p1的下一个轨迹点p2,构建起点向量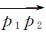
第2步:从p3开始依次遍历,计算当前点与其下一个轨迹点构成向量与起点向量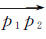
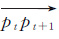
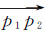

第3步:将pt替换第1步的p1,并作为新的起点,连接pt的下一个轨迹点pt+1,重复第2步计算,直到剩余轨迹点与当前点及其向量之间的角度值和距离值都小于角度阈值与距离阈值。
2.1.2 轨迹分割阈值分析分割阈值(角度阈值A,距离阈值D)决定了轨迹分割粒度的大小。目前,很多关于轨迹分割的研究在阈值设定过程中倾向于用户自定义,其缺陷主要体现在两个方面。一方面增加了用户确定最佳分割阈值的困难,另一方面图形复杂度不一的轨迹数据都采用同一个分割阈值,使得分割结果不理想。轨迹分割阈值的大小其实受制于两个因素:①用户分割需求;②轨迹数据自身的图形复杂度。用户分割需求通常是一种比较粗略的心理估算,在整体分割过程中具有规范整体分割阈值范围的作用。轨迹数据自身的图形复杂度则具体决定了该条轨迹在用户分割需求的基础上最终的分割阈值,即如果轨迹数据图形复杂度高,被分割的粒度就应该大,分割阈值相对较小;如果轨迹数据图形简单,则被分割的粒度就相对较小,分割阈值也相对较大。本文从影响轨迹分割阈值的两个因素出发,提出了一种顾及用户分割需求及轨迹图形复杂度的轨迹分割阈值确定方法。
假设轨迹T={p1,p2,…,pn},则T的分割阈值A和D可以定义为
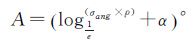 (1)
(1)
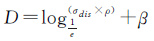 (2)
(2)
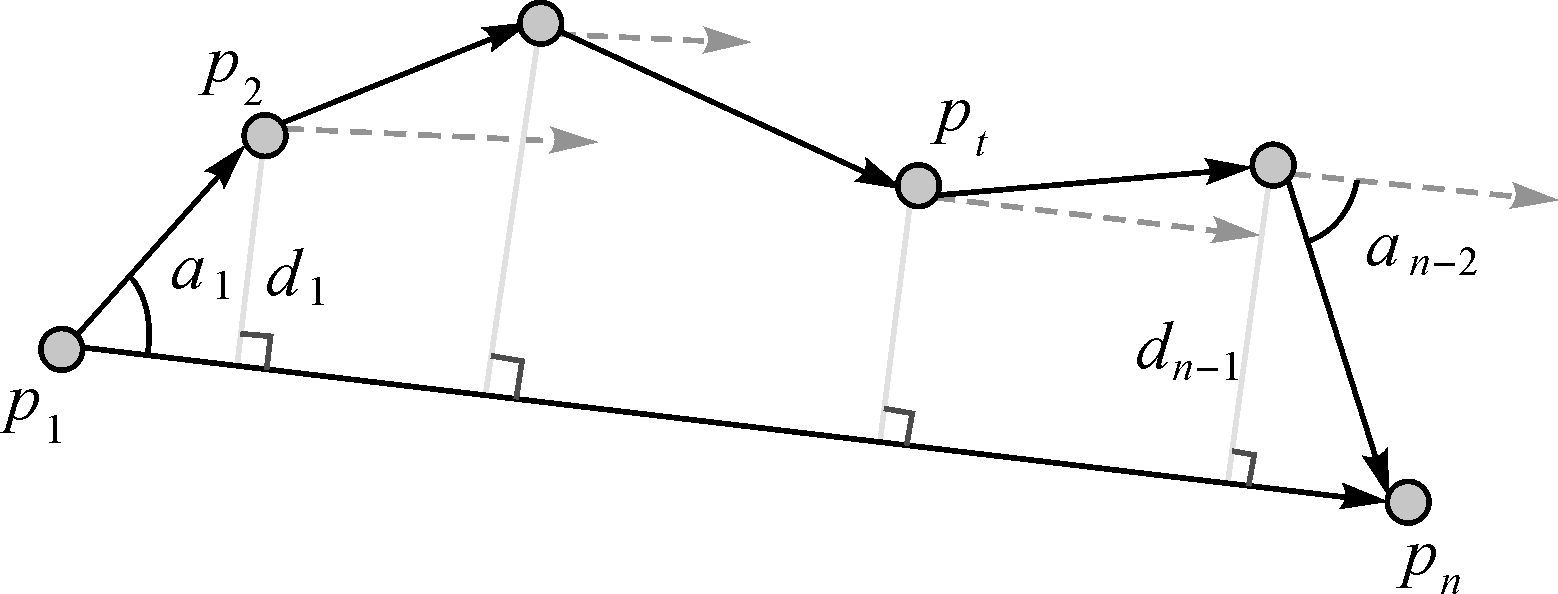
式中,α和β为常数项,在分割阈值确定过程中体现了用户分割需求约束,具体值可以由用户制定;ang表示轨迹点pt到轨迹向量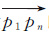
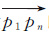
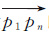
|
| 图 3 GPS轨迹数据的图形复杂度 Fig. 3 Graph complexity of GPS traces |
按照式(1)和式(2),当用户需求确定后,即可计算出每一条轨迹的分割阈值,最终获取最理想的轨迹分割结果。
2.2 轨迹滤选按照正常的车辆行驶规则:车辆会遵守交通规则,沿着车道中心线的延伸方向稳定行驶除非遇到转弯或者快速变换车道。因此,反映车辆真实行驶状态的高精度GPS轨迹数据的线性连接应该是一条平滑且无明显锯齿状的平滑线条,即处于同一条子轨迹段内的高精度轨迹点在航向和位置上存在较高的空间一致性。根据这个特点,本文利用RANSAC算法原理,以直线方程作为数学模型,对每一个子轨迹段构建其参考基线。RANSAC算法相较于其他线性拟合算法,如最小二乘法、模糊加权拟合法,RANSAC算法抗噪性强,可以不受噪音点的干扰,找出轨迹段内高度一致的轨迹点并拟合成线。
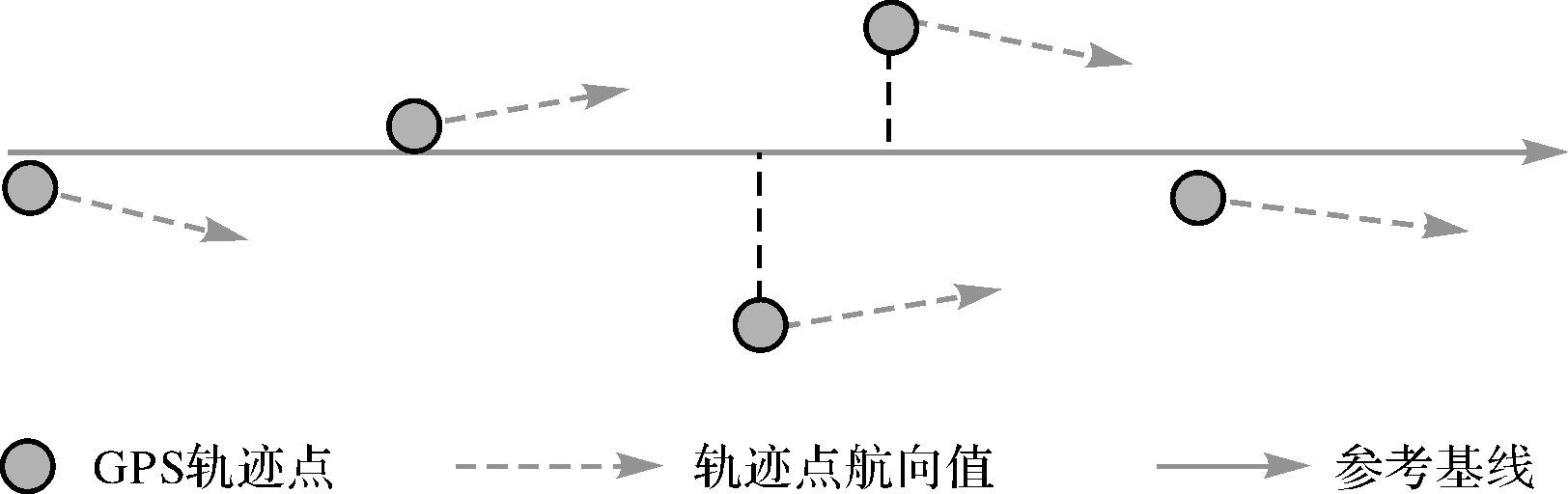
虽然参考基线并不能代表轨迹点真值的空间位置,但是参考基线是最能代表轨迹点的基线。轨迹滤选过程中,参考基线一般用来作为控制滤选轨迹整体线性平滑度的标尺。在参考基线构建过程中,需要选择合适的模型去模拟轨迹行驶的线性特征。本文采用直线方程作为RANSAC算法模型(图 4),利用子轨迹段内每一个轨迹点的位置构建参考基线方程,其中RANSAC算法原理可以参见文献[15]。另外,子轨迹段的参考基线本质上是一条没有方向的直线段。本文为了方便后期滤选,将子轨迹段的前进方向作为参考标准,对参考基线赋予方向属性,即参考基线的方向与子轨迹段的移动方向一致(图 4)。
|
| 图 4 参考基线构建 Fig. 4 Construction of reference baseline |
2.2.1 向量相似度模型
参考基线在滤选的过程中,可以通过计算子轨迹段内其他轨迹向量与参考基线向量的相似度,按照相似度阈值进行滤选。目前评估向量相似度的模型主要包含向量的模、夹角及向量间距离等因子[24-25]。由于行驶车辆的速度对GPS定位精度的影响可以忽略不计,因此,本文提出了一种顾及夹角和距离的向量相似度评价模型。
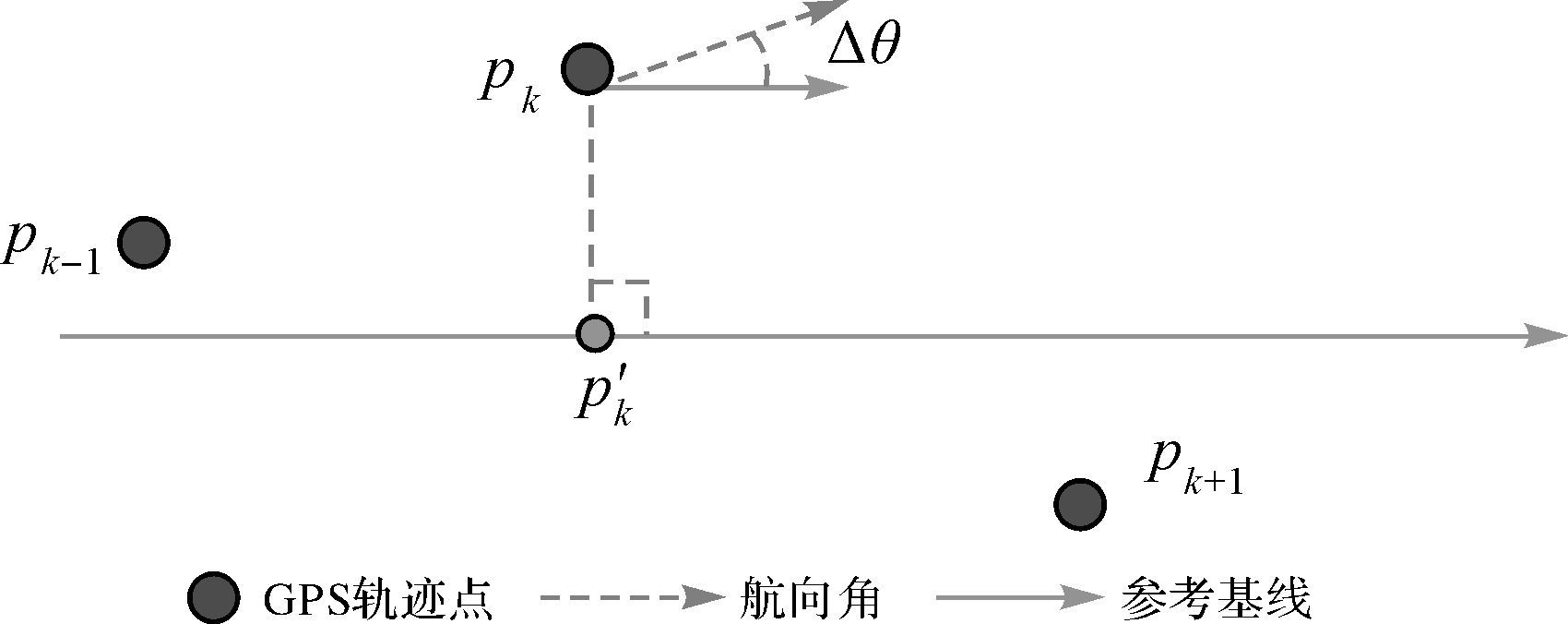
假设子轨迹段为S={pi,pi+1,…,pt},其参考基线如图 5所示。
|
| 图 5 GPS轨迹点与其参考基线间的相似度 Fig. 5 Similarity between GPS points with reference baseline |
根据轨迹点pk的航向值及其空间位置,构成的向量与参考基线向量之间的相似度可定义为
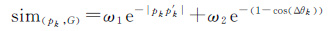 (3)
(3)
式中,sim(pk,G)表示轨迹向量pk与基线向量G之间的相似度值;|pkp′k|表示轨迹向量点pk与其投影在参考基线上的点p′k的垂直距离;角度Δθk表示轨迹向量pk与参考基线的夹角;ω1和ω2为距离和角度因子的权重值,ω1+ω2=1。相似度sim的取值范围为[0,1]。当sim=0时,表示两者完全不相同;当sim=1表示两者完全相同。相似度值越高,表示轨迹点与参考基线的相似程度越高,其轨迹点线性平滑度也越高。
2.2.2 滤选阈值分析轨迹滤选最关键的一步是如何设定滤选阈值。假设相似度阈值与GPS定位精度存在某种函数关系如下
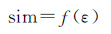 (4)
(4)
式中,ε表示GPS轨迹数据的定位精度。当滤选数据的定位精度为τ时,即可通过式(4)得到相应的相似度阈值。为了进一步理清相似度滤选阈值与数据定位精度之间的关系,本文在文献[14]的基础上,通过对不同采集区域、整体定位精度不同的大量低精度GPS轨迹数据及其同步高精度DGPS轨迹数据(精度为厘米级)的相似度进行计算,分析低精度轨迹点的定位误差及其相似度的关系。在相似度计算过程中,采用式(3)所示相似度评估模型,权重参数参考文献[14],而轨迹点与其真值之间的距离参数|pkp′k|是该轨迹点的定位误差。大量试验结果表明,GPS轨迹数据的相似度与定位精度呈现稳定的指数分布,如下
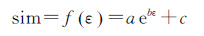 (5)
(5)
式中,a、b、c分别是相似度与定位精度函数关系式的系数,其具体值与相似度评价模型内距离和角度的权重系数息息相关,而与原始GPS数据集的整体定位精度不相关。因此,无论是来自哪种型号的GPS接收机,只要采用统一的相似度评价模型,则GPS数据定位误差与GPS数据和其理想值之间相似度之间的函数关系是确定的。GPS轨迹点与参考基线之间的相似度实际上与GPS轨迹点与其真值之间的相似度存在差异,但是当参考基线被作为参考基准时,这种衡量GPS轨迹点与参考基线之间的相似度阈值可采用式(5)来确定。当滤选GPS轨迹数据的期望精度为τ时,可计算出相似度滤选阈值为f(τ)。
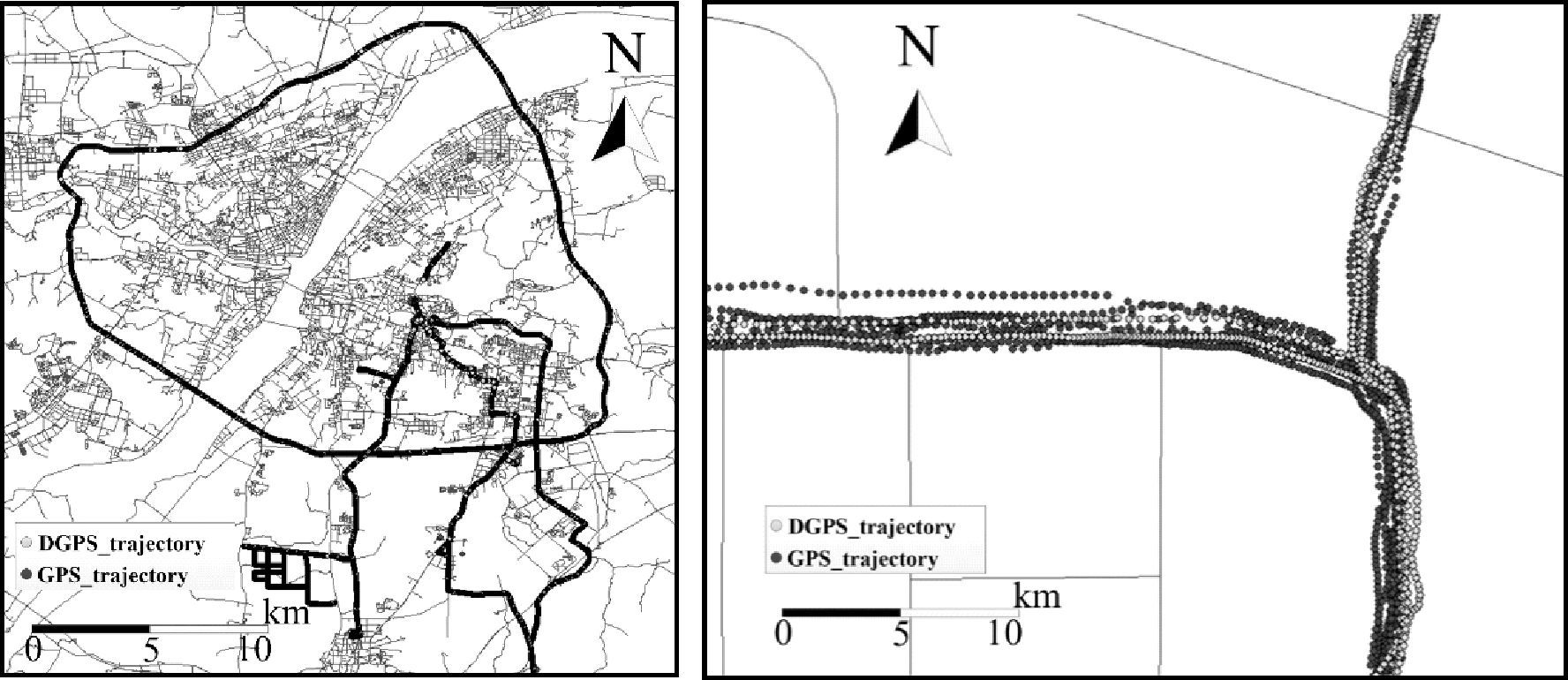
3 试验分析本文以武汉市作为GPS轨迹数据采集区域,利用多辆GPS测量车分不同周期对武汉市郊区和市区进行数据采集,其中测量车内的GPS接收器包括:Trimble R9、洛基山手持GPS接收器、智能手机(华为、iPhone 5、 魅族等)。所获取的GPS数据主要包含3类:一类是由Trimble R9采集的低精度GPS轨迹数据,定位精度为5~10 m,采样间隔为1 s;一类是由手持GPS接收器采集的低精度GPS轨迹数据,定位精度为5~10 m,采样间隔为1 s;一类是由手机采集的GPS轨迹数据,定位精度为10~15 m。这3类数据的同步高精度数据由CORS基站系统采集,定位精度为0.05 m,采样间隔为1 s。试验数据一共包含900万个GPS轨迹点,采集周期为1周,采集区域遍布武汉市郊区和市区,如图 6所示。
|
| 图 6 试验数据 Fig. 6 Experimental data |
在下述试验中,低精度GPS轨迹数据将被作为待滤选数据,高精度DGPS轨迹数据(定位精度为厘米级)将作为参考值,以便对滤选结果进行评价和检验。
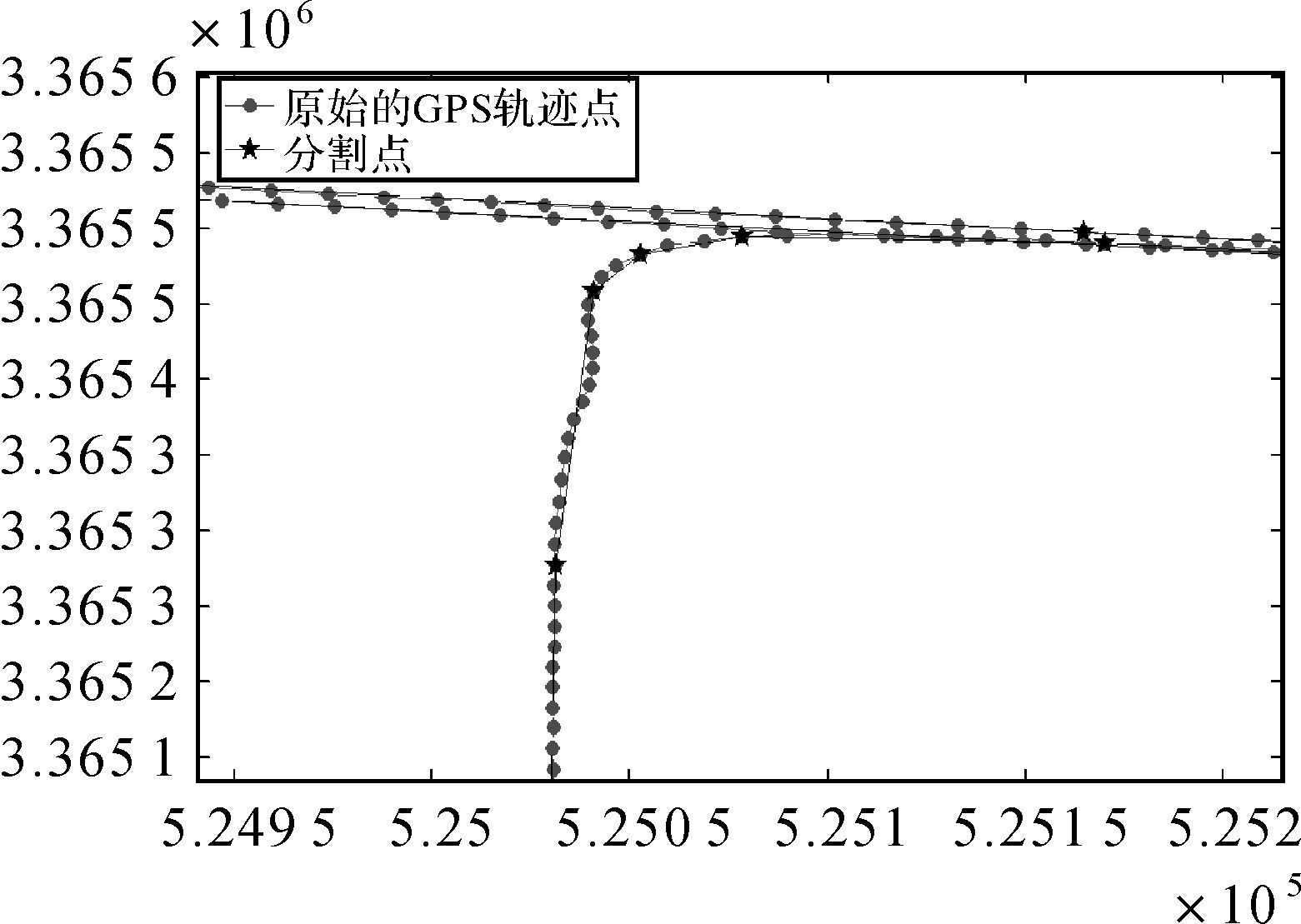
3.1 轨迹分割按照轨迹分割算法,需要对待分割轨迹的图形复杂度进行计算,然后确定分割阈值。在确定每一条轨迹的分割阈值前,需要对常量α和β 赋值。α和β根据用户需求设定,本文根据现有交通规则和道路建设标准,将常量α和β分别设为45°和30 m。每一条轨迹的最终分割阈值则通过计算该轨迹的图形复杂度进行自适应确定。试验结果如图 7所示,其中实心圆表示原始的GPS轨迹数据,星型符号表示分割点。在进行滤选时,由于分割点在角度与距离上与其他轨迹点存在较大的差异,因此可以将其首先作为异常值去除,然后再对子轨迹段进行滤选。
|
| 图 7 轨迹分割结果 Fig. 7 The result of partition |
3.2 滤选阈值确定
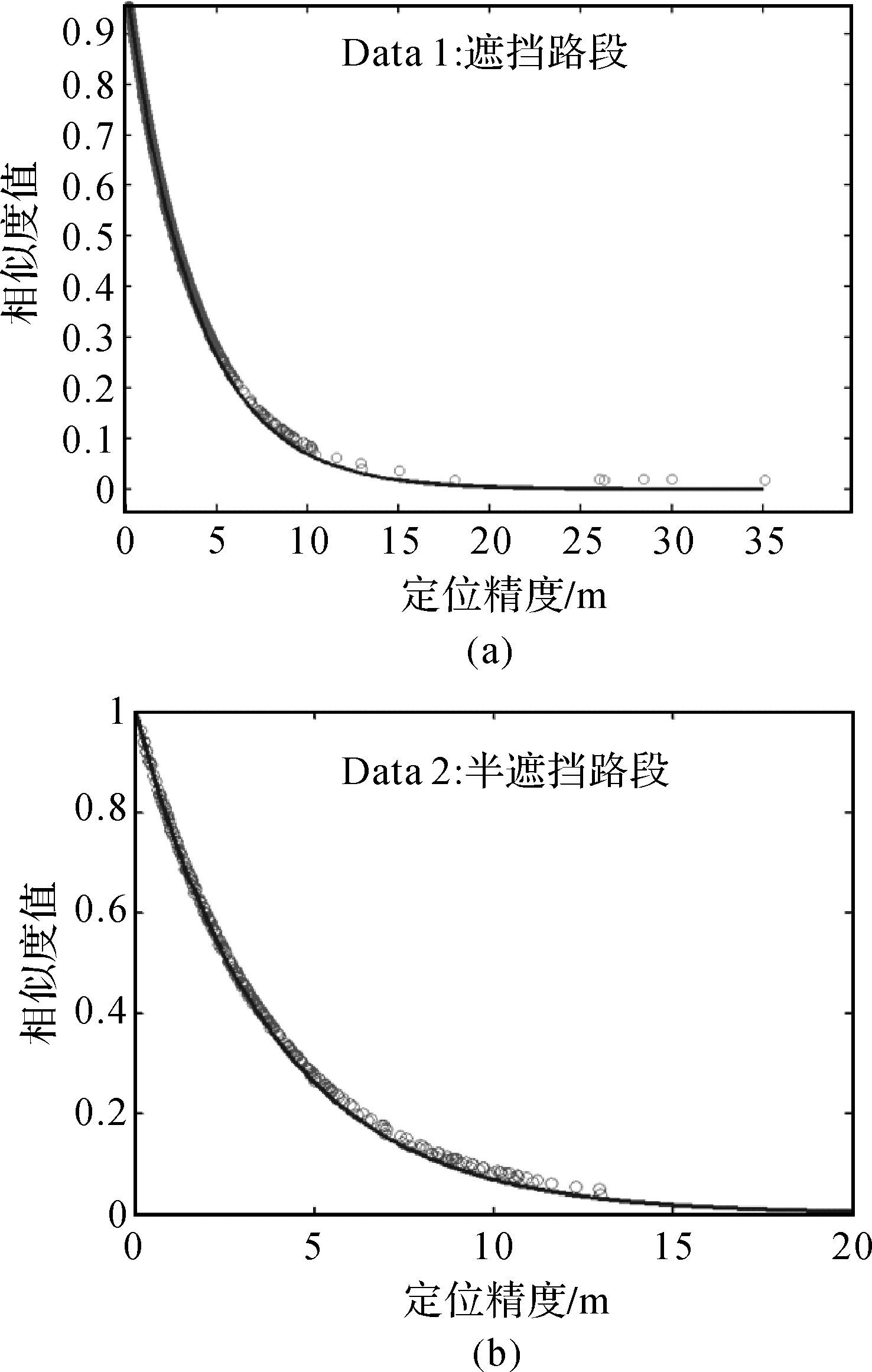
轨迹滤选阈值决定了最终滤选数据的整体精度。本文利用文献[16]的模型,度量距离和角度因素对GPS测量值定位精度的结果,将相似度评价模型的权值分别设为0.87和0.13。从原始数据中选择一部分采集于不同区域、拥有不同误差分布的低精度GPS轨迹数据作为试验数据,分析这些GPS数据与其参考值的相似度及其测量误差之间的函数关系(由于试验数据采集于城市道路,真值获取相对困难,因此在计算过程中将定位精度为厘米级的高精度差分数据作为GPS数据的参考真值),确定相似度阈值和GPS定位精度函数模型的相关参数。试验结果表明,不论GPS轨迹点集的定位精度是多少,每一个低精度GPS轨迹点的定位精度与其真值的相似度值遵从指数函数关系,其中系数a=1,b=-0.267 1,c=0,见图 8。
|
| 图 8 相似度阈值与GPS轨迹点定位精度的函数关系拟合 Fig. 8 Function relation fitting between similarity threshold and GPS locus point positioning accuracy |
图 8(a)的试验数据采集于城市遮挡路段,图 8(b)的试验数据采集于城市半遮挡路段,其GPS接收器为Trimble R9。图 8表明,即使GPS轨迹数据集整体误差分布不一样,定位精度也存在差异,但是GPS轨迹数据的相似度及定位误差存在稳定的指数分布。另外,通过计算,两类数据集的相似度与定位精度和指数模型的拟合相关度为0.992及0.986。因此,确定滤选数据的期望定位精度后,可利用GPS轨迹点的定位精度与其参考值的相似度指数函数关系式计算滤选阈值,见表 1。
| 期望精度: τ /m | 相似度阈值 |
| 1 | 0.765 7 |
| 2 | 0.586 3 |
| 3 | 0.448 9 |
| 4 | 0.343 7 |
| 5 | 0.263 2 |
3.3 轨迹滤选
根据滤选算法,构建子轨迹段的参考基线向量,计算子轨迹段内各GPS轨迹向量与参考基线向量之间的相似度。在相似度计算过程中,距离和角度权值的大小与相似度阈值分析一样都设定为0.87、0.13。然后,根据表 1的相似度阈值依次对原始GPS数据进行滤选(见图 9)。
|
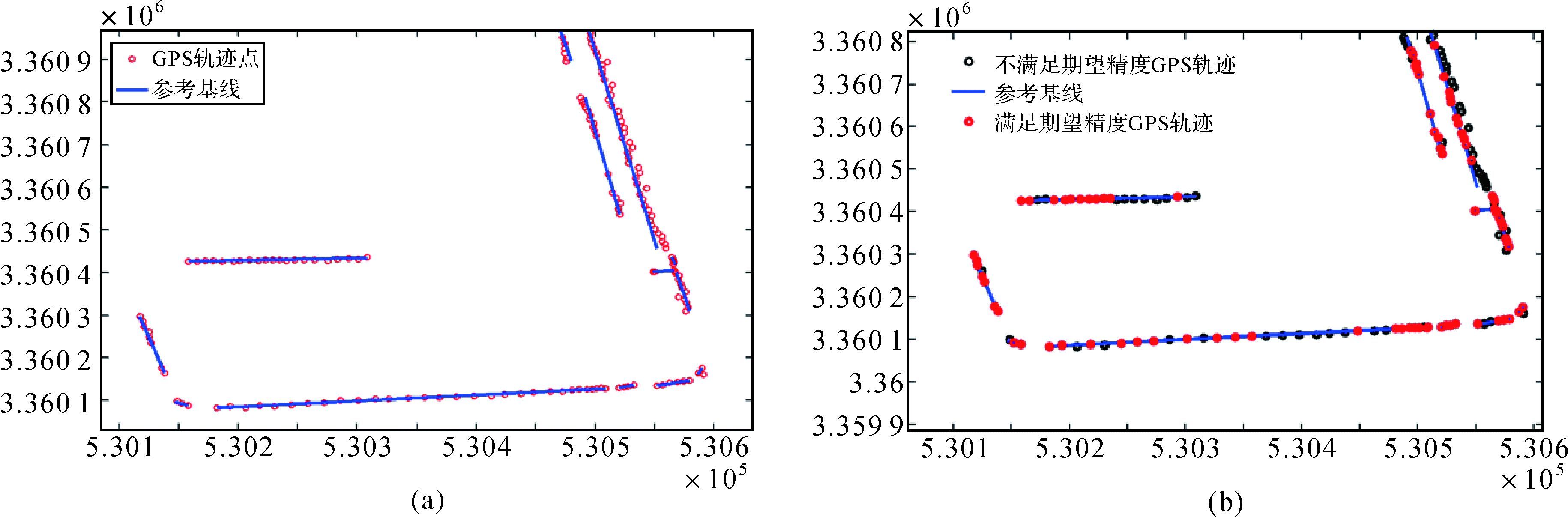
| 图 9 轨迹滤选结果 Fig. 9 The results of filtering |
图 9表示了试验区内一部分轨迹数据进行分割后构建参考基线,然后按照滤选阈值进行滤选后的结果。其中,图 9(a)展示了子轨迹段的参考基线,图 9b反映了滤选阈值设定为3 m时的滤选结果。
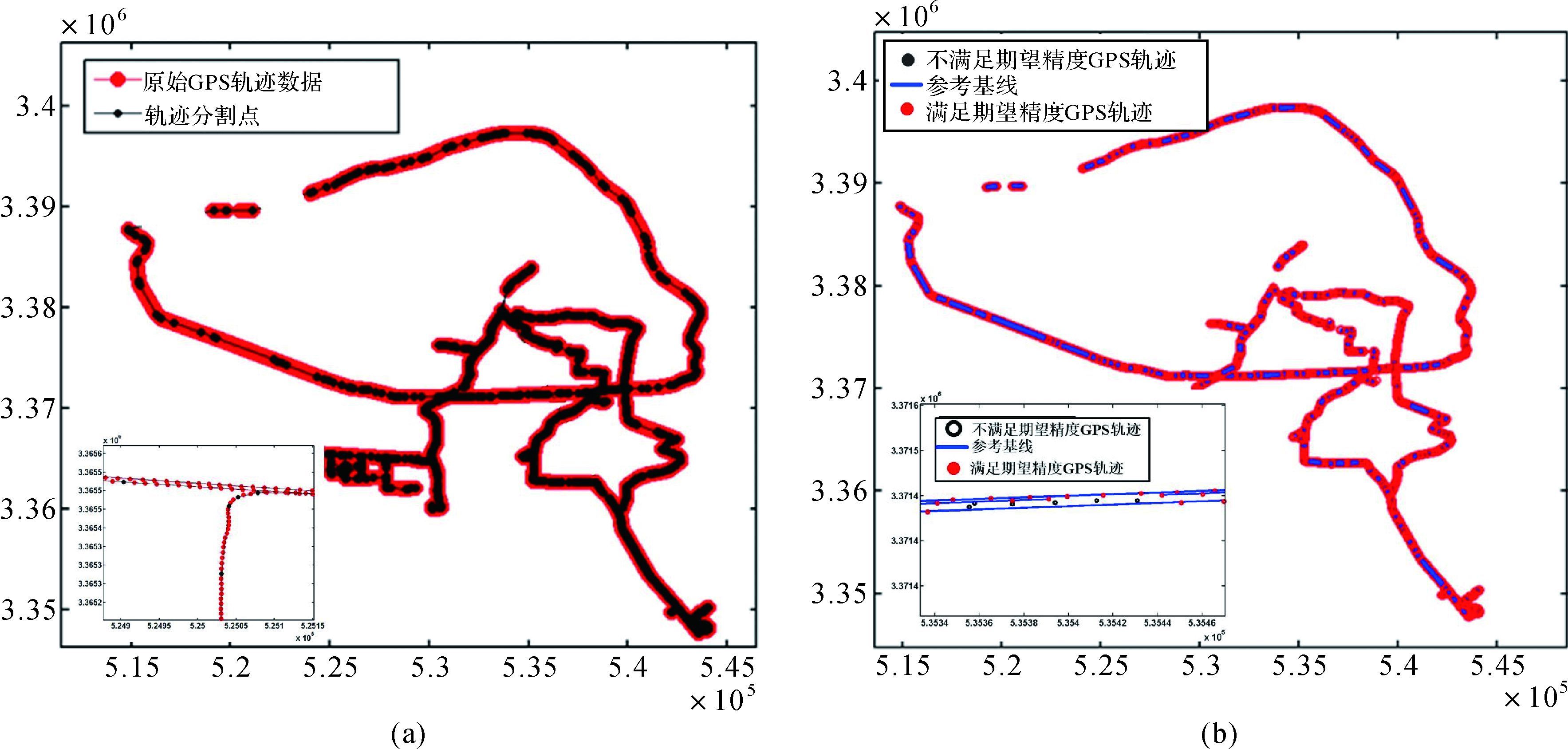
3.4 滤选评价为了进一步验证分割滤选模型方法的有效性,本文对试验区内的所有低精度GPS轨迹数据进行滤选,如图 10(a)所示。通过比较滤选数据与其真值,计算不同阈值约束下获取的滤选GPS数据测量误差的平均值和标准差,见表 2。
|
| 图 10 试验区原始低精度GPS轨迹数据分割滤选结果 Fig. 10 The filtering results of the raw and low accuracy GPS trajectory data in experimentation area |
| GPS接收器 | 期望精度: τ/m | 滤选数据占总体数据比例/(%) | 滤选数据测量误差的平均值/m | 滤选数据测量误差的标准差/m |
| Trimble R9 | 1 | 31.58 | 2.0 | 0.92 |
| 2 | 47.62 | 2.1 | 0.95 | |
| 3 | 58.67 | 2.8 | 1.02 | |
| 4 | 67.30 | 3.4 | 1.73 | |
| 5 | 74.48 | 3.9 | 1.79 | |
| 手持GPS接收器 | 1 | 25.7 | 2.0 | 0.8 |
| 2 | 37.86 | 2.0 | 0.8 | |
| 3 | 42.38 | 2.4 | 1.0 | |
| 4 | 45.32 | 2.9 | 1.3 | |
| 5 | 49.76 | 3.7 | 2.3 | |
| 智能手机 | 1 | 23.52 | 3.6 | 2.2 |
| 2 | 28.23 | 3.6 | 2.2 | |
| 3 | 32.67 | 4.6 | 2.7 | |
| 4 | 40.23 | 5.0 | 3.0 | |
| 5 | 48.11 | 5.1 | 3.2 |
表 2结果表明,分割-滤选模型可以实现众源车载轨迹数据按需滤选,且经过滤选后原始数据的质量得到不同程度的改善,然而该方法同样存在局限性。首先,当期望滤选精度为1 m或者更高时,滤选数据的定位精度无法满足滤选需求,例如,对于3种GPS接收器采集的原始数据集,当滤选期望精度为1 m时,所滤选结果的整体精度与期望精度相差甚远;其次,滤选数据最终的滤选结果与原始数据集内数据的定位精度息息相关,即原始数据集内如果没有包含高精度的轨迹点,则该方法就会失效,如,由手机采集的GPS轨迹数据,其定位精度较低,导致滤选结果的整体精度与期望精度之间存在相对差异;最后,如果一条子轨迹段内的所有轨迹点定位精度都非常低,且保持了高度一致性,那么就会导致参考基线出现错误,从而滤选结果失效。在未来的研究工作中,本文将继续对众源轨迹数据按需滤选进行研究。
4 总结本文在国内外GPS轨迹数据优化方法的基础上,提出了一种基于分割-滤选模型的众源车载GPS轨迹大数据自适应滤选方法。该方法可以基于信息提取精度需求,从原始GPS轨迹数据集中滤选出满足期望精度的轨迹数据。试验结果表明,该方法可以实现众源轨迹大数据按精度需求滤选,降低数据冗余度,为未来不同精度需求的信息提取提供可靠的数据源。然而本文所提方法同样存在局限性:①当期望精度高于原始GPS轨迹数据集内数据的最高精度,那么滤选结果与期望精度存在较大差异;②当原始GPS轨迹数据集内数据精度达到期望精度,但其比例相对较少时,滤选结果不理想。未来研究中,本文将进一步通过分析低高同步GPS轨迹数据的空间特征,对分割-滤选模型进行优化。
| [1] | 刘瑜, 肖昱, 高松, 等. 基于位置感知设备的人类移动研究综述[J]. 地理与地理信息科学, 2011, 27(4): 8–13. LIU Yu, XIAO Yu, GAO Song, et al. A Review of Human Mobility Research Based on Location Aware Devices[J]. Geography and Geo-Information Science, 2011, 27(4): 8–13. |
| [2] | 牟乃夏, 张恒才, 陈洁, 等. 轨迹数据挖掘城市应用研究综述[J]. 地球信息科学, 2015, 17(10): 1136–1142. MOU Naixia, ZHANG Hengcai, CHEN Jie, et al. A Review on the Application Research of Trajectory Data Mining in Urban Cities[J]. Journal of Geo-information Science, 2015, 17(10): 1136–1142. |
| [3] | 李德仁. 多学科交叉中的大测绘科学[J]. 测绘学报, 2007, 36(4): 363–365. LI Deren. On Geomatics in Multi-discipline Integration[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(4): 363–365. DOI:10.3321/j.issn:1001-1595.2007.04.001 |
| [4] | 李清泉, 黄练. 基于GPS轨迹数据的地图匹配算法[J]. 测绘学报, 2010, 39(2): 207–212. LI Qingquan, HUANG Lian. A Map Matching Algorithm for GPS Tracking Data[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(2): 207–212. |
| [5] | 唐炉亮, 常晓猛, 李清泉, 等. 基于蚁群优化算法与出租车GPS数据的公众出行路径优化[J]. 中国公路学报, 2011, 24(2): 89–95. TANG Luliang, CHANG Xiaomeng, LI Qingquan, et al. Public Travel Route Optimization Based on Ant Colony Optimization Algorithm and Taxi GPS Data[J]. China Journal of Highway and Transport, 2011, 24(2): 89–95. |
| [6] | 唐炉亮, 刘章, 杨雪, 等. 符合认知规律的时空轨迹融合与路网生成方法[J]. 测绘学报, 2015, 44(11): 1271–1276. TANG Luliang, LIU Zhang, YANG Xue, et al. A Method of Spatio-temporal Trajectory Fusion and Road Network Generation Based on Cognitive Law[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(11): 1271–1276. DOI:10.11947/j.AGCS.2015.20140591 |
| [7] | CHEN Yihua, KRUMM J. Probabilistic Modeling of Traffic Lanes from GPS Traces[C]//Proceedings of the 18th SIGSPATIAL International Conference on Advances in Geographic Information Systems. New York, NY:ACM, 2010:81-88. |
| [8] | TANG Luliang, YANG Xue, KAN Zihan, et al. Lane-level Road Information Mining from Vehicle GPS Trajectories Based on Naïve Bayesian Classification[J]. ISPRS International Journal of Geo-Information, 2015, 4(4): 2660–2680. DOI:10.3390/ijgi4042660 |
| [9] | 唐炉亮, 杨雪, 阚子涵, 等. 一种基于朴素贝叶斯分类的车道数量探测[J]. 中国公路学报, 2016, 29(3): 116–123. TANG Luliang, YANG Xue, KAN Zihan, et al. Traffic Lane Numbers Detection Based on the Naïve Bayesian Classification[J]. China Journal of Highway and Transport, 2016, 29(3): 116–123. |
| [10] | LEE W C, KRUMM J. Trajectory Preprocessing[M]//ZHENG Yu, ZHOU Xiaofang. Computing with Spatial Trajectories. New York:Springer, 2011:3-33. |
| [11] | 杨元喜, 何海波, 徐天河. 论动态自适应滤波[J]. 测绘学报, 2001, 30(4): 293–298. YANG Yuanxi, HE Haibo, XU Tianhe. Adaptive Robust Filtering for Kinematic GPS Positioningg[J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(4): 293–298. DOI:10.3321/j.issn:1001-1595.2001.04.004 |
| [12] | 杨元喜, 唐颖哲, 李庆田, 等. 用于GIS道路信息修测的动态GPS自适应滤波试验[J]. 测绘科学, 2003, 28(4): 9–11. YANG Yuanxi, TANG Yingzhe, LI Qingtian, et al. Experiments of Adaptive Filters for Kinemetic GPS Positioning Applied in Road Information Updating in GIS[J]. Science of Surveying and Mapping, 2003, 28(4): 9–11. |
| [13] | YANG Yuanxi, HE H, XU Guochang. Adaptively Robust Filtering for Kinematic Geodetic Positioning[J]. Journal of Geodesy, 2001, 75(2-3): 109–116. DOI:10.1007/s001900000157 |
| [14] | YANG Yuanxi, GAO Weiguang. An Optimal Adaptive Kalman Filter[J]. Journal of Geodesy, 2006, 80(4): 177–183. DOI:10.1007/s00190-006-0041-0 |
| [15] | WANG Jing, RUI Xiaoping, SONG Xianfeng, et al. A Novel Approach for Generating Routable Road Maps from Vehicle GPS Traces[J]. International Journal of Geographical Information Science, 2015, 29(1): 69–91. DOI:10.1080/13658816.2014.944527 |
| [16] | TANG Luliang, YANG Xue, DONG Zhen, et al. CLRIC:Collecting Lane-based Road Information via Crowdsourcing[J]. IEEE Transactions on Intelligent Transportation Systems, 2016, 17(9): 2552–2562. DOI:10.1109/TITS.2016.2521482 |
| [17] | YANIV Z. Random Sample Consensus (RANSAC) Algorithm:A Generic Implementation[Z]. Washington, DC:Georgetown University Medical Center, 2010. |
| [18] | 高为广, 杨元喜, 崔先强, 等. IMU/GPS组合导航系统自适应Kalman滤波算法[J]. 武汉大学学报(信息科学版), 2006, 31(5): 466–469. GAO Weiguang, YANG Yuanxi, GUI Xianqiang, et al. Application of Adaptive Kalman Filtering Algorithm in IMU/GPS Integrated Navigation System[J]. Geomatics and Information Science of Wuhan University, 2006, 31(5): 466–469. |
| [19] | 周乐韬, 黄丁发, 袁林果, 等. 网络RTK参考站间模糊度动态解算的卡尔曼滤波算法研究[J]. 测绘学报, 2007, 36(1): 37–42. ZHOU Letao, HUANG Dingfa, YUAN Linguo, et al. A Kalman Filtering Algorithm for Online Integer Ambiguity Resolution in Reference Station Network[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(1): 37–42. DOI:10.3321/j.issn:1001-1595.2007.01.007 |
| [20] | 丁仁杰, 闵勇, 冯亚东, 等. 基于GPS的全网同步时钟的建立和误差校正[J]. 清华大学学报(自然科学版), 1997, 37(7): 74–77. DING Renjie, MIN Yong, FENG Yadong, et al. Development of Power System Dynamic Monitoring Unit Based on GPS[J]. Journal of Tsinghua University (Science & Technology), 1997, 37(7): 74–77. |
| [21] | LEE J G, HAN Jiawei, WHANG K Y. Trajectory Clustering:A Partition-and-group Framework[C]//Proceedings of the 2007 ACM SIGMOD International Conference on Management of Data. New York, NY:ACM, 2007:593-604. |
| [22] | 张治华. 基于GPS轨迹的出行信息提取研究[D]. 上海:华东师范大学, 2010. ZHANG Zhihua. Deriving Trip Information from GPS Trajectories[D]. Shanghai:East China Normal University, 2010. |
| [23] | 欧阳鸿, 刘建勋, 刘毅志, 等. 基于步行GPS轨迹的路网提取方法[J]. 计算机与现代化, 2014(2): 124–128. OUYANG Hong, LIU Jianxun, LIU Yizhi, et al. An Extraction Method of Road Network Based on Walking GPS Trajectories[J]. Computer and Modernization, 2014(2): 124–128. |
| [24] | 赵东保, 盛业华. 全局寻优的矢量道路网自动匹配方法研究[J]. 测绘学报, 2010, 39(4): 416–421. ZHAO Dongbao, SHENG Yehua. Research on Automatic Matching of Vector Road Networks Based on Global Optimization[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(4): 416–421. |
| [25] | 唐炉亮, 李清泉, 杨必胜. 空间数据网络多分辨率传输的几何图形相似性度量[J]. 测绘学报, 2009, 38(4): 336–340. TANG Luliang, LI Qingquan, YANG Bisheng. Shape Similarity Measuring for Multi-resolution Transmission of Spatial Datasets over the Internet[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(4): 336–340. DOI:10.3321/j.issn:1001-1595.2009.04.009 |



