2. 武汉大学城市设计学院, 湖北 武汉 430072;
3. 武汉大学测绘遥感信息工程国家重点实验室, 湖北 武汉 430079
2. School of Urban Design, Wuhan University, Wuhan 430072, China;
3. State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan 430079, China
遥感影像聚类是遥感图像处理的关键技术之一,通过像元的相似性判别准则,将特征相似的像元划分为同一聚类[1-3],为遥感影像信息解译提供认知基础,常见的遥感影像聚类算法包括k-means[4]、ISODATA[5]、模糊聚类[6-7]等。对于低分辨率遥感影像,因其空间分辨率限制,导致混合像元现象普遍出现,影像具有模糊性与不确定性。因此,相较于硬聚类方法,模糊聚类方法能够保留更多的原始数据信息[8],在这些模糊聚类算法中,模糊C-均值聚类算法(FCM)很受欢迎并且被广泛地应用于遥感影像聚类中[9-11]。
随着遥感影像空间分辨率的提高,影像空间细节信息和像元间的空间相关信息更加丰富,而基于像元光谱的遥感影像聚类方法只利用了遥感影像的光谱信息,会产生聚类“离群点”或“椒盐噪声”的现象,严重影响了遥感影像的聚类效率与精度。近年来国内外学者针对基于像元光谱的聚类算法缺乏空间信息的问题进行研究,提出了众多改进算法。文献[8]提出了利用空间上下文信息分割后聚类的方法,属于面向对象的聚类方法,该类方法通过图像分割技术,保证了聚类的空间形态特征,避免了聚类椒盐噪声点的出现。但这种方法难以针对不同的遥感图像获得图像分割和局部窗口的最佳尺度,往往存在过度平滑、无法保持原始数据细节的问题。文献[13]提出借助Delaunay三角网构建多尺度的空间邻近关系,而遥感影像本身数据量就很庞大,这样做会过量增加算法的计算复杂度。文献[15—16]提出将马尔科夫随机场(MRF)引入FCM算法中,将像元特征域相似性与空间域邻近性结合起来,实现了在无空间尺度参数选择的情况下光谱信息与空间信息的融合,改善了聚类效果。然而基于马尔科夫随机场的聚类算法,数据分布必须服从各像元之间条件独立的模型假设,而实际上遥感影像临近像元之间是相关的。
综上所述,虽然当前结合空间信息的光谱聚类算法研究取得了进展,但是光谱信息与空间信息之间没有建立耦合的关系,忽视了邻近像元所属类别的空间关联约束。条件随机场(conditional random fields,CRF)模型是一种经典的随机场模型,区别于MRF模型,它不存在严格的条件独立假设,并且由于观测场的存在,能够考虑光谱相关性[19, 23],具有融合任意多特征和上下文信息的能力。同时,CRF的模型推测过程是一个像元先验分类置信度传播的过程,根据像元置信度的大小,可以自适应地确定该像元的分类信息对临近空间的影响范围,避免了面向对象的分类算法难于选择分割尺度的问题。因此,本文提出利用CRF改进FCM算法,提出空间信息与光谱信息耦合的遥感影像聚类算法。
1 理论基础 1.1 模糊C-均值FCM算法采用隶属度来度量像元属于每一类别的概率,相对于硬聚类方法(k-means、ISODATA等)而言,模糊聚类方法反映了真实地物的模糊性和不确定性[13],在中低分辨率遥感影像聚类分析中发挥了重要作用。FCM通过迭代优化目标函数得到隶属度,并根据隶属度最大原则来划分类别。
FCM的目标函数[14]如下
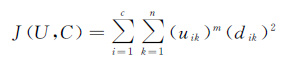 (1)
(1)
式中,U表示所有像元的模糊度集合;C表示聚类中心的集合;uik表示第k个像元对于第i类的隶属度,隶属度的取值区间为[0,1],根据归一化原则,数据隶属不同类别的概率总和等于1;m表示权重系数,取值区间通常为[1.5,3];dik表示第k个像元和第i个聚类中心的欧氏距离。
利用拉格朗日乘子法,构造新的目标函数[6, 7, 15],拉格朗日乘子法构造函数表示如下
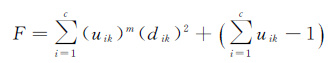 (2)
(2)
对式(2)求偏导,得到式(3)和式(4),计算更新每个像元的隶属度并同步获得新的聚类中心。当两次迭代的聚类中心变化小于设定阈值时,迭代结束
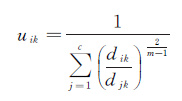 (3)
(3)
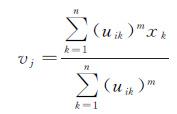 (4)
(4)
CRF是一种判别式条件概率无向图模型。在CRF中,将遥感影像像元灰度阵列称作观测序列,将每个像元的分类信息称作标记序列,由Hammersley-Clifford定理,在观测序列x条件下标记序列y的后验概率分布服从Gibbs分布[17, 21]
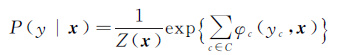 (5)
(5)
式中,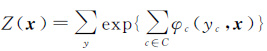
势函数的选择适应于需要解决的实际问题, 在遥感图像处理领域,一般使用二阶的条件随机场模型,其数学形式[21-22]见式(6)
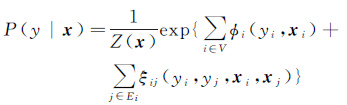 (6)
(6)
式中,V表示图像空间集合;Ei表示中心像元i的邻域空间,通常是4领域或8邻域;φi(yi,xi)为一阶势函数,称为光谱项;提取光谱特征,ξij(yi,yj,xi,xj)为二阶势函数,称为空间项[20],提取空间特征,具体计算模型根据实际应用构造。
2 条件随机场模型约束下的模糊C-均值聚类算法 2.1 算法原理条件随机场模型约束下的模糊C-均值聚类算法(CRF-FC)由二阶条件随机场衍生而来,Hammersley-Clifford定理证明了式(6)中子势团c服从的后验概率分布在势团C中均成立。由图 1可知,对子势团c进行分析,这里描述4-邻域,8-邻域原理相同。在子势团c中,中心像元与邻域像元邻接,标记序列包含先验标记值,即先验类别,同时标记序列与像元本身灰度信息关联,考虑各邻域像元与中心像元标记值是否相符及二者的光谱相似性,邻域像元会对中心像元的分类进行约束,空间项就是对这种约束进行量化,从而提取空间相关信息。光谱项是模糊C-均值初步聚类得到的像元分类先验概率。结合光谱项和空间项,根据式(6)后验概率分布可以得到子势团c上像元的分类后验概率,将后验概率分布推广到整个势团C可以得到影像中每个像元的分类后验概率。

|
| 图 1 CRF-FC算法模型 Fig. 1 Model of CRF-FC |
对于光谱项φi(yi,xi),通过FCM可以得到各像元属于每一类别的先验概率,基于这些先验概率构造条件随机场的光谱项
 (7)
(7)
式中,c表示类别数,每个像元的光谱项都是一个维数为类别数的特征向量,每一维表示该像元属于某一类别的概率。
对于空间项ξij(yi,yj,xi,xj)的构造,CRF模型大多采用Ising/Potts模型来构建空间领域范围内标记场和观测场之间的潜在关系[18],然而这些模型都没有考虑图像数据集间的上下文关系。本文采用了一种马氏距离边界约束模型作为空间项[19, 23],该模型构造中心像元的邻域系统,通过邻域像元的先验分类信息对中心像元的分类进行约束,从而将局部空间相关信息融入聚类
 (8)
(8)
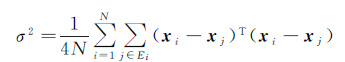 (9)
(9)
 (10)
(10)
 (11)
(11)
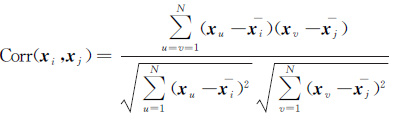 (12)
(12)
式中,d(xi,xj)是xi和xj之间的相似性测度,两像元相似时较大,不相似则较小;σ2是归一化项,将ξij(yi,yj,xi,xj)限制在[0,1)的范围内;DM是xi和xj之间的马氏距离,马氏距离可以自适应地根据数据调整几何分布,将像元的光谱相关性融入CRF的空间项;Corr(xi,xj)是Pearson矩阵相关系数,解决了马氏距离夸大微小变化量的弊端[19],xi和xj表示光谱向量xi和xj的均值。分析上式,ξij(yi,yj,xi,xj)的作用在于结合邻域像元对中心像元的分类进行约束,类似于置信度的概念。当中心像元与邻域像元的标记值不一致时,若两像元差异性也较大,与标记值不相等的现状相符,则d(xi,xj)较大,计算出的ξij(yi,yj,xi,xj)较大,即认为当前中心像元分类的置信度高;但若两像元相似性较大,则与标记值不相等的现状不符,d(xi,xj)较小,计算出的ξij(yi,yj,xi,xj)较小,即认为当前分类的置信度低。当邻域像元的标记值一致时,ξij(yi,yj,xi,xj)取得最大值为1,起到了图像平滑的作用。
2.2 算法流程(1) 由式(7)计算光谱项,由式(8)—式(12)计算空间项;
(2) 结合光谱项和空间项,由式(6)构建CRF-FC算法模型
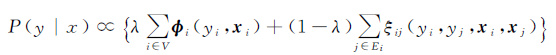 (13)
(13)
直接将光谱项和空间项进行整合可能会造成过拟合的问题,因此引入结构化参数λ,通过网格搜索和交叉验证的方法可以得到λ最优取值。为了简化计算,本文中使λ在[0.1,1]之间变化,在不同的λ下分别进行模型推测。
(3) 使用环形置信度迭代(LBP)算法对模型进行推测。LBP算法将整幅影像看作是一个有向图,每个像元看作一个结点,包含光谱信息,将像元之间的连接看作边,包含空间信息。使结点信息和边信息在有向图中传递,进而得到P(y|x)近似的全局最优推测。基本步骤如下:
a. 分别将结点Vi和边Eij初始化为μi和ηij,其中
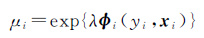 (14)
(14)
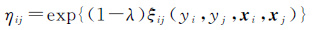 (15)
(15)
b. 通过传递结点信息和边信息,对网络中的边进行更新,i表示中心像元,k∈δi表示结点k属于结点i的邻域,k∈δi\j表示除去与结点j相连接的边。这是一个迭代的过程,直至整个网络收敛,即|Eijn+1-Eijn|<σ
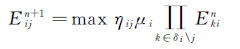 (16)
(16)
c. 根据结点信息和边信息计算置信度
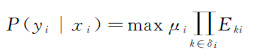 (17)
(17)
在每次迭代过程中通过置信度传播的方法,使结点自身信息与邻域节点构成的边信息在条件随机场网络中进行传递,实现了局部信息近似在全局的传递,从而能够得到全局的最优推测。
(4) 通过最大似然判别准则判定像元所属类别。通过LBP算法得到的标记序列对应于每一个像元仍然是一个多概率值,选取最大概率对应的类别作为该像元的所属类别。
3 试验及结果分析 3.1 QuickBird多光谱高分辨率遥感影像如图 3(a)所示,该影像共4个波段,空间分辨率为2.4 m,影像尺寸为400×400像素,实际地物分布如图 3(b)所示。本试验选取建筑物、水系、阴影、林地、草地、道路、裸地共7类,分别用k-means、ISODATA、FCM和本文提出的CRF-FC聚类算法进行试验。

|
| 图 2 算法流程图 Fig. 2 Flow chart of algorithm |

|
| 图 3 原始影像与地物分布 Fig. 3 Image and distribution of objects |
由图 4可知,4种聚类算法均将水系和阴影、道路和建筑物分成一类,原因在于4种算法均使用欧氏距离作为相似性测度,欧氏距离是灰度空间距离,由于传感器和外界因素的影响,不同类别像元的灰度空间距离较近,造成错分。在精度评定时,将水系和阴影归为“水系/阴影”类,将建筑和道路归为“建筑/道路”类。

|
| 图 4 4种算法聚类结果 Fig. 4 Results of four clustering algorithms |
4种聚类算法结果类块分布基本一致,直观来看,本文提出算法结果最明显的特征在于噪声大量减少,图像目视效果更平滑,而其他3种传统的聚类算法结果均存在不同程度的噪声。
对右上角林地区域进行放大可以看出,使用3种传统的聚类算法林地的提取效果均不好,将林地错分为草地。如图 5(d),本文所提出算法提取的林地区域噪声小,轮廓清晰,提取效果明显优于另外3种算法。

|
| 图 5 部分植被区域分类结果 Fig. 5 Classification results of part of the plant |
图 6是部分建筑及其阴影的提取情况。k-means、ISODATA和FCM算法建筑物类别中均参杂其他类别,出现明显错分,本文所提出算法结果中并不存在,建筑物形状特征保持较好。

|
| 图 6 部分建筑物区域分类结果 Fig. 6 Classification results of part of the building |
根据影像对应区域的实际地物分布,使用Envi软件制作ROI进行精度评定。选取建筑/道路、水系/阴影、树林、草地、裸地5类的ROI(图 7),通过OA系数及Kappa系数来定量对比4种算法的分类精度,各算法的分类精度见表 1。

|
| 图 7 ROI Fig. 7 ROI |
| k-means | ISODATA | FCM | CRF-FC | |
| OA系数/(%) | 73.16 | 70.74 | 68.64 | 81.68 |
| Kappa系数 | 0.65 | 0.62 | 0.59 | 0.76 |
由表 1知,OA系数和Kappa系数从小到大的顺序依次为:FCM、ISODATA、k-means、CRF-FC,CRF-FC的两项指标明显优于其他3种算法,相比于FCM算法,OA系数高出13.04%,Kappa系数高出0.17。这说明结合局部空间相关信息的CRF-FC算法实现了对传统FCM算法的改进,相比于硬聚类经典算法k-means和ISODATA更适合处理较高分辨率遥感影像的聚类问题。
3.2 湖北十堰QuickBird影像影像大小为250×250像素,共4个波段,空间分辨率为4 m,分别使用FCM算法、基于马尔科夫随机场的模糊C-均值聚类算法(MRF-FCM)、本文提出的CRF-FC算法进行分类,分类结果如下:
分析图 8,MRF-FCM和CRF-FC相对于FCM的分类结果平滑度有所提高。其中,CRF-FC在保证分类正确性的情况下,平滑度更优于MRF-FCM,部分间断的建筑物被连接在一起,同时地物边界更加明确。各算法的分类精度见表 2。

|
| 图 8 分类结果 Fig. 8 Classification results |
| FCM | MRF-FCM | CRF-FC | |
| OA系数/(%) | 84.70 | 85.64 | 86.89 |
| Kappa系数 | 0.80 | 0.81 | 0.83 |
分析表 2,CRF-FC和MRF-FCM考虑了空间相关信息,OA系数和Kappa系数均高于FCM算法。CRF-FC基于像元光谱信息构造邻域提取空间相关信息,相比MRF-FCM能够建立标记场和观测场之间的联系,试验表明CRF-FC分类精度确实高于MRF-FCM,OA系数高出1.25%,Kappa系数高出0.02。
4 结论遥感影像像元及其邻域的空间相关信息十分丰富,而基于像元光谱的聚类算法往往只考虑了光谱信息,聚类效果并不理想。因此,本文提出了一种条件随机场模型约束下的模糊C-均值聚类算法,将模糊C-均值计算的像元属于每一类别的先验概率作为光谱项,马氏距离边界约束模型构造中心像元及其邻域,提取空间特征作为空间项,构造二阶条件随机场,实现了光谱信息和空间相关信息的耦合。试验表明,CRF-FC聚类算法在分类结果的平滑度上相比传统基于像元光谱的聚类算法更加优越,同时在保持地物的形状特征及地物表面的连续性方面具有一定优势。CRF-FC聚类算法也有一定的不足,在一部分区域出现了过度腐蚀与过度膨胀的现象,并且4-邻域系统对于纹理丰富的区域显得有些不足,这些方面有待进一步的改进。
| [1] | TAŞDEMIR K, MERÉNYI E. A Validity Index for Prototype-based Clustering of Data Sets with Complex Cluster Structures[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 2011, 41(4): 1039–1053. DOI:10.1109/TSMCB.2010.2104319 |
| [2] | JAIN A K. Data Clustering:50 Years beyond K-means[J]. Pattern Recognition Letters, 2010, 31(8): 651–666. DOI:10.1016/j.patrec.2009.09.011 |
| [3] | MAULIK U, SAHA I. Modified Differential Evolution Based Fuzzy Clustering for Pixel Classification in Remote Sensing Imagery[J]. Pattern Recognition, 2009, 42(9): 2135–2149. DOI:10.1016/j.patcog.2009.01.011 |
| [4] | LLOYD S. Least Squares Quantization in PCM[J]. IEEE Transactions on Information Theory, 1982, 28(2): 129–137. DOI:10.1109/TIT.1982.1056489 |
| [5] | BALL G H, HALL D J. ISODATA, A Novel Method of Data Analysis and Pattern Classification[R]. Technical Report AD0699616. Menlo Park, CA:Stanford Research Institute, 1965. |
| [6] | 李雷, 罗红旗, 丁亚丽. 自适应约束模糊C均值聚类算法[J]. 模糊系统与数学, 2010, 24(5): 126–130. LI Lei, LUO Hongqi, DING Yali. Adaptive Constrained FCM Clustering Algorithm[J]. Fuzzy Systems and Mathematics, 2010, 24(5): 126–130. |
| [7] | 耿连英, 贺兴时, 贺飞跃. 基于模糊分类的MRF图像恢复方法[J]. 计算机工程, 2011, 37(10): 198–199. GENG Lianying, HE Xingshi, HE Feiyue. MRF Image Restoration Method Based on Fuzzy Classification[J]. Computer Engineering, 2011, 37(10): 198–199. |
| [8] | ZHONG Yanfei, MA Ailong, ZHANG Liangpei. An Adaptive Memetic Fuzzy Clustering Algorithm with Spatial Information for Remote Sensing Imagery[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 7(4): 1235–1248. DOI:10.1109/JSTARS.4609443 |
| [9] | BANDYOPADHYAY S, MAULIK U, MUKHOPADHYAY A. Multiobjective Genetic Clustering for Pixel Classification in Remote Sensing Imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(5): 1506–1511. DOI:10.1109/TGRS.2007.892604 |
| [10] | GHOSH A, MISHRA N S, GHOSH S. Fuzzy Clustering Algorithms for Unsupervised Change Detection in Remote Sensing Images[J]. Information Sciences, 2011, 181(4): 699–715. DOI:10.1016/j.ins.2010.10.016 |
| [11] | NIAZMARDI S, HOMAYOUNI S, SAFARI A. An Improved FCM Algorithm Based on the SVDD for Unsupervised Hyperspectral Data Classification[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2013, 6(2): 831–839. DOI:10.1109/JSTARS.2013.2244851 |
| [12] | AHMED M N, YAMANY S M, MOHAMED N, et al. A Modified Fuzzy C-means Algorithm for Bias Field Estimation and Segmentation of MRI Data[J]. IEEE Transactions on Medical Imaging, 2002, 21(3): 193–199. DOI:10.1109/42.996338 |
| [13] | 刘启亮, 邓敏, 石岩, 等. 一种基于多约束的空间聚类方法[J]. 测绘学报, 2011, 40(4): 509–516. LIU Qiliang, DENG Min, SHI Yan, et al. A Novel Spatial Clustering Method Based on Multi-constraints[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(4): 509–516. |
| [14] | HAMASUNA Y, ENDO Y, MIYAMOTO S. On Mahalanobis Distance Based Fuzzy C-means Clustering for Uncertain Data Using Penalty Vector Regularization[C]//Proceedings of 2011 IEEE International Conference on Fuzzy Systems. Taipei, Taiwan, China:IEEE, 2011:810-815. |
| [15] | 杨红磊, 彭军还. 基于马尔可夫随机场的模糊C-均值遥感影像分类[J]. 测绘学报, 2012, 41(2): 213–218. YANG Honglei, PENG Junhuan. Remote Sensing Classification Based on Markov Random Field and Fuzzy C-Means Clustering[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(2): 213–218. |
| [16] | 张路, 廖明生. 一种顾及上下文的遥感影像模糊聚类[J]. 遥感学报, 2006, 10(1): 58–65. ZHANG Lu, LIAO Mingsheng. Contextual Fuzzy Clustering of Remote Sensing Imagery[J]. Journal of Remote Sensing, 2006, 10(1): 58–65. |
| [17] | 姜文志, 顾佼佼, 胡文萱, 等. 条件随机场模型的应用研究及改进[J]. 计算机与现代化, 2011(11): 55–58. JIANG Wenzhi, GU Jiaojiao, HU Wenxuan, et al. Research on Applications of Conditional Random Fields and Its Improvement[J]. Jisuanji Yu Xiandaihua, 2011(11): 55–58. |
| [18] | 李祖传, 马建文, 张睿, 等. 利用SVM-CRF进行高光谱遥感数据分类[J]. 武汉大学学报(信息科学版), 2011, 36(3): 306–310. LI Zuchuan, MA Jianwen, ZHANG Rui, et al. Classifying Hyperspectral Data Using Support Vector Machine Conditional Random Field[J]. Geomatics and Information Science of Wuhan University, 2011, 36(3): 306–310. |
| [19] | ZHONG Yanfei, LIN Xuemei, ZHANG Liangpei. A Support Vector Conditional Random Fields Classifier with a Mahalanobis Distance Boundary Constraint for High Spatial Resolution Remote Sensing Imagery[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 7(4): 1314–1330. DOI:10.1109/JSTARS.4609443 |
| [20] | WANG Yang, RAJAPAKSE J C. Contextual Modeling of Functional MR Images with Conditional Random Fields[J]. IEEE Transactions on Medical Imaging, 2006, 25(6): 804–812. DOI:10.1109/TMI.2006.875426 |
| [21] | SYMONS C T, SAMATOVA N F, KRISHNAMURTHY R, et al. Multi-criterion Active Learning in Conditional Random Fields[C]//Proceedings of the 18th IEEE International Conference on Tools with Artificial Intelligence. Arlington, VA:IEEE, 2006:323-331. |
| [22] | NOMOTO T. Discriminative Sentence Compression with Conditional Random Fields[J]. Information Processing & Management, 2007, 43(6): 1571–1587. |
| [23] | ZHANG Guangyun, JIA Xiuping. Simplified Conditional Random Fields with Class Boundary Constraint for Spectral-Spatial Based Remote Sensing Image Classification[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(5): 856–860. DOI:10.1109/LGRS.2012.2186279 |



