2. 中国科学院大学, 北京 100049;
3. 中国资源卫星应用中心, 北京 100094
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. China Center for Resources Satellite Data and Application, Beijing 100094, China
随着城市化和工业化的快速发展,大量抽取地下水所造成地面沉降的状况呈现上升趋势,已成为世界性的地质灾害,给城市基础设施造成了巨大的经济损失。星载合成孔径雷达干涉测量技术(interferometric synthetic aperture radar,InSAR)作为新兴的空间测量技术,全天时、全天候、覆盖广等优点使其在地表形变的监测中得到广泛的关注;特别是近年来时序多基线InSAR技术的发展,大大提高了地表形变监测精度和应用范围。时序多基线InSAR技术开始于20世纪90年代后期,经过十多年的发展,国内外学者提出了干涉图堆栈技术(Stacking)[1]、最小二乘法(least square,LS)[2]、永久散射体法(permanent scatterer,PS)[3-6]、小基线子集法(small baseline subset,SBAS)[7-9]、相干目标方法(coherence target,CT)[10-12]、多时相InSAR技术(multi temporal InSAR,MTI)[13]、多尺度InSAR时间序列分析法(multiscale InSAR time series,MInTS)[14]等多种技术方法。这些时序多基线InSAR技术的散射机制均以像素中占主导优势的散射体为主,当应用于城区建筑密集区域时,会产生严重的叠掩效应使得单个雷达分辨率单元中包含了来自不同地面目标的多个散射目标信号,如果不能有效地将这些混叠的多个散射目标信号分离开来,就无法获取准确的地表形变信息。
针对上述方法对城区建筑密集区中高分辨SAR数据由叠掩效应带来的无法正确解算地表形变量这一问题,文献[15]提出了差分SAR层析成像技术:在SAR层析成像技术(tomography SAR,TomoSAR)基础上,通过对时序多基线InSAR数据集在层析向-斜距形变速率向形成合成孔径,获得目标方位向-距离向-层析向-形变速率向的四维空间信息。在该方法提出之初,文献[15]采用Capon谱估计法实现了地表形变速率估计,但是该方法需要使用多视数据估计观测协方差矩阵,降低了方位向-距离向的分辨率且旁瓣较高。为了解决上述问题,文献[16]采用了SVD奇异值分解法,文献[17] 采用了Backus-Gilber逆问题求解法,但它们在高度向-形变速率向的分辨率较低且还需要处理奇异值矩阵的病态问题。对于此问题,文献[18]采用了RELAX算法,该方法虽然提高了层析向-形变速率向的分辨率,但需要进行目标信号源数目的估计,当估计的信号源数目与真实的信号源数目不一致时会产生严重的误差。针对上述问题文献[19-22]采用了压缩感知技术(compressive sensing,CS)[23],该方法不仅保持了方位向-距离向的分辨率而且还实现了层析向-斜距形变速率向的高分辨率聚焦,然而随着层析向采样间隔的减小,叠掩效应中每个层析向上的散射目标将会出现多个空间上呈聚集块的采样散射点,使得叠掩效应中散射目标的多个散射点具有块结构特性,但是该方法对块结构信号进行反演时其估计性能较差[24-26]。
为了解决CS方法对块结构散射目标进行反演时的不足,本文利用叠掩效应中散射目标的块结构特性与差分TomoSAR中参数矩阵所具有的Khatri-Rao积性质,提出采用联合Khatri-Rao子空间与块压缩感知[27](Khatri-Rao subspace and block compressive sensing,KRS-BCS)的方法对城区地表进行反演,通过模拟仿真数据和Envisat卫星ASAR数据与一等水准点及GPS实时测量数据进行对比分析,结果表明本文所采用的KRS-BCS方法不仅保持了CS方法的优点而且还更好地实现了城区地表形变信息的估计。
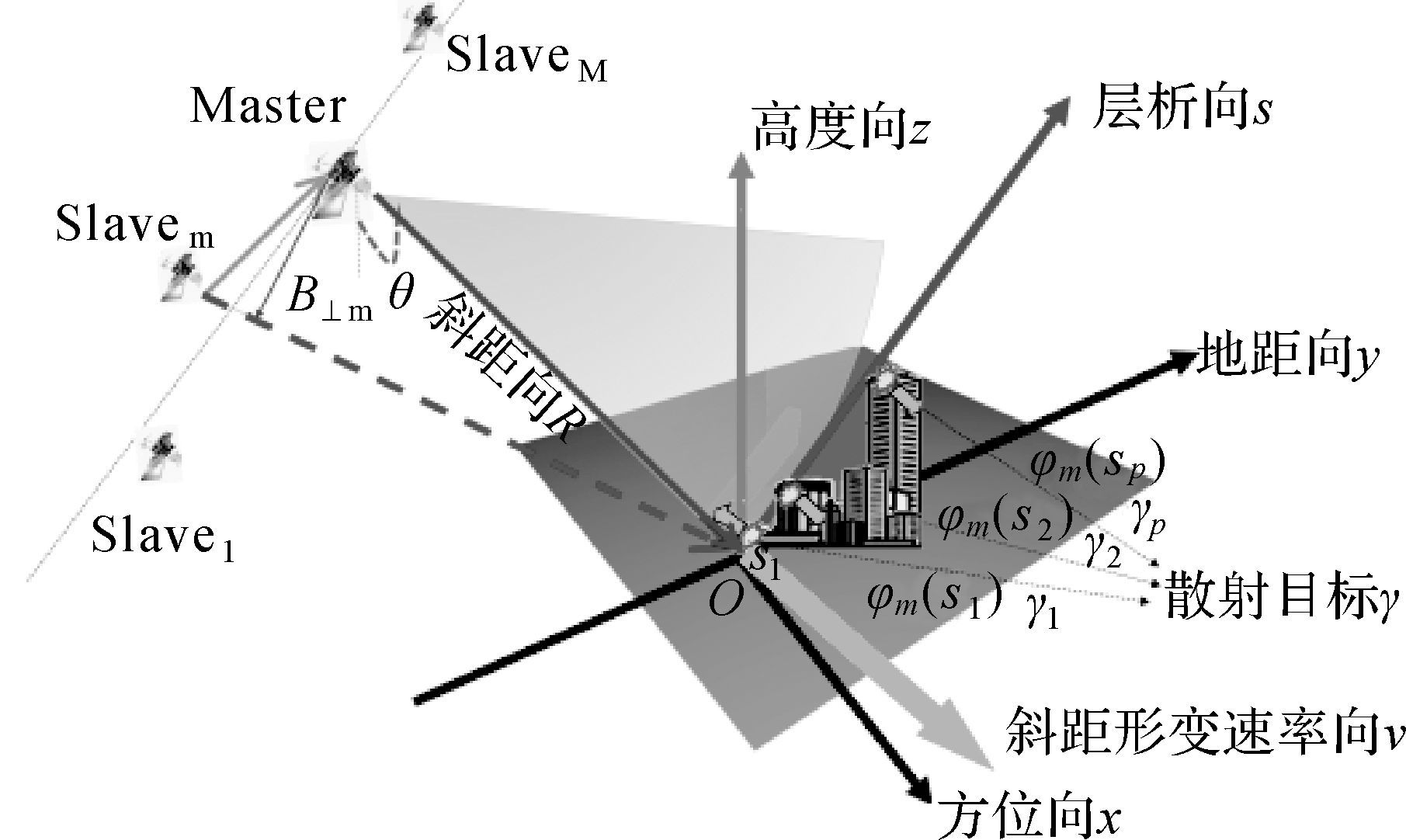
1 差分TomoSAR原理差分TomoSAR成像示意图如图 1所示。假设从不同空间和时间位置获得了同一目标区的M+1景航过SAR单视复图像数据集,在对时序SAR单视复图像数据集进行主图影像选取、图像序列配准、去斜、相位补偿去除大气延迟以及基线估计等预处理步骤后,除主图像外第m(m=1,2,…,M)航过影像中每个方位向-斜距向分辨率单元的复数值gm可看作是相同方位同一斜距下P个散射目标信号在层析向-斜距形变速率向平面上的二维联合谱,其表达式为
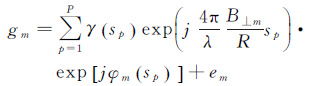 (1)
(1)
式中,s为层析向,垂直于方位向-斜距向平面,且与高度向z的关系为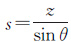
在线性形变速率模型下,形变相位φmsp可记为
 (2)
(2)
式中,Tm为第m航过影像与主图像的时间基线;v(sp为层析向采样点sp处的线性斜距形变速率。
将式(2)代入方程式(1),有
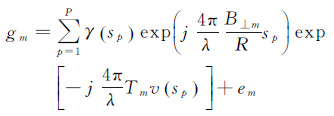 (3)
(3)
若令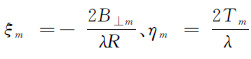
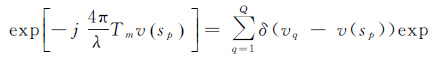
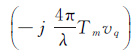
 (4)
(4)
式中,vq(q=1,2,…,Q$\gg $M)为斜距形变速率向采样点,并记斜距形变速率向采样点间隔ρv=vq-vq-1;δ(·)为狄克拉函数。
对于上述方程令G=[g1 g2… gM]T,γ={γ1δ[v1-v(s1)]…γ1δ[vQ-v(s1)]…γPδ[vQ-v(sP)]…γPδ[vQ-v(sP)]}T,e=[e1 e2 … eM]T,则可将其进一步写成矩阵形式
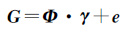 (5)
(5)
式中
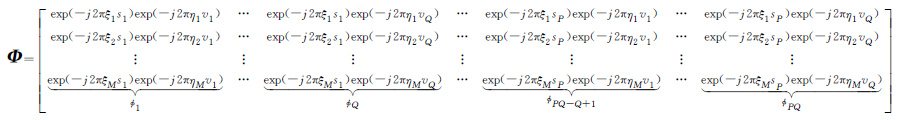
差分TomoSAR技术主要解决的问题是根据方程式(5)中的观测向量G,通过各种方法反演层析向-斜距形变速率向二维平面上目标信号的γ值,进而不同方法采用不同准则依据其值的位置确定散射点的层析向位置和斜距形变速率向的大小,从而实现差分SAR层析成像的四维成像。
2 KRS-BCS差分TomoSAR方法对于方程式(5),采用CS的差分TomoSAR方法通过l1范数最小化求解γ值,通过γ值的非零位置确定散射点的层析向位置和斜距形变速率向的大小,一般认为散射目标信号的少数几个非零γpδ[vq-v(sp)]值出现在层析向-斜距形变速率向二维平面上的任意位置,可是对于中高分辨星载数据,若层析向采样间隔ρs较小,则叠掩效应中每个层析向上的散射目标将采样多个散射点,即层析向上的一个散射目标由多个散射点组成,尽管这一散射目标中的多个散射点在反射量上各不相同,但他们在空间上呈现聚集块的结构形式不再满足信号的任意稀疏性,而CS方法并没有考虑目标的这种特性,故对同时具有稀疏特性和结构特性的目标进行估计时性能较差。因此本文针对CS方法的不足,从散射目标的块结构特性分析入手,建立Khatri-Rao子空间下的差分TomoSAR块压缩感知观测模型,提出KRS-BCS差分TomoSAR方法。
2.1 散射目标的块结构特性从差分TomoSAR成像示意图(图 1)可知,同一散射目标中散射点数目或块长度b与层析向采样间隔ρs存在以下关系
 (6)
(6)
|
| 图 1 差分TomoSAR成像示意图 Fig. 1 Differential TomoSAR imaging diagram |
由上面分析和式(6)可知,散射目标由散射点组成,散射点的多少随层析向采样间隔的大小变化,层析向采样间隔减小,散射目标中获得了更多的散射点,可以更全面地刻画散射目标的整体情况;层析向采样间隔变大,散射目标中获得了较少的散射点,只能突出散射目标的主要特性。块结构是散射目标在压缩感知中的另一种表述,叠掩中有几个散射目标就对应几个块结构,若层析向间隔ρs增大到以Δs 采样,则b=1,散射目标中只有一个散射点,此时散射目标不再具有块结构特性;另外,由于每一个块结构中多个散射点来自于同一个散射目标,因此可认为每一个块结构或散射目标中多个散射点形变速率一样。
2.2 差分TomoSAR的块压缩感知观测模型依据2.1节散射目标的块结构特性,将散射目标中散射点的反射能量矩阵γs按块长度b分为N块
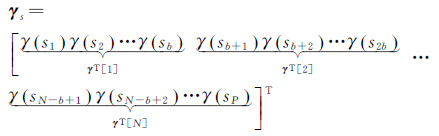 (7)
(7)
式中,P=N×b;γT[n]表示第n(n=1,2,…N)个子块,子块中的值是同为零或非零的。
依据每一个散射目标中多个散射点形变速率一样,可将每块对应的δvq-v(sp函数矩阵也分为N块
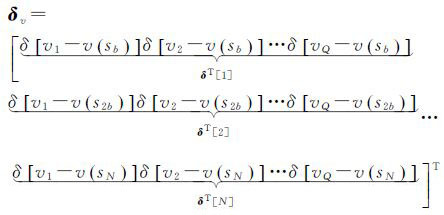 (8)
(8)
则目标信号的γ值为
 (9)
(9)
式中,“⊙”和“⊗”分别表示为Khatri-Rao积和Kronecker积;设
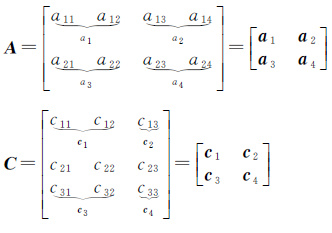
Khatri-Rao积定义为
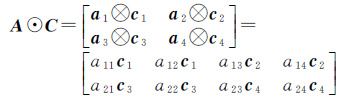
按照与目标信号γ相似的块分块,可将观测矩阵Φ分块定义为
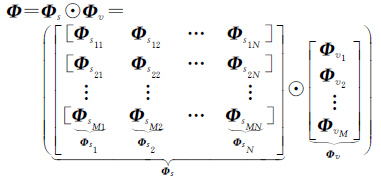 (10)
(10)
式中
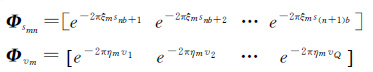
依据上述块结构特性,差分SAR层析成像的观测模型可进一步表示成N个Khatri-Rao子空间下的块压缩感知观测模型,其表达式为
 (11)
(11)
根据稀疏重构理论,欲在块压缩感知框架下对方程式(11)进行精确重构,需要满足块结构目标信号γ的可稀疏表示性和观测矩阵Φ的限制等距特性,文献[19-22]已证明其满足。因此,方程式(11)可通过混合l1/l2范数最小化求解将其准确地重构出来
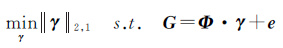 (12)
(12)
式中,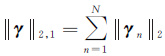
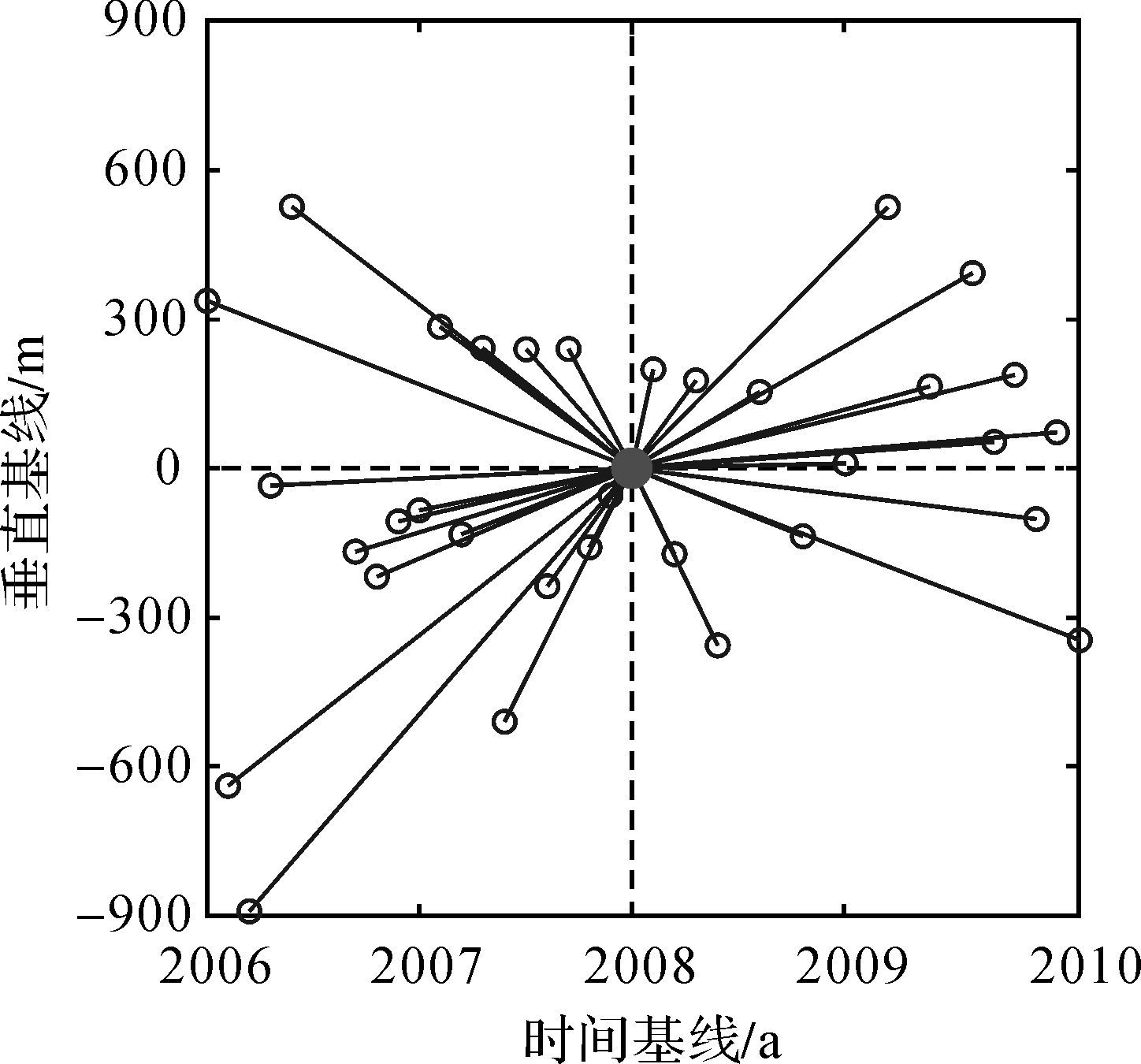
分辨能力和重构估计性能是衡量成像方法的两个重要方面,本文采用以Envisat卫星34景ASAR数据集为实际参数(拍摄时间为2006年9月至2010年8月,主图为2008年8月4日的垂直基线与时间基线分布如图 2所示)的仿真试验(试验对象为不受各种误差影响的理想散射目标)对其进行评价。
|
| 图 2 垂直基线-时间基线分布图 Fig. 2 Perpendicular baseline and time baseline distribution |
2.3.1 分辨能力
由Envisat卫星ASAR主图数据的中心视角θc=22.83°,主图的中心斜距Rc=864 766.98 m,垂直基线的总长度B⊥=1 417.43 m,时间基线的总跨度T约为5 a(T≈5 a),可知层析向瑞利分辨率
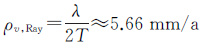
仿真中为了分析KRS-BCS差分TomoSAR方法和CS差分TomoSAR方法的分辨率性能及两者的对比情况,斜距形变速率向采样间隔ρv和层析向采样间隔ρs斜距形变速率向都以远小于瑞利分辨率进行采样,取 
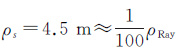
图 3和图 4是块稀疏数k=1、2、3和b=4时两方法在层析向-斜距形变速率向三维平面上和二维平面上的重构图,其中绿色、青色和蓝色的实矩形区是k=1、2、3时的真实位置,假定同一块稀疏数中散射点的散射能量相同且γ1=1.0、γ2=0.4、γ3=0.7,红色圆形是KRS-BCS方法重构的位置,黑色实点是CS方法重构的位置。从图中可以看出,在块稀疏数k=1、2、3时,KRS-BCS方法和CS方法都能清晰分辨出不同散射目标中4个4.5 m间隔的散射点,这充分展现了两种方法具有相同的高分辨性能,但两种方法在重构估计性能方面差别较大,具体分析见2.3.2节。
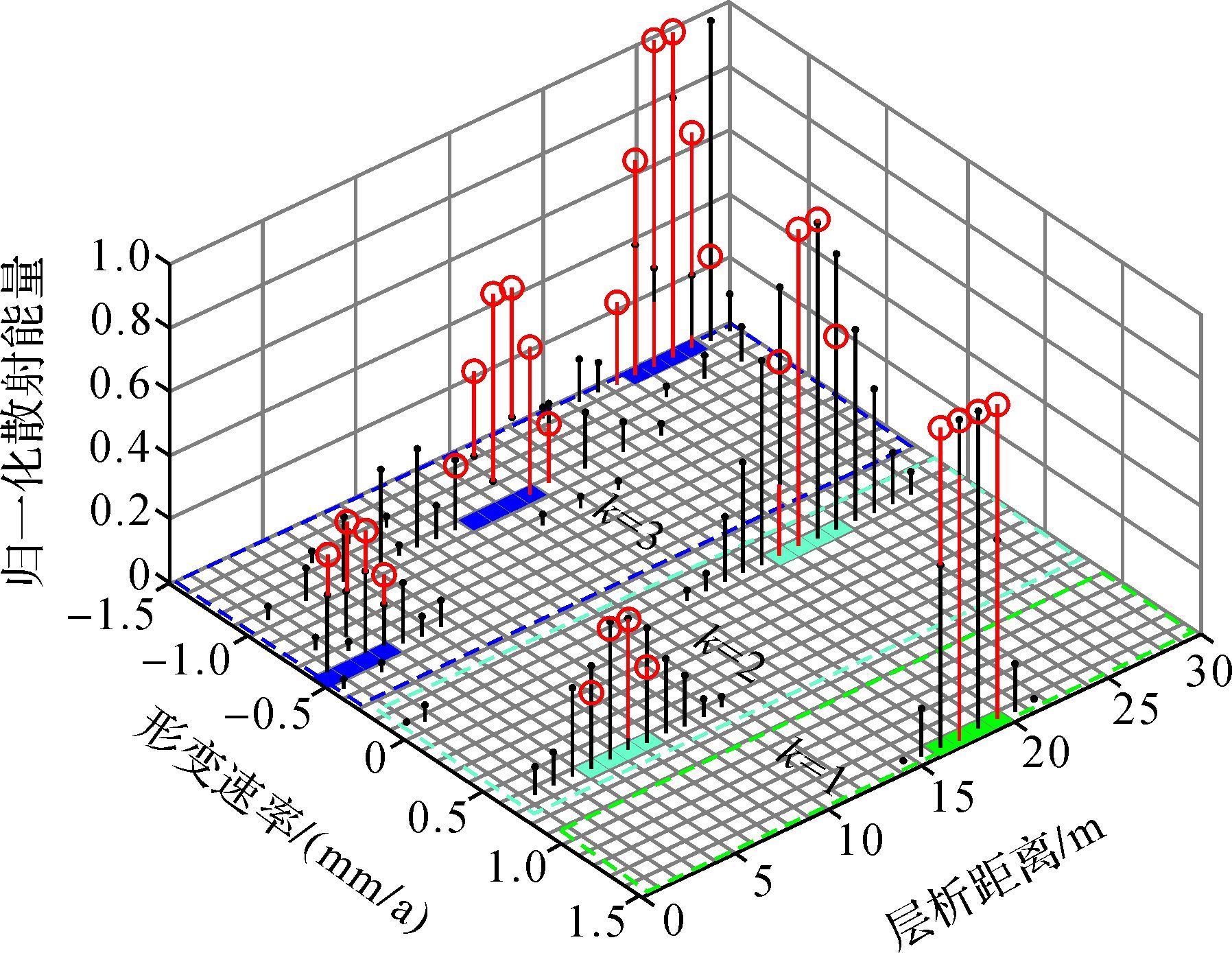
|
| 图 3 b=4、不同k时的三维重构位置 Fig. 3 3D reconstruction position of using b=4 and different k |
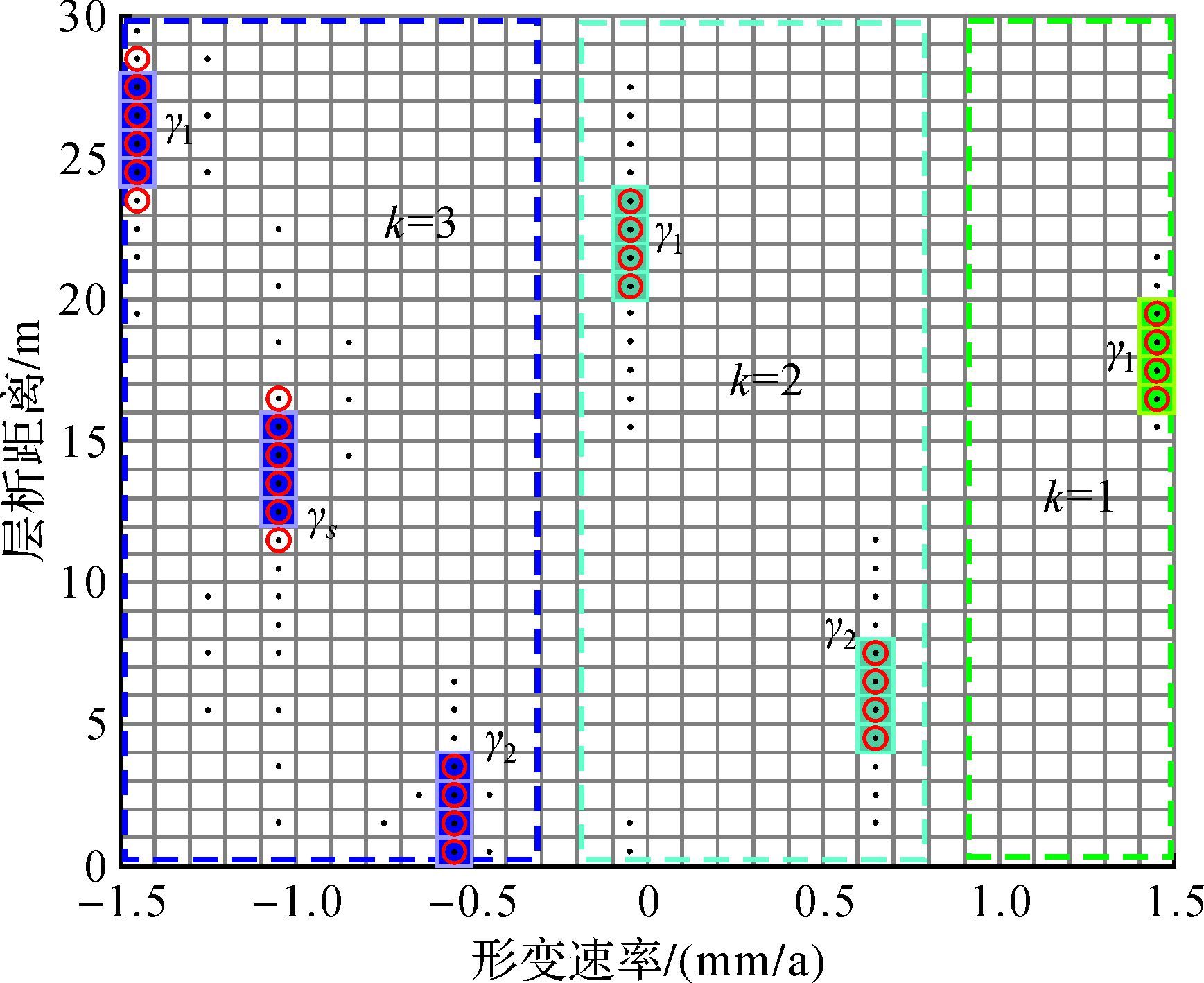
|
| 图 4 b=4、不同k时的二维重构位置 Fig. 4 2D reconstruction position of using b=4 and different k |
2.3.2 重构估计性能
虚假散射目标出现概率和准确重构率是重构估计性能的主要指标,其由观测矩阵Φ的RIP决定。RIP要求Φ对观测向量G作用具有保距性,Φ的RIP性能越好保距性越好,保距性越好其重构性能越好;由于实际应用中RIP很难判断,常用Φ中原子间的相似性μ代替,μ越小Φ的RIP性能越好;对于CS方法和KRS-BCS方法中的μ和μb其表达式分别为
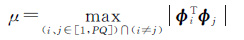 (13)
(13)
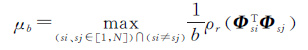 (14)
(14)
式中,ρr(·)为谱半径。
依2.2节分析可知,随着层析向采样间隔的减少,目标信号的总体采样数目增加,Φ的维数也相应地增加,但Φ的维数增加相当于在各列向量间进行了插值,因此Φ的各列向量间差异随着层析向采样间隔的减少也逐渐减小。结合式(13)可知CS方法中Φ的相似性μ是列与列的相似性,因此μ的值将变大,其RIP性能将变差,故其重构估计性能也将变差;而对于KRS-BCS方法中Φ的相似性μb,由式(14)可知μb是块与块的相似性,因此块的大小变化不会对μb产生很大的影响,故其重构估计性能稳定。
为了更加合理地验证上述理论分析,本文进行了仿真试验。通过不同参数的设置,对KRS-BCS方法和CS方法的重构估计性能从定性和定量两个方面加以分析。
(1) 定性方面:采用2.3.1节的仿真,从图 3和图 4可以看出,在块稀疏数k=1、2时,KRS-BCS方法和CS方法都没有虚假散射目标,但CS方法在每个散射目标的周边多出2~4个错误散射点,而KRS-BCS方法完整地恢复原始信号;在块稀疏数k=3时,KRS-BCS方法还没有虚假散射目标出现,仅在周边多出1个错误散射点,但CS方法出现大量虚假散射目标且周边都有错误散射点。
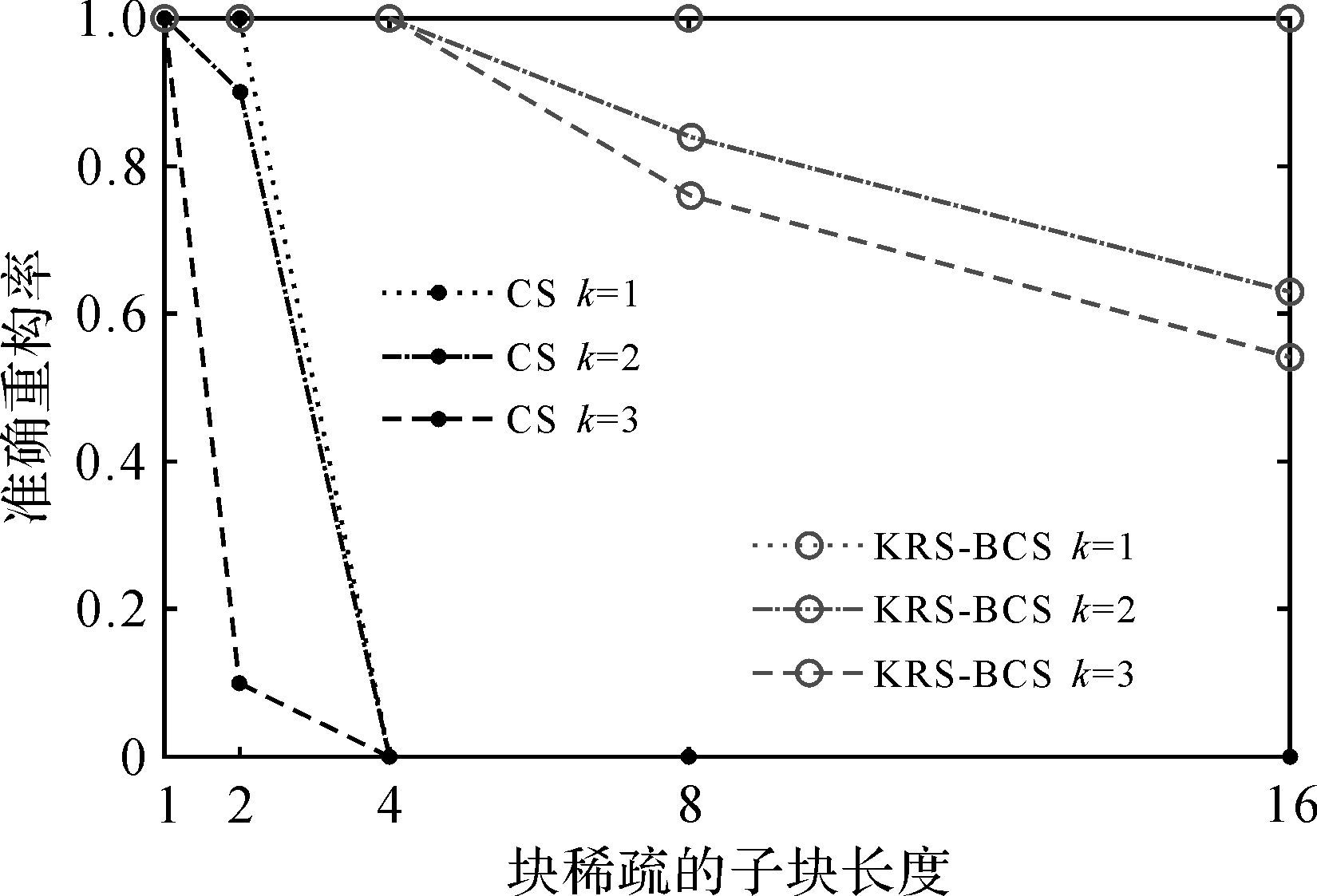
(2) 定量方面:保持2.3.1节的仿真参数不变,层析向采样间隔ρs以18.5 m、8.5 m、4.5 m、2.5 m、1.2 m进行采样,对应子块长度b=1、2、4、8、16,每个块的斜距形变速率相同并以0.1 mm/a的分辨率在区间[-1.5 1.5]内随机产生。分析块稀疏数k=1、2、3的情况下,不同子块长度下的虚假散射目标的出现概率和散射目标中散射点的准确重构概率,结果如图 5和图 6所示。从图 5和图 6中可以看出,随着块稀疏数的增加,KRS-BCS方法和CS方法的虚假散射目标的出现概率都相应增加且散射点位置的准确重构率减小,但CS方法的增加和减小的幅度明显大于KRS-BCS方法的增加和减小的幅度。另外,CS方法在块稀疏数k=3和子块长度b大于2时虚假散射目标出现的概率就已大于0.8且准确重构率已衰减到0,在块稀疏数k=1和子块长度b大于4时虚假散射目标出现概率大于0.2且准确重构率也已衰减到0,而KRS-BCS方法在子块长度b大于4后才开始出现虚假散射目标且最大虚假散射目标出现概率不大于0.2,准确重构率也开始衰减但其最小值仍大于0.5,这一结果也表明KRS-BCS方法的性能明显优于CS方法。

|
| 图 5 不同k、b时虚假散射目标出现概率 Fig. 5 Probability of false scattering target using different k and b |
|
| 图 6 不同k、b时散射点准确重构率 Fig. 6 Reconstruction accurate of scattering point using different k and b |
依据上述理论分析与仿真试验的结果,可以得出本文所采用的KRS-BCS方法不仅保持了高分辨率的优点,而且有效地降低了虚假目标出现概并和大幅度地提高了散射点准确重构概率,切实可行地解决了CS方法的不足。
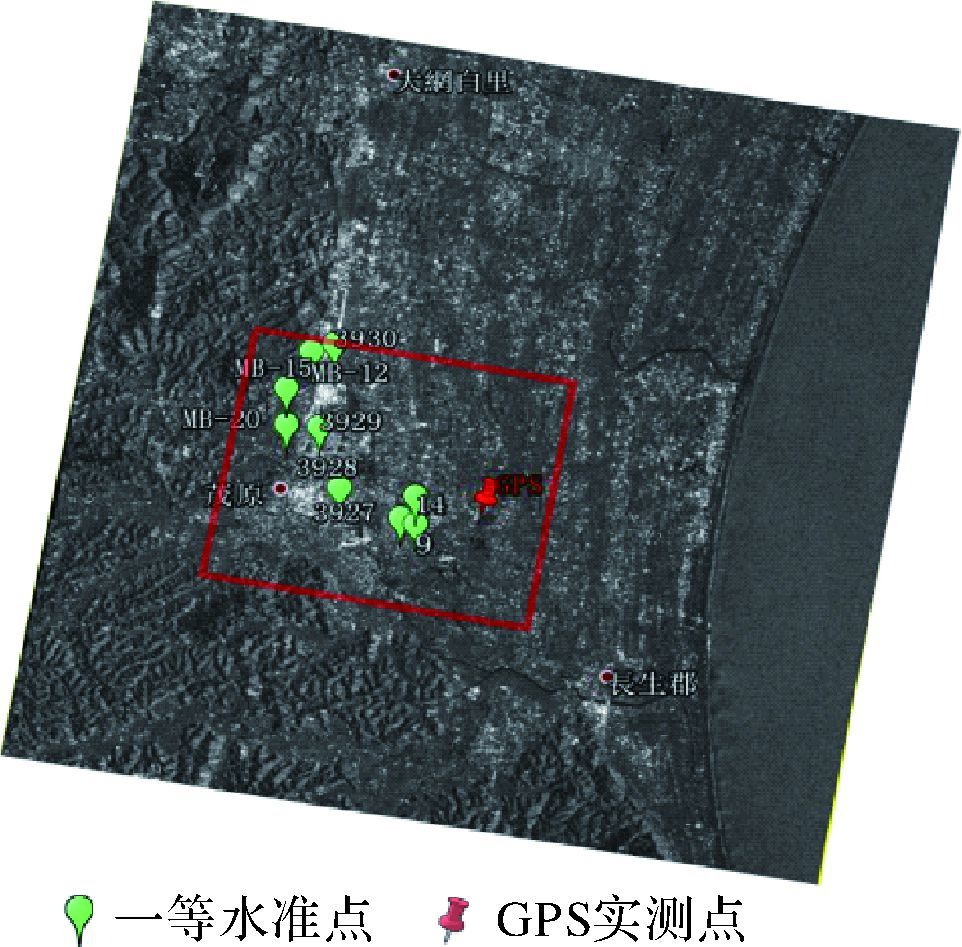
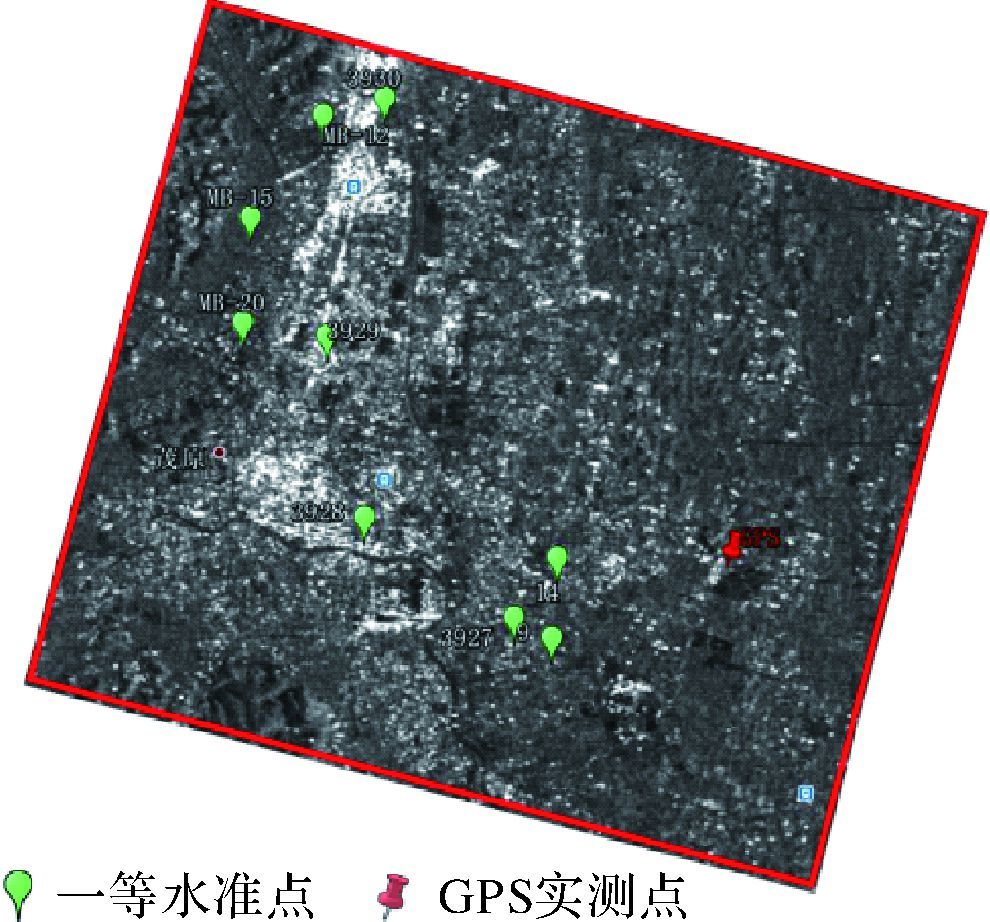
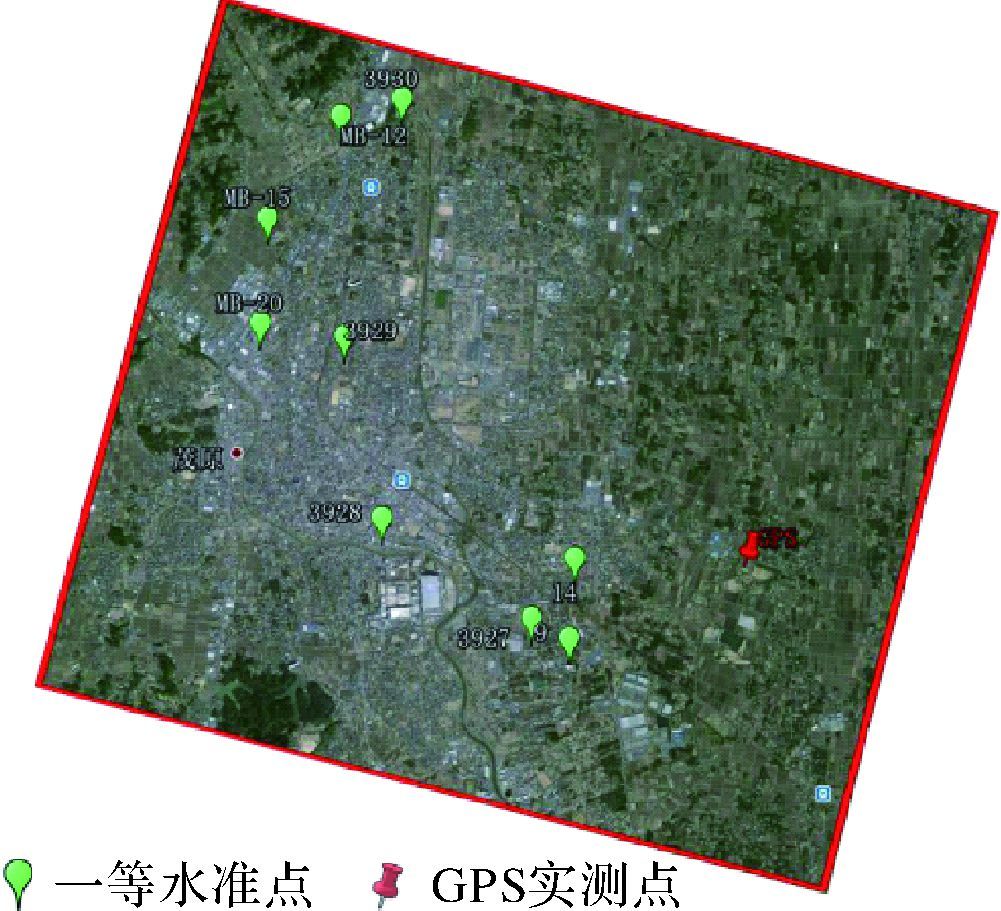
3 研究区域地表形变提取与验证 3.1 研究区域概括为了验证KRS-BCS方法在城区地表形变监测应用中的可行性,本文选取日本千叶县作为试验研究区,该区域位于关东平原的东南部,具有丰富的天然气资源和含盐量很高的地下水,由于天然气和地下水的过度开采,千叶县成为日本地表形变最严重的区域。试验选取了该区域2006年9月至2010年8月获取的34景Envisat卫星ASAR影像(2008年8月4日的垂直基线与时间基线分布如图 2所示),拍摄范围为35.34°N—35.55°N、140.22°E—140.47°E,如图 7所示。为进行针对性的分析对比,将试验区进一步选定为高层建筑物较多的茂原市区,如图 8所示。图 9为试验区的光学图像,其中雨点状标记为一等水准点、图钉状标记为茂原区曾根尼之台综合公园GPS实时测量站点。
|
| 图 7 Envisat ASAR拍摄范围 Fig. 7 Scene acquired by Envisat ASAR |
|
| 图 8 试验区的SAR幅度图像 Fig. 8 SAR magnitude image of the test area |
|
| 图 9 试验区的光学图像 Fig. 9 Corresponding Optical image of the test area |
3.2 研究区域概括形变结果与精度验证
试验区在KRS-BCS差分TomoSAR成像处理中斜距形变速率采样间隔的选取,依据2.3节的分析选择为ρv=0.1 mm/a和块稀疏的子块长度选择为b=4,此时虚假散射目标出现概率为0和准确重构概率为1.0,可以充分保证重构的准确度,重构结果如图 10和图 11所示。
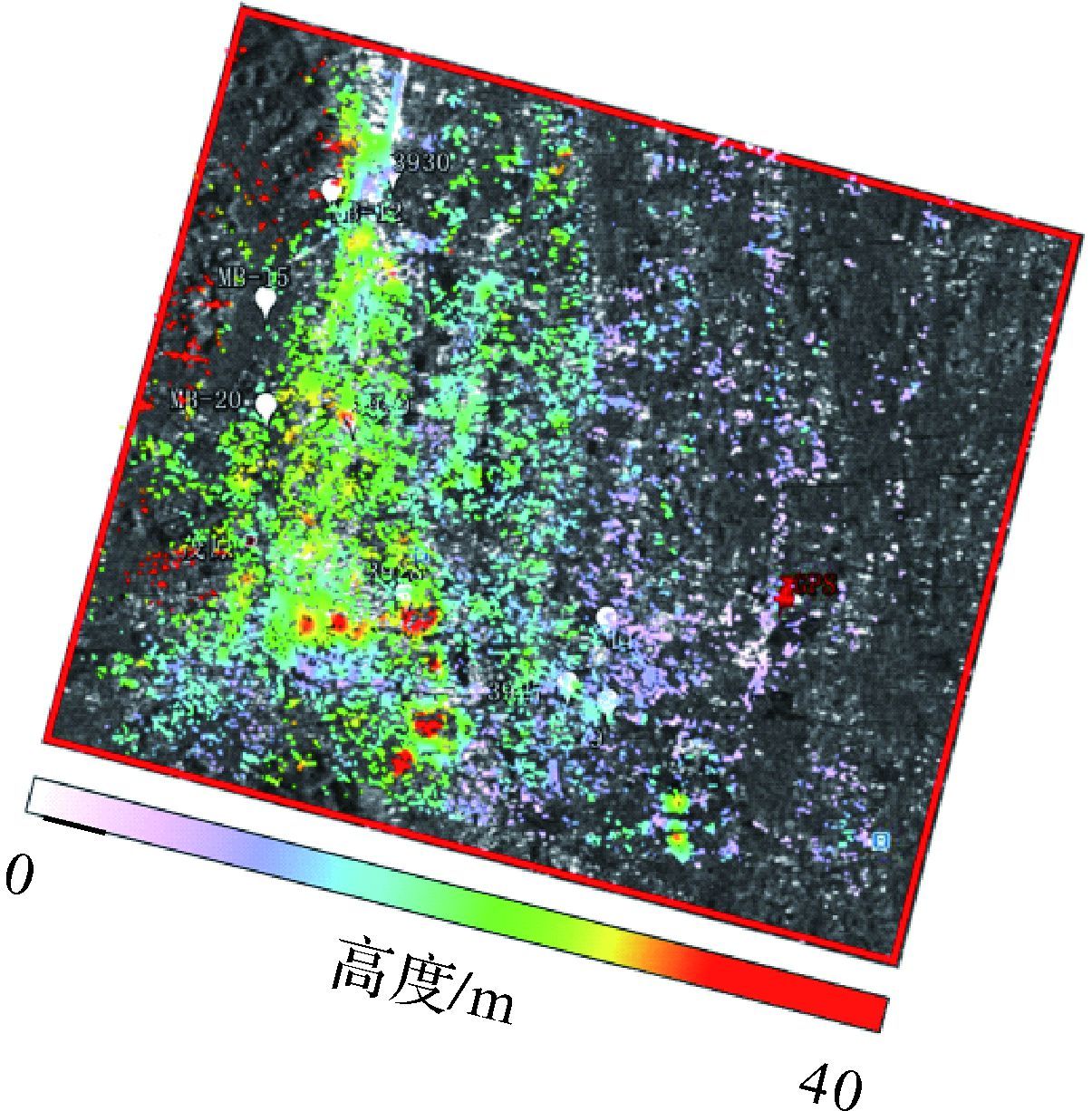
|
| 图 10 KRS-BCS方法重构的测试区高度与SAR幅度图像叠加 Fig. 10 Reconstructing height from KRS-BCS overlapped SAR magnitude image of the test area |
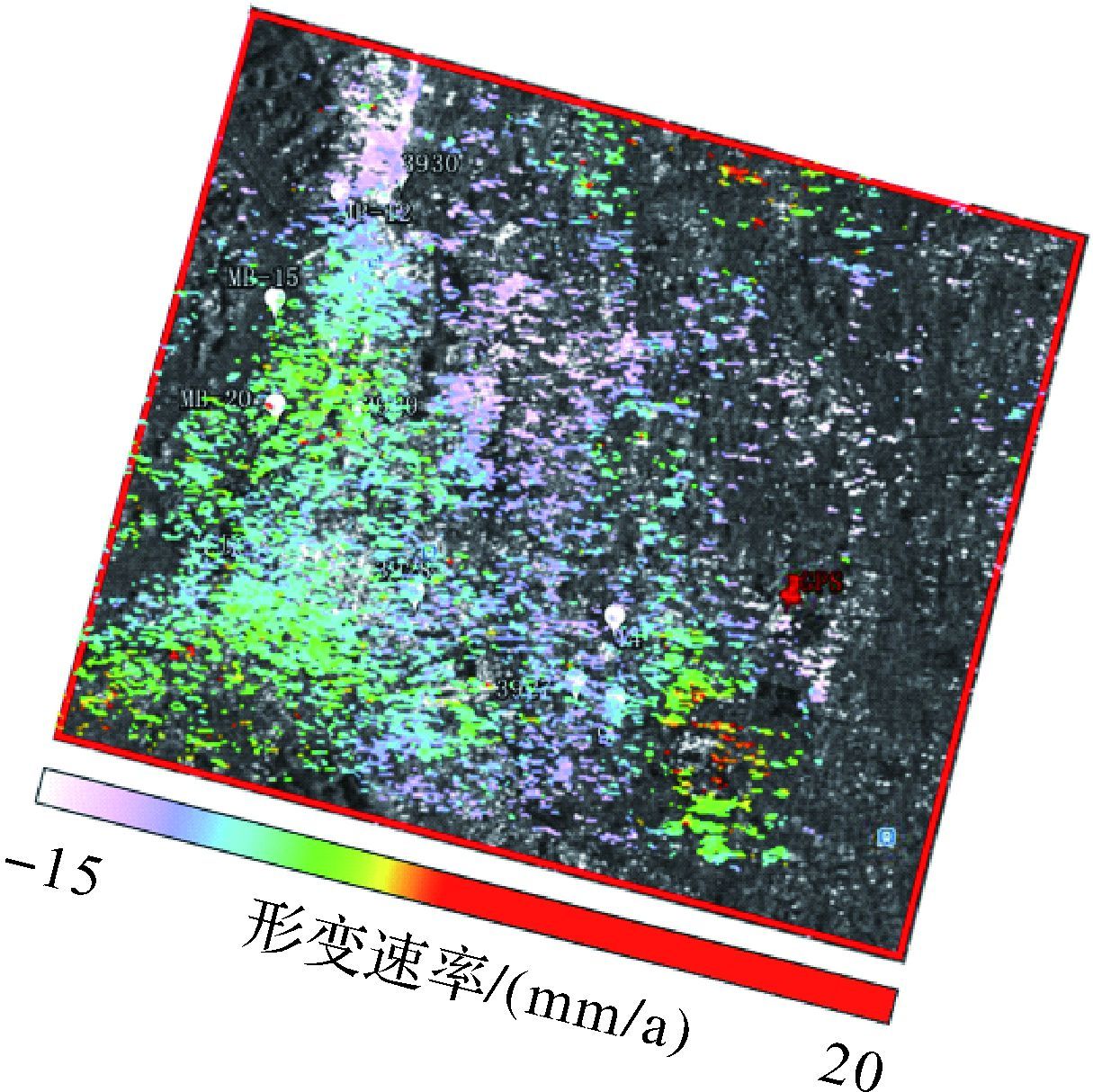
|
| 图 11 KRS-BCS方法重构的测试区形变速率与SAR幅度图像叠加 Fig. 11 Reconstructing deformation velocity from KRS-BCS overlapped SAR magnitude image of the test area |
图 10是依据层析向与高度向转换关系获得的重构高度与SAR幅度图像的叠加图,从中可以获知测试区的高度从城区中心到沿海岸边呈递减趋势,城区高层建筑物较多其高度大多分布在20~40 m区间内,城区外以低矮建筑为主其高度分布在0~20 m区间内,整个测试区的高度分布及趋势与Google地图中的三维建筑物高度呈整体一致性。图 11是斜距形变速率向的形变速率图与SAR幅度图像的叠加图,从中可知测试区的小部分区域斜距形变速率大于0、呈现抬高趋势、上升形变速率达20 mm/a,大部分区域斜距形变速率小于0、呈现下沉趋势、下沉形变速率可达-15 mm/a,其整体趋势与千叶县环境生活部发布的形变趋势基本吻合。
为进一步验证KRS-BCS方法重构的形变速率,本文选取了9个一等水准点和1个GPS实时测量站点作为检验点,对比结果如图 12和图 13所示。图 12是2007年至2011年期间每年1月测量的9个水准点形变量、线性拟合后的形变量与KRS-BCS方法重构的线性形变量对比图,为了便于分析将水准点实测形变量转化到斜距向或斜距形变速率向形变量,从图 12可知,KRS-BCS方法重构的形变与水准点测量的形变都呈下沉趋势且保持了整体一致性,除3930水准点外KRS-BCS方法重构的形变速率均偏低于水准点测量的形变速率且偏差也不大,在水准点3927、3928、MB-12的偏差小于1.5 mm/a,在水准点14、3230的偏差小于2 mm/a,与水准点9、MB-15的偏差小于4 mm/a,与水准点3929、MB-20的偏差在6 mm/a左右,所有点的整体偏差小于3.2 mm/a。
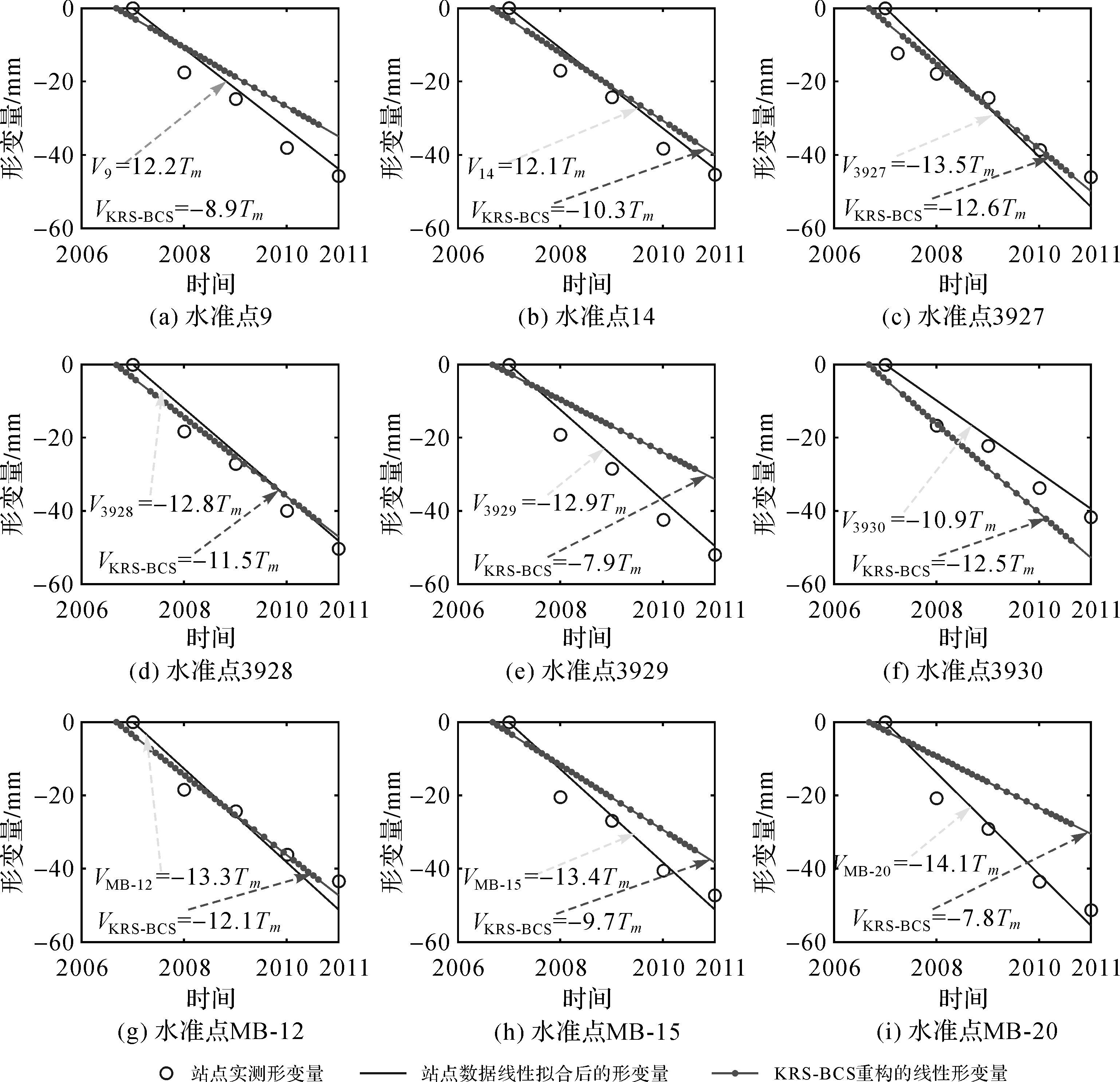
|
| 图 12 KRS-BCS方法重构形变量与站点实测形变量的对比 Fig. 12 Comparison of reconstructing deformation from KRS-BCS and measuring deformation from first level point data |
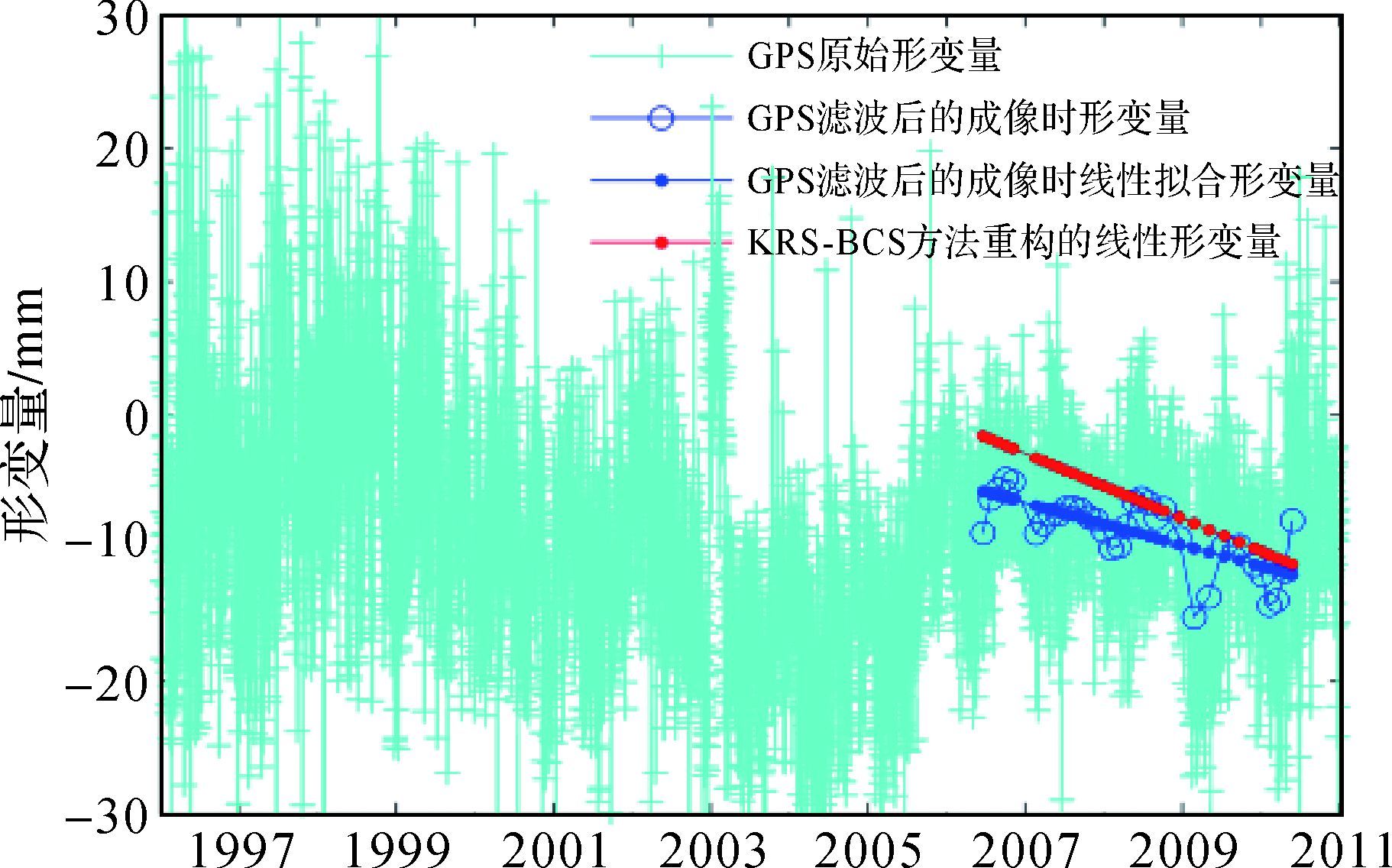
|
| 图 13 KRS-BCS方法重构形变量与GPS实测形变量的对比 Fig. 13 Comparison of reconstructing deformation from KRS-BCS and measuring deformation from GPS tracking data |
图 13是1996年5月至2011年1月间获得的GPS实测形变量与KRS-BCS方法重构的线性形变量对比图,在分析前先将GPS实时测量数据进行滤波、ASAR数据成像时间重采样、线性形变拟合以及高程向形变量到斜距向或斜距形变速率向形变量转化等处理,然后比较GPS滤波后的成像时线性拟合形变量与KRS-BCS方法重构的线性形变量,从图 13可知,以1996年5月数据采集起始点为参考点的GPS实时测量站点在ASAR数据成像期间呈现上升和下沉的交替沉降模式但其整体趋势呈现下沉,KRS-BCS方法重构的形变趋势与GPS滤波后的成像时线性拟合形变趋势保持了良好的一致性,都呈现下沉趋势,且KRS-BCS方法重构的线性形变速率-6.7 mm/a与GPS滤波后的成像时线性拟合形变速率-4.3 mm/a相差也较小,为2.4 mm/a。
4 结论本文提出了一种基于KRS-BCS差分TomoSAR技术的城区地表形变监测方法,利用了城区地表叠掩效应中散射目标随层析向采样间隔变化而产生的块结构特性,构建了Khatri-Rao子空间下的块压缩感知观测模型,采用混合l1/l2范数最小化求解实现了反演参数的重构,通过理论分析和仿真试验说明了CS方法存在的不足,并进一步对比分析了KRS-BCS方法对CS方法不足之处的切实改进:分辨力方面KRS-BCS方法保持了CS方法的高分辨率优点,可以实现0.1 mm/a级的地表形变监测、重构估计性能方面KRS-BCS方法,可以保证在不同块稀疏和不同子块长度下,最大虚假散射目标出现概率不大于0.2和最小准确重构率仍大于0.5,而CS方法在块稀疏数k=1和子块长度b大于4时虚假散射目标出现概率已大于0.2,且准确重构率也已衰减到0;在实例研究应用中,利用Envisat卫星ASAR数据集对日本千叶茂原区进行地表形变监测,并利用一等水准点和实时测量的GPS站点数据进行精度验证,试验结果表明本文采用KRS-BCS方法反演的结果不仅与一等水准点及GPS结果保持了良好的一致性,而且形变速率整体偏差也较小,分别为3.2 mm/a和2.4 mm/a,进一步验证了该方法的可靠性和精确性。在后续的研究中尝试更加复杂的非线性形变模式和周期形变模式,使本文方法能满足复杂条件下的地表形变监测需求。
| [1] | SANDWELL D T, SICHOIX L. Topographic Phase Recovery from Stacked ERS Interferometry and A Low-resolution Digital Elevation Model[J]. Journal of Geophysical Research:Atmospheres, 2000, 205(B12): 28211–28222. |
| [2] | USAI S. A New Approach for Long Term Monitoring of Deformations by Differential SAR Interferometry[D]. Delft:Delft University of Technology, 2001. |
| [3] | FERRETTI A, PRATI C, ROCCA F. Permanent Scatterers in SAR Interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(1): 8–20. DOI:10.1109/36.898661 |
| [4] | HOOPER A, ZEBKER H, SEGALL P, et al. A New Method for Measuring Deformation on Volcanoes and Other Natural Terrains Using InSAR Persistent Scatterers[J]. Geophysical Research Letters, 2004, 31(23). |
| [5] | KAMPES B M. Radar Interferometry:Persistent Scatterer Technique[M]. Netherlands: Springer, 2006. |
| [6] | 李德仁, 廖明生, 王艳. 永久散射体雷达干涉测量技术[J]. 武汉大学学报(信息科学版), 2004, 29(8): 664–668. LI Deren, LIAO Mingsheng, WANG Yan. Progress of Permanent Scatterer Interferometry[J]. Geomatics and Information Science of Wuhan University, 2004, 29(8): 664–668. |
| [7] | BERARDINO R, FORNARO G, LANARI R, et al. A New Algorithm for Surface Deformation Monitoring Based on Small Baseline Differential SAR Interferograms[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(11): 2375–2383. DOI:10.1109/TGRS.2002.803792 |
| [8] | 邓琳, 刘国祥, 张瑞, 等. 多平台MC-SBAS长时序建模与形变提取方法[J]. 测绘学报, 2016, 45(2): 213–223. DENG Lin, LIU Guoxiang, ZHANG Rui, et al. A Multi-platform MC-SBAS Method for Extracting Long Gterm Ground Deformation[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(2): 213–223. DOI:10.11947/j.AGCS.2016.20140614 |
| [9] | 许文斌, 李志伟, 丁晓利, 等. 利用InSAR短基线技术估计洛杉矶地区的地表时序形变和含水层参数[J]. 地球物理学报, 2012, 55(2): 452–461. XU Wenbin, LI Zhiwei, DING Xiaoli, et al. Application of Small Baseline Subsets D-InSAR Technology to Estimate the Time Series Land Deformation and Aquifer Storage Coefficients of Los Angeles Area[J]. Chinese Journal of Geophysics, 2012, 55(2): 452–461. |
| [10] | PERISSIN D, WANG Teng. Repeat-pass SAR Interferometry with Partially Coherent Targets[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(1): 271–280. DOI:10.1109/TGRS.2011.2160644 |
| [11] | 张永红, 龚文瑜, 张继贤, 等. 基于SAR干涉点目标分析技术的城市地表形变监测[J]. 测绘学报, 2009, 38(6): 482–487. ZHANG Yonghong, GONG Wenyu, ZHANG Jixian, et al. Monitoring Urban Subsidence Based on SAR Interferometric Point Target Analysis[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(6): 482–487. DOI:10.3321/j.issn:1001-1595.2009.06.003 |
| [12] | 王明洲, 李陶, 江利明, 等. 地表形变监测的改进相干目标法[J]. 测绘学报, 2016, 45(1): 36–43. WANG Mingzhou, LI Tao, JIANG Liming, et al. An Improved Coherent Targets Technology for Monitoring Surface Deformation[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(1): 36–43. DOI:10.11947/j.AGCS.2016.20140617 |
| [13] | HOOPER A. A Multi-temporal InSAR Method Incorporating Both Persistent Scatterer and Small Baseline Approaches[J]. Geophysical Research Letters, 2008, 35(16): L16302. DOI:10.1029/2008GL034654 |
| [14] | HETLAND E A, MUSÉ P, SIMONS M, et al. Multiscale InSAR Time Series(MinTS) Analysis of Surface Deformation[J]. Journal of Geophysical Research:Solid Earth, 2012, 117(B2): B02404. |
| [15] | LOMBARDINI F. Differential Tomography:A New Framework for SAR Interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(1): 37–44. DOI:10.1109/TGRS.2004.838371 |
| [16] | SERAFINO F, SOLDOVIERI F,LOMBARDINI F, et al. Singular Value Decomposition Applied to 4D SAR Imaging[C]//Proceedings of International Geoscience and Remote Sensing Symposium. Seoul, Korea:IEEE, 2005:2701-2704. |
| [17] | 任笑真, 杨汝良. 一种基于逆问题的差分干涉SAR层析成像方法[J]. 电子与信息学报, 2010, 32(3): 582–586. REN Xiaozhen, YANG Ruliang. An Inverse Problem Based Approach for Differential SAR Tomography Imaging[J]. Journal of Electronics & Information Technology, 2010, 32(3): 582–586. |
| [18] | 孙希龙, 余安喜, 董臻, 等. 一种差分SAR层析高分辨成像方法[J]. 电子与信息学报, 2012, 34(2): 273–278. SUN Xilong, YU Anxi, DONG Zhen, et al. A High Resolution Imaging Method for Differential SAR Tomography[J]. Journal of Electronics & Information Technology, 2012, 34(2): 273–278. |
| [19] | ZHU Xiaoxiang, BAMLER R. Superresolving SAR Tomography for Multidimensional Imaging of Urban Areas:Compressive Sensing-based TomoSAR Inversion[J]. IEEE Signal Processing Magazine, 2014, 31(4): 51–58. DOI:10.1109/MSP.2014.2312098 |
| [20] | WANG Yuanyuan, ZHU Xiaoxiang, BAMLER R. An Efficient Tomographic Inversion Approach for Urban Mapping Using Meter Resolution SAR Image Stacks[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(7): 1250–1254. DOI:10.1109/LGRS.2013.2290833 |
| [21] | 廖明生, 魏恋欢, 汪紫芸, 等. 压缩感知在城区高分辨率SAR层析成像中的应用[J]. 雷达学报, 2015, 4(2): 123–129. LIAO Mingsheng, WEI Lianhuan, WANG Ziyun, et al. Compressive Sensing in High-resolution 3D SAR Tomography of Urban Scenarios[J]. Journal of Radars, 2015, 4(2): 123–129. |
| [22] | SIDDIQUE M A, HAJNSEK I, AERSOSPACE G, et al. Investigating the Combined Use of Differential SAR Tomography and PSI for Spatio-temporal Inversion[C]//Proceedings of 2015 Joint Urban Remote Sensing Event(JURSE). Lausanne, Switzerland:IEEE, 2015:1-4. |
| [23] | DONOHO D L. Compressed Sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289–1306. DOI:10.1109/TIT.2006.871582 |
| [24] | ZHU Xiaoxiang, BAMLER R. Super-resolution Power and Robustness of Compressive Sensing for Spectral Estimation with Application to Spaceborne Tomographic SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(1): 247–258. DOI:10.1109/TGRS.2011.2160183 |
| [25] | 张冰尘, 王万影, 毕辉, 等. 基于压缩多信号分类算法的森林区域极化SAR层析成像[J]. 电子与信息学报, 2015, 37(3): 625–630. ZHANG Bingchen, WANG Wanying, BI Hui, et al. Polarimetric SAR Tomography for Forested Areas Based on Compressive Multiple Signal Classification[J]. Journal of Electronics & Information Technology, 2015, 37(3): 625–630. |
| [26] | 王爱春, 向茂生. 基于块压缩感知的SAR层析成像方法[J]. 雷达学报, 2016, 5(1): 57–64. WANG Aichun, XIANG Maosheng. SAR Tomography Based on Block Compressive Sensing[J]. Journal of Radars, 2016, 5(1): 57–64. |
| [27] | ELDAR Y C, KUPPINGER P, BOLCSKEI H. Block-sparse Signals:Uncertainty Relations and Efficient Recovery[J]. IEEE Transactions on Signal Processing, 2010, 58(6): 3042–3054. DOI:10.1109/TSP.2010.2044837 |
| [28] | FU Yuli, LI Haifeng, ZHANG Qiheng, et al. Block-sparse Recovery via Redundant Block OMP[J]. Signal Processing, 2014, 97: 162–171. DOI:10.1016/j.sigpro.2013.10.030 |



