2. 北斗导航应用技术河南省协同创新中心, 河南 郑州 450001
2. BeiDou Navigation Technology Collaborative Innovation Center of Henan, Zhengzhou 450001, China
Swarm星座于2013年11月22日成功发射,是欧洲航天局(ESA)第4个“地球探测者”任务卫星[1]。该星座由A、B、C 3颗卫星组成,分别运行在2个轨道面上,其中Swarm-A和Swarm-C卫星为运行在高度450 km、87.4°极轨道的成对卫星;Swarm-B卫星运行在高度530 km、倾角88°的极轨道。Swarm星座主要用于地球核心、地幔、地壳、海洋、电离层科学研究以及地磁场反演[2]。高精度的轨道信息是其利用卫星载荷有效完成科学任务的前提条件,因此研究Swarm卫星精密定轨技术对其科学任务的实现与应用有十分重要的意义。
自从星载GPS测轨技术成功应用于TOPEX/Poseidon卫星[3]以来,该技术已成为低轨(low earth orbit,LEO)卫星精密定轨当前最有效的技术手段。特别是近年来,多颗LEO卫星相继发射,如CHAMP、GRACE、Jason等,在LEO卫星动力学模型及精密定轨方法等方面取得了突破性进展,使得利用星载GPS数据确定Swarm卫星轨道成为其首选技术手段[4-6]。但是,通过星载GPS接收机实际测定的是卫星信号发射天线到接收机信号接收天线间的距离,而在实际定轨时是以其天线参考点为基准。因此,天线相位中心的正确标定是实现Swarm卫星精密定轨的重要前提。GPS卫星端的天线相位中心可通过地面监测站精确标定[7-9],接收机端的天线相位中心虽然可以在发射之前对其进行精确标定,但是由于LEO卫星所处的空间环境与地面差异较大,接收机天线的特性会发生较大变化,且在轨飞行时易受近场多路径、环境多路径等因素的影响,地面的标定值与卫星实际在轨的相位中心差异较大,无法满足实际需求[10-12]。
长期以来,国内外学者对LEO卫星天线相位中心标定进行了大量的研究,并取得了丰硕的研究成果[10-13]。目前在轨标定方法主要有残差法和直接估计法两种方法。残差法最初由文献[14]提出使用约化动力学轨道的载波相位残差来弥补天线相位中心变化(phase center variation,PCV)误差,并被率先应用于Jason-1卫星天线相位中心标定。由于该方法简单易于实现,且能够实现分辨率为1°×1°的PCV估计,已被应用于多个LEO卫星,但是该方法容易受接收机钟差、模糊度等参数误差的影响,且需进行多次迭代,计算效率较低。直接估计法通过将PCV作为未知参数与轨道、经验力模型等参数一同估计[15],该方法优点是不受接收机钟差、模糊度等参数的影响,但是在多天PCV解综合时,需要用到每天解算的法方程以及轨道参数信息,对轨道等参数信息依赖性强,对计算机存储要求较高,进而影响计算效率[10]。
基于上述分析,在传统PCV综合方法的基础上,本文提出了一种改进的PCV综合方法。该方法只需存储前一天的PCV估值及其协方差信息,每增加一天新的观测,只需对前一天的PCV估值及其协方差阵进行适当的修正,即可得到包含当前观测信息的新PCV估值及其协方差阵。另外,该方法的优势还在于其每天都能够生成一组PCV估值(包含先前的观测信息),这样根据需求能够及时提供一组可靠的PCV估值,极大方便了用户PCV校正,提高了用户获取PCV信息的效率。最后,通过Swarm卫星实测数据对该方法的有效性进行了验证。
1 天线相位中心改正模型假定接收机PCV主要与观测GPS卫星的方位角α和高度角z相关,则由Swarm卫星接收机天线相位中心改正所引起的等效距离误差ΔρANT(α,z)[16]可表示为
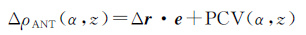 (1)
(1)
式中,Δr为接收机天线相位中心偏差(phase center offset,PCO),即平均天线相位中心(mean antenna phase center,MAPC)与天线相位中心参考点(antenna reference point,ARP)间的偏差矢量;PCV(α,z)表示PCV改正值;e为卫星信号入射方向的单位矢量,如图 1所示。在天线相位中心标定时,首先对PCO进行标定,将PCO参数引入观测方程中与轨道等参数同时求解,然后将多天解取平均即可得到PCO参数,下面重点讨论PCV参数估计方法。

|
| 图 1 Swarm卫星接收机天线相位中心校正示意图 Fig. 1 Sketch map of Swarm satellite receiver antenna phase center correction |
目前主要的PCV模型有球谐函数模型和分段线性函数模型两种模型[17],在实际估计过程中两种方法得到的PCV差异很小,但分段线性函数模型因更易于实现而被广泛使用。本文采用分段线性函数模型,即假设PCV模型由不同的网格点构成,每个格网均由4个待求PCV点组成,如图 2所示,落入该格网内的PCV值可通过以高度角和方位角为自变量的分段线性函数模型PCV(α,z)可表示为
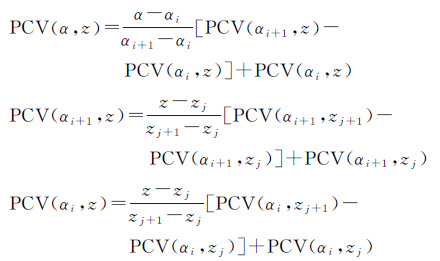 (2)
(2)
式中,PCV(αi,zj)为待估的天线相位中心变化参数(i=1,2,…,n;j=1,2,…,m),n和m的取值与PCV格网的分辨率有关。
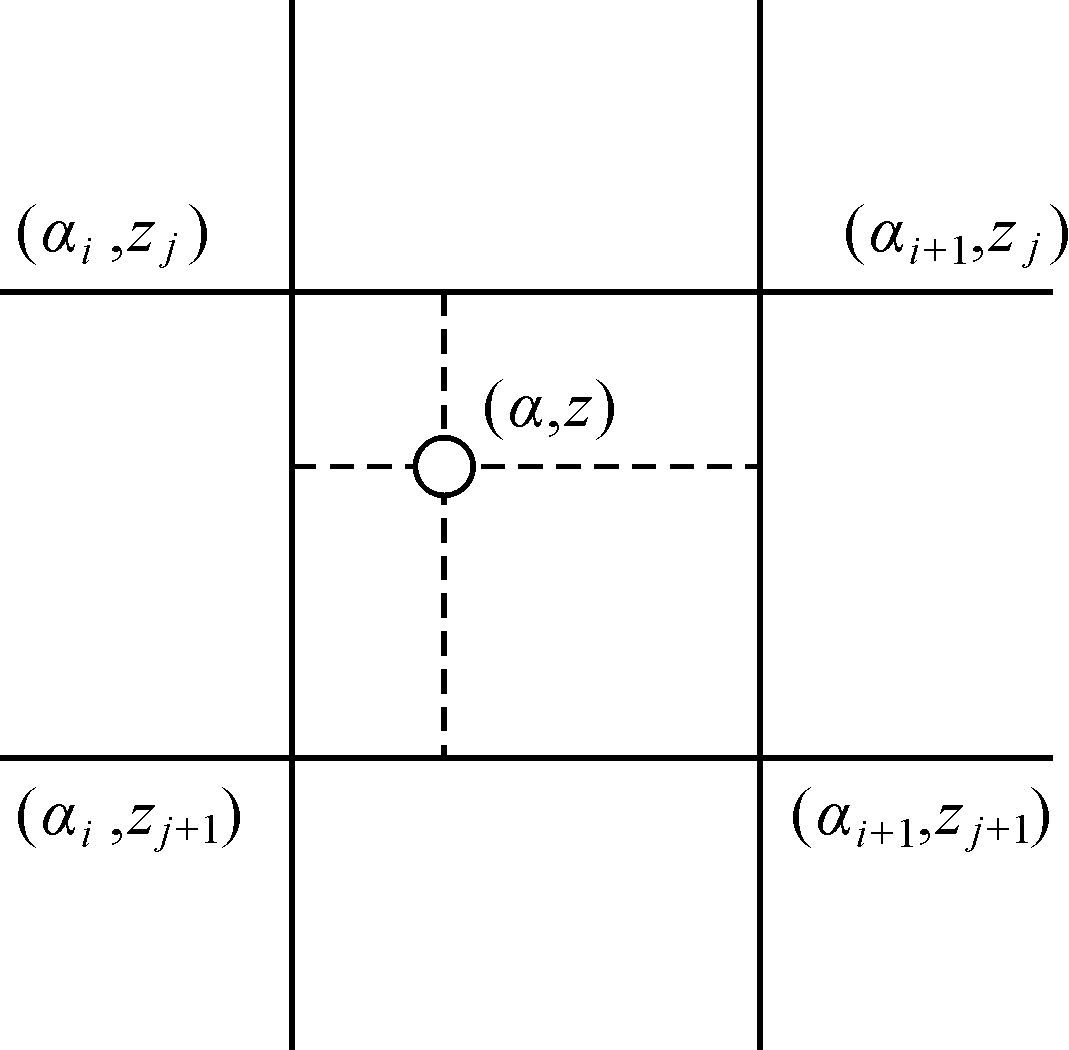
|
| 图 2 Swarm卫星PCV网格点线性插值示意图 Fig. 2 PCV grids linear interpolation for Swarm satellite |
2 多天PCV综合方法
Swarm卫星星载GPS接收机可同时获得L1和L2两个频点上的相位和码观测量,将两个频率间的相位和伪距观测值分别构成消电离层组合[18],其观测方程可表示为
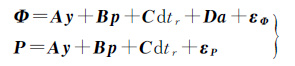 (3)
(3)
式中,2表示消电离层组合码观测向量;2表示消电离层组合载波相位观测向量;y2=[a e i Ω ω T0 a0,d … an,d]T表示待估的初始轨道参数和经验加速度参数向量;A=GA0为其系数矩阵,G和A0分别为状态转移矩阵和初始历元参数的系数矩阵;p表示PCV参数向量;B为相应的系数矩阵;dtr表示接收机钟差参数;C为相应的系数向量;a为消电离层组合模糊度参数向量;D为相应的系数矩阵;εP和εΦ分别表示码和相位的观测噪声。
在进行Swarm卫星PCV估计时,Swarm卫星钟差和模糊度等参数并不是用户所关心的参数,为了提高计算效率在参数估计之前对其进行预消除,详细推导见文献[19]。根据最小二乘原理,可得包含有轨道、经验加速度和PCV参数的法方程
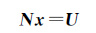 (4)
(4)
式中,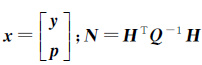
在利用单天解进行PCV综合处理的过程中,每个单天解所包含的PCV参数是相同的,但每个单天解轨道参数和经验加速度参数不同,设对n个连续单天解进行综合处理,根据方程式(4)可表示为
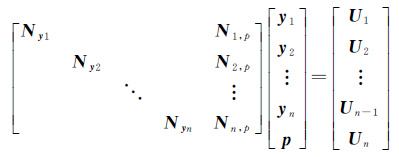 (5)
(5)
式中,yk(k=1,2,…,n)为每天的轨道和经验加速度参数;Nyk、Nk,p(k=1,2,…,n)为相应的法方程系数矩阵;Uk(k=1,2,…,n)为法方程自由项向量。
根据式(5)可知,只有计算完成所有天PCV后才能进行综合,且在每天计算完成后必须保存当天的法方程信息以及待估参数的先验信息,这势必会浪费大量的存储资源,同时也会降低PCV估计的效率。为此,本文提出了一种改进的PCV综合处理方法。
2.2 改进的PCV综合方法针对传统PCV综合方法存在的问题,将待估的轨道参数、经验加速度参数和PCV参数进行分类处理,减小PCV综合时对其他参数信息的依赖性,以提高PCV综合效率。设yk表示第k天法方程中轨道和经验加速度参数,pk表示第k天待估的PCV参数,根据方程(4),可得第k天的法方程
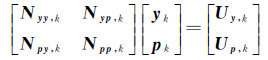 (6)
(6)
式中,Nyy,k表示轨道和经验参数对应的法方程矩阵;Npp,k表示PCV参数对应的法方程矩阵;Nyp,k和Npy,k表示轨道和经验参数与PCV参数间的互协方差阵;Uy,k和Up,k表示法方程相应的自由项向量。
在方程(6)的基础上,左右两边同时乘以[-Npy,k Nyy,k-1 I]并对方程进行整理可得
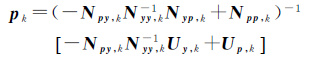 (7)
(7)
记${\tilde{N}}$k=(-Npy,k Nyy,k-1 Nyp,k+Npp,k),${\tilde{U}}$k=-Npy,k Nyy,k-1 Uy,k+Up,k,可得
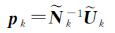 (8)
(8)
将第k-1天的PCV估值${\hat{p}}$k-1及相应的协方差矩阵Q${\hat{p}}$k-1=${\tilde{N}}$k-1-1作为第k天PCV估计的先验信息,根据文献[20]序贯最小二乘参数平差原理可得第k天的PCV估值${\hat{p}}$k及相应的协方差矩阵Q${\hat{p}}$k
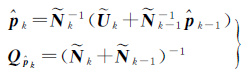 (9)
(9)
根据方程(9)即可获得多天PCV综合的递推公式
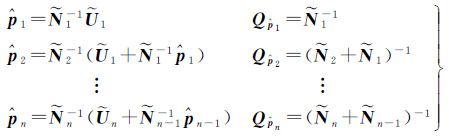 (10)
(10)
该方法充分利用了PCV前期的估计结果与当前观测样本,随着观测天数的增加,多余观测量逐步累积,可有效提高PCV精度及可靠性,且无需存储历史观测数据,无需对大维数的矩阵求逆即可获得与整体估计相同的最优解。利用2014年11月02至30日共29天星载GPS观测数据,估计了Swarm-A、B、C 3颗卫星消电离层组合观测量L3所对应的PCV。估计过程中PCV的分辨率设为5°×5°,并进行2次迭代求解。图 3给出了A、B、C 3颗Swarm卫星的PCV估计结果。
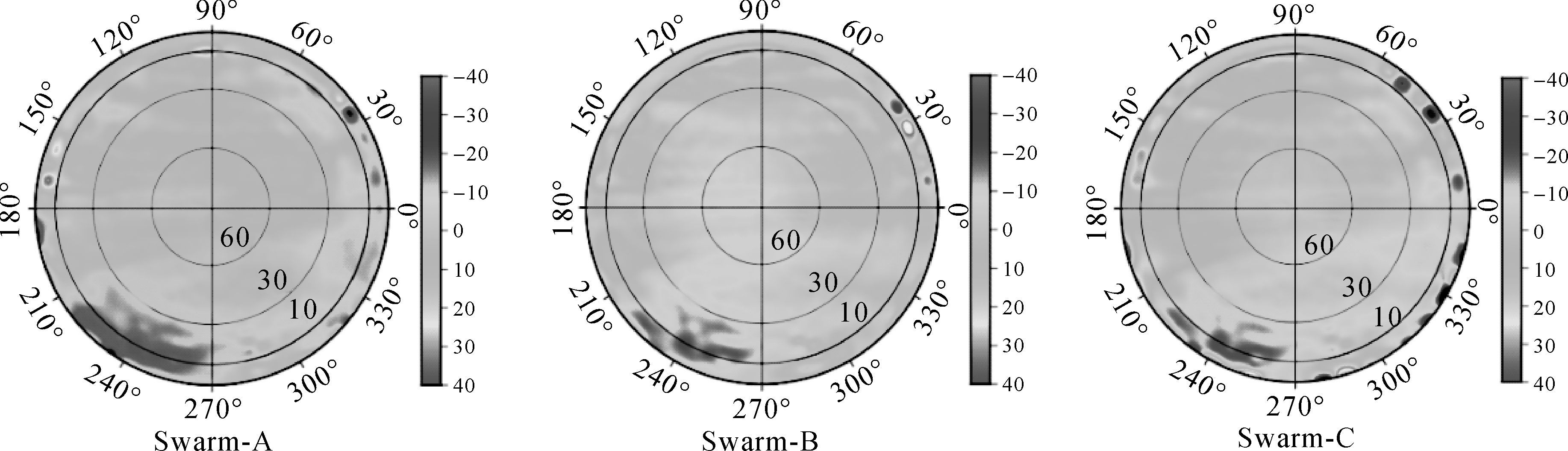
|
| 图 3 Swarm卫星PCV估计结果(单位:mm) Fig. 3 Results of PCV for Swarm satellites (mm) |
从图 3可以看出,3颗Swarm卫星的PCV非常相似,整体上PCV值的大小在1 cm左右,当高度角低于10°时,PCV的值较大,这一方面是由于Swarm卫星低于10°高度角观测量较少,另一方面是因为低高度角的观测数据质量较低。根据上述获得的PCV模型值,采用线性插值方法即可获得对应方位角和天顶距的PCV值。结合PCO信息,利用式(1)即可实现相应的天线相位中心校正。
3 试验结果及分析为进一步验证PCV综合算法的有效性以及PCV改正对Swarm卫星精密定轨的影响,本文采用Swarm-A、B、C卫星2014年11月02日至30日共29天的星载GPS码和相位观测数据,进行约化动力学精密定轨实验。在试验过程中,GPS卫星的PCO和PCV来自于igs08.atx[21],其中GPS卫星天底角在0°~14°的PCV值由地面观测量处理得到,天底角在15°~17°部分的PCV值由CODE等分析中心使用多颗LEO卫星数据联合求解获得[22]。估计PCV过程中,Swarm卫星PCV的初值设为0。另外,为了更好地吸收太阳光压、大气阻力以及其他力学因素的影响,试验采用了分段线性经验加速度模型,该模型需估计3个初始常数加速度参数,并每隔一定时间间隔再估计一组经验加速度参数。表 1给出了Swarm精密定轨涉及的动力学模型、观测模型和待估参数详细情况。
| 类别 | 详细描述 |
| 观测量 | 消电离层组合L3,5 s采样间隔 |
| 高度截止角 | 0° |
| GPS卫星轨道及钟差 | CODE最终轨道及5 s采样间隔钟差产品 |
| 地球重力场模型 | EGM2008 120×120 |
| N体摄动力 | 太阳、月球以及其他行星摄动(JPL DE405) |
| 潮汐摄动 | 固体潮汐和极潮(IERS 2010);海洋潮汐(FES2004) |
| 太阳光压和大气阻力 | 通过经验加速度参数吸收 |
| 卫星轨道状态参数 | 6个初始轨道根数+3个常数经验加速度参数 |
| 接收机钟差 | 伪距估计+高斯白噪声,参数估计前对其进行预消除 |
| 载波相位模糊度 | 浮点解,参数估计前对其进行预消除 |
| 经验加速度 | 每6 min估计一组 |
| GPS卫星天线相位中心改正 | igs08.atx |
3.1 不同PCV综合方法对比分析
为了便于对比分析,试验中采用以下两种方案进行PCV综合处理。由于改进的PCV综合方法与传统PCV综合方法的主要差异是参数的求解策略,各参数之间的相关性及其约束条件等都未改变,因此所得PCV估计结果与传统PCV综合方法完全相同。这里仅比较两种方法计算耗时和所需存储空间情况,以评估改进的PCV综合方法的有效性。这里计算耗时统计的是两种PCV综合方法在综合相同天数PCV参数所需要的时间,试验采用CPU为Intel i5、内存为4 GB的普通计算机进行数据处理。
方案1 采用传统的PCV综合方法进行PCV估计;
方案2 采用改进的PCV综合方法进行PCV估计。
图 4给出了上述两种方案PCV综合计算耗时和所需存储空间的对比情况。

|
| 图 4 Swarm卫星PCV综合计算耗时和所需存储空间的对比情况 Fig. 4 The contrast of Swarm satellite PCV computing time and required storage space |
由图 4结果可见,改进的PCV综合方法在计算效率上明显优于传统PCV综合方法,尤其是随着PCV综合天数的增加,传统PCV综合方法的估计参数数量累积增加,相应的计算耗时迅速增大,而改进的PCV综合方法却依然能够保持较高的计算效率。在所需存储空间方面,改进的PCV综合方法同样优于传统PCV综合方法,每天仅需存储叠加后的一个PCV先验值及其协方差矩阵,所需存储空间仅为几MB,而传统方法需要存储每天的PCV和轨道先验信息以及它们所对应的法方程,所需存储空间随PCV综合天数的增加呈线性增长。
3.2 与外部精密轨道比较ESA提供了Swarm卫星运动学和约化动力学两种标准轨道供用户使用,这两种标准轨道均由Delft大学通过GHOST软件处理生成,其约化动力学轨道精度优于2 cm,运动学轨道精度约为4~5 cm[23-24]。将ESA公布的Swarm卫星约化动力学轨道作为参考轨道,对本文的Swarm卫星约化动力学定轨结果进行精度评定。径向、切向和法向各分量的RMS计算方法如下
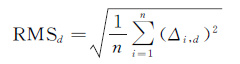 (11)
(11)
式中,Δi,d表示Swarm约化动力学定轨结果与参考轨道在径向、切向和法向的残差;n表示历元数。图 5给出了Swarm卫星约化动力学轨道与参考轨道在径向、切向和法向对比的RMS序列,表 2给出了采用PCV前后Swarm轨道与参考轨道差异的RMS均值统计情况。
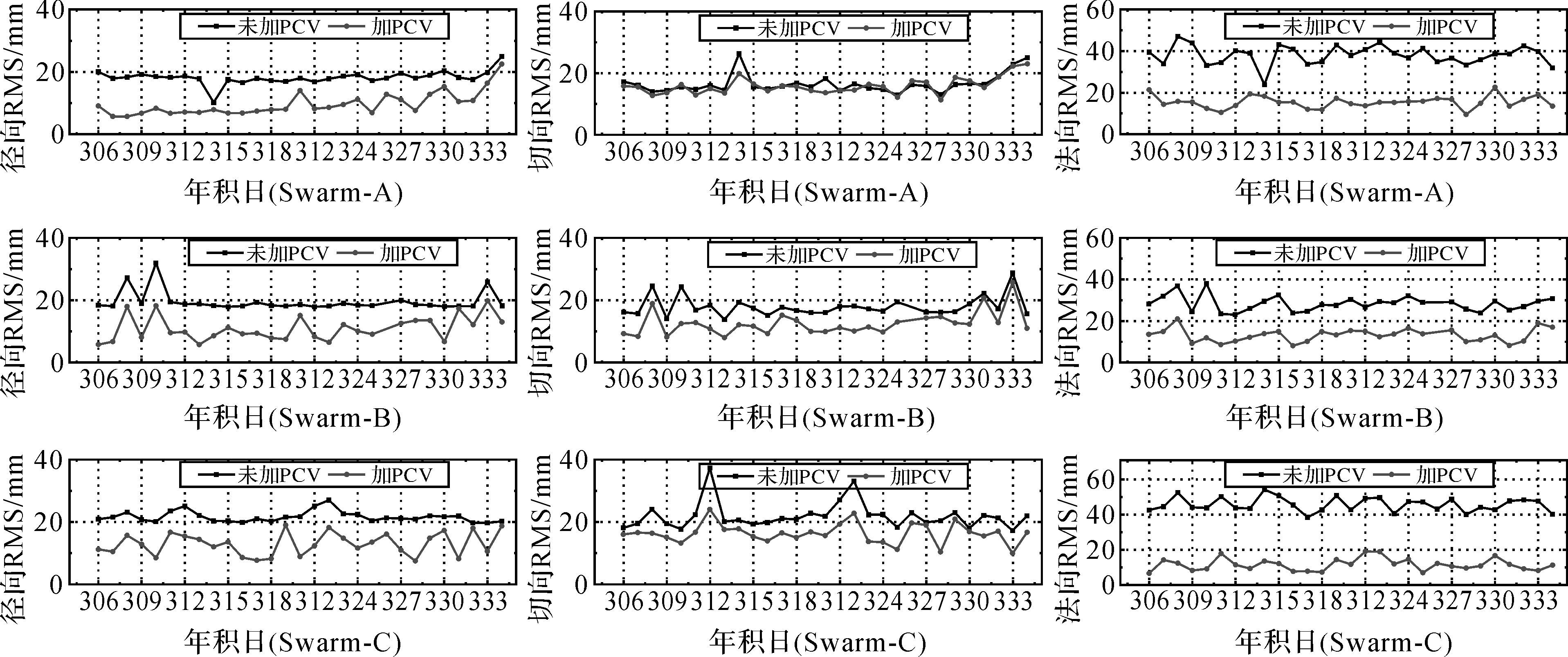
|
| 图 5 采用PCV前后Swarm轨道与参考轨道差异的RMS Fig. 5 The RMS of Swarm orbit and the reference orbit before and after PCV correction |
| mm | |||||||||||
| 卫星 | 径向(R) | 切向(t) | 法向(N) | 三维(3D) | |||||||
| 未加PCV | 加PCV | 未加PCV | 加PCV | 未加PCV | 加PCV | 未加PCV | 加PCV | ||||
| A | 18.4 | 10.2 | 17.7 | 17.2 | 38.0 | 15.8 | 45.8 | 25.5 | |||
| B | 19.5 | 11.0 | 18.0 | 12.1 | 28.4 | 13.1 | 38.9 | 21.0 | |||
| C | 21.7 | 13.0 | 21.9 | 16.3 | 45.7 | 11.6 | 55.1 | 23.9 | |||
(1) 对比PCV改正前后,Swarm-A、B、C 3颗卫星的各个方向的定轨精度均有不同程度的提高,尤其是对轨道法向的精度改善最为明显,法向RMS分别改进了22.2 mm、15.3 mm、34.2 mm,平均提高了23.9 mm。上述结果与Bock等采用残差法进行GOCE卫星PCV估计的实验结果相类似[12]。
(2) 对比PCV改正前后,PCV改正对轨道径向和切向精度改善程度相对较小,其中,A、B、C卫星的径向RMS分别改进了8.2 mm、8.5 mm和8.7 mm,定轨精度平均提高8.5 mm;切向RMS分别改进了0.5 mm、5.9 mm和5.6 mm,定轨精度平均提高4 mm。径向和切向精度改善程度相对较小,一方面主要是因为未被模型化的观测误差对Swarm卫星轨道径向的影响较大,而切向较弱的几何约束以及大气阻力等模型误差的也会影响到PCV的精度;另一方面可能是因为Swarm卫星本身PCV在切向方向较小。
(3) 整体上,进行PCV改正后,Swarm卫星各个方向的定轨精度都优于20 mm,三维定轨精度优于30 mm,PCV改正对Swarm卫星精密定轨的最大影响约为20 mm。
4 结论本文针对传统PCV综合方法的不完善,提出了一种改进的PCV综合方法。该方法通过递推的方式,既不需要存储多天的法方程及先验信息,又能及时提供PCV信息,从而提高了PCV校正的效率,为实现LEO卫星PCV参数估计法的快速求解提供了一种新的途径。利用Swarm卫星星载GPS数据分析表明:
(1) 采用改进的PCV综合方法,能够有效提高PCV校正的效率,降低存储空间的需求。随着PCV综合天数的增加,传统PCV综合方法的估计参数数量累积增加,相应的计算耗时迅速增大,而改进的PCV综合方法却依然能够保持较高的计算效率。在所需存储空间方面,改进的PCV综合方法同样优于传统PCV综合方法,改进的综合方法每天仅需存储叠加后的一个PCV先验值及其协方差矩阵,所需存储空间仅为几个MB,而传统方法需要存储每天的PCV和轨道先验信息以及它们所对应的法方程,所需存储空间随PCV综合天数的增加呈线性增长。
(2) 通过与外部精密轨道比较表明,进行PCV改正后,Swarm卫星轨道径向、切向和法向的精度均有不同程度的提高,尤其是对法向精度改善最为明显,平均提高约23.3 mm,轨道径向精度平均提高8.5 mm,轨道切向精度平均提高4 mm。径向和切向精度改善程度相对较小,一方面主要是因为未模型化的相位观测误差对Swarm卫星轨道径向的影响较大,而切向较弱的几何约束以及大气阻力等模型误差的也会影响到PCV的精度,另一方面可能是因为Swarm卫星本身PCV在切向方向较小。
| [1] | 付郁, 云成. ESA首个磁场监测卫星星座"蜂群"[J]. 卫星应用, 2014(3): 73. FU Yu, YUN Cheng. ESA's First Field Monitoring Satellite Constellation[J]. Satellite Applications, 2014(3): 73. |
| [2] | OLSEN N, FRIIS-CHRISTENSEN E, FLOBERGHAGEN R, et al. The Swarm Satellite Constellation Application and Research Facility (SCARF) and Swarm Data Products[J]. Earth, Planets and Space, 2013, 65(11): 1189–1200. DOI:10.5047/eps.2013.07.001 |
| [3] | TAPLEY B D, RIES J C, DAVIS G W, et al. Precision Orbit Determination for TOPEX/Poseidon[J]. Journal of Geophysical Research:Oceans (1978-2012), 1994, 99(C12): 24383–24404. DOI:10.1029/94JC01645 |
| [4] | HAINES B, BERTIGER W, DESAI S, et al. Initial Orbit Determination Results for Jason-1:Towards a 1 cm Orbit[J]. Navigation, 2003, 50(3): 171–180. DOI:10.1002/navi.2003.50.issue-3 |
| [5] | ŠVEHLAD, ROTHACHERM. Kinematic and Reduced-dynamic Precise Orbit Determination of Low Earth Orbiters[J]. Advances in Geosciences, 2003, 1: 47–56. |
| [6] | KANG Zhigui, TAPLEY B, BETTADPUR S, et al. Precise Orbit Determination for the GRACE Mission Using only GPS Data[J]. Journal of Geodesy, 2006, 80(6): 322–331. DOI:10.1007/s00190-006-0073-5 |
| [7] | SCHMID R, STEIGENBERGER P, GENDT G, et al. Generation of a Consistent Absolute Phase-center Correction Model for GPS Receiver and Satellite Antennas[J]. Journal of Geodesy, 2007, 81(12): 781–798. DOI:10.1007/s00190-007-0148-y |
| [8] | 胡志刚, 赵齐乐, 郭靖, 等. GPS天线相位中心校正对低轨卫星精密定轨的影响研究[J]. 测绘学报, 2011, 40(S): 34–38. HU Zhigang, ZHAO Qile, GUO Jing, et al. Research on Impact of GPS Phase Center Variation on Precise Orbit Determination of Low Earth Orbit Satellite[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(S): 34–38. |
| [9] | 马洋, 欧吉坤, 袁运斌, 等. 导航卫星天线相位中心变化估计及对LEO精密定轨影响[J]. 武汉大学学报(信息科学版), 2015, 40(7): 894–900. MA Yang, OU Jikun, YUAN Yunbin, et al. Estimation of GPS Antenna Phase Center Variation and Its Effect on Precise Orbit Determination of LEOs[J]. Geomatics and Information Science of Wuhan University, 2015, 40(7): 894–900. |
| [10] | JÄGGI A, DACH R, MONTENBRUCK O, et al. Phase Center Modeling for LEO GPS Receiver Antennas and Its Impact on Precise Orbit Determination[J]. Journal of Geodesy, 2009, 83(12): 1145–1162. DOI:10.1007/s00190-009-0333-2 |
| [11] | MONTENBRUCK O, GARCIA-FERNANDEZ M, YOON Y, et al. Antenna Phase Center Calibration for Precise Positioning of LEO Satellites[J]. GPS Solutions, 2009, 13(1): 23–34. DOI:10.1007/s10291-008-0094-z |
| [12] | BOCK H, JÄGGI A, MEYER U, et al. Impact of GPS Antenna Phase Center Variations on Precise Orbits of the GOCE satelLite[J]. Advances in Space Research, 2011, 47(11): 1885–1893. DOI:10.1016/j.asr.2011.01.017 |
| [13] | 马洋, 欧吉坤, 袁运斌. JASON-2天线相位中心变化估计及1cm精密轨道确定[J]. 大地测量与地球动力学, 2015, 35(2): 186–189. MA Yang, OU Jikun, YUAN Yunbin. Antenna Phase Center Variation Estimation of JASON-2 and Its Precise Orbit Determination Towards 1cm[J]. Journal of Geodesy and Geodynamics, 2015, 35(2): 186–189. |
| [14] | HAINES B, BAR-SEVER Y, BERTIGER W, et al. One-centimeter Orbit Determination for Jason-1:New GPS-based Strategies[J]. Marine Geodesy, 2004, 27(1-2): 299–318. DOI:10.1080/01490410490465300 |
| [15] | LUTHCKE S B, ZELENSKY N P, ROWLANDS D D, et al. The 1-centimeter orbit:Jason-1 Precision Orbit Determination Using GPS, SLR, DORIS, and Altimeter Data[J]. Marine Geodesy, 2003, 26(3-4): 399–421. |
| [16] | DACH R, LUTZ S, WALSER P, et al. Bernese GNSS Software Version 5.2[M]. Switzerland: Astronomical Institute, University of Bern, 2015. |
| [17] | SCHMID R, ROTHACHER M, THALLER D, et al. Absolute Phase Center Corrections of Satellite and Receiver Antennas[J]. GPS Solutions, 2005, 9(4): 283–293. DOI:10.1007/s10291-005-0134-x |
| [18] | JÄGGI A.Pseudo-stochastic Orbit Modelling of Low Earth Satellites Using the Global Positioning System[D]. Switzerland:University of Bern, 2007. |
| [19] | 田英国, 郝金明, 刘伟平, 等. 星载GNSS低轨卫星精密定轨快速解算方法[J]. 大地测量与地球动力学, 2014, 34(1): 157–160. TIAN Yingguo, HAO Jinming, LIU Weiping, et al. A Rapid Solution Method on Precise Orbit Determination of LEOs Using GNSS[J]. Journal of Geodesy and Geodynamics, 2014, 34(1): 157–160. |
| [20] | 杨元喜. 自适应动态导航定位[M]. 北京: 测绘出版社, 2006. YANG Yuanxi. Adaptive Navigation and Kinematic Positioning[M]. Beijing: Surveying and Mapping Press, 2006. |
| [21] | KHACHIKYAN R. IGS08_1745. atx:Update Including GPS Satellite Antenna PCV Extension[R]. IGS MAIL 6786. Pasadena:IGS Central Bureau, 2013. |
| [22] | JÄGGI A, DILSSNER F, SCHMID R, et al. Extension of the GPS Satellite Antenna Patterns to NADIR Angles Beyond 14°[C]//IGS Workshop 2012. Olsztyn, Poland:EGU, 2012. |
| [23] | VAN DEN IJSSEL J, ENCARNAÇÃO J, DOORNBOS E, et al. Precise Science Orbits for the Swarm Satellite Constellation[J]. Advances in Space Research, 2015, 56(6): 1042–1055. DOI:10.1016/j.asr.2015.06.002 |
| [24] | JÄGGI A, DAHLE C, ARNOLD D, et al. Swarm Kinematic Orbits and Gravity Fields from 18 Months of GPS Data[J]. Advances in Space Research, 2016, 57(1): 218–233. DOI:10.1016/j.asr.2015.10.035 |


