变量间的关系包括确定性的函数关系与非确定性的相关关系[1]。回归分析是处理随机变量间相关关系的数学工具,目的是根据自变量和因变量以及关于变量的一些合理假设建立变量间的统计关系,即(线性或者非线性的)函数模型[2-4]。由于变量间的非线性关系往往可以通过变量变换等转化为线性关系,因此线性回归模型是回归分析中最常用的模型。
建立回归模型的最终目的是进行自变量的控制或因变量的预测。通常,先通过回归分析建立回归模型,然后根据回归模型控制自变量或者预测因变量,因此回归分析是模型应用的基础。传统的回归分析认为只有因变量含有观测误差(下文中都指随机误差),采用最小二乘求解回归系数。然而,实际应用中的自变量和因变量都来源于观测,不可避免地都含有观测误差,如果回归分析时忽略自变量的观测误差,则会影响求解的回归系数。对此,同时顾及自变量和因变量观测误差的(加权)整体最小二乘理论及其方法近年来得到了广泛的研究与应用[5-11],文献[12-13]在回归分析时还进一步考虑了自变量和因变量观测误差间的相关性并获得了合理的回归系数。
尽管采用同时顾及自变量和因变量观测误差及其相关性的回归分析方法能建立合理的回归模型,但采用该模型预测因变量时,现有方法依然忽略了待预测自变量的观测误差,从而影响了模型因变量的预测效果。为此,本文提出无缝线性回归和预测模型,该模型将回归系数解算与因变量预测联合处理,除了考虑解算回归系数时的自变量和因变量观测误差及其相关性,还严格考虑待预测自变量的观测误差。无缝线性回归和预测模型的本质是在求解回归系数的同时估计变量的观测误差;再根据变量观测误差间的相关性对待预测自变量的观测误差进行估计并改正,进而提高模型因变量的预测效果。
1 无缝线性回归和预测模型 1.1 自变量观测误差对模型预测的影响根据给定的自变量观测值预测对应的因变量是回归模型的主要应用。利用回归系数β预测自变量观测值AP对应的因变量yP有
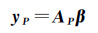 (1)
(1)
式(1)忽略了AP的观测误差EAP。若考虑EAP,则有
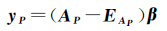 (2)
(2)
由于AP通常来自实际观测且不可避免地含有观测误差,因此考虑EAP的式(2)较式(1)更为合理。从式(2)可以看出,提高模型预测效果的关键是对EAP的有效处理和对回归系数β的合理求解。记yP的真值为yP,回归系数估值为${\hat{\beta }}$,式(1)和式(2)的预测值分别为${\hat{y}}$P,WO和${\hat{y}}$P,W,则预测值的均方误差分别为MSEWO=E((${\hat{y}}$P,WO-yP)(${\hat{y}}$P,WO-yP)T)和MSEW=E((${\hat{y}}$P,W-yP)(${\hat{y}}$P,W-yP)T),其中,E(·)表示期望算子。均方误差的差异为
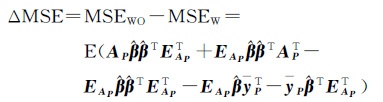 (3)
(3)
当EAP=0时,差异ΔMSE=0;但事实上,通常EAP≠0,即差异ΔMSE≠0且受EAP、${\hat{\beta }}$和AP等多因素影响。可以肯定的是,考虑EAP的式(2)得到的均方误差MSEw更能真实地反映模型的实际预测效果。
1.2 无缝线性回归与预测模型对于未知的观测误差EAP,如果能对其进行估计(记估值为${\tilde{E}}$AP)并改正,利用误差改正后的观测值${\tilde{A}}$P=AP-${\tilde{E}}$AP预测因变量,则可在一定程度上提高模型的预测效果。以同时顾及自变量和因变量观测误差及其相关性的线性回归分析模型[12-13]为基础,联合预测模型式(2)有
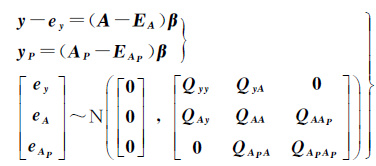 (4)
(4)
式中,第1个方程是顾及自变量和因变量观测误差及误差相关性的回归模型,第2个方程是顾及待预测自变量观测误差的预测模型。向量y=[y1y2…ym]T由m个已知因变量观测值构成;设每个因变量对应n个自变量和1个常数项,则未知回归系数β=[β0 β1…βn]T;矩阵A=[A1A2…Am]T,其中Ai=[1 X1i…Xni]T已知;向量yP=[y1y2…yk]T由k个未知因变量构成;已知矩阵AP=[AP,1AP,2…AP,k]T,其中AP,i=[1XP,1i…XP,ni]T;向量ey和矩阵EA分别为y和A的观测误差。向量EA=vec(EA),EAP=vec(EAP),运算符vec(·)为矩阵向量化算子。正定矩阵Qyy为ey的方差阵;非负定矩阵QAA和QAPAP分别是EA和EAP的方差阵;QAy和QyA是ey和EA的协方差矩阵,且QAy=QyAT;QAAP和QAPA是EA和EAP协方差阵,且QAAP=QAPAT。为了简单起见,式(4)忽略回归分析中的因变量和待预测自变量观测误差之间的相关特性。式(4)将回归分析和模型预测联合处理,并严格考虑了所有变量的观测误差及误差特性,因此称其为无缝线性回归和预测模型。
通常,回归模型中包含常数项,因而模型系数矩阵A和AP的第1列通常为常数,即矩阵EA和EAP的第1列都为0。对矩阵作如下变换
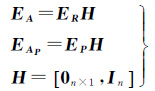 (5)
(5)
则新矩阵ER和EP中的所有元素不为0。根据向量化算子和克罗内克积运算法则[14-15]有
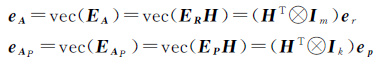
又根据等式EAβ=(βT⊗Im)eA=(βTHT⊗Im)er和EAPβ=(βT⊗Ik)eAP=(βTHT⊗Ik)ep将式(4)等价表达为
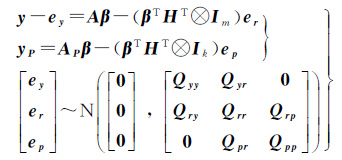 (6)
(6)
采用最小二乘准则求解式(6),有
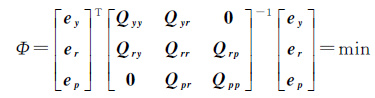 (7)
(7)
对应的拉格朗日条件函数为
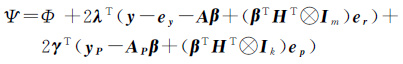 (8)
(8)
式中,λ和γ是拉格朗日乘常数向量。对各未知量求偏导数并令其等于0,则
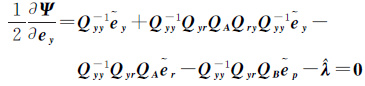 (9a)
(9a)
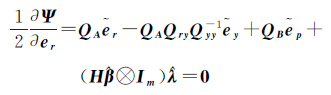 (9b)
(9b)
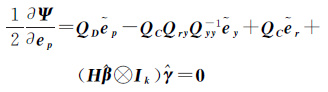 (9c)
(9c)
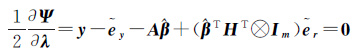 (9d)
(9d)
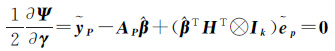 (9e)
(9e)
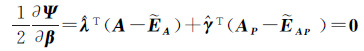 (9f)
(9f)
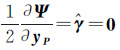 (9g)
(9g)
式中,QA=Qr|y-1+Qr|y-1QrpQp|ry-1QprQr|y-1;QB=-Qr|y-1QrpQp|ry-1;QC=-Qp|ry-1QprQr|y-1=QBT;QD=Qp|ry-1;Qp|ry=Qpp-QprQr|y-1Qrp;Qr|y=Qrr-QryQyy-1Qyr。给(9b)两边同乘以Qyy-1Qyr并与(9a)相加得
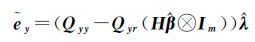 (10)
(10)
由(9c)和(9g)得
 (11)
(11)
将式(10)、式(11)代入(9b)得
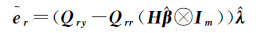 (12)
(12)
由(9d)可得
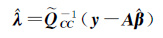 (13)
(13)
式中,正定矩阵${\tilde{Q}}$CC=Qyy-QyrH${\hat{\beta }}$⊗Im-${\hat{\beta }}$THT⊗ImQry+${\hat{\beta }}$THT⊗ImQrrH${\hat{\beta }}$⊗Im。显然,正定矩阵${\tilde{Q}}$CC是向量EC=ey-EA${\hat{\beta }}$的协方差阵。由(9f)得
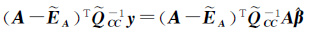 (14)
(14)
非线性方程式(14)的解即为回归系数估值${\hat{\beta }}$。
1.3 迭代公式对于非线性方程式(14),设计迭代算法求解回归系数估值${\hat{\beta }}$。令${\tilde{A}}$=A-${\tilde{E}}$A,将式(14)两边同时减去${\tilde{A}}$T${\tilde{Q}}$CC-1${\tilde{E}}$A${\hat{\beta }}$,得[16]
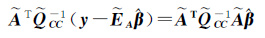 (15)
(15)
则回归系数估值为
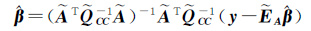 (16)
(16)
将式(16)中的${\tilde{E}}$A替换成A-${\tilde{A}}$,并忽略${\tilde{A}}$和${\hat{\beta }}$的随机性,则回归系数${\hat{\beta }}$的协方差阵为[7]
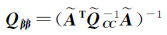 (17)
(17)
单位权方差估值为
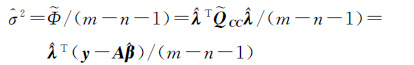 (18)
(18)
比较发现,无缝模型式(4)获得的回归系数估值及其协方差阵、单位权方差估值与文献[12]的结果相同,说明模型式(4)中的预测方程不影响回归模型的建立。
将式(13)分别代入式(10)—式(12),得各类变量的观测误差估值为
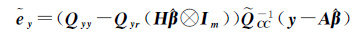 (19a)
(19a)
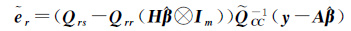 (19b)
(19b)
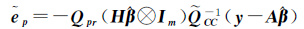 (19c)
(19c)
根据误差传播定理导出它们的协方差阵为
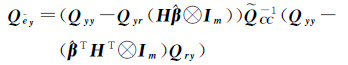 (20a)
(20a)
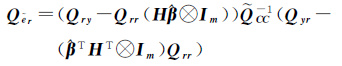 (20b)
(20b)
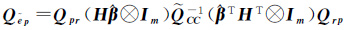 (20c)
(20c)
设观测误差EA和EAP的相关系数为ρpr,则Qpr=ρprQppCkn,mnQrr(其中矩阵ρprCkn,mn描述了EAP和EA的相关性),估值${\tilde{e}}$p及其协方差阵Q${\tilde{e}}$P分别为
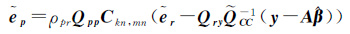 (21a)
(21a)
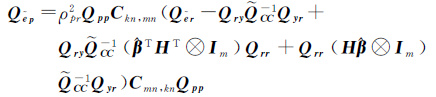 (21b)
(21b)
显然,${\tilde{e}}$P和Q${\tilde{e}}$P分别受${\tilde{e}}$r和Q${\tilde{e}}$r的影响,影响程度取决于相关系数 ρpr和方差阵Qpp。当相关系数ρpr=0时,估值${\tilde{e}}$p=0,即式(4)无法估计观测误差EAP。
1.4 几种回归和预测模型的比较无缝线性回归和预测模型式(4)严格考虑了所有变量的观测误差,若QAPAP=0,则无需估计并修正观测误差EAP;若QAAP=0,则无法估计EAP。此时式(4)的预测方程与式(1)相同,相应的回归模型为
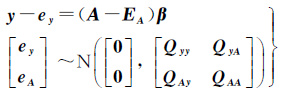 (22)
(22)
该模型即文献[12-13, 17-20]中的回归模型,此时式(4)与式(22)的回归分析和预测效果都相同;但当AP的确包含观测误差时,采用无缝模型式(4)能有效地估计并修正该误差,从而得到更加合理的预测结果。
若QAAP=0且QAy=0,则式(4)的预测方程与式(1)相同,对应的回归模型为
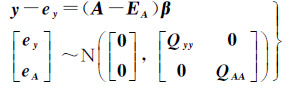 (23)
(23)
对加权总体最小二乘(WTLS)的大多研究[5-8]是针对式(23)的,此时${\tilde{Q}}$CC=Qyy+(${\hat{\beta }}$THT⊗Im)Qrr(H${\hat{\beta }}$⊗Im)。注意,式(23)与式(22)的区别是随机模型不同,因此两者获得的回归系数和预测结果也不同。
若QAAP=0且QAA=0(即EA=0),则式(4)的预测方程与式(1)相同,相应的回归模型为
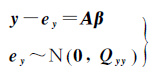 (24)
(24)
该模型常采用最小二乘求解[21]。此时,回归系数的估值及其协方差阵退化为${\hat{\beta }}$=(ATQyy-1A)-1ATQyy-1y 和Q${\hat{\beta }}$ ${\hat{\beta }}$=(ATQyy-1A)-1。
综上所述,现有的几种回归和预测模型都是式(4)的特例。因此,顾及所有变量观测误差及误差特性的无缝线性回归和预测模型式(4)更具一般性。
1.5 预测值偏差最小二乘解${\hat{\beta }}$LS无偏[21],相应的预测值${\hat{y}}$P,LS也无偏,即E(${\hat{y}}$P,LS)-P=0。${\hat{y}}$P,LS的均方误差为
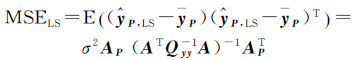 (25)
(25)
式中,σ2为单位权方差。无缝模型式(4)估计并改正观测误差EAP,利用误差改正后的自变量${\tilde{A}}$P预测因变量,因此将观测误差估值(19c)代入预测方程可得因变量预测值为
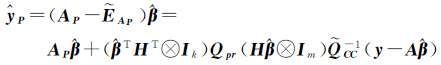 (26)
(26)
该预测值已经在一定程度上扣除了EAP的影响。由于式(4)是非线性模型,求得的回归系数${\hat{\beta }}$必然有偏,记其偏差为 b${\hat{\beta }}$=E${\hat{\beta }}$-β。则预测值${\hat{y}}$P对应的偏差为
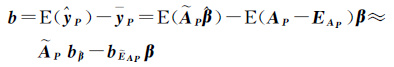 (27)
(27)
式中,b${\bar{E}}$AP为估值${\tilde{E}}$AP的偏差。预测值${\hat{y}}$P的均方误差为
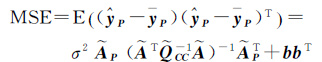 (28)
(28)
对比均方误差式(28)和式(25)可发现,由于预测值${\hat{y}}$P有偏(回归系数有偏),其均方误差由预测值的方差和偏差两部分组成,且受回归系数${\hat{\beta }}$(偏差 b${\hat{\beta }}$)和观测误差估值${\tilde{E}}$AP(偏差b${\bar{E}}$AP)等多种因素的影响。
2 试验与分析设计模拟试验进行一元线性回归与预测,分别采用无缝线性回归与预测模型和现有几种线性回归模型进行回归分析和因变量预测,通过比较试验结果,分析无缝线性回归与预测模型的应用效果。
2.1 试验设计设自变量x和因变量y以及待预测自变量xP服从正态分布
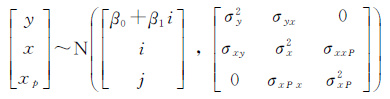 (29)
(29)
式中,i和j为整数;σx2、σy2、σxp2为各变量观测误差的方差;σxy=σyx=ρxyσxσy,σxxp=σxpx=ρxxpσxσxp为变量观测误差的协方差。由于随机模型满足非负定条件,因此|ρxy|≤1,|ρxxp|≤1且 ρxy2+ρxxp2≤1。通过调整σx、σy、σxp及相关系数ρxy和 ρxxp可改变观测值的误差特性。给定整数区间[0,1,…,10],对区间内任意i模拟N个点,因此共有m=11×N个观测点用于建立回归模型。不失一般性,取j=i+11,即将自变量x向右平移11作为待预测自变量xP,因此共有m个待预测因变量。对应于无缝模型式(4)有:y=[y1y2…ym]T;A=[emx]且x=[x1x2…xm]T,em为元素都为1的列向量;β=[β0β1]T;AP=[emxp]且xp=[xp,1xp,2…xp,m]T;Qyy=σy2Im;Qxx=σx2Im;Qxy=Qyx=σxyIm;Qxpxp=σxp2Im;Qxxp=Qxpx=σxxpIm,Im为维数为m的单位阵。
根据回归系数的求解和因变量的预测设计4种模型,如表 1所示。其中,ETLS(extended total least squares)模型的求解参考文献[12—13],GTLS(general total least squares)模型即本文提出的无缝线性回归与预测模型,按2.3节的算法进行求解。LS只考虑因变量观测误差ey,是常用的回归分析和预测模型;WTLS同时考虑了ey和EA,但模型预测时忽略了EAP;ETLS不仅考虑了ey和EA,还考虑了它们的相关性QyA,但预测因变量时依然忽略了EAP。本文提出的无缝GTLS严格考虑了所有变量观测误差ey,EA和EAP以及它们之间的相关性QAy及QAAP。按预测值是否有偏又能将4种模型分为两类,即无偏预测模型(LS)和有偏预测模型(WTLS、ETLS、GTLS)。
| 模型 | 函数模型 | 随机模型 | 回归系数 | 预测值 |
| LS | y-ey=Aβ yP=APβ | ey~N(0,Qyy) | ${\hat{\beta }}$LS | ${\hat{y}}$P,LS |
| WTLS | y-ey=(A-EA)β yP =APβ | 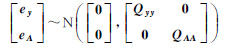 | ${\hat{\beta }}$WS | ${\hat{y}}$P,WS |
| ETLS | y-ey=(A-EA)β yP=APβ | 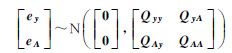 | ${\hat{\beta }}$ES | ${\hat{y}}$P,ES |
| GTLS | 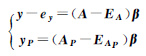 | 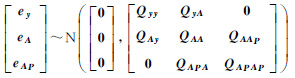 | ${\hat{\beta }}$GS | ${\hat{y}}$P,GS |
试验中取β0=9,β1=2,分别模拟不同精度和观测误差相关性的观测数据。分别用表 1中的4种模型求解回归系数并进行因变量预测,并统计预测值的均方根误差
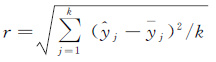 (31)
(31)
式中,${\hat{y}}$j和yj分别表示模型预测值和对应的真值。
2.2 试验分析无缝线性回归和预测模型在回归分析时考虑了变量的观测误差及其特性,在模型预测时考虑了待预测自变量的观测误差EAP并利用变量观测误差间的相关性对其进行估计和改正,利用解算的回归系数和误差改正的待预测自变量预测相应的因变量。因此,本文着重分析变量观测误差相关性和待预测自变量观测误差对模型预测效果的影响。
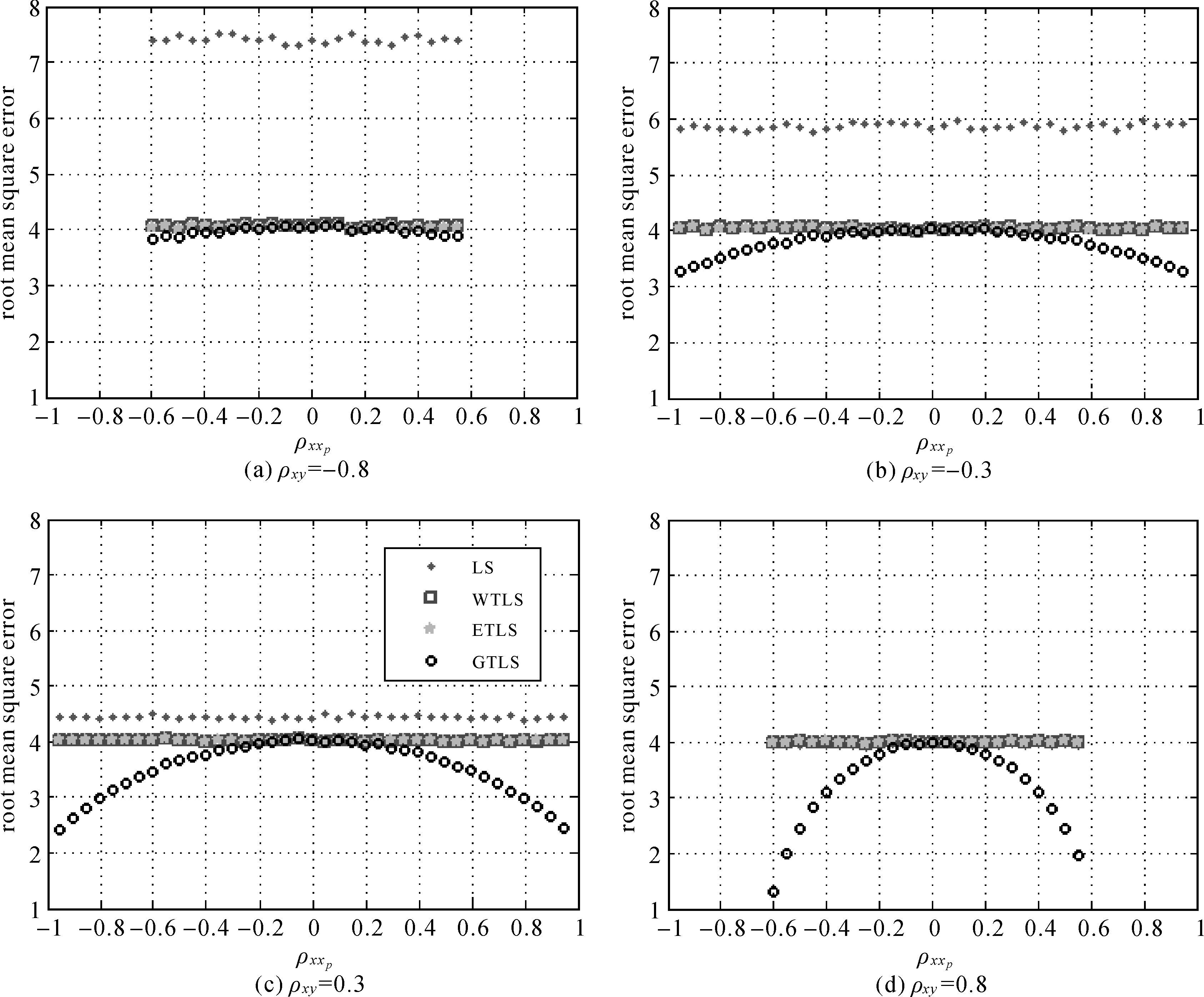
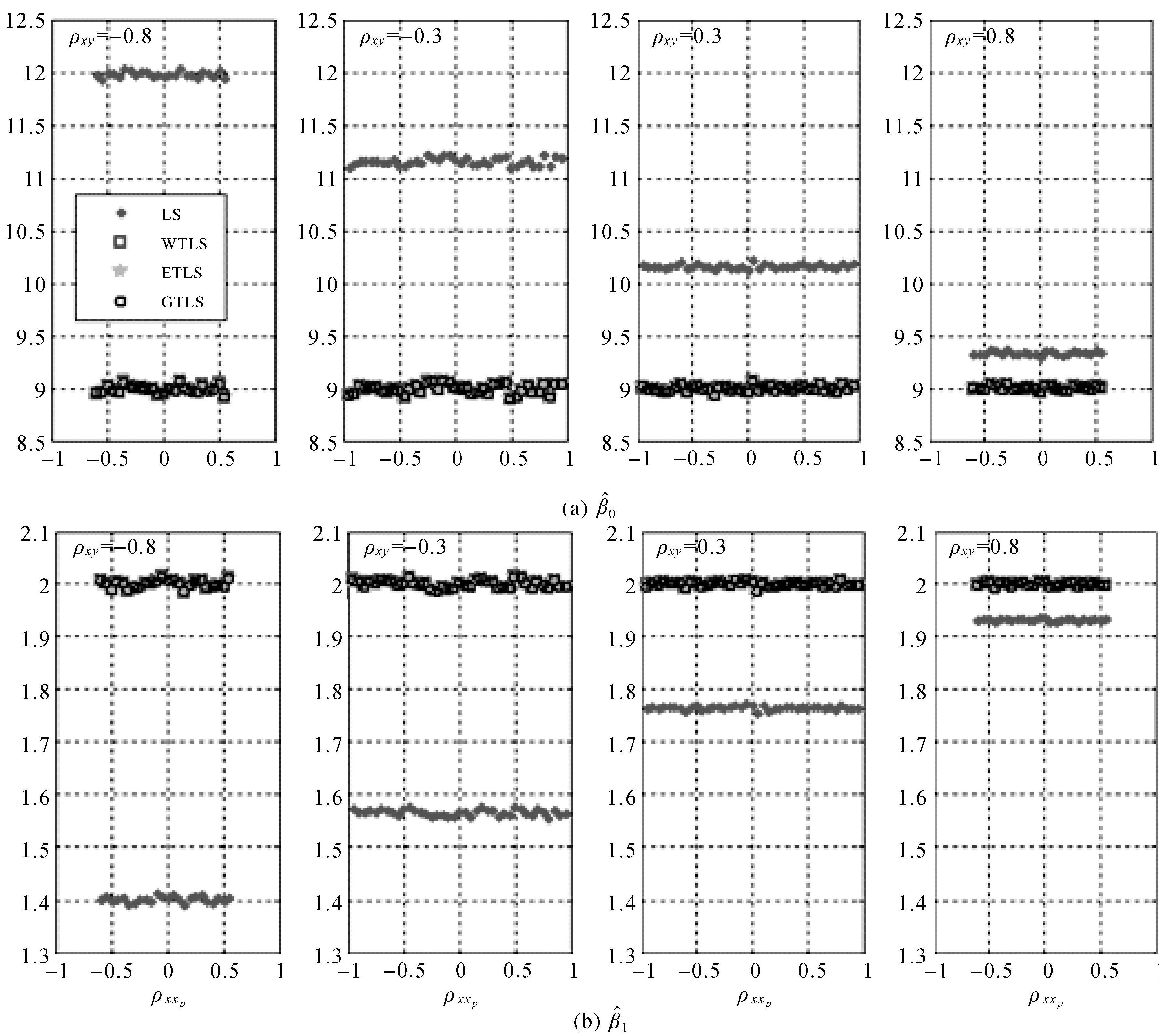
首先,分析误差相关系数ρxxp对因变量预测效果的影响。取变量方差σx2=2,σy2=8和σxp2=2σx2 ,相关系数ρxy分别取-0.8、-0.3、0.3和0.8,在满足|ρxxp|≤1和 ρxy2+ρxxp2≤1的条件下改变ρxxp。根据式(29)模拟观测数据并利用表 1中的4种模型进行解算。对每组方差和相关系数的设置,模拟计算50次得到预测值均方根误差的均值如图 1所示,相应的回归系数如图 2所示。
|
| 图 1 不同误差相关性的观测数据获得的预测值均方根误差 Fig. 1 Root mean squares of predicted dependent variables with different error correlated observations |
|
| 图 2 不同误差相关性的观测数据获得的回归系数估值${\hat{\beta }}$0和${\hat{\beta }}$1 Fig. 2 Estimated regression coefficients ${\hat{\beta }}$0 (top) and ${\hat{\beta }}$1 (bottom) from observations with different error correlations |
因变量的预测效果受回归系数${\hat{\beta }}$及自变量AP的影响,${\hat{\beta }}$越接近真值,AP的观测误差EAP越小,则因变量预测效果越好。LS、WTLS和ETLS均采用忽略EAP的模型(1)预测因变量,然而由于3种模型获得的${\hat{\beta }}$不同,对应的预测效果不同。相比LS方法,WTLS和ETLS考虑了误差的特性,获得的回归系数更接近真值,因而预测值的均方根误差较小。随着ρxy逐渐接近于1,LS解算的回归系数逐渐接近真值,其预测效果也逐渐获得改善。
对于GTLS和ETLS,虽然有${\hat{\beta }}$ES=${\hat{\beta }}$GS,但GTLS估计并改正AP中的观测误差EAP,即采用误差改正后的自变量${\tilde{A}}$P=AP-EAP预测因变量,因而其预测效果优于ETLS。由式(21a)可知,GTLS对EAP的有效估计受多因素影响,试验中(给定变量观测精度)主要受误差估值Er(相关系数ρxy)和相关系数ρxxp的影响。相关系数ρxy越接近1,且ρxxp的绝对值越接近1,GTLS对EAP的估计改正能力越强,对因变量预测效果的改善越明显。当ρxxp=0时(观测误差EA和EAP不相关),GTLS无法估计误差EAP,此时GTLS和ETLS等价,两者的预测效果相同。
为了分析AP中的观测误差EAP(以观测精度σxp2描述)对因变量预测效果的影响,给定精度σx2=2,σy2=8,取相关系数ρxy分别为-0.6、-0.3、0.3和0.6,ρxxp分别取0.1和0.8,令方差σxp2=χ·σx2,试验取χ为0~10。根据式(29)分别模拟观测数据并利用表 1中的4种模型进行解算。对每组方差和相关系数的设置,模拟计算50次得到预测值均方根误差的均值如图 3所示。

|
| 图 3 不同误差特性的观测数据获得的预测值均方根误差 Fig. 3 Root mean square errors of predicted dependent variables obtained from observations with different error characteristics |
预测因变量时,若AP不含有观测误差,则预测效果完全取决于回归系数${\hat{\beta }}$;否则,预测效果还受EAP的影响。从图 3可以看出,当χ=0时(AP不包含误差),由于${\hat{\beta }}$ES和${\hat{\beta }}$GS更加接近真值,因而两者的预测效果较好,WTLS的预测效果次之;而${\hat{\beta }}$LS与真值有较大差异,相应的预测效果较差。当χ≠0时(AP含有误差),各方法的预测效果受误差EAP影响且预测效果随误差EAP的增大而变差。对于LS,回归系数${\hat{\beta }}$LS和预测值${\hat{y}}$P,LS无偏,均方误差MSELS受误差EAP的影响且随χ变大而增大。对于GTLS,其回归系数${\hat{\beta }}$GS和预测值${\hat{y}}$P,GS有偏,均方误差MSEGS不仅与预测值的方差有关还和其偏差有关,且两者都随χ变大而变大,因此,MSEGS随χ变大而变大。WTLS和ETLS的均方误差与MSEGS相似且都随χ的变大而变大。
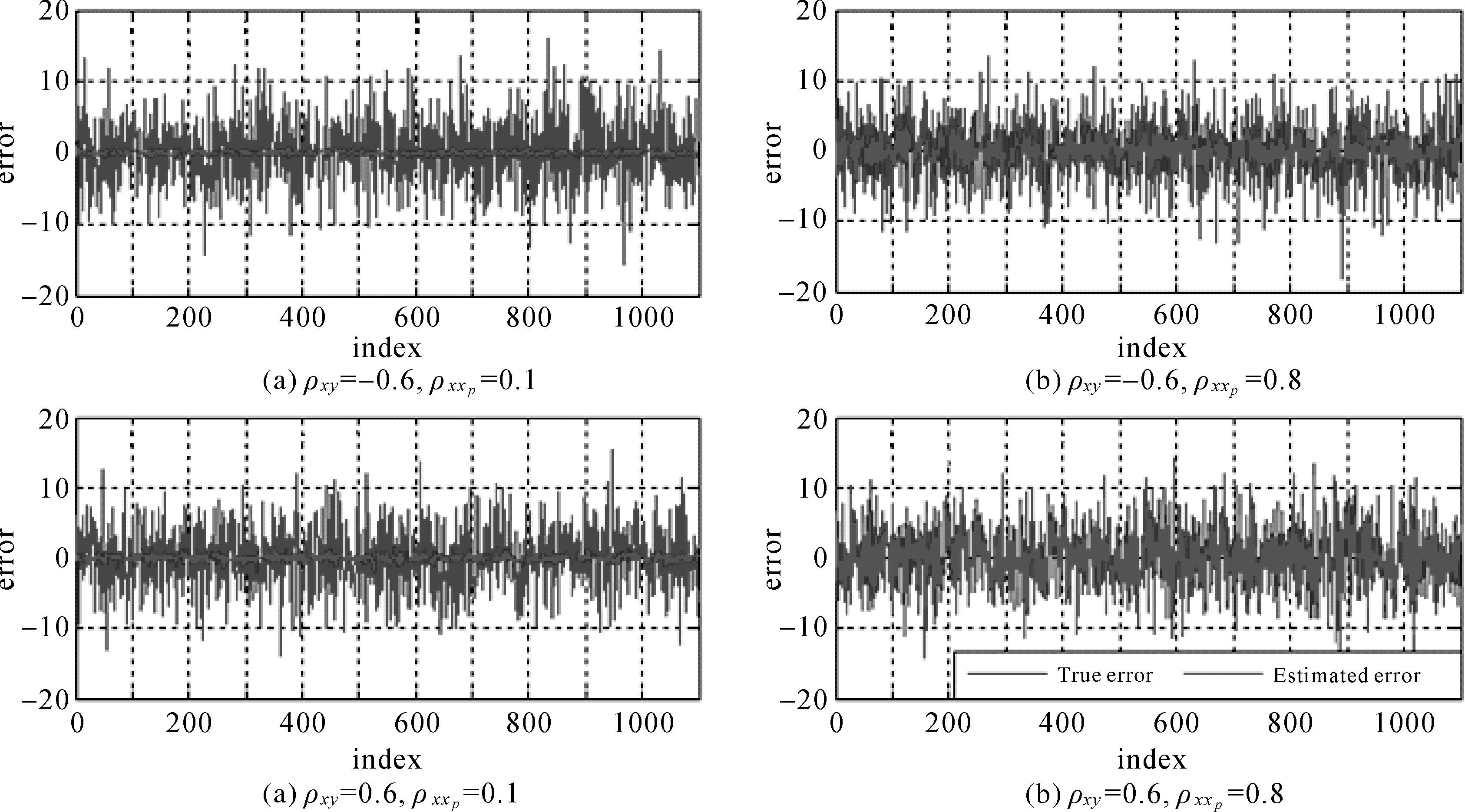
虽然GTLS利用误差改正后的自变量${\tilde{A}}$P预测因变量,其预测效果优于其他3种模型,但它对误差EAP的改正能力受ρxy和ρxxp等多种因素影响。图 4给出对应图 3((a)、(b)、(g)、(h))中σxp2=10σx2时的模拟误差EAP和GTLS的估计误差EAP。显然,GTLS对误差的恢复能力取决于变量误差的相关性。当相关性ρxy和ρxxp都较大时,GTLS能够有效地估计恢复EAP并将其改正,从而显著提高因变量的预测效果。
|
| 图 4 观测误差σxp2=10σx 2时模拟的自变量误差与GTLS估计的误差 Fig. 4 The simulated and estimated (by GTLS) observation errors of independent variables when σxp2=10σx 2 |
为了分析不同相关系数ρxy和ρxxp以及观测精度σxp2与预测值均方根误差的关系,给定观测精度σx2=2、σy2=8,取σxp2分别为σx2、5σx2和10σx2。根据式(29)分别模拟观测数据并利用表 1中的4种模型分别进行解算。对每组方差和相关系数进行设置,模拟计算50次得到预测值均方根误差的均值如图 5所示。图 5较为完整地说明不同模型对因变量的预测效果与误差相关系数ρxy和ρxxp以及观测误差EAP精度的关系。总体上,LS的预测效果较差,WTLS次之,ETLS优于WTLS,而GTLS的预测效果较好。虽然GTLS对误差EAP的估计改正能力受多种因素影响,但其对误差的有效处理明显提高了因变量的预测效果。

|
| 图 5 不同观测精度及不同误差相关性的观测数据获得的预测值均方根误差 Fig. 5 Root mean square errors of the predicted dependent variables obtained from observations with different precisions and error correlations |
3 结论
提高回归分析与模型因变量预测效果的关键是合理有效地处理各变量的观测误差。本文研究了回归分析及其预测应用中自变量和因变量的观测误差及其特性。
(1) 提出了具有一般性的、综合考虑所有变量观测误差及误差特性的无缝线性回归和预测模型。该模型不仅考虑回归分析时自变量和因变量的观测误差及其相关性,还严格考虑模型预测时待预测自变量的观测误差。
(2) 无缝模型将回归分析和因变量预测联合处理。其本质是利用变量观测误差间的相关性估计并改正待预测自变量的观测误差,利用误差改正的自变量预测因变量,进而提高因变量的预测效果。
(3) 无缝模型对观测误差的估计修复能力受误差相关性等多种因素影响,误差相关性越强,无缝模型对误差的修复能力越强,对因变量预测效果的改善越明显。
总之,提出的综合考虑所有变量观测误差及误差特性的无缝线性回归和预测模型可明显提高回归分析和回归模型的应用效果。
本文提出的无缝线性回归与预测模型的核心是采用最小二乘配置方法推估待预测自变量的观测误差EAP。最小二乘配置不可避免地涉及信号(观测误差)的协方差矩阵,而实际应用中变量观测误差的相关性通常难以准确获得,可通过协方差函数拟合或相关性分析等方法,并根据实际情况和经验判断给出观测误差的相关特性。
| [1] | 邓勃. 分析测试数据的统计处理方法[M]. 北京: 清华大学出版社, 1995. DENG Bo. Statistical Processing Method for Data of Analytic and Test[M]. Beijing: Tsinghua University Press, 1995. |
| [2] | CHAMBERS J M, CLEVELAND W S, KLEINER B, et al. Graphical Methods for Data Analysis[M]. Belmont: Duxbury Press, 1983. |
| [3] | CAMPBELL D, CAMPBELL S. Introduction to Regression and Data Analysis[R]. New Haven:StatLab Workshop Series, Yale University Center for Science and Social Science Information, 2008. |
| [4] | SYKES A O. An Introduction to Regression Analysis[R]. Chicago:The Inaugural Coase Lecture, Law School, University of Chicago, 1993. |
| [5] | SCHAFFRIN B, WIESER A. On Weighted Total Least-squares Adjustment for Linear Regression[J]. Journal of Geodesy, 2008, 82(7): 415–421. DOI:10.1007/s00190-007-0190-9 |
| [6] | SHEN Yunzhong, LI Bofeng, CHEN Yi. An Iterative Solution of Weighted Total Least-squares Adjustment[J]. Journal of Geodesy, 2011, 85(4): 229–238. DOI:10.1007/s00190-010-0431-1 |
| [7] | LI Bofeng, SHEN Yunzhong, LI Weixiao. The Seamless Model for Three-dimensional Datum Transformation[J]. Science China Earth Sciences, 2012, 55(12): 2099–2108. DOI:10.1007/s11430-012-4418-z |
| [8] | XU Peiling, LIU Jingnan, SHI Chuang. Total Least Squares Adjustment in Partial Errors-in-variables Models:Algorithm and Statistical Analysis[J]. Journal of Geodesy, 2012, 86(8): 661–675. DOI:10.1007/s00190-012-0552-9 |
| [9] | 刘经南, 曾文宪, 徐培亮. 整体最小二乘估计的研究进展[J]. 武汉大学学报(信息科学版), 2013, 38(5): 505–512. LIU Jingnan, ZENG Wenxian, XU Peiliang. Overview of Total Least Squares Methods[J]. Geomatics and Information Science of Wuhan University, 2013, 38(5): 505–512. |
| [10] | 曾文宪, 方兴, 刘经南, 等. 附有不等式约束的加权整体最小二乘算法[J]. 测绘学报, 2014, 43(10): 1013–1018. ZENG Wenxian, FANG Xing, LIU Jingnan, et al. Weighted Total Least Squares Algorithm with Inequality Constraints[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(10): 1013–1018. DOI:10.13485/j.cnki.11-2089.2014.0173 |
| [11] | 王乐洋, 赵英文, 陈晓勇, 等. 多元总体最小二乘问题的牛顿解法[J]. 测绘学报, 2016, 45(4): 411–417. WANG Leyang, ZHAO Yingwen, CHEN Xiaoyong, et al. A Newton Algorithm for Multivariate Total Least Squares Problems[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(4): 411–417. DOI:10.11947/j.AGCS.2016.20150246 |
| [12] | LI Bofeng, WANG Miaomiao, YANG Yuanxi. Multiple Linear Regression with Correlated Explanatory Variables and Responses[J]. Survey Review, 2015. DOI:10.1179/1752270615Y.0000000006 |
| [13] | 王苗苗, 李博峰, 沈云中. 顾及自变量与因变量误差及相关性的线性回归[J]. 同济大学学报(自然科学版), 2016, 44(3): 446–453. WANG Miaomiao, LI Bofeng, SHEN Yunzhong. Linear Regression with Corrected Errors of Independent and Dependent Variables[J]. Journal of Tongji University (Natural Science), 2016, 44(3): 446–453. |
| [14] | KOCH K R. Least Squares Adjustment and Collocation[J]. Bulletin Géodésique, 1977, 51(2): 127–135. DOI:10.1007/BF02522282 |
| [15] | KOCH K R. Parameter Estimation and Hypothesis Testing in Linear Models[M]. 2nd ed. Berlin Heidelberg: Springer, 1999. |
| [16] | LI Bofeng, SHEN Yunzhong, ZHANG Xingfu, et al. Seamless Multivariate Affine Error-in-variables Transformation and Its Application to Map Rectification[J]. International Journal of Geographical Information Science, 2013, 27(8): 1572–1592. DOI:10.1080/13658816.2012.760202 |
| [17] | FANG Xing. Weighted Total Least Squares Solution for Application in Geodesy[D]. Hanover:Leibniz University Hanover, 2011. |
| [18] | FANG Xing. Weighted Total Least Squares:Necessary and Sufficient Conditions, Fixed and Random Parameters[J]. Journal of Geodesy, 2013, 87(8): 733–749. DOI:10.1007/s00190-013-0643-2 |
| [19] | FANG Xing. Weighted Total Least-squares with Constraints:A Universal Formula for Geodetic Symmetrical Transformations[J]. Journal of Geodesy, 2015, 89(5): 459–469. DOI:10.1007/s00190-015-0790-8 |
| [20] | SNOW K. Topics in Total Least-squares Adjustment within the Errors-in-variables Model:Singular Cofactor Matrices and Priori Information[D]. Columbus:The Ohio State University, 2012. |
| [21] | TEUNISSEN P G J. Adjustment Theory:An Introduction (Mathematical Geodesy and Positioning)[M]. Delft, The Netherlands: VSSD, Delft University Press, 2000. |



