2. 地球空间信息技术协同创新中心, 湖北 武汉 430079
2. Collaborative Innovation Center for Geospatial Technology, Wuhan 430079, China
利用IGS发布的GPS事后精密轨道与钟差产品,基于载波相位观测数据的精密单点定位(PPP)技术可以实现厘米甚至毫米级的定位精度。但IGS发布的GPS事后精密星历产品都存在不同程度的时间延迟,因此无法应用于实时导航定位。虽然目前IGS发布的实时精密轨道产品(IGU-P)的轨道精度已达到厘米级,但其钟差外推精度仅为3 ns左右,严重影响IGU产品在实时精密导航定位中的应用。因此,GPS卫星钟差实时精密确定与中短期高精度预报已成为高精度实时导航应用中的关键技术之一[1-3]。
GPS卫星钟差的预报精度与卫星原子钟的频率稳定度紧密相关,而不同类型卫星钟的频率稳定度也存在较大差异。研究表明,卫星钟原子频标的频率主要存在5种独立的随机噪声:调相白噪声、调相闪变噪声、调频白噪声、调频闪变噪声和调频随机游走噪声[4-7]。这些噪声会对钟频标输出信号的相位和频率产生影响,引起频率的随机变化,从而导致卫星钟差难以准确预报。截至2016年4月1日,GPS星座中共出现过BLOCK I、II、IIA、IIR、IIR-M与IIF等6种型号的卫星,主要搭载铯原子钟(Cs)与铷原子钟(Rb)。相较于Cs钟,Rb钟的短期稳定度相对较高。在GPS卫星钟差预报中,通常基于精密定轨得到的卫星钟差数据,采用线性模型、二次多项式或灰色模型等进行钟差拟合与预报,在卫星钟频率稳定度较高的情况下,能够获得较好的钟差预报结果[8-10]。由于部分GPS卫星使用年限较长,原子钟频率稳定度较差,钟差预报精度相对较差。
GPS卫星钟差预报精度除与卫星钟本身的频率稳定度有关外,还需考虑外部环境的影响。卫星钟受在轨运行的温度与空间环境等因素的影响,原子频标的频率呈现周期性变化。为了提高预报精度,通常在线性模型或二次多项式预报模型中增加周期项[11-16]。在早期发布的IGU预报钟差产品中,GPS IIA卫星的Cs钟和IIR卫星的Rb钟都采用附加约12 h周期项的线性模型,II/IIA卫星的Rb钟则采用附加约12 h周期项的二次多项式模型来预报钟差[17]。部分Cs钟和稳定度较差的Rb钟的钟差预报精度较差,与广播星历的钟差精度相当。为了提高IGU产品的精度,IGS将这些卫星排除在外,总体预报精度从2~4 ns提高到1 ns[18],但这种排除策略将引起可用卫星数量的减少而影响用户的定位。
目前所采用的卫星钟差预报方法,通常是对精确估计的卫星钟差数据进行拟合建模,然后利用所建立的模型来预报后续时刻的卫星钟差。本文提出一种基于卫星钟差变化率序列的钟差建模与预报新方法,采用附加周期项的线性模型或多项式模型对卫星钟的钟差变化率进行拟合,建立钟差的预报模型并预报后续时刻的卫星钟差。最后使用当前GPS星座的卫星钟差数据为试验对象,验证与分析该方法的有效性与可行性。
1 基于钟差变化率拟合的钟差建模当前,GPS卫星钟差常采用线性、二次多项式和附加周期项的线性或二次多项式模型进行建模与预报。对钟差数据进行拟合,附加周期项的二次多项式模型可表示为
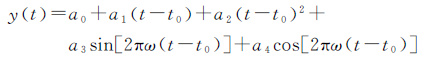 (1)
(1)
式中,y(t)为t时刻的钟差;t0为预报钟差的初始时刻;a0、a1与a2为多项式系数;a3与a4为附加周期项的系数;ω为周期项频率,根据IGS钟差预报策略,将周期设置为GPS卫星的轨道周期[17]。
对式(1)求导,即可得到钟差变化率的拟合模型
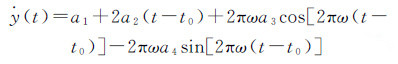 (2)
(2)
式中,$\dot{y}$(t)为t时刻的钟差变化率。根据卫星的钟差序列y(t),可以采用一阶中心差分近似法计算钟差变化率
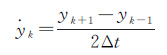 (3)
(3)
式中,$\dot{y}$k为k时刻的卫星钟差变化率;yk+1和yk-1分别为k+1和k-1时刻的卫星钟差;Δt为卫星钟差的时间间隔。采用式(2)对钟差变化率序列进行建模,将式(2)中的ai(i=1,2,…,4)作为待估参数,采用加权最小二乘方法进行估计,由此建立钟差变化率的拟合与预报模型。设tj(j=1,2,…,n)时刻的卫星钟差变化率为j,可建立误差方程
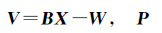 (4)
(4)
式中,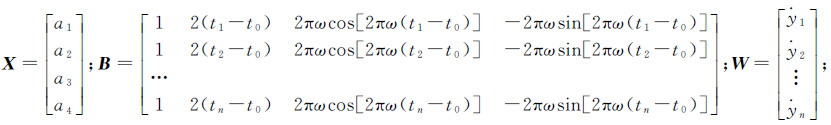
根据加权最小二乘准则,可得
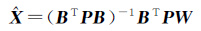 (5)
(5)
图 1给出了基于钟差变化率序列进行钟差建模估计与钟差预报的时间关系。通过对[tn,t0]时间段内的钟差变化率序列进行拟合,估计出a1、a2、a3和a4模型参数,然后根据[tj,t0]较短时间段内的精确钟差,估计a0参数,由此建立基于钟差变化率拟合建模的预报模型。在钟差预报阶段,按照式(1)预报t0时刻之后轨道弧段的卫星钟差。本文的a0参数是直接依据用于模型拟合的IGS精密星历中t0时刻的精密钟差计算得到,有a0=y(t0)-a4。

|
| 图 1 钟差建模与预报 Fig. 1 Clock modeling and prediction |
根据式(1)与式(2)可知,基于钟差观测值和基于钟差变化率观测值这两种建模方法的基础模型是一致的,都是附加周期项的二次多项式模型。虽然基于钟差变化率观测值的基础模型经过求导后,消除了a0项,模型次数降低,但考虑到该拟合模型来自于基础模型,而且两者的预报模型是完全一致的,因此下文在讨论基于钟差变化率的拟合模型,仍沿用其采用的基础模型来表述。
2 两种钟差建模方法的比较传统的基于钟差序列的建模方法采用“一步法”原理,利用全弧段的钟差数据整体估计ai(i=0,1,…,4);而基于钟差变化率序列的建模方法采用“二步法”原理,先拟合估计ai(i=1,2,…,4)参数,确定卫星钟差的变化趋势,然后利用与预报时刻相近的短弧段精密钟差估计预报钟差的基准项a0,建立完整的钟差预报模型。
根据上文分析可知,两种建模方法的数学模型是完全一致的,预报模型参数ai(i=0,1,…,4)的物理意义也相同,两者的主要区别在于估计a0项所使用的钟差数据长度不一致。采用“一步法”原理,使用了整个弧段内的数据来估计预报钟差的基准a0,而“两步法”仅使用与预报初始时刻相近的短弧段数据来估计,由此导致两种建模方法得到的a0不同,同时会引起趋势项参数ai(i=1,2,…,4)出现微小差异。通过大量的试验分析,在卫星钟频率稳定度较高的情况下,两种方法估计得到的a0差异不大,当卫星钟频率稳定度较差时,结果差异较大。
通过比较分析,采用本文提出的基于钟差变化率拟合的钟差预报方法,在数据处理过程中还存在以下优势:
(1) 对于精密定轨的单天解或者弧段解结果,如果没有经过轨道综合处理,会存在不同弧段解之间的钟差不连续现象[19],对“一步法”钟差建模存在较大的影响,严重时导致建模失败,但是对“两步法”的影响只有跳变点附近的两个历元,可以通过粗差检测来消除,不影响钟差变化趋势的估计。
(2) 从钟差建模角度来看,“两步法”通过整体估计钟差的变化趋势项,利用精密钟差作为基准,如果预报时间段内钟差的变化趋势与建模时段相同,就可以获得很高的预报精度。而采用“一步法”,虽然在建模时间段内,钟差建模结果是最优的,但建模得到的钟差基准项受到全弧段数据的影响,与预报初始时刻的精密钟差可能会存在一定的差异,由此会引起预报钟差存在系统性的偏差。
3 基础模型确定截至2016年4月1日,GPS星座由12颗IIR卫星、8颗IIR-M卫星与12颗IIF卫星组成,除2颗IIF卫星(G8,G24)采用Cs钟外,其余卫星都采用Rb钟。表 1列出了GPS卫星以及卫星钟的基本信息。可以看出,不同型号的GPS卫星启用的时间相差10~20 a,考虑到不同时期各种型号原子钟的频率稳定度以及时间基准的维持技术都会有所不同,因此需要根据不同型号原子钟的钟差变化特性,选择合适的基础模型,才能获得较高的预报精度。
| 卫星型号 | 卫星号(PRN) | 原子钟类型 | 卫星启用时间 |
| IIR | 2、11、13、14、16、18、19、20、21、22、23、28 | Rb | 1997—2004 |
| IIR-M | 4、5、7、12、15、17、29、31 | Rb | 2005—2009 |
| IIF | 1、3、6、9、10、25、26、27、30、32 8、24 | Rb Cs | 2010—2016 |
对于IIR与IIR-M卫星,IGS采用附加周期项的线性模型对钟差进行建模与预报[17],因此本文仍沿用附加周期项的线性模型作为基础模型。对于最新型号的IIF卫星,IGS没有给出具体的预报模型,本文将通过试验分析钟差变化率的变化特性,确定合理的基础模型。IIF卫星存在Rb钟与Cs钟两种原子钟,分别采用线性模型、二次多项式、附加周期项的线性模型与附加周期项的二次多项式共4种基础模型对两种原子钟的钟差变化率进行拟合,如图 2所示。可以看出,IIF卫星Rb钟的钟差变化率序列具有明显的周期变化特性,并存在趋势项变化,因此采用附加周期项的二次多项式作为基础模型;而Cs钟的周期性并不明显。图 3统计了Rb钟与Cs钟在4种模型下钟差变化率拟合误差的均方根值(RMS)。可以看出,对于搭载Rb钟的IIF卫星(G01与G30),附加周期项的二次多项式模型拟合误差明显最小;对于搭载Cs钟的G08与G24卫星,4种模型的拟合误差都基本相当,但附加周期项的二次多项式模型相对较小。因此对于IIF卫星的钟差,无论是Rb钟还是Cs钟,本文将统一采用附加周期项的二次多项式模型作为基础模型,进行拟合建模并预报。
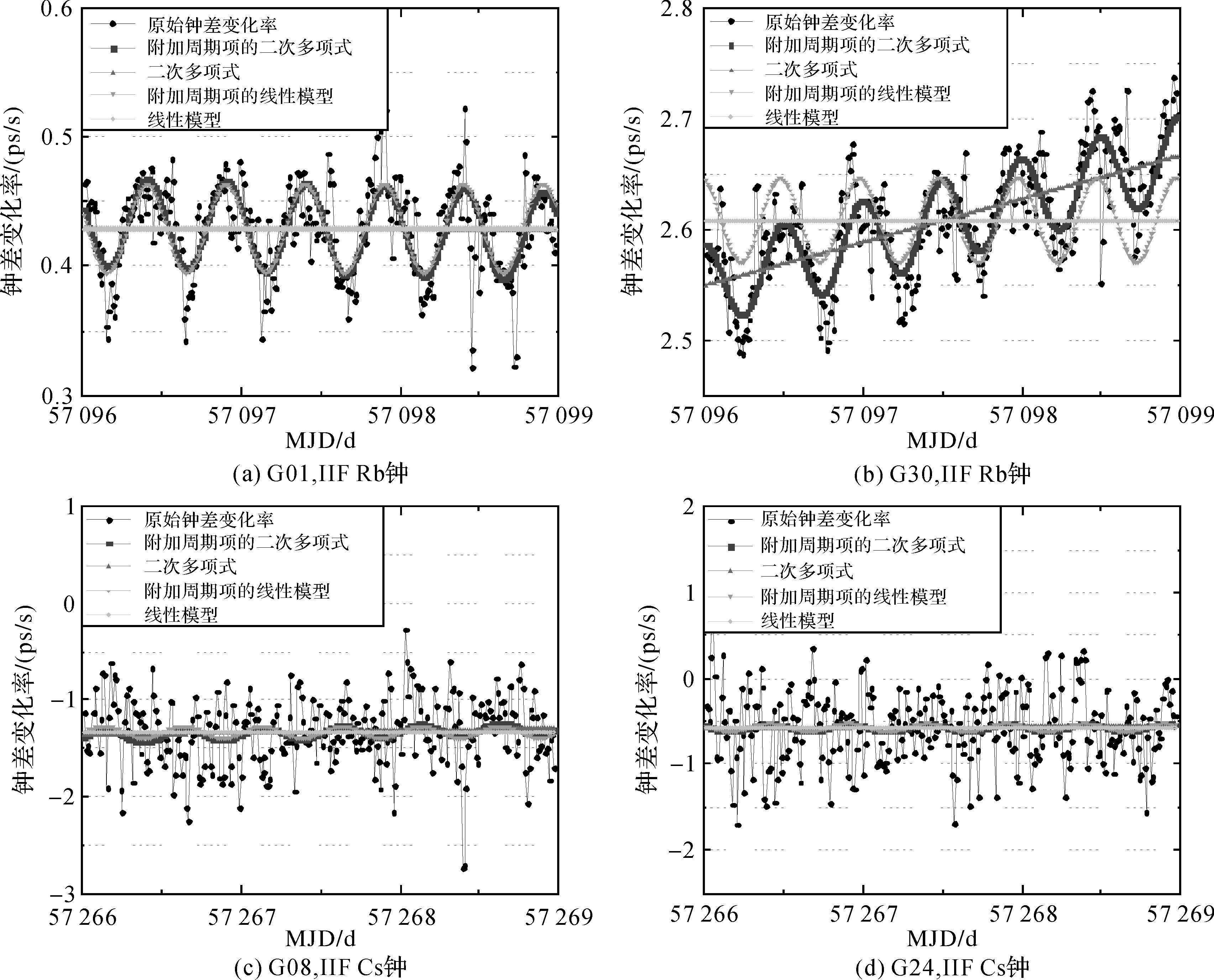
|
| 图 2 卫星钟差变化率及其拟合结果 Fig. 2 Clock offset rates and their fitting results |
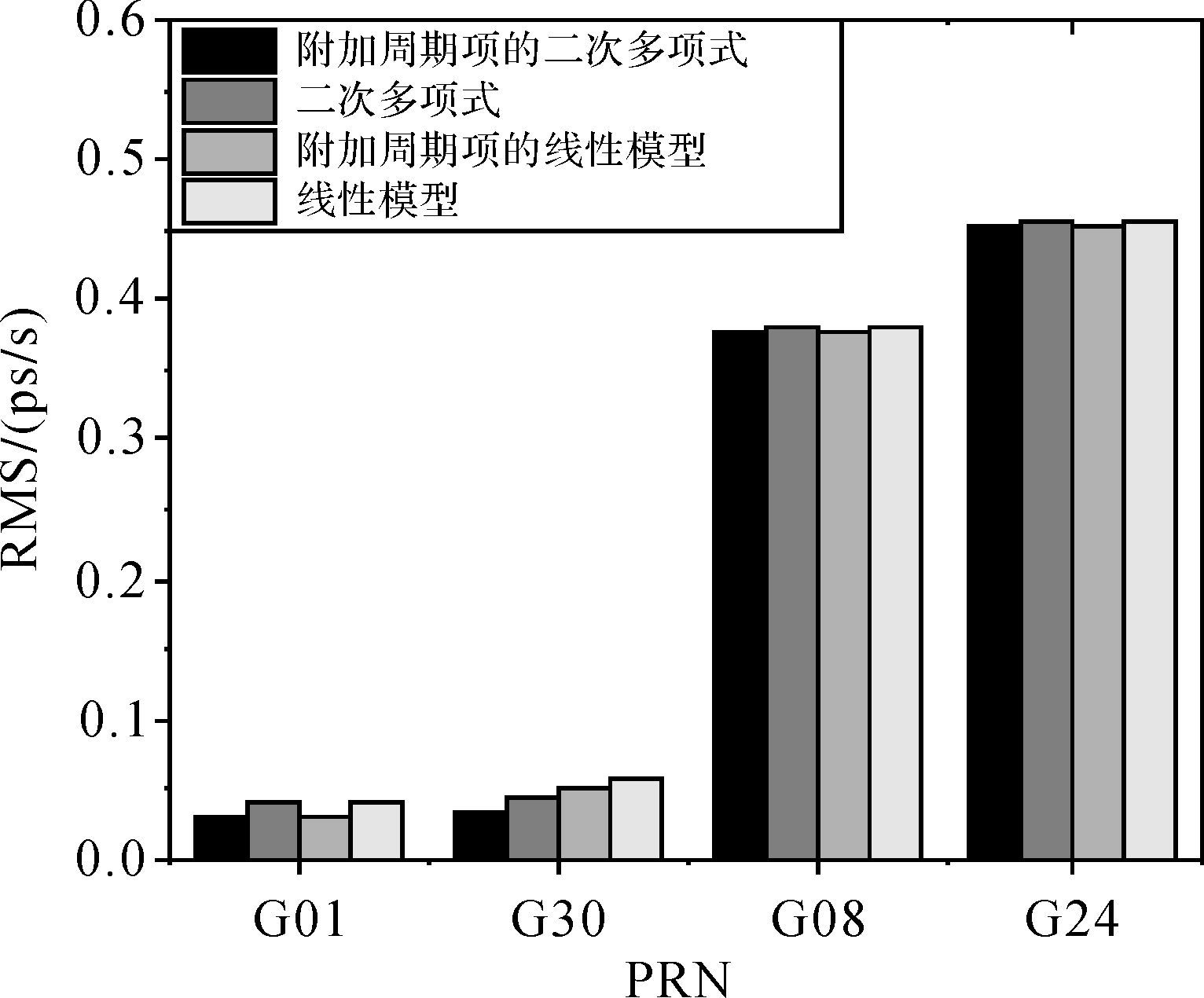
|
| 图 3 卫星钟差变化率拟合的精度统计 Fig. 3 Accuracy statistics of clock offset rate fitting |
4 试验结果与分析
IGS发布的精密轨道与钟差产品包括超快速星历(IGU)、快速星历(IGR)与最终精密星历(IGS)。最终精密星历的精度最高,但其发布存在12~18 d的时间延迟,其30 s的钟差产品精度可达0.075 ns(3σ)。快速星历的精度次之,钟差精度为0.075 ns(2σ),存在17~41 h的发布时延。超快速星历包括观测部分(IGU-O)与预测部分(IGU-P),观测部分存在3~9 h的发布时延,预测部分可以实时使用[21]。IGU-O的钟差通过对多个IGS数据分析中心估计钟差的综合加权得到,精度为0.15 ns;IGU-P的钟差基于多个IGS数据分析中心估计的钟差经过复杂的综合加权外推得到,并非某种单一预报模型的预报结果,其钟差精度为3 ns左右[22]。
以2016年4月1—9日IGR钟差产品为试验对象,分别采用本文提出的基于钟差变化率拟合的预报方法(方案1)以及传统的基于钟差拟合的预报方法(方案2)对3 d的IGR钟差进行拟合建模,并向后预报1 d的卫星钟差,与IGR钟差比较,统计分析钟差的预报精度。无论是基于钟差拟合还是钟差变化率拟合,两种方案下的基础模型都相同,对于IIR与IIR-M卫星,都采用附加周期项的线性模型;对于IIF卫星,则采用附加周期项的二次多项式模型。此外,试验中将同时列出IGU预报钟差(IGU-P)的精度,作为钟差预报精度的参照。
4.1 钟差预报精度统计使用4月1—3日3 d的IGR钟差产品,分别采用方案1和方案2进行建模,预报4月4日的钟差,以该天IGR的钟差为参考,计算预报钟差的精度;依此类推,分别预报4月5—9日的钟差。图 4给出了4月4—9日两种预报方案下每颗GPS卫星的钟差预报精度(RMS),同时列出了IGU预报钟差的精度,期间内IGU没有给出G08卫星钟差预报结果。可以看出:
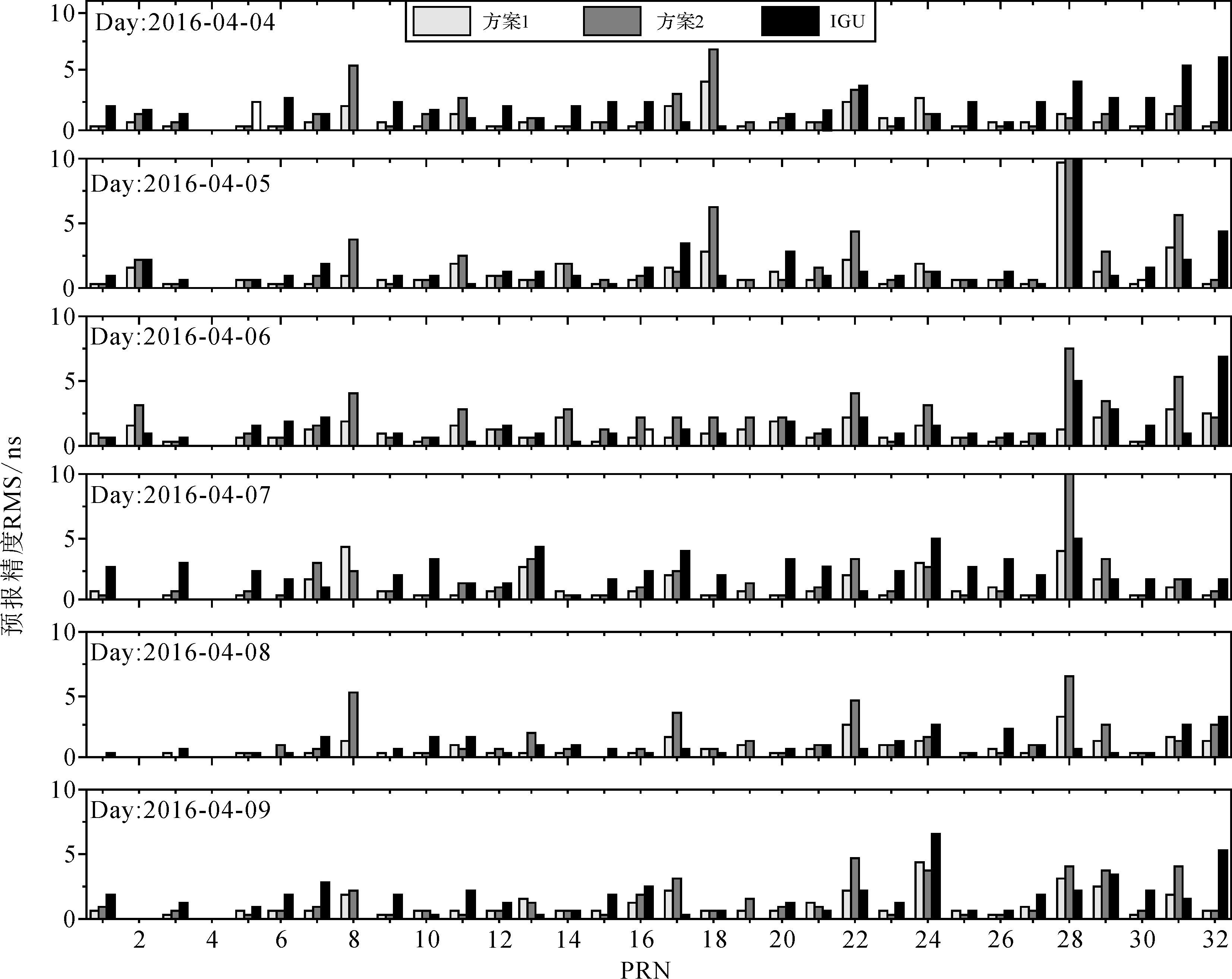
|
| 图 4 卫星钟差的1 d预报精度 Fig. 4 Accuracy statistics of the clock prediction for one day |
(1) GPS星座中60%以上的卫星为IIR与IIR-M卫星,对于IIR与IIR-M卫星的Rb钟,在大多数情况下特别是在卫星钟差稳定度较差时,方案1的钟差预报精度优于方案2,且优于IGU预报钟差。
(2) 少数IIR与IIR-M卫星的预报误差较大,如G28,这是由拟合建模期间和预报期间卫星钟差的变化趋势不一致引起的。在此情况下,两种方法都无法准确预报。
(3) 对于IIF卫星的Rb钟(G01、G03、G06、G09、G10、G25、G26、G27、G30与G32),因为卫星钟稳定度较高,方案1的钟差预报精度与方案2相当,但两种方案的钟差预报精度都明显优于IGU预报钟差。
(4) 对于IIF卫星的Cs钟(G08与G24),由于短期稳定度较差,预报精度整体较差,方案1的预报钟差精度略优于方案2,大多数时候也优于IGU预报钟差。
(5) 存在少量几例情况,方案1的预报精度略低于方案2,主要是由基准项a0不精确引起的,即用于拟合的精密钟差存在一定的误差。
表 2统计了4月4—9日两种预报方案下各种型号卫星钟预报时长分别为3、6、12以及24 h的钟差预报精度,作为对比,同时也列出了IGU预报钟差的精度,其中“IIR Rb”表示IIR卫星搭载的Rb钟,类似的,“IIR-M Rb”、“IIF Rb”与“IIF Cs”分别表示IIR-M、IIF卫星搭载的Rb钟或Cs钟,“all”表示对所有卫星的钟差预报精度进行统计。从表 2可以明显发现:
| 卫星钟类型 | 钟差预报精度/ns | 方案1精度提高/(%) | 钟差预报精度/ns | 方案1精度提高/(%) | |||||||||
| 预报时长 | 方案1 | 方案2 | IGU | 相比方案2 | 相比IGU | 预报时长 | 方案1 | 方案2 | IGU | 相比方案2 | 相比IGU | ||
| IIR Rb | 3 h | 0.36 | 1.73 | 0.56 | 79.2 | 35.7 | 6 h | 0.57 | 1.94 | 0.85 | 70.6 | 32.9 | |
| IIR-M Rb | 0.37 | 1.19 | 0.36 | 68.9 | -2.8 | 0.43 | 1.3 | 0.54 | 66.9 | 20.4 | |||
| IIF Rb | 0.21 | 0.3 | 0.35 | 30 | 40 | 0.26 | 0.34 | 0.57 | 23.5 | 54.4 | |||
| IIF Cs | 1.17 | 2.69 | 1.42 | 56.5 | 17.6 | 1.5 | 2.76 | 1.92 | 45.7 | 21.9 | |||
| all | 0.43 | 1.4 | 0.51 | 69.3 | 15.7 | 0.58 | 1.52 | 0.76 | 61.8 | 23.7 | |||
| IIR Rb | 12 h | 1.03 | 2.35 | 1.36 | 56.2 | 24.3 | 24 h | 1.88 | 3.15 | 2.33 | 40.3 | 19.3 | |
| IIR-M Rb | 0.65 | 1.51 | 0.95 | 57 | 31.6 | 1.21 | 2 | 1.85 | 39.5 | 34.6 | |||
| IIF Rb | 0.35 | 0.43 | 1.07 | 18.6 | 67.3 | 0.61 | 0.67 | 2.22 | 9 | 72.5 | |||
| IIF Cs | 2.05 | 3.28 | 2.64 | 37.5 | 22.3 | 2.45 | 3.4 | 3.58 | 27.9 | 31.6 | |||
| all | 0.9 | 1.82 | 1.24 | 50.5 | 27.4 | 1.47 | 2.34 | 2.24 | 37.2 | 34.4 | |||
(1) 对于各种型号的卫星钟,本文提出的基于钟差变化率拟合的预报方法(方案1)相比于基于钟差拟合的预报方法(方案2),其钟差预报精度都有不同程度的提高,但随着预报时长增大,钟差预报精度的提高幅度有所降低。如对于IIR卫星的Rb钟,预报时长为3、6、12与24 h对应的精度提高幅度分别为79.2%、70.6%、56.2%与40.3%。
(2) 相比于IGU产品,对于IIR-M卫星的Rb钟,方案1的3 h钟差预报精度与IGU基本相当,下降2.8%,对于其余卫星钟,方案1的预报钟差精度都有不同程度的提高。与相较于方案2的精度提高幅度变化不同,对于IIR卫星Rb钟,方案1相较于IGU的钟差预报精度随着预报时长增大而逐渐下降,3、6、12与24 h对应的精度提高幅度分别为35.7%、32.9%、24.3%与19.3%。但对于其他型号卫星钟,方案1的精度提高幅度随着预报时间增长逐渐提高,如对于IIF卫星的Rb钟,方案1对3、6、12与24 h钟差预报的精度提高幅度分别为40.0%、54.4%、67.3%与72.5%。
(3) 本文提出的新方法,对IIF卫星Rb钟的钟差预报精度最优,3、6、12与24 h的钟差预报精度分别可达0.21、0.26、0.35与0.61 ns,相比于IGU预报钟差,其精度提高幅度也较大。其原因在于,IIF卫星Rb钟的钟差变化率具有较为明显的周期性趋势,本文采用附加周期项的多项式模型对钟差变化率进行拟合,能够很好地反映出钟差变化的趋势,从而实现更为准确的预报。对于IIF卫星的Cs钟,本文方法3、6、12与24 h的钟差预报精度相对较低,分别为1.17、1.50、2.05与2.45 ns,相比于IGU的提高幅度也相对较小。原因在于Cs钟的短期稳定度较差,虽然采用本文方法对钟差预报精度有一定的提高,仍然无法达到Rb钟的预报精度。
(4) 总的来说,本文提出的方法3、6、12与24 h的钟差预报精度分别可达0.43、0.58、0.90与1.47 ns,方案2对3、6、12与24 h的钟差预报精度分别为1.40、1.52、1.82与2.34 ns,相比于方案2,本文方法预报精度分别可提高69.3%、61.8%、50.5%与37.2%;IGU预报钟差3、6、12与24 h的精度分别为0.51、0.76、1.24与2.24 ns,相比于IGU预报钟差,本文方法的预报精度分别可提高15.7%、23.7%、27.4%与34.4%,这说明本文提出的预报方法精度要优于目前IGS超快速星历钟差预报所采用的方法。
4.2 钟差预报精度分析相比传统的基于钟差拟合的预报方法,本文提出的基于钟差变化率拟合的预报方法可以较大幅度地提高卫星钟差的中短期预报精度,其主要原因在于本文方法将钟差拟合模型的趋势项系数(a1,a2,a3,a4)与基准项a0分为两步计算,减小基准项的建模误差。
图 5给出了两种方案下IIR Rb钟、IIR-M Rb钟在拟合建模期间的拟合残差,可以看出:
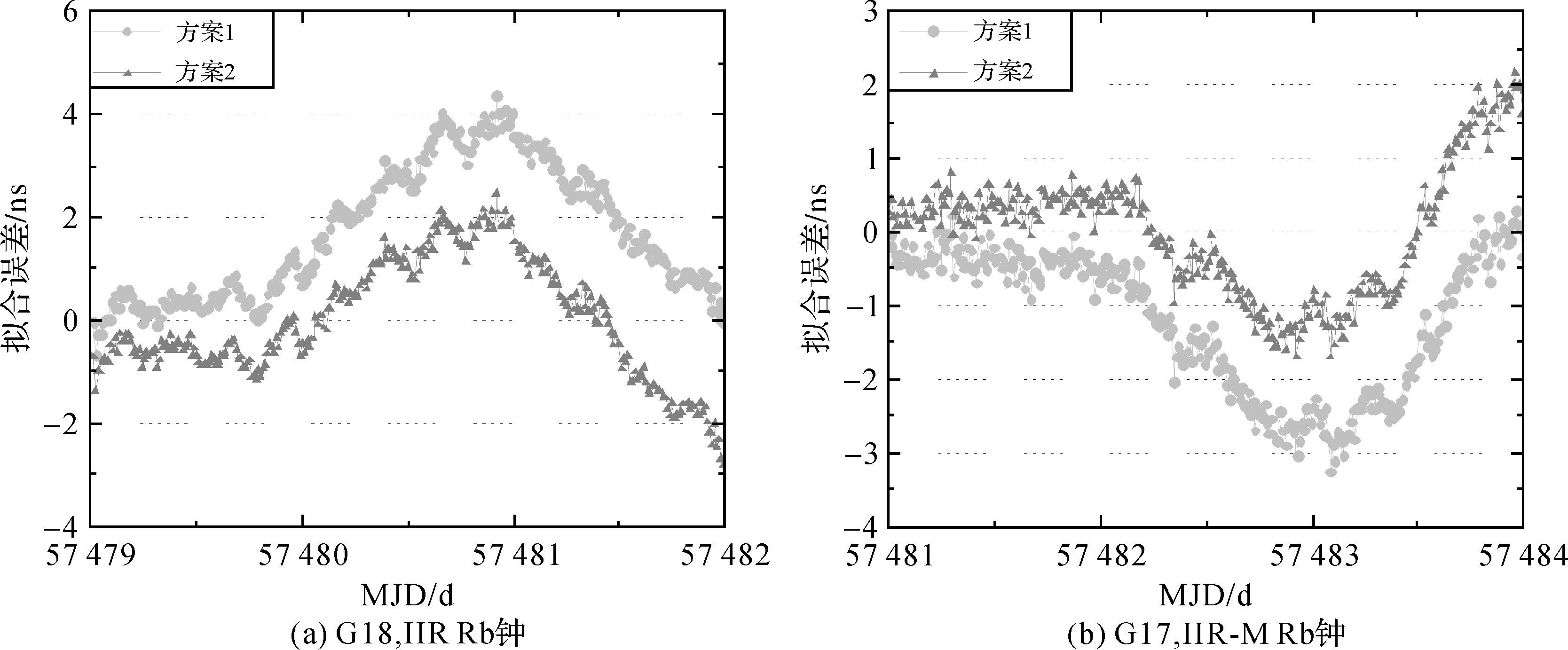
|
| 图 5 GPS卫星钟的钟差拟合误差 Fig. 5 The fitting residuals for GPS clocks |
(1) 方案2对钟差进行拟合,根据拟合残差平方和最小准则,可以获得(a0,a1,a2,a3,a4)参数的最优解,能够保证钟差拟合误差最小,因此(a)和(b)图中方案2的拟合误差曲线整体在0附近,整体的偏差相对较小。
(2) 本文提出的方法(方案1)对钟差变化率进行拟合,根据最小二乘准则可以获得(a1,a2,a3,a4)参数基于钟差变化率拟合残差最小的最优解,a0项根据钟差拟合时段末尾时刻的精密钟差计算得到,因此所得模型参数并非钟差数据拟合的最优解,并不能保证钟差拟合误差最小。
(3) 方案1与方案2的钟差拟合误差变化趋势基本相同,这说明两种方案下钟差拟合的趋势项参数(a1,a2,a3,a4)的差异很小。两种方案的拟合误差存在明显的系统性差异,这主要来自于a0项的影响。在钟差拟合时段的末尾时刻,方案1能够约束该时刻的钟差拟合误差为0,而方案2则可能存在较大的拟合误差。
图 6给出了方案1与方案2在一天内所有GPS卫星的钟差预报误差曲线。可以看出,在初始时刻,方案1的预报误差为0,一天内预报误差在±6 ns范围内;而方案2,部分卫星初始时刻预报误差较大,高达±4 ns,一天内钟差预报误差最大可达±10 ns。两种方案钟差预报误差的变化趋势基本相同,误差增大幅度也基本一致,这说明两种方案预报精度统计结果的差异主要来自于初始时刻的预报偏差。而初始时刻的钟差预报误差主要取决于a0项,这也验证了基于钟差变化率数据采用“两步法”建模结果更有利于提高钟差预报的精度。
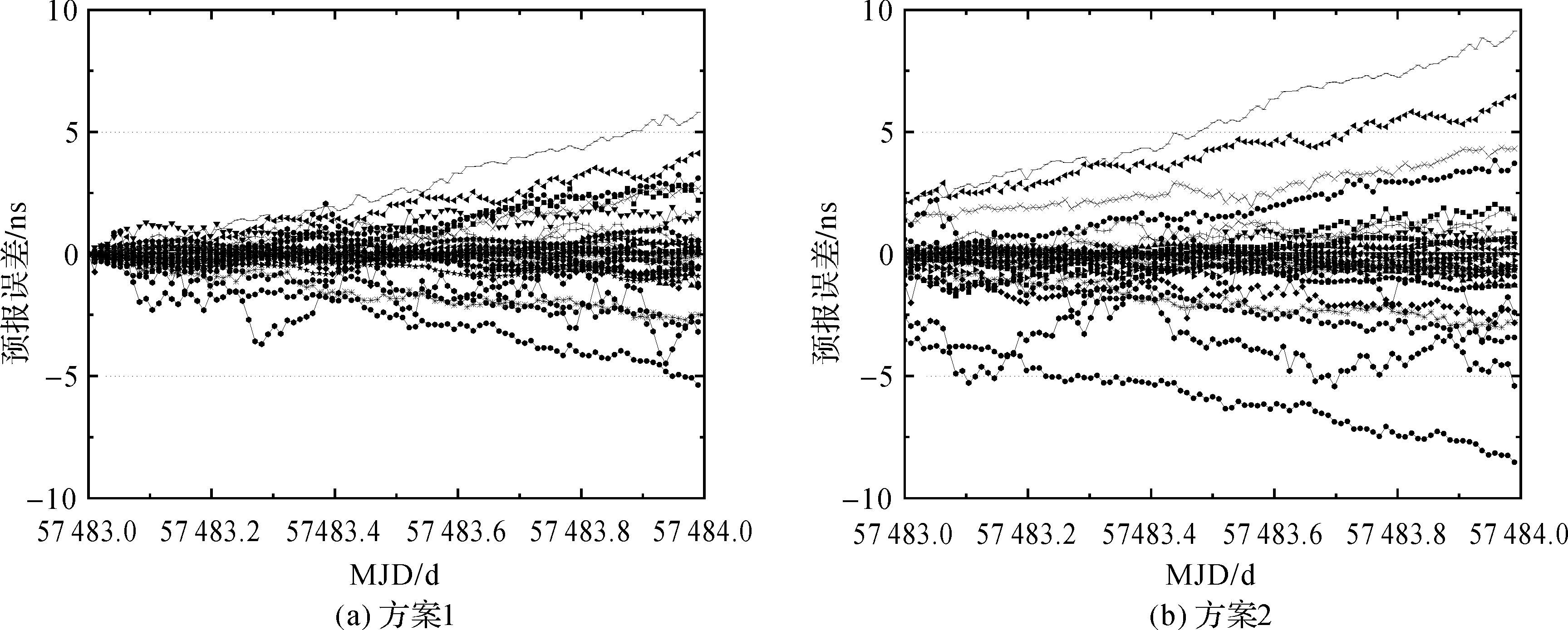
|
| 图 6 所有GPS卫星的钟差预报误差 Fig. 6 The prediction residuals for all GPS clocks |
通过上述初步分析,两种方案的预报精度差异主要取决于a0项。为了进一步验证这个结论,设计一种新的钟差预报方案(即方案3):取方案1的a0项与方案2的趋势项(a1,a2,a3,a4)组成新的预报模型。图 7给出了方案1与方案3对3与24 h的钟差预报精度统计。可以看出,对于3与24 h预报,方案3与方案1的钟差预报精度不存在明显差异,相对于方案2,预报精度得到大幅提高,进一步验证了本文提出的基于“两步法”预报方法,在卫星钟频率稳定度较差的情况下,能够更为准确地进行钟差预报。
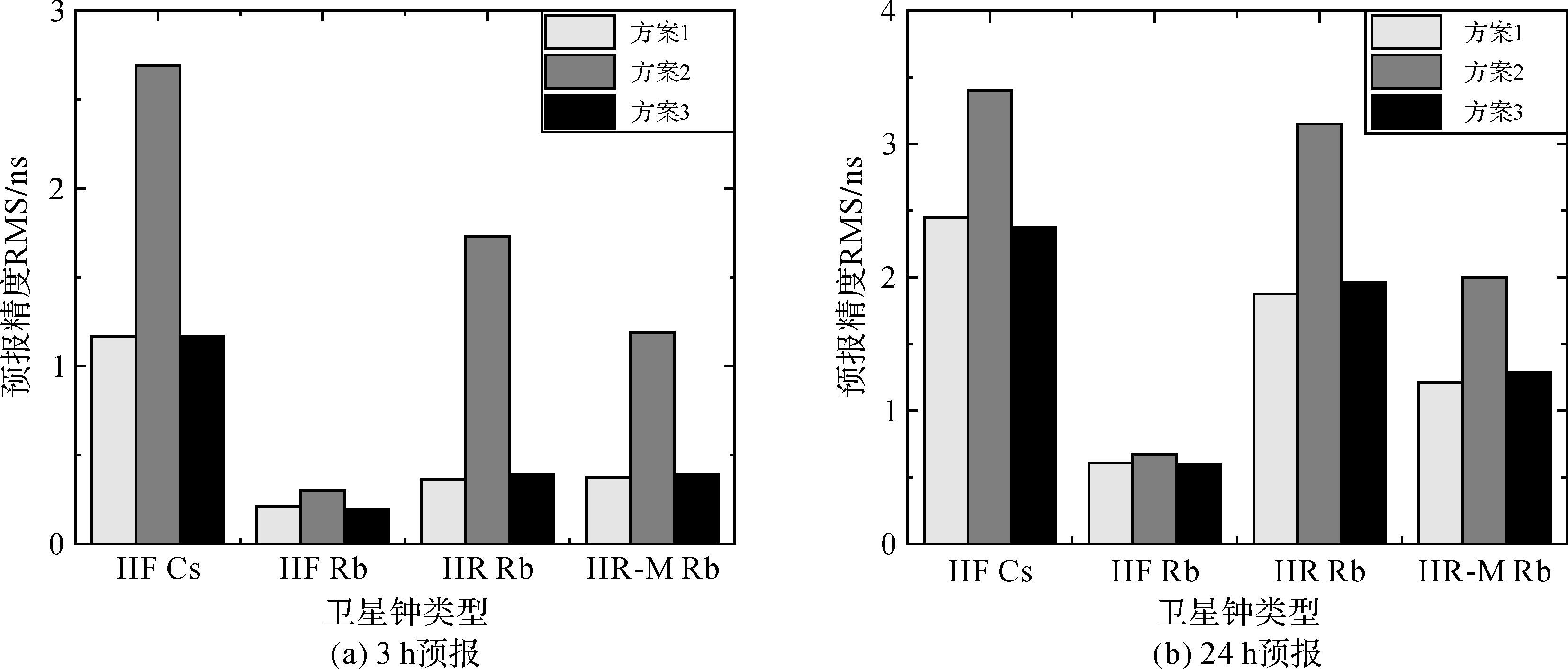
|
| 图 7 钟差预报精度比较 Fig. 7 Accuracy comparisons of clock prediction |
5 结论
本文提出了一种基于钟差变化率拟合的钟差建模与预报方法。该方法采用附加周期项的线性模型与二次多项式模型对钟差变化率序列进行拟合,估计钟差模型的趋势项参数(a1,a2,a3,a4),同时根据预报初始时刻的精密钟差来计算a0项,由此建立钟差预报模型参数(a0,a1,a2,a3,a4),预报后续时刻的钟差。该方法的数学模型本质上与传统的基于钟差拟合的预报方法相同,但模型参数的建立方法与数据处理方案不同,通过减小全弧段数据拟合引起的基准项a0的计算误差,来提高预报时段内的钟差预报精度。
使用IGR钟差产品,对所有GPS卫星钟进行钟差预报试验。结果表明:本文方法3、6、12与24 h的预报精度分别可达0.43、0.58、0.90与1.47 ns,相比于传统的基于钟差拟合的预报方法,分别提高了69.3%、61.8%、50.5%与37.2%;同时新方法的预报钟差精度也优于IGU产品中的预报钟差,钟差精度分别提高了15.7%、23.7%、27.4%与34.4%。因此,基于钟差变化率拟合的钟差预报方法,可以较大幅度提高实时钟差的中短期预报精度。
| [1] | 宋伟伟. 导航卫星实时精密钟差确定及实时精密单点定位理论方法研究[D]. 武汉:武汉大学, 2011. SONG Weiwei. Research on Real-time Clock Offset Determination and Real-time Precise Point Positioning[D]. Wuhan:Wuhan University, 2011. |
| [2] | GONZALEZ MARTINEZ F J. Performance of New GNSS Satellite Clocks[D]. München:Deutsche Geodätische Kommission, 2014. |
| [3] | BHATTARAI S. Satellite Clock Time Offset Prediction in Global Navigation Satellite Systems[D]. London:University of London, 2015. |
| [4] | 冯遂亮, 宋力杰. GPS卫星原子钟频率稳定度表征方法分析[J]. 全球定位系统, 2009, 34(1): 19–23. FENG Suiliang, SONG Lijie. The Analysis of Frequency Stability's Presenting Methods for Atomic Clocks of GPS Satellites[J]. GNSS World of China, 2009, 34(1): 19–23. |
| [5] | 王宇谱, 吕志平, 陈正生, 等. 卫星钟差预报的小波神经网络算法研究[J]. 测绘学报, 2013, 42(3): 323–330. WANG Yupu, LÜ Zhiping, CHEN Zhengsheng, et al. Research on the Algorithm of Wavelet Neural Network to Predict Satellite Clock Bias[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(3): 323–330. |
| [6] | HEO Y J, CHO J, HEO M B. Improving Prediction Accuracy of GPS Satellite Clocks with Periodic Variation Behaviour[J]. Measurement Science and Technology, 2010, 21(7): 073001. DOI:10.1088/0957-0233/21/7/073001 |
| [7] | ALLAN D W. Time and Frequency (Time-domain) Characterization, Estimation, and Prediction of Precision Clocks and Oscillators[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 1987, 34(6): 647–654. DOI:10.1109/T-UFFC.1987.26997 |
| [8] | 付文举. GNSS在轨卫星钟特性分析及钟差预报研究[D]. 西安:长安大学, 2014. FU Wenju. Research on Prediction and Characteristics of GNSS Satellite Clock on Orbit[D]. Xi'an:Chang'an University, 2014. |
| [9] | MONTENBRUCK O, HUGENTOBLER U, DACH R, et al. Apparent Clock Variations of the Block IIF-1(SVN-62) GPS Satellite[J]. GPS Solutions, 2012, 16(3): 303–313. DOI:10.1007/s10291-011-0232-x |
| [10] | 王国成, 柳林涛, 徐爱功, 等. 径向基函数神经网络在GPS卫星钟差预报中的应用[J]. 测绘学报, 2014, 43(8): 803–817. WANG Guocheng, LIU Lintao, XU Aigong, et al. The Application of Radial Basis Function Neural Network in the GPS Satellite Clock Bias Prediction[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(8): 803–817. DOI:10.13485/j.cnki.11-2089.2014.0078 |
| [11] | LEI Yu, ZHAO Danning, HU Zhaopeng, et al. Prediction of Navigation Satellite Clock Bias by Gaussian Process Regression[C]//Proceedings of China Satellite Navigation Conference (CSNC). Berlin:Springer, 2015:411-423. |
| [12] | GRIGGS E, KURSINSKI E R, AKOS D. An Investigation of GNSS Atomic Clock Behavior at Short Time Intervals[J]. GPS Solutions, 2014, 18(3): 443–452. DOI:10.1007/s10291-013-0343-7 |
| [13] | HUANG Guanwen, ZHANG Qin, XU Guochang. Real-time Clock Offset Prediction with an Improved Model[J]. GPS Solutions, 2014, 18(1): 95–104. DOI:10.1007/s10291-013-0313-0 |
| [14] | 王继刚, 胡永辉, 何在民, 等. 基于修正线性组合模型的原子钟钟差预报[J]. 天文学报, 2011, 52(1): 54–61. WANG Jigang, HU Yonghui, HE Zaimin, et al. Modified Linear Combination Model for Atomic Clock Prediction[J]. Acta Astronomica Sinica, 2011, 52(1): 54–61. |
| [15] | SENIOR K L, RAY J R, BEARD R L. Characterization of Periodic Variations in the GPS Satellite Clocks[J]. GPS Solutions, 2008, 12(3): 211–225. DOI:10.1007/s10291-008-0089-9 |
| [16] | 郑作亚, 党亚明, 卢秀山, 等. 附有周期项的预报模型及其在GPS卫星钟差预报中的应用研究[J]. 天文学报, 2010, 51(1): 95–102. ZHENG Zuoya, DANG Yaming, LU Xiushan, et al. Prediction Model with Periodic Item and Its Application to the Prediction of GPS Satellite Clock Bias[J]. Acta Astronomica Sinica, 2010, 51(1): 95–102. |
| [17] | RAY J. Summary of Clock Prediction Strategy[DB]. IGS Analysis Center Coordinator:IGSMAIL 2962, 2001. |
| [18] | RAY J, GRIFFITHS J. Change to Exclude Some IGU Clock Predictions[DB]. IGSMIAL 5965. IGS Analysis Center Coordinator, 2009. |
| [19] | DACH R, SCHILDKNECHT T, HUGENTOBLER U, et al. Continuous Geodetic Time-transfer Analysis Methods[J]. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, 2006, 53(7): 1250–1259. DOI:10.1109/TUFFC.2006.1665073 |
| [20] | U.S. Coast Guard Navigation Center. GPS Constellation Status[DB/OL].[2016-04-01]. http://www.navcen.uscg.gov/?Do=constellationStatus. |
| [21] | IGS. IGS Products[DB/OL].[2016-04-01]. http://www.igs.org/products/data. |
| [22] | IGS. IGS Analysis Center Coordinator[DB/OL].[2016-04-01]. http://acc.igs.org/. |



