2. 西南交通大学地球科学与环境工程学院, 四川 成都 611756
2. Faculty of Geosciences and Environmental Engineering, Southwest Jiaotong University, Chengdu 611756, China
传统遥感影像定位对控制点的依赖程度较高,控制点的数量与分布直接影响遥感影像地面目标定位的精度。但对于境外、海岛(礁)以及沙漠等地区,即使是稀少的控制点也较难获得。因此,在全球背景下,遥感影像采用无控定位是优先选择,也是势在必行的。
目前我国卫星装备的星敏感器精度较低,无控条件下不经过平差的直接前方交会(简称直接定位)的高程精度达不到1:5万比例尺地形图的精度要求(平面坐标误差15 m,高程误差6 m (1σ))[1],在这种条件下,进行区域网平差是提高定位精度的有效方法[2]。在仅布设少量控制点,通过区域网平差即可将影像的定位精度提高到像素级[3-5]。无控条件下,文献[1, 6]分别对天绘一号和资源三号影像进行区域网平差,多个试验区的检查结果均表明能满足1:5万比例尺地形图的精度要求,但平差过程较复杂,且无控条件下的区域网平差方法会受区域大小等的限制[7-8]。此外,除了利用地面控制点,目前仍然缺少其他更有效的对区域网平差所得的高精度定位结果进行检核的手段。
上述利用稀少控制点或在无控条件下的区域网平差均能达到较高的定位精度,都说明单景影像直接定位的误差大部分来自系统误差,因此,可得到与德国MOMS工程一致的结论:当星敏精度较低时,可利用已有的DEM、正射影像等数据提高影像的无控定位精度[9]。文献[10-11]利用经过纠正的光学影像和SAR影像辅助影像实现高精度的无控定位。这类方法受制于辅助数据,若待定位区域缺少这些数据则难以实施。全球公开DEM也用于辅助影像进行定位和纠正,文献[12-14]采用一定方式将基准DEM转换成影像,并通过与待定位影像进行匹配从基准DEM中提取控制信息;文献[15]对将DEM匹配用于补偿线阵影像定位误差的模型进行了理论推导与试验验证,结果表明对于姿态较稳定的线阵影像,DEM匹配可以用于辅助影像无控定向,但该方法需要较多的人工参与,自动化程度较低;文献[7]通过DEM的区域网平差从基准DEM中提取控制点用于重新解算RPC参数,有效提高了正射纠正的精度。
通过分析可知,上述各种方法利用基准数据进行辅助定位时,仍然未摆脱传统的基于地面控制点的影像定位思路,即通过匹配建立待定位数据与基准数据之间的对应关系,再采用一些策略从中提取少量信息用于定位。由于基准数据在各点位上的精度不完全相同,上述方法的定位精度存在一定的随机性;此外,这些方法忽略了基准数据在整个影像覆盖区域内精度的稳定性,难以充分发挥基准数据的优势,也很难达到很高的定位精度。针对上述问题,为了充分利用辅助数据的可靠性和稳定性,本文提出利用全球公开DEM辅助国产卫星影像无控定位(简称DEM辅助定位)的方法,旨在利用公开DEM提高国产卫星影像的无控定位精度,同时也为其他高精度定位方法提供一种新的有效的检核手段。
1 全球公开DEM及其辅助定位的基本原理SRTM DEM等全球公开DEM具有较高的全球陆地面积覆盖率,将这些公开数据用于辅助定位,可有效解决全球测绘的基准数据的问题。下面首先对文中所采用的全球公开DEM进行简要介绍,再对本文提出的DEM辅助的卫星影像无控定位的基本原理进行介绍。
1.1 全球公开DEMSRTM DEM和ASTER GDEM是目前应用最广泛的两种公开的全球DEM数据,本文利用两种DEM的最新版本,部分参数如表 1所示。
SRTM DEM V4.1是由国际热带农业中心(CIAT)利用文献[18]中的插值算法得到的新版本数据,该方法利用SRTM 30等多种辅助DEM对SRTM V3中的空洞进行了填补,其标称的绝对平面精度和绝对高程精度分别为±20 m、±16 m,置信度均为90%。2011年公布的ASTER GDEM V2在前一版本的基础上进行了部分改正,并填补了数据空洞,其标称的平面精度和高程精度分别为±30 m、±20 m,置信度均为95%。两种DEM的水平基准和高程基准均分别为WGS-84坐标系和EGM96模型。公开DEM自发布以来就受到了研究者的广泛关注,而数据的精度直接决定了数据的用途,研究者们采用诸多方法和数据对这些DEM的精度进行了评价[17, 19]。无论是官方公布数据还是研究者的评价结果,都表明SRTM DEM具有更高的精度。由于两种公开DEM的高程基准均为EGM96模型,因此,需要对影像定位结果和GPS控制点的大地高进行EGM96模型的改正,后文讨论的高程均为EGM96模型下的高程。
1.2 DEM辅助定位的基本原理利用公开DEM进行辅助定位时,文献[12-13]等将DEM降维成二维影像与待定位影像进行匹配,虽然在将DEM转换为影像时也利用了坡度、坡向等地形信息,但仍然损失了其中大量的有用信息;而对于采用DEM匹配的方法,也是在实现基准DEM与待定位DEM的匹配后从前者提取少量信息加以利用[7, 15]。
因此,目前诸多方法对基准DEM加以利用时仍未摆脱传统的基于地面控制点的影像定位思路,在建立待定位数据与基准数据之间的对应关系后,选取少量信息(如匹配确定的同名点)作为控制数据用于影像的定位,而忽略了基准DEM在整个影像覆盖区域内精度的稳定性和一致性,难以得到较高且较稳定的定位结果。由于基准DEM不仅在各种地形区的精度存在差异,在同一种地形区内各点位的精度也不完全相同,因此,仅利用其中部分数据进行辅助定位,其结果存在一定的随机性,定位精度会因匹配方法和控制数据提取方法的不同而有所差异。
考虑到公开DEM在全球范围内具有较稳定的精度[17-19],对各种地形均能较好的表达,为了充分利用公开DEM的丰富信息及其在较大范围内精度的一致性,本文对公开DEM进行利用时,直接对其整个表面数据加以利用,通过DEM匹配方法将待定位DEM与其进行准确的匹配。同时,也不再试图从基准DEM中提取控制数据,匹配确定的待定位DEM的改正参数即用于对影像直接定位结果进行改正,以充分发挥基准DEM具有较高整体精度的优势。
因此,DEM辅助定位的基本原理为:通过密集匹配等过程从影像数据中提取待定位DEM,然后采用DEM匹配方法与对应区域的公开DEM进行匹配,计算待定位DEM的包括旋转、平移、缩放的7个改正参数,并利用其对影像直接定位结果进行物方改正以改善无控定位的精度。
由于文中参与DEM匹配的待定位DEM是采用“航天泰坦”商业软件利用线阵影像和RPC参数提取的,故后文仅对该软件提取DEM时所需设置的“匹配点间隔”参数进行说明,具体理论不再赘述。
2 引入截尾最小二乘估计的DEM匹配 2.1 DEM匹配方法的选择对于DEM匹配,最小高差(least Z-difference, LZD)法是结合DEM自身数据结构特点的匹配方法,无需任何预处理步骤,是应用最广泛的DEM匹配方法[20]。文献[21]设计的多组对比试验表明,对于格网DEM的匹配,LZD法在拉入范围、精度、效率等方面的性能均优于迭代最邻近点(iterative closest point, ICP)法和最小二乘3D表面匹配(least squares 3D surface matching,LS3D)法[22]。LZD法将如式(1)所示的“所有对应点间高差平方和最小”作为目标函数。
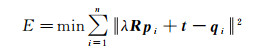 (1)
(1)
式中,pi=[pix piy piz]T和qi=[qix qiy qiz]T分别为待定位DEM中i点及其在基准DEM中对应点的坐标向量;λ为缩放系数;R为由3个旋转角度ω、φ、κ确定的旋转矩阵;t=[tx ty tz]T为平移向量,表示沿3个坐标轴方向的平移量。ω、φ、κ、λ、tx、ty、tz即为LZD法待求的7个变换参数。
由于依靠最小二乘理论的经典LZD法不具备抗差性,研究者将其与不同的稳健估计相结合,得到很多稳健的DEM匹配方法。截尾最小二乘(least trimmed squares,LTS)估计作为一种具有高崩溃污染率的稳健估计,具有光滑的目标函数,对局部影响不敏感,具有确定的数值计算结果,利用其进行DEM匹配时每次迭代过程一致,可很好地与LZD法的框架进行融合[20],其定义如下
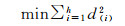 (2)
(2)
式中,(i)表示升序排列后的序号,d(i)2即为升序排列后第i个余差的平方;h∈[n/2, n],对于大数据集而言,当h≈n/2时,崩溃污染率≈50%。
文献[20]将LTS估计与LZD法进行结合,提出一种LTS-LZD法,对DEM之间的差异具有很好的探测能力,当DEM之间存在较大变形时也能实现准确的匹配。由于本文中参与匹配的DEM是不同时相的,原始影像数据获取时间前后甚至超过十年,地表存在或多或少的变化,数据获取的技术手段也可能不同。此外,DEM生成过程中还可能引入一定的粗差、随机误差等,这些都会增加参与匹配的DEM之间的差异,为了避免这些差异影响匹配结果,本文在进行DEM匹配时也采用引入LTS估计的LZD法。下面就对本文提出的自动探测和剔除DEM间差异的方法的基本原理进行重点介绍。
2.2 DEM间差异的自动探测与剔除采用LZD法进行DEM匹配是一个迭代的过程,由于在匹配过程中姿态差异、地表变化、粗差、随机误差等因素的共同影响,使得对应点的高差分布是不断变化的[20],为实现方法的自动化,应能在匹配过程中自适应的确定截断高差,从而避免表面差异对匹配带来不利影响。文献[20]重点在于提高DEM匹配方法的差异探测能力,主要对存在较大变形区的DEM进行讨论,DEM之间较大的变形区使得对应点间高差绝对值(在不产生歧义的情况下,后文直接称作高差)的直方图会出现代表变形区的第二个波峰,因此,通过搜索直方图的波谷确定的截断高差即可自动的对DEM间的变形区和非变形区进行区分。
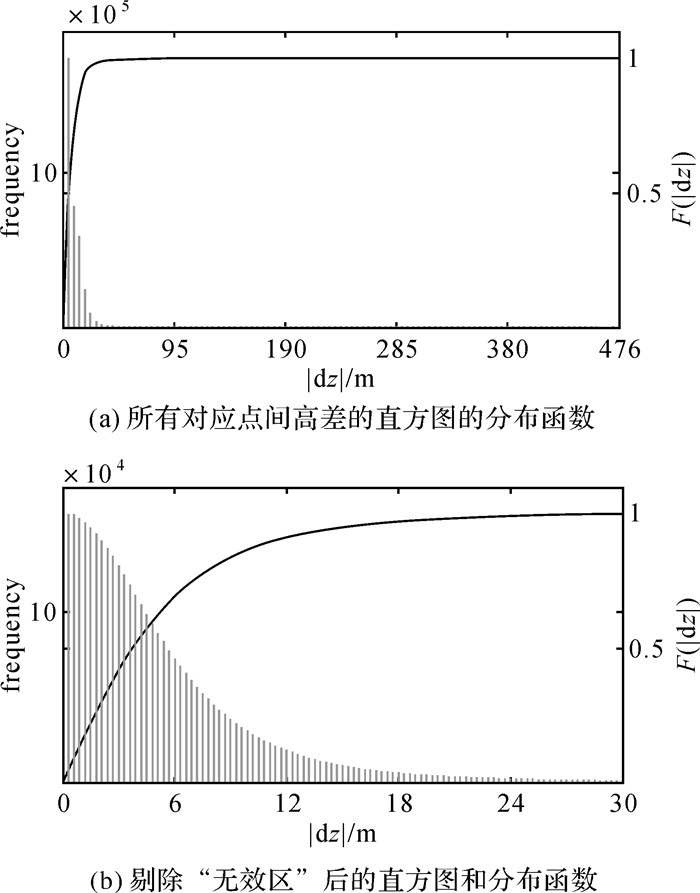
通过分析可知,虽然本文中参与匹配的DEM之间存在一定差异,但一景卫星影像的覆盖范围较大,地表变化、粗差等导致的DEM间差异所占面积比例不会太大,LZD法确定的对应点间的高差直方图基本不会出现两个波峰,更多地表现为随着高差增大频数迅速减少的形式。图 1(a)所示的则为某景试验影像的待定位DEM与SRTM DEM匹配时某次迭代所得的高差直方图。因此,本文利用LTS估计时不能通过上述方法确定截断高差。
|
| 图 1 高差直方图“无效区”的剔除 Fig. 1 Elimination of Z-difference histgram "invalid area" |
2.2.1 高差直方图“无效区”的剔除
通过对LZD法确定的对应点间的高差分布进行分析可知,变形、粗差等原因导致高差所覆盖的数值范围较大,但高差直方图中较大数值区的频数却远远小于较小数值区,绝大部分频数集中在起始的几个区间内。若直方图数值较小或较大一侧超过50%的统计区间的频数和不足1%,则称其存在“无效区”,“无效区”的面积则为在“无效区”存在一侧,频数和为1%的区间数占总区间数的比例。如图 1(a)所示,高差大于95 m的点不足1%,但对应的区间数却占整个直方图的80%,故该直方图的“无效区”面积超过80%。这种直方图很难表现出正确对应点间高差的分布特点,也难以直接对其进行分析与利用,因此,首先对由变形、粗差等导致的“无效区”进行剔除,再根据高差的分布确定截断高差。
根据LZD法的基本原理可知,当DEM实现较好的匹配时,对应点间的高差服从均值为0的正态分布,而对于正态分布有:P(|x-μ|≤σ)≈68.3%,P(|x-μ|≤3σ)≈99.7%,即与均值的距离超过3倍标准差的点在统计学上的概率不足0.5%。因此,此处根据正态分布的3σ准则对变形、粗差等造成的直方图“无效区”进行剔除,主要步骤如下:
(1) 根据对应点高差的最大值m1和最小值m2将数值区间均分为N1段,并统计高差的分布函数F1。
(2) 求得分布函数F1大于68.3%的第一个区间的上界u1。
(3) 判断r×u1是否小于m1,若是,则认为仍有残留的“无效区”,将大于r×u1的高差剔除,并令m1=r×u1,重复进行步骤(1)-(2),直至r×u1不小于m1;反之,则完成“无效区”的剔除。其中r是所取的标准差倍数,即保留大小不超过r倍标准差的高差,根据上述分析,r≥3。
按照上述步骤对图 1(a)所示的直方图进行处理(令r=5),可得到如图 1(b)所示的能较好体现正确对应点间高差的分布特点的直方图。
2.2.2 截断高差的自适应确定对“无效区”内的对应点进行剔除后,仍然会存在少量数值较小的变形区、粗差对应的高差值。前文已分析,在迭代过程中高差分布是不断变化的,为保证方法的自动化水平,应能在每次迭代中根据高差的分布特点自适应的确定截断高差。此处则利用高差分布函数的增长率自适应确定截断高差,并将平均增长率的1/m设置为增长率阈值T,具体步骤如下:
(1) 将经过“无效区”剔除的高差分为N2段,并统计高差的分布函数F2,增长率阈值T则为1/(mN2)。
(2) 从分布函数F2大于p的第一个分段开始,依次计算各段的增长率,将增长率小于阈值T的第一个区间的上界u2确定为截断高差,其中p应不小于LTS估计的最大崩溃污染率50%。
试验结果表明,当m较大时,其取值对定位结果的影响很小,为保证本文方法的稳定性,尽量剔除变形区、粗差点,文中m取2。
3 试验及结果分析 3.1 试验数据本文的试验数据包括登封测区的天绘一号影像数据和法国测区的资源三号影像数据。登封测区范围为112.556°E-113.964°E,33.896°N-34.953°N,包括山地、丘陵等多种地形,且以山地为主,高程范围约为50~1400 m,该测区包括河南登封地区3景1B级三线阵全色影像及对应的RPC参数,每景影像包括5 m分辨率的前下后三视,数据获取时间为2015年6月至7月。此外,将该区域利用ADS40航空影像采用“像素工厂”制作的5 m分辨率的DEM也作为基准DEM加以使用,影像于2010年5月获取,空间分辨率0.4 m,DEM的平面坐标是UTM投影6°分带坐标(简称UTM坐标),高程是大地高,为便于叙述,后文简称ADS40 DEM。试验区内共30个已知点,均采用野外控制测量,通过RTK方式在WGS-84坐标系下获取,平面精度优于0.1 m,高程精度优于0.2 m,像点坐标采用人工转刺,精度优于1个像元[5]。各景影像、ADS40 DEM的覆盖范围和已知点的分布如图 2(a)所示。

|
| 图 2 试验数据 Fig. 2 Distribution of experimental data |
法国测区范围为6.196°E-6.968°E,43.031°N-43.628°N,高程范围约为0~900 m,该测区包括法国Sainte-Maxime地区的1景经过相对辐射校正和传感器校正的影像数据,包括3.5 m分辨率的前后两视线阵全色影像和RPC参数,数据获取时间为2014年8月,数据由国家测绘地理信息局卫星测绘应用中心提供[23]。影像覆盖范围和12个已知点分布如图 2(b)所示。
为便于后文分析DEM辅助定位方法的性能,此处首先利用高差法对基准DEM的精度进行评价。基准DEM在各已知点处高程误差的中误差如表 2所示,由结果可知,SRTMDEM和ADS40 DEM的高程精度较ASTER GDEM高,这与两种公开DEM标称的精度高低是一致的。
| m | |||
| SRTM-DEM | ASTER GDEM | ADS40 DEM | |
| 登封测区 | 3.300 | 7.887 | 2.331 |
| 法国测区 | 2.707 | 6.598 | - |
3.2 试验方案设计
为了验证本文方法的可行性以及分析其精度、抗差性等性能,设计如下3种试验方案。
方案1:为了验证利用本文方法辅助国产卫星影像进行无控定位的可行性,分别利用天绘一号和资源三号卫星影像进行试验,将DEM辅助定位的结果与直接定位、有控定位的精度进行定量比较。
方案2:为了验证本文方法能对基准DEM中的信息充分利用,定位结果具有较好的稳定性,分别采用不同分辨率的基准DEM和待定位DEM进行DEM匹配确定改正参数,并将本文方法的定位结果与匹配时采用经典LZD法的定位结果进行比较。
方案3:为了验证本文方法的稳健性,利用本文方法对通过密集匹配提取的DEM中存在较大面积粗差的影像进行辅助定位试验,并与匹配时采用经典LZD法的定位结果进行比较。
3.3 试验结果及分析 3.3.1 方案1的试验结果分别利用基准DEM辅助登封测区的影像004-135和法国测区的影像进行试验,并与直接定位以及不同布控方案的有控定位的精度进行比较。两景影像中分别有9个、12个已知点,所有已知点均作为直接定位和DEM辅助定位结果的检查点;对于有控定位,方案A、B分别选择靠近影像中心的一个点和靠近影像各角点且分布均匀的3个点作为控制点,其余点作为检查点。
由于公开DEM和ADS40 DEM的平面坐标分别是地理坐标和UTM坐标,为避免不必要的坐标转换,从影像中提取两种坐标系下的待定位DEM,并分别与相同坐标系下的基准DEM进行匹配。通过计算可知,登封测区所处位置经纬度方向0.000 1°在UTM坐标系中的长度约为10 m,故本文后续试验近似认为格网间距为0.000 1°s和10s m的DEM的分辨率一致(s≥1)。本方案利用0.000 3°和30 m分辨率的待定位DEM进行试验,提取DEM时的匹配点间隔为5像素。为尽量避免剔除正确对应点的高差,且考虑到影像覆盖范围内的变形不会太大,本文所有试验在对DEM间差异进行自动探测与剔除时,标准差倍数r取5,p取0.6。两景影像在各种定位方案中的定位结果如表 3、4所示,其中max为误差绝对值的最大值,文中X方向、Y方向和平面上的误差均是在高斯投影6°带坐标系下统计的。
| m | |||||||||||||
| 方案 | X | Y | 平面 | 高程 | |||||||||
| max | STD | RMSE | max | STD | RMSE | RMSE | max | STD | RMSE | ||||
| 直接定位 | 12.970 | 2.029 | 9.756 | 21.998 | 3.002 | 17.861 | 20.351 | 14.835 | 2.754 | 9.693 | |||
| 有控定位方案A | 6.305 | 1.832 | 3.699 | 7.568 | 2.965 | 4.654 | 5.945 | 7.980 | 2.780 | 3.809 | |||
| 有控定位方案B | 3.057 | 1.607 | 2.120 | 7.185 | 3.058 | 3.169 | 3.813 | 6.085 | 2.349 | 3.681 | |||
| SRTM DEM | 4.531 | 3.041 | 2.875 | 9.685 | 2.964 | 3.798 | 4.763 | 6.134 | 2.668 | 2.666 | |||
| ASTER GDEM | 13.895 | 2.478 | 9.535 | 19.826 | 4.162 | 14.980 | 17.757 | 4.140 | 2.704 | 3.137 | |||
| ADS40 DEM | 4.380 | 1.733 | 2.215 | 5.664 | 2.954 | 2.790 | 3.562 | 4.770 | 2.550 | 2.411 | |||
| m | |||||||||||||
| 方案 | X | Y | 平面 | 高程 | |||||||||
| max | STD | RMSE | max | STD | RMSE | RMSE | max | STD | RMSE | ||||
| 直接定位 | 15.206 | 2.538 | 12.425 | 9.851 | 2.125 | 7.188 | 14.354 | 12.784 | 4.121 | 6.227 | |||
| 有控定位方案A | 6.456 | 2.344 | 4.398 | 5.458 | 2.044 | 3.089 | 5.374 | 7.658 | 4.226 | 5.143 | |||
| 有控定位方案B | 5.090 | 2.257 | 2.313 | 3.574 | 2.168 | 2.267 | 3.238 | 8.823 | 5.024 | 5.007 | |||
| SRTM DEM | 11.849 | 2.090 | 7.292 | 5.030 | 2.244 | 3.035 | 7.898 | 9.253 | 3.992 | 4.253 | |||
| ASTER GDEM | 9.070 | 2.119 | 5.125 | 7.638 | 2.547 | 4.716 | 6.965 | 12.249 | 4.298 | 5.980 | |||
从试验结果可知,单景影像直接定位的精度较低,但误差的均方差均很小,这说明直接定位的结果存在很大的系统误差;在有少量控制点参与定位时即可大大提高定位精度。DEM辅助定位的结果表明,利用SRTM DEM能得到比利用ASTER GDEM更高的定位精度,前者的平面和高程精度分别优于8 m和5 m,高程精度甚至优于有少量控制点参与定位的结果;利用ADS40 DEM能得到最高的定位精度,这与表 2中评价的各种基准DEM精度的高低顺序是一致的,说明DEM辅助定位的精度与基准DEM的精度直接相关。此外,部分有控定位方案和DEM辅助定位方案误差的均方差较直接定位有所减小,这表明本文方法可达到与有控定位类似的效果。
试验结果及相关分析表明,在有SRTM DEM以及其他一些局部的高精度DEM参与辅助定位时,利用本文方法辅助国产卫星影像进行无控定位是切实可行的。
3.3.2 方案2的试验结果由于影像006-135覆盖范围内主要是山地地形,地形起伏较大,利用其进行试验更能体现本文方法对各种地形的适应性,因此,本方案选用该景影像进行试验。为验证本文方法能对基准DEM整体信息加以充分利用,设计如下两组试验:第1组分别从影像中提取不同分辨率的待定位DEM (TH DEM)与公开DEM进行匹配;第2组将原始ADS40 DEM进行降采样得到不同分辨率的基准DEM (具体分辨率如表 5所示),并分别与不同分辨率的TH DEM进行匹配。利用匹配确定的变换参数对检查点的直接定位结果进行改正,最后对DEM辅助定位的精度进行比较分析。首先利用影像内22个已知点采用高差法对本方案所采用的基准DEM进行精度评价,评价结果如表 5所示。提取不同分辨率的TH DEM时,当s取1、2、3、4、5时,匹配点密度分别为3、3、5、7、9像素;当s≥6时,匹配点密度为11像素。
| m | ||||||||||||
| 基准DEM | SRTM DEM | ASTER GDEM | ADS40 DEM | |||||||||
| 5 | 10 | 20 | 30 | 40 | 50 | 60 | 80 | 100 | 120 | |||
| 精度 | 3.640 | 8.629 | 2.661 | 2.980 | 3.086 | 3.738 | 3.821 | 3.900 | 4.169 | 4.371 | 4.157 | 4.481 |
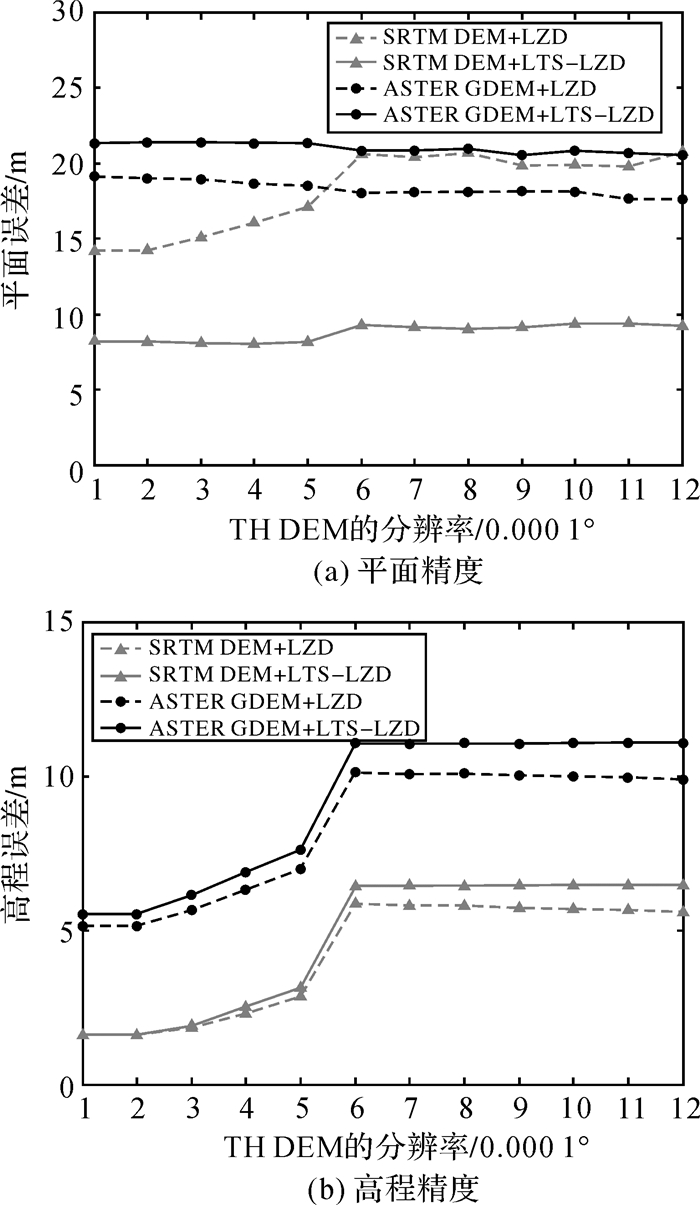
对于第1组试验,利用不同的匹配方法、基准DEM以及待定位DEM所得的平面和高程精度如图 3所示,其中小三角形标记的和小圆点标记的分别是利用SRTM DEM和ASTER GDEM的结果,虚线和实线分别是采用经典LZD法和本文匹配方法的结果。
|
| 图 3 TH DEM的分辨率对定位结果的影响 Fig. 3 The influence of the TH DEM resolution to positioning result |
当匹配采用经典LZD法时,随着TH DEM分辨率的变化,辅助定位的精度不太稳定,且随着分辨率的降低,精度有逐渐降低的趋势。引入稳健估计后,平面精度基本不受TH DEM分辨率的影响,利用SRTM DEM时,平面精度有大幅度的提高,能保持在较高的精度水平,而利用ASTER GDEM时,平面精度反而有一定程度的降低;高程精度整体有一定的降低,在TH DEM分辨率较高时精度较高,当分辨率降到一定数值时精度会出现一定幅度的骤降,此后分辨率再降低,精度保持稳定。通过分析可知,这是因为引入LTS估计将高差较大的对应点剔除而不参与平差,但这些点不完全是变形区和粗差点,也可能是姿态差异等原因导致的,这就使得迭代可能未到最理想匹配状态即达到停止条件,从而造成定位精度甚至有所降低,但这并不妨碍高精度基准DEM辅助影像得到较高的无控定位精度。对于两种公开DEM,虽然SRTM DEM的分辨率较ASTER GDEM低,但其辅助定位的精度远高于后者。
总的来说,由于本文方法对基准DEM中的整体信息加以充分利用,定位结果具有较好的稳定性;利用SRTM DEM能得到更高的辅助定位精度,当待定位DEM的分辨率较高时,能达到测制1:5万比例尺地形图的精度要求。
第2组试验分别利用不同分辨率的ADS40 DEM与TH DEM进行匹配,定位的结果如图 4所示。

|
| 图 4 DEM的分辨率对定位结果的影响 Fig. 4 The influence of the DEM resolution to positioning result |
由图 4可知,当参与匹配的TH DEM分辨率较高时,平面精度和高程精度均较高,具有较好的稳定性,基本不受ADS40 DEM的分辨率的影响;分辨率较低时,ADS40 DEM的分辨率对平面精度有一定的影响。关于TH DEM分辨率对定位结果的影响与第1组试验的结论一致,不再赘述。
此外,需要指出的是,若TH DEM分辨率较高,利用SRTM DEM和不同分辨率的ADS40 DEM时,所得的高程精度约为2 m,均高于表 5所列的各种基准DEM的高程精度,这说明DEM辅助定位的精度虽然直接受基准DEM精度的影响,但不是唯一因素,也不限于其精度,当影像内部几何稳定性较高时,采用本文方法有突破基准DEM精度的潜力。
综合本方案两组试验的结果及分析可得:本方法对基准DEM中的整体信息进行了充分利用,定位结果具有较好的稳定性;基准DEM的分辨率对定位结果影响较小,其精度则直接影响着影像的定位精度,但不是唯一因素和决定性因素;利用SRTM DEM时能得到更高的定位精度。
3.3.3 方案3的试验结果在提取影像006-136的DEM时,由于匹配算法等原因使得提取的DEM出现较大区域的粗差,如图 5(a)中东南角高程较大的区域,约占整个DEM区域的7%,图 5(b)为对应区域的SRTM DEM,因此利用该景影像验证本文方法的稳健性。由方案2的试验结果可知,当TH DEM分辨率高于0.000 5°时,能得到较高的水平精度和高程精度,故本方案采用分辨率为0.000 4°(或40 m)的TH DEM进行匹配。分别采用本文匹配方法和经典LZD法利用各种基准DEM对该影像进行定位,试验结果如表 6所示,第1列按“基准DEM+DEM匹配方法”的格式给出,其中“SD”“AG”“AD”分别代表SRTM DEM、ASTER GDEM和ADS40 DEM,“L-L”和“LZD”分别代表本文提出的LTS-LZD法和经典LZD法,本方案采用原始ADS40 DEM进行试验。

|
| 图 5 从影像006-136中提取的DEM和对应的SRTM DEM Fig. 5 TH DEM extracted from image 006-136 and SRTM DEM |
| m | ||||
| 方法 | X | Y | 平面 | 高程 |
| SD+LZD | - | - | - | - |
| SD+L-L | 3.981 | 7.612 | 8.590 | 2.044 |
| AG+LZD | 97.494 | 106.017 | 144.030 | 24.216 |
| AG+L-L | 21.263 | 17.730 | 27.685 | 6.116 |
| AD+LZD | 8.364 | 10.293 | 13.263 | 2.582 |
| AD+L-L | 3.804 | 5.496 | 6.684 | 2.966 |
由表 6可知,经典LZD法的抗差性较差,利用公开DEM辅助定位时不能收敛或迭代停止在错误的匹配位置,定位精度低;本文方法则能有效剔除上述粗差区的影响,定位精度有大幅度的提高,利用两种公开DEM所得的定位精度与前几组试验的结果一致。利用ADS40 DEM辅助定位时,采用经典LZD法也能得到较准确的定位结果,这是因为该影像覆盖范围只有北侧部分有基准DEM,匹配时粗差区域无对应点,故未参与匹配,不会对定位结果产生影响;本文方法虽然得到的高程精度有一定降低,但平面精度得到了有效的提高,这与方案2的试验结果一致;还需要指出的是,此处的定位精度均低于前两方案采用ADS40 DEM辅助定位的精度,这说明基准DEM的有效面积也会影响定位结果,要保证具有更高、更稳定的辅助精度,应尽量利用覆盖整个影像区域的基准DEM。
试验结果表明,本文方法能有效消除DEM中粗差、变形等的影响,具有较好的稳健性,从而保证达到较高的无控定位精度。
4 结论本文针对国产卫星影像无控定位的问题,提出一种将公开DEM用于辅助定位的方法,并设计多组对比试验对该方法的性能进行了充分的验证,根据试验结果可得如下几点结论:
(1) 在有SRTM DEM等具有较高精度的DEM参与辅助定位时,本文方法切实可行,能用于实现国产卫星影像的无控定位。
(2) 本文方法对基准DEM的整体高精度特性和丰富信息进行了充分的利用,定位结果具有较好的稳定性;基准DEM的精度直接影响着最终的定位结果,但不是唯一因素和决定性因素;当待定位DEM分辨率较高时,定位结果基本不受参与匹配的DEM分辨率的影响。
(3) 本文方法具有较好的稳健性,能有效消除DEM间粗差、变形等的影响。
(4) 当参与匹配的待定位DEM分辨率不低于0.000 5°(或50 m)时,利用SRTM DEM辅助单景国产卫星(包括天绘一号和资源三号)影像进行无控定位,平面精度和高程精度分别优于9 m、5 m,能较好地满足测制1:5万比例尺地形图的精度要求。
(5) 本文方法还为卫星影像定位精度的检核提供了一种新的便捷有效的手段,其定位结果可用于对其他方法的定位结果进行检核。
当然,本文所进行的试验还很有限,需要进一步利用更多的数据验证本文方法的性能,以得到更可靠、更具说服力的结论。此外,通过分析影像重叠区内检查点的定位结果发现,利用各景影像的改正参数对直接定位结果进行改正所得的辅助定位结果存在一定差异,因此,后续研究将把DEM匹配结果纳入区域网平差中,以保证较大区域范围得到更稳定和更一致的定位结果。
| [1] | 王任享, 胡莘, 王建荣. 天绘一号无地面控制点摄影测量[J]. 测绘学报, 2013, 42(1): 1–5. WANG Renxiang, HU Xin, WANG Jianrong. Photogrammetry of Mapping Satellite-1 without Ground Control Points[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(1): 1–5. |
| [2] | 王任享. 天绘一号卫星无地面控制点摄影测量关键技术及其发展历程[J]. 测绘科学, 2013, 38(1): 5–7, 43. WANG Renxiang. Key Photogrammetric Progress of TH-1 Satellite without Ground Control Point[J]. Science of Surveying and Mapping, 2013, 38(1): 5–7, 43. |
| [3] | 刘楚斌, 张永生, 范大昭, 等. 资源三号卫星三线阵影像自检校区域网平差[J]. 测绘学报, 2014, 43(10): 1046–1050. LIU Chubin, ZHANG Yongsheng, FAN Dazhao, et al. Self-calibration Block Adjustment for Three Line Array Image of ZY-3[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(10): 1046–1050. DOI:10.13485/j.cnki.11-2089.2014.0148 |
| [4] | ZHANG Guo, WANG Taoyang, LI Deren, et al. Block Adjustment for Satellite Imagery Based on the Strip Constraint[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(2): 933–941. DOI:10.1109/TGRS.2014.2330738 |
| [5] | 张艳, 王涛, 冯伍法, 等. "天绘一号"卫星三线阵CCD影像自检校区域网平差[J]. 遥感学报, 2015, 19(2): 219–227. ZHANG Yan, WANG Tao, FENG Wufa, et al. Self-calibration Block Adjustment for Mapping Satellite-1 Three Linear CCD Image[J]. Journal of Remote Sensing, 2015, 19(2): 219–227. |
| [6] | WANG Taoyang, ZHANG Guo, LI Deren, et al. Geometric Accuracy Validation for ZY-3 Satellite Imagery[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(6): 1168–1171. DOI:10.1109/LGRS.2013.2288918 |
| [7] | 张浩, 张过, 蒋永华, 等. 以SRTM-DEM为控制的光学卫星遥感立体影像正射纠正[J]. 测绘学报, 2016, 45(3): 326–331. ZHANG Hao, ZHANG Guo, JIANG Yonghua, et al. A SRTM-DEM-controlled Ortho-rectification Method for Optical Satellite Remote Sensing Stereo Images[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(3): 326–331. DOI:10.11947/j.AGCS.2016.20150358 |
| [8] | BOUILLON A, BERNARD M, GIGORD P, et al. SPOT5 HRS Geometric Performances: Using Block Adjustment as a Key Issue to Improve Quality of DEM Generation[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2006, 60(3): 134–146. DOI:10.1016/j.isprsjprs.2006.03.002 |
| [9] | EBNER H, STRUNZ G. Combined Point Determination Using Digital Terrain Models as Control Information[J]. International Archives of Photogrammetry and Remote Sensing, 1988, 27(B11/3): 578–587. |
| [10] | GLANINETTO M, SCAIONL M. Automated Geometric Correction of High-resolution Pushbroom Satellite Data[J]. Photogrammetric Engineering and Remote Sensing, 2008, 74(1): 107–116. DOI:10.14358/PERS.74.1.107 |
| [11] | REINARTZ P, MÜLLER R, SCHWIND P, et al. Orthorectification of VHR Optical Satellite Data Exploiting the Geometric Accuracy of TerraSAR-X Data[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2011, 66(1): 124–132. DOI:10.1016/j.isprsjprs.2010.10.003 |
| [12] | LEPRINCE S, BARBOT S, AYOUB F, et al. Automatic and Precise Orthorectification, Coregistration, and Subpixel Correlation of Satellite Images, Application to Ground Deformation Measurements[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(6): 1529–1558. DOI:10.1109/TGRS.2006.888937 |
| [13] | SCHNEIDER M, SURI S, LEHNER M, et al. Matching of High-resolution Optical Data to a Shaded DEM[J]. International Journal of Image and Data Fusion, 2012, 3(2): 111–127. DOI:10.1080/19479832.2011.618468 |
| [14] | 贺宏. DEM辅助无地面控制点卫星影像定位技术研究[D].郑州:信息工程大学, 2013. HE Hong. Research on Satellite Image Positioning without Ground Control Point Assisted by DEM[D]. Zhengzhou: Information Engineering University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-90005-1013353652.htm |
| [15] | KIM T, JEONG J. DEM Matching for Bias Compensation of Rigorous Pushbroom Sensor Models[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2011, 66(5): 692–699. DOI:10.1016/j.isprsjprs.2011.06.002 |
| [16] | JARVIS A, REUTER HI, NELSON A, et al. Hole-filled Seamless SRTM Data V4, International Centre for Tropical Agriculture (CIAT)[DB/OL]. (2008-08-19)[2016-06-10]. http://srtm.csi.cgiar.org. |
| [17] | TACHIKAWA T, KAKU M, IWASAKI A, et al. ASTER Global Digital Elevation Model Version 2.Summary of Validation Results[R].[S.l.]: NASA. |
| [18] | REUTER H I, NELSON A, JARVISA. An Evaluation of Void-filling Interpolation Methods for SRTM Data[J]. International Journal of Geographical Information Science, 2007, 21(9): 983–1008. DOI:10.1080/13658810601169899 |
| [19] | RODRÍGUEZ E, MORRIS C S, BELZ J E. A Global Assessment of the SRTM Performance[J]. Photogrammetric Engineering & Remote Sensing, 2006, 72(3): 249–260. |
| [20] | 张同刚, 岑敏仪, 冯义从, 等. 采用截尾最小二乘估计的DEM匹配方法[J]. 测绘学报, 2009, 38(2): 144–151. ZHANG Tonggang, CEN Minyi, FENG Yicong, et al. DEMMatching Algorithm Using Least Trimmed Squares Estimator[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(2): 144–151. DOI:10.3321/j.issn:1001-1595.2009.02.009 |
| [21] | 杨容浩.无控制DEM匹配算法性能比较与改进研究[D].成都:西南交通大学, 2012. YANG Ronghao.The Research on Performance Comparison and Improvement of DEM Matching Algorithms without Ground Control Point[D]. Chengdu: Southwest Jiaotong University, 2012. |
| [22] | GRUEN A, AKCA D. Least Squares 3D Surface and Curve Matching[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2005, 59(3): 151–174. DOI:10.1016/j.isprsjprs.2005.02.006 |
| [23] | ISPRS. ZY-3 Satellite High Resolution Stereo Image[DB/OL]. (2015-09-25)[2016-06-10]. http://www.isprs.org/data/zy-3/default.aspx. |


