2. 浙江省地理信息中心, 浙江 杭州 310012
2. Geomatics Center of Zhejiang, Hangzhou 310012, China
地理信息科学在21世纪遇到了数据密集、计算密集、并发访问密集和时空密集的挑战[1]。近年来在IT领域飞速发展的云计算技术的超大规模、虚拟化、高性能、高可靠性等特点给大规模空间数据处理提供了机遇[2-6]。云存储是在云计算环境下针对数据存储发展出来的一个新概念,是指通过计算机集群的应用、分布式文件系统或网格技术等,把网络中各种类型的存储设备在应用软件协助下集合起来,共同为用户提供透明的数据存储服务[7]。目前主流的云数据管理系统,如HBase、Cassandra和亚马逊的Amazon Simple Storage,底层存储系统都是基于BigTable管理系统发展而来,存储系统采用的“键-值”存储模型,具有很高的扩展性、可用性和容错性。但是“键-值”模型是一种一维存储结构,仅支持基于主键的快速查询,因缺乏索引机制,所以不能提供高效的多维查询,这限制了云计算在地理信息科学中的应用。利用云计算推进地理信息科学的发展首先需要面对的就是空间数据的云存储,而云存储环境下的空间索引技术又是其中需要研究的首要问题。目前分布式空间索引主要有两个研究方向:一种是改进传统的用于单服务器的多维数据索引的扩展性,使之支持多服务器分布式空间检索,如SD-Rtree[8]、P2PR-Tree[9]、KR+-索引[10]、HQ-Tree[11]和DQuadtree[12],它们大部分都是基于经典的空间数据索引:R-树或四叉树,但是这种索引结构会带来空间冗余或数据量负载的不均衡,且这种自顶向下的多级索引结构无法利用MapReduce并行构建;另一种是利用线性化技术将多维的空间数据降为一维,在“键-值”模型上直接利用已有一维索引进行空间操作[13-15],这种方法支持高扩展性,并行度高,但是仅能保持较宽松的位置邻近,不适合空间范围查询,且更新数据后无法解决数据平衡问题。
本文针对云存储环境的特点,在吸取现有分布式空间索引优点的基础上,设计了一种适合云存储环境的分布式空间索引:M-Quadtree索引,以解决现有分布式空间索引存在的数据存储量负载不均衡、算法较难并行化或空间查询效率低等问题。该索引基于一种改进的空间数据划分策略,在MapReduce并行框架下完成空间数据的划分和索引的构建。本文同时给出了M-Quadtree索引在云环境中的并行构建、查询和更新算法,并和现有的分布式空间索引进行了相应的对比试验。
1 M-Quadtree索引方法云存储环境下的空间索引,要求数据具有较好的存储位置邻近性和负载平衡性,能满足云存储环境下大数据量和高扩展性等要求,同时有较高的索引构建效率。本文设计了两级索引结构--全局索引和块内索引。全局索引在数据并行划分过程中构造,负责索引数据块;块内索引在各个数据节点内并行构造,负责索引数据块内的空间对象。
1.1 空间数据划分空间数据划分是建立云环境下空间数据索引的基础,采用不同的划分方法直接影响索引的构建效率和查询效率。目前建立云环境下空间数据索引所采用的划分策略主要分为3种:
(1) 基于k-means等空间聚类的划分[16-17],该划分算法能较好地保持空间数据的位置邻近性,得到较好的查询效果,但是算法时间效率较低,无法满足大数据量要求。
(2) 基于四叉树的划分,该划分算法能保持空间数据的位置邻近性,但是这种递归划分方法会对读取的空间数据重复计算,不能利用MapReduce并行化,在数据分布不均匀的情况下,会导致划分后子区域间的数据存储量不平衡,甚至产生空数据节点,导致查询效率降低。
(3) 基于Hilbert或Z-Order等空间填充曲线的划分[18-19],该划分算法适合并行化,时间效率高,但是单纯的空间填充曲线方法在搜索的过程中会带来一些额外的不必要的搜索空间(false-positive search)[20],且该方法仅能保持较宽松的位置邻近,查询的上下界之间可能包含大量的无关子查询区域,不适空间合范围查询。
本文基于MapReduce并行计算框架的特点和云环境对数据均衡存储的要求,改进现有四叉树划分方法,使之能满足MapReduce并行化的要求,并解决划分后可能出现空查询区域的问题。假设空间数据总量为D,划分后每个数据块容量上限为M,则最少会产生D/M个数据块。先对整个空间区域利用四叉树划分方法进行划分,并建立索引四叉树,树的深度n取
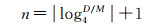 (1)
(1)
由于空间数据分布的不均衡,落在该四叉树某个叶子区域的数据量会出现大于或小于M,甚至出现为空的情况。若某叶子区域内数据量大于M,对其继续划分;若叶子区域内数据量小于M,并且和相邻的子区域数据量之和也小于M,则将其与相邻子区域合并为一个子区域,作为叶子节点。这时,四叉树的叶子节点所对应的各子区域不再是传统四叉树划分后的4个面积均等的区域,而是如图 1所示的“□”型、“I”型和“L”型等3类12种形状的区域。其中,“□”型区代表单独某个象限组成的叶子节点,4种形状如图 1(a),编码为0-3;“I”型区代表相邻两个象限合并后形成的叶子节点,4种形状如图 1(b),编码为4-7;“L”型区代表相邻3个象限合并形成的叶子节点,4种形状如图 1(c),编码由A-D表示。传统的四叉树在叶子节点区域合并后,父节点所对应的子节点由传统的4个变为12个。

|
| 图 1 M-Quadtree划分编码模型 Fig. 1 The coding model of M-Quadtree partition |
数据块的编码类似四叉树编码,由从根节点到叶子节点的各层节点编码组成。唯一与四叉树不同的是叶节点,四叉树叶节点的编码只有0-3 4种,而本文介绍的编码方法由于进行了节点间的合并,叶节点的编码有0-7和A-D等12种。为了表示与传统四叉树划分方法的区别与联系,本文称这种划分方式为M-Quadtree划分(M:Modified),相应的编码为M-Quadtree编码,以此编码为基础构建的索引为M-Quadtree索引。M-Quadtree划分针对云环境的特点对传统四叉树划分进行了改进,其优势有两点:①M-Quadtree划分规定了子区域的最小数据量,消除了空区域,在保持子区域间数据量平衡方面可以表现得更好;②M-Quadtree划分提高了空间数据加载和划分的并行性,如果用传统四叉树方法并行划分,其无法处理划分后的那些空数据区域,而M-Quadtree并行划分后可以将这些空数据区域合并。具体的并行划分和索引构建算法见下文。
1.2 空间数据块内索引基于“键-值”存储模型的云存储系统提供了两种基本的数据读取方法:多键扫描(Scan)和单键读取(Get),其中Scan操作可以根据连续的键一次读取多条记录,Get操作只能根据一个键一次读取一条记录。文献[10]已经证明了在读取同样的数据量时,Scan操作有更高的读取效率。
本文基于此特征设计空间数据块内索引,将在同一数据块内的空间对象按照Hilbert次序存储,能较好地保证空间数据的存储位置邻近性,以空间对象的Hilbert码作为键,可以尽可能以连续的键访问相邻的空间对象,以提高Scan操作的使用率。相对于其他的空间填充曲线如Z-曲线、Gray code曲线等,Hilbert曲线已被证明是能够获得最佳聚类效果和最高空间查询效率的空间填充曲线[21-22],因此本文选用Hilbert曲线映射空间对象。
空间对象的Hcode (Hilbert码)以其最小外包矩形中心点所在网格的Hilbert码表示,其中点对象的Hcode以其坐标所在网格的Hilbert码表示。重组后的空间数据块是一种具有特殊格式的数据文件,包含两部分:局部索引部分和数据内容部分。局部索引部分依次记录数据块的编码(Dcode,划分数据块时得到)、单元网格的行高和列高(ΔX、ΔY)、区域的数据量大小(length of region)、第一个网格的中心点坐标(X0,Y0),然后依次是根据Hilbert次序从第一至最后一个空间对象的Hcode、空间对象所在数据块文件内的偏移量(offset)和长度(length)。第i个空间对象偏移量由式(2)得出
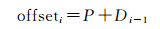 (2)
(2)
式中,P为数据块内索引所占存储空间的大小,Di-1为前i-1个空间对象的数据量大小。根据经典Hilbert码生成算法[21],已知对象的坐标信息就可以计算其Hcode,再根据Hcode查出空间对象的块内偏移和长度,即可得出空间对象。因为Hcode是按照顺序排列,可用折半查找,时间复杂度为o(log2n)。
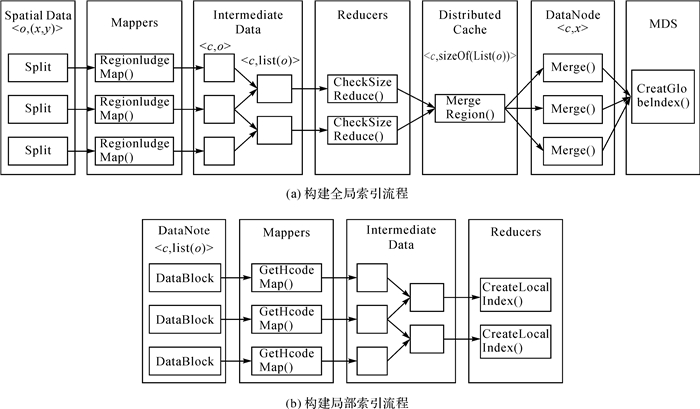
2 M-Quadtree索引构建算法MapReduce框架的Reduce阶段可使用用户自定义的数据划分算法,以提高负载均衡和计算效率,本文设计的M-Quadtree数据划分方法适合在此阶段采用。如图 2所示,算法通过两个MR (MapReduce)阶段来实现M-Quadtree索引的快速构建。算法描述如下。
|
| 图 2 M-Quadtree索引构建算法流程 Fig. 2 Flow chart of M-Quadtree index construction algorithm |
(1) 在加载数据以及构建全局索引的MR过程中, 依次进行下述操作:
a.为便于并行计算,先利用传统四叉树方法对整个空间区域进行划分,并建立索引四叉树T,树的深度由式(1)得出。
b. m1个mappers并行地读取输入的数据切片,对map函数读取的每个对象o,根据其坐标与T表计算其所属子区域编码,输出〈key Ci, value o〉键值对,其中,Ci为该对象所属子区域i的四叉树编码。
c. r1个reducers接收所有划分到该reducer的对象子集〈Ci, list (o)〉,每个reducer计算list (o)数据量大小,若大于上限M,则对该区域继续四叉树划分,直到没有子区域数据量大于M为止。计算后将数据块〈Ck,list (o)〉分发到各数据节点,并将〈Ck, sizeOf (list (o))〉存入系统分布式缓存中,其中Ck为数据量小于M的子区域四叉树编码,sizeOf (list (o))为该子区域数据量。
d.在分布式缓存中计算,若相邻子区域数据量之和小于M,合并相邻的区域编码为Xk,并生成〈Ck, Xk〉通知各数据节点完成数据块的合并。
e.使用元数据服务器MDS收集数据块的编码,并建立全局索引表。
(2) 在局部索引构建的MR过程中, 依次进行下述操作:
a. m2个mappers并行地读取前一阶段生成的数据块〈Ck, list (o)〉,对map函数读取的每个对象o,计算其Hcode,输出〈key Ck, value 〈Hcode, o〉〉键值对。
b. r2个reducers接收所有划分到该reducer的对象子集〈Ck, list (〈Hcode, o〉)〉,将对象子集中每个元组〈Hcode, o〉插入到列表L中,并对列表L按Hcode进行排序。
c.对排序后的对象建立局部索引,并序列化到HDFS文件中。
在步骤(1) a建立索引四叉树是为了步骤(1) b、(1) c中mappers、reducers可以并行执行。数据迁移在第一个Reducers阶段已经完成。步骤(1) d合并数据块的计算是在分布式缓存中完成,时间消耗可忽略不计。利用该算法建立的索引有以下优势:①采用M-Quadtree数据划分算法,利用了四叉树划分不会有重叠空间的优势,又弥补了可能会导致数据不平衡的不足;②M-Quadtree编码有一定的空间聚集性,有利于数据的快速读取;③全局索引在数据加载过程中即建立,并且是一种“扁平结构”,没有层层中间节点,利于数据块的快速定位。④局部索引在各个节点内部建立,充分利用MapReduce的并行优势。⑤由于采用了均衡的数据划分方法。当数据规模扩大时,每个数据块容量并没有变化,只增大了数据块数量,系统只需扩大节点数量和mapper、reducer数量,索引具有扩展性。
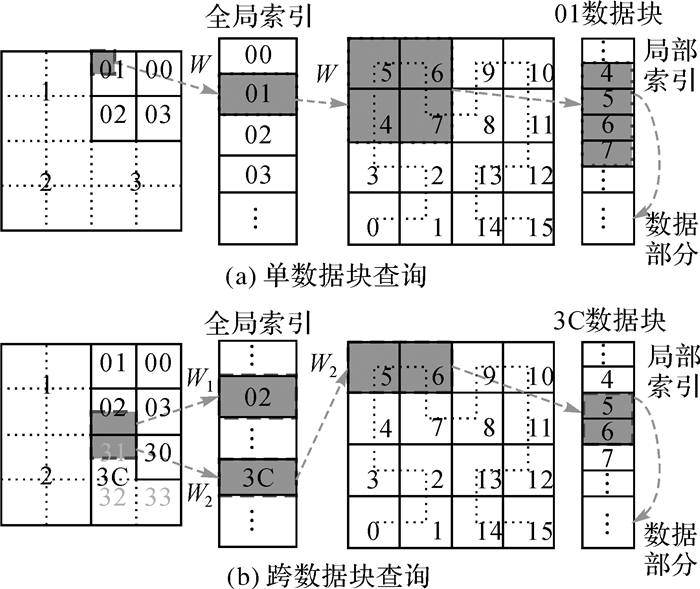
3 M-Quadtree索引查询算法以空间范围查询为例,查询客户端以窗口范围W向元数据服务器MDS发送消息,查找与W相交的空间目标。由于M-Quadtree划分后会有“I”、“L”型叶子节点存在,为了精确查找,在MDS中保存一张对数据集空间范围进行逻辑四叉树划分的坐标范围映射表,先查出与W相交的四叉树叶子节点编码,再根据此编码在MDS目录(全局索引)中查找其对应的数据块,然后在各个数据块中利用局部索引查找空间对象。查询过程如图 3所示。
|
| 图 3 基于M-Quadtree索引的空间查询 Fig. 3 The spatial query based on M-Quadtree index |
图 3(a)为查询区域在单数据块内的查询,与查询范围W相交的逻辑四叉树叶子节点编号为01,全局索引中匹配的Dcode为01,根据Dcode在全局索引中查出01数据块所在的IOS节点,再在该IOS节点中根据W坐标范围和Hilbert码生成算法算出Hcode范围,根据Hcode范围查找在此范围的空间对象。图 3(b)为查询区域跨数据块查询,与查询范围相交的逻辑四叉树叶子节点编号为02和31,全局索引中匹配的Dcode为02和3C,此时将W分为W1和W2,分别在两个数据块中并行查找空间对象。具体查询算法如下。
输入:W(查询范围)
输出:与W相交的空间对象实体集
(1) 查询客户端将W发给MDS,在MDS中查出与W相交的各数据块Dcode。
(2) 根据全局索引查找匹配各Dcode的数据块和IOS节点位置。
a.在MDS索引表中查找与各Dcode匹配的数据块。
b.搜索各数据块所在的IOS节点Si。
c.由MDS将Dcode和W发给对应的Si。
(3) 在Si中根据局部索引查找空间对象。
a.根据W坐标范围和Hilbert码生成算法,求得W的Hcode范围。
b.由Hcode在块内查找空间对象的块内偏移和长度,进而取出所有空间对象Oi。
(4) 将各个Si中取出的空间对象Oi发往客户端,即组成了与W相交的空间对象实体集。
步骤(1)、(2)在MDS完成,仅含少量计算,并无大量数据输入输出,所需时间极少;步骤(3)、(4)在各个IOS节点并行完成,最终查询时间由查询时间最长的IOS节点决定。
4 M-Quadtree索引更新算法在数据的增删过程中,会导致数据块间的容量不平衡,进而影响索引效率。因此,需要对数据块分裂或合并。但是频繁的分裂合并数据块同样会导致数据更新效率的降低,为避免这种情况,可设数据量上限M的P%大小为容量缓冲范围,在此范围内的容量变化不进行数据块的分裂或合并,仅更新局部索引。
4.1 数据插入数据插入可能会导致数据块的分裂,对某数据块进行数据插入操作时,具体更新算法如下。
输入:待插入的数据O
输出:索引更新
(1) 利用索引查询算法查找数据O所在的数据块,O可能分布在多个数据块内。
(2) 向目标数据块D插入数据O。
(3) 如果数据块大小size (D)≤(1+P%)·M,计算数据O的Hcode,在局部索引中插入数据记录的Hcode、在数据块文件内的偏移量(offset)和长度(length)。
(4)10如果size (D) > (1+P%)·M。
a.分裂数据块,并对数据量之和小于M的相邻数据块合并,产生若干新的数据块编码。
b.将新数据块编码和原数据块编码发回的MDS,在MDS全局索引中删除原编码并记录新生成的编码。
4.2 数据删除数据删除可能会导致数据块的合并,对某数据块进行数据删除操作时,具体更新算法如下。
输入:待删除的数据O
输出:索引更新
(1) 利用索引查询算法查找数据O所在的数据块,数据O可能分布在多个数据块内。
(2) 删除目标数据块D中的数据O。
(3) 如果数据块大小size (D)≥(1-P%)·M,仅删除数据块内数据O的局部索引记录。
(4) 如果size (D) < 1-P%)·M。
a.根据该数据块编码,在MDS中查找与之空间相邻的子区域。
b.对数据量之和小于下限m的相邻子区域合并生成新的数据块。
c.更新合并后数据块局部索引。
d.将新数据块编码和原数据块编码发回的MDS,在MDS全局索引中删除原编码并记录新生成的编码。
5 试验与结果分析 5.1 试验环境与数据本文试验平台由Hadoop-2.4.1集群组成,搭建在12个节点上,每两个节点部署在一台物理机上。每台物理机包含两个虚拟系统、4 GB内存、500 GB硬盘和64位Ubuntu 14.04操作系统。两个节点作为MDS (NameNode),另外10个节点作为IOS (DataNode)。测试数据为北京市12 000辆出租车在2012年11月所产生的所有GPS数据。该数据完整全面地记录了该市出租车的移动轨迹。数据大小压缩前为50 GB。本文抽取80 000 000个数据点测试本文索引的可用性和效率,每个数据点包含空间坐标等9个属性。
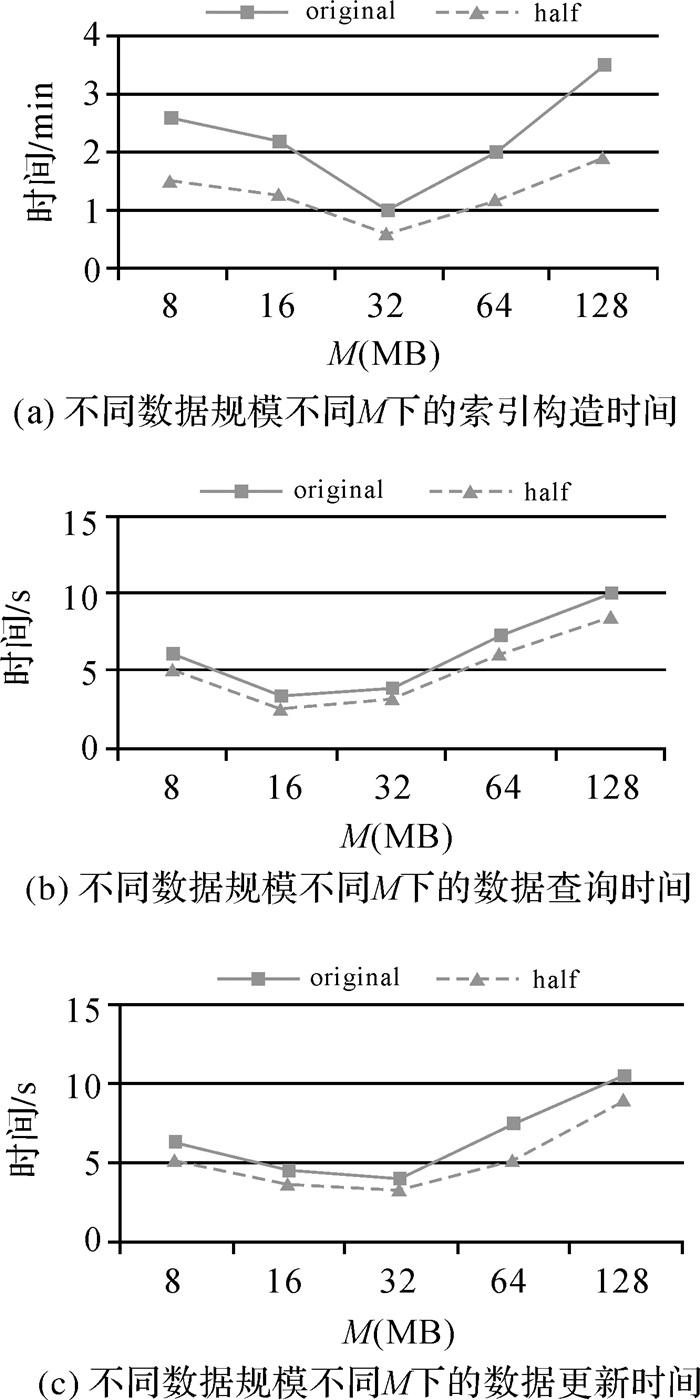
5.2 M对索引效率的影响HDFS默认数据块大小为64 MB,这个数字是系统综合考虑NameNode内存消耗、MapReduce框架的效率等设定的默认值[23]。本文中M作为数据块容量的上限,也是M-Quadtree划分和合并子区域的容量标准,不对其非空间数据应用下的一般性作讨论,仅讨论其在空间数据环境下的一般性,即仅研究在存储空间数据时,不同M对M-Quadtree索引效率造成的影响。图 4显示了当数据量为80 000 000个数据点(original)和40 000 000个数据点(half),M分别为8 MB、16 MB、32 MB、64 MB和128 MB时索引的构造、查询、更新所用的时间。
|
| 图 4 参数M对索引效率的影响 Fig. 4 The effect of parameter M in the index |
图 4(a)显示了在不同数据规模、不同数据块容量M下的索引构建时间。相同数据规模下,当M=32 MB时,构造索引所需时间最少。这是因为当M>32 MB时,数据块容量增大导致构造块内索引所需时间延长;当M < 32 MB时,虽然减少了块内索引的构造时间,但是数据块数目增多,系统在并行划分数据块时超过了所能提供的最大并行度。
图 4(b)显示了在不同数据规模、不同M下,查询整体区域的0.5%范围内数据所需的响应时间。相同数据规模下,M=16 MB时数据查询时间最少。这是因为当M>16 MB时,跨块查询减少,并行查询几率降低,数据块容量的增大也会导致块内查询时间延长,此时查询时间主要由块内查询时间决定;当M < 16 MB时,跨块查询增多,系统会花更多的时间查找数据块。
图 4(c)显示了在不同数据规模、不同M下,系统更新100 MB数据时的响应时间。相同数据规模下,当M=32 MB时索引更新时间最少。这是因为当M>32 MB时,数据块容量增大,增删数据导致的块分裂合并几率降低,但是块内查询所需时间增多同样会影响索引更新效率;当M < 32 MB,块内查询时间减少,但是块分裂合并几率提高,会对索引更新效率产生影响。
由此试验可知,在存储空间数据时,不同数据块大小确实对M-Quadtree索引的效率有影响。对比不同数据规模下M在试验中的5组取值,当M取32 MB时,索引有最好的构造和更新效率,虽然此时查询效率不是最优,但与取16 MB时相差不到1 s。故综合考虑,一般情况下可取M=32 MB。
5.3 空间数据划分效率分析空间数据划分策略是并行空间索引结构建立的基础,它的优劣直接影响了云计算环境下系统的处理效率。本节测试基于M-Quadtree划分和两种常用空间数据划分的效率对比,包括划分时间效率、数据量负载均衡度和选用不同划分方法时的空间查询效率。
表 1对比了M-Quadtree划分与3种现有的空间数据划分方法所用的划分时间,同时为了测试块内Hilbert编码构造带来的额外时间开销,也与不采用Hilbert块内编码的M-Quadtree划分进行对比。这几种方法均在数据划分过程中完成了索引的构建,故可认为此试验是索引的构建效率对比。由试验可以看出,基于Hilbert的划分方法时间效率最好,因为其不需要多次遍历空间对象,只需要加载数据时,一次性编码获取对象的空间排列即可。基于K-means的方法需要根据聚类中心的变化不断迭代,所需时间远远大于其他方法。本文提出的M-Quadtree划分在传统四叉树基础上针对并行性进行改进,虽然在时间效率上稍逊于Hilbert,但与传统的四叉树划分方法HQ-Tree相比,效率已经有了很大提高。同时可以看出,采用Hilbert编码索引块内数据确实增加了整个划分的时间开销,但此开销跟整个划分时间相比并不大,这是因为编码时数据已经加载完毕,并且块内索引的构建是利用MapReduce框架在各个节点内并行完成的。
| s | |||||
| 划分方法 | Hilbert | K-means | HQ-Tree | M-Quad | M-Quad (NoHilbert) |
| 划分时间 | 50 | 600 | 210 | 60 | 55 |
本文用划分后得到的数据块数据量标准差衡量划分后各数据块的数据量负载均衡度,标准差越小表示划分后各数据块的数据量越均衡。由表 2可以看出,使用Hilbert划分后的数据量均衡度最好,使用传统四叉树方法划分的均衡度最差,并且会产生更多的数据块, M-Quadtree稍逊于Hilbert方法,但优于K-means和传统的四叉树方法。
| 划分方法 | Hilbert | K-means | HQ-Tree | M-Quadtree |
| 数据块数量/个 | 160 | 176 | 200 | 170 |
| 标准差/MB | 1.93 | 6.41 | 12.02 | 3.43 |
分布式环境下的空间查询效率是反映一个空间数据划分方法优劣的最重要指标。图 5显示了云环境下,采用不同划分方法在不同查询范围下的空间查询效率对比。在查询范围较小时(R < 0.1%),3种方法的查询时间都很接近;但是当查询范围增大,M-Quadtree显示了最高的查询效率。Hilbert的查询效率最差,这是因为线性化只能较宽松地保持数据存储邻近性,随着查询范围的增大,查询的线性上下界之间会包含大量的无关子查询区域。M-Quadtree的查询效率比基于传统四叉树划分的HQ-Tree更好,这是因为当查询范围增大,HQ-Tree数据不均衡划分的劣势显现出来,同样的数据量会查到更多的数据块,甚至会产生不包含任何数据的“空数据块”,并且数据块内部没有采用索引,只能通过全局查询来获得具体的数据。而采用M-Quadtree划分的数据块大小相似(接近阈值M),查询的数据量越大,相对HQ-Tree查询到的数据块数量越少,而且数据块内部采用了基于Hilbert组织的索引结构,可以充分利用系统内置的Scan操作获得需要查询的空间数据,故所用的查询时间相对越少。

|
| 图 5 不同划分方法不同查询范围下查询效率对比 Fig. 5 Efficiency comparison of spatial querying on different range and different partitioning method |
本文设计的M-Quadtree划分方法的各项性能都优于传统的四叉树方法,虽然在构建效率和数据量负载均衡度上稍逊于基于Hilbert的划分方法,但在空间查询效率上远远优于后者。
5.4 并发环境下索引查询效率分析本节用两组试验来测试并发环境下索引的查询效率。一组测试不同索引方法下的并发查询效率,另一组测试M-Quadtree索引下多机与单机环境下的查询时间加速比。试验将压力测试标准套件Loadrunner-9.10部署在云环境中用于评估系统性能。
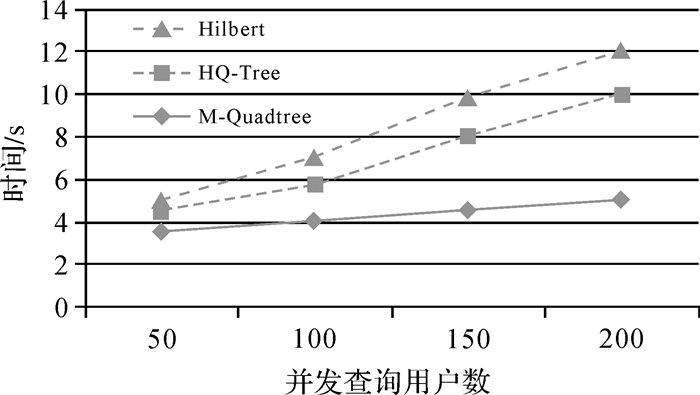
图 6显示了并发用户数在50、100、150、200下查询范围为0.1%的3种索引方法的平均查询响应时间对比。从图中结果可以看出,随着并发用户数的增多,M-Quadtree基本维持在一个恒定水平,而另外两种索引方法的响应时间均呈不同的增长趋势。主要原因是Hilbert采用的一级索引结构,并发查询的增多会给系统主节点MDS带来更大的内存压力;HQ-Tree采用了不均衡的划分方式,会查询到更多的数据块,高并发查询带来的影响更加明显;M-Quadtree的负载更均衡,故其性能并没有因为并发查询的增多而降低。
|
| 图 6 并发查询响应时间对比 Fig. 6 Comparison of response time of concurrent queries |
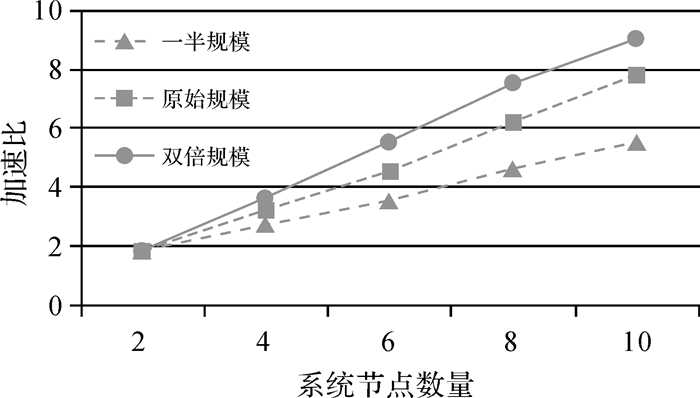
图 7显示了不同问题规模下,采用M-Quadtree索引的系统查询时间加速比。原始规模指并发用户数为100,查询范围为0.5%;一半规模指并发用户数为50,查询范围为0.25%;双倍规模指并发用户数为200,查询范围为1%。从图中可以看到,加速比不仅会随着云环境中处理节点规模的扩大而增大,同时也会随着问题规模的增大而增大。因此当问题规模越大,使用云系统处理空间数据作用越明显。
|
| 图 7 不同问题规模下并行查询的加速比 Fig. 7 Speedup of parallel query under different scale of the problem |
5.5 索引更新效率分析
本节测试索引更新效率,同样与Hilbert和HQ-Tree作对比。图 8显示了3种索引在插入20 MB、50 MB、100 MB和200 MB数据所用的时间,数据删除所用时间对比与此类似。当插入数据较小时(P < 50 MB),三者更新数据所用时间相差不大;但是当数据插入量变大时,Hilbert和HQ-Tree显然耗费了更多的时间。这是因为虽然Hilbert在开始划分数据时能保证数据量的负载均衡,但随着数据插入量增大无法对其继续保持,而HQ-Tree则会导致更多的数据块分裂,并且Hilbert和HQ-Tree只有一层索引,任何数量的数据插入都会导致索引的整体更新;而M-Quadtree划分使数据分布更平衡,并且大部分数据块的更新不会对全局索引造成影响,可在节点内并行执行。

|
| 图 8 索引更新效率对比 Fig. 8 Efficiency comparison of index updating |
6 结论
本文根据云存储环境的特点,改进现有的空间数据划分方法,设计了一种M-Quadtree划分方法,该方法将四叉树划分的4种编码拓展为12种,提高了算法的并行度和划分效率,同时能满足云环境下数据存储量负载均衡的要求。基于此划分方法,提出了一种适用于key-value数据模型的云存储环境下的分布式空间索引--M-Quadtree索引。相比现有分布式环境中单纯基于树或线性化降维的两种索引结构,本文提出的索引在数据负载均衡、查询更新效率和并发访问的应对方面表现得更好。该索引在云环境中的各项性能均优于现有的四叉树索引结构,并发环境下的空间查询也优于基于Hilbert空间填充曲线的索引,但是索引构建效率和负载均衡度方面仍逊于基于线性化技术的索引。同时块内索引仍采用传统的索引方法,当数据块容量变大,块内查询会降低空间查询的效率,故该索引结构仍需进一步优化。
| [1] | YANG Chaowei, GOODCHILD M, HUANG Qunying, et al. Spatial Cloud Computing: How Can the Geospatial Sciences Use and Help Shape Cloud Computing?[J]. International Journal of Digital Earth, 2011, 4(4): 305–329. DOI:10.1080/17538947.2011.587547 |
| [2] | 李德仁. 展望大数据时代的地球空间信息学[J]. 测绘学报, 2016, 45(4): 379–384. LI Deren. Towards Geo-Spatial Information Science in Big Data Era[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(4): 379–384. DOI:10.11947/j.AGCS.2016.20160057 |
| [3] | VAQUERO L M, RODERO-MERINO L, CACERES J, et al. A Break in the Clouds: Towards a Cloud Definition[J]. ACM SIGCOMM Computer Communication Review, 2009, 39(1): 50–55. |
| [4] | 李德仁, 张良培, 夏桂松. 遥感大数据自动分析与数据挖掘[J]. 测绘学报, 2014, 43(12): 1211–1216. LI Deren, ZHANG Liangpei, XIA Guisong. Automatic Analysis and Mining of Remote Sensing Big Data[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(12): 1211–1216. DOI:10.13485/j.cnki.11-2089.2014.0187 |
| [5] | CARY A, YESHA Y, ADJOUADI M, et al. Leveraging Cloud Computing in Geodatabase Management[C]//Proceedings of the 2010 IEEE International Conference on Granular Computing. Washington, DC: IEEE Computer Society, 2010: 73-78. |
| [6] | 郭仁忠, 刘江涛, 彭子凤, 等. 开放式空间基础信息平台的发展特征与技术内涵[J]. 测绘学报, 2012, 41(3): 323–326. GUO Renzhong, LIU Jiangtao, PENG Zifeng, et al. Technologies Connotation and Developing Characteristics of Open Geospatial Information Platform[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 323–326. |
| [7] | ZENG Wenying, ZHAO Yuelong, OU Kairi, et al. Research on Cloud Storage Architecture and Key Technologies[C]//Proceedings of the 2nd International Conference on Interaction Sciences: Information Technology, Culture and Human. New York: ACM, 2009: 1044-1048. |
| [8] | MOUZA C D, LITWIN W, RIGAUX P. Large-Scale Indexing of Spatial Data in Distributed Repositories: the SD-Rtree[J]. The VLDB Journal, 2009, 18(4): 933–958. DOI:10.1007/s00778-009-0135-4 |
| [9] | MONDAL A, YI Lifu, KITSUREGAWA M. P2PR-Tree: an R-Tree-Based Spatial Index for Peer-to-Peer Environments[M]//LINDNER W, MESITI M, TüRKER C, et al. Current Trends in Database Technology-EDBT 2004 Workshops. Berlin Heidelberg: Springer, 2004: 516-525. |
| [10] | WEI Lingyin, HSU Y T, PENG W C, et al. Indexing Spatial Data in Cloud Data Managements[J]. Pervasive and Mobile Computing, 2014, 15: 48–61. DOI:10.1016/j.pmcj.2013.07.001 |
| [11] | FENG Jun, TANG Zhixian, WEI Mi'an, et al. HQ-Tree: a Distributed Spatial Index Based on Hadoop[J]. China Communications, 2014, 11(7): 128–141. DOI:10.1109/CC.2014.6895392 |
| [12] | TANIN E, HARWOOD A, SAMET H. Using a Distributed Quadtree Index in Peer-To-Peer Networks[J]. The VLDB Journal, 2007, 16(2): 165–178. DOI:10.1007/s00778-005-0001-y |
| [13] | NISHIMURA S, DAS S, AGRAWAL D, et al. MD-HBase: Design and Implementation of an Elastic Data Infrastructure for Cloud-Scale Location Services[J]. Distributed and Parallel Databases, 2013, 31(2): 289–319. DOI:10.1007/s10619-012-7109-z |
| [14] | LAWDER J K, KING P J H. Querying Multi-Dimensional Data Indexed Using the Hilbert Space-Filling Curve[J]. ACM SIGMOD Record, 2001, 30(1): 19–24. DOI:10.1145/373626 |
| [15] | CARY A, SUN Zhengguo, HRISTIDIS V, et al. Experiences on Processing Spatial Data with MapReduce[C]//Proceedings of the 21st International Conference on Scientific and Statistical Database Management. Berlin, Heidelberg: Springer-Verlag, 2009. |
| [16] | CARY A, YESHA Y, ADJOUADI M, et al. Leveraging Cloud Computing in Geodatabase Management[C]//Proceedings of the 2010 IEEE International Conference on Granular Computing. Washington, DC: IEEE, 2010: 73-78. |
| [17] | 吴明光. 一种空间分布模式驱动的空间索引[J]. 测绘学报, 2015, 44(1): 108–115. WU Mingguang. A Spatial Distribution Pattern-driven Spatial Index[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(1): 108–115. DOI:10.11947/j.AGCS.2015.20130245 |
| [18] | 王永杰, 孟令奎, 赵春宇. 基于Hilbert空间排列码的海量空间数据划分算法研究[J]. 武汉大学学报(信息科学版), 2007, 32(7): 650–653. WANG Yongjie, MENG Lingkui, ZHAO Chunyu. Spatial Partitioning of Massive Data Based on Hilbert Spatial Ordering Code[J]. Geomatics and Information Science of Wuhan University, 2007, 32(7): 650–653. |
| [19] | LIU Yi, JING Ning, CHEN Luo, et al. Parallel Bulk-Loading of Spatial Data with MapReduce: an R-tree Case[J]. Wuhan University Journal of Natural Sciences, 2011, 16(6): 513–519. DOI:10.1007/sl1859-011-0790-3 |
| [20] | 马友忠, 孟小峰. 云数据管理索引技术研究[J]. 软件学报, 2015, 26(1): 145–166. MA Youzhong, MENG Xiaofeng. Research on Indexing for Cloud Data Management[J]. Journal of Software, 2015, 26(1): 145–166. |
| [21] | MOON B, JAGADISH H V, FALOUTSOS C, et al. Analysis of the Clustering Properties of the Hilbert Space-Filling Curve[J]. IEEE Transactions on Knowledge and Data Engineering, 2001, 13(1): 124–141. DOI:10.1109/69.908985 |
| [22] | ABEL D J, MARK D M. A Comparative Analysis of Some Two-Dimensional Orderings[J]. International Journal of Geographical Information Systems, 1990, 4(1): 21–31. DOI:10.1080/02693799008941526 |
| [23] | SHVACHKO K, KUANG H, RADIA S, et al. The Hadoop Distributed File System[C]//Proceedings of the 2010 IEEE 26th Symposium on Mass Storage Systems and Technologies. Washington, DC: IEEE Computer Society, 2010: 1-10. |


