空间同位模式挖掘作为空间数据挖掘领域的重要研究内容之一,已经引起了国内外学者的广泛关注[1-3]。空间同位模式挖掘旨在发现空间数据集中满足一定邻域关系的、频繁发生的要素或事件集合[4]。空间同位模式挖掘可以发现空间现象中隐藏的、有意义的模式,从而揭示深层次的领域知识并服务于决策支持。目前,空间同位模式挖掘已应用于生物研究、疾病防控、犯罪分析、移动位置服务等领域。
空间同位模式挖掘算法的一般框架最初由文献[4]提出,并给出一种Colocation Miner算法。Colocation Miner算法大致可分为两个步骤:①确定空间邻域,并产生候选同位模式,其中,空间邻域关系通常由用户给定的欧氏距离阈值来确定;②对候选同位模式的兴趣度(频繁度)进行度量,并根据兴趣度度量指标对候选同位模式进行过滤,其中,在计算候选模式的兴趣度时,Colocation Miner采取的是实例连接的方法,计算量较大。为提升算法效率,不同学者陆续针对实例连接方法作了改进,如部分连接的方法[5]、无连接方法[6]和基于密度的方法[7]等。此外,空间数据的异质特性导致空间同位模式可能仅存在局部的空间区域,空间同位模式挖掘的另一重要研究内容是如何挖掘局部空间同位模式[8-11]。
尽管国内外学者陆续发展了不同的空间同位模式的挖掘方法,但这些方法的大多仍遵循Colocation Miner算法的框架。在此框架下,模式挖掘结果主要受到挖掘参数阈值(邻近距离阈值和兴趣度阈值)的影响。而实际中,这些参数阈值的设置通常缺乏先验知识,从而影响了挖掘结果的可靠性。以兴趣度度量指标为例,若设置太高会导致模式的遗漏,而设置太低又会导致挖掘结果中包含太多的模式,从而造成模式解译及应用的难题。为减轻挖掘结果对参数阈值的依赖,国内外诸学者开展了积极的探索。具体而言,对于距离阈值的设置,通常由两种策略,基于最近邻的方法和基于空间自相关指标的方法[13];对于兴趣度阈值的设置,文献[12]给出一种TOP-N空间同位模式的挖掘策略,文献[13]则假设同位模式的兴趣度指标服从正态分布,进而结合拉依达准则筛选出显著模式。最近,文献[14]给出一种降低兴趣度参数影响的新方法(SSCSP)。该方法首先假设数据中不包含任何同位模式(即零假设),进而对候选模式进行假设检验,最终不满足零假设的模式即为显著模式。该方法的优势在于将模式判别转化为假设检验问题,避免了人为设置兴趣度阈值。具体而言,该方法主要包含3个步骤:①点分布模式拟合,若点分布体现较强的空间自相关特征,则假设由泊松类聚过程生成[15],否则假设由一般泊松过程生成,在此假设的基础上,对每种类型的点要素分布模型的参数进行估计;②模拟数据生成,根据上一步骤中估计的模型生成模拟数据,从而使得模拟数据尽量保持和原始数据相似的分布特征;③显著空间同位模式发现,以同位模式的兴趣度作为统计量,通过比较零假设和实际数据中模式的兴趣度的差异来确定同位模式是否显著。
分析上述空间同位模式挖掘的相关研究可发现,当前同位模式挖掘工作尚存在以下不足:①当前同位模式挖掘算法大多试图发现单一的、最佳的邻近距离阈值,而事实上,采用不同的距离阈值时,空间同位模式挖掘结果不同[16],因而很难确定最佳的距离阈值;②为避免兴趣度阈值的设置,现有方法均对数据特征或模型进行了特定假设。例如,SSCSP方法假设空间自相关的点模式由泊松类聚类型产生,而实际上单一的泊松类聚类型并不能描述所有类型的空间点模式。因此,若这些假设未能很好地满足,由此带来的误差就会影响最终模式挖掘的结果。为解决以上问题,本文提出一种基于模式重建的显著空间同位模式多尺度挖掘方法。
1 基于模式重建的显著空间同位模式多尺度挖掘 1.1 研究策略如上文中指出,空间同位模式挖掘结果会随着邻近距离阈值的改变而变化,确定单一的、最佳的距离阈值并不现实。一种更为合理的策略是在不同的距离阈值下发现和评价空间同位模式,即实现空间同位模式的多尺度挖掘。为此,需要解决以下3个问题:①给定数据集,首先确定空间同位模式可能存在的空间范围,即:邻域距离取何值时可能发现同位模式;②选定某一距离阈值,模式的兴趣度阈值设置应该采取一种较为客观的方法,而不是人为设定兴趣度阈值;③综合多个尺度的挖掘结果,对空间同位模式的有效性作出评价,筛选出数据集中最显著的模式。
鉴于以上考虑,本文提出一种显著空间同位模式的多尺度挖掘方法,包含以下3个步骤:
(1) 邻近距离阈值有效范围的确定。引入一种新的度量指标--互邻近距离,该指标可以刻画不同要素实例间的邻近分布特征,从而界定邻近距离阈值的有效取值范围。
(2) 零模型构建和显著空间同位模式挖掘。假设不同要素之间相互独立(零模型),在此基础上借助一种非参数方法(模式重建)生成模拟数据。模拟数据中保持各类要素的分布特征,但却破坏不同类别要素实例间的依赖关系。进而,将空间同位模式挖掘转化为统计假设检验问题,避免了人为设置兴趣度的困境。最终,不满足原假设的模式即为显著同位模式。
(3) 显著空间同位模式多尺度挖掘结果评价,引入生存期的概念对不同尺度下的挖掘结果进行评价,从而确定数据中主要的模式,下文将对方法给出详细的描述。
1.2 邻近距离阈值估计为了确定邻近距离阈值的有效取值范围,首先给出以下相关定义。
定义1:互最近邻距离(mutual nearest neighbor distance, MNND)。给定K个要素类型集合T={f1, f2, …, fK},记Ei为要素类型fi对应的实例集合,Ek为要素类型fk对应的实例集合,Ei中第j个实例记为eij,则eij与要素类型fk的互最邻近距离定义为
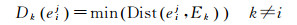 (1)
(1)
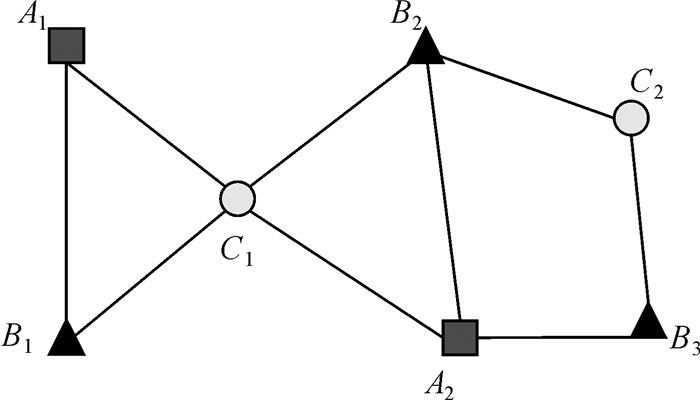
式中,Dist (eij, Ek)表示eij与Ek中所有邻近实例距离的集合。如图 1中,3种要素类型{A, B, C}共7个实例{A1, A2, B1, B2, B3, C1, C2}。黑色实线表示不同实例间互为空间邻近,则实例C1与要素类型A间的互邻近距离为DA(C1)=min (LengthA1-C1, LengthA2-C1)。同理,DB(C1)=min (LengthB1-C1, LengthB2-C1)。
|
| 图 1 要素实例邻近关系 Fig. 1 Neighboring relationship of feature instances |
定义2:空间同位模式参与指数(participation index, PI)[5]。给定同位模式C,其参与指数定义为
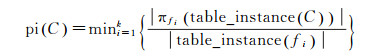 (2)
(2)
式中,k表示同位模式共包含的要素类型数目;fi对应其中某一种要素类型;table_instance表示空间同位模式包含的实例集合;π表示删除重复项的关系映射操作。由式(2)可知,分母为要素类型fi的实例总数目,分子为满足同位关系C中的fi实例数目。显然,参与指数的取值范围为[0~1]。
定义3:邻近距离域(neighboring distance range, NDR)。记数据集中所有实例的互最近邻距离集合为DC,DC中以最小值和最大值为界构成的距离范围定义为邻近距离域。结合定义1可知:MNND刻画的是不同类型要素间邻近距离的特征,当距离阈值小于min (DC)时,任意两个不同类型要素实例均不相邻,此时参与指数为0;而当距离阈值大于max (DC)时,任意实例的邻域内均含有其他类型要素,参与指数达到最大值1。因此,邻近距离域对应的范围即为有效的邻近距离阈值取值。
1.3 显著空间同位模式判别空间同位模式是很难凭借经验进行判别的。一个更为合理策略是假设空间数据集中不存在空间同位模式,进而比较实际挖掘所得模式与零假设的差异,将显著偏离原假设的模式视为真实的空间同位模式。为此,需设计零模型并根据零模型生成模拟数据。其中,零模型主要满足两个条件:①不同要素间相互独立;②对于同一要素,模拟数据和真实数据具有相似的空间分布特征。由于不同空间要素分布模式的复杂性和差异性,条件②是零模型构建中的难点问题,也是关键所在。
为此,本文在零模型构建中采取了模式重建[17]的方法。模式重建方法的核心思想在于采用不同空间统计量组合对空间模式进行描述,进而生成具有相同模式特征的数据集。假设观测数据的空间模式Ψ可由M个空间统计量的特征fiψ(x)(i=1, 2, …, M)进行表征。若第j次的模拟结果ϕ的特征记为fiφj(x),模拟结果ϕ与真实的模式Ψ间的特征差异表达为Eψ(φj),则有
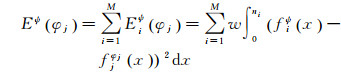 (3)
(3)
式中,Eiψ(φj)为第i个统计量对应的空间特征;w表示空间统计量对应的权值;x为统计量函数对应的距离。至此,模拟数据和真实数据的差异可以根据式(3)进行定量表达。进而,可将式(3)作为目标函数,在模拟过程中对生成数据不断调整,直至目标函数取值足够小,即可认为模拟数据和真实数据具有相同的空间分布特征。文献[17-19]中相关研究结果证明,二阶空间统计量(如K函数、L函数等)是描述刻画空间点模式的最重要的统计量,其中尤以成对相关函数(pair correlation function)描述能力最强。此外,不同类型的统计量相互补充,完整刻画较为复杂的空间模式一般需要3~5个统计量。为此,本文选取3种不同类型的空间统计量组合,分别为成对相关函数g(r),最近邻分布函数D(r)和空白空间分布函数H(r)[19]。
给定观测数据D,根据式(3)可生成N个具有相同要素分布特征的模拟数据集{D1, D2, Di, …, DN}。记实际数据集D中同位模式C对应的参与指数记为PIobs(C), 同一模式在数据Di的参与指数记为PIi(C), 则同位模式C的显著性根据下式进行计算
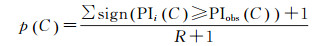 (4)
(4)
式中,sign为取值为0或1的符号运算。给定显著性水平α, 若p(C)小于α, 则C为显著同位模式。
1.4 多尺度挖掘结果评价单个距离阈值下挖掘得到的同位模式通常不能充分刻画数据特征,更有意义的是在多个距离阈值下挖掘空间同位模式,即实现空间同位模式的多尺度挖掘。然而,多尺度挖掘结果中通常包含较多的模式,若返回所有的模式会造成结果分析困难,不利于辅助决策,因此需对多尺度挖掘结果进行评价和筛选。
文献[20]指出,模式稳定性和视觉显著性存在明显的对应关系,即:显著的模式会在较广的视觉范围内被优先感知。基于此,文献[21]首次定义了生存期的概念,并用来描述尺度空间聚类算法中聚类模式的稳定性。类似的,文献[22]定义了聚类数目的生存期,并将其作为多尺度聚类算法结果的筛选标准。鉴于此,本文引入生存期的概念对空间同位模式多尺度挖掘结果进行评价,空间同位模式的生存期定义如下。
定义4:生存期(living time, LT)。将邻近距离域均分为N等份,并在此N个距离上分别进行同位模式挖掘。若同位模式C在其中连续的P个距离上均统计显著,则同位模式C的生存期定义为:LT(C)=P。生存期P对应距离阈值的范围即为同位模式存在的空间范围。需指出,生存期度量的是模式的相对重要性,模式的生存期越长,表示该模式相对越重要,这对于模式挖掘结果的筛选有着重要的指导作用。
2 试验分析与应用试验首先采用模拟数据集将本文方法与经典Colocation Miner方法、SSCSP方法进行对比分析,以验证本文方法的有效性和可靠性;在此基础上,进一步给出实际应用中的空间同位挖掘实例分析。
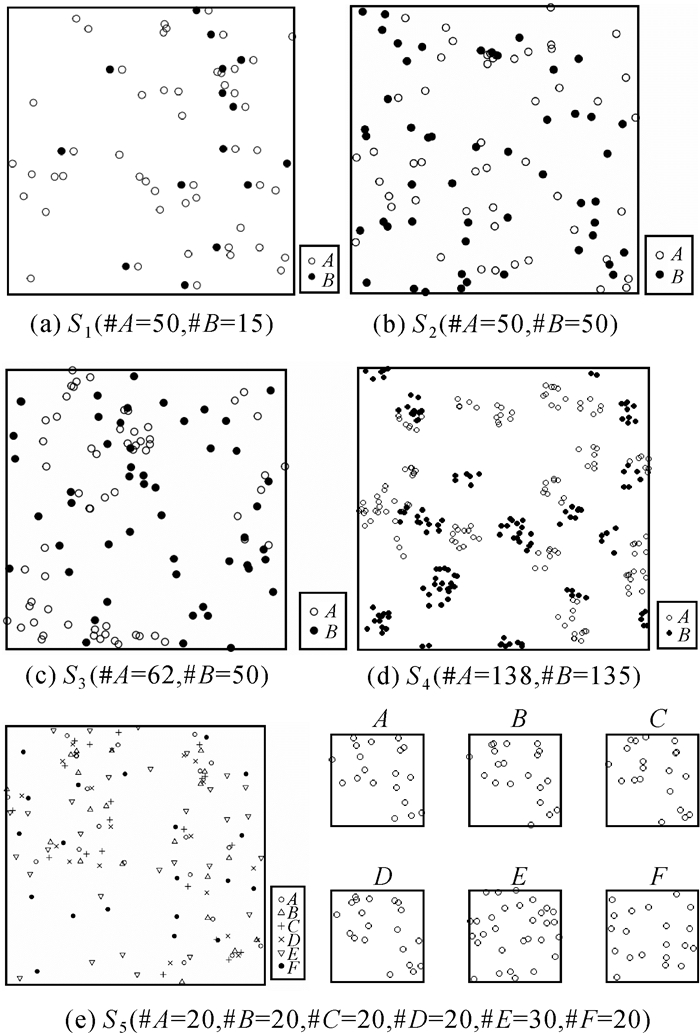
2.1 模拟数据试验分析模拟试验中包含5组数据(S1-S5),分布范围均为10×10的单元, 空间分布如图 2所示。主要考虑以下3种情形:多要素实例、空间自相关、多要素类型。其中,S1、S2对应多要素实例情形。S1中所有B要素实例均位于A要素实例的邻域,但两类要素数目差别较大;S2中两类要素数据均较多,且都随机分布在研究区域。S3、S4对应空间自相关的情形。其中,S3中A要素分布呈空间自相关;B要素随机分布;S4中A、B要素均表现出空间自相关,但两者相互独立。S5对应多要素类型的情形,其中人为设定了两种模式,同位模式{A, B, C, D}和互斥模式{E, F}。其中,同位模式由多要素类聚过程产生,邻近距离为1;互斥模式由多类型Strauss过程[15](作用半径为1,核半径为0.5)生成。空间同位模式挖掘过程中,Colocation Miner和SSCSP算法中邻近距离阈值设置采取文献[12]中的建议,根据改进的L函数进行设置。本文方法多尺度中,模拟次数为999次,并将邻近距离域均分为20等分。
|
| 图 2 5组模拟数据集 Fig. 2 Five simulated datasets |
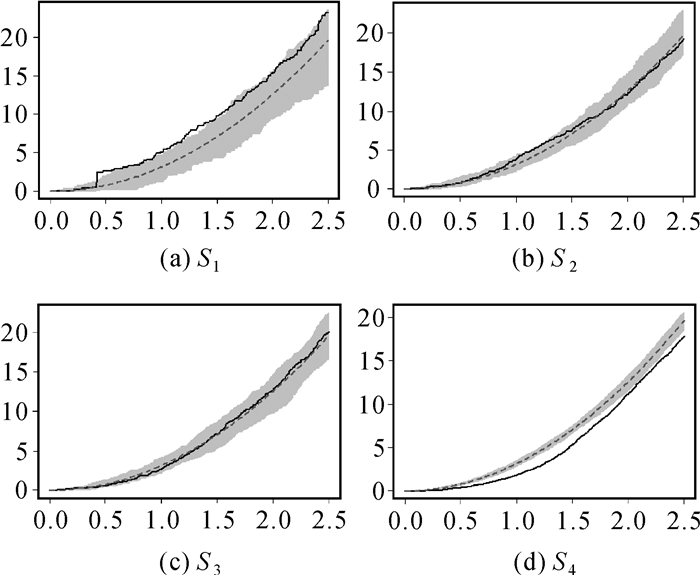
由于S1-S4数据集仅包含两类要素,将Cross-K函数结果作为基准对空间同位模式挖掘结果进行评价(图 3),本文方法挖掘结果列于表 1,对比分析图 3和表 1,可得到如下结论:
|
| 图 3 S1-S4数据集的Cross-K函数值(虚线:理论值; 实线:观测值; 灰色条带:95%置信区间) Fig. 3 Cross-K function of S1-S4(dotted line:expected value; solid line:observed value; grey band:95% confidence interval) |
| 数据集 | 同位模式 | 最小距离阈值 | 最大距离阈值 | 生存期 | 同位距离 |
| S1 | {A-B} | 0.18 | 3.34 | 8 | [0.48~0.95] |
| S2 | {A-B} | 0.06 | 1.62 | 0 | |
| S3 | {A-B} | 0.03 | 2.64 | 0 | |
| S4 | {A-B} | 0.06 | 3.28 | 0 |
(1) 数据S1对应Cross-K函数结果表明要素A-B呈现较强的集聚效应。若采用Colocation Miner算法,由于两类要素实例数目差别较大,参与指数值较低(0.34),故模式{A-B}容易发生漏判。本文方法与SSCSP方法均可有效识别该模式。
(2) 数据S2对应Cross-K函数结果表明要素A-B间无集聚效应。若采用Colocation Miner算法,由于两类要素实例数目均较多,会导致较高的参与指数值(0.86),故模式{A-B}会误判定为同位模式。本文方法和SSCSP法探测结果与Cross-K函数结果一致,无误判发生。
(3) 数据S3对应的Cross-K函数结果表明要素A-B间无集聚效应。Colocation Miner将模式{A-B}误判为同位模式(PI=0.82),而本文方法和SSCSP算法均可作出正确判定。
(4) 对于数据集S4, Cross-K函数结果表明要素A-B间实为排斥作用。若采用Colocation Miner算法,由于两类要素数目较多,且部分簇发生重叠,参与指数值较高(0.79),故模式{A-B}被误判为显著的同位模式。本文方法和SSCSP算法均可作出正确判定。
上述结果表明,对于包含两种要素类型的简单数据集,SSCSP方法和本文方法均可有效识别真实的同位模式。进一步,研究了多要素类型的空间同位挖掘,挖掘结果列于表 2。
| 模式长度 | 本文方法 | SSCSP方法 |
| 2 | {A-B, A-C, A-D, B-C, B-D, C-D} | {A-B, A-C, A-D, B-C, B-D, C-D, E-F} |
| 3 | {A-B-C, A-B-D, A-C-D, B-C-D} | {A-B-C, A-B-D, A-C-D, B-C-D, A-B-E, A-B-F, A-C-E, A-C-F, A-D-E, A-D-F, A-E-F} |
| 4 | {A-B-C-D} | {A-B-C-D} |
S5数据集中, 预设同位模式为{A-B-C-D}, 真实的同位模式应为{A-B-C-D}的子集。由表 2可知,尽管SSCSP算法可以发现所有正确的同位模式,但同时也存在着误判现象,如模式{A-E-F}。这可能是由于模式拟合过程中存在误差,且误差随要素类型的数目而累积。本文方法很好地识别本实例中所有的空间同位模式,既无漏判现象,也无误判现象。
2.2 实际应用与分析实际应用中采取我国东北洪河湿地部分区域的生态群落数据。数据中包含毛果苔草、狭叶甜茅、漂筏苔草、小叶章、沼柳等类别。各类物种的空间分布如图 4所示,同位模式挖掘结果列于表 3。

|
| 图 4 不同物种的空间分布图 Fig. 4 Distribution of five species |
| 模式 | 生存期 | 同位距离 |
| {毛果苔草,狭叶甜茅} | 9 | [20~180] |
| {漂筏苔草,小叶章} | 7 | [20~140] |
| {狭叶甜茅,沼柳} | 1 | [20~40] |
| {漂筏苔草,沼柳} | 1 | [20~40] |
| {毛果苔草,狭叶甜茅,沼柳} | 2 | [40~60] |
| {漂筏苔草,小叶章,沼柳} | 3 | [40~80] |
空间同位模式挖掘在生态群落分析中有着重要的应用价值,结合物种的空间分布及本文方法挖掘结果,可知:显著同位模式挖掘可避免模式的误判发生。如图 4(e)所示, 沼柳数目最多且散布在整个研究区域,Colocation Miner方法易将沼柳和其他所有物种误判为同位模式。本文方法由于不受兴趣度参数阈值的影响,可避免误判发生;不同邻近距离阈值下,同位模式挖掘结果并不完全相同。本文方法可以挖掘不同距离阈值下显著同位模式,对数据中的同位模式进行完整的描述;生存期可较好地度量多尺度挖掘结果中同位模式的相对重要性,从而使结果筛选和分析更加简单。显然,该数据集中最显著的同位模式为{毛果苔草-狭叶甜茅}和{漂筏苔草-小叶章},且对应的同位距离范围分别为[20~180]和[20~140]。
3 结论针对空间同位模式挖掘中参数阈值设置缺乏先验的问题,本文发展了一种基于模式重建的显著空间关联模式多尺度挖掘方法。具体而言,通过互邻近距离来界定邻近距离的有效取值范围,借助模式重建和假设检验策略从而避开了兴趣度阈值设置的难题,并引入生存期的概念对多尺度挖掘结果进行评价。试验结果表明:本文方法可避免挖掘参数的设置问题及由此造成的模式误判问题;算法挖掘结果中不仅包含了同位模式的类型,同时反映了模式存在的空间范围,挖掘结果更加精确。
进一步的研究工作主要集中在两个方面:本文方法在模式重建的过程仅考虑了单一要素的分布特征,需进一步研究协变量对空间分布的影响(如:土壤类型对某植物空间分布的影响);方法采用了蒙特卡洛模拟,计算量较大,需研究分布式计算框架下的算法实现,以进一步提升算法效率。
| [1] | 李光强, 邓敏, 朱建军. 基于Voronoi图的空间关联规则挖掘方法研究[J]. 武汉大学学报(信息科学版), 2008, 33(12): 1242–1245. LI Guangqiang, DENG Min, ZHU Jianjun. Spatial Association Rules Mining Methods Based on Voronoi Diagram[J]. Geomatics and Information Science of Wuhan University, 2008, 33(12): 1242–1245. |
| [2] | 谢超, 陈毓芬, 王英杰. Apriori算法在ACViS中用户行为监测数据挖掘中的应用研究[J]. 测绘学报, 2010, 39(4): 397–403. XIE Chao, CHEN Yufen, WANG Yingjie. Application of Apriori Algorithm in User Action Monitoring Data Mining in Adaptive Cartographic Visualization System[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(4): 397–403. |
| [3] | 田晶, 王一恒, 颜芬, 等. 一种网络空间现象同位模式挖掘的新方法[J]. 武汉大学学报(信息科学版), 2015, 40(5): 652–660. TIAN Jing, WANG Yiheng, YAN Fen, et al. A New Method for Mining Co-location Patterns between Network Spatial Phenomena[J]. Geomatics and Information Science of Wuhan University, 2015, 40(5): 652–660. |
| [4] | HUANG Yan, SHEKHAR S, XIONG Hui. Discovering Colocation Patterns from Spatial Data Sets: A General Approach[J]. IEEE Transactions on Knowledge and Data Engineering, 2004, 16(12): 1472–1485. DOI:10.1109/TKDE.2004.90 |
| [5] | YOO J S, SHEKHAR S, SMITH J, et al. A Partial Join Approach for Mining Co-Location Patterns[C]//Proceedings of the 12th Annual ACM International Workshop on Geographic Information Systems. New York: ACM, 2004: 241-249. |
| [6] | YOO J S, SHEKHAR S. A Joinless Approach for Mining Spatial Colocation Patterns[J]. IEEE Transactions on Knowledge and Data Engineering, 2006, 18(10): 1323–1337. DOI:10.1109/TKDE.2006.150 |
| [7] | XIAO Xiangye, XIE Xing, LUO Qiong, et al. Density Based Co-Location Pattern Discovery[C]//Proceedings of the 16th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems. New York: ACM, 2008. |
| [8] | EICK C F, PARMAR R, DING Wei, et al. Finding Regional Co-Location Patterns for Sets of Continuous Variables in Spatial Datasets[C]//Proceedings of the 16th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems. New York: ACM, 2008. |
| [9] | DING Wei, EICK C F, YUAN Xiaojing, et al. A Framework for Regional Association Rule Mining and Scoping in Spatial Datasets[J]. GeoInformatica, 2011, 15(1): 1–28. DOI:10.1007/s10707-010-0111-6 |
| [10] | MOHAN P, SHEKHAR S, SHINE J A, et al. A Neighborhood Graph based Approach to Regional Co-Location Pattern Discovery: A Summary of Results[C]//Proceedings of the 19th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems. New York: ACM, 2011: 122-132. |
| [11] | QIAN Feng, CHIEW K, HE Qinming, et al. Mining Regional Co-Location Patterns with k NNG[J]. Journal of Intelligent Information Systems, 2014, 42(3): 485–505. DOI:10.1007/s10844-013-0280-5 |
| [12] | YOO J S, BOW M. Mining Spatial Colocation Patterns: A Different Framework[J]. Data Mining and Knowledge Discovery, 2012, 24(1): 159–194. DOI:10.1007/s10618-011-0223-0 |
| [13] | QIAN Feng, HE Qinming, CHIEW K, et al. Spatial Co-Location Pattern Discovery Without Thresholds[J]. Knowledge and Information Systems, 2012, 33(2): 419–445. DOI:10.1007/s10115-012-0506-9 |
| [14] | BARUA S, SANDER J. Mining Statistically Significant Co-location and Segregation Patterns[J]. IEEE Transactions on Knowledge and Data Engineering, 2014, 26(5): 1185–1199. DOI:10.1109/TKDE.2013.88 |
| [15] | GELFAND A E, DIGGLE P, GUTTORP P, et al. Handbook of Spatial Statistics[M]. Boca Raton, Florida: CRC Press, 2010. |
| [16] | BARUA S, SANDER J. Mining Statistically Sound Co-Location Patterns at Multiple Distances[C]//Proceedings of the 26th International Conference on Scientific and Statistical Database Management. New York: ACM, 2014. |
| [17] | ILLIAN J, PENTTINEN A, STOYAN H, et al. Statistical Analysis and Modelling of Spatial Point Patterns[M]. Chichester: Wiley, 2008. |
| [18] | WIEGAND T, HE Fangliang, HUBBELL S P. A Systematic Comparison of Summary Characteristics for Quantifying Point Patterns in Ecology[J]. Ecography, 2013, 36(1): 92–103. DOI:10.1111/j.1600-0587.2012.07361.x |
| [19] | WIEGAND T, MOLONEY K A. Handbook of Spatial Point-Pattern Analysis in Ecology[M]. New York, NY: Chapman and Hall/CRC Press, 2014. |
| [20] | WITKIN A. Scale-Space Filtering: A New Approach to Multi-Scale Description[C]//Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing. San Diego, California, USA: IEEE, 1984: 150-153. |
| [21] | LEUNG Y, ZHANG Jiangshe, XU Zongben. Clustering by Scale-Space Filtering[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(12): 1396–1410. DOI:10.1109/34.895974 |
| [22] | PEI Tao, ZHU A-Xing, ZHOU Chenghu, et al. A New Approach to the Nearest-Neighbour Method to Discover Cluster Features in Overlaid Spatial Point Processes[J]. International Journal of Geographical Information Science, 2006, 20(2): 153–168. DOI:10.1080/13658810500399654 |



