随着车载和手持GPS设备的普及,GPS轨迹数据(如浮动车数据(floating car data,FCD)等)已成为交通状态模拟分析的重要数据源之一。由于采集高频轨迹数据通信成本高,因此,60%以上的GPS轨迹数据均属于低频采样[1]。但低频轨迹数据在采样间隔内可能会经过多条道路和交叉口,增加了车辆行驶路线的不确定性,致使轨迹数据无法准确地反映出车辆在路网中真实的行驶轨迹和状态,降低了数据应用价值。因此,如何根据低频采样GPS轨迹数据获取车辆真实行驶路线已成为国内外学者研究的重点内容之一[2-15]。
文献[2]设计了基于D-S证据理论的导航数据地图匹配方法。文献[4, 7]在顾及轨迹曲线和路网相似性等因素的基础上研究了高频轨迹数据的匹配方法。文献[6]设计了基于曲率积分约束的浮动车匹配算法。文献[16]在考虑路网几何拓扑结构和时间、速度限制等因素的基础上,构造了ST-Matching轨迹数据匹配算法。文献[17]在ST-Matching算法的基础上,设计了基于邻近GPS轨迹点相关性的最佳路径选择算法。文献[18]采用条件随机场方法结合上下文信息进行低频轨迹数据的匹配。文献[5, 19]将低频GPS轨迹点数据作为输入端,将待匹配路段作为隐马尔科夫模型(hidden Markov model,HMM)的表现端,设计了基于HMM的低频轨迹匹配算法。为避免HMM模型的“标注偏移”问题,文献[20]采用条件随机场(condition random fields,CRFs)实现了手机GPS定位数据与地图的匹配。但上述算法均未使用历史轨迹数据,导致GPS轨迹与道路网匹配的准确率不高。文献[3]基于武汉出租车数据构建了历史轨迹经验库,设计了轨迹数据的匹配算法。文献[1, 21]基于出租车群体的历史轨迹数据和概率推断模型,构建基于历史经验的出行系统(history based route inference system, HIRS),轨迹匹配准确率和运算效率都得到了提升,但HIRS算法的求解效率不高。为此,本文拟构建基于强化学习和马尔科夫决策过程的低频轨迹匹配算法,以提高匹配的准确率和求解效率。
1 基于强化学习的轨迹匹配算法原理轨迹匹配问题可描述如下:给定路网G={E,V},其中E为边集,V为顶点集;假设一辆浮动车从t0到ti时刻包含n个GPS轨迹点{pi|i=0, 1, …, n},轨迹匹配即求一条最可能的行车路径T,使T位于G上。基于强化学习和历史轨迹的匹配算法整体流程如图 1所示。算法主要包括3个部分:候选点集选取、候选路径集选取、最优路径求解。候选点集选取时,首先根据GPS点的位置寻找路网中邻近路段,然后将GPS点分别投影到对应的路段上,形成候选点集。候选路径集选取主要依据候选点之间是否存在历史轨迹;若存在,则将历史轨迹和候选点间最短路径作为候选路径;否则,则将最短路径作为候选路径集。在确定候选路径集后,依据马尔科夫决策过程和强化学习来获取最佳的匹配路径。其中,历史经验库构建、候选路径选取、基于强化学习的最优路径求解是低频轨迹数据匹配算法的关键。下面将对算法各主要实现步骤分别进行详细说明。
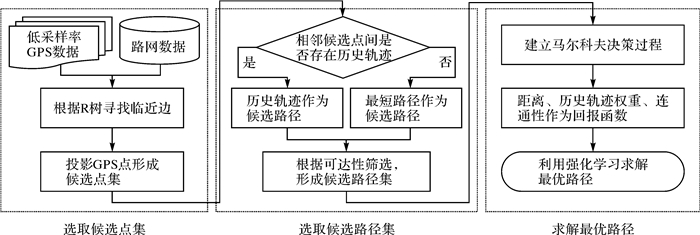
|
| 图 1 基于强化学习的地图匹配算法流程 Fig. 1 The flow chart of the map matching algorithm based on reinforcement learning |
1.1 构建历史经验库
历史轨迹是构建马尔科夫决策过程回报函数的重要基础。因此,如何利用原始高频采样轨迹数据构建历史轨迹经验库则是首先需要完成的任务。轨迹数据中的每条GPS日志均记录了一辆车在较长时间段内的GPS点位置信息,包括了多条行驶路径信息。为此,需将GPS日志划分成多条路段,保证每个路段只有唯一的起点和终点。GPS日志记录划分过程可参见文献[21]。文献[21]首先引入stay point的概念,每个stay point是上一路段终点和下一路段的起点;然后通过检测GPS日志记录中的stay point可将日志拆分为多个连续的路段。最后,利用文献[22]提出的增量算法将历史高频轨迹数据匹配到对应的道路上,把匹配获得的结果存入历史经验库,作为构建回报函数的基础。
1.2 候选路径集选取理论上轨迹数据均应位于道路上,但由于GPS定位误差等因素的影响,致使GPS点偏离真实的路网,因此需要将GPS点匹配到路网上。本文依据邻近性原则选取待匹配GPS点的候选点集。候选点选取过程如下:查找GPS点误差范围内的邻近道路,计算GPS点在邻近道路上的投影点,将投影点作为候选点;若投影点位于道路的延长线上,则选取距离该投影点最近的道路顶点作为候选点。
由于相邻候选点间可能存在多条路径,需要判断是否存在同时经过它们的历史轨迹;如果存在,则将它们和候选点间的最短路径加入候选路径集中。如图 2,GPS点候选点c1、c2间存在很多路径,如果在历史经验库中存在L1、L2、L33条路径同时经过候选点c1、c2,则将L1、L2、L3以及c1、c2最短路径作为它们的候选路径集;若不存在,则将它们的最短路径作为候选路径。此外,需根据可达性对候选路径进行筛选,即候选路径不应该超过车辆在该时间间隔内能够行驶的最大距离,从而形成更加符合现实的候选路径集。
1.3 基于强化学习的全局最优路径求解如何在相邻的GPS点间多条候选路径中选取一条路径,使组成的路径最接近真实的行车轨迹,是本算法需解决的关键问题。马尔科夫决策过程是随机动态系统的最优决策过程,是解决该类问题的有力工具之一。为此,本文将轨迹匹配问题转换为马尔科夫决策过程,采用强化学习中Q-learning算法求解连续GPS点序列的全局最优解,通过不断试错的方法获得经验知识,然后根据经验知识完善行动策略,进而完成轨迹数据的匹配。
1.3.1 马尔科夫决策过程马尔科夫决策过程(Markov decision processes,MDPs)包含一个环境状态集S,行为(agent)集合A,以及状态之间的转移概率P和在某个状态下执行行为的期望回报R组成。在t时刻,环境(environment)发送一个状态信号st∈S给agent;agent做出行为(action)at∈A(st);行为反过来影响环境,改变其状态,同时得到一个即时的回报(reward);重复上述过程,直到满足设定退出条件为止。
轨迹匹配转换为MDP过程的描述如下:
(1)状态(state):在每次决策过程中,agent均位于某个GPS候选点上,因此某时刻agent所处的GPS候选点即为MDP的状态。
(2)决策(action):agent选择连接当前候选点和下一个候选点的路径。
(3)回报值(reward):评估action选出的路径优劣性,将评估结果作为回报值。
(4)转移概率P:依据回报值不断更新转移概率,回报值大的状态其对应的转移概率大。
agent在不断进行决策、状态转移的同时,根据得到的回报值更新对环境的认知,进而影响决策过程,直到获得最优路径为止。
1.3.2 强化学习算法在马尔科夫决策过程中,回报值最大对应的路径为轨迹数据最佳匹配路径。由于强化学习利用了蒙特卡罗抽样方法和动态规划单步迭代方法的优点,克服了蒙特卡罗策略演化问题和动态规划随状态数增加时复杂性呈指数增加的缺点;因此本文采用强化学习算法中Q-learning方法进行最佳匹配路径的寻找。但强化学习算法要求agent初始状态具有唯一性。轨迹数据中第一个GPS点的候选点不唯一(每个GPS点对应若干个候选点)。因此,需要虚构一个虚拟点,设定虚拟点到第一个GPS候选点的路径长度都为1。轨迹匹配从虚拟点开始,agent通过一次决策可到达第一个GPS点对应的候选点,再依据马尔科夫决策过程依次选择后续的道路节点,直到完成轨迹与路网的匹配。
Q-learning算法是在状态转移概率和奖惩未知的情况下来估计最优策略的Q值。Q值函数是在环境状态st时执行动作at的评价函数与按最优动作序列执行时得到强化信号折扣的和
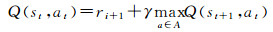 (1)
(1)
式中,rt+1为在状态st执行动作at到达状态st+1时获得的瞬时奖惩值;γ为折扣率,保证返回的奖惩是有限的;A为状态st+1时可执行的动作集。
为了简化计算过程,本文采取单步Q学习策略,即学习过程中,首先根据状态st选择执行动作at,然后观察下一个状态st+1,收到瞬时奖惩信号rt+1,根据Q学习更新规则更新Q值,再根据st+1执行动作at+1,重复上述过程直至满足设定的退出条件为止。
1.3.3 回报函数agent执行策略a,从状态s变为状态s′时,都会得到一个回报函数R,agent是要获取最大化的累积回报。本文算法中回报函数R由历史经验回报值R1, 偏移距离回报值R2组成,均需要归一化处理,计算公式如下
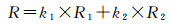 (2)
(2)
式中,R为回报函数;k1、k2表示权重系数,k1与K2的和为1;R1为历史经验回报值;R2为偏移距离回报值。
计算历史经验路径回报值R1时,需统计每条候选路径在历史经验库中出现的次数作为流行度popular (Li),计算见式(3),其中,n表示候选路径Li被历史轨迹经过的次数
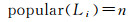 (3)
(3)
则历史经验路径回报值R1的公式表达如下,其中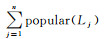
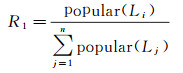 (4)
(4)
偏移距离回报值R2是指候选点和GPS点之间偏移距离,表达公式如下
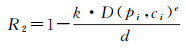 (5)
(5)
式中,D(pi, ci)表示GPS点pi和候选点ci之间的距离;k、d、e是比例因子。
2 算法验证为了验证算法的正确性和有效性,本文应用某市的浮动车轨迹数据(2013年8月1日-8月31日2000多辆出租车的GPS数据,共一千多万个GPS点)和OpenstreetMap路网数据进行了试验。试验中,首先将高频采样数据(采样频率为30 s)与地图数据进行匹配,获取车辆真实的行驶轨迹;然后将高频采样轨迹数据进行抽稀,分别构建了采样间隔为1 min、2 min、4 min、8 min和16 min的低频数据集;接着利用本文算法将低频数据集分别匹配到地图中;最后对比分析高频采样轨迹数据与低频采样数据匹配结果差异,计算匹配的准确率。
2.1 试验数据预处理数据预处理直接影响地图匹配算法的精度和性能。为了实现轨迹与路网数据的高效匹配,需要对路网数据和浮动车轨迹数据进行处理,流程如图 2所示。利用OpenstreetMap数据构建路网拓扑结构;处理后的路网共有19 974条边和22 672个节点。由于GPS点存在“漂移”问题,因此,应利用缓冲区分析剔除轨迹数据中的“漂移”点。本文采用两级缓冲区技术[21]剔除漂移的GPS点,具体流程如下:首先利用缓冲区删除偏离道路300 m以上的GPS点,然后利用小尺度缓冲区对距离道路300 m以内的数据点进行过滤(缓冲区半径由式(6)计算获得);再分别设置浮动车轨迹数据的瞬时速度和经纬度位置变化阈值的上限,剔除超过阈值的GPS点;最后为了消除由于浮动车静止或低速运行时GPS定位精度不高造成的“假行驶”现象,需要根据车辆行驶模式剔除上述的GPS轨迹点数据。
 (6)
(6)
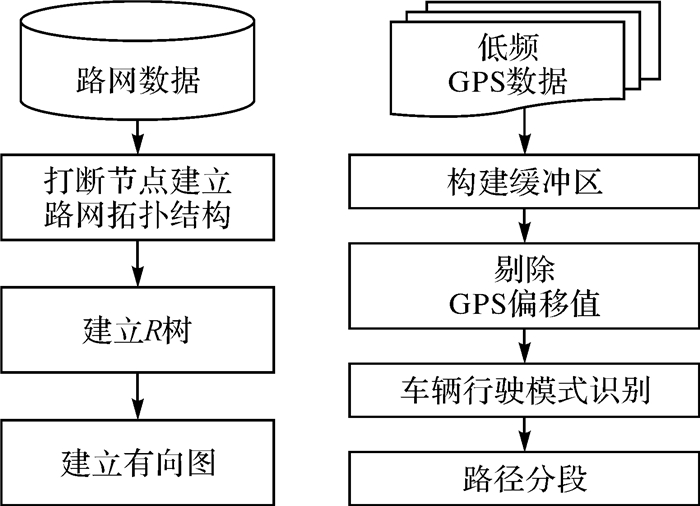
|
| 图 2 数据预处理流程图 Fig. 2 The flow chart of the map matching algorithm based on reinforcement learning |
其中,路网定位误差为α,车辆定位误差最大为β,高速公路单向路宽为ω,车宽为m。本文假定路网精度为α=10 m,车辆最大定位误差β为50 m,出租车宽度为1.6 m,道路宽度依据城市道路等级确定。
2.2 试验结果浮动车系统没有相应辅助设备记录车辆的真实行驶路径;但高频采样数据与真实行驶路径非常相近,采用增量法可实现轨迹数据与道路的正确匹配。文献[12-15]均将高频采样轨迹数据当作为真实行驶路径(ground truth),即将高频轨迹匹配结果作为真值来衡量低频轨迹数据匹配的准确率,本文也采用该标准进行相关试验分析(图 3)。
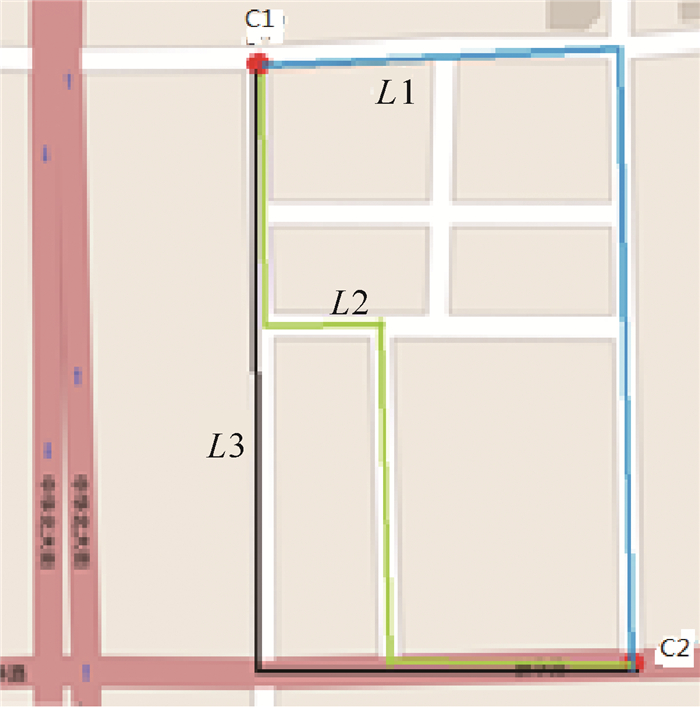
|
| 图 3 候选路径的选取 Fig. 3 The selection of candidate path |
为了衡量匹配精确度,使用文献[17]中的标准评价轨迹数据匹配的准确度,具体公式如下
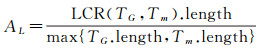 (7)
(7)
式中,TG为高采样率匹配路段;Tm为低采样率匹配路段;LCR (TG, Tm)为路段TG、Tm最长重合路段。
为了获取最优的匹配效果,试验测试分析了历史轨迹和偏离道路权重对匹配结果的影响。k1分别取0.1、0.2、…、0.9,对应k2分别取0.9、0.8、…、0.1;1、2、4、8 min采样间隔的轨迹匹配准确率情况如图 4所示(偏移权重公式中d=250,k=1,e=1.4)。由图 4可知,历史经验路径回报值在总回报值中所占比重小于0.6时,匹配准确度随着历史经验路径回报值比重的增大而增大;当超过0.6时,随着偏移距离回报值的比重减小,轨迹匹配的准确率也随之下降。由此可见,当k1=0.6时,低频轨迹数据匹配的准确率最高;因此,将回报函数中k1确定为0.6,k2确定为0.4。
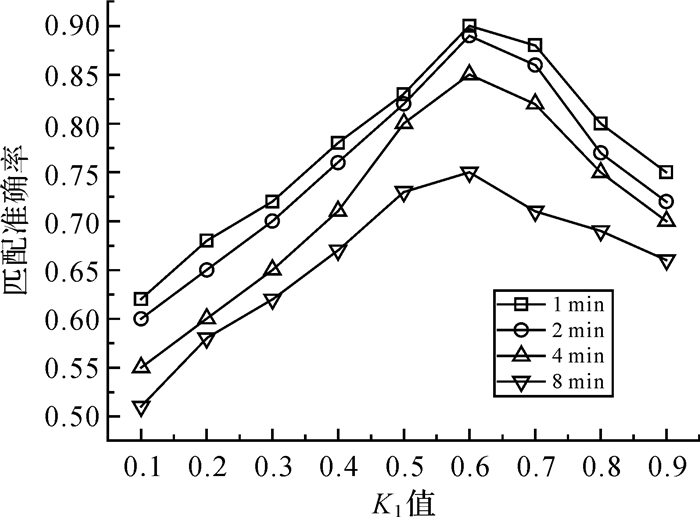
|
| 图 4 不同采样率下k1值对地图匹配准确率的影响 Fig. 4 Algorithm accuracy of different k1 under different sampling rate |
为了验证匹配结果的正确性,本文将低频轨迹与高频轨迹数据的匹配结果进行了可视化表达,如图 5所示(高频数据采样间隔为30 s;低频轨迹数据采样间隔为2 min)。图 5中,蓝色圆点表示原始轨迹中GPS点,橙色点表示低频采样间隔GPS点,蓝色轨迹线为低频采样轨迹匹配的最优路径。图 5(a)和5(b)分别表示在交叉路口和立交桥的匹配结果。

|
| 图 5 匹配结果的可视化表达效果 Fig. 5 Visualization of trajectory mapping results |
为了测试算法匹配的准确率,对比分析了该算法(history Markov decision processes Q-learning,HMDP-Q)与IVMM (interactive voting-based map matching)[17]在不同采样频率下匹配情况。IVMM算法是应用最广泛的低频轨迹数据匹配算法之一,该算法考虑了邻近和次邻近GPS轨迹点对匹配结果的影响,算法匹配精度优于ST-Matching等方法。为此,本文对比分析了HMDP-Q与IVMM算法匹配精度,结果如图 6所示。采样频率为1 min时,HMDP-Q算法匹配准确率达89.2%,而IVMM匹配准确率为73%;随着采样间隔的增大,HMDP-Q和IVMM算法匹配准确率均呈下降的趋势;当采样间隔为16 min时,HMDP-Q算法匹配准确率为61.4%,而IVMM匹配准确率仅为34%。各采样频率的HMDP-Q匹配准确率均高于IVMM算法。与IVMM算法相比,HMDP-Q算法加入历史轨迹库,充分考虑了司机习惯性路段选择,利用强化学习提取出了稀疏数据条件下的路段相关性,从而提高了浮动车轨迹数据匹配的准确率。
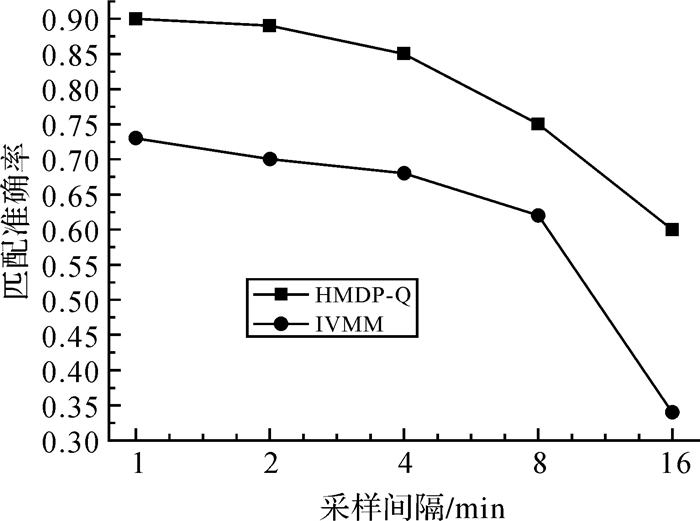
|
| 图 6 不同采样率下HMDP-Q和IVMM算法准确率对比 Fig. 6 Algorithm accuracy of HMDP-Q and IVMM under different sampling rate |
此外,本文利用普通笔记本计算机(具体配置如下:Intel i3 CPU,2.30 GHz,4 GB内存)测试分析了HMDP-Q算法的运行效率,结果如图 7所示。由图 7可知,随着轨迹数据采样间隔的增大,HMDP-Q算法和IVVM算法求解所需时间均呈下降的趋势;当轨迹采样频率为12 min时,HMDP-Q和IVVM算法求解所需时间基本相当;当轨迹采样频率小于12 min时,HMDP-Q算法求解效率优于IVVM算法,且轨迹采样时间间隔越小,相对于IVVM算法而言,HMDP-Q求解效率越高。
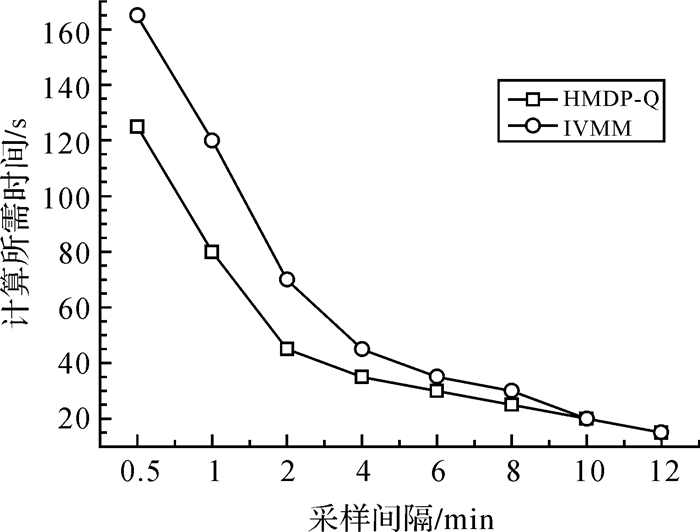
|
| 图 7 不同采样率下HMDP-Q和IVMM算法运行时间对比 Fig. 7 Consuming time of HMDP-Q and IVMM under different sampling rate |
3 结论
针对低频轨迹数据匹配精确不高的缺陷,本文提出了一种基于强化学习和历史轨迹的低频轨迹数据匹配算法。首先根据高频轨迹数据建立历史轨迹经验数据库,然后以历史轨迹经验数据库和GPS点偏移距离作为回报函数构建马尔科夫决策模型,并引入强化学习来进行马尔科夫决策过程求解。应用浮动车轨迹数据和OpenstreetMap路网数据进行了试验。试验结果表明:随着采样间隔增大,HMDP-Q和IVMM匹配的准确率均呈下降的趋势;HMDP-Q算法的匹配准确率明显高于IVMM算法;在采样率为1 min的低频浮动车轨迹数据下匹配精度达到89.2%,即使采样率为16 min,其匹配精度也能达到61.4%;算法解算效率也明显高于IVMM算法。
| [1] | ZHENG Kai, ZHENG Yu, XIE Xing, et al. Reducing Uncertainty of Low-Sampling-Rate Trajectories[C]//Proceedings of the IEEE 28th International Conference on Data Engineering. Washington, DC, USA: IEEE, 2012: 1144-1155. |
| [2] | 王美玲, 程林. 浮动车地图匹配算法研究[J]. 测绘学报, 2012, 41(1): 133–138. WANG Meiling, CHENG Lin. Study on Map-matching Algorithm for Floating Car[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(1): 133–138. DOI:10.13485/j.cnki.11-2089.2014.0030 |
| [3] | 李珂, 杨杨, 邱雪松. 城市汽车导航中一种改进的D-S证据理论地图匹配算法[J]. 测绘学报, 2014, 43(2): 208–213. LI Ke, YANG Yang, QIU Xuesong. An Improved Map Matching Algorithm Based on D-S Evidence Theory in City Vehicle Navigation[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(2): 208–213. DOI:10.13485/j.cnki.11-2089.2014.0030 |
| [4] | 唐炉亮, 常晓猛, 李清泉. 出租车经验知识建模与路径规划算法[J]. 测绘学报, 2010, 39(4): 404–409. TANG Luliang, CHANG Xiaomeng, LI Qingquan. The Knowledge Modeling and Route Planning Based on Taxi' Experience[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(4): 404–409. |
| [5] | 李清泉, 黄练. 基于GPS轨迹数据的地图匹配算法[J]. 测绘学报, 2010, 39(2): 207–212. LI Qingquan, HUANG Lian. A Map Matching Algorithm for GPS Tracking Data[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(2): 207–212. |
| [6] | 唐进君, 刘芳. 基于路径预测的不确定性推理组合地图匹配算法[J]. 测绘学报, 2010, 39(5): 546–550. TANG Jinjun, LIU Fang. A Driver Route Prediction Based Map-matching Algorithm Integrating Uncertain Reasoning[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(5): 546–550. |
| [7] | 曾喆, 李清泉, 邹海翔, 等. 曲率积分约束的GPS浮动车地图匹配方法[J]. 测绘学报, 2015, 44(10): 1167–1176. ZENG Zhe, LI Qingquan, ZOU Haixiang, et al. Curvature Integration Constrained Map Matching Method for GPS Floating Car Data[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(10): 1167–1176. DOI:10.11947/j.AGCS.2015.20140352 |
| [8] | 唐进君, 曹凯. 一种自适应轨迹曲线地图匹配算法[J]. 测绘学报, 2008, 37(3): 308–315. TANG Jinjun, CAO Kai. An Adaptive Trajectory Curves Map-matching Algorithm[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(3): 308–315. DOI:10.3321/j.issn:1001-1595.2008.03.008 |
| [9] | DAI Jian, DING Zhiming, XU Jiajie. Context-Based Moving Object Trajectory Uncertainty Reduction and Ranking in Road Network[J]. Journal of Computer Science and Technology, 2016, 31(1): 167–184. DOI:10.1007/s11390-016-1619-5 |
| [10] | SCHULZE G, HORN C, KERN R. Map-Matching Cell Phone Trajectories of Low Spatial and Temporal Accuracy[C]//Proceedings of the IEEE 18th International Conference on Intelligent Transportation Systems. Washington, DC, USA: IEEE, 2015: 180-187. |
| [11] | CHEN Ling, TANG Yanlin, LV Mingqi, et al. Partition-Based Range Query for Uncertain Trajectories in Road Networks[J]. GeoInformatica, 2015, 19(1): 61–84. DOI:10.1007/s10707-014-0206-6 |
| [12] | DING Zhiming, YANG Bin, GüTING R H, et al. Network-Matched Trajectory-Based Moving-Object Database: Models and Applications[J]. IEEE Transactions on Intelligent Transportation Systems, 2015, 16(4): 1918–1928. DOI:10.1109/TITS.2014.2383494 |
| [13] | CHIANG M F, ZHU Wenyuan, PENG W C, et al. Distant-Time Location Prediction in Low-Sampling-Rate Trajectories[C]//Proceedings of the IEEE 14th International Conference on Mobile Data Management. Washington, DC: IEEE, 2013: 350-359. |
| [14] | LI Yang, HUANG Qixing, KERBER M, et al. Large-scale Joint Map Matching of GPS Traces[C]//Proceedings of the 21st ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems. New York: ACM, 2013: 1320-1321. |
| [15] | CHIANG M F, LIN Y H, PENG W C, et al. Inferring Distant-Time Location in Low-Sampling-Rate Trajectories[C]//Proceedings of the 19th ACM SIGKDD international Conference on Knowledge Discovery and Data Mining. New York, USA: ACM, 2013: 1234-1241. |
| [16] | LOU Yin, ZHANG Chengyang, ZHENG Yu, et al. Map-Matching for Low-Sampling-Rate GPS Trajectories[C]//Proceedings of the 17th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems. New York, USA: ACM, 2009: 352-361. |
| [17] | YUAN Jing, ZHENG Yu, ZHANG Chengyang, et al. An Interactive-Voting Based Map Matching Algorithm[C]//Proceedings of the 2010 Eleventh International Conference on Mobile Data Management. Washington, DC, USA: IEEE, 2010: 43-52. |
| [18] | YANG Jian, MENG Liqiu. Feature Selection in Conditional Random Fields for Map Matching of GPS Trajectories[M]//GARTNER G, HUANG Haosheng. Progress in Location-Based Services 2014. Switzerland: Springer International Publishing, 2015: 121-135. |
| [19] | NEWSON P, KRUMM J. Hidden Markov Map Matching through Noise and Sparseness[C]//Proceedings of the 17th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems. New York, USA: ACM, 2009: 336-343. |
| [20] | HUNTER T, ABBEEL P, BAYEN A. The Path Inference Filter: Model-Based Low-Latency Map Matching of Probe Vehicle Data[J]. IEEE Transactions on Intelligent Transportation Systems, 2014, 15(2): 507–529. DOI:10.1109/TITS.2013.2282352 |
| [21] | ZHENG Yu, ZHANG Lizhu, XIE Xing, et al. Mining Interesting Locations and Travel Sequences from GPS Trajectories[C]//Proceedings of the 18th International Conference on World Wide Web. New York, USA: ACM, 2009: 791-800. |
| [22] | BRAKATSOULAS S, PFOSER D, SALAS R, et al. On Map-Matching Vehicle Tracking Data[C]//Proceedings of the 31st International Conference on Very Large Data Bases. New York, USA: ACM, 2005: 853-864. |



