在开展卫星影像高精度规模化应用过程中,减少控制点需求,开展稀少控制甚至是无控制的航天摄影测量处理,是降低生产成本、提升生产效率的有效途径。开展无地面控制条件下的1: 50 000甚至更大比例尺测绘应用一直是当前国产卫星追求的理想目标,而确保无地面控制点条件下影像处理后的几何精度达到1:50 000比例尺测图要求是实现这一目标的前提。我国各尺度基础地理信息产品的高程精度要求相较于平面精度通常要高出许多倍,例如1:50 000比例尺地形图在丘陵地区的平面精度要求是25 m,而高程精度要求却比平面精度整整高出5倍,达到5 m,其他地形类型也存在同样的现象。大量学者的研究和试验表明,在无地面控制条件下,主要的国产测绘遥感卫星(如资源三号卫星)的平面中误差一般为5~25 m,立体影像对的高程中误差一般为6~15 m[1-2]。这表明在无地面控制条件下,国产测绘遥感卫星影像平面精度基本可以满足我国1:50 000比例尺测图的平面精度要求,但高程精度却达不到1:50 000比例尺测图的高程精度要求,因此在无地面控制条件下的卫星测绘应用中,高程精度是制约卫星影像测图精度的关键因素。在不借助地面控制资料条件下,通过区域网平差方法实现卫星影像高程精度的较大幅度提升并满足1:50 000甚至更大比例尺的测图要求,这对基于国产卫星的全球1:50 000比例尺测图以及控制获取困难地区的高精度测图都拥有非常重要的实际意义和研究价值。
推扫式卫星影像的区域网平差主要包括基于严密成像几何模型和基于有理多项式模型(rational function model,RFM)的区域网平差两种,其中基于严密成像几何模型的平差研究主要集中在对其姿态、轨道模型进行改正[3-5]。基于RFM的区域网平差研究主要集中在采用像方的多项式模型补偿模型误差,而基于像方补偿的RFM区域网平差可以很好地消除影像的系统误差[6-8]。而在SRTM辅助的区域网平差研究方面,文献[9-10]研究了SRTM约束的弱交会条件下的区域网平差方法,通过在平差迭代解算中直接利用SRTM来获取连接点的物方高程的方法,有效保障了弱交会影像区域网平差的正确性。文献[11]提出了先通过卫星立体影像对制作DEM,并以SRTM作为控制基准,开展独立模型法DEM区域网平差,获得DEM的定向参数并改正立体影像的成像几何模型参数,试验结果将资源三号正视全色影像的平面定向精度由12.93像素提高到6.85像素。
针对SRTM数据在部分平坦地形区域的几何精度远远高于其标称精度的情况,提出并设计了在不使用地面控制点情况下采用SRTM (shuttle radar topography mission)辅助的立体影像区域网平差方法:通过在区域网中布设密集且均匀的连接点,且连接点的物方高程初始值直接通过SRTM数据获取,并为位于平坦地形区域连接点的物方高程值赋予较大的合适权值,在平差解算过程中亦使用SRTM作为连接点物方高程改正值的参考,进而实现整个区域网平差高程精度的较大幅度提升。
1 SRTM约束的立体影像区域网平差原理 1.1 SRTM精度2000年2月美国太空总署(NASA)和国防部国家测绘局(NIMA)以及德国与意大利航天机构共同合作,开展了“航天飞机雷达地形测绘(SRTM)”计划,利用搭载在“奋进”号航天飞机上的C波段航天图像雷达和X波段合成孔径雷达,获取了覆盖60°N-56°S之间,占全球陆地表面总面积80%以上的规则格网的数字高程模型产品。SRTM的数字高程模型拥有两种分辨率,分别是3″×3″(约90 m分辨率)的SRTM 3和1″×1″(约30 m分辨率)的SRTM 1。目前全球范围的SRTM 3数据可提供公开免费下载。本文的研究工作采用的SRTM为SRTM 3数据,为了便于后文描述,后文中SRTM指的即是SRTM 3数据。
SRTM的高程基准采用EGM96(Earth Gravitational Model 96)水准面,高程坐标单位为米,平面基准采用WGS-84大地基准、平面坐标采用经纬度。SRTM标称的绝对高程精度为16 m (LE90),相对高程精度为10 m (LE90),绝对平面精度为20 m (CE90),相对平面精度为15 m (CE90)。LE90和CE90是美国摄影测量界常用的高程和平面精度表示方法,表示90%(1.64倍中误差)的高程和平面误差不超过精度数值。将其换算为我国常用的以中误差形式表达的几何精度,则SRTM标称的绝对高程精度为10 m (1σ),相对高程精度为6 m (1σ),绝对平面精度为12 m (1σ),相对平面精度为9 m (1σ)[12]。国内外众多机构和学者已经对全球范围SRTM数据精度开展了广泛的研究和验证,结果表明,SRTM的高程精度与地形类型存在较强的相关性,在高程较小的平坦地区其高程精度较高,中误差甚至可以优于2~6 m,而在山地、高山地等高程起伏较大区域的精度相对较差,但也至少优于其标称精度[13-16]。
1.2 基于RFM的立体影像区域网平差模型主要的国产测绘遥感卫星影像产品均主要提供RFM作为成像几何模型。RFM是利用有理多项式建立影像的像方(影像像素坐标)与其对应的物方(地面大地坐标)之间的数学映射关系,基本方程定义如下[17]
 (1)
(1)
式中,为避免计算过程中参数数值量级差别过大而引入舍入误差,需要将影像像点坐标和对应的地面点坐标均归一化到-1~1之间,以增强参数求解的稳定性;(P, L, H)为归一化后的地面坐标;(x, y)为归一化后的影像坐标;NumS(P, L, H)、DenS(P, L, H)、NumL(P, L, H)和DenL(P, L, H)分别表示一般多项式,多项式中每一个变量P、L、H的幂均不超过3次,所有变量的幂之和也不超过3次[18]。
因其参数不具备具体的物理意义,在区域网平差过程中也就无法通过严密分析误差来源来改正模型误差,而是通过采用偏移补偿的方式进行模型误差改正,目前主要采用像方补偿策略。基于像方的补偿模型是建立一个影像像方坐标点的多项式模型,通过该多项式模型针对RFM计算获得的像点坐标进行补偿[6, 17, 19-20]。
采用像方补偿方案的多项式模型形式(也即基于RFM的平差模型)如下
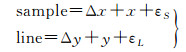 (2)
(2)
式中,(sample, line)为像点在影像上的归一化后量测坐标,可以是控制点或者连接点;εL和εS为随机非观测误差;(x, y)为利用有理函数模型式(1)计算之像方坐标。
(Δx, Δy)为RFM计算的像方坐标的补偿多项式模型,其形式如下
 (3)
(3)
式中,(a0, a1, a2, …, b0, b1, b2, …)表示系统误差的补偿参数。
当系统误差补偿多项式(Δx, Δy)仅取一次项时,即为像方仿射变换模型
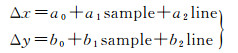 (4)
(4)
在式(2)和式(4)基础上, 将影像像方的仿射变换参数(a0, a1, a2)、(b0, b1, b2)和连接点对应的物方大地坐标(lat, lon, h)一并求解,即可建立基于RFM的区域网平差的误差方程,如下所示
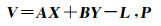 (5)
(5)
式中,V表示像点行和列坐标观测值的残差向量:V=[vxvy]T;X=[Δa0Δa1Δa2Δb0Δb1Δb2]T为像方坐标系统误差补偿参数(即6个仿射变换参数)的改正数向量;Y=[Δlat Δlon Δh]T为连接点对应地面大地坐标的改正数向量;A=

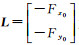
针对控制点而言,误差方程中需要改正的是仿射变换参数,而对于连接点而言,误差方程中需要同时改正仿射变换参数和其相应的物方大地坐标。
1.3 SRTM约束的无地面控制立体区域网平差策略通过式(5)可知,基于RFM的区域网平差中的未知数包括影像像方的仿射变换参数改正值,以及连接点对应的物方大地坐标的改正值。在平差解算过程中,连接点对应的物方大地坐标的初始值和改正值均是通过立体像对前方交会获取,在无地面控制条件下,显然这些物方大地坐标的精度由参与平差立体影像的原始精度决定。当参与平差影像精度较低(含有不同程度的系统误差),且区域网中不同区域的影像精度不一致时,将导致各连接点对应的物方大地坐标中都残存有不同量级的误差,而最终的平差结果相当于对所有连接点物方大地坐标误差进行了一次均衡处理。因此不使用控制点的自由网平差是对所有参与平差影像的误差进行了一次平均,并不能够显著提升区域内影像的整体平面和高程定位精度。
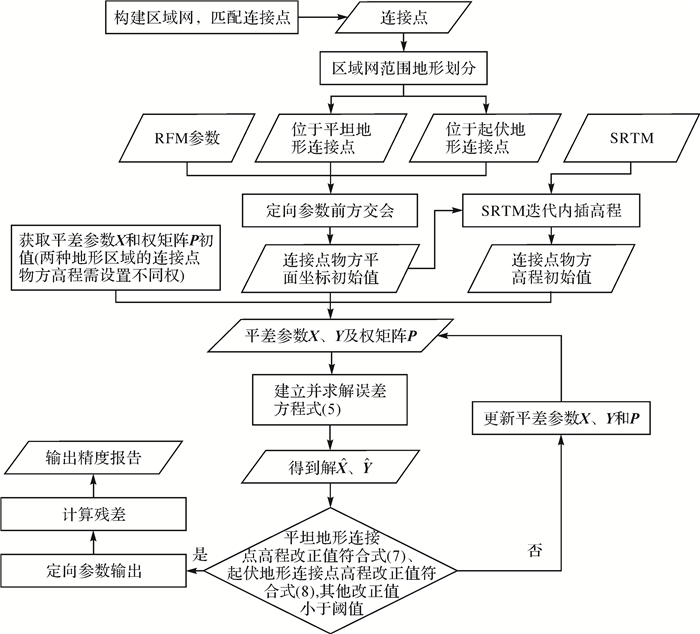
为了提升自由网平差后立体影像的高程精度,本文设计了采用SRTM约束连接点物方高程解算的无地面控制立体区域网平差方案。其基本流程如图 1所示。
|
| 图 1 SRTM约束的无地面控制立体区域网平差流程图 Fig. 1 SRTM assisted block adjustment process for stereo imagery without GCPs |
具体过程描述如下:
(1)针对SRTM数据在平坦地形区域的精度优于起伏地形(指山地和高山地地形)区域的特点,将区域网覆盖范围概略地划分为平坦地形区域和起伏地形区域。
(2)在区域网平差解算前,所有连接点物方大地坐标的平面初始值由立体像对前方交会获取,但是高程初始值则利用SRTM数据获取。
地形类型的划分时,既可以基于SRTM的显示效果通过人工目视方法划分,也可以参照我国测绘相关标准中地形类型划分原则,即按图幅范围内大部分的地面倾斜角和高差划分不同地形类型[21],通过将区域网覆盖范围按一定规则划分成若干图幅,利用SRTM计算各图幅的地面倾斜角和高差,并按表 1的划分标准确定各图幅的地形类型。
| 地形类别 | 地面倾斜角/(°) | 高差/m |
| 平坦地形 | ≤6 | ≤150 |
| 起伏地形 | >6 | >150 |
| 注:当高差与地面倾斜角矛盾时,以地面倾斜角为准。 | ||
(3)根据SRTM的高程精度经验值(一般可认为地形平坦区域的SRTM高程中误差σSRTM-plan为3~6 m,地形起伏区域的高程中误差σSRTM-hill为6~10 m),分别为位于平坦地形区域和位于起伏地形区域的连接点的物方大地坐标的高程值设置一个合理的不同权重,不同观测值的权值可按如下方法确定:
a.像点坐标观测值的精度为σx(mm),设其权Px=1。
b.所参考外部数字高程数据的高程精度为σch(m),则连接点物方大地坐标的高程值的权Pch为
 (6)
(6)
式中,f/H为摄影比例尺;当所参考的数字高程模型的精度越高,即σch越小,则权值越大,其对平差结果的贡献也越大。
(4)在平差迭代解算过程中,根据需要对连接点物方大地坐标和影像像方的仿射变换参数进行改正,但每次迭代后位于平坦地形区域的连接点物方高程改正值hplan_corr应符合下式要求
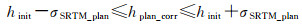 (7)
(7)
位于起伏地形区域的连接点物方高程改正值hhill_corr应符合下式要求
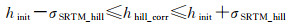 (8)
(8)
式中,hinit为连接点通过外部高程模型获得的物方大地坐标的高程初始值。
将改正后的连接点物方大地坐标的平面值和高程值,以及影像像方仿射变换改正参数一起代入下一次平差迭代解算,直至平差结果收敛,平差结束。
此外,为了避免SRTM局部区域高程值错误或精度低下等偶然因素对整体高程精度的影响,在区域网平差中连接点数量应尽量充足且点位分布应尽量均匀。根据实践经验,针对资源三号卫星前后视立体影像建议在行和列方向上分别每隔1500个像素布设一个连接点,即每一标准景立体影像对上均匀布设约100个连接点。通过密集且均匀的连接点分布,可以有效降低SRTM中偶然误差的影响,提升区域网平差整体精度水平。
2 试验与分析 2.1 试验区域和试验数据本试验选定湖北省全境作为试验区域。湖北省位于我国中部,东西长约740 km,南北宽约470 km。全省国土总面积18.59万km2,其中山地占56%,丘陵占24%,平原湖区占20%。全省地势大致为东、西、北三面环山,中间低平,略呈向南敞开的不完整盆地,地形起伏从海拔20 m到3105 m。
为了验证试验精度,收集到分布于试验区域内的180个采用GPS CORS技术测量的高精度外业GPS点,其大地基准为WGS-84坐标系,高程基准为WGS-84椭球高,平面和高程精度均优于0.2 m。
试验影像选用2012年3月-2014年12月期间获取的412对ZY-3卫星传感器校正三线阵立体影像对(其中265对三线阵立体影像上有GPS点分布),影像附带有理函数模型参数文件,前、正、后视影像分辨率分别为3.5 m、2.1 m、3.5 m。
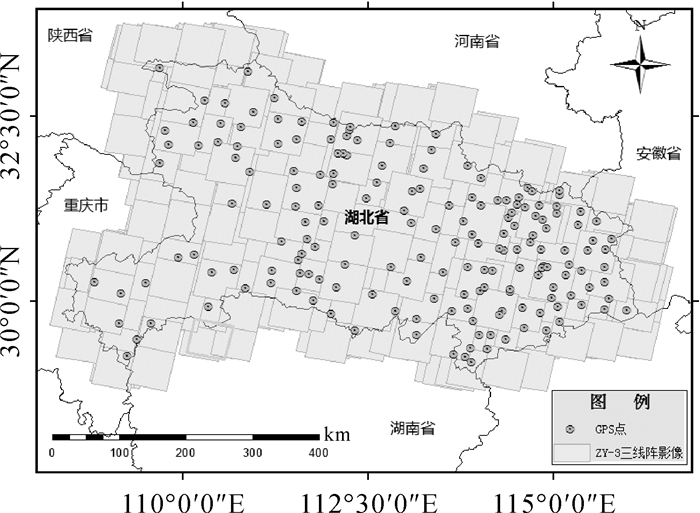
试验区域、试验影像和GPS点地理分布如图 2所示。
|
| 图 2 湖北试验区域区域网平差试验影像和GPS点分布 Fig. 2 Experimental images and GPS points distribution |
GPS点在试验影像上的像点坐标由人工刺点获取,像点量测精度优于0.5像元。
作为高程参考的SRTM数据是从“国际农业研究协商小组的空间信息协会”(CGIAR-CSI)官网(http://srtm.csi.cgiar.org/)免费下载90 m格网SRTM3,数据版本号为V4.1,数据范围覆盖整个试验区域。其大地基准为WGS-84坐标系,平面采用经纬度坐标,高程基准为EGM96水准面,高程单位为米。
由于资源三号卫星采用GPS作为轨道测量设备,因此其立体影像的高程基准为WGS-84椭球高,且作为检查资料的外业GPS点的高程基准也采用了WGS-84椭球高,均与SRTM所采用的EGM96水准面存在差异。为了消除高程基准面不同造成的试验结果误差,本文将SRTM高程基准由EGM96水准面转换到WGS-84椭球高,转换过程中采用公开获取的1 km格网的EGM96水准模型(常用的商业遥感和GIS软件,如ArcGIS、ENVI等均附带该模型)来获取SRTM各格网的WGS-84椭球高与大地水准面的垂直差距并进行改正。EGM96水准模型是美国利用全球大量重力数据计算获得的全球范围高精度大地水准面模型,其在美国本土50 km范围内达厘米级精度[22]。由于该模型构建过程中没有参考我国的重力资料,造成其在国内精度偏低,但其精度也应至少优于0.5 m[23],相对于SRTM数据标称的高程精度而言,尚在可以接受的范围。
同时通过人工目视判断SRTM渲染图上地形起伏,将试验区域概略地分为平坦地形区域和起伏地形区域,其中平坦地形区域面积约10万km2,起伏地形区域面积约8.6万km2。SRTM数据地理分布及不同地形区域划分如图 3所示。

|
| 图 3 SRTM地理分布及不同地形类型划分 Fig. 3 SRTM geographic distribution and the different terrain area division |
2.2 SRTM数据自身高程精度验证
为了有效开展和分析基于SRTM约束的无控制立体区域网平差,需要先行开展SRTM数据自身的高程精度验证。
将180个GPS点全部作为检查点,根据GPS点的大地平面坐标获取SRTM数据上对应位置的高程值,并与GPS点的高程值相减即可以获取SRTM数据的高程精度如表 2所示。
| m | ||||
| 地形区域 | 中误差 | 平均差 | 最大误差 | 最小误差 |
| 全区域 | 3.85 | 2.48 | 16.18 | 0.10 |
| 平坦地形区域 | 2.72 | 2.12 | 8.82 | 0.10 |
| 起伏地形区域 | 6.02 | 3.51 | 16.29 | 0.13 |
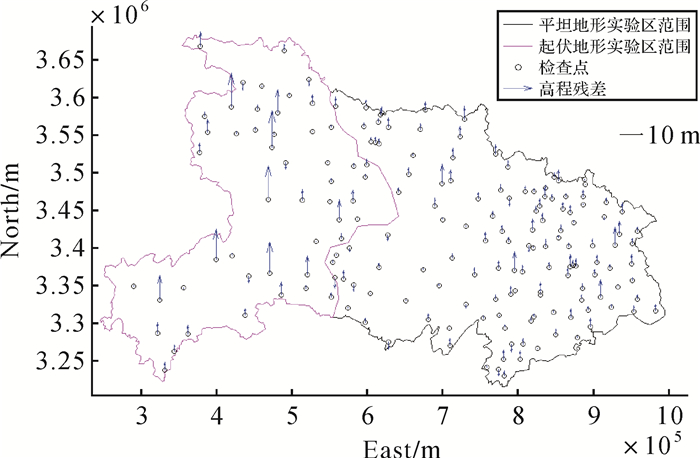
SRTM数据在整个试验区域的高程中误差为3.85 m,最大误差为16.18 m;在按图 3划分的平坦地形区域的高程中误差为2.75 m,最大误差为8.82 m;起伏地形区域的高程中误差为6.02 m,最大误差为16.29 m。证实了本试验区的SRTM实际高程精度远高于其标称的10 m (1σ)精度,且在地形平缓区域,其高程精度远远高于其在山地等起伏地形区域的高程精度,已经达到了我国1:50 000比例尺地形图在平原地形的精度要求。
所有检查点的高程残差如图 4所示。
|
| 图 4 SRTM上检查点的高程残差图 Fig. 4 SRTM elevation residuals |
从图 4可以看出,SRTM在局部范围某些区域(尤其是起伏地形区域的局部范围)的高程残余误差较大。验证了本文前面的论述,即在区域网平差中需要布设密集连接点,以避免局部区域高程值错误或精度低下等偶然因素对整体高程精度的影响。
2.3 SRTM约束的无控制立体区域网平差试验为了有效验证并对比分析无地面控制条件下SRTM高程约束对立体区域网平差的影响效果,分别开展如下3组区域网平差试验:
(1)开展无任何约束的自由网平差。
(2)按照1.3节所述方法,开展无地面控制条件下SRTM高程约束的区域网平差。平差前,通过判断各景影像中心位置所处图 3所示的不同地形区域,将影像划分为位于平坦地形区域影像和位于起伏地形区域影像,通过SRTM获取所有立体影像连接点的物方高程初值。平差过程中,设定地形平坦区域的SRTM高程中误差σSRTM-plan为3 m,山地区域的SRTM高中程误差σSRTM-hill为8 m,通过式(6)分别为位于平坦地形区域和位于起伏地形区域的影像设置其上连接点物方高程的权值;分别通过式(7)和式(8)作为每次迭代解算中位于平坦地形区域影像和位于起伏地形区域影像上连接点物方高程改正值的约束条件。
(3)采用公开获取的地球科学激光测高仪系统(geoscience laser altimeter system,GLAS)数据作为高程控制,开展GLAS高程控制的区域网平差。GLAS数据来源于美国2003年发射的ICESat卫星上搭载的GLAS传感器, GLAS数据可分为GLA01-GLA15共15种类别的标准数据产品。其中GLA14级产品为陆地高程数据,由于其记录的是GLAS每个激光脉冲对应的70 m直径地面光斑足印范围内的一个平均高程值,因此为了确保GLAS数据的精度,需要选择足印内地形平坦且地物单一区域的GLAS数据作为高程控制。大量研究表明, 在该类区域的GLAS数据的激光足印平面精度为10 m,高程精度约15 cm[24]。由于GLAS发射的激光脉冲为高斯型,在地形平坦且地物单一区域的回波波形应该严格符合高斯分布且只有一个波峰,因此通过对GLAS数据的回波波形信息进行高斯拟合,当拟合后的标准差小于5 ns,并对照足印区域的影像块,即可挑选出用于高程控制的高精度GLAS数据[25]。经过筛选,本试验共采用了326个GLA14级数据产品作为高程控制,数据获取时间为2003年10月6日-2009年4月8日,其点位分布见图 6(c)。在平差过程中,GLAS高程控制点待求解的未知数为其对应的物方平面坐标和影像像方的仿射变换参数(a0, a1, a2, b0, b1, b2),将高程控制点的高程值作为真实值代入式(5),则有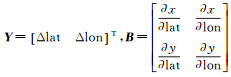
此外,为了避免平差试验中因连接点的不同而引入的额外误差,上述各组区域网平差试验均采用了同一套连接点,即通过将所有三线阵立体影像构建区域网,按照每个立体像对上至少均匀布设100个连接点的设计方案,通过自动匹配技术获取密集的连接点(本文试验中采用了像素工厂软件V4.0辅助开展了连接点自动匹配工作)。且每个连接点在其所分布的所有影像上均有刺点。区域网中的连接点的分布如图 5所示。

|
| 图 5 SRTM高程约束的立体影像自由网平差连接点分布示意图 Fig. 5 Tie Points distribution of block adjustment for stereo image |
上述各组区域网平差中,连接点在像方X向(垂轨向)和Y向(沿轨向)中误差均小于0.25像素,最大残差均小于1.5像素。
将所有GPS外业点全部作为检查点,各组区域网平差试验中检查点精度如表 3所示。
| m | |||||||||||
| 平差类型 | 地形区域 | 高程精度/m | 平面精度/m | ||||||||
| 中误差 | 平均差 | 最大差 | 平面 中误差 |
平面 最大差 |
垂轨向 中误差 |
垂轨向 最大差 |
沿轨向 中误差 |
沿轨向 最大差 |
|||
| 无约束的自由网平差 | 全区域 | 7.19 | 6.41 | 19.98 | 10.97 | 23.30 | 7.48 | 21.48 | 7.78 | 14.12 | |
| 平坦地形区域 | 7.25 | 0.07 | 19.98 | 11.62 | 23.27 | 8.12 | 21.48 | 8.43 | 14.12 | ||
| 起伏地形区域 | 7.04 | -2.89 | 19.67 | 8.56 | 11.73 | 6.04 | 11.31 | 5.81 | 10.20 | ||
| SRTM高程约束区域网平差 | 全区域 | 2.01 | 1.47 | 6.86 | 12.05 | 21.66 | 10.12 | 18.52 | 6.71 | 15.68 | |
| 平坦地形区域 | 1.44 | 0.29 | 4.66 | 13.40 | 21.66 | 11.25 | 18.52 | 7.29 | 15.68 | ||
| 起伏地形区域 | 3.05 | 2.31 | 6.86 | 7.14 | 12.25 | 5.29 | 9.73 | 4.80 | 8.52 | ||
| GLAS高程控制区域平差 | 全区域 | 2.49 | -1.48 | 8.10 | 12.64 | 19.33 | 10.80 | 19.33 | 6.56 | 15.28 | |
| 平坦地形区域 | 1.69 | -1.18 | 4.28 | 14.16 | 22.73 | 12.27 | 19.33 | 7.06 | 15.28 | ||
| 起伏地形区域 | 3.92 | -2.28 | 8.10 | 6.96 | 12.24 | 4.89 | 9.73 | 4.95 | 9.19 | ||
| 注:GLAS高程控制点的高程中误差0.12 m,平均高程误差0.000 3 m,最大高程误差0.65 m | |||||||||||
SRTM高程约束区域网平差中,整体高程中误差为2.01 m、最大误差为6.86 m,相对于无任何约束的自由网平差提升了3倍以上;整体平面中误差为12.05 m,最大误差为21.66 m,与无任何约束的自由网平差的平面精度基本相当,表明采用本文提出的SRTM高程约束的区域网平差方法可以显著提升整体区域的高程精度。
GLAS高程控制区域平差的高程中误差为2.49 m,而平面精度也与无任何约束的自由网平差的平面精度基本相当,表明采用GLAS高程数据作为高程控制,也可以显著提升区域网的平差高程精度。
SRTM高程约束区域网平差的高程精度略微优于GLAS高程控制区域平差,初步分析其原因为:虽然GLAS数据的高程精度要远高于SRTM数据高程数据,但是受限于激光数据获取机理以及ICESat卫星GLAS较大的光斑足印直径,只有分布在地形平坦且地物单一区域的GLAS数据才拥有较高的高程精度。这极大限制了GLAS数据的使用,因此在本试验中的GLAS高程控制点主要分布于试验区东部平坦区域,而西部山地区域则严重缺乏GLAS数据分布。表明在大范围区域网平差的实际应用中,SRTM高程约束区域网平差的高程精度可以达到甚至略优于高精度GLAS数据作为高程控制的区域网平差水平。
SRTM高程约束的自由网平差的整体高程精度相对于SRTM自身的高程精度提升了约2倍,其中平坦地形区域高程精度比SRTM的自身精度提高了约1 m,起伏地形区域的高程精度提高了约3 m。造成这一现象的主要原因是SRTM的格网尺寸仅为90 m,相当程度地综合了地形细节,极大影响了检查点的高程精度检查结果,而在立体影像对上则不存在这一问题,因此区域网平差后可能获得比SRTM更高的高程精度水平。
各组区域网平差的残差对比如图 6所示。

|
| 图 6 各组区域网平差残差对比 Fig. 6 Comparison of each group block adjustment residuals |
从图 6可以看出,3组区域网平差的平面残余误差呈现出明显的系统性,其误差大小、方向和分布特点均基本一致。总体上为自西向东误差大小逐渐变大,误差方向均主要由西南向指向东北向。这说明无论是SRTM高程约束区域网平差还是GLAS高程控制区域网平差,由于均未作任何平面约束,所以并未明显改变区域内影像的平面误差特性和误差大小。
无约束自由网平差的高程残余误差在整个区域而言系统性不强,但在局部区域还是呈现出一定的系统性,在试验区域中部地区的高程残差较大,高程残差数值达到20 m左右,误差方向均为低于检查点真实高程。
SRTM高程约束区域网平差的高程残余误差在整个区域内显著减小,且误差大小比较平均,没有明显的误差值较大区域。表明采用本文提出的SRTM高程约束的平差方案可以显著降低整体区域的系统误差、提升影像的高程精度。
GLAS高程控制区域网平差的高程残余误差在整个区域内也显著减小。但是由于山地地形区域内的GLAS高程控制点数量稀少,导致该区域的高程残差显著大于平坦地形区域的高程残差,且残差方向还表现出一定的系统性,其中山地地形西部区域高程残差方向向上,山地地形中东部区域的高程残差方向向下。表明GLAS数据作为高程控制的区域网平差虽然也可以显著提升影像的高程精度,但却与GLAS数据的几何分布状态和数量密切相关,在局部区域,尤其是山地地形区域的使用上受到了一定限制。
3 结论本文针对SRTM数据在部分平坦地形区域的几何精度可以达到我国1:50 000比例尺基础地理信息产品几何精度的情况,提出并设计了在不使用地面控制点情况下采用SRTM辅助的立体影像区域网平差方法,并利用湖北省全境412对资源三号卫星传感器校正三线阵立体影像对进行了试验。结果证实:采用SRTM约束的立体影像自由网平差在不对平面精度造成影响的情况下可以显著提升影像的高程精度,其高程精度水平满足我国1:25 000比例尺地理信息产品各地形区域的精度要求。
| [1] | TANG Xinming, ZHOU Ping, ZHANG Guo, et al. Verification of ZY-3 Satellite Imagery Geometric Accuracy without Ground Control Points[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(10): 2100–2104. DOI:10.1109/LGRS.2015.2450251 |
| [2] | TANG Xinming, ZHOU Ping, ZHANG Guo, et al. Geometric Accuracy Analysis Model of the Ziyuan-3 Satellite without GCPs[J]. Photogrammetric Engineering & Remote Sensing, 2015, 81(12): 927–934. |
| [3] | TOUTIN T. Multisource Data Fusion with an Integrated and Unified Geometric Modelling[J]. EARSeL-Advances in Remote Sensing, 1995, 4(2): 118–129. |
| [4] | POLI D. A Rigorous Model for Spaceborne Linear Array Sensors[J]. Photogrammetric Engineering & Remote Sensing, 2007, 73(2): 187–196. |
| [5] | TEO T A. Bias Compensation in a Rigorous Sensor Model and Rational Function Model for High-resolution Satellite Images[J]. Photogrammetric Engineering & Remote Sensing, 2011, 77(12): 1211–1220. |
| [6] | GRODECKI J, DIAL G. Block Adjustment of High-resolution Satellite Images Described by Rational Polynomials[J]. Photogrammetric Engineering & Remote Sensing, 2003, 69(1): 59–68. |
| [7] | 张力, 张继贤, 陈向阳, 等. 基于有理多项式模型RFM的稀少控制SPOT-5卫星影像区域网平差[J]. 测绘学报, 2009, 38(4): 302–310. ZHANG Li, ZHANG Jixian, CHEN Xiangyang, et al. Block-adjustment with SPOT-5 Imagery and Sparse GCPs Based on RFM[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(4): 302–310. |
| [8] | 唐新明, 张过, 祝小勇, 等. 资源三号测绘卫星三线阵成像几何模型构建与精度初步验证[J]. 测绘学报, 2012, 41(2): 191–198. TANG Xinming, ZHANG Guo, ZHU Xiaoyong, et al. Triple Linear-array Imaging Geometry Model of Ziyuan-3 Surveying Satellite and Its Validation[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(2): 191–198. |
| [9] | ZHANG Yongjun, WAN Yi, HUANG Xinhui, et al. DEM-Assisted RFM Block Adjustment of Pushbroom Nadir Viewing HRS Imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(2): 1025–1034. DOI:10.1109/TGRS.2015.2472498 |
| [10] | WANG Taoyang, ZHANG Guo, LI Deren, et al. Planar Block Adjustment and Orthorectification of ZY-3 Satellite Images[J]. Photogrammetric Engineering & Remote Sensing, 2014, 80(6): 559–570. |
| [11] | 张浩, 张过, 蒋永华, 等. 以SRTM-DEM为控制的光学卫星遥感立体影像正射纠正[J]. 测绘学报, 2016, 45(3): 326–331. ZHANG Hao, ZHANG Guo, JIANG Yonghua, et al. A SRTM-DEM-controlled Ortho-rectification Method for Optical Satellite Remote Sensing Stereo Images[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(3): 326–331. DOI:10.11947/j.AGCS.2016.20150358 |
| [12] | 王任享. 天绘一号卫星无地面控制点摄影测量关键技术及其发展历程[J]. 测绘科学, 2013, 38(1): 5–7, 43. WANG Renxiang. Key Photogrammetric Progress of TH-1 Satellite without Ground Control Point[J]. Science of Surveying and Mapping, 2013, 38(1): 5–7, 43. |
| [13] | SUN G, RANSON K J, KHARUK V I, et al. Validation of Surface Height from Shuttle Radar Topography Mission Using Shuttle Laser Altimeter[J]. Remote Sensing of Environment, 2003, 88(4): 401–411. DOI:10.1016/j.rse.2003.09.001 |
| [14] | RODRÍGUEZ E, MORRIS C S, BELZ J E. A Global Assessment of the SRTM Performance[J]. Photogrammetric Engineering & Remote Sensing, 2006, 72(3): 249–260. |
| [15] | BHANG K J, SCHWARTZ F W, BRAUN A. Verification of the Vertical Error in C-band SRTM DEM Using ICESat and Landsat-7, Otter Tail County, MN[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(1): 36–44. DOI:10.1109/TGRS.2006.885401 |
| [16] | 杜小平, 郭华东, 范湘涛, 等. 基于ICESat/GLAS数据的中国典型区域SRTM与ASTER GDEM高程精度评价[J]. 地球科学--中国地质大学学报, 2013, 38(4): 887–897. DU Xiaoping, GUO Huadong, FAN Xiangtao, et al. Vertical Accuracy Assessment of SRTM and ASTER GDEM over Typical Regions of China Using ICESat/GLAS[J]. Earth Science:Journal of China University of Geosciences, 2013, 38(4): 887–897. |
| [17] | FRASER C S, HANLEY H B. Bias-compensated RPCs for Sensor Orientation of High-resolution Satellite Imagery[J]. Photogrammetric Engineering & Remote Sensing, 2005, 71(8): 909–915. |
| [18] | FRASER C S, DIAL G, GRODECKI J. Sensor Orientation via RPCs[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2006, 60(3): 182–194. DOI:10.1016/j.isprsjprs.2005.11.001 |
| [19] | TAO C V, HU Y, JIANG W. Photogrammetric Exploitation of IKONOS Imagery for Mapping Applications[J]. International Journal of Remote Sensing, 2004, 25(14): 2833–2853. DOI:10.1080/01431160310001618392 |
| [20] | TONG Xiaohua, LIU Shijie, WENG Qihao. Bias-corrected Rational Polynomial Coefficients for High Accuracy Geo-positioning of QuickBird Stereo Imagery[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2010, 65(2): 218–226. DOI:10.1016/j.isprsjprs.2009.12.004 |
| [21] | 中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. GB/T 12343.1-2008国家基本比例尺地图编绘规范第1部分: 1:25 000 1:50 000 1:100 000地形图编绘规范[S].北京:中国标准出版社, 2008. State Administration of Quality Supervision, Inspection and Quarantine, People's Republic of China, China National Standardization Management Committee. GB/T 12343.1-2008 Compilation Specifications for National Fundamental Scale Maps-Part 1: Compilation Specifications for 1:25 000 1:50 000 1:100 000 Topographic Maps[S]. Beijing: Chinese Standard Publishing House, 2008. |
| [22] | LEMOINE F G, KENYON S C, FACTOR J K, et al. The Development of the Joint NASA GSFC and the National Imagery and Mapping Agency (NIMA) Geopotential Model EGM96[R]. NASA/TP-1998-206861. Greenbelt, Maryland: Goddard Space Flight Center, 1998. |
| [23] | 冯林刚, 杨润甫, 李胜. 基于EGM96的GPS高程转换方法[J]. 测绘通报, 2006(3): 22–23, 47. FENG Lingang, YANG Runfu, LI Sheng. EGM96 Based GPS Height Transform Method[J]. Bulletin of Surveying and Mapping, 2006(3): 22–23, 47. |
| [24] | ZWALLY H J, SCHUTZ B, ABDALATI W, et al. ICESat's Laser Measurements of Polar Ice, Atmosphere, Ocean, and Land[J]. Journal of Geodynamics, 2002, 34(3-4): 405–445. DOI:10.1016/S0264-3707(02)00042-X |
| [25] | LI Guoyuan, TANG Xinming, GAO Xiaoming, et al. ZY-3 Block Adjustment Supported by GLAS Laser Altimetry Data[J]. The Photogrammetric Record, 2016, 31(153): 88–107. DOI:10.1111/phor.2016.31.issue-153 |


