随着激光雷达(light detection and ranging,LiDAR)[1]测量、多视影像密集匹配[2]技术的完善和行业应用的深入,点云滤波的重要性日益突出。本文的点云涉及机载LiDAR点云和航空、航天多视立体影像密集匹配的点云等3种类型。在点云处理和信息提取领域,滤波是指区分点云中的地面点和非地面点的过程[1, 3],它是生成数字高程模型(DEM)、分类、目标识别和三维重建的基础和必经的步骤[4]。文献[1, 4-5]对目前众多点云滤波方法进行了系统的介绍。其中,有代表性的方法有三角网(triangular irregular network,TIN)渐进加密(TIN progressive densification,TPD)[6-7]、分层稳健线性内插[8]、坡度滤波[9]、数学形态学滤波[10]、基于聚类/对象的滤波[11-12]等。已有方法中涉及的基元(基本处理单元)有点[6-7]、对象[11-12]、体素[13]或剖面[14]等多种类型;且后3种基元具有一定的共性,本质上是点基元的一种集合和再组织方式,本文仅关注其中的对象。由于点易受粗差、地形断裂的负面影响,而对象比点更能增强点云处理效果[15],因此基于对象的点云滤波方法[16-21]是研究的一个热点。然而,与基于点的滤波方法相比,尽管基于对象的滤波方法可以在一定程度上提高滤波精度,但是也存在效率低下的问题[21]。
文献[22]提出基于多实体的点云分类方法,在分类的不同阶段使用不同的实体以实现更优的分类效果。借鉴上述策略,本文设计一种既能继承基于对象方法的优势、又不显著降低基于点方法的效率的滤波技术,即同时提高基于点的TPD方法[6]精度和基于对象的三角网渐进加密(object-based TPD,OTPD)方法[21]效率,本文称之为基于多基元的三角网渐进加密(multiple-primitives-based TPD,MPTPD)方法。它有3个创新点:①使用多基元、而非单一的基元参与运算,其中多基元包括点、对象、关键点等3种类型,且在不同阶段使用不同类型的基元;②使用关键点代替对象参与判别,即在核心判别步骤中,使用对象的关键点替代对象进行运算以提高效率;③提出一种简单、快捷的关键点检测算法。
特别指出,本文的一个“对象”指“点云分割后具有同一标号的点集”,“关键点”又是对象点集的一个子集,即关键点本质上仍然是原始点云中的点,而非额外创造的,但是关键点具有特殊性。另外,处理一个“对象”,可以通过处理该对象包含的点集来实现,也可以通过处理“关键点”来实现。
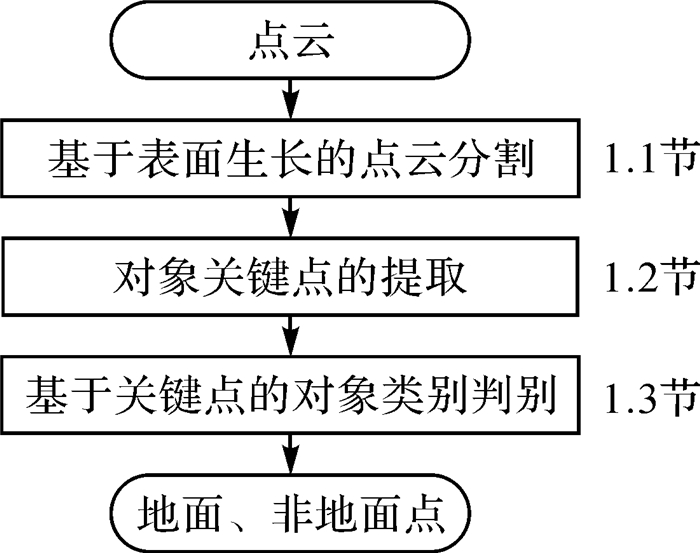
1 本文的滤波方法MPTPD方法包括基于表面生长的点云分割、对象关键点提取、基于关键点的对象类别判别等3个主要步骤。整体技术框架如图 1所示;图 2展示了某一点云各个处理步骤的效果,文中数字“1”代表“非地面点类”,数字“2”代表“地面点类”。
|
| 图 1 本文方法的整体技术流程图 Fig. 1 The whole work flow of the proposed method |
1.1 基于表面生长的点云分割
点云分割是对点云数据中每个点按照一定的判别规则进行标号的过程。分割后,满足同一规则的点集被赋予同一标号,且每一点集称为一个对象。本文判别的是3D空间中邻近且共平面的点。另外,不满足上述判别规则的孤立点、邻近点数目不足的点、共平面性差的点亦会被标号。鉴于表面生长[23]算法具有所需参数少、分割效果好、普适性好的特点,本文使用它对点云进行分割,其主要步骤如下。
第1步,估计法向量和残差,处理过程如下。
(1)加载点云数据,并将所有点的类别标记为“1”、标号状态记为“未分割”,设共计有n个点。
(2)建立点云的三维kd-tree[24]空间索引。
(3)逐一处理每一个点,即对第i(i=0, 2, …,n-1)个点,首先利用kd-tree求取其k个最临近点,然后利用特征值法[25]求当前点及k个邻近点构成点集的拟合平面方程,即可确定第i个点的法向量φi及其残差λi。
第2步,进行区域生长。
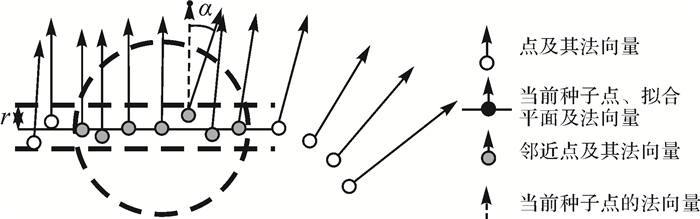
图 2展示了表面生长过程。该过程需要设定两个参数,包括法向量间角度差异阈值α、距离阈值r。其中,α的使用规则为:对于当前要扩张的种子点,利用kd-tree查询其某一邻接点作为待处理的点,设当前种子点的法向量为αi,待处理的邻接点法向量为αj,且αi和αj均为单位法向量;如果待处理的邻接点与种子点之间法向量的点积‖αiαj‖小于阈值cos α,则将该待处理的邻接点加入到种子点队列中,并作为新的种子点,继续判别其他的未处理点;反之,则跳过该待处理的邻接点,处理其他的未处理点。r的使用规则为:如果待处理的邻接点到种子点确定的种子平面的距离小于给定距离阈值r,则将该待处理的邻接点加入到种子点队列中,并作为新的种子点,继续判别其他的未处理点;反之,则跳过该待处理的邻接点,处理其他的未处理点。具体处理如下。
|
| 图 2 表面生长过程的示意图 Fig. 2 Illustration of the surface growing process |
(1)记“区域标记号”从0开始。
(2)检查“未分割”点集中点的数量,如果数量为0,则转到步骤(6);否则,接着从“未被分割”的点集中,寻找出残差λ最小的点,以该点为种子点并将该点压入一个种子点的队列,且将该点的处理状态标记为“未处理”,开始进行区域生长。
(3)取种子点队列中第一个“未处理”的种子点,利用kd-tree求取该种子点的k个最临近点。
(4)逐一对于每一个临近点进行判别。如果临近点已经被赋予分割号,则不予以处理;另外,若临近点已经在种子点的队列中,则不予以处理;接着,分别按照法向量间角度差异和距离差异的规则进行当前种子点和该邻近点的相似性判别。如果该邻近点同时满足两个相似性的条件,则将该邻近点加入到种子点队列中;反之,如果该邻近点没有同时满足两个相似性的条件,则不予以处理。邻近点判别完毕后,将该种子点的处理状态标记为“已处理”。
(5)顺序检查种子点队列中是否有“未处理”的点。如果有,返回步骤(3);否则,将种子点队列中的点集的标号记为“区域标记号”,状态记为“已分割”,同时“区域标记号”自增1,清空种子点队列后返回步骤(2)。
(6)结束。
经过上述分割后,任意一点被划到一个对象,但是部分对象的点的数量较少。个别情况下,一个对象仅仅包含一个点。图 3(a)展示了某机载LiDAR点云数据,图 3(b)展示了其分割效果,其中地面点被聚为若干个对象,多数地面对象包含点的数量较多;一个建筑物可以被聚为一个或者若干个对象,这与其类型、点云密度、精度等多个因素有关;孤立的植被点、粗差点也往往被分割为一个对象。

|
| 图 3 本文提出滤波方法的关键步骤处理效果示意图 Fig. 3 Illustration of the process of the proposed filtering method |
1.2 对象关键点的提取
本文的关键点包括外轮廓点、内特征点、最高点和最低点。
第1步,计算每个对象包含点的数量。如果数量不大于经验阈值4,则将该对象的点集记为对象的关键点。反之,进入第2步。
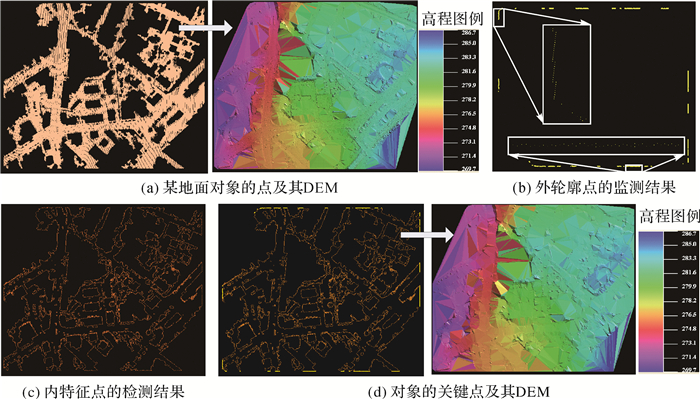
第2步,识别每个对象的关键点。图 4展示了某对象关键点检测的主要过程。提取的基本原理是仅利用某一对象点集的水平坐标信息生成TIN。该TIN中,处于边缘的三角形仅有两个三角形通过边相邻;而处于非边缘的三角形有3个三角形通过边相邻。因此,可以通过一个三角形的一边为邻边的邻接三角形的数量来判断该三角形是否处于边缘。处于边缘的三角形涉及的3个顶点记为“外轮廓点”,如图 4(b)所示。接着,删除该TIN中的短边,并以删除短边后的TIN为索引进行连通区域分析(connected component analysis)。则该对象被分割为若干子对象。若子对象包含的点的数量大于经验阈值4,则该子对象的点集被认为是“内特征点”,如图 4(c)所示。注意上述关键点无需有序排列,这与Alpha shape[26]算法有着显著的差别。第2步具体内容如下。
(1)建立某一对象的二维TIN。
(2)检测“外轮廓点”。通过上述邻接三角形数量的规则识别“外轮廓点”,如图 4(b)所示。
(3)删除短边。假设输入原始点云的平均点间距为g(单位:m),且g已知。删除TIN中二维边缘长度小于经验阈值3g的边。
(4)检测“内特征点”。通过上述连通区域分析获取的子对象包含点的数量的规则识别“内特征点”,如图 4(c)所示。
(5)检测最高点、最低点。另外,外轮廓点、内特征点、最高点、最低点不可重复。如有重复,则只保留其中一个。
图 4(a)展示了某一地面对象包含321 998个点,其外轮廓点、内特征点和关键点分别如图 4(b)、(c)和(d)所示,图 4(d)只包含19 875个点。从图 4(a)和(d)中的DEM看,尽管构建DEM的点的数量差别悬殊,但是DEM的表达效果却趋于一致。对两个DEM,不仅最高、最低值一致,且相应像素值之差的绝对值的平均值和标准差分别为0.05和0.01,这反映了提取的关键点既能显著地减少点的数量、又能逼近真实的对象原始形态。另外,图 2(c)展示了图 2(a)中点云的关键点检测结果,其中原始点云包含826 416个点、而关键点只包含64 257个点,关键点数量只占原始点数量的7.78%。
|
| 图 4 对象关键点检测的示意图 Fig. 4 Illustration of detection of the key points of an object |
1.3 基于关键点的对象类别判别
经典TPD方法的运算过程中,TIN构建和点类别判别占整个滤波时间的比重很大[27]。本文采用关键点替代对象的目的是能同时显著地减少参与TIN构建的、参与判别的点的数量以提高效率,又可使构建的TIN尽可能地逼近区域真实的DEM以确保精度。
本节是一个迭代过程。共涉及4个参数:最大建筑物长度b(单位:m)、最大角度阈值θ(单位:°)、最大距离阈值d(单位:m)和最大地形角度阈值t(单位:°)。具体过程如下。
第1步:格网划分。求点云在XOY平面上的最小外包矩形,并在XOY平面上对该最小外包矩形进行格网划分、且格网的尺寸为b×b。
第2步:将全部对象处理状态均标记为“未处理”。
第3步:选择初始地面种子点。逐一选择每一个格网的地面种子点。即对每一个格网,找到格网中高程值最低的点所在的对象。如果对象的面积小于4.00 m2,则继续找到高程值次低的点所在的对象直至找到面积大于4.00 m2的对象。将该对象的关键点作为该格网的地面种子点,且该对象的类别被标记为“2”、处理状态被标记为“已处理”。
第4步:构建初始地面种子点的TIN。该TIN代表该区域初始的DEM。
第5步:迭代的判别对象类别。子步骤包括:
(1)迭代次数记为0。
(2)以对象为基本处理单元,逐一通过每一个“未处理”对象的关键点的判别,实现该对象类别的判别。
对每一个“未处理”对象逐一判别其“未处理”关键点,找到该关键点落入的三角形,计算该关键点到三角形构成的平面的距离及该关键点到三角形3点的夹角,并找出3个夹角中的最大角。进行下述判别:如果同时满足距离小于d、最大夹角小于θ,则认为该关键点是地面点,将该关键点的类别号标记为“2”,处理状态标记为“已处理”,继续处理下一个“未处理”关键点;否则,检查三角形构成的平面的倾角,进行下述判别:如果倾角小于,继续处理下一个“未处理”关键点;反之,将当前关键点以所在三角形的最高点为中心做一个镜像点(参考文献[6, 12]),且该镜像点的高等于该关键点。对该镜像点进行类似的判别。如果该镜像点被判别为“2”,则将该关键点的类别号标记为“2”,处理状态标记为“已处理”;继续处理下一个“未处理”关键点。
判别完毕,统计该对象的关键点的数量、关键点属于地面点的比例。如果该比例大于50%,将该对象的处理状态标记为“已处理”,类别为“2”;否则,将该对象的处理状态重新标记为“未处理”,类别为“1”。
(3)利用新识别的属于地面点的关键点更新TIN,同时迭代次数自增1。
(4)重复上述步骤(1)至(3),继续执行直至迭代次数达到经验阈值5,或者没有新识别的地面点则停止迭代。
2 试验与分析基于Visual Studio 2010 C++集成开发环境实现了本文提出的MPTPD方法,同时对TPD[6]、OTPD[21]两种方法进行性能比较,上述3种方法均采用串行计算,未采用并行计算技术。其中,TPD包括低位粗差点剔除和1.3节描述的5个主要步骤,其基元为点;OTPD包括1.1节和1.3节两个相似部分,其基元为对象。为了增加效率的可比性,尽管3种滤波方法的基元的不同,但相似步骤涉及的算法一致。试验平台的配置:ThinkPad W520笔记本,CPU为Intel酷睿i7-2760QM 2.4 GHz,内存2.98 GB,装配Windows XP系统。
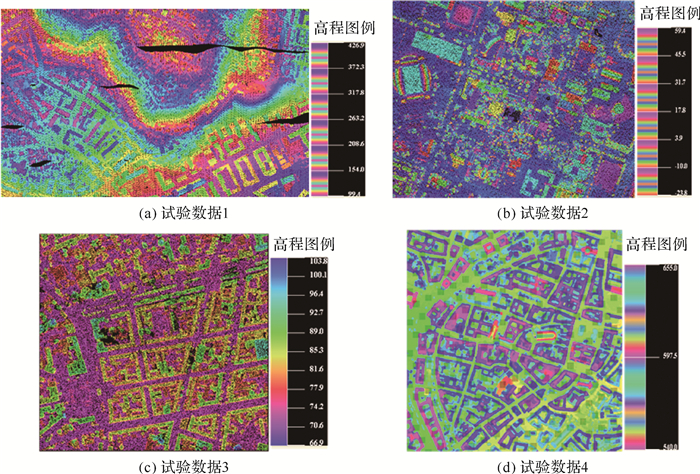
2.1 试验数据及结果本文共使用了4个场景的点云开展试验(图 5),它们的基本信息见表 1。前两个场景的点云为开放的机载LiDAR数据;后两个为摄影测量点云,其中,第3个场景的原始影像由Trimble Germany GmbH公司免费提供、点云由中国测绘科学研究院的PixelGrid软件生成,第4个场景的点云由德国宇航局免费提供。另外,试验数据1为国际摄影测量与遥感协会第三委员会提供的测试数据CSite1,该数据位于德国,如图 5(a)所示;试验数据2由IEEE GRSL Fusion Contest 2013提供,该数据位于美国休斯敦大学附近,本文截取了原始点云的一部分,如图 5(b)所示;试验数据3对应的斜影像由天宝公司AOS系统获取,该数据位于德国柏林市和波茨坦市附近,本文截取了由影像生成的摄影测量点云的一部分,如图 5(c)所示;试验数据4由GeoEye-1的立体影像对生成,该数据位于德国的慕尼黑市,本文截取了该摄影测量点云的一部分,如图 5(d)所示。
|
| 图 5 4个试验数据 Fig. 5 The four testing datasets |
| 试验数据 | 点云类型 | 点数/个 | 长/m×宽/m | 平均点间距/m | 是否有粗差 | 地形类型 |
| 1 | 机载LiDAR | 1 366 408 | 1 100.71×701.46 | 0.69 | 有 | 城区与森林 |
| 2 | 机载LiDAR | 2 335 048 | 1 087.47×889.51 | 0.64 | 有 | 城区 |
| 3 | 航空影像匹配 | 2 044 447 | 655.12×624.39 | 0.44 | 有 | 城区 |
| 4 | 卫星影像匹配 | 2 497 638 | 1 011.85×1 035.85 | 0.50 | 有 | 城区 |
对4个试验数据进行滤波时,使用的相关参数的值见表 2。其中,TPD、OTPD和MPTPD 3种方法对1.3节的参数b、θ、d、t采用了相同的参数值,OTPD和MPTPD两种方法对1.1节的参数k、d、r采用了相同的参数值。鉴于篇幅的原因未展示3种方法的滤波结果。后续试验分析表明3种滤波方法均能正确地区分多数的地面点和非地面点,且OTPD和MPTPD两种方法的滤波效果相当、并优于TPD方法的滤波效果。
| 方法 | TPD | OTPD和MPTPD | |||||
| 参数 | b/m | t/(°) | θ/(°) | d/m | k/点 | α/(°) | r/m |
| 试验数据1 | 20 | 80.00 | 6.00 | 1.40 | 20 | 30.00 | 0.50 |
| 试验数据2、3、4 | 60 | 88.00 | 6.00 | 1.40 | 20 | 10.00 | 0.50 |
2.2 精度评价
本文采用文献[4]中的一类误差I (将地面点错分为非地面点的数量占地面点数量的比例)、二类误差Ⅱ(将非地面点错分为地面点的数量占非地面点数量的比例)和总误差T (错分点数量占全部点数量的比例)3个指标定量衡量滤波精度。同时,使用了人工半自动解译的方式识别了4个试验数据的地面点和非地面点,并将每个试验数据的人工识别结果作为真值计算滤波方法的误差。4个试验数据的3类误差值见表 3。
| 试验数据 | 误差类型 | TPD/(%) | OTPD/(%) | MPTPD/(%) |
| 1 | Ⅰ | 34.74 | 11.35 | 11.36 |
| Ⅱ | 2.39 | 4.21 | 4.16 | |
| T | 17.92 | 7.64 | 7.62 | |
| 2 | Ⅰ | 22.46 | 6.81 | 6.98 |
| Ⅱ | 3.02 | 0.79 | 0.77 | |
| T | 13.35 | 4.04 | 4.07 | |
| 3 | Ⅰ | 23.71 | 1.29 | 1.33 |
| Ⅱ | 1.80 | 5.74 | 5.81 | |
| T | 9.40 | 4.20 | 4.26 | |
| 4 | Ⅰ | 27.45 | 0.39 | 0.43 |
| Ⅱ | 1.87 | 0.24 | 0.36 | |
| T | 9.40 | 0.28 | 0.38 |
表 3中,TPD方法的Ⅰ、Ⅱ、T 3类误差的平均值分别为27.09%、2.27%和12.52%,OTPD方法相关误差的平均值分别为4.96%、2.75%和4.04%,MPTPD方法相关误差的平均值分别为5.03%、2.78%和4.08%。数字说明OTPD方法与MPTPD方法的各类误差均十分接近。且,一类误差I和总误差T均呈现TPD>OTPD≈MPTPD的趋势,而二类误差Ⅱ呈现TPD < OTPD≈MPTPD的趋势。另外,MPTPD和OTPD两种方法的一类误差I、总误差T的平均值比TPD的分别低约22.10%、8.46%,而两种方法的二类误差Ⅱ的平均值比TPD的高约0.49%。可见,与TPD相比,MPTPD和OTPD两者会轻微地提高二类误差Ⅱ,但会显著地降低一类误差I、总误差T。可知,OTPD和MPTPD两种方法的滤波精度相当、且高于TPD方法的滤波精度。
2.3 效率评价本文采用时间花费来衡量滤波效率。为此,分别记录了3种方法对4个试验数据进行滤波的各个阶段耗时及总耗时,具体的统计数据见表 4。其中,将滤波过程划分为5个阶段:低位粗差点剔除、基于表面生长的点云分割(1.1节)、对象关键点提取(1.2节)、基于关键点的对象类别判别(1.3节)前3步和后两步,在表 4中分别称为阶段1、阶段2、阶段3、阶段4、阶段5。
| 试验数据 | 方法 | 阶段1耗时/s | 阶段2耗时/s | 阶段3耗时/s | 阶段4耗时/s | 阶段5耗时/s | 总耗时/s |
| 1 | TPD | 261.13 | - | - | 5.34 | 7.85 | 274.32 |
| OTPD | - | 171.26 | - | 59.27 | 135.29 | 356.82 | |
| MPTPD | - | 171.26 | 47.78 | 4.21 | 1.37 | 224.62 | |
| 2 | TPD | 179.40 | - | - | 34.77 | 33.84 | 248.04 |
| OTPD | - | 237.45 | - | 35.88 | 161.48 | 433.81 | |
| MPTPD | - | 237.45 | 55.34 | 17.13 | 2.94 | 312.86 | |
| 3 | TPD | 251.70 | - | - | 13.03 | 33.97 | 298.70 |
| OTPD | - | 316.20 | - | 18.39 | 531.06 | 865.65 | |
| MPTPD | - | 316.20 | 84.05 | 10.23 | 4.98 | 415.46 | |
| 4 | TPD | 150.72 | - | - | 9.45 | 13.79 | 173.96 |
| OTPD | - | 344.57 | - | 109.70 | 342.64 | 796.91 | |
| MPTPD | - | 344.57 | 113.63 | 7.78 | 2.09 | 468.07 |
表 4的统计数据表明,在4个试验数据中,有3个出现了3种滤波方法的总效率均呈现TPD>MPTPD>OTPD的规律。以试验数据3为例,TPD、MPTPD、OTPD 3种方法的总耗时由少到多依次为约299 s、415 s、866 s。但在第1个试验数据中,MPTPD的效率高于TPD、OTPD。整体上,TPD效率最高,MPTPD次之,OTPD最低。表 4还表明TPD、MPTPD、OTPD 3种方法在每个试验数据上的总耗时平均分别为248.76 s、355.26 s、613.30 s。如果以效率最慢的OTPD的基准,TPD和MPTPD的效率分别是OTPD的2.47倍、1.73倍。
而且,表 4还表明每种滤波方法的各个阶段的耗时的比例也有着显著的差别,表现为:
(1) TPD方法中,阶段1、阶段4和阶段5这3个阶段的耗时占总耗时比例的平均值分别为84.61%、6.44%、8.95%,可见,阶段1和阶段5这两个阶段占了TPD方法总耗时的绝大部分比例,其中粗差剔除的相关比例最大、且点云中的粗差越复杂相应的比例越大。例如,试验数据1的粗差多且多样,粗差剔除的时间花费占总时间花费的95.19%,是4个试验数据中比例最大的,这是在第1个试验中MPTPD的效率高于TPD的原因。
(2) OTPD方法中,阶段2、阶段4、阶段5等3个阶段的耗时占总耗时比例的平均值分别为45.62%、10.19%、44.87%。可见,OTPD的3个阶段中,除了第2个阶段外,其他两个阶段均比较耗时、且占总耗时的比例相当。
(3) MPTPD方法中,阶段2、阶段3、阶段4、阶段5等4个阶段的耗时占总耗时比例的平均值分别为75.47%、20.86%、2.87%、0.80%。可见,MPTPD的4个阶段中,前两个阶段的累计耗时占了总耗时的绝大部分,而后两个阶段的累计耗时占总耗时的比例极小。这是MPTPD与OTPD尽管在阶段2的耗时相同、但是MPTPD的总耗时显著的低于OTPD的原因。
另外,表 4展示了一个很有兴趣的现象。3种滤波方法均有阶段4、阶段5两个阶段,但由于基元的不同导致两个阶段(尤其是阶段5)的效率有着显著差别。例如,第4个试验数据中,TPD和OTPD两种方法的阶段4的耗时分别为9.45 s、109.70 s,但MPTPD的相应耗时仅为7.78 s;TPD、OTPD、MPTPD 3种方法在阶段5的耗时分别为13.79 s、342.64 s、2.09 s,即MPTPD方法在此阶段的耗时仅为TPD的15.16%、OTPD的0.61%。其他3个试验数据亦表现出类似的规律。这证明了基元对滤波效率有着显著的影响,MPTPD方法的关键点显著提高了其后续阶段的效率。但是,与TPD方法相比,MPTPD方法的点云分割和关键点提取耗费了较多的时间,因此该方法的整体效率低于TPD方法。
2.4 分析与讨论文献[4]指出TPD方法对具有不同场景复杂度的点云数据均具有较高的滤波精度。本文的统计数据表明,TPD方法的总误差T平均值约12.52%,精度较高,符合既有结论。另外,表 2表明TPD方法所需的4个参数的取值对场景的变化不是很敏感,且具有显著的物理意义,根据实际情况微调参数取值即可。但TPD方法存在对低位粗差、地形断裂敏感的问题,因此该滤波方法仍然存在一定的误差。表 3表明TPD方法的一类误差I平均值约27.09%,显著地高于其他两种滤波方法的相关误差值。
OTPD方法是对TPD方法的改进,具有对低位粗差、地形断裂不敏感的优势,但是比较耗时。统计数据表明,与TPD相比,OTPD方法的一类误差I、总误差T比TPD的分别低约22.13%、8.48%,但耗时是TPD的2.47倍。
本文提出的MPTPD方法,既有与OTPD方法相当的滤波精度,又有更高的效率。统计数据表明,MPTPD方法与OTPD方法的一类误差Ⅰ、二类误差Ⅱ、总误差T的差值绝对值分别为0.07%、0.03%、0.04%,但是MPTPD方法的平均耗时却仅有OTPD方法的约58%。与OTPD方法的滤波精度相当、但效率显著提升的原因在于,MPTPD方法中的关键点既能逼近原始点云的三维形态、又能显著地减少参与后续判别的计算量。
另外,与TPD方法相比,MPTPD和OTPD两种方法需要额外的3个参数。但是,表 2表明4个试验数据中k和r两个参数的取值可相同,而α的取值在3个试验数据亦相同。这表明额外的3个参数亦“具有显著的物理意义,根据实际情况微调参数取值即可”。
3 结论点云是一种新型的数据源,其数据处理方法亟待研究。滤波是点云数据处理的一个必要的关键环节。目前,多数滤波方法采用单一的基元,但采用单一基元的滤波方法很难平衡滤波精度和滤波效率。为此,本文提出了MPTPD方法,该方法在滤波的不同阶段采用了不同的基元。其涉及的基元包括点、对象、关键点等3种,且滤波的基本原理与TPD、OTPD方法相似。采用4个有代表性的点云数据进行了试验。试验表明,MPTPD方法具有整体上最优的性能。其中,精度方面,MPTPD与OTPD两种方法的精度相当,MPTPD方法的一类误差I、总误差T比TPD的相应误差低分别约22.07%、8.44%;效率方面,多数情况下TPD、MPTPD、OTPD方法的效率依次降低,但少数情况下MPTPD的效率最高,且MPTPD的平均耗时是OTPD平均耗时的57.93%。笔者下一步的研究围绕两个方面开展:①采用并行计算技术提高滤波效率;②探索多基元的点云分类。
| [1] | 黄先锋, 李卉, 王潇, 等. 机载LiDAR数据滤波方法评述[J]. 测绘学报, 2009, 38(5): 466–469. HUANG Xianfeng, LI Hui, WANG Xiao, et al. Filter Algorithms of Airborne LiDAR Data: Review and Prospects[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(5): 466–469. |
| [2] | 王竞雪, 朱庆, 王伟玺. 多匹配基元集成的多视影像密集匹配方法[J]. 测绘学报, 2013, 42(5): 691–698. WANG Jingxue, ZHU Qing, WANG Weixi. A Dense Matching Algorithm of Multi-view Image Based on the Integrated Multiple Matching Primitives[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(5): 691–698. |
| [3] | 张小红. 机载激光雷达测量技术理论与方法[M]. 武汉: 武汉大学出版社, 2007. ZHANG Xiaohong. Theories, Methods of Airborne LiDAR Technique[M]. Wuhan: Wuhan University Press, 2007. |
| [4] | SITHOLE G, VOSSELMAN G. Experimental Comparison of Filter Algorithms for Bare-earth Extraction from Airborne Laser Scanning Point Clouds[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2004, 59(1-2): 85–101. DOI:10.1016/j.isprsjprs.2004.05.004 |
| [5] | MENG Xuelian, CURRIT N, ZHAO Kaiguang. Ground Filtering Algorithms for Airborne LiDAR Data: A Review of Critical Issues[J]. Remote Sensing, 2010, 2(3): 833–860. DOI:10.3390/rs2030833 |
| [6] | AXELSSON P E. DEM Generation from Laser Scanner Data Using Adaptive TIN Models[J]. International Archives of Photogrammetry and Remote Sensing, 2000, 33: 110–117. |
| [7] | 隋立春, 张熠斌, 张硕, 等. 基于渐进三角网的机载LiDAR点云数据滤波[J]. 武汉大学学报(信息科学版), 2011, 36(10): 1159–1163. SUI Lichun, ZHANG Yibin, ZHANG Shuo, et al. Filtering of Airborne LiDAR Point Cloud Data Based on Progressive TIN[J]. Geomatics and Information Science of Wuhan University, 2011, 36(10): 1159–1163. |
| [8] | BRIESE C, PFEIFER N, DORNINGER P. Applications of the Robust Interpolation for DTM Determination[J]. International Archives of Photogrammetry and Remote Sensing, 2002, 34: 55–61. |
| [9] | SITHOLE G. Filtering of Laser Altimetry Data Using a Slope Adaptive Filter[J]. International Archives of Photogrammetry and Remote Sensing, 2001, 34: 203–210. |
| [10] | ZHANG Keqi, CHEN Shuching, WHITMAN D, et al. A Progressive Morphological Filter for Removing Nonground Measurements from Airborne LiDAR Data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(4): 872–882. DOI:10.1109/TGRS.2003.810682 |
| [11] | TÓVÁRI D, PFEIFER N. Segmentation Based Robust Interpolation-A New Approach to Laser Data Filtering[J]. International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, 2005, 36: 79–84. |
| [12] | ZHANG Jixian, LIN Xiangguo. Filtering Airborne LiDAR Data By Embedding Smoothness-constrained Segmentation in Progressive TIN Densification[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2013, 81: 44–59. DOI:10.1016/j.isprsjprs.2013.04.001 |
| [13] | 唐菲菲, 刘经南, 张小红, 等. 基于体素的森林地区机载LiDAR数据DTM提取[J]. 北京林业大学学报, 2009, 31(1): 55–59. TANG Feifei, LIU Jingnan, ZHANG Xiaohong, et al. A Voxel-based Filtering Algorithm for DTM Data Extraction in Forest Areas[J]. Journal of Beijing Forestry University, 2009, 31(1): 55–59. |
| [14] | 郑辑涛, 张涛. 基于可变半径圆环和B样条拟合的机载LiDAR点云滤波[J]. 测绘学报, 2015, 44(12): 1359–1366. ZHENG Jitao, ZHANG Tao. Filtering of Airborne LiDAR Point Cloud Based on Variable Radius Circle and B-spline Fitting[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(12): 1359–1366. DOI:10.11947/j.AGCS.2015.20140514 |
| [15] | FILIN S, PFEIFER N. Segmentation of Airborne Laser Scanning Data Using A Slope Adaptive Neighborhood[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2006, 60(2): 71–80. DOI:10.1016/j.isprsjprs.2005.10.005 |
| [16] | LOHMANN P. Segmentation and Filtering of Laser Scanner Digital Surface Models[J]. International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, 2002, 34(Pt 3): 311–315. |
| [17] | CHEN Z, XU B, GAO B. An Image-segmentation-based Urban DTM Generation Method Using Airborne LiDAR Data[J]. IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing, 2016, 9(1): 496–506. |
| [18] | SITHOLE G, VOSSELMAN G. Filtering of Airborne Laser Scanner Data based on Segmented Point Clouds[J]. International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, 2005, 36: 66–71. |
| [19] | SHEN J, LIU J P, LIN X G, et al. Object-based Classification of Airborne Light Detection and Ranging Point Clouds in Human Settlements[J]. Sensor Letters, 2012, 10(1-2): 221–229. |
| [20] | YAN Menglong, BLASCHKE T, LIU Yu, et al. An Object-based Analysis Filtering Algorithm for Airborne Laser Scanning[J]. International Journal of Remote Sensing, 2012, 33(22): 7099–7116. DOI:10.1080/01431161.2012.699694 |
| [21] | LIN Xiangguo, ZHANG Jixian. Segmentation-based Filtering of Airborne LiDAR Point Clouds By Progressive Densification of Terrain Segments[J]. Remote Sensing, 2014, 6(2): 1294–1326. DOI:10.3390/rs6021294 |
| [22] | XU S, VOSSELMAN G, ELBERINK O S. Multiple-Entity Based Classification of Airborne Laser Scanning Data in Urban Areas[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2014, 88: 1–15. DOI:10.1016/j.isprsjprs.2013.11.008 |
| [23] | RABBANI T. Automatic Reconstruction of Industrial Installations Using Point Clouds and Images[D]. Delft, the Netherlands:Netherlands Commission of Geodesy, 2006. |
| [24] | ARYA S, MOUNT D M, NETANYAHU N S, et al. An Optimal Algorithm for Approximate Nearest Neighbor Searching Fixed Dimensions[J]. Journal of the ACM, 1998, 45(6): 891–923. DOI:10.1145/293347.293348 |
| [25] | 官云兰, 程效军, 施贵刚. 一种稳健的点云数据平面拟合方法[J]. 同济大学学报(自然科学版), 2008, 36(7): 981–984. GUAN Yunlan, CHENG Xiaojun, SHI Guigang. A Robust Method for Fitting a Plane to Point Clouds[J]. Journal of Tongji University (Natural Science), 2008, 36(7): 981–984. |
| [26] | EDELSBRUNNER H, KIRKPATRICK D, SEIDEL R. On the Shape of A Set of Points in the Plane[J]. IEEE Transactions on Information Theory, 1983, 29(4): 551–559. DOI:10.1109/TIT.1983.1056714 |
| [27] | 亢晓琛, 刘纪平, 林祥国. 多核处理器的机载激光雷达点云并行三角网渐进加密滤波方法[J]. 测绘学报, 2013, 42(3): 331–336. KANG Xiaochen, LIU Jiping, LIN Xiangguo. Parallel Filter of Progressive TIN Densification for Airborne LiDAR Point Cloud Using Multi-core CPU[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(3): 331–336. |


