2. 武汉大学动力与机械学院, 湖北 武汉 430072
2. School of Power and Mechanical Engineering, Wuhan University, Wuhan 430072, China
多波束测深声呐(multibeam echo sounder, MBES)是目前广为使用的海洋测绘仪器之一,在海洋调查、海洋底质、海洋环境等应用中发挥着重要作用[1]。多波束声呐测深与后向散射回波由同一换能器获得,测深点和后向散射图像的地理位置完全相关,经过简单的地理编码及叠加等操作,可同时获得具有高精度位置信息的海底三维地形和二维声呐图像。国内对于多波束的研究主要侧重于测深方面[2-3],而对多波束图像研究较少。传统多波束声呐仅能获得每个波束的平均强度,形成的声呐图像分辨率与测深一致,难以用于对海底地貌的精细描述。近年来,多波束声呐增加了海底扫测功能,即在每个波束中按片段(snippet)接收后向散射回波,形成片段图像,相对传统多波束声呐波束平均波束强度形成的图像分辨率提高了20~50倍,可实现对海底地貌特征较精细的描述[4-6]。多波束声呐后向散射数据在实际测量中受到海底地形起伏、传播损失、环境和仪器噪声等多种因素影响,大多可以通过仪器自带改正和后期处理消除或减弱。而多波束声呐后向散射数据受到散射模型机理影响,在不同的角度下会得到完全不同的回波强度系数,称之为角度响应(angular response,AR),且角度响应对于后向散射数据的影响是难以消除的。受角度响应和增益综合影响,多波束声呐图像质量偏低,无法真实地反映海底地貌、底质等特征变化。消除角度响应影响的传统方法为角变增益(angle varying gain,AVG),目前主要有数学模型法和声学模型法两类。前者利用数据间的连续性修正异常的中央波束数据,往往没有很好地考虑角度响应变化的特点,主要方法有移动平均法[7]、内插法[8]、经验模型法[9]等;后者借助声学理论形成一种统一的改正模型,如Lambertian模型[10]、综合声学模型[11]、EM角度响应模型[12-13]。以上两类方法在适用性、对复杂底质响应程度上均难以满足目前的实际应用需要。为此,本文根据回波强度与波束角响应关系,给出角度响应改进模型,以期改善多波束图像质量。
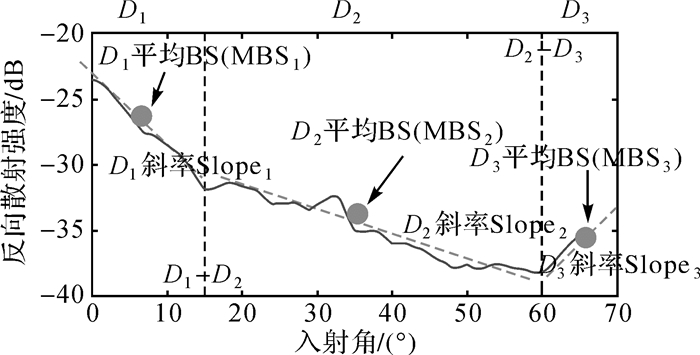
1 角度响应参数提取及改进的角度响应模型多波束后向散射强度(backscatter strength, BS)同时受入射角和底质特性影响[14]。后向散射强度在不同入射角下变化模式不同。随着入射角A的增大,后向散射强度一般经历小入射角区(D1区,A < 15°)、漫反射区(D2区,A为15°~60°)和高入射角区(D3区,A>60°)。后向散射强度与入射角间的关系可通过角度响应参数来描述(图 1)[15-17],借助角度响应参数也可实现海底底质分类[18-19]。理想环境下,角度响应参数的提取可以通过角度响应曲线的二次微分曲线获得,D1D2区的边界通过角度响应曲线二次微分的最大值确定,而D2D3区的边界通过角度响应曲线二次微分最小值获得[15]。实际测量中,由于复杂水域和仪器自身问题,以上方法难以准确获得角度响应参数,进而导致角度响应的影响无法消除,严重影响多波束图像质量。为此,本文给出一种改进方法,实现角度响应参数准确提取的同时,给出一种改进模型以适应底质的变化和实现角度响应影响的有效补偿。改进算法的基本思想是:首先通过连续声呐脉冲(Ping,后文简称脉冲)的平均消除随机误差,获得角度响应曲线;再通过对角度响应曲线滑动平均和微分处理,获取角度响应参数;最后,借助角度响应参数,构建新的角度响应模型。
|
| 图 1 后向散射数据的角度响应曲线及对应的角度响应参数 Fig. 1 The AR curve and corresponding AR parameters of multibeam backscatter |
1.1 连续脉冲取平均及角度响应曲线的获取
由于单次脉冲数据随机性较大,选择连续脉冲处理[17, 20-21]来提取角度响应参数。本文选取50次脉冲来获得平均的角度(A)-波束回波强度(R)曲线,连续脉冲中的每次脉冲按照原有采样点密度进行等角距重采样,然后对每次脉冲的重采样序列取平均值,获得平均的角度响应曲线。
在底质变化复杂时,连续脉冲的平均角度响应曲线会存在较大波动,传统方法[15]无法获得准确的分类结果。为了解决此问题,首先对角度响应曲线进行加权滑动平均。由于采样数据为离散数据,在统计学中加权滑动滤波实际是一种卷积计算。采样波束强度序列b和加权窗口序列w的有限离散卷积计算可以表示为
 (1)
(1)
式中,b为重采样后的等角距回波强度序列;N为每次脉冲的回波个数;w为窗口大小为M的加权窗口函数。由于Hanning函数适用于非周期性的连续信号,可以很好地消去高频(偶然误差)干扰,故本文选取Hanning函数为加权窗口w, 计算公式如下
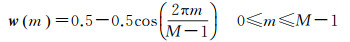 (2)
(2)
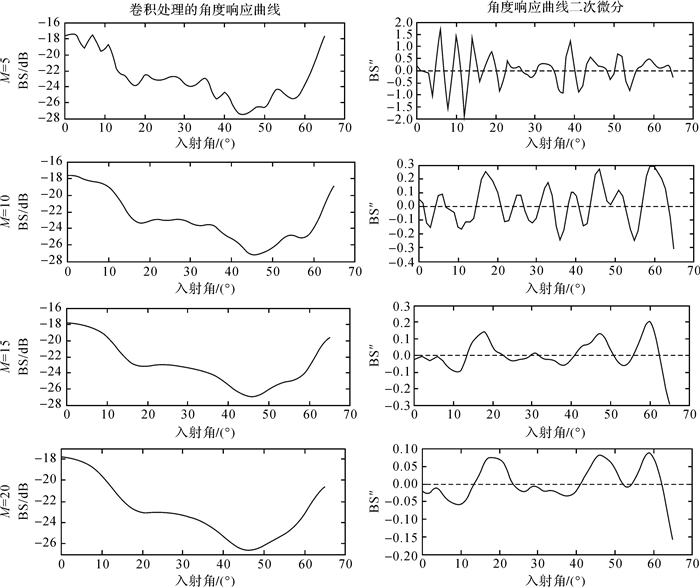
为了确定合理的窗口大小取值,分别选取不同的窗口大小M对平均角度响应曲线进行卷积处理,并获取对应的二次微分曲线。本文将M依次为5、10、15和20情况下得到的不同卷积结果列于图 2。可以看出,M为15时角度响应二次曲线可以较准确地判断出角度响应参数中不同区域的边界。
|
| 图 2 窗口大小M对角度响应二次曲线结果的影响 Fig. 2 The effect of the Window Size M on AR second differential curves |
1.2 角度响应参数的提取
借助以上获得的角度响应曲线,下面研究角度响应参数提取。参数提取中,首先应获得每个区域的边界位置,其次再获得区域内声强的变化斜率slope和平均回波强度MBS。
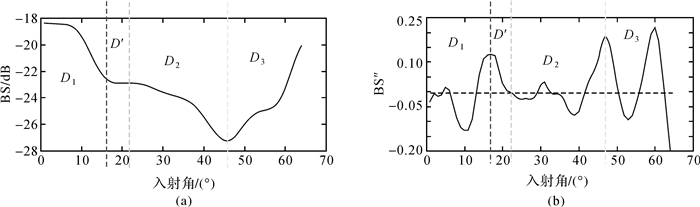
小入射角区(D1)和漫反射区(D2)两个区的边界角已被证实为在5°~30°之间变化的任意值,不同类型海底底质的边界角是不同的[12]。由图 2可以看出,随着窗口的不断增大,50次脉冲的平均角度响应曲线逐渐趋于平滑。M=15时,曲线已经十分平滑,且二次微分的曲线中5°~30°的最大值可以直接判读D1和D2的位置,如图 3所示。理想数据下D3的回波强度应该是进一步下降的过程,D2和D3边界角可以通过寻找40°~60°间的二次微分最小值来获得[15]。但是实际生产中,因某些仪器厂商提供的时变增益(time varying gain,TVG)存在过增益现象且难以消除,导致高入射角区域D3的后向散射强度不是下降而是升高的趋势,如图 3所示。对于这种情况,本文通过选取40°~60°区间内回波强度的最小值即对应该区间二次微分最大值位置得到D2和D3边界角,如图 3所示。
|
| 图 3 角度响应参数中边界的提取 Fig. 3 Extraction of the boundaries in AR parameters. 注:通过(b)中二次曲线中特征点位置确定(a)角度响应曲线中的区域分界位置,按角度增加方向3条虚线依次代表D1结束位置,D2开始位置和D3开始位置 |
为了消除区间过渡边界角度响应改正产生的跳变问题,在区间还应设立过渡区。D′为D1、D2的过渡区,D2的开始范围可以通过D1D2边界角之后第1个二次曲线为0位置判定(图 3)。而D2到D3过渡区在大多数情况下很小可以忽略。对D1、D2和D3利用线性回归法获得每个区域的斜率slope,并计算各自的平均值MBS,获得各自的角度响应参数,用于角度响应模型构建。
1.3 角度响应模型构建根据上述分析,角度响应曲线中的后向散射强度在不同的入射角区域的变化方式是不同的,因此需要对入射角分段进行分析。传统的EM多波束官方角度响应模型考虑小入射角区和漫反射区分段处理[12]模型如式(3)所示
 (3)
(3)
式中,BSN、BSO分别是在0°和25°的后向散射强度;φ是波束入射角。
大量的实践表明,EM模型存在如下方面的不足:边界角度固定在25°,未充分考虑底质变化影响,仅顾及D1和D2区域(忽略D′、D3)和不能适应增益误差的影响。本文通过完善方法与模型解决这些问题,即利用1.2节中参数提取获得角度响应参数,充分考虑底质对于边界位置的影响,将角度响应分成3个主要区域和一个过渡区域,同时考虑不易消除的增益误差在D2、D3进行相应的补偿。
改进模型实则是参考了EM模型、结合实际回波序列在单次脉冲内变化特点给出。为了克服传统模型的缺点,利用前面获得的角度响应参数,在3个主区(D1、D2、D3)和1个过渡区(D′)构建角度响应模型。式(4)为本文给出的4个区域的角度响应模型
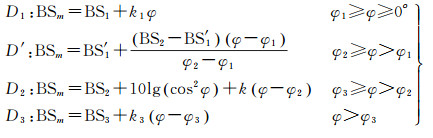 (4)
(4)
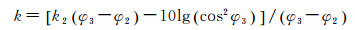 (5)
(5)
式中,φ1为小入射角区的边界角;φ2为漫反射区的开始边界角;φ3为高入射角区的边界角;k1、k3分别是小入射角区和高入射角区的斜率slope;k为漫反射区的补偿斜率(补偿自适应模型与Lambert法则的差值);BS1′是D1的结束强度;BS1、BS2和BS3是D1、D2和D3的开始强度。区域开始、结束强度可以通过该区域的斜率slope和平均强度MBS计算获得。
1.4 角度响应改正不同波束角下原始的后向散射强度,减去构建模型计算出的角度响应改正值,再加上D2区域的平均强度MBS2(图 1),便可以实现角度响应改正和BS的归一化
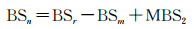 (6)
(6)
式中,BSn为最终的归一化的回波强度值;BSr为原始的回波强度;BSm为由模型(4)计算出来的改正值,而MBS2代表D2的平均回波强度值。
2 多波束片段图像角度响应改正流程21世纪以来新一代的主流多波束系统都已经具有片段回波数据采样的能力,且强度分辨率逐步提高。片段数据选取自波束振幅采样数据,振幅采样数据沿着海底构成一个连续的回波强度数据序列,而片段数据就是每个波束连续振幅采样数据开始与结束门限之间的一个片段。序列中的数据根据多波束系统的采样频率和使用的采样模式(等角或等距)来保证固定的间隔[12]。
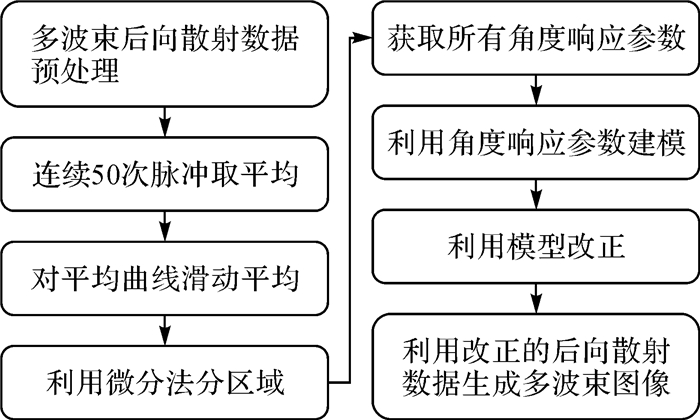
多波束后向散射经仪器采集,首先要经过预处理(包括各项改正),然后对所有的测线数据依次利用本文上述方法提取角度响应参数,构建式(4)所示的角度响应模型,再借助该角度响应模型对后向散射数据改正,最终利用改正后的后向散射数据通过地理编码得到整个区域的多波束图像。数据处理流程如图 4所示。
|
| 图 4 多波束后向散射数据图像角度响应改正流程图 Fig. 4 The workflow of AR correction on multibeam backscatter images |
3 试验与分析
为了验证文中所提方法,选取2009年由EM3002多波束(工作频率300 kHz,单头最大开角130°,工作时最大采样点数131,测深分辨率为1 cm,声强振幅分辨率0.5 dB)在胶州湾某水域实测的多波束数据进行试验。测量区域约2 km2,水深20~40 m,测区内具有明显的底质变化和一些地物。测区为斜长形状,实测了7个测线。多波束测深的同时记录了测深和对应的片段回波数据。实测的片段回波强度数据进行各项预处理(包括传播误差改正、地形起伏改正、粗差剔除等),得到原始声呐图像。
为说明图 3过程,任选测线中一段,通过连续50次脉冲取平均,得到图 5(a)所示虚线数据,利用本文方法建模得到图 5(a)中的模型,利用式(6)改正,得到图 5(b)的改正结果。可以看出,改正后的回波强度在3个区域变化均匀,很好地削弱了角度响应因素的影响。

|
| 图 5 一段测线的角度响应改正结果 Fig. 5 AR correction result in a small segment |
原始声呐图像如图 6(a)所示,整个区域按照图 3的过程依次完成,得到图 6(c)的结果。为了方便对比,EM仪器的默认角度响应改正结果如图 6(b)所示。可以看出,原始图像图 6(a)中角度响应影响明显,表现为一条条“亮线”,条带图像拼接痕迹明显;比较EM角度响应模型改正结果,发现图像的灰度虽有改善,但“亮线”问题依然存在(如图 6(b)),分析认为由于EM模型对底质变化的适应性较差所致,角度响应改正效果不理想;而本文方法的改正结果明显削弱了“亮线”的影响,拼接的痕迹也因为归一化到平均回波强度上而明显地削弱,基本还原了底质的原有变化。

|
| 图 6 整个区域的角度响应改正 Fig. 6 The AR correction of the multibeam images of the whole survey area |
为分析不同测线重叠区改正后结果的一致性,选取一对相邻测线试验。分别针对3个区域进行角度响应改正,相邻测线(A和B)对应区域(即测线A中的D1对应测线B中的D1,A中D2对B中D2,A中D3对B中D3)中的地理位置重叠的回波强度的差值的平均值统计如表 1所示。可以看出,EM改正模型由于无法适应复杂海底变化,改正效果一般;而本文方法效果较好,小入射角区和漫反射区的平均偏差在改正后较EM改正模型的差值平均值降低了一倍以上,高入射角区也有较大的改善。
| dB | |||
| 区域 | 原始 | 仪器默认改正 | 本文模型 |
| 小入射角区 | 0.62 | 0.63 | -0.31 |
| 漫反射区 | -0.82 | 0.34 | 0.19 |
| 高入射角区 | 1.54 | 1.32 | 0.91 |
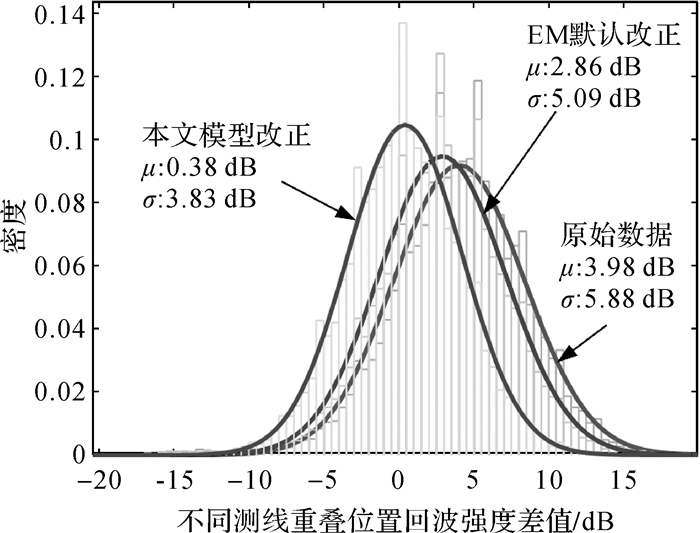
选取相交叉的两条测线,统计其中一条测线的小入射角区与另一个测线中与之位置重叠区域的回波强度差值。为了对比分析,原始数据、默认仪器改正和本文模型改正3批数据的统计参数结果和各自误差的概率密度函数(probability density function, PDF)曲线如图 7所示。
|
| 图 7 原始数据及不同改正方法位置重叠的回波强度差值的PDF曲线 Fig. 7 Probability density functions of discrepancies of overlapped backscatter intensities 注:μ代表均值,σ代表标准差 |
由图 7可以看出,由于小入射角区的强度普遍高于其他区域,未改正的数据存在明显系统性偏差,EM的角度响应改正仍然无法消除系统偏差。而通过本文模型方法改正后,系统偏差基本消除,地理位置重叠区域的差值都基本符合高斯分布,属于随机分布,同时标准差也有一定的减小。以上试验验证了本文方法的有效性。
4 结论本文提出的角度响应模型构建和改正方法,考虑到声波在不同入射角下的回波响应机制,改善了现有角度响应模型构建方法中的不足,利用更为详细的分段模型来改正角度响应,有效地削弱了多波束声呐片段图像中角度响应影响,改善了多波束片段图像的质量,并得到了试验的验证。
本文的方法适合于削弱各项改正之后仍然无法消除的角度响应影响,通过角度响应改正可以获得高质量高分辨率的片段图像,更好地反映海底底质的变化,有利于海底底质调查、勘探等进一步工作。
| [1] | CLARKE J E H, MAYER L A, WELLS D E. Shallow-water Imaging Multibeam Sonars: A New Tool for Investigating Seafloor Processes in the Coastal Zone and on the Continental Shelf[J]. Marine Geophysical Researches, 1996, 18(6): 607–629. DOI:10.1007/BF00313877 |
| [2] | 阳凡林, 李家彪, 吴自银, 等. 浅水多波束勘测数据精细处理方法[J]. 测绘学报, 2008, 37(4): 444–450. YANG Fanlin, LI Jiabiao, WU Ziyin, et al. The Methods of High Quality Post-processing for Shallow Multibeam Data[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(4): 444–450. DOI:10.3321/j.issn:1001-1595.2008.04.008 |
| [3] | 王海栋, 柴洪洲, 王敏. 多波束测深数据的抗差Kriging拟合[J]. 测绘学报, 2011, 40(2): 238–242. WANG Haidong, CHAI Hongzhou, WANG Min. Multibeam Bathymetry Fitting Based on Robust Kriging[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(2): 238–242. |
| [4] | GARDNER J V, DARTNELL P, MAYER L A, et al. Geomorphology, Acoustic Backscatter, and Processes in Santa Monica Bay from Multibeam Mapping[J]. Marine Environmental Research, 2003, 56(1-2): 15–46. DOI:10.1016/S0141-1136(02)00323-9 |
| [5] | SACCHETTI F, BENETTI S, GEORGIOPOULOU A, et al. Geomorphology of the Irish Rockall Trough, North Atlantic Ocean, Mapped from Multibeam Bathymetric and Backscatter Data[J]. Journal of Maps, 2011, 7(1): 60–81. DOI:10.4113/jom.2011.1157 |
| [6] | MEDIALDEA T, SOMOZA L, LEóN R, et al. Multibeam Backscatter as a Tool for Sea-floor Characterization and Identification of Oil Spills in the Galicia Bank[J]. Marine Geology, 2008, 249(1-2): 93–107. DOI:10.1016/j.margeo.2007.09.007 |
| [7] | FONSECA L, CALDER B. Geocoder: An Efficient Backscatter Map Constructor[C]//The US Hydrographic Conference. San Diego: CCOM JHC, 2005. |
| [8] | 唐秋华, 周兴华, 丁继胜, 等. 多波束反向散射强度数据处理研究[J]. 海洋学报, 2006, 28(2): 51–55. TANG Qiuhua, ZHOU Xinghua, DING Jisheng, et al. Study on Processing of Multibeam Backscatter Data[J]. Acta Oceanologica Sinica, 2006, 28(2): 51–55. |
| [9] | 王煜.多波束声纳图像入射角效应和镜面反射区异常的改正[D].青岛:山东科技大学, 2009. WANG Yu. Correction of Incidence Effection and Mirror Reflection Exception on Multibeam Sonar Image[D]. Qingdao: Shandong University of Science and Technology, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10424-2009254560.htm |
| [10] | HAMMERSTAD E, POHNER F, PARTHIOT F, et al. Field Testing of a New Deep Water Multibeam Echo Sounder[C]//Proceedings of the Ocean Technologies and Opportunities in the Pacific for the 90's. Honolulu, Hawaii: IEEE, 1991, 2: 743-749. |
| [11] | HELLEQUIN L, BOUCHER J M, LURTON X. Processing of High-frequency Multibeam Echo Sounder Data for Seafloor Characterization[J]. IEEE Journal of Oceanic Engineering, 2003, 28(1): 78–89. DOI:10.1109/JOE.2002.808205 |
| [12] | HAMMERSTAD E. Backscattering and Seabed Image Reflectivity[R]. EM Technical Note, 2000. |
| [13] | 金绍华, 翟京生, 刘雁春, 等. 海底入射角对多波束反向散射强度的影响及其改正[J]. 武汉大学学报(信息科学版), 2011, 36(9): 1081–1084. JIN Shaohua, ZHAI Jingsheng, LIU Yanchun, et al. Influence of Seafloor Incidence Angle on Multibeam Backscatter Intensity and Corrected Method[J]. Geomatics and Information Science of Wuhan University, 2011, 36(9): 1081–1084. |
| [14] | WAITE A D. Sonar for Practising Engineers[M]. 3rd ed. New York, NY: John Wiley & Sons, 2002. |
| [15] | CLARKE J E H, DANFORTH B W, VALENTINE P. Areal Seabed Classification Using Backscatter Angular Response at 95 kHz[C]//SACLANTCEN Conference on High Frequency Acoustics in Shallow Water. Lerici, Italy:[s.n.], 1997: 243-250. |
| [16] | FONSECA L, MAYER L. Remote Estimation of Surficial Seafloor Properties through the Application Angular Range Analysis to Multibeam Sonar Data[J]. Marine Geophysical Researches, 2007, 28(2): 119–126. DOI:10.1007/s11001-007-9019-4 |
| [17] | 金绍华, 肖付民, 边刚, 等. 利用多波束反向散射强度角度响应曲线的底质特征参数提取算法[J]. 武汉大学学报(信息科学版), 2014, 39(12): 1493–1498. JIN Shaohua, XIAO Fuming, BIAN Gang, et al. A Method for Extracting Seabed Feature Parameters Based on the Angular Response Curve of Multibeam Backscatter Strength[J]. Geomatics and Information Science of Wuhan University, 2014, 39(12): 1493–1498. |
| [18] | CUTTER G R JR, DEMER D A. Seabed Classification Using Surface Backscattering Strength Versus Acoustic Frequency and Incidence Angle Measured with Vertical, Split-Beam Echosounders[J]. ICES Journal of Marine Science, 2014, 71(4): 882–894. DOI:10.1093/icesjms/fst177 |
| [19] | HANIOTIS S, CERVENKA P, NEGREIRA C, et al. Seafloor Segmentation Using Angular Backscatter Responses Obtained at Sea with A Forward-looking Sonar System[J]. Applied Acoustics, 2015, 89: 306–319. DOI:10.1016/j.apacoust.2014.09.025 |
| [20] | DÍAZ J V M. Analysis of Multibeam Sonar Data for the Characterization of Seafloor Habitats[D]. California: University of New Brunswick, 2000. |
| [21] | FONSECA L, BROWN C, CALDER B, et al. Angular Range Analysis of Acoustic Themes from Stanton Banks Ireland: A Link between Visual Interpretation and Multibeam Echosounder Angular Signatures[J]. Applied Acoustics, 2009, 70(10): 1298–1304. DOI:10.1016/j.apacoust.2008.09.008 |



