2. 山东农业大学信息科学与工程学院, 山东 泰安 271018;
3. 北京市农林科学院蔬菜研究中心, 北京 100097
2. College of Information Science and Engineering, Shandong Agricultural University, Taian 271018, China;
3. Beijing Vegetable Research Center, Beijing 100097, China
GNSS-R技术是利用导航卫星信号及其前向散射信号作为信号源的遥感技术。与传统微波遥感技术相比,具有受大气影响小,众多的导航卫星可提供大量的免费信号源以及可获取的信息丰富等优点,已成功应用于海风海浪反演[1-2]、土壤湿度测量[3-4]等领域。在用导航卫星反射信号进行土壤湿度测量的配置模式中干涉测量法发展迅速,其利用的是GNSS直射与反射信号的干涉效应,理论上只用一根天线就能够完成测量,因此逐渐在该领域以及水面测高[5]、积雪深度探测[6]等领域中受到广泛关注。
从干涉法利用的反射信号极化类型可将该方法分为3类:①使用竖直极化(V-POL)天线接收干涉信号,通过竖直极化反射系数的布鲁斯特角获取土壤介电常数,进而反演土壤湿度[7];②使用水平极化(H-POL)天线接收干涉信号,从干涉功率峰谷值中提取介电常数,进而反演土壤湿度[8];③使用右旋圆极化(RHCP)天线接收干涉信号,其振荡幅度可以反映土壤湿度的变化[9]。上述3种方法中,方法③与普通导航接收机的应用模式最为接近,实际应用中较为简便,易于推广。文献[9]证明了干涉信号振荡幅度与土壤湿度有关,但未给出反演算法,且文献[9-14]中都用一个标准正弦信号逼近接收机输出SNR观测值,并将该标准正弦信号的幅度作为干涉信号幅度,这种定义虽然能够反映土壤湿度变化,但都无法给出确切的反演表达式,实际上接收机输出SNR振荡幅度随时间和卫星仰角的变化而变化,如用幅度恒定的正弦信号逼近则会损失这一信息。方法②的提出者最早对利用H-POL干涉功率振荡峰谷值进行土壤湿度反演的方法进行了仿真,并考虑了干涉信号振荡幅度的变化,但仿真时未考虑噪声和接收机信噪比估计方法的影响,此外由于利用H-POL天线接收干涉信号,直反射信号干涉效应始终存在,反射信号影响难以剥离,因此对直射信号功率的估计十分困难。文献[15]描述了一套GPS多径干涉仿真器,但其仿真也未考虑噪声和接收机信号估计算法的影响。
本文结合方法②和方法③的特点,首先从电磁场与电磁波的角度阐述了干涉测量的本质,给出利用归一化干涉功率反演介电常数的表达式,然后结合接收机信噪比估计原理给出GNSS接收机中归一化干涉功率的估计模型,基于此给出土壤介电常数和土壤湿度反演方法;根据所研究问题的特点,提出使用AMPD算法[16],从含有噪声的归一化干涉功率中提取干涉峰值与谷值用于反演,并对信号模型与反演过程进行了仿真和性能分析。
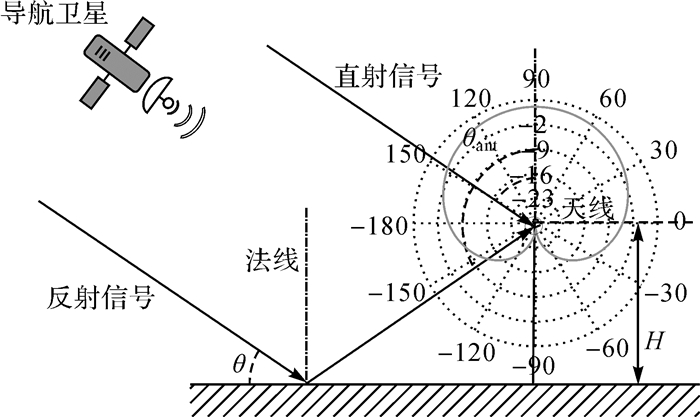
1 GNSS干涉信号模型 1.1 干涉信号的物理模型GNSS土壤湿度干涉测量利用的是直射信号与反射信号的干涉效应,在电磁场与电磁波理论中,干涉效应可用干涉功率P描述,该物理量反映了干涉的本质[10]
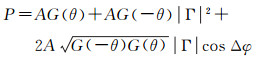 (1)
(1)
式中,A为信号到达天线前端的平均功率;G(·)为天线增益;θ为卫星高度角;Γ为右旋-右旋(RR)反射系数;|Γ|为反射系数模值;AG(θ)为天线输出的直射信号平均功率;AG(-θ)|Γ|2为天线输出的反射信号平均功率;Δφ为干涉功率瞬时相位
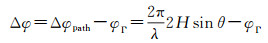 (2)
(2)
式中,Δφpath为直射信号与反射信号的路径差导致的相位差;λ为载波波长;φΓ为反射系数相角;H为右旋圆极化天线的架设高度,其场景如图 1所示。
式中,反射系数Γ由土壤相对介电常数εr和卫星高度角θ决定,在忽略电导率的情况下,Γ可由式(3)表示[17]
 (3)
(3)
将式(1)两端用AG(θ)进行归一化,得到归一化干涉功率Pnorm
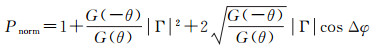 (4)
(4)
由式(2)和式(4)可知,Δφ随卫星高度角的增大而增大,使Pnorm呈现周期性振荡。当Δφ=±2kπ时,Pnorm达到局部峰值Ppeak;当Δφ=±(2k+1)π时,Pnorm达到局部谷值Pvalley。于是
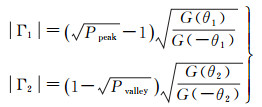 (5)
(5)
式中,θ1为局部峰值对应的卫星高度角;θ2为局部谷值对应的卫星高度角;Γ1、Γ2为相应的反射系数。根据式(3)和式(5)即可获取土壤介电常数,从而反演土壤湿度。
1.2 接收机干涉信号估计模型在仅有一条土壤镜面反射路径的情况下,根据文献[18]可得,GNSS接收机相关器输出的复信号p可表示为
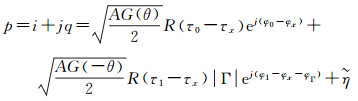 (6)
(6)
式中,i、q表示相关器IQ两路输出;R(·)为归一化码自相关函数;τi、φi分别为码相位和载波相位;i取0、1、x时分别表示直射信号、反射信号、接收机本地信号;ῆ为复数噪声项,其实部与虚部可用独立同分布的高斯白噪声描述。
在天线架设高度较低的情况下,直射与反射信号间的多径延时可忽略,因此τ0≈τ1≈τx,R(·)≈1,在忽略噪声的情况下,相关功率|p|2可用式(7)表示
 (7)
(7)
文献[18]给出了利用极大似然(ML)估计理论估计接收机信噪比的方法,该文献证明了在不考虑导航电文影响的情况下,相关功率|p|2的估计式如下
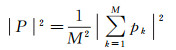 (8)
(8)
式(8)表示用连续M个相关器输出值pk估算相关功率,并假设在此期间干涉信号的各参量近似不变,这一假设对于地基应用来说是合理的。由于式(8)的平均作用,干涉信号的噪声将降低,因此反演利用的归一化干涉功率可用式(9)估计
 (9)
(9)
式(9)表明从相关功率估计值中剔除直射信号功率A和天线增益G(θ)的影响,即可得到归一化干涉功率。
2 归一化干涉功率峰谷值提取方法 2.1 AMPD算法简介AMPD (automatic multiscale-based peak detection)算法是文献[16]提出的一种多尺度峰值检测算法,主要解决周期或类周期信号在噪声影响下的峰值检测问题,应用领域主要在生物医药以及天文信号处理,与传统的峰值检测算法相比,此方法具有不宜陷入噪声引起的局部毛刺、通用性强和算法复杂度低的优点。
AMPD算法的基本原理是设置一个用于数据比较的滑动窗(window),对窗内的序列数据进行比较,得到一个局部峰值,通过改变窗的尺度(scale),改变参与比较的数据范围,直到窗覆盖所有数据。对于时间序列X=[x1, x2, ..., xN-1, xN]:
(1)建立一个L×N的矩阵M,矩阵M的每个元素的定义如下
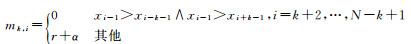 (10)
(10)
式中,L为窗的个数,L=|N/2|-1;|z|为不小于z的最小整数;窗的长度wk为{wk=2k|k=1, 2,…, L};r是在[0, 1]之间均匀分布的随机数;α为一个常数(可取1)。
(2)对矩阵M的每一行进行求和运算
 (11)
(11)
得到一个L维列向量,求出该列向量的最小值所对应的下标,记为λ=argmin (γk),并取矩阵M的前λ行,构成一个新矩阵Mr。
(3)对矩阵Mr求每一列的标准差
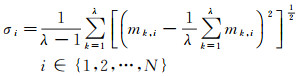 (12)
(12)
则所有σi=0的元素所对应的下标就是原始序列峰值所在的位置。
如果时间序列X中含有线性或非线性趋势项,可用最小二乘等方法先将其从中剔除,再进行上述步骤,以避免误检[16]。需要说明的是,在本问题中,趋势项是有其物理含义的,根据式(7),该趋势项主要由天线增益导致(暂时忽略大气衰减影响),如果能够得知天线在各个仰角处的增益(实际应用中可通过仿真或暗室测量得到),则可将其剔除,如果盲目使用最小二乘等方法,会导致观测量失真。
2.2 归一化干涉功率峰谷值提取根据式(9),从相关功率值中估计和剔除直射信号功率A和天线增益G(θ)的影响,即可得到归一化干涉功率。天线G(θ)假定为已知。由于高仰角处反射信号受天线增益和RR反射系数衰减(高仰角处RR反射系数本身趋于0)的影响而趋于0,因此对直射信号A的估计可在剔除G(θ)后取高仰角处多个相关功率的均值得到,如果用H-POL天线接收干涉信号,反射信号影响将一直存在,影响对直射信号功率的估计。因干涉效应在低仰角时效果明显,应用中多采用低仰角范围内振荡明显的数据,以0°~35°的数据为例,运用AMPD算法搜索含有噪声的归一化干涉功率曲线的峰值与谷值,结果如图 2(a)所示,可以看出搜索到的干涉峰谷值位于理论峰谷值周围,没有陷入其他毛刺中,如果采用求函数极值的方法则会将所有毛刺都判断为峰谷值,如图 2(b)所示。
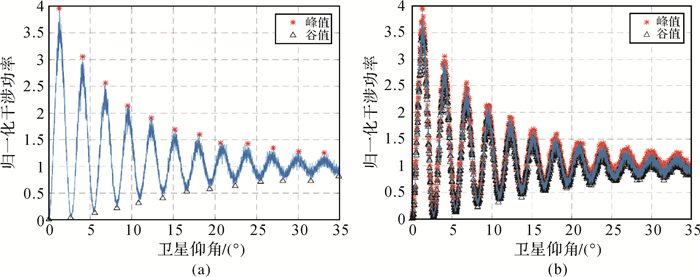
|
| 图 2 AMPD算法与传统算法搜索效果对比 Fig. 2 Searching results comparison between AMPD algorithm and traditional algorithm |
3 土壤湿度反演与结果分析 3.1 仿真参数设置
仿真参数设置如下:
(1)天线高度H设为2 m。
(2)载波频率设为1 575.42 MHz,码速率设为1.023 MHz。
(3)直射信号功率A设为-160 dBW,热噪声功率谱密度N0设为-205.2 dBW/Hz (载噪比为45.2 dBHz),接收机相干积分时间Tcoh设为1 ms,于是相关器I、Q两路噪声方差可用式(13)计算[18]
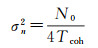 (13)
(13)
在上述载噪比设置下,若直射信号功率A为1 W时,相关器输出的噪声方差为0.007 6 W。
(4) ML估计算法中M∈{1, 10, 20, 100, 200, …, 1000},相关功率估计值输出频率为1 Hz。
(5)卫星上升段仰角变化范围设为0°~90°,仰角变化率设为0.006 7°/s。
(6)土壤相对介电常数与土壤体积湿度S之间的关系采用Wang模型[19],并忽略虚部
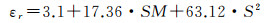 (14)
(14)
土壤体积湿度S设为0.28,于是相对介电常数εr为12.9。
(7)接收天线为右旋圆极化,其增益满足式(15)[7]
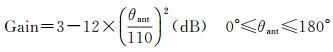 (15)
(15)
天线主瓣最大增益方向朝向天顶,θant表示信号入射方向与主瓣最大增益方向的夹角,如图 1所示,由于直射信号从天线上部入射,此时θant=90°-θ,而反射信号从天线底部入射,根据反射信号几何关系,θant=90°+θ。
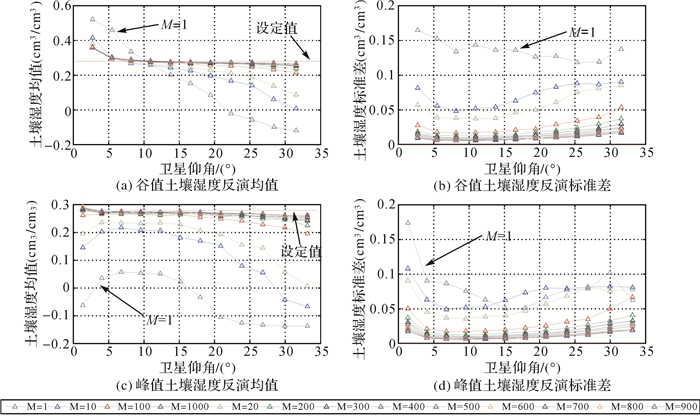
3.2 累加次数M变化时反演性能分析根据式(8),在假设IQ两路噪声为高斯白噪声的情况下,归一化干涉功率估计方法本质是取平均,因此参与平均的点数M越多,对噪声抑制作用也越大,因此M变化时将有不同的反演性能,本文按仿真参数设置(4)改变M值,并针对每个M值进行了800次仿真,当M≤20时,ML估计得到的归一化干涉功率曲线噪声仍较大(如图 2所示,M=20),为了保证反演性能,后续使用Lomb-Scargle功率谱估计算法[20]辅助RLS滤波[21](遗忘因子设为0.975)对其进行进一步降噪,其中利用Lomb-Scargle算法估计振荡频率能够增加RLS算法的稳健性[22],800次仿真统计结果如图 3所示。
|
| 图 3 800次仿真土壤湿度反演统计结果 Fig. 3 Soil moisture retrieval statistical results via 800 simulation runs |
(1) 图 3中,当累加次数M≤20时,峰值与谷值反演结果均较差,无论是反演均值和方差,当累加次数M≥100时,噪声减小,反演接近设定值。
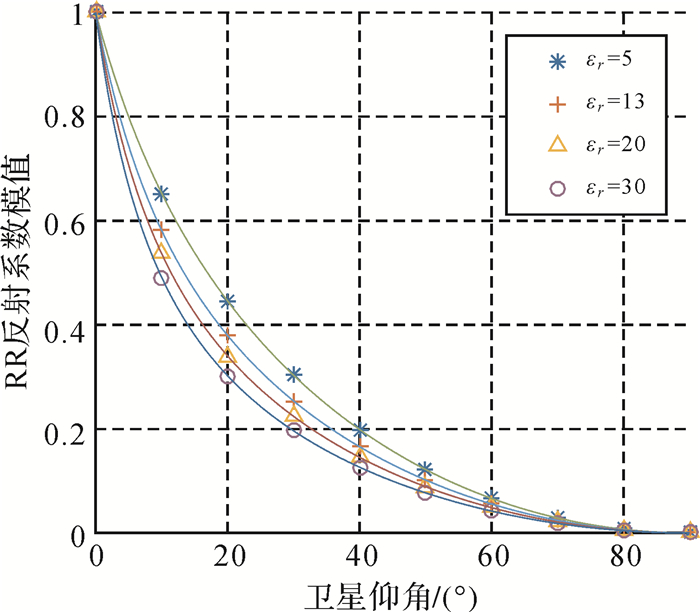
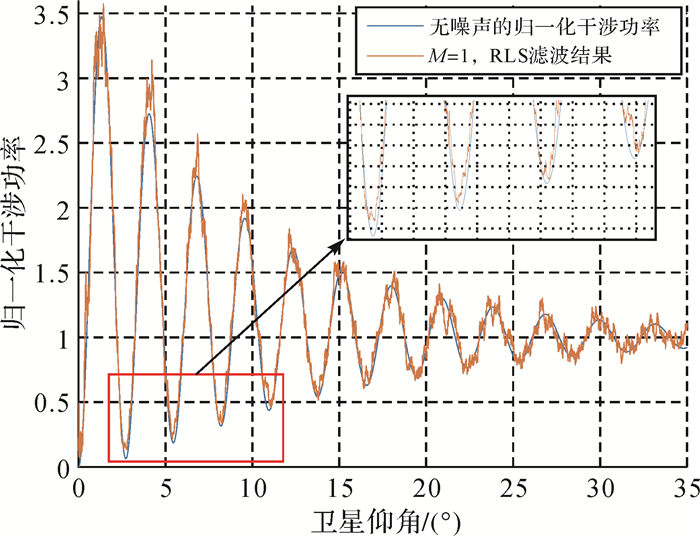
(2) 图 3中,峰值与谷值反演表现不同,根据式(5),峰值与谷值的估计误差对土壤湿度反演误差的影响不同,对于利用峰值反演,如果估计的峰值功率高于理论值,则得到的反射系数将高于理论值,由于RR反射系数与介电常数和土壤湿度呈负相关(图 4),导致最终土壤湿度反演结果低于理论值,而用谷值反演影响恰好相反。由于归一化干涉功率的峰值噪声普遍高于谷值噪声(如图 2所示,M=20),导致估计出来的峰值大于理论值,且仰角越低,峰谷值噪声差别越大,这样的噪声特点导致RLS滤波后归一化干涉功率的低仰角部分上翘。即仰角大约小于12°时,干涉功率谷值大于理论值;仰角大于12°时,干涉功率谷值小于理论值。当M=1时,这种效果最明显,如图 5所示,因此峰值反演结果绝大多数小于设定值,而谷值反演结果在仰角小于12°时大于理论值,在仰角大于12°时小于理论值。
|
| 图 4 RR反射系数与介电常数之间的关系 Fig. 4 Relationship between RR reflection coefficient and permitivity |
(3) 图 3中,峰值与谷值反演标准差在低仰角和高仰角处都偏大,但两者成因不同,低仰角处(小于5°) RR反射系数与卫星仰角的关系曲线非常密集(图 4),说明这一段仰角范围内反射系数对介电常数的敏感性高,误差放大系数大,即较小的反射系数估计误差将导致较大的土壤湿度反演误差,标准差也被放大;高仰角处(大于25°),反射系数对介电常数的敏感性明显降低,误差放大系数减小,但由于反射信号功率受天线增益与反射系数衰减的影响,干涉功率曲线的信噪比降低(图 5),导致反演的方差较大。
|
| 图 5 M=1时归一化干涉功率RLS滤波结果 Fig. 5 Results after normalized interference power being filtered by RLS filter with M=1 |
(4) AMPD算法完全基于对窗内数据进行大小比较,因此其在搜索干涉峰谷值时依然受叠加在峰谷值周围毛刺的影响,使得搜索到的干涉功率峰谷值在一定程度上偏离理想位置,从而造成一定程度的反演误差, 如果存在某一处毛刺明显偏离理想位置,且功率值明显高于周围的正常峰谷值(如图 6实线框所示),则此异常值的存在将影响周围峰谷值的搜索,AMPD算法无法控制这样的异常值。

|
| 图 6 异常值对AMPD算法影响分析 Fig. 6 Outlier value effect on AMPD algorithm |
(5)综上所述,利用5°~25°内的谷值进行土壤湿度反演效果较好,M的取值应大于等于100,但M的取值也不应过大,应保证“在此期间干涉信号的各参量近似不变”这一假设成立。
3.3 不同土壤湿度下反演性能分析同一仰角下土壤湿度与地表反射系数Γ的关系为非线性,且反射系数随仰角的不同而不同,敏感性也不一致,因此在不同土壤湿度下利用干涉功率反演将会有不同的误差放大系数,为了验证不同土壤湿度下该方法的反演效果,本文在选择M=100的条件下,设置了多个土壤湿度(从0.04开始以0.02为间隔直到0.5),对其分别进行800次仿真,每次取5°~25°内归一化干涉功率谷值反演结果的平均值,800次仿真的统计结果如图 7所示。

|
| 图 7 土壤湿度变化时仿真统计结果 Fig. 7 Statistical results under different soil moisture |
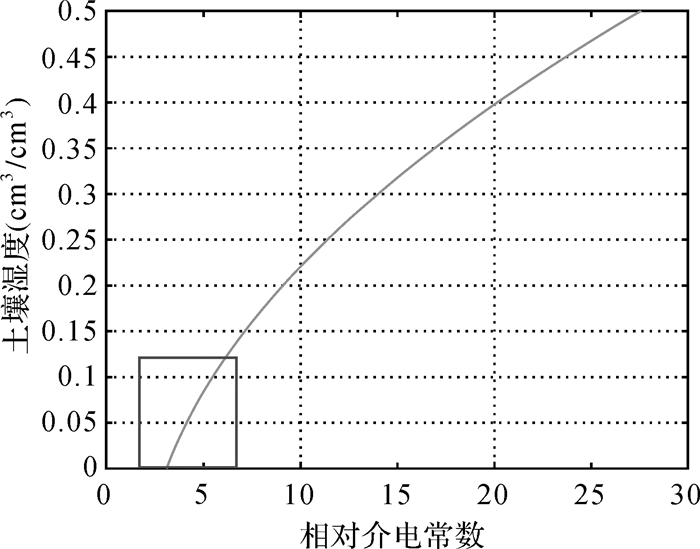
从图 7中可以看出,土壤湿度越大(大于0.06 cm3/cm3),反演结果越接近于设定值,反演结果标准差在0.008 6~0.015 4 cm3/cm3之间波动,当土壤湿度小于0.06 cm3/cm3时,误差值略大一些,这是因为土壤湿度较小时,归一化干涉功率经RLS滤波后的曲线偏离真实曲线的程度较大,导致较大的介电常数估计误差,且根据图 8,土壤湿度低时土壤湿度反演误差对介电常数估计误差较敏感(斜率大,如图 8实线框部分所示),误差放大系数较大,导致反演结果明显偏离设定值。
|
| 图 8 土壤湿度与介电常数关系曲线 Fig. 8 Relationship between soil moisture and relative permittivity |
4 结论
本文研究了GNSS土壤湿度干涉测量法,推导了从GNSS接收机相关功率中提取归一化干涉功率,再从干涉功率峰谷值中提取介电常数的公式,并对反演过程进行了仿真,仿真过程考虑了天线方向图、噪声、相关功率估计方法的影响,根据所研究问题的特点提出使用AMPD算法提取归一化干涉功率曲线峰谷值用于反演土壤湿度,并得到如下结论:
(1) AMPD算法能够有效地从含有噪声的归一化干涉功率中提取到干涉峰值与谷值,克服了传统方法的缺点。
(2)相关功率的估计方法会影响归一化干涉功率曲线上的噪声,进而影响到后续反演结果,噪声越小反演越准确。
(3)利用干涉功率谷值进行土壤湿度反演性能优于峰值。
(4)反演结果的准确性与不同仰角下介电常数对反射系数估计误差的敏感性有关,反演时应选取敏感性弱的仰角范围,5°~25°是一种性能优越的选择,利用这段仰角内的谷值进行反演,土壤湿度大于0.06 cm3/cm3时结果更为准确。
上述仿真过程中,假设反射路径仅有一条,但实际上土壤表面有一定粗糙度,反射路径会多于一条,导致SNR产生一定程度的畸变,修正粗糙度带来的反演误差是重要的研究方向之一。
| [1] | ZAVOROTNY V U, VORONOVICH A G. Scattering of GPS Signals from the Ocean with Wind Remote Sensing Application[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(2): 951–964. DOI:10.1109/36.841977 |
| [2] | WANG Feng, YANG Dongkai, LI Weiqiang, et al. A New Retrieval Method of Significant Wave Height Based on Statistics of Scattered BeiDou GEO Signals[C]//Proceedings of the 28th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+2015). Tampa, Florida: Tampa Convention Center, 2015: 3953-3957. |
| [3] | EGIDO A, RUFFINI G, CAPARRINI M, et al. Soil Moisture Monitorization Using GNSS Reflected Signals[J]. arXiv preprint arXiv:0805.1881, 2008. |
| [4] | 邹文博, 张波, 洪学宝, 等. 利用北斗GEO卫星反射信号反演土壤湿度[J]. 测绘学报, 2016, 45(2): 199–204. ZOU Wenbo, ZHANG Bo, HONG Xuebao, et al. Soil Moisture Retrieval Using Reflected Signals of BeiDou GEO Satellites[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(2): 199–204. DOI:10.11947/j.AGCS.2016.20150135 |
| [5] | RODRIGUEZ-ALVAREZ N, BOSCH-LLUIS X, CAMPS A, et al. Water Level Monitoring Using the Interference Pattern GNSS-R Technique[C]//Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium. Vancouver, BC, Canada: IEEE, 2011: 2334-2337. |
| [6] | CHEN Qiang, WON D, AKOS D M. Snow Depth Sensing Using the GPS L2C Signal with a Dipole Antenna[J]. EURASIP Journal on Advances in Signal Processing, 2014, 2014: 106. DOI:10.1186/1687-6180-2014-106 |
| [7] | RODRIGUEZ-ALVAREZ N, MARCHAN J F, CAMPS A, et al. Soil Moisture Retrieval Using GNSS-R Techniques: Measurement Campaign in a Wheat Field[C]//Proceedings of the 2008 IEEE International Geoscience and Remote Sensing Symposium. Boston, Massachusetts: IEEE, 2008: Ⅱ-245-Ⅱ-248. |
| [8] | ARROYO A A, CAMPS A, AGUASCA A, et al. Dual-Polarization GNSS-R Interference Pattern Technique for Soil Moisture Mapping[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 7(5): 1533–1544. DOI:10.1109/JSTARS.2014.2320792 |
| [9] | LARSON K M, SMALL E E, GUTMANN E, et al. Using GPS Multipath to Measure Soil Moisture Fluctuations: Initial Results[J]. GPS Solutions, 2008, 12(3): 173–177. DOI:10.1007/s10291-007-0076-6 |
| [10] | ZAVOROTNY V U, LARSON K M, BRAUN J J, et al. A Physical Model for GPS Multipath Caused by Land Reflections: Toward Bare Soil Moisture Retrievals[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2010, 3(1): 100–110. DOI:10.1109/JSTARS.2009.2033608 |
| [11] | CHEW C C, SMALL E E, LARSON K M, et al. Effects of Near-Surface Soil Moisture on GPS SNR Data: Development of a Retrieval Algorithm for Soil Moisture[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(1): 537–543. DOI:10.1109/TGRS.2013.2242332 |
| [12] | YAN Songhua, LI Zhengyong, YU Kegen, et al. GPS-R L1 Interference Signal Processing for Soil Moisture Estimation: An Experimental Study[J]. EURASIP Journal on Advances in Signal Processing, 2014, 2014: 107. DOI:10.1186/1687-6180-2014-107 |
| [13] | 万玮, 李黄, 洪阳, 等. GNSS-R遥感观测模式及陆面应用[J]. 遥感学报, 2015, 19(6): 882–893. WAN Wei, LI Huang, HONG Yang, et al. Definition and Application of GNSS-R Observation Patterns[J]. Journal of Remote Sensing, 2015, 19(6): 882–893. |
| [14] | ROUSSEL N, FRAPPART F, RAMILLIEN G, et al. Detection of Soil Moisture Content Changes by Using a Single Geodetic Antenna: The Case of an Agricultural Plot[C]//Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium. Milan, Italy: IEEE, 2015. |
| [15] | NIEVINSKI F G, LARSON K M. An Open Source GPS Multipath Simulator in Matlab/Octave[J]. GPS Solutions, 2014, 18(3): 473–481. DOI:10.1007/s10291-014-0370-z |
| [16] | SCHOLKMANN F, BOSS J, WOLF M. An Efficient Algorithm for Automatic Peak Detection in Noisy Periodic and Quasi-Periodic Signals[J]. Algorithms, 2012, 5(4): 588–603. DOI:10.3390/a5040588 |
| [17] | 万玮, 李黄, 洪阳. 作为外辐射源雷达的GNSS-R遥感多极化问题[J]. 雷达学报, 2014, 3(6): 641–651. WAN Wei, LI Huang, HONG Yang. Issues on Multi-polarization of GNSS-R for Passive Radar Detection[J]. Journal of Radars, 2014, 3(6): 641–651. |
| [18] | SATYANARAYANA S, BORIO D, LACHAPELLE G. C/N0 Estimation: Design Criteria and Reliability Analysis under Global Navigation Satellite System (GNSS) Weak Signal Scenarios[J]. IET Radar, Sonar & Navigation, 2012, 6(2): 81–89. |
| [19] | WANG J R, SCHMUGGE T J. An Empirical Model for the Complex Dielectric Permittivity of Soils as a Function of Water Content[J]. IEEE Transactions on Geoscience and Remote Sensing, 1980, GE-18(4): 288–295. DOI:10.1109/TGRS.1980.350304 |
| [20] | SCARGLE J D. Studies in Astronomical Time Series Analysis. Ⅱ-Statistical Aspects of Spectral Analysis of Unevenly Spaced Data[J]. Astrophysical Journal, 1982, 263: 835–853. DOI:10.1086/160554 |
| [21] | NEHORAI A, PORAT B. Adaptive Comb Filtering for Harmonic Signal Enhancement[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1986, 34(5): 1124–1138. DOI:10.1109/TASSP.1986.1164952 |
| [22] | BILICH A, LARSON K M, AXELRAD P. Modeling GPS Phase Multipath with SNR: Case Study from the Salar de Uyuni, Boliva[J]. Journal of Geophysical Research: Solid Earth, 2008, 113(B4): B04401. |