2. 北斗导航应用技术河南省协同创新中心, 河南 郑州 450001
2. BeiDou Navigation Technology Collaborative Innovation Center of Henan, Zhengzhou 450001, China
在高精度远程时间传递中卫星双向时间频率传递(two way satellite time and frequency transfer,TWSTFT)和精密单点定位(precise point positioning,PPP)时间传递技术是精度最高的两种方法[1-3]。TWSTFT需要专门的中介卫星建立通信链路,且参与双方都需要专门的发射接收设备,设备价格昂贵,目前世界上只有少数较大的实验室应用。而PPP时间传递算法是单站作业,操作灵活方便,时间传递的精度可达亚纳秒量级,其短期稳定度甚至优于TWSTFT技术[1-3],已经被广泛应用于时间传递领域。随着国际GNSS服务组织(International GNSS Services, IGS)和国际时频机构的深入合作,许多实验室已经将PPP方法用于时间传递和原子时的计算[3],国际计量局还将其用于维护协调世界时的运作[1]。文献[1-5]对PPP时间传递技术进行了研究,并取得了良好效果。文献[6-7]还对非组合PPP时间传递方法进行了研究,该方法能有效避免传统PPP算法由于观测值组合过程中观测噪声及多路径效应误差被放大而造成的对接收机钟差解算的不利影响,解算结果优于传统PPP算法。传统的PPP时间传递算法通常是将各历元接收机钟差看作相互独立的白噪声逐历元进行估计,未充分发掘接收机钟差参数在相邻历元间变化可能较为平稳的约束信息。同时由于接收机钟差、测站高程和对流层参数的高度相关,解算得到的钟差序列往往会偏离接收机钟差序列多项式的特性[8-9],时间传递结果还会存在一定时间的收敛过程。为此,本文利用原子钟的物理特性对接收机钟差建模来进一步提高PPP时间传递的精度和稳定性。
利用接收机钟物理特性对钟差进行建模的思想并不是最新提出的,美国喷气推进实验室(Jet Propulsion Laboratory,JPL)在20世纪80年代为了提高GNSS轨道等相关参数的精度就采用不同的随机过程模型来对接收机钟差和对流层进行建模[10]。但由于早期的接收机一般采用稳定度较差的石英钟,即使采用复杂的数学模型也无法准确描述石英钟的运行特征,钟差建模对解算结果的影响微乎其微。而目前许多时间实验室都已经配备了高稳定度的原子钟,这使通过钟差物理建模提高时间传递精度变得可能。近年来众多学者对钟差建模进行了大量的研究,取得了丰硕的成果。在卫星原子钟建模方面,文献[11]在顾及原子钟物理模型的基础上提出了适用于原子钟的Kalman滤波器;文献[12-15]进一步研究了原子钟滤波过程中状态矩阵和观测噪声矩阵的确定方法;文献[16]利用原子钟物理特性对钟差建模实现了对铷原子钟的状态监测。在接收机钟差建模方面,文献[17-19]对低轨卫星星载接收机端的钟差建模方法进行了研究;文献[9]对高稳定性地面接收机钟的随机模型进行了研究;文献[8, 20-21]对通过接收机钟物理建模来提高定位精度和收敛速度进行了研究,并取得了一定的效果。目前针对接收机钟差建模提高时间传递性能方面的研究较少,且处于起步阶段。文献[22]通过接收机钟差建模对接收机钟差参数估计进行了一些研究,但主要是针对石英晶振接收机,并不能有效提高时间传递精度。文献[1]也对基于原子钟钟差模型的时间传递算法进行了初步的研究。
因此,本文利用原子钟的物理特性,采用Kalman滤波方法对接收机钟差进行建模,给出了Kalman滤波过程噪声协方差矩阵、初始状态向量及其协方差矩阵的确定方法,并重点分析了附加原子钟物理模型对单站时间传递及站间时间同步结果的影响。
1 附加原子钟物理模型的PPP时间传递算法 1.1 基本观测模型对于双频接收机,PPP时间传递算法一般采用消电离层组合观测量[1],观测方程如下
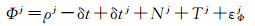 (1)
(1)
 (2)
(2)
式中,j为卫星号;Φ和P分别为载波相位和伪距消电离层组合观测量;ρ为卫星到接收机的几何距离;δt、δtj分别为接收机和卫星钟差;N为消电离层组合模糊度;T为对流层延迟;εΦj、εPj为观测噪声及多路径等未模型化的误差影响。
1.2 附加原子钟物理模型原子钟具有较高的频率稳定度,其钟差通常采用简单的一次多项式或二次多项式进行描述[23]。限于篇幅,本文仅以二次多项式为例进行分析
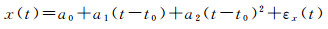 (3)
(3)
式中,x(t)为t时刻的接收机钟差;a0、a1、a2为确定性分量,分别表示参考时刻t0的初始钟差、钟速、钟漂,当a2=0时,式(3)可简化为线性模型;εx(t)为随机变化的不确定性分量。
PPP时间传递算法通常采用Kalman滤波进行参数估计,一般是将接收机钟差当作独立的白噪声,逐历元估计钟差参数,未充分发掘接收机钟差参数在相邻历元间变化可能较为平稳的约束信息。若考虑接收机钟差历元间的关系,可附加原子钟的物理模型进行约束,拓展传统PPP模型中的接收机钟差参数,使解算的钟差序列仍然体现原子钟的物理特性。具体做法是在PPP时间传递基本观测方程式(1)与式(2)估计接收机钟差参数的基础上,同时估计钟速和钟漂参数。此时观测方程中未知参数为测站三维坐标参数、钟差、钟速、钟漂、对流层和模糊度参数。为了便于推导和直观地显示附加钟差模型的方法,公式推导过程仅考虑钟差模型参数,观测方程简化为
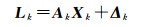 (4)
(4)
式中,Lk为观测量;Ak=[1 0 0]为设计矩阵;Xk=[x(t+τ)y(t+τ)z(t+τ)]T为tk时刻的三维状态向量,x(t)、y(t)、z(t)为接收机钟差(时差)、钟速(频率)和钟漂(频漂),τ为tk时刻与tk-1时刻的时间间隔;Δk为观测噪声。
Kalman滤波三维状态空间方程为
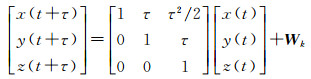 (5)
(5)
令
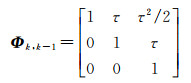 (6)
(6)
可得状态空间方程的简化形式
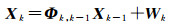 (7)
(7)
式中,Φk, k-1为状态转移矩阵;Wk为三维过程噪声向量,其协方差矩阵Q可以表示成过程噪声参数的函数[13]
 (8)
(8)
式中,q1、q2和q3分别可用调频白噪声、调频随机游走噪声和调频随机奔跑噪声来描述。
若原子钟线性频漂不明显,可采用二维状态模型来描述接收机的动态过程,此时状态转移矩阵和协方差阵需要根据三维状态模型进行相应的调整。
2 过程噪声协方差矩阵的确定系统过程噪声协方差矩阵的确定是Kalman滤波的关键,可由原子钟的滤波过程噪声参数来表示。过程噪声参数可以通过哈达玛总方差或阿伦方差进行估计。
2.1 基于哈达玛总方差的过程噪声估计原子钟频漂较明显时,可采用哈达玛总方差来估计过程噪声参数。基于时差数据的哈达玛总方差计算公式为[5, 24]
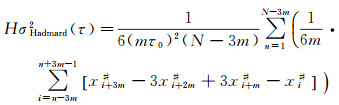 (9)
(9)
式中,HσHadmard2(τ)为采样间隔为τ的哈达玛总方差;τ=mτ0;τ0为原始数据采样间隔;m为平滑因子;N为时差数据个数;{xi#}为去除频漂的原始时差数据子序列映射延伸得到的子序列。
当同时考虑调相白噪声和状态方程中存在的3种调频噪声,且假设调相白噪声与其他3种噪声不相关时,可推导出公式[5]
 (10)
(10)
式中,q0为对应于调相白噪声的测量噪声参数。
2.2 基于阿伦方差的过程噪声估计原子钟频漂不明显时,可以采用阿伦方差来估计过程噪声参数。基于时差数据阿伦方差计算公式为[5, 24-25]
 (11)
(11)
式中,HσAllan2(τ)为采样间隔为τ的阿伦方差;N′=int (N/M)+1为测量间隔为τ的时差数据个数。
当同时考虑调相白噪声和状态方程中存在的3种调频噪声时,可推导出公式[5]
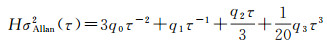 (12)
(12)
设定不同的采样间隔,就可以得到不同的哈达玛总方差(或阿伦方差)公式,联立各式利用最小二乘算法即可解得过程噪声参数q0、q1、q2和q3,进而确定系统过程噪声协方差矩阵。
3 初始状态向量及协方差确定Kalman滤波算法需要给定初始状态向量及其协方差矩阵。在无先验信息时,通常令初始状态向量为零向量,协方差矩阵为aI,其中a为很大的正数,I为单位矩阵,以确保滤波结果的无偏性。但在没有先验信息时,滤波器初始化会比较困难,且会影响滤波器的稳定性。在进行连续解算或已知先验信息时,若已知3个时差测量值l(0)、l(1)、l(2),τ1、τ2为这3个观测量的采样间隔,则根据式(13)-式(21)即可确定状态向量初值X(2)=[x(2)y(2)z(2)]以及协方差矩阵P(2),其中协方差矩阵为对角阵[15-16]
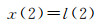 (13)
(13)
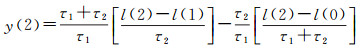 (14)
(14)
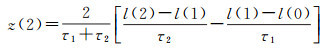 (15)
(15)
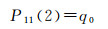 (16)
(16)
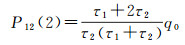 (17)
(17)
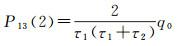 (18)
(18)
 (19)
(19)
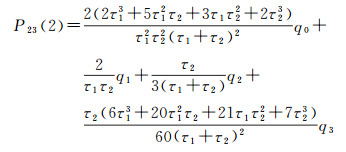 (20)
(20)
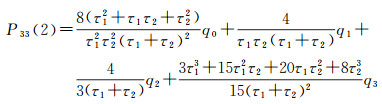 (21)
(21)
由JPL发布的“loglist.txt”文件可知,截至2016年6月2日,IGS已经有超过130个跟踪站配备了高频稳度的原子钟,其中71个配备了氢原子钟[26],这为本文算法性能的验证提供了很大的便利。为了验证附加原子钟物理模型的PPP时间传递算法的应用效果,选取2015年1月5日配备了氢原子钟的WAB2、CRO1、PTBB、NRC1和MDVJ 5个IGS跟踪站的观测数据进行试验分析。观测数据采样间隔为30 s,采用伪距和载波相位消电离层组合观测量,伪距与载波相位的权比为1/10 000,高度截止角设为10°。试验采用静态模式进行处理,利用卡尔曼滤波估计三维坐标、接收机钟差、钟速、对流层延迟和模糊度参数。卫星轨道和钟差采用IGS提供的事后精密星历和钟差产品,为了避免卫星和接收机硬件延迟偏差对接收机钟差造成的系统性偏差影响,利用CODE发布的DCB产品对其进行改正[27]。分别采用以下两种方案进行PPP解算。
方案1:将接收机钟差当作白噪声,采用传统的逐历元估计一维钟差参数的方法。
方案2:顾及接收机钟差历元间的相关性,采用附加原子钟物理模型的方法进行解算,过程噪声由阿伦方差根据IGS事后精密产品解算得到。
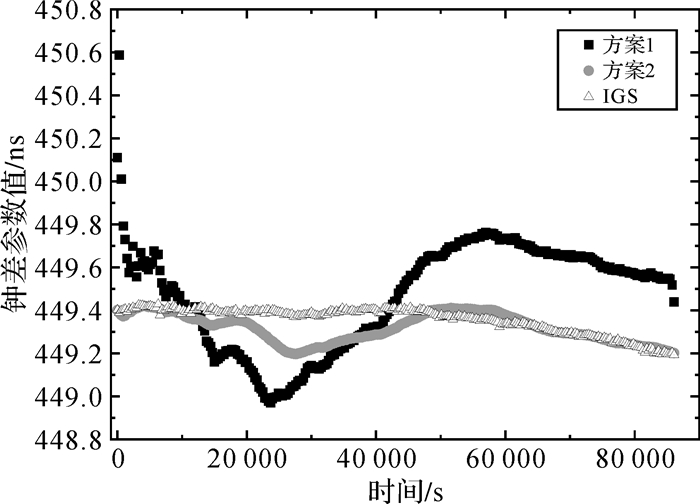
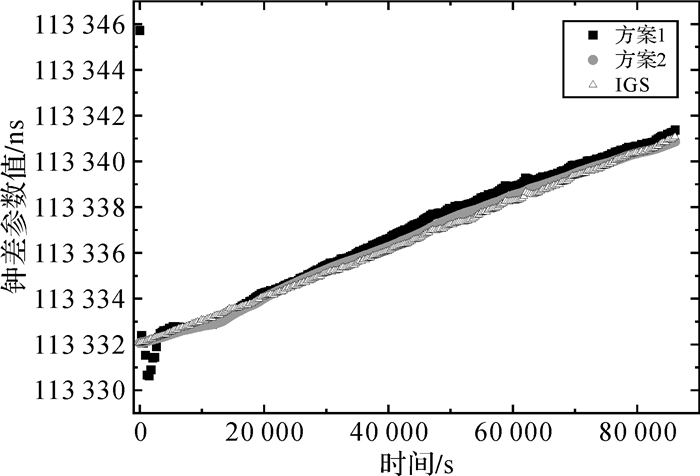
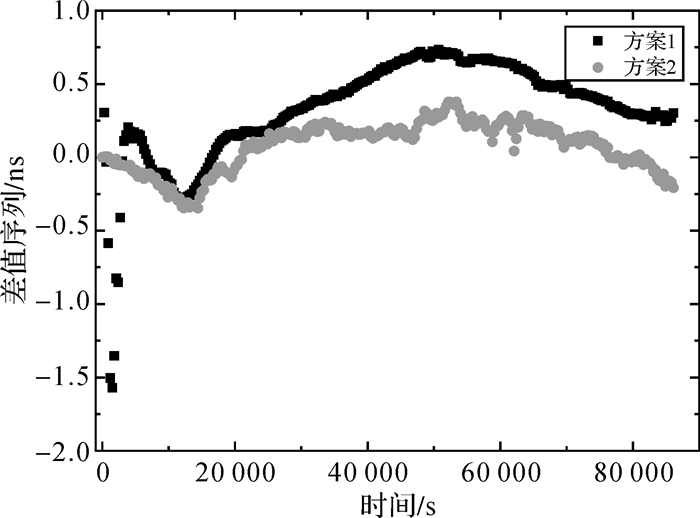
目前IGS提供的事后接收机钟差产品精度为75 ps,可将其作为真值进行比对。由于IGS事后精密钟差产品的采样间隔为5 min,因此本文以5 min为采样间隔对方案1和方案2的时间传递精度进行分析。限于篇幅,仅给出了WAB2和CRO1两跟踪站采用两种方案得到的结果与IGS时间序列对比,分别如图 1与图 2所示。同时将两种方案的钟差结果分别与IGS最终结果作差可以得到对应的差值序列,图 3与图 4分别给出了WAB2和CRO1两跟踪站单站时间传递结果的差值序列。
|
| 图 1 WAB2-GPST两种方案结果与IGS时间序列对比 Fig. 1 WAB2-GPST results of the two schemes compared with IGS time series |
|
| 图 2 CRO1-GPST两种方案结果与IGS时间序列对比 Fig. 2 CRO1-GPST results of the two schemes compared with IGS time series |

|
| 图 3 WAB2-GPST两种方案时间传递结果与IGS差值序列 Fig. 3 Difference between WAB2-GPST results and IGS from two schemes |
|
| 图 4 CRO1-GPST两种方案时间传递结果与IGS差值序列 Fig. 4 Difference between CRO1-GPST results and IGS from two schemes |
(1)方案2的收敛速度明显快于方案1,单历元就可以达到很高的精度。而方案1由于未使用原子钟物理模型作为先验信息进行约束,需要一定时间的收敛过程才能达到较高的精度,WAB2和CRO1两测站分别需要22 min、35 min才能收敛。另外,对方案2得到的坐标,对流层和模糊度结果进行分析,其收敛速度均有一定程度的提高。
(2)方案2由于附加了原子钟物理模型,得到的接收机钟差时间序列的连续性和稳定性明显优于方案1,与IGS发布的事后精密钟差结果的一致性较高,更能准确地描述接收机钟差序列的变化规律。
(3)从图 1明显可以看出,方案1解算的钟差序列略微偏离了接收机钟本身的多项式特性,这是由于方案1解算的钟差序列之间是相互独立的,解算的过程中吸收了许多不属于钟差的其他误差源而造成。方案2的滤波结果更能准确可靠地反映原子钟的物理特性。
表 1中给出了WAB2、CRO1、PTBB、NRC1和MDVJ 5个跟踪站相应的误差统计结果。表中SD为标准差(standard deviation),用来衡量钟差误差序列自身的离散程度,RMS为均方根误差用来衡量钟差估计值同真值之间的误差。
| ns | ||||
| 测站 | 统计 类型 |
方案1 | 方案2 | 精度提高 程度/(%) |
| WAB2 | SD | 0.27 | 0.07 | |
| RMS | 0.28 | 0.08 | 71 | |
| CRO1 | SD | 0.34 | 0.17 | |
| RMS | 0.47 | 0.18 | 62 | |
| PTBB | SD | 0.29 | 0.06 | |
| RMS | 0.30 | 0.08 | 73 | |
| NRC1 | SD | 0.21 | 0.10 | |
| RMS | 0.32 | 0.15 | 53 | |
| MDVJ | SD | 0.23 | 0.08 | |
| RMS | 0.24 | 0.16 | 33 | |
由表 1可知,各测站方案2时间传递结果的SD和RMS均优于方案1,方案1的钟差解相对较为离散,方案2的钟差解稳定度较高,与IGS结果的符合程度更高。方案2附加原子钟物理模型后,能够显著提高PPP时间传递的精度,可将WAB2、CRO1、PTBB、NRC1和MDVJ 5个跟踪站的单站时间传递精度(RMS)分别提高71%、62%、73%、53%和33%,平均提高58%。该算法对于促进PPP时间传递技术在国际时间实验室等高精度时间同步领域的应用具有一定意义。
为了进一步分析本文算法应用于站间时间同步中的精度,将各站利用PPP获得的原子钟的钟差结果相减即可得到站间时间同步结果,表 2给出了两种方案得到的不同时间链路的时间同步序列的精度统计结果,为更好地观察时间同步序列变化情况,图 5以CRO1-WAB2时间链路为例给出了站间时间同步结果同IGS结果的差值序列图。
| ns | ||||
| 测站 | 统计 类型 |
方案1 | 方案2 | 精度提高 程度/(%) |
| CRO1-WAB2 | SD | 0.37 | 0.18 | |
| RMS | 0.43 | 0.21 | 51 | |
| CRO1-PTBB | SD | 0.28 | 0.17 | |
| RMS | 0.37 | 0.19 | 49 | |
| CRO1-NRC1 | SD | 0.23 | 0.17 | |
| RMS | 0.24 | 0.17 | 29 | |
| CRO1-MDVJ | SD | 0.31 | 0.10 | |
| RMS | 0.52 | 0.14 | 73 | |

|
| 图 5 CRO1-WAB2链路两方案时间同步结果与IGS结果差值序列 Fig. 5 Difference between CRO1-WAB2 results and IGS from two schemes |
根据表 2和图 5可知,方案2得到的站间时间同步结果的精度明显优于方案1,与IGS时间同步结果一致性较高,能够可靠地描述测站间时间同步序列的变化规律。由图 5可知,方案1采用传统算法CRO1-WAB2链路需要大约35 min才能收敛,而方案2附加原子钟物理模型后几乎不需要收敛时间即可达到很高的精度。方案2相比方案1,能够将CRO1-WAB2、CRO1-PTBB、CRO1-NRC1和CRO1-MDVJ链路的站间时间同步精度分别提高51%、49%、29%和73%,平均提高51%。
5 结论鉴于当前许多国际时频实验室和IGS跟踪站均配置有高性能原子钟,本文通过附加原子钟物理模型对现有PPP时间传递模型进行改进,使用Kalman滤波对接收机原子钟进行钟差建模,研究了Kalman滤波中系统过程噪声协方差矩阵、初始状态向量及协方差的确定方法,并重点分析了附加原子钟物理模型对单站时间传递及站间时间同步结果的影响。试验结果表明:附加原子钟物理模型后,解决了传统算法中收敛过程的耗时问题,显著提高单站时间传递和站间时间同步的精度,可将单站时间传递精度平均提高58%,尤其是WAB2和PTBB站精度提高水平高达71%和73%,同时可将站间时间同步精度平均提高51%。研究附加原子钟物理模型的PPP时间传递算法,对于国际时间实验室实现高精度的时间传递具有一定的参考意义,对于拓展GNSS在时频传递领域的应用具有重要意义。本文算法并非适用于所有的GNSS接收机,其前提是要判定接收机钟本身的物理特性。它要求接收机配备有高精度和高稳定的原子钟,否则加入钟差物理模型后不但不能提高时间传递精度,反而会引起比较大的误差。
| [1] | 李红涛.基于GPS和GLONASS的单站授时和时差监测研究[D].西安:长安大学, 2012. LI Hongtao. Research on the Single Station Time Service and Time Offset Based on the GPS and GLONASS Data[D]. Xi'an: Chang'an University, 2012. |
| [2] | DEFRAIGNE P, AERTS W, HARMEGNIES A, et al. Advances in Multi-GNSS Time Transfer[C]//2013 Joint European Frequency and Time Forum & International Frequency Control Symposium (EFTF/IFC). Prague, Czech Republic: IEEE, 2013: 508-512. |
| [3] | DEFRAIGNE P, AERTS W, POTTIAUX E. Monitoring of UTC (k)'s Using PPP and IGS Real-time Products[J]. GPS Solutions, 2015, 19(1): 165–172. DOI:10.1007/s10291-014-0377-5 |
| [4] | 张小红, 蔡诗响, 李星星, 等. 利用GPS精密单点定位进行时间传递精度分析[J]. 武汉大学学报(信息科学版), 2010, 35(3): 274–278. ZHANG Xiaohong, CAI Shixiang, LI Xingxing, et al. Accuracy Analysis of Time and Frequency Transfer Based on Precise Point Positioning[J]. Geomatics and Information Science of Wuhan University, 2010, 35(3): 274–278. |
| [5] | 黄观文. GNSS星载原子钟质量评价及精密钟差算法研究[D].西安:长安大学, 2012. HUANG Guanwen. Research on Algorithms of Precise Clock Offset and Quality Evaluation of GNSS Satellite Clock[D]. Xi'an: Chang'an University, 2012. |
| [6] | 闫伟, 袁运斌, 欧吉坤, 等. 非组合精密单点定位算法精密授时的可行性研究[J]. 武汉大学学报(信息科学版), 2011, 36(6): 648–651. YAN Wei, YUAN Yunbin, OU Jikun, et al. Feasibility of Precise Timing with Uncombined PPP[J]. Geomatics and Information Science of Wuhan University, 2011, 36(6): 648–651. |
| [7] | 张宝成, 欧吉坤, 袁运斌, 等. 基于GPS双频原始观测值的精密单点定位算法及应用[J]. 测绘学报, 2010, 39(5): 478–483. ZHANG Baocheng, OU Jikun, YUAN Yunbin, et al. Precise Point Positioning Algorithm Based on Original Dual-frequency GPS Code and Carrier-phase Observations and Its Application[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(5): 478–483. |
| [8] | 张小红, 陈兴汉, 郭斐. 高性能原子钟钟差建模及其在精密单点定位中的应用[J]. 测绘学报, 2015, 44(4): 392–398. ZHANG Xiaohong, CHEN Xinghan, GUO Fei. High-performance Atomic Clock Modeling and Its Application in Precise Point Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(4): 392–398. DOI:10.11947/j.AGCS.2015.20140287 |
| [9] | WANG Kan, ROTHACHER M. Stochastic Modeling of High-stability Ground Clocks in GPS Analysis[J]. Journal of Geodesy, 2013, 87(5): 427–437. DOI:10.1007/s00190-013-0616-5 |
| [10] | LICHTEN S M, BORDER J S. Strategies for High-precision Global Positioning System Orbit Determination[J]. Journal of Geophysical Research: Solid Earth, 1987, 92(B12): 12751–12762. DOI:10.1029/JB092iB12p12751 |
| [11] | JONES R H, TRYON P V. Continuous Time Series Models for Unequally Spaced Data Applied to Modeling Atomic Clocks[J]. SIAM Journal on Scientific and Statistical Computing, 1987, 8(1): 71–81. DOI:10.1137/0908007 |
| [12] | 林旭, 罗志才. 一种新的卫星钟差Kalman滤波噪声协方差估计方法[J]. 物理学报, 2015, 64(8): 080201. LIN Xu, LUO Zhicai. A New Noise Covariance Matrix Estimation Method of Kalman Filter for Satellite Clock Errors[J]. Acta Physica Sinica, 2015, 64(8): 080201. |
| [13] | 郭海荣, 杨元喜, 何海波, 等. 导航卫星原子钟Kalman滤波中噪声方差-协方差的确定[J]. 测绘学报, 2010, 39(2): 146–150. GUO Hairong, YANG Yuanxi, HE Haibo, et al. Determination of Covariance Matrix of Kalman Filter Used for Time Prediction of Atomic Clocks of Navigation Satellites[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(2): 146–150. |
| [14] | SU W, FILLER R L. Application of Kalman Filtering Techniques to the Precision Clock with Non-constant Aging[C]//Proceedings of the 46th Frequency Control Symposium. Hershey, PA: IEEE, 1992: 231-237. |
| [15] | STEIN S R, FILLER R L. Kalman Filter Analysis for Real Time Applications of Clocks and Oscillators[C]//Proceedings of the 42nd Annual Frequency Control Symposium. Baltimore, MD: IEEE, 1988: 447-452. |
| [16] | 张清华, 隋立芬, 贾小林. 应用Jones-Tryon Kalman滤波器对在轨GPS Rb钟进行状态监测[J]. 武汉大学学报(信息科学版), 2012, 37(4): 436–440. ZHANG Qinghua, SUI Lifen, JIA Xiaolin. Monitor State of GPS Rb Clock Using Jones-Tryon Kalman Filter[J]. Geomatics and Information Science of Wuhan University, 2012, 37(4): 436–440. |
| [17] | YANG Yang, YUE Xiaokui, YUAN Jianping, et al. Enhancing the Kinematic Precise Orbit Determination of Low Earth Orbiters Using GPS Receiver Clock Modelling[J]. Advances in Space Research, 2014, 54(9): 1901–1912. DOI:10.1016/j.asr.2014.07.016 |
| [18] | WEINBACH U, SCHÖN S. Improved GRACE Kinematic Orbit Determination Using GPS Receiver Clock Modeling[J]. GPS Solutions, 2013, 17(4): 511–520. DOI:10.1007/s10291-012-0297-1 |
| [19] | WEINBACH U, SCHON S. Improved GPS Receiver Clock Modeling for Kinematic Orbit Determination of the GRACE Satellites[C]//Proceedings of European Frequency and Time Forum. Gothenburg, Sweden: IEEE, 2012: 157-160. |
| [20] | 肖国锐, 隋立芬, 陈泉余, 等. 利用接收机钟差建模提升PPP收敛速度及精度[J]. 测绘科学技术学报, 2015, 32(6): 555–558. XIAO Guorui, SUI Lifen, CHEN Quanyu, et al. Improving PPP Convergence and Accuracy Using Receiver Clock Modeling[J]. Journal of Geomatics Science and Technology, 2015, 32(6): 555–558. |
| [21] | WEINBACH U, SCHÖN S. GNSS Receiver Clock Modeling When Using High-precision Oscillators and Its Impact on PPP[J]. Advances in Space Research, 2011, 47(2): 229–238. DOI:10.1016/j.asr.2010.06.031 |
| [22] | FILHO E A M, KUGA H K, LOPES R V F. Real Time Estimation of GPS Receiver Clock Offset by the Kalman Filter[J]. Personal Communication, 2003. |
| [23] | 于合理, 郝金明, 刘伟平, 等. 一种卫星钟差异常实时监测算法[J]. 武汉大学学报(信息科学版), 2016, 41(1): 106–110. YU Heli, HAO Jinming, LIU Weiping, et al. A Real-time Anomaly Monitoring Algorithm for Satellite Clock[J]. Geomatics and Information Science of Wuhan University, 2016, 41(1): 106–110. |
| [24] | RILEY W J. Handbook of Frequency Stability Analysis[R]. NIST Special Publication 1065, 2007: 1-123. |
| [25] | MANNING D M. AF/NGA GPS Monitor Station High-performance Cesium Frequency Standard Stability 2005/2006: from NGA Kalman Filter Clock Estimates[C]//Proceedings of the 38th Annual Precise Time and Time Interval Systems and Applications Meeting. Reston, Virginia:[s.n.], 2006: 137-152. |
| [26] | CLKLOG. A Summary File of the Deployment History for GPS Receiver, Antenna, Frequency Standards, and Other Equipment at IGS Stations[EB/OL]. (2010-01-20)[2016-06-02]. ftp://igscb.jpl.nasa.gov/igscb/station/general/loghist.txt. |
| [27] | 于合理, 郝金明, 谢建涛, 等. 硬件延迟偏差对卫星钟差解算的影响[J]. 导航定位学报, 2015, 3(1): 71–73. YU Heli, HAO Jinming, XIE Jiantao, et al. Impact of DCB on the Estimate of Satellite Clock Bias[J]. Journal of Navigation and Positioning, 2015, 3(1): 71–73. |


