2. 湖北水利水电职业技术学院, 湖北 武汉 430070
2. Hubei Water Resource Technical College, Wuhan 430070, China
欧空局(ESA) SWARM地球探测计划已于2013年11月22日成功实施,该计划最初目标是为了研究地磁场机制及其相互作用[1]。为了满足地磁探测的任务需要,该计划由3颗同等卫星组成,其中SWARM-A与SWARM-C轨道高度为480 km,SWARM-B轨道高度为530 km。此外,SWARM卫星搭载了热离子成像仪、朗缪尔探针以及用于精密定轨的设备(星载加速度仪、星载GPS接收机以及激光测距仪[2-3])。确定高精度的地球重力场模型需要低轨卫星精密轨道。文献[4-7]分别利用CHAMP、GRACE、GOCE、SWARM等精密轨道数据反演地球重力场模型,均获得较好的结果。因此,研究SWARM卫星精密定轨对后续相关工作的开展有很强的现实意义。
低轨卫星精密定轨方法有动力学法、运动学法以及简化动力学法。传统的定轨方法大多采用动力学法,其优点是能够提供连续的卫星轨道位置和轨道预报。但是由于地球非球形引力、大气阻力、太阳光压辐射压等摄动力难以用精确的模型表示[8],从而制约了低轨卫星定轨精度进一步的提高。星载双频GPS接收机安装在低轨卫星上以后,可获得大量连续、实时的GPS数据,扩展了定轨方法,发展了一种仅仅依赖星载GPS观测值的运动学定轨。这种定轨方法的优点是不需要知道卫星的受力情况,星载GPS观测不受天气的影响,定轨精度与卫星高度无关[9],缺点是易受GPS卫星几何图形结构的制约,导致定轨精度不稳定。针对运动学法与动力学法的不足,文献[8-10]提出了简化动力学定轨方法。该方法将动力学轨道作为先验轨道,在后续的平滑过程中,附加伪随机参数(伪随机脉冲、分段常量加速度、分段线性加速度)来吸收动力学模型误差和未被模型化的误差,通过在动力学模型和星载GPS观测值提供的几何信息之间最优选权,以充分利用动力学信息和几何信息,从而提高低轨卫星简化动力学定轨精度。文献[10]首次将简化动力学方法成功运用到TOPEX/POSEIDON卫星精密定轨,定轨精度达到3 cm。随着星载GPS技术的快速发展,简化动力学方法得到了广泛的应用。文献[9]将简化动力学方法应用到CHAMP卫星上,定轨精度为4~5 cm;文献[11-12]将简化动力学方法应用到GRACE双星上,径向定轨精度达到1 cm;文献[13-14]将简化动力学方法运用到GOCE卫星上,定轨精度达到2 cm;文献[15]将简化动力学方法运用到JASON-2卫星上,定轨精度达到厘米级;文献[16]将简化动力学方法应用到海洋2A卫星上,径向定轨精度达到1~2 cm。
SWARM计划成功实施后,学者们对SWARM精密定轨展开研究。文献[3]基于GHOST软件,在简化动力学法的基础上,将分段常量加速度引入卫星确定性运动方程中,对SWARM进行精密定轨,轨道精度优于2 cm;文献[7]基于BERNESE软件,采用运动学定轨方法对SWARM进行精密定轨,获得较好的定轨结果。而在简化动力学法中,将伪随机脉冲参数引入卫星确定性运动方程,对SWARM进行精密定轨却少有研究。因此,在简化动力学法中引入优选的伪随机脉冲参数进行SWARM精密定轨有一定的研究价值。
本文在简化动力学法的基础上,采用SWARM星载GPS双频观测值,结合目前较好的简化动力学模型,将优选的伪随机脉冲参数引入卫星确定性运动方程,将伪随机脉冲参数与其他确定性参数一起估计,成功解算SWARM卫星精密轨道。为了客观评价本文定轨结果的可靠性,利用星载GPS相位观测值残差、重叠轨道偏差以及与外部轨道对比等一系列内外符合精度评定方法对本文定轨结果进行综合评估。
1 SWARM卫星简化动力学定轨基本理论 1.1 伪随机脉冲定义与数学模型伪随机脉冲就是某个历元时刻、预定方向上的瞬时速度变化,一般是在径向、切向、法向3个方向上每隔一段时间各设置一个伪随机脉冲参数[8]。假设历元时刻为ti,预设方向为e(t),则伪随机脉冲参数pi表示为
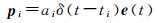 (1)
(1)
式中,δ(t-ti)表示狄拉克函数,δ(t-ti)=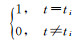
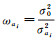
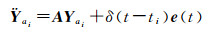 (2)
(2)
式中,δ(t-ti)表示狄拉克函数;Yai表示初始历元的6个轨道根数的偏导数的线性组合;A表示相应的系数阵;e(t)表示伪随机脉冲预设方向。
1.2 简化动力学定轨方法低轨卫星在距离地球表面几百公里的轨道上高速运转,受到多种摄动力的作用,包括N体摄动、地球非球形摄动、固体潮摄动、海潮摄动、大气阻力摄动、太阳辐射压摄动、地球辐射压摄动以及相对论效应等引起的摄动[8]。低轨卫星运动方程为
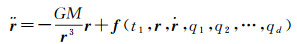 (3)
(3)
式中,r、ṙ和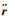
首先假设先验轨道r0(t)和先验参数pi0是已知的,动力学定轨的核心思想是轨道的不断改善过程。将r(t)作Taylor级数展开,并消去未知摄动力,将其他摄动力进行偏微分。采用最小二乘法同时处理星载GPS双频观测值与他相关参数,求得先验轨道参数pi0的改正值,对初始轨道进行修正得到精密轨道,如式(4)所示
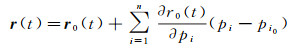 (4)
(4)
式中,pi表示轨道参数;pi0为pi的先验值。
简化动力学定轨法与动力学法类似,采用力学模式与数值积分求解低轨卫星轨道,其区别在于简化动力学法通过使用较少的动力学模型,联合运动学法与动力学法。通过增加伪随机脉冲参数将几何信息引入动力学模型中,通过相关时间间隔和先验标准差来进行动态调节,从而在几何信息和动力学信息中最优选权。在简化动力学定轨中引入伪随机脉冲参数的最大优点是伪随机脉冲参数可以有效吸收动力学模型误差与未被模型化的误差,从而提高低轨卫星简化动力学定轨精度。
2 数据来源与处理策略采用欧空局(ESA)提供的SWARM星载双频GPS观测值、CODE提供的15 min采样间隔的GPS精密星历、地球自转参数ERP以及30 s采样间隔的精密卫星钟差等数据,时间为2015年11月23-25日(年积日(DOY)为327-329),定轨弧长为24 h。根据其他低轨卫星简化动力学定轨中伪随机脉冲参数的设置为参考依据[8, 17],结合SWARM卫星自身定轨的特点,优选了一组伪随机脉冲先验值,即伪随机脉冲时间间隔为6 min,径向、切向以及法向先验标准差为10-3 m/s。首先,联合M-W线性组合和电离层残差组合进行周跳的探测与修复[18],从而获得“干净”的非差观测值,然后利用SWARM星载GPS双频伪距消电离层组合的非差观测值和消电离层组合的历元间差分相位观测值作为基本观测值,并加上天线相位中心改正、地球自转改正以及相对论效应等改正。在简化动力学定轨方法的基础上,利用最小二乘法[19]对伪随机脉冲与其他参数进行联合估计,SWARM卫星简化动力学定轨数据处理策略见表 1。
| 类别 | 参数 | 具体内容 |
| 观测值 | 观测量 | SWARM星载GPS相位与伪距观测值 |
| 采样率 | 30 s | |
| 卫星高度截止角 | 3° | |
| 误差改正 | 相位中心偏差改正 | PCV_COD.I08 |
| 相对论效应 | IERS2003 | |
| GPS轨道 | CODE提供的精密轨道(采样间隔5 min) | |
| GPS卫星钟差 | CODE提供的卫星钟差(采样率30 s) | |
| 电离层改正 | 非差消电离层组合 | |
| 地球自转形变 | IERS2003 | |
| 章动 | IAU2000R06 | |
| 单日极移 | IERS2010XY | |
| 动力学模型 | 地球重力场 | EGM2008(100阶) |
| 固体潮 | TIDE2000 | |
| 海潮 | FES2004 | |
| 行星星历 | JPL DE405 | |
| 太阳光压 | ECOM | |
| 大气阻力 | DTM94 | |
| 参数估计 | 6个初始条件 | a、e、i、w、Ω、M0 |
| 9个经验力学模型参数 | 3个常数和6个一圈一次的参数 | |
| 星载GPS接收机钟差 | 历元估计 | |
| 模糊度参数 | 非差模糊度估计 | |
| 伪随机脉冲参数 | 径向、切向、法向 |
3 SWARM卫星简化动力学定轨精度评估
目前,卫星精密定轨精度评估方法可分为内符合精度评估与外符合精度评估两大类。内符合精度评估在对卫星轨道进行精度评估时未使用其他的独立观测数据与定轨结果,而是依靠卫星定轨过程中获取的相关数据或结果来进行对比分析,包括观测值残差统计、轨道重叠差值统计等[12]。外符合精度评估通过与国际权威机构发布的轨道进行对比分析或者利用未参与精密定轨的其他观测数据进行精度评估。本文将从内符合精度和外符合精度两个方面评估SWARM卫星简化动力学定轨精度。内符合精度评估采用星载GPS相位观测值残差统计与重叠轨道偏差统计,外符合精度评估则将本文定轨结果与ESA提供的事后精密轨道进行对比分析。
3.1 观测值残差分析观测值残差是评价GPS定轨精度的指标之一[12],当所采用的动力学模型和观测数据的质量及其预处理都很理想时,观测值残差接近观测噪声水平。表 2显示SWARM-A、SWARM-B、SWARM-C等3颗卫星定轨后星载GPS非差相位观测值残差RMS,不同年积日不同卫星的相位残差RMS均分布在7~10 mm之间。结果表明:本文选取的简化动力学模型以及观测模型与实际情况吻合较好,本文提供的星载GPS数据预处理方法可以较好的探测和处理周跳。此外,SWARM-B星载GPS非差相位观测值残差RMS小于SWARM-A和SWARM-C,这是由于SWARM-B卫星轨道高度与SWARM-A卫星、SWARM-C卫星相比要高一些,而动力学模型误差(如大气阻力)随着轨道的降低而增大。因此,在相同条件下,SWARM-B卫星的动力学模型以及观测模型与实际情况吻合程度要优于SWARM-A卫星以及SWARM-C卫星。
| mm | ||
| satellite | DOY | residual RMS |
| SWARM-A | 327 | 8.5 |
| 328 | 8.6 | |
| 329 | 8.9 | |
| SWARM-B | 327 | 7.0 |
| 328 | 7.2 | |
| 329 | 7.1 | |
| SWARM-C | 327 | 9.9 |
| 328 | 10.7 | |
| 329 | 9.2 | |
3.2 重叠轨道差值分析
选取2015年11月23-25日3 d的实测数据参与轨道计算,每天0:00:00-14:59:59为第1时段,定轨弧长为15 h,9:00:00-23:59:59为第2时段,定轨弧长为15 h,9:00:00-14:59:59为重叠弧段,有6 h的重叠数据。图 1为2015年11月23日两个时段的重叠轨道示意图,尽管这6 h的观测数据相同,但是两端轨道是通过两次独立定轨运算获得,这6 h的重叠轨道不相关。因此,重叠轨道的吻合程度可以反映轨道的定轨精度[12, 20-20]。将每天的第1时段与第2时段重叠轨道进行对比分析,重叠轨道差值RMS统计结果见表 3。表 3表明,SWARM-A在径向、切向、法向重叠轨道差值RMS在0.48~2.16 cm之间波动,3D RMS为1~2 cm;SWARM-B在径向、切向、法向重叠轨道差值RMS在0.54~1.67 cm之间波动,3D RMS为1~2 cm;SWARM-C在径向、切向、法向重叠轨道差值RMS在0.73~1.68 cm之间波动,3D RMS为1~2 cm。因此,径向、切向以及法向均无明显的系统误差,6 h重叠轨道差值RMS均在1~2 cm左右,满足精密定轨的需求。
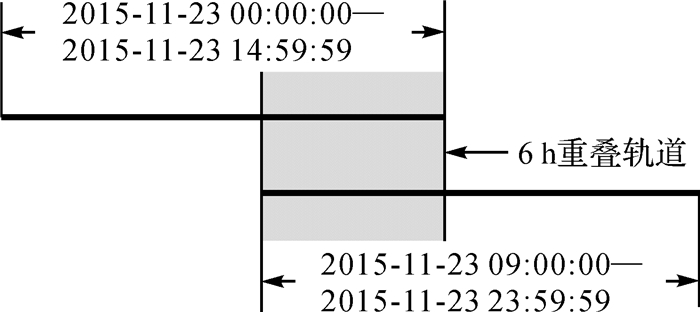
|
| 图 1 重叠轨道示意图 Fig. 1 Sketch map of overlap orbit |
| cm | |||||
| satellite | DOY | R | T | N | 3D |
| SWARM-A | 327 | 1.17 | 0.79 | 0.93 | 1.69 |
| 328 | 0.97 | 1.37 | 0.48 | 1.75 | |
| 329 | 2.16 | 1.56 | 0.82 | 2.79 | |
| SWARM-B | 327 | 0.82 | 0.60 | 1.10 | 1.50 |
| 328 | 0.86 | 0.71 | 0.54 | 1.24 | |
| 329 | 1.52 | 0.64 | 1.67 | 2.35 | |
| SWARM-C | 327 | 0.84 | 0.86 | 1.36 | 1.82 |
| 328 | 1.14 | 0.77 | 0.73 | 1.56 | |
| 329 | 1.68 | 1.65 | 1.50 | 2.79 | |
| 注:R表示径向;T表示切向;N表示法向;3D表示三维位置 | |||||
3.3 简化动力学定轨结果与ESA轨道对比分析
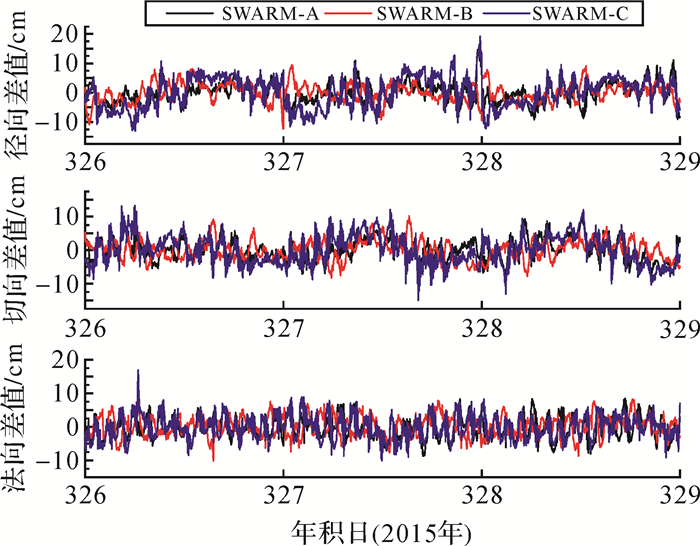
解算SWARM卫星精密轨道是卫星星群应用与研究机构(SCARF)的一项任务[22],荷兰代尔夫特理工大学航空工程学院是卫星星群应用与研究机构(SCARF)的成员,承担此次任务。该学院采用GHOST软件解算SWARM简化动力学精密轨道,运用SLR观测数据对其进行检核,轨道精度优于2 cm,定轨结果已在ESA网站上发布[3],本文将其作为参考轨道。根据表 1给出的定轨策略,定轨结果与参考轨道进行对比分析,结果见表 4和图 2。表 4和图 2表明,SWARM-A在R、T、N 3个方向的轨道差值RMS在2.63~3.89 cm之间波动,3D轨道差值RMS为4~6 cm;SWARM-B在R、T、N 3个方向的轨道差值RMS在2.49~3.65 cm之间波动,3D轨道差值RMS为4~5 cm;SWARM-C在R、T、N 3个方向的轨道差值RMS在2.97~5.72 cm之间波动,3D轨道差值RMS为6~7 cm;不同年积日不同卫星的定轨精度差异不大,3D轨道差值RMS在4~7 cm之间波动。定轨结果与ESA事后轨道之间无明显的系统误差,差异主要来源于卫星轨道周期的随机误差。由图 2可以很明显地发现3个方向(径向、切向以及法向)的轨道差值均存在周期性变化规律。此外,SWARM-B的轨道差值RMS整体优于SWARM-A和SWARM-C,这与星载GPS相位观测值残差RMS结果保持一致。因此,SWARM卫星径向、切向以及法向轨道差值RMS均达到了厘米级,满足精度要求。
| cm | |||||
| satellite | DOY | R | T | N | 3D |
| SWARM-A | 327 | 3.14 | 2.63 | 2.76 | 4.94 |
| 328 | 3.71 | 2.80 | 3.33 | 5.72 | |
| 329 | 3.60 | 3.89 | 3.46 | 6.33 | |
| SWARM-B | 327 | 3.65 | 2.49 | 2.81 | 5.24 |
| 328 | 2.72 | 3.44 | 3.13 | 5.39 | |
| 329 | 2.81 | 2.63 | 2.88 | 4.81 | |
| SWARM-C | 327 | 5.01 | 3.75 | 3.42 | 7.13 |
| 328 | 5.72 | 4.19 | 3.54 | 7.93 | |
| 329 | 3.99 | 4.31 | 2.97 | 6.58 | |
| 注:R表示径向;T表示切向;N表示法向;3D表示三维位置 | |||||
|
| 图 2 年积日327-329的简化动力学定轨结果与ESA轨道差值 Fig. 2 Difference between reduced-dynamic orbit results and ESA orbit solutions on DOY 327-329 |
为了进一步验证本文定轨策略的可靠性。选取2015年8月2-8日(年积日为214-220)一个星期的观测数据,采用本文的定轨策略进行SWARM卫星精密定轨,定轨结果与ESA事后精密轨道进行对比分析。
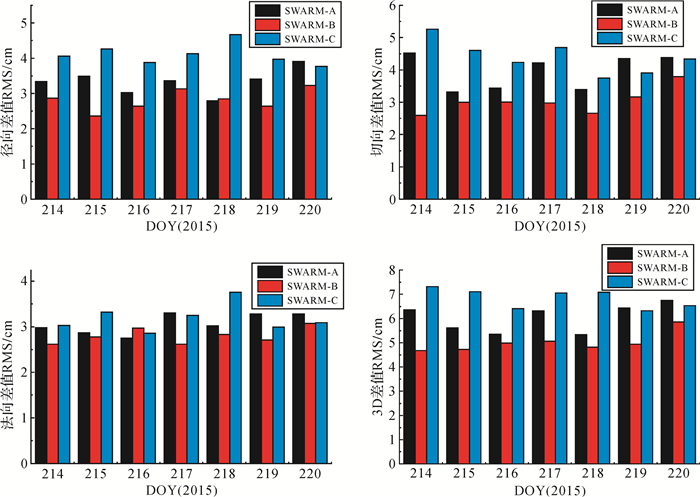
图 3为3颗SWARM卫星一个星期(2015年8月2日-8日)的定轨结果与ESA事后轨道在径向、切向、法向以及3D的差值RMS统计图。由图 3可知,在径向上,SWARM-A差值RMS为2~4 cm,SWARM-B差值RMS为2~3 cm,SWARM-C差值RMS为3~5 cm;在切向上,SWARM-A差值RMS为3~4 cm,SWARM-B差值RMS为2~3 cm,SWARM-C差值RMS为3~5 cm;在法向上,SWARM-A差值RMS为2~3 cm,SWARM-B差值RMS为2~3 cm,SWARM-C差值RMS为2~4 cm;在3D上,SWARM-A差值RMS为5~7 cm,SWARM-B差值RMS为4~6 cm,SWARM-C差值RMS为6~7 cm;SWARM-B的定轨精度优于SWARM-A与SWARM-C,与上一时段的结论保持一致,从而进一步验证了本文定轨策略的有效性以及结果的稳定性。
|
| 图 3 一个星期的定轨结果与ESA事后轨道的差值RMS Fig. 3 Difference RMS between orbit results and ESA orbit solutions for one week |
综合两个时段的试验结果表明:无论在径向、切向、法向以及3D上,SWARM定轨结果与ESA事后轨道差异较小,均无明显的系统误差,定轨精度达到厘米级水平;SWARM-B定轨精度优于SWARM-A与SWARM-C。因此,采用简化动力学定轨方法结合文中给出的定轨策略进行SWARM卫星精密定轨是可行的,定轨结果稳定可靠。
4 结束语本文在简化动力学方法的基础上,采用SWARM星载GPS非差观测值,结合目前较好的简化动力学模型,在卫星确定性运动方程中引入优选的伪随机脉冲参数(时间间隔为6 min,先验标准差为10-3 m/s),对SWARM进行精密定轨。通过SWARM星载GPS相位观测值残差、轨道重叠偏差以及与外部轨道对比等一系列内外符合精度评定方法对本文定轨结果进行综合评估,得到如下结论:
(1) SWARM星载GPS相位观测值残差RMS为7~10 mm,经过预处理的星载GPS观测数据与简化动力学模型符合较好。
(2)对同一天两个时段的6 h重叠轨道偏差进行统计分析,SWARM卫星径向、切向以及法向轨道差值RMS均在1 cm左右,3个方向均无明显的系统误差,重叠轨道之间符合较好。
(3)通过与ESA发布的精密轨道进行对比分析,SWARM径向轨道差值RMS为2~5 cm,切向轨道差值RMS为2~5 cm,法向轨道差值RMS为2~4 cm,3D轨道差值RMS为4~7 cm。定轨结果与ESA事后轨道之间无明显的系统误差,定轨精度达到厘米级。
(4) SWARM-B定轨精度优于SWARM-A与SWARM-C。
因此,在卫星确定性运动方程中引入优选的伪随机脉冲参数进行SWARM卫星简化动力学精密定轨可以获得与ESA精度相当的定轨结果,定轨精度达到厘米级。
致谢: 感谢CODE提供GPS精密星历、卫星钟差以及地球定向参数,感谢ESA提供星载GPS观测值与SWARM精密轨道。
| [1] | FRIIS-CHRISTENSEN E, LÜHR H, KNUDSEN D, et al. SWARM--An Earth Observation Mission Investigating Geospace[J]. Advances in Space Research, 2008, 41(1): 210–216. DOI:10.1016/j.asr.2006.10.008 |
| [2] | VISSER P, DOORNBOS E, VAN DEN IJSSEL J, et al. Thermospheric Density and Wind Retrieval from Swarm Observations[J]. Earth, Planets and Space, 2013, 65(11): 1319–1331. DOI:10.5047/eps.2013.08.003 |
| [3] | VAN DEN IJSSEL J, ENCARNAÇÃ O J, DOORNBOS E, et al. Precise Science Orbits for the SWARM Satellite Constellation[J]. Advances in Space Research, 2015, 56(6): 1042–1055. DOI:10.1016/j.asr.2015.06.002 |
| [4] | 徐天河, 杨元喜. 利用CHAMP卫星星历及加速度计数据推求地球重力场模型[J]. 测绘学报, 2004, 33(2): 95–99. XU Tianhe, YANG Yuanxi. Recoverying the Gravitational Potential Model from the Ephemerides and Accelermeter of CHAMP[J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(2): 95–99. |
| [5] | 陈秋杰, 沈云中, 张兴福, 等. 基于GRACE卫星数据的高精度全球静态重力场模型[J]. 测绘学报, 2016, 45(4): 396–403. CHEN Qiujie, SHEN Yunzhong, ZHANG Xingfu, et al. GRACE Data-based High Accuracy Global Static Earth's Gravity Field Model[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(4): 396–403. DOI:10.11947/j.AGCS.2016.20150422 |
| [6] | 周浩, 罗志才, 钟波, 等. 利用最小二乘直接法反演卫星重力场模型的MPI并行算法[J]. 测绘学报, 2015, 44(8): 833–839. ZHOU Hao, LUO Zhicai, ZHONG Bo, et al. MPI Parallel Algorithm in Satellite Gravity Field Model Inversion on the Basis of Least Square Method[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(8): 833–839. DOI:10.11947/j.AGCS.2015.20140396 |
| [7] | JÄGGI A, DAHLE C, ARNOLD D, et al. SWARM Kinematic Orbits and Gravity Fields from 18 Months of GPS Data[J]. Advances in Space Research, 2016, 57(1): 218–233. DOI:10.1016/j.asr.2015.10.035 |
| [8] | JÄGGI A, HUGENTOBLER U, BEUTLER G. Pseudo-stochastic Orbit Modeling Techniques for Low-Earth Orbiters[J]. Journal of Geodesy, 2006, 80(1): 47–60. DOI:10.1007/s00190-006-0029-9 |
| [9] | SVEHLA D, ROTHACHER M. Kinematic and Reduced-Dynamic Precise Orbit Determination of Low Earth Orbiters[J]. Advances in Geosciences, 2003, 1: 47–56. DOI:10.5194/adgeo-1-47-2003 |
| [10] | YUNCK T P, BERTIGER W I, WU S C, et al. First Assessment of GPS-based Reduced Dynamic Orbit Determination on TOPEX/POSEIDON[J]. Geophysical Research Letters, 1994, 21(7): 541–544. DOI:10.1029/94GL00010 |
| [11] | 陈俊平, 王解先. 附加Helmert变换参数的低轨卫星约化动力学精密定轨[J]. 测绘学报, 2008, 37(3): 394–399. CHEN Junping, WANG Jiexian. Reduced-dynamic Precise Orbit Determination of Low Earth Orbiter Using Helmert Transformation Model[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(3): 394–399. |
| [12] | KANG Zhigui, TAPLEY B, BETTADPUR S, et al. Precise Orbit Determination for the GRACE Mission Using only GPS Data[J]. Journal of Geodesy, 2006, 80(6): 322–331. DOI:10.1007/s00190-006-0073-5 |
| [13] | BOCK H, JÄGGI A, BEUTLER G, et al. GOCE: Precise Orbit Determination for the Entire Mission[J]. Journal of Geodesy, 2014, 88(11): 1047–1060. DOI:10.1007/s00190-014-0742-8 |
| [14] | BOCK H, JÄGGI A, MEYER U, et al. GPS-derived Orbits for the GOCE Satellite[J]. Journal of Geodesy, 2011, 85(11): 807–818. DOI:10.1007/s00190-011-0484-9 |
| [15] | 秦建, 郭金运, 孔巧丽, 等. Jason-2卫星星载GPS数据厘米级精密定轨[J]. 武汉大学学报(信息科学版), 2014, 39(2): 137–141. QIN Jian, GUO Jinyun, KONG Qiaoli, et al. Precise Orbit Determination of Jason-2 with Precision of Centimeters Based on Satellite-borne GPS Technique[J]. Geomatics and Information Science of Wuhan University, 2014, 39(2): 137–141. |
| [16] | 郭靖, 赵齐乐, 李敏, 等. 利用星载GPS观测数据确定海洋2A卫星厘米级精密轨道[J]. 武汉大学学报(信息科学版), 2013, 38(1): 52–55. GUO Jing, ZHAO Qile, LI Min, et al. Centimeter Level Orbit Determination for HY2A Using GPS Data[J]. Geomatics and Information Science of Wuhan University, 2013, 38(1): 52–55. |
| [17] | 韩保民. 基于星载GPS双频观测值的简化动力学定轨方法[J]. 南京航空航天大学学报, 2007, 39(2): 149–153. HAN Baomin. Reduced-Dynamic Orbit Determination Using Dual-Frequency Onboard GPS Observations[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2007, 39(2): 149–153. |
| [18] | CAI Changsheng, LIU Zhizhao, XIA Pengfei, et al. Cycle Slip Detection and Repair for Undifferenced GPS Observations under High Ionospheric Activity[J]. GPS Solutions, 2013, 17(2): 247–260. DOI:10.1007/s10291-012-0275-7 |
| [19] | JÄGGI A, BEUTLER G, HUGENTOBLER U. Efficient Stochastic Orbit Modeling Techniques Using Least Squares Estimators[M]//SANSÒ F. A Window on the Future of Geodesy. Berlin: Springer, 2005: 175-180. |
| [20] | WU S C, MUELLERSCHOEN R J, BERTIGER W I, et al. Automated Precision Orbit Determination for TOPEX/POSEIDON with GPS[R]. Jet Propulsion Laboratory Technical Report, 1993. |
| [21] | 郭金运.由星载GPS数据进行CHAMP卫星定轨和地球重力场模型解算[D].泰安:山东科技大学, 2004. GUO Jinyun. Determination of CHAMP's Orbit and Earth Gravity Model from Onboard GPS Data[D]. Tai'an: Shandong University of Science and Technology, 2004. |
| [22] | OLSEN N, FRIIS-CHRISTENSEN E, FLOBERGHAGEN R, et al. The SWARM Satellite Constellation Application and Research Facility (SCARF) and SWARM Data Products[J]. Earth, Planets and Space, 2013, 65(11): 1189–1200. DOI:10.5047/eps.2013.07.001 |



