2. 北京环球信息应用开发中心, 北京 100094
2. Beijing Global Information Application and Development Center, Beijing 100094, China
GNSS星座的精密轨道和卫星钟差信息的连续一致性,是用户导航定位和授时服务质量的重要保证。在一年的轨道运行期间,GNSS普遍采用的中高轨导航卫星都要经历两次相隔半年的地影季[1]。在地影季期间,太阳位于卫星轨道面附近,当日、地和卫星近似在一条直线上时,卫星进入地影,称为星蚀[2]。由于导航卫星地影季期间每天一至两次地进出地影,造成力模型中太阳辐射压的间断,并且地影季前后星体偏航角调整引起的姿控较为复杂,建模精度不高,对相关时段的轨道、卫星钟差以及卫星天线相位中心的偏差归算和SLR外部检核等影响较大[3],文献[4-10]分别讨论了GPS Ⅱ/ⅡA、GLONASS-M、QZS-1和我国BDS的非GEO卫星的轨道、卫星钟差和SLR外部轨道径向等数据产品的精度不一致性。此外,星蚀期间卫星星体不能接收太阳光线照射并感知太阳位置,从而影响星上太阳能帆板和太阳敏感器等的正常工作,也需要对卫星的温控和姿控系统进行策略调整和切换[11]。因此,常常需要仿真分析或提取实测的各类卫星的地影季时段数据。若能够对地影季进行解析建模(如地影季分布、每天出入地影频度以及每次进出时刻和持续时间、偏航角等),则可依据少量的地影参数,为精密定轨、偏航姿控和卫星能源等分系统的设计和数据验证提供快速而精确的参考依据。
由于涉及日、地和卫星3个星体的相对运动,分析卫星进出地影的常见方法是两步法。首先,基于日地关系建立地影模型,即严格的锥形地影模型和简化的柱形地影模型[12-13];其次,在选取的地影模型上,根据某颗卫星的轨道运动特性,分析该卫星的地影季和星蚀参数[12]。目前,两步法对卫星地影的讨论多是针对某些特定轨道的数值仿真[1, 4-7],计算精度高,但是难以快速而全面地给出卫星地影参数的变化和分布规律。
本文提出一种新的一体化分析方法,即直接基于日、地和卫星三者关系的卫星地影建模法。首先,由轨道高度确定卫星地影的大小,由太阳的周年视运动确定卫星地影的运动规律。其次,将黄道和卫星轨道面投影在赤道坐标系的YOZ平面内,建立它们与卫星地影的几何关系;利用球面三角推导了常用卫星地影参数的计算公式以及扁率摄动等对长期预报的影响改正公式。以GEO/IGSO/MEO 3类中高轨轨道为例,分析了GNSS星座地影参数的变化和分布规律。
1 卫星地影模型为了区别,这里把仅涉及日地位置关系的称为地影,而把顾及日-地-卫星三者相互关系的称为卫星地影。卫星地影包括大小和周年运动两个特性参数。
1.1 卫星地影的半径如图 1所示,若将太阳视为理想的无穷远天体,则其退化为点光源,入射光线为平行光,即对应有简化的柱形地影模型。对进入地影的近圆轨道卫星S1和S2,分别以其空间高度为视场基点,在其轨道高度处观察到的地球视盘大小基本固定,且随轨道高度增大而减小。

|
| 图 1 卫星地影的大小 Fig. 1 Size of the earth shadow projected at satellite altitude |
对于近圆轨道,卫星地影的大小由卫星轨道高度决定。卫星地影的半径即为地球视盘的角半径de,即
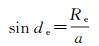 (1)
(1)
式中,Re和a分别表示地球平均半径和卫星轨道半长轴。例如,BDS的地球同步卫星GEO和IGSO的半长轴a约为6.6Re,其卫星地影的角半径de为8.7°,而MEO的半长轴约为4.4Re,相应的de为13.2°。
当考虑太阳为有限距离天体时,由于日地距离远大于卫星轨道高度,可认为卫星轨道高度与地心处看到的太阳视盘ds一致,约为0.267°。此时,卫星地影与锥形地影类似,也有本影和半影。本影和全影(即本影+半影)为两同心圆,半径分别为dumbra=de-ds和dshadow=de+ds。
1.2 卫星地影中心的位置变化卫星地影中心的位置由太阳位置决定,与卫星轨道无关。因为地影的中心始终位于地日连线的反方向,即其始终位于黄道上与太阳相对,且其位置变化由视太阳(以下均指太阳质心)每年沿黄道的运动决定。
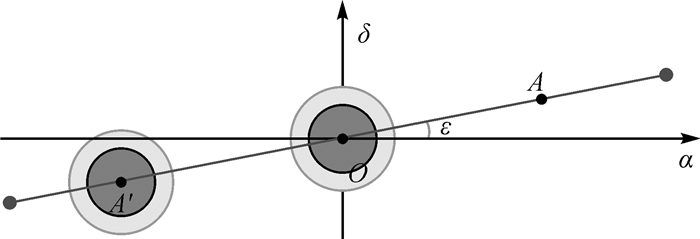
图 2为黄道在地心赤道坐标系的YOZ平面的投影,两坐标轴分别对应赤经α和赤纬δ,春分点(即X轴指向)和秋分点与地心O点重合,黄赤交角为ε。
|
| 图 2 卫星地影的周年运动 Fig. 2 Annual motion of the satellite earth shadow |
在太阳的周年视运动过程中,当太阳在春分点时,卫星地影中心位于秋分点,即图 2的O点;当太阳从春分点出发沿黄道向夏至点方向运动至A点时,卫星地影则从秋分点出发沿黄道反向运动至A′点,两者的运动速率相同,约为每天1°。
因此,对于不同高度的近圆卫星,其卫星地影表现为沿黄道作周年运动的同心圆;轨道越高,圆半径越小。
2 卫星的地影季参数在图 3中,将卫星轨道升交段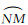

|
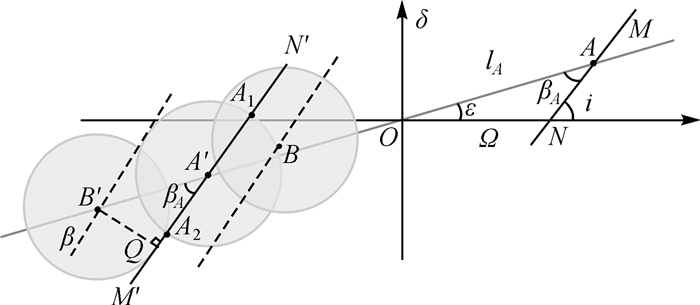
| 图 3 地心赤道坐标系下黄道、卫星轨道升交段/降交段的投影关系 Fig. 3 The ecliptic and the ascending/descending sections of the satellite projected onto the equatorial coordinate system |
太阳相对卫星轨道面的高度角称为太阳β角,这里取与轨道角动量方向一致时为正[14-15]。因为卫星地影中心与太阳关于地心镜像对称,太阳高于轨道面时,卫星地影中心则低于轨道面,因此,卫星地影中心相对卫星轨道面的高度角与β角数值相等,符号相反,如B′Q。特别的,当太阳位于黄道与卫星轨道面的交点A和A′点时,β角为零。
随着太阳沿黄道从南向北向卫星轨道面A点运动,卫星地影反向向A′点运动,太阳β角逐渐变小。当卫星地影中心到达B点和B′点时,卫星轨道与地影相切,即|β|=de。因此,卫星地影中心经过BA′B′的时段,有|β|≤de,卫星轨道每圈均会穿过卫星地影出现星蚀,该时段称为卫星的地影季。
地影季期间,随着卫星地影的运动,每圈的星蚀持续时间表现为由零变大直至最大再逐渐变小至零的对称过程。其中,当卫星地影中心到达A′点时(β=0),卫星轨道恰好穿越卫星地影中心,星蚀持续时间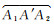
一般情况下,太阳一年两次经过卫星轨道面(即A点和A′点),因此,地影季和最长地影日一年两次,且相隔半年。特别的,若卫星的轨道面与黄道面重合,太阳始终位于卫星轨道面内,则地影季为全年。
2.1 最长地影日最长地影日由卫星的轨道倾角和升交点赤经决定。以太阳运动到与卫星升交段的交点A为例,在图 3的球面三角形AON中,太阳平黄经lA可由四元素公式计算
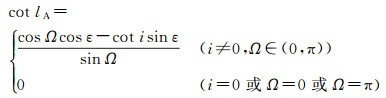 (2)
(2)
则最长地影日距离春分日(一般为3月21日)的日数为
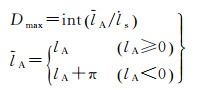 (3)
(3)
式中,int表示取整;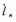
地影季的持续时间还与卫星地影半径有关。当太阳β角超过卫星地影半径de,地影季结束。在图 3的球面直角三角形A′QB′中,有A′B′的平黄经之差
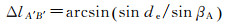 (4)
(4)
式中,黄道面与卫星轨道面的夹角βA,可由球面三角形AON的角的余弦定理得到
 (5)
(5)
特别的,当i=0(理想GEO)时,βA=ε;当Ω=0时,βA=|i-ε|;当Ω=π时,βA=i+ε。
因为地影季关于最长地影日对称,其持续天数ΔD为
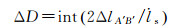 (6)
(6)
对于所有GEO卫星,总有βA=ε,de=8.7°,代入式(4),ΔlA′B′的计算值约为23°,因此GEO的单次地影季共持续46 d左右。
2.3 摄动对地影季预报的影响地影季每年两次,但是并非严格相差半年。对于长达半年的预报时段,精化预报需要进行以下两方面的修正。
(1)太阳黄经的日平均变率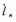
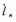
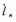
(2)地球扁率J2项摄动等引起的卫星轨道面的长期进动即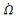
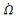
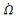
对于GEO卫星,其赤道轨道面不受地球扁率摄动的影响,但是地球赤道的椭率J22项摄动会引起其定点经度的长周期漂移,不过有频繁的位置保持机动,可忽略其摄动影响。
综合上述两方面改进,对于MEO和IGSO,由式(2)的误差方程可预报半年后的最大地影日相对于A′点的黄经偏差
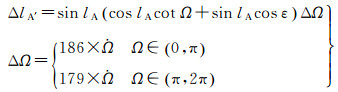 (7)
(7)
因此,下一次的最大地影日的预报偏差为
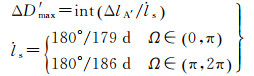 (8)
(8)
式(8)中第2次最大地影日对应半年后,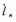
已知卫星地影季参数后,可以进一步确定任意时刻的星蚀参数。
3.1 太阳β角太阳β角是地影季星上能源和姿态转换的主要考察参数之一[14-15]。如图 4所示的降交段

|
| 图 4 星蚀和卫星地影 Fig. 4 Satellite eclipse and the satellite earth shadow |
通过球面直角三角形A′FC的计算式,有
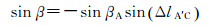 (9)
(9)
式中,ΔlA′C=I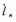
在地影季附近,卫星的轨道运动计量经常要求从星上子夜时刻开始起算[18-19]。在图 4中,F点是降交段
若已知近圆轨道某时刻ts0及其轨道角μ0,则任意时刻的轨道角近似为
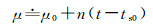 (10)
(10)
式中,n为卫星运动平均角速率。
但是,对于近圆卫星,通常给出的轨道运动快变量是从升交点开始计量的,即幅角u=ω+f,其中,ω和f分别为近地点幅角和真近点角。
因此,若已知卫星沿降交段轨道运动到某S点的时刻ts0及其幅角u0,需要计算该时刻的轨道角μ0。计算过程如下(见图 4):
(1)在球面直角三角形A′FC中,计算
 (11)
(11)
(2)在球面三角形A′OM′(或图 3的球面三角形AON)中,由四元素公式计算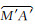
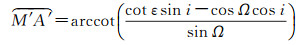 (12)
(12)
(3)从降交点M′计量的S点幅角uπ=u0-π
(4) S点的轨道角μ0为
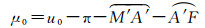 (13)
(13)
地影季期间,卫星每圈均过地影。令最长地影日的卫星子夜时刻为t0,此时卫星地影中心C点与星蚀穿越的中间点A′是重合的。但是,随后两点将沿不同轨迹运动(见图 4),即卫星地影中心C点沿黄道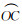


如图 4所示,若从最长地影日过A′的卫星子夜时刻t0开始计量,卫星运动m整圈后回到A′,而该段时间内,卫星地影中心已经从A′点移动到C点。因此,卫星还需要沿轨道从A′点继续运动到F点才能到达其子夜时刻tm。这里可以忽略
因此,第m圈卫星子夜时刻tm为
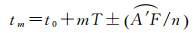 (14)
(14)
式中,T为卫星轨道运动周期,等号右边最后一项是卫星
(1) m>0时,表示超过了最长地影日,F点比A′点晚到,式中取正号;m < 0时,则是还没到最长地影日,F点比A′点早到,式中取负号。
(2)由于
第m圈的星蚀持续时间Pm可以由轨道与地影圆相割的弦长计算,即
 (15)
(15)
进而可以计算地影的进出时刻变化。这里可以根据需要,采用本影圆和半影圆取代地影圆[20-21],得到本影和半影的相关参数。
特别的,对于GEO卫星,还可直接由卫星的定点经度(即星下点经度)确定地影穿越的子夜时刻。
对于定点在λ的GEO卫星,由于GEO的静地特性,其卫星子夜就是该地的地方时子夜,且地影季内每天的卫星子夜时刻相同。因此,定点在东经120°的GEO卫星,该时刻恰为北京时间零时。
对于定点在λ的GEO,采用北京时间T8表示的卫星子夜时刻为
 (16)
(16)
若T8为负,则加24 h。
需要说明的是,这里的时刻均为平太阳时刻,若需要较高精度的分析,应考虑平太阳时与真太阳时之间的时差改正。
3.4 卫星偏航角常用的卫星星固系定义较多,其中与太阳指向相关的星固系定义为[3]:Z轴沿卫星信号发射天线方向指向地心;Y轴为太阳帆板旋转轴并垂直于太阳、地球和卫星所构成的平面;X轴垂直于Y轴和Z轴构成右手坐标系并背离太阳光入射方向。
卫星偏航角是卫星指向或背离太阳方向的投影偏离卫星轨道运动方向的角度[3, 6, 19]。在图 4中,卫星运动到S点,背离太阳(即指向卫星地影中心)的投影方向为+X方向,有偏航角ψ=π-∠N′SC。
在球面直角三角形CFS中,已知卫星轨道角μ=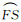
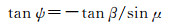 (17)
(17)
或者扩展反正切函数的取值范围至-π,π,有[18]
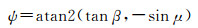 (18)
(18)
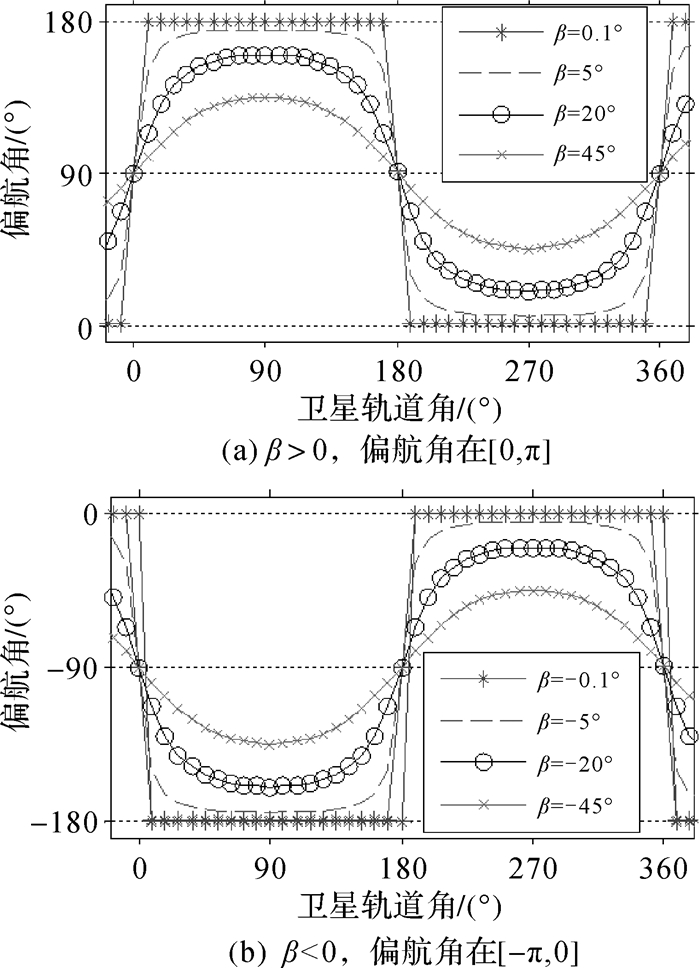
观察图 4可以看出,当β=0,太阳和卫星地影中心分别位于轨道面上的A和A′点。每当地影穿越的卫星子夜和正午时刻,指向卫星地影中心的方向均发生方向的逆转,即对应于图 5中β=±0.1°时,偏航角ψ由0到±π或±π到0的跳变。
|
| 图 5 偏航角与太阳β角和卫星轨道角的关系 Fig. 5 Relation of yaw attitude with solar β and the satellite time angle |
由式(18)计算偏航角速率,有[3]
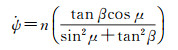 (19)
(19)
图 6是北斗MEO和IGSO卫星的偏航角速率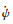

|
| 图 6 偏航角速率与太阳β角和卫星轨道角的关系 Fig. 6 Relation of the change rate of yaw attitude with solar β and the satellite time angle |
根据式(18)、式(19)和图 5、图 6,偏航姿态通常包括:
(1)动偏模式;太阳β角较大情况下,如图 5(a)中β=45°,随着卫星轨道角μ的周期变化,MEO和IGSO的偏航姿态ψ及其角速率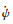
(2)零偏模式。由式(19)看出,在卫星子夜和正午(轨道角μ为0°和180°)时刻,有|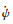
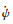
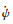
偏航姿态调整的动偏转零偏和零偏恢复为动偏,会对光压和卫星天线相位中心等的建模带来影响。注意动偏和零偏的转换并非一定与地影季始末时间一致,还与卫星姿态控制装置和控制策略相关。
4 试验和分析以北斗导航系统的混合星座为参考,分析GEO/IGSO/MEO 3类中高轨卫星的地影参数[3, 6]。3类轨道的偏心率均取为0,IGSO和MEO的轨道倾角为55°,取升交点赤经Ω∈0, π,MEO的半长轴为27 906 km。分析解的计算结果与STK仿真计算结果基本符合。
4.1 GEO的地影参数GEO的地影参数相对简单:
(1)一年两次的地影季均为46 d,最长地影日分别为春分日和秋分日,太阳β角的变化等于太阳赤纬的变化。
(2)定点经度分别为东经160°、140°、110.5°、84°和55°的GEO卫星,地影季内每天进出地影一次,且卫星子夜时刻即为其各自星下点经度的本地子夜时刻,分别为北京时间21:20/22:40/0:38/2:24/4:20;春/秋分日的地影持续时间最长,达到72 min,其中半影时间在前后两端,各2 min左右。
4.2 IGSO/MEO的地影参数图 7和图 8给出了IGSO/MEO的地影季和星蚀参数。可以看出:
(1)当不考虑摄动影响时,最长地影日仅与空间定向参数i, Ω有关,与轨道高度无关。因此,两类轨道的最长地影日基本相同,如图 7(a)所示。升交点赤经为零时,最长地影日为春/秋分日,随着升交点赤经的增加,最长地影日逐渐延后,当升交点赤经达到180°时,最长地影日回归春/秋分日。
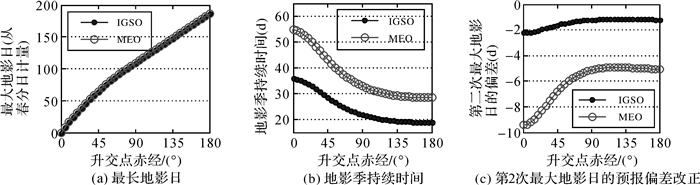
|
| 图 7 IGSO/MEO的卫星地影参数 Fig. 7 Satellite shadow parameters vs. the RAAN of IGSO/MEO |
(2) 图 7(b)给出了IGSO/MEO地影季天数与升交点赤经的关系。倾角55°的条件下,两类轨道均在升交点赤经为180°时地影季最短,此时黄道面与卫星轨道面的夹角βA达到最大值(i+ε)。因此若想缩短地影季,应考虑选取卫星轨道的升交点赤经在180°附近,从而尽量偏离黄道面。IGSO卫星地影季最短18 d,最长35 d;而MEO的卫星地影半径更大,其地影季比同一轨道面上的IGSO卫星要长,最短28 d,最长54 d。
(3) 图 7(c)是预报半年后的第2次最大地影日的摄动影响偏差。两类轨道的预报日期均比半年提前,提前量随升交点赤经的增加而减小;其中IGSO卫星受地球扁率摄动影响较小,仅提前1~2 d,而MEO卫星会有4~10 d的提前量。
(4) 图 8给出了升交点赤经为160°的MEO卫星在半个地影季内(14 d)每圈的子夜时刻和星蚀持续时间,分别用方框和圆点表示。MEO卫星的轨道周期12.887 h,基本上每天有两次星蚀,星蚀持续时间则由最长地影日的58 min减少到最短的12 min。
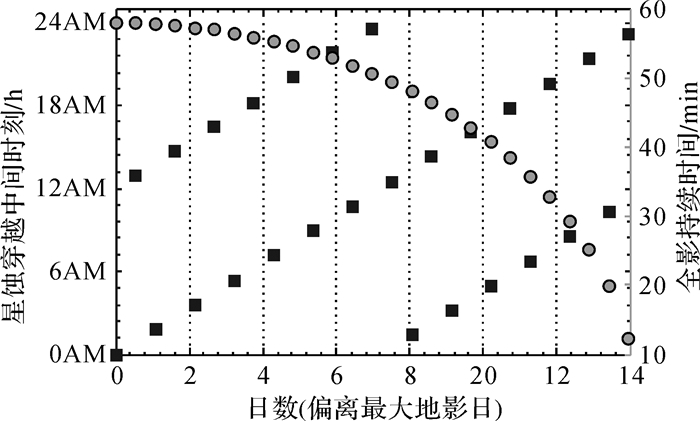
|
| 图 8 MEO子夜时刻(方框)和全影持续时间(圆点)的变化 Fig. 8 Variations of satellite midnights (square) and eclipsing periods (spot) |
需要指出的是,解析法既可以单独计算每颗导航卫星的星蚀参数,也能够为该类轨道计算整体星蚀规律性。例如本算例仅指定了IGSO/MEO的部分轨道参数,升交点赤经并未固定,因此可以快速地看出地影季和星蚀参数随不同轨道面的变化关系。
同理,利用解析法可以计算其他GNSS星座卫星的卫星地影和星蚀参数。
这里未采用定轨数值计算结果来对比解析法星蚀参数,一方面,定轨算法并不针对和涵盖各星蚀参数,此外,解析法的目的之一就是摆脱定轨算法,从建模原理和图形化理解星蚀问题。
5 结论在卫星轨道和姿态的确定及控制计算中,经常需要针对卫星进出地影时段进行大量的事先设计分析和事后的数据调试及建模优化等工作。对于大型成熟软件,通常针对具体卫星,逐一采用严格的日-地-卫星的位置计算(即日-地和地影-卫星的两步法),但是因为涉及大量的数值积分运算,并不适合对某类(如中高轨)卫星的大时间跨度的地影规律统计和计算。
本文依据日地和卫星三者的几何关系建立了卫星地影的一体化模型,并且利用地心赤道坐标系的YOZ平面投影进行了图形化表征,推导给出了常用地影参数的计算式和图形几何表达关系。该方法仅需要利用卫星的6个轨道根数,且顾及了一阶长期摄动对地影季预报的影响,因此,在保证分析精度的前提下,计算简单,形象直观,易于理解,尤其适合多GNSS星座的相关地影季数据快速判断和地影参数批量计算。
卫星地影的中心点位于黄道,且与太阳相对,其轨迹运动速率为太阳公转速率,但运动方向相反;卫星地影的半径由卫星高度处的地球和太阳视盘角半径决定,轨道越高,卫星地影半径越小。
对于GNSS的中高轨近圆导航卫星,依据卫星地影模型和轨道参数,可得出以下结论:
(1)中高轨卫星通常一年两次地影季,最长地影日是太阳经过卫星轨道与黄道两个交点的日期,两个最长地影日相隔半年左右。地影季持续天数由黄道面与卫星轨道面的夹角βA和卫星地影半径决定。地影季期间,太阳β角的绝对值先是从等于卫星地影半径逐渐减小至零,然后再逐渐增大直至超过卫星地影半径,从而结束地影季进入长期光照期。
(2)地影季期间,卫星每圈均过地影,其地影穿越过程称为星蚀。每次星蚀的子夜位置变化轨迹沿卫星轨道,且与卫星地影中心沿黄道的南北运动方向一致。根据星蚀的子夜位置变化可以计算得到近圆轨道每次星蚀进出时刻的变化规律。
(3)卫星轨道角和偏航角均与太阳指向方向有关。卫星轨道角是从卫星子夜时刻(远日点)开始计量的轨道快变量,可以根据太阳位置变化和近圆轨道快变量-幅角计算得到。偏航角的变化可以充分利用卫星地影模型进行图形化直观反映。
本文的分析建模方法适用于近圆轨道卫星,但是得到的卫星地影规律是针对中高轨卫星的。地影季参数与卫星轨道高度和轨道的空间定向参数(i, Ω)关系密切。随着轨道高度的降低,卫星地影半径和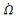
致谢: 特别感谢国家留学基金委对笔者在德国地学研究中心公派访学的资助。
| [1] | 毛悦, 宋小勇, 贾小林, 等. 北斗导航卫星地影状态分析[J]. 测绘学报, 2014, 43(4): 353–359. MAO Yue, SONG Xiaoyong, JIA Xiaolin, et al. Earth Eclipse Status Analysis of BeiDou Navigation Satellites[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(4): 353–359. DOI:10.13485/j.cnki.11-2089.2014.0053 |
| [2] | HUBAUX C, LEMAITRE A, DELSATE N, et al. Symplectic Integration of Space Debris Motion Considering Several Earth's Shadowing Models[J]. Advances in Space Research, 2012, 49(10): 1472–1486. DOI:10.1016/j.asr.2012.02.009 |
| [3] | 郭靖.姿态、光压和函数模型对导航卫星精密定轨影响的研究[D].武汉:武汉大学, 2014. GUO Jing. The Impacts of Attitude, Solar Radiation and Function Model on Precise Orbit Determination for GNSS Satellites[D]. Wuhan: Wuhan University, 2014. |
| [4] | GUO Jing, ZHAO Qile, GENG Tao, et al. Precise Orbit Determination for COMPASS IGSO Satellites during Yaw Maneuvers[M]//SUN Jiadong, JIAO Wenhai, WU Haitao, et al. China Satellite Navigation Conference (CSNC) 2013 Proceedings. Berlin Heidelberg: Springer, 2013: 41-53. |
| [5] | DAI Xiaolei, GE Maorong, LOU Yidong, et al. Estimating the Yaw-attitude of BDS IGSO and MEO Satellites[J]. Journal of Geodesy, 2015, 89(10): 1005–1018. DOI:10.1007/s00190-015-0829-x |
| [6] | 毛悦, 宋小勇, 王维, 等. IGSO姿态控制模式切换期间定轨策略研究[J]. 武汉大学学报(信息科学版), 2014, 39(11): 1352–1356. MAO Yue, SONG Xiaoyong, WANG Wei, et al. IGSO Satellite Orbit Determining Strategy Analysis with the Yaw-steering and Orbit Normal Attitude Control Mode Switching[J]. Geomatics and Information Science of Wuhan University, 2014, 39(11): 1352–1356. |
| [7] | 陈刘成. 地影模型对导航卫星轨道数值积分的影响及改进[J]. 武汉大学学报(信息科学版), 2007, 32(5): 450–453. CHEN Liucheng. How Navigation Satellite Orbit Numerical Integration Affected by Shadow Model and Its Correcting Methods[J]. Geomatics and Information Science of Wuhan University, 2007, 32(5): 450–453. |
| [8] | DILSSNER F, SPRINGER T, GIENGER G, et al. The GLONASS-M Satellite Yaw-attitude Model[J]. Advances in Space Research, 2011, 47(1): 160–171. DOI:10.1016/j.asr.2010.09.007 |
| [9] | STEIGENBERGER P, HAUSCHILD A, MONTENBRUCK O, et al. Orbit and Clock Determination of QZS-1 Based on the CONGO Network[J]. Navigation, 2013, 60(1): 31–40. DOI:10.1002/navi.v60.1 |
| [10] | 彭汉兵, 杨元喜, 王刚, 等. 星蚀期北斗卫星轨道性能分析--SLR检核结果[J]. 测绘学报, 2016, 45(6): 639–645. PENG Hanbing, YANG Yuanxi, WANG Gang, et al. Performance Analysis of BDS Satellite Orbits during Eclipse Periods: Results of Satellite Laser Ranging Validation[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(6): 639–645. DOI:10.11947/j.AGCS.2016.20150637 |
| [11] | 郑军, 陈宏, 李于衡. GEO卫星能源分系统状态切换时间精确预报算法[J]. 上海航天, 2011, 28(5): 30–33. ZHENG Jun, CHEN Hong, LI Yuheng. Algorithm Analysis on Energy System State Switch Time Accurate Prediction in GEO Satellite Eclipse[J]. Aerospace Shanghai, 2011, 28(5): 30–33. |
| [12] | LONGO C R O, RICKMAN S L. Method for the Calculation of Spacecraft Umbra and Penumbra Shadow Terminator Points[R]. NASA Technical Paper 3547, 1995. |
| [13] | MONTENBRUCK O, GILL E. Satellite Orbits: Models, Methods and Applications[M]. Berlin Heidelberg: Springer-Verlag, 2000. |
| [14] | BROUWER D, CLEMENCE G M. Methods of Celestial Mechanics[M]. London: Academic Press, 1961. |
| [15] | HUBAUX C, LIBERT A S, DELSATE N, et al. Influence of Earth's Shadowing Effects on Space Debris Stability[J]. Advances in Space Research, 2013, 51(1): 25–38. DOI:10.1016/j.asr.2012.08.011 |
| [16] | 苏宜. 天文学新概论[M]. 4版. 北京: 科学出版社, 2009. SU Yi. A Brief Introduction of Astronomy[M]. 4th ed. Beijing: Science Press, 2009. |
| [17] | 郑军, 鲍明涛, 王鑫, 等. 升交点赤经与轨道倾角对地球同步卫星地影的影响[J]. 上海航天, 2005, 22(3): 34–36. ZHENG Jun, BAO Mingtao, WANG Xin, et al. Affection of Longitude Ascending Node and Orbit Inclination on the Eclipse for Geosynchronous Satellite[J]. Aerospace Shanghai, 2005, 22(3): 34–36. |
| [18] | BAR-SEVER Y E. A New Model for GPS Yaw Attitude[J]. Journal of Geodesy, 1996, 70(11): 714–723. DOI:10.1007/BF00867149 |
| [19] | KOUBA J. A Simplified Yaw-attitude Model for Eclipsing GPS Satellites[J]. GPS Solutions, 2009, 13(1): 1–12. DOI:10.1007/s10291-008-0092-1 |
| [20] | MULLINS L D. Calculating Satellite Umbra/Penumbra Entry and Exit Positions and Times[J]. Journal of the Astronautical Sciences, 1991, 39: 411–422. |
| [21] | 张世杰, 曹喜滨. 卫星进/出地影位置和时间的计算算法[J]. 上海航天, 2001, 18(6): 9–22. ZHANG Shijie, CAO Xibin. Calculating Method of Satellite Entry and Exit Positions and Times through Umbra/Penumbra[J]. Aerospace Shanghai, 2001, 18(6): 9–22. |


