2. 信息工程大学地理空间信息学院, 河南 郑州 450001;
3. 海军工程大学导航工程系, 湖北 武汉 430033
2. Institute of Geospacial Information, Information Engineering University, Zhengzhou 450001, China;
3. Department of Navigation, Naval University of Engineering, Wuhan 430033, China
海洋重力场信息在大地测量学、空间科学、海洋学、地球物理学、地球动力学等诸多学科领域都具有重要的应用价值[1]。精化大地水准面一直是测定海洋重力场的主要目的之一。由于地球重力场与地球内部质量密切相关,因此海洋重力测量可为确定地球内部质量密度分布提供数据支持。海洋重力异常既可应用于地球动力学板块构造理论研究,又可应用于海底地壳年龄、地球内部质量迁移、板块冰后回跳等多种地球物理现象的解释。随着空间技术的发展,海洋重力测量的实用价值更加凸显,因为自然天体(月亮、行星)和人造天体(卫星、飞行器)的轨道计算都离不开地球重力场信息的支持。海洋重力测量在海洋矿产资源开发、惯性导航、水下匹配辅助导航等工程应用领域也发挥着非常重要的作用[2]。很显然,不同应用领域对海洋重力测量精确度、分辨率及覆盖域大小的需求是有区别的,很多时候这种区别还比较显著[3-4]。卫星测高反演重力和海面船载重力测量是当前获取海洋重力场信息的两种主要手段,虽然最新推出的卫星测高反演重力异常成果的网格间距已经达到1′×1′,其精度达到了±3~5 mGal (1 mGal=10-5 m/s2)[5],但这样的精度水平仍无法完全满足某些领域的应用需求。因此,海面船载重力测量仍然是目前获取高精度和高分辨率海洋重力场信息的重要手段。
沿预先设计好的测线作连续动态测量是海面船载测量作业模式的主要特点。如何依据不同目的的应用需求,规划最佳的测线布设方案是海洋重力测量技术设计的核心内容,此项工作在平衡测量成果质量和测量效率两个方面都发挥着重要甚至是决定性的作用[6-7]。在开展海洋重力测量初期,我国学者曾就测线布设问题作过比较深入的研究和探讨[8],但由于受当时资料条件和需求指标不明确的制约,大部分研究结论已经明显无法适应当今各个领域的应用需求。我国现行的国家和行业标准虽然对海洋重力测量测线布设都提出来了比较明确的技术要求[3-4],但针对具体的专题应用需求,目前还缺少完整而深入的研究论证工作,往往会导致测前技术设计的盲目性。为此,本文尝试从分析地球重力场对远程飞行器飞行轨迹的影响出发,重点围绕飞行轨道计算对地球重力场参数的保障需求,开展相应的海洋重力测量测线布设方案设计与论证。
1 重力场对远程飞行器落点的影响由文献[9-10]知,发动机和控制系统(包括制导系统和姿态稳定系统)是无人驾驶飞行器的两个重要组成部分,其作用是将飞行器沿预定的轨迹投送到预定的目标区。根据远程飞行器在飞行中的受力情况,一般将飞行轨迹划分为主动段和被动段两个部分,前者指从发射平台起飞到发动机主令关机点的一段飞行轨迹,后者是指从发动机主令关机点到飞行器着地的一段飞行轨迹(又分自由段和再入段)。在飞行轨迹的主动段,飞行器除了受到发动机推力和控制系统的调控作用外,还会受到空气动力、地球引力和由于地球自转引起的惯性力的影响。而在被动飞行阶段,飞行器则完全依靠在主动段终点获得的动能飞行,不再受发动机推力和控制系统的调控作用。因此,飞行器落点的精确度主要取决于控制系统在主动段终点获得的飞行器运动参数的可靠性。但确定运动参数的准确性又完全取决于飞行器在飞行过程中的受力分析、建模和计算。随着飞行器制造工艺和控制技术的不断突破和完善,地球重力扰动场计算误差已经成为限制飞行器落点精度进一步提高的主要因素[11-13]。因此,要想有效控制飞行器的落点偏差,必须首先解决地球外部空间特别是近地空间扰动引力场的精密计算问题。
地球重力场对飞行器落点的精度影响主要体现在两个方面:一是飞行器的初始定位(也叫初始化过程);二是飞行器的飞行控制。飞行器发射前必须对载体和控制系统传感器进行精确的垂直定位和定向,以建立制导坐标系。由于飞行器在发射台竖直及惯性系统标定过程都是以发射点的铅垂线为基准的,而飞行轨迹计算则是以发射点椭球法线为基准的发射坐标系作为参照系。因此,如果不对两者之间的差异(即垂线偏差)进行修正,必然会引起飞行器落点的偏差。理论分析和实际计算都表明[11-12],垂线偏差对飞行器落点的影响不仅与其量值大小有关,而且随发射点位置、射程和方位角的改变而变化。对于10 000 km左右射程的飞行器,1″垂线偏差的影响量一般不超过50 m。在飞行器的初始化阶段,除了载体的姿态影响因素外,发射点位置误差特别是高程分量误差对飞行器落点的影响也不容忽视。高程分量误差主要体现为高程异常计算误差,其影响大小既与飞行器的射程有关,又与飞行器的飞行轨道特性有关。根据理论分析估计[11-12],1 m高程异常误差对飞行器落点的影响一般不超过15 m。
在空中飞行阶段,飞行器始终受到地球重力异常场的作用,当计算飞行轨道使用的引力场模型存在误差时,也必然会引起飞行器落点产生一定的偏差,其影响量主要取决于飞行器射程大小和扰动引力场沿飞行轨迹的变化激烈程度。根据动力学原理,飞行器飞行轨迹可简单用下列的动力和运动方程组进行描述[10]
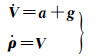 (1)
(1)
式中,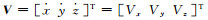
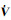
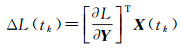 (2)
(2)
式中,tk代表主动段关机时刻;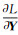
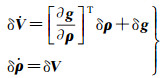 (3)
(3)
式中,δg代表地球重力加速度的扰动矢量。根据线性微分方程理论,采用状态转移矩阵,可导出上述摄动方程的解析表达式。考虑到对应于δVz、δx和δz的3项导航误差系数相对于其他3项系数要小的多,忽略它们的影响只会带来10 m左右的误差,这里直接给出射程偏差的简化估算公式如下[9]
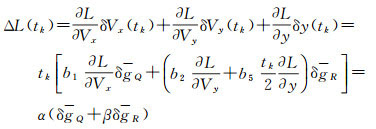 (4)
(4)
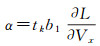 (5)
(5)
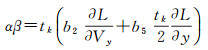 (6)
(6)
式中,δgQ=δgNcos A+δgEsin A;δgR、δgN和δgE分别代表扰动引力在北东天惯性坐标系中的3个分量沿飞行轨迹的积分平均值;A为射向角;b1、b2和b5为导航误差模型解系数,其大小主要与主动段关机时刻有关。通过对不同类别的飞行轨迹特性进行理论分析和数值计算,文献[9]给出了误差系数α和β的估值变化范围,具体见表 1。
| 射程L/km | 6000~7500 | 8000~9000 | 10 000 | 12 000 |
| α | 8.7~14.0 | 15.6~18.0 | 22~24 | 28 |
| β | 0.75~0.65 | 0.6~0.45 | 0.42~0.35 | 0.25 |
空中扰动引力一般由地面重力异常观测数据计算得到,其误差大小主要与地面数据的观测精度、密度及计算模型逼近度有关。假设扰动引力三分量计算误差之间没有显著的相关性,则由式(4)可得射程偏差的中误差为
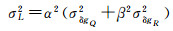 (7)
(7)
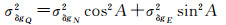 (8)
(8)
式中,σδgR、σδgN和σδgE分别代表扰动引力三分量的计算中误差。若近似取σδgR=σδgN=σδgE=σδg,则有
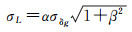 (9)
(9)
根据表 1给出的α和β估值,由式(7)可计算得到不同大小的扰动引力误差所引起的射程偏差变化情况,具体如表 2所示。
| m | ||||
| σδg /mGal |
射程L/km | |||
| 6000~7500 | 8000~9000 | 10 000 | 12 000 | |
| 3 | 33~50 | 55~59 | 72~76 | 87 |
| 4 | 44~67 | 73~79 | 95~102 | 115 |
| 5 | 54~83 | 91~99 | 119~127 | 144 |
| 6 | 65~100 | 109~118 | 143~153 | 173 |
| 30 | 326~501 | 546~592 | 716~763 | 866 |
| 50 | 544~835 | 910~987 | 1193~1271 | 1443 |
由表 2得知,如果忽略掉几十毫伽量值的扰动引力影响,那么可能给远程飞行器带来千米级的射程偏差。扰动引力场除了影响飞行器的主动段飞行外,对被动段飞行也会产生不可忽略的影响,但由于被动段飞行轨迹离地面较高,通常在200 km以上,与主动段相比,一方面扰动引力对被动段飞行的作用会相对减小,另一方面高空扰动引力的计算误差也相对容易控制。因此,在实际应用中,一般都以主动段扰动引力的计算精度要求作为地面或海面重力测量技术设计的基本依据。
根据当前及今后一个时期飞行器技术的发展水平和实际应用需求,笔者认为,将扰动引力场单一要素对10 000 km以上射程的飞行器落点偏差影响量限定为100 m的量值是比较适宜的。由表 2计算结果可以看出,如果以100 m作为限差量,那么扰动引力计算精度的要求应设定为:优于4 mGal。但由于在靠近发射点的低空段求得高精度的扰动引力参数要比高空段困难得多,在重力场变化激烈的区域要比变化相对平缓的区域困难得多。因此,对于扰动引力的计算精度要求,在不同区域、不同高度应有所区别,“优于4 mGal”可理解为一种平均精度要求。又由前面的论述得知,1 m高程异常误差对飞行器落点的影响一般不超过15 m,1″垂线偏差的影响量一般不超过50 m。显然,在当前的技术条件下,高程异常的计算精度完全能够满足飞行器落点偏差100 m的限差要求。而对于垂线偏差参量,根据重力场参数之间的泛函关系(即δgφ=-γξ和δgλ=-γη),2″垂线偏差的误差量相当于扰动引力水平分量10 mGal的偏差,这个量值已经远远超过前面的扰动引力4 mGal的精度要求。由此得知,只要确保扰动引力的计算精度满足“优于4 mGal”的要求,那么,2″垂线偏差的计算精度要求也自然会得到保障。
2 扰动引力计算精度估计 2.1 数据截断误差估计扰动引力计算误差主要由模型误差和数据误差两部分组成[1, 14-15],模型误差主要包括积分离散化误差、远区截断误差和数据截断误差,数据误差主要包括使用移去恢复技术引入的位系数误差和观测数据传播误差。为了突出主要影响因素,同时考虑到次要因素的可控性,这里重点讨论数据截断和数据观测两项误差对扰动引力计算精度的影响。
首先将扰动引力三分量的谱展开式表示为重力异常的n阶球谐函数式
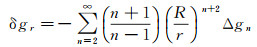 (10)
(10)
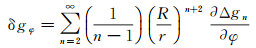 (11)
(11)
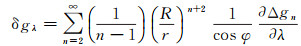 (12)
(12)
式中,R为地球椭球平均半径;r=R+h为地心向径;h为计算高度;(φ,λ)为计算点坐标;Δgn为重力异常的n阶球谐函数式
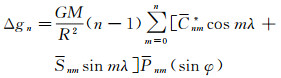 (13)
(13)
利用球函数的正交性和重力异常阶方差的定义,可写出扰动引力垂直和水平分量在某个频段上能量谱的全球均方值计算式
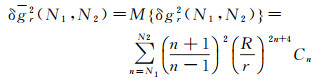 (14)
(14)
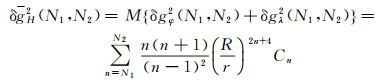 (15)
(15)
式中,(N1, N2)代表频段N1~N2;Cn为重力异常的阶方差,其计算式采用文献[16]推出的分段拟合模型
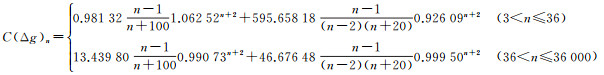 (16)
(16)
根据当前在计算重力场参数时惯用的地面数据分辨率组合[1, 17],由式(14)-(16)可计算得到扰动引力在相应频段的能量谱,具体见表 3。
| mGal | |||||||
| 频段(N1~N2) | 2~180 | 181~540 | 541~2160 | 2161~5400 | 5401~10 800 | 10 801~36 000 | |
| 对应数据分辨率 | 1° | 20′ | 5′ | 2′ | 1′ | 高于1′ | |
| δgr | h=0 km | 30.94 | 15.08 | 6.66 | 2.83 | 0.93 | 0.18 |
| h=1 km | 30.70 | 14.41 | 5.72 | 1.75 | 0.33 | 0.03 | |
| h=5 km | 29.81 | 12.06 | 3.32 | 0.31 | 0.01 | 0.00 | |
| δgH | h=0 km | 29.25 | 15.05 | 6.66 | 2.83 | 0.93 | 0.18 |
| h=1 km | 29.00 | 14.38 | 5.72 | 1.75 | 0.33 | 0.03 | |
| h=5 km | 28.07 | 12.04 | 3.32 | 0.31 | 0.01 | 0.00 | |
由表 3可以看出,计算扰动引力时,如果使用的数据分辨率截断到5′,那么截断误差可达到3 mGal;如果截断到2′,那么截断误差可减小到1 mGal。但由于表 3估计结果是全球意义上的平均值,在重力场变化特性比较突出的地区,实际截断误差可能存在较大的差异,特别是在陆部的山区和海部的海沟区域,由数据分辨率不够精细引起的截断误差可能远远大于表 3所列的估计值。因此,在实际应用中,应针对具体情况作具体分析和判断。就表 3的统计结果而言,如果以前面的扰动引力“优于4 mGal”计算精度要求为依据,那么至少应当采用精细到2′分辨率的地面观测数据。
2.2 数据传播误差估计根据文献[1, 14],可将扰动引力三分量的数值积分计算式表示为
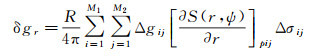 (17)
(17)
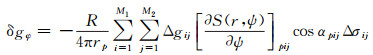 (18)
(18)
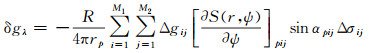 (19)
(19)
式中,p为计算点;Δgij代表地面网格平均重力异常;M1和M2分别代表纬线和经线方向的数据网格数;其他参量计算式为
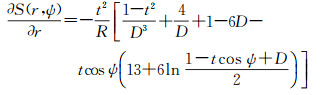
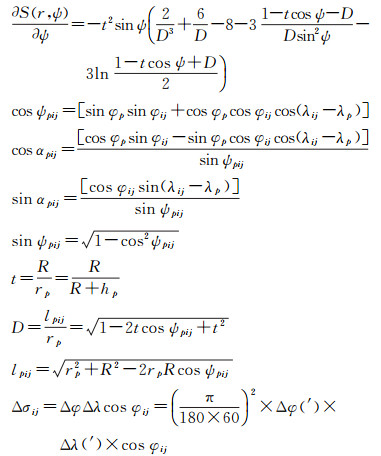
假设网格平均重力异常为等精度观测量,且相互独立,则根据误差传播律可得扰动引力的数据传播误差估计式为
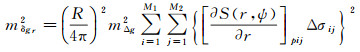 (20)
(20)
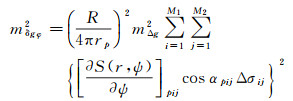 (21)
(21)
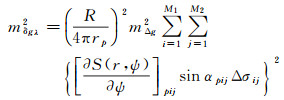 (22)
(22)
式中,mΔg代表地面平均重力异常的中误差。
这里以p(φ=40°, λ=120°)为计算点,以40°×40°为数据覆盖范围(此范围足以忽略积分远区影响)[15, 17],分别采用5′×5′、2′×2′和1′×1′ 3种网格数据,同时分别取mΔg=3、5、7 mGal,依次计算mδgr、mδgφ、mδgλ,具体见表 4。
| mGal | |||||||||
| 数据 | 5′×5′ | 2′×2′ | 1′×1′ | ||||||
| 误差 | 3 | 5 | 7 | 3 | 5 | 7 | 3 | 5 | 7 |
| mδgr | 0.008 | 0.014 | 0.021 | 0.004 | 0.006 | 0.008 | 0.002 | 0.003 | 0.005 |
| mδgφ | 1.536 | 2.560 | 3.584 | 1.534 | 2.557 | 3.577 | 1.534 | 2.556 | 3.576 |
| mδgλ | 1.246 | 2.077 | 2.905 | 1.245 | 2.074 | 2.904 | 1.244 | 2.073 | 2.903 |
由表 4可以看出,数据网格大小对数据误差传播几乎没有影响,但扰动引力数据传播误差随数据误差的增大而增大,当数据误差为5 mGal时,扰动引力计算误差已接近3 mGal。很显然,如果仍然以前面的4 mGal精度要求为基本依据,同时考虑数据截断误差等其他因素的综合影响,那么,5 mGal就应当是数据误差的限定指标。表 4结果同时显示,扰动引力径向分量的数据传播误差比两个水平分量要小几个数量级,这是因为当r→R时,径向分量计算核函数涉及的三维空间Dirac函数值趋近于零而导致计算结果失真的缘故。利用恒等式变换可以消除由三维空间Dirac函数引起的数值矛盾[1, 14]。这方面的内容已经超出本文的讨论范围,不再详述。
3 海洋重力测量测线布设由前面的论述得知,要想确保地球重力场单一扰动要素对空间飞行器落点的影响不超过100 m的限差,扰动引力三分量的计算精度必须优于4 mGal,由此要求地球表面重力异常观测量的数据分辨率应不低于2′×2′,网格平均重力异常精度应优于5 mGal。这样的要求对地面测点和海面测线布设又提出了什么样的量化约束指标,这是本文接下来需要研究解决的核心问题。需要指出的是,前面所指的网格数据精度既与重力异常的观测精度有关,又与计算网格内布设测点的数量和均匀度有关,前者主要取决于测量传感器的技术性能和作业模式,后者主要涉及作业效益和工作难度,取决于测量区域重力场的变化复杂程度。人们习惯上将后者称为网格数据的代表误差[18-19]。在陆地区域,由于重力观测误差远远小于网格平均值的代表误差,故在讨论网格数据精度时一般都忽略前者的影响,但在海洋区域,由于受测量动态效应的影响,重力观测误差明显增大,通常可达1~2 mGal[20-21],因此在讨论海洋重力网格数据精度时,必须同时顾及观测误差和代表误差的影响。
由文献[18-19]知,计算网格重力异常代表误差经验模型可表达为
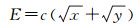 (23)
(23)
式中,x和y分别为计算网格的长、宽边长,单位为千米;c称为代表误差系数,主要体现网格区块内重力场变化的激烈程度。显然,对应于不同地形类别的区块,代表误差系数c应当取不同的数值,因为地球表面形状起伏直接反映地球重力场变化的不规则性。笔者利用最新卫星测高重力数据集,结合海洋重力实测资料,通过统计计算获得了对应于4种类别(1类--浅海大陆架;2类--海盆;3类--大陆坡;4类--岛弧、海山和海沟)海底地形的海洋重力异常代表误差模型(另文讨论),具体结果如表 5所示。
| 地形类别 | 1类 | 2类 | 3类 | 4类 |
| 误差系数c | 0.546 | 1.490 | 2.442 | 3.650 |
将表 5中的误差系数代入式(23)即可估算以网格内任意点观测值代表该网格平均值引起的代表误差。但当计算网格内存在一个以上重力测点时,网格数据代表误差估算公式需要作相应的改变。首先将面积为A=xy的网格等分为(n1×n2)个小网格,每个小网格的边长为(x/n1)和(y/n2),假设在每个小网格中均匀布设了一个重力测点,则对应于小网格的代表误差为
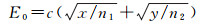 (24)
(24)
将分布于小网格的(n1×n2)个重力观测值取中数作为大网格的平均值,此时大网格的代表误差为
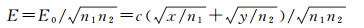 (25)
(25)
需要指出的是,式(25)只是一种理想条件下的误差估算公式,即必须保证每个小网格都存在一个重力测点。很显然,在实际应用中,无论是主观还是客观条件都很难满足这样的布点要求。现实中更为常见的情形是,在大网格中按一定要求布设了n个测点,这些测点分布有一定的规律性,但在二维空间不一定是均匀的。以测线测量方式获取海洋重力场信息的过程就属于这种情形,此时的重力测点集中分布在测线上,测线之间是空白区域,因此无法保证测点分布的均匀性。在这种情形下,可考虑采用两组近似公式来估算网格平均值的代表误差,一组是继续沿用前面的思路,即顾及重力测点的实际分布而忽略测点分布的均匀性,此时,n≠n1 n2,近似估算公式可表示为
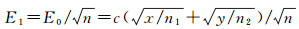 (26)
(26)
另一组是不顾及重力测点的实际分布但在理论上考虑了测点分布的均匀性,这一思路与目前陆地区域重力测点布设使用的代表误差估算公式相吻合,公式形式为[12, 19]
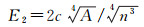 (27)
(27)
不难证明,当同时满足x=y、n1=n2、n=n1n2时,式(26)和式(27)将取得一致。
海面测量平台虽然能够以非常高的采样率(如1 Hz)沿测线进行重力信息采集,但由于受测量动态环境噪声的干扰和重力传感器测量能力的限制,这种超高采样率下的观测成果其实并没有太多实质性的意义。因为要想获取有效的重力场信息,必须采用低通滤波器对观测数据进行滤波处理,以剔除各类噪声干扰。因此,海洋重力测量的实际空间分辨率ρ(半波长λ/2)最终取决于数据滤波处理所采用的截止频率f(其倒数称为滤波尺度T)大小,它们与测量载体航行速度v之间的关系可表示为[22]
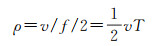 (28)
(28)
文献[4]规定,开展海洋重力测量时的航行速度应控制在18 kn以内,当滤波尺度取为T=200 s (正常取值)时,由式(28)可求得与其相对应的空间分辨率约为ρ=0.9 km。据此可以认为,在穿越2′×2′网格的测线段上至少拥有4个有效测点。按此推算,如果在2′×2′网格内均匀布设4条测线(间隔为0.5′,相当于测量比例尺1:10万,简称方案1),那么就表示每个网格至少拥有n=16个有效测点,相当于在每个0.5′×0.5′小网格内均匀布设了一个测点,此时n=n1n2;如果只在2′×2′网格内的一个方向上均匀布设2条测线(间隔为1′,相当于测量比例尺1:20万,简称方案2),那么就表示每个网格至少拥有n=8个有效测点,相当于只有一半数量的0.5′×0.5′小网格布设了测点,此时n≠n1n2;如果只在2′×2′网格内的一个方向上布设1条测线(间隔为2′,相当于测量比例尺1:40万,简称方案3),那么就表示每个网格至少拥有n=4个有效测点,相当于只有四分之一数量的0.5′×0.5′小网格布设了测点,此时n≠n1n2。这里分别就上述测线布设方案,依据表 5提供的代表误差系数,按照式(26)和式(27)依次计算了不同方案所对应的2′×2′网格重力代表误差估值,具体结果如表 6所示。
| mGal | |||||
| 地形类别 | 1类 | 2类 | 3类 | 4类 | |
| E1 | 方案1 | 0.259 | 0.707 | 1.158 | 1.731 |
| 方案2 | 0.366 | 1.000 | 1.638 | 2.448 | |
| 方案3 | 0.518 | 1.414 | 2.317 | 3.463 | |
| E2 | 方案1 | 0.259 | 0.707 | 1.158 | 1.731 |
| 方案2 | 0.436 | 1.189 | 1.948 | 2.912 | |
| 方案3 | 0.733 | 1.999 | 3.276 | 4.897 | |
从表 6结果可以看出,使用式(26)和式(27)进行误差估算时,3种测线布设方案所对应的2′×2′网格重力代表误差估值都不超过5 mGal。单就上述结果而言,在绝大多数海区,在2′×2′网格内布设1条测线就能满足网格重力平均值精度优于5 mGal的指标要求。但实际情况并非这么简单,首先是前面使用的两组误差估算公式都是近似公式,它们给出的估计值普遍过于乐观,其原因之一是:两组误差估算公式都来源于最基础的代表误差经验模型即式(23),而已有的统计分析研究结果已经证实[12],式(23)的最佳适用条件是:10 km≤x, y≤50 km。当x, y < 10 km时,由式(23)给出的估算值通常偏小;而当x, y>50 km时,由式(23)给出的估算值又通常偏大。本文讨论的2′×2′网格及其内部的小网格边长都远远小于10 km,故可以推断表 6给出的误差估值是偏小的。原因之二是:除了方案1外,两组误差公式给出的估算值都没有顾及测点分布的非均匀性,由此带来的误差估计偏差不容忽视,但相比较而言,理论上第1组公式的估算结果要比第2组公式更可靠一些。其次是表 5给出的代表误差系数来源于大量的统计分析结果,是一种平均值参数,主要反映该参数的统计特性,很难反映局部重力场变化的全貌,因此,制定测线布设方案时应适当考虑在地形变化比较剧烈的区域增加一定的保险系数(即在原估值上乘以一个略大于1的系数,其效果相当于将表 6结果按比例略加放大),以补偿由统计代表误差系数带来的平滑效应。此外,海洋重力网格数据精度估计除了要考虑代表误差因素外,还应考虑重力测点观测误差的影响。因此,如果综合考虑上面所述的各种影响因素,同时考虑前面将线状测量转换为点状测量过程可能存在一定的余量因素,那么,为了保证海洋2′×2′网格平均重力异常精度优于5 mGal,比较稳妥的重力测线布设方案应当是:在1类和2类海区使用方案3,即在2′×2′网格中央布设1条测线;在3类和4类海区使用方案2,即在2′×2′网格内均匀布设2条测线。文献[4]规定的重力测线布设密度指标为:飞行器发射首区测线间隔1′,常规测量测线间隔2′。由此可见,在某种意义上,本文给出的布设方案与文献[4]的规定是相吻合的,前面的分析论证也从另一个侧面证明现行国军标规定的测线布设密度指标是合理可行的。
综合前面的分析、论证、计算和讨论,可得出以下基本结论:
(1)地球重力扰动对远程飞行器飞行轨迹具有不可忽略的影响,几十毫伽量值的扰动引力可给远程飞行器带来千米级的落点偏差;如果以100 m作为飞行器落点偏差的限差量,那么扰动引力计算精度的限定指标为优于4 mGal。
(2)要想使扰动引力的计算精度达到4 mGal限定指标,地面重力异常的观测分辨率至少应当精细到2′×2′,相应网格平均重力异常的测量精度应优于5 mGal。
(3)要想使2′×2′网格平均重力异常的计算精度达到5 mGal限定指标,在地形变化比较平坦的1类和2类海区,应在2′×2′网格内至少布设1条海洋重力测线;在地形变化比较激烈的3类和4类海区,应在2′×2′网格内至少布设2条海洋重力测线。
4 结语针对远程飞行器飞行轨道控制重力场保障需求,本文开展了空中扰动引力计算和地面重力异常测量精度指标及海洋重力测量测线布设方案的设计、分析与论证工作,得出了一些具有量化指标的初步结论,为制定海洋重力场保障规划和海上作业方案提供了必要的理论支撑。这里需要补充说明的是,由于干扰飞行器飞行轨迹的误差源种类繁多,影响海洋重力测量精度的环境因素也相当复杂多变,飞行器落点偏差、海洋重力测量精度与海上测线布设密度之间的对应关系,只能使用某种简化的方式及一些经验公式来进行描述和估算,由此得到的量化指标不具有绝对的代表性和精准性,只能作为制定海上作业技术方案的参考。因此,从这个意义上讲,本文的工作仍然是初步的,下一步需要利用海上测量积累的实测数据,对不同的布设方案进行验证、分析和评价,并提出相应的修正意见和建议,最终目标是形成比较完整的海洋重力场保障技术体系。
| [1] | 黄谟涛, 翟国君, 管铮, 等. 海洋重力场测定及其应用[M]. 北京: 测绘出版社, 2005. HUANG Motao, ZHAI Guojun, GUAN Zheng, et al. The Determination and Application of Marine Gravity Field[M]. Beijing: Surveying and Mapping Press, 2005. |
| [2] | 黄谟涛, 翟国君, 欧阳永忠, 等. 海洋磁场重力场信息军事应用研究现状与展望[J]. 海洋测绘, 2011, 31(1): 71–76. HUANG Motao, ZHAI Guojun, OUYANG Yongzhong, et al. Prospects and Development in the Military Applications of Marine Gravity and Magnetic Information[J]. Hydrographic Surveying and Charting, 2011, 31(1): 71–76. |
| [3] | 中华人民共和国国家质量监督检疫总局. GB/T 12763.8-2007海洋调查规范第8部分:海洋地质地球物理调查[S].北京:中国标准出版社, 2008. General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China.GB/T 12763.8-2007 Specifications for Oceanographic Survey-Part 8: Marine Geology and Geophysics Survey[S]. Beijing: China Standard Press, 2008. |
| [4] | GJB 890A-2008海洋重力测量规范[S].北京:总装备部军标出版发行部, 2008. GJB 890A-2008 Specification for Marine Gravity Survey[S].Beijing: Military Standard Press of the Headquarters of General Equipment, 2008. |
| [5] | ANDERSEN O B, KNUDSEN P, BERRY P A M. The DNSC08GRA Global Marine Gravity Field from Double Retracked Satellite Altimetry[J]. Journal of Geodesy, 2010, 84(3): 191–199. DOI:10.1007/s00190-009-0355-9 |
| [6] | 石磐, 孙中苗. 航空重力测量的测线设计[J]. 测绘科学与工程, 2003, 23(2): 5–8. SHI Pan, SUN Zhongmiao. Survey-Line Design for Airborne Gravimetry[J]. Geomatics Science and Engineering, 2003, 23(2): 5–8. |
| [7] | 边刚, 金绍华, 夏伟, 等. 线性插值的海洋磁力测量测线布设评价方法[J]. 测绘学报, 2014, 43(7): 675–680. BIAN Gang, JIN Shaohua, XIA Wei, et al. Evaluating Method of the Survey Line Layout Based on the Linear Interpolation in Marine Magnetic Survey[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(7): 675–680. DOI:10.13485/j.cnki.11-2089.2014.0115 |
| [8] | 黄谟涛. 论海洋重力测线布设[J]. 海洋测绘, 1988(4): 31–35. HUANG Motao. On the Design of Surveying Line for Marine Gravimetry[J]. Hydrographic Surveying and Charting, 1988(4): 31–35. |
| [9] | 陈国强. 异常重力场中飞行器动力学[M]. 长沙: 国防科技大学出版社, 1982. CHEN Guoqiang. Spacecraft Dynamics in Gravity Anomaly Field[M]. Changsha: National University of Defense Technology Press, 1982. |
| [10] | 贾沛然, 陈克俊, 何力. 远程火箭弹道学[M]. 长沙: 国防科技大学出版社, 1993. JIA Peiran, CHEN Kejun, HE Li. Long Range Rocket Ballistics[M]. Changsha: National University of Defense Technology Press, 1993. |
| [11] | 黄谟涛.潜地战略导弹弹道扰动引力计算与研究[D].郑州:解放军测绘学院, 1991. HUANG Motao.Calculation and Study of Gravity Disturbances in Ballistic Computation for Strategic Submarine Missile[D]. Zhengzhou: PLA Institute of Surveying and Mapping, 1991. |
| [12] | 陆仲连, 吴晓平, 丁行斌, 等. 弹道导弹重力学[M]. 北京: 八一出版社, 1993. LU Zhonglian, WU Xiaoping, DING Xingbin, et al. Gravimetry in Ballistic Missile[M]. Beijing: Bayi Press, 1993. |
| [13] | 张金槐, 贾沛然, 唐雪梅, 等. 远程火箭精度分析与评估[M]. 长沙: 国防科技大学出版社, 1995. ZHANG Jinhuai, JIA Peiran, TANG Xuemei, et al. Accuracy Analysis and Evaluation for Long Range Rocket[M]. Changsha: National University of Defense Technology Press, 1995. |
| [14] | HEISKANEN W A, MORITZ H. Physical Geodesy[M]. San Francisco: Freeman W H and Company, 1967. |
| [15] | ZHANG Chuanding, LU Zhonglian, WU Xiaoping. Truncation Error Formulae for the Disturbing Gravity Vector[J]. Journal of Geodesy, 1998, 72(3): 119–123. DOI:10.1007/s001900050153 |
| [16] | 翟振和, 任红飞, 孙中苗. 重力异常阶方差模型的构建及在扰动场元频谱特征计算中的应用[J]. 测绘学报, 2012, 41(2): 159–164. ZHAI Zhenhe, REN Hongfei, SUN Zhongmiao. Construction of Gravity Anomaly Degree Variance Model and Application in Computation of Spectral Sensitivity of Disturbing Gravity Functions[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(2): 159–164. |
| [17] | 吴晓平. 在推求地球外部扰动重力场中数据的采用[J]. 测绘学院学报, 1992(4): 1–10. WU Xiaoping. Applications of Data in the Determination of the External Disturbing Gravity Field outside the Earth[J]. Journal of the Institute of Surveying and Mapping, 1992(4): 1–10. |
| [18] | 管泽霖, 宁津生. 地球形状及外部重力场[M]. 北京: 测绘出版社, 1981. GUAN Zelin, NING Jinsheng. Shape of the Earth and Its External Gravity Field[M]. Beijing: Surveying and Mapping Press, 1981. |
| [19] | 陆仲连. 地球重力场理论与方法[M]. 北京: 解放军出版社, 1996. LU Zhonglian. Theory and Method of the Earth's Gravity Field[M]. Beijing: PLA Publishing House, 1996. |
| [20] | 欧阳永忠.海空重力测量数据处理关键技术研究[D].武汉:武汉大学, 2013. OUYANG Yongzhong.On Key Technologies of Data Processing for Air-sea Gravity Surveys[D]. Wuhan: Wuhan University, 2013. http://mall.cnki.net/magazine/Article/CHXB201404018.htm |
| [21] | 黄谟涛, 刘敏, 孙岚, 等. 海洋重力测量动态环境效应分析与补偿[J]. 海洋测绘, 2015, 35(1): 1–6. HUANG Motao, LIU Min, SUN Lan, et al. Compensation and Analysis of Dynamic Environment Effect on Marine Gravimetry[J]. Hydrographic Surveying and Charting, 2015, 35(1): 1–6. |
| [22] | 孙中苗, 翟振和, 李迎春. 航空重力测量的分辨率和精度分析[J]. 地球物理学进展, 2010, 25(3): 795–798. SUN Zhongmiao, ZHAI Zhenhe, LI Yingchun. Analysis on the Resolution and Accuracy of Airborne Gravity Survey[J]. Progress in Geophysics, 2010, 25(3): 795–798. |


