面目标空间聚类旨在通过计算面目标间的相似性来识别具有近似特征或聚集分布模式的面目标集合,进而有效地发现地理实体的空间分异规律,广泛运用于城市功能区划[1-2]、面状地物的制图综合[3-5]、聚落或城镇结构扩张分析[6]等领域。面目标间的相似性分为空间信息相似性和非空间信息相似性,前者根据空间认知原理与格式塔完形原则,主要涉及面目标的方向、尺寸、形状、位置邻近等几何信息的相似性[7-8];后者则针对面目标功能、性质、状态等的类似程度进行定性描述。不同的信息相似性需根据不同的应用导向进行选取和计算,非空间信息相似性常用于目标的类型识别与分类领域,一般采用传统聚类分析中的角度系数、相关系数、指数相似系数、匹配测度等进行测算[9]。而空间信息主要用于目标形状与分布的一致性或聚集性识别,其中,方向相似性或以面目标顶点计算标准差椭圆,或以最长边法、加权平分线法、最小外接矩形法等计算建筑物的墙的方向来计算[10];尺寸相似性采用面目标的周长、面积或最小外接矩形的宽长比等方式计算;形状相似性可通过面目标边数、角度、维数等进行衡量;位置相似性则是点目标位置距离测算的扩展,在克服面目标因不规则形状导致的距离不确定性的基础上,准确计算目标的位置接近程度。
面目标的聚集性识别中,位置相似性的准确判断是空间聚类的核心问题,研究以准确发现面目标位置分布的聚集模式为切入点,通过分析现有的目标位置相似性测算方法,构建不受面目标形状、尺寸限制,且在空间障碍实体约束条件下,能准确识别并测算面目标位置接近程度的相似性准则。
1 面目标的位置相似性研究进展空间事物或现象的属性、功能、关系等相互牵引与驱动,使其位置分布具有显著的空间异质性,以面状目标表示则呈现聚集分布且有意义的面目标簇,如聚落、建筑群、石漠化区等。面目标的位置相似性是对面目标聚集程度进行有效衡量的重要指标,纵观已有的面目标空间聚类研究,主要从距离与拓扑关系两方面判断面目标的位置相似性。
1.1 距离测算距离测算是通过计算面目标间的局部距离和边界距离等来定义位置相似性。
局部距离是通过计算面目标的质心、最近点[11-12]或最远点间的欧氏距离来判断其位置远近,但方法忽略了面目标面积的限制。以质心距离为例(图 1),面目标A1、A2、A3,对应质心为P1、P2、P3,经目视判读可得,相较于A1到A2的距离,A1与A3更为靠近,但以质心距离计算得到P1与P3间的距离大于P1与P2间的距离,与空间认知不符,因而质心距离对面目标位置相似性的判断具有局限性。同理,最值距离也受到目标尺寸的影响。
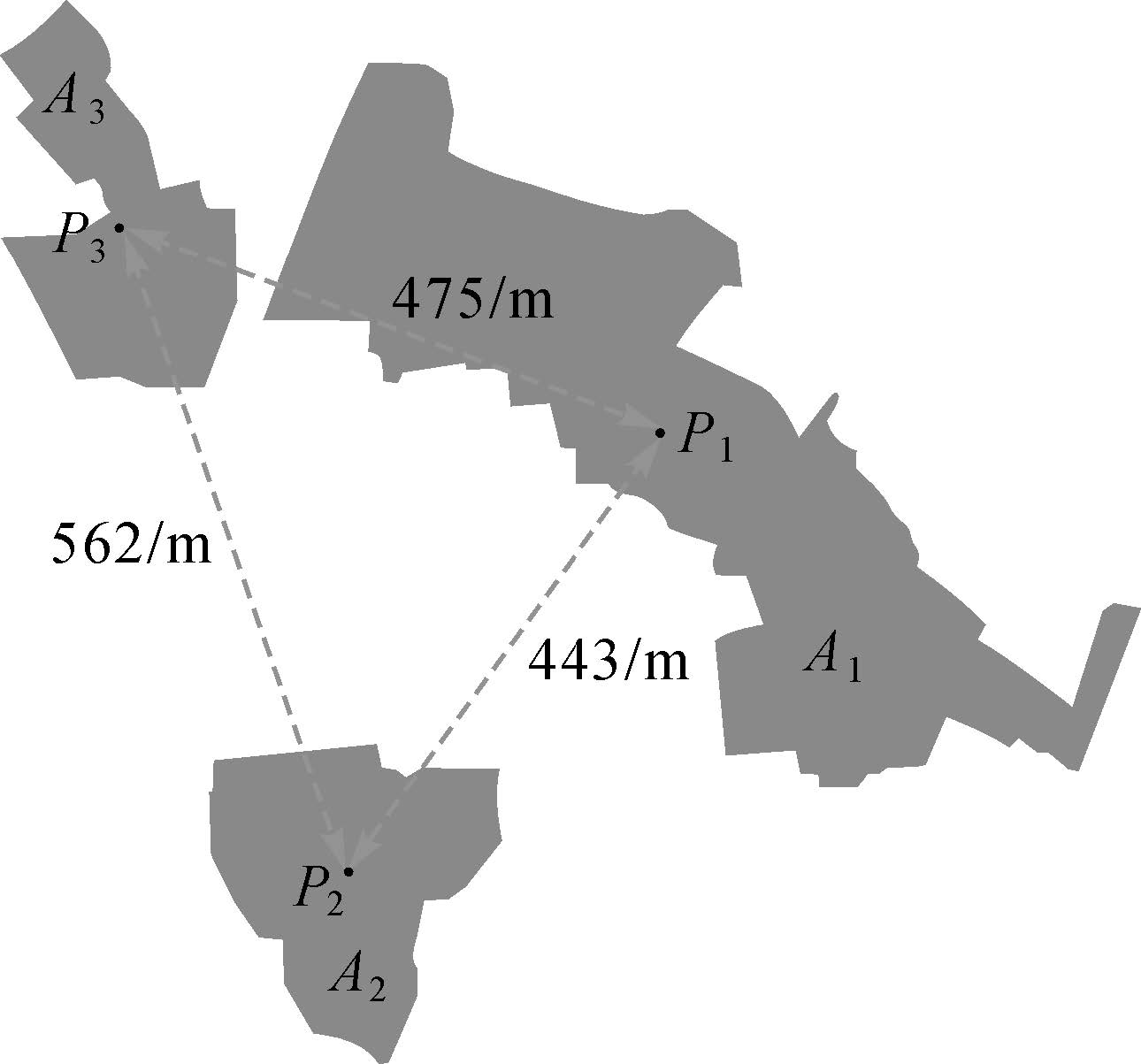
|
| 图 1 质心距离的计算 Fig. 1 The calculation of centroid distance between polygons |
边界距离是通过提取面目标边界的特征点对,采用Hausdorff距离[13-14]、改进Hausdorff距离[15-17]、平均距离[18]以及栅格距离[19]等计算目标间的位置相似性,但面目标的不规则几何形状导致难以准确找到距离为最值处的几何点对,且几何点对的数量随面目标数量的增加呈倍数增长,当空间数据量大且聚类算法迭代次数多时,会导致距离计算的时间复杂度大大增加。为提升算法效率,也有部分算法以最小外包矩形简化面目标边界[20],但易造成图形信息的损失,甚至产生拓扑关系的错误。同时,平均距离采用Delaunay三角网剖分目标,并计算目标间公共三角网边的平均长度[7],所得距离精度与边界点的内插步长相关,计算准确度与效率难以有效平衡;而栅格距离在将矢量数据二值图像化处理过程中,也存在信息和精度损失。
1.2 拓扑关系测算拓扑关系测算是以面目标间的拓扑关系判断位置相似性,GDBSCAN(generalizing density-based spatial clustering of applications with noise)算法[21]采用相交或相遇的空间关系判断面目标的邻近关系,但缺乏对相离空间目标的处理;DBCANESO(density-based clustering algorithm with noise for extended spatial objects)算法[22]以目标缓冲区内包含目标的面积与目标缓冲区面积的比值计算密度值作为相似性,存在缓冲区半径设置缺乏依据且主观性强的问题;SCGML_IR(spatial clustering in geography markup language data based on inclusion relations)和SCGML_IR*算法[23]根据GML(geography markup language)文档判断点/线/面目标之间的包含关系作为相似性度量准则,但算法以特定数据源和单一拓扑关系作为判断准则,应用较为局限。
综上所述,面目标的位置相似性计算既需要克服自身尺寸和形状的影响,又需尽可能准确并高效地测算目标间位置的接近程度。同时考虑到空间障碍阻隔了面目标聚集分布的连续性,相似性的判断也需要对障碍进行识别与区分。在目标几何信息和空间障碍的双重约束下,研究选择扩展点目标多尺度聚类方法(multi-scale spatial clustering,MSSC)[24]进行面目标的聚类分析,原因有以下几点:Voronoi图在无需简化不规则多边形边界的情况下,能够对面目标进行整体剖分,符合格式塔原理的连续性和闭合性定律[25],既不会造成图形信息损失,又能准确提取目标的邻近关系;Voronoi图在“颈”和“链”目标处的势力范围远大于聚集目标,易于识别“颈”和“链”目标;MSSC方法在无须用户自定义参数的基础上实现目标的多尺度聚类,具有较好的自适应性。鉴于此,研究以Voronoi邻近关系判断面目标间、面目标与障碍间的通达性;通过对比分析面目标的几何特征对其位置聚集性的影响,构建了强度函数以计算面目标与其邻近目标的聚集性强弱来表征位置相似性;最后采用评价指数对聚类质量进行评估。
2 强度函数的构建根据地理学第一定律[26]阐述,目标距离越近,关联程度越强,本文通过对比分析,构建适宜的强度函数以识别空间障碍约束下位置关联性强、聚集程度高的不规则面目标集合。
2.1 指标的对比分析MSSC方法验证了点目标位置分布与其Voronoi图空间格局之间的密切相关,当点目标的位置分布越密集时,生成的Voronoi势力范围越小,由此可得,以空间目标为生长元所得到的Voronoi多边形的面积是判断目标分布特征的重要指标之一。但与零维点目标不同,面目标属于二维对象,其Voronoi图的剖分格局除了受生长元位置影响外,还依赖于目标自身不规则形状与尺寸的约束。本文采用Voronoi图对面目标的势力范围进行剖分,在完整包含面目标的同时,Voronoi图不仅充分表达了目标的不规则几何形状特征,而且能够通过Voronoi图的一阶邻近特性判断面目标在空间障碍约束下的通视情况;进而,结合目标尺寸约束下Voronoi面积变化的分析,以确定目标位置的接近程度。
研究选择“面目标Voronoi面积”“面积差”和“比率”3项指标进行对比分析,旨在寻求不同离散程度、不同目标尺寸大小下,能稳定判断面目标聚集特征的计算方法。其中,“面积差”表示面目标的Voronoi面积与自身面积的差值;“比率”表示面积差与面目标周长的比值,为清晰显示指标对比结果,当存在右坐标轴时,“比率”指标值由右坐标轴显示。
(1) 相同目标尺寸,不同离散程度分布的指标变化。图 2(a)中存在21个尺寸一致的面目标,细线表示Voronoi边,经目视判读,面目标1-9属于聚集分布,10-21的分布相对分散。对应于“面目标Voronoi面积”“面积差”和“比率”3项指标的变化趋势如图 2(b)所示,皆表现为目标在不同聚集程度分布下,指标值随聚集程度的减弱而数值增大,同一聚集程度分布下,指标值会因边界和转角的分布而略有增加,但指标值仍远小于离散分布的目标。
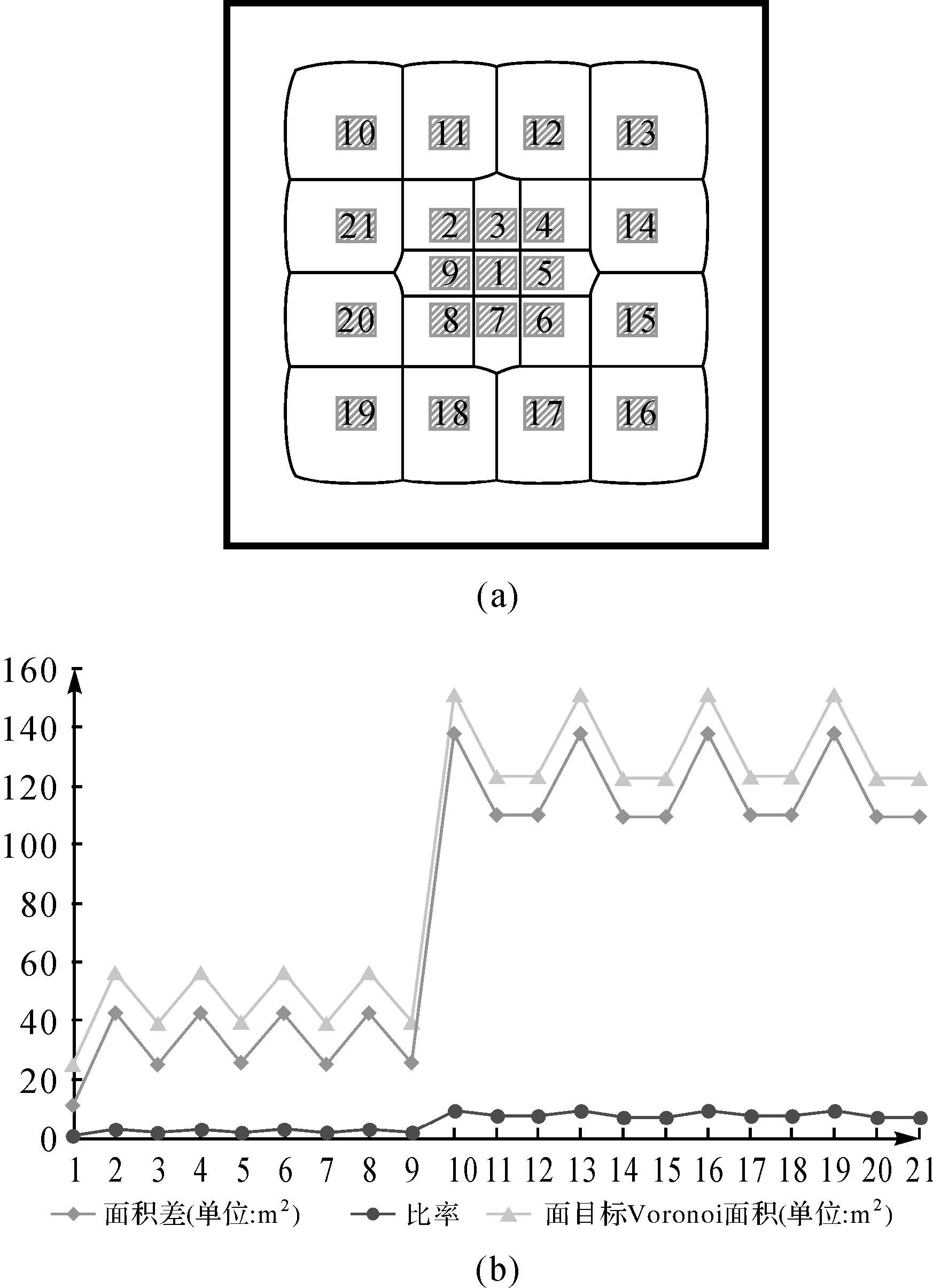
|
| 图 2 相同目标尺寸下的指标变化 Fig. 2 Changes of indicators under given object size |
(2) 相同离散程度分布,不同目标尺寸的指标变化。图 3(a)中存在13个尺寸不同但等距离分布的面目标,细线表示Voronoi边,经目视判读,所有面目标均匀分布,应具有相同的位置相似性,即指标值应近似相等。对应于“面目标Voronoi面积”“面积差”和“比率”3项指标值的变化趋势(图 3(b)),表现为:“面目标Voronoi面积”和“面积差”随面目标尺寸的增大而指标值增加,相较而言,“面积差”的增加幅度较弱,但两者在判断目标位置相似性时,易受到目标自身尺寸大小的影响,准确度低。而“比率”指标加入了对目标面积和周长的约束,指标值近似相等,在不受面目标尺寸影响的情况下,能准确反映目标的分布特性,较为稳定。
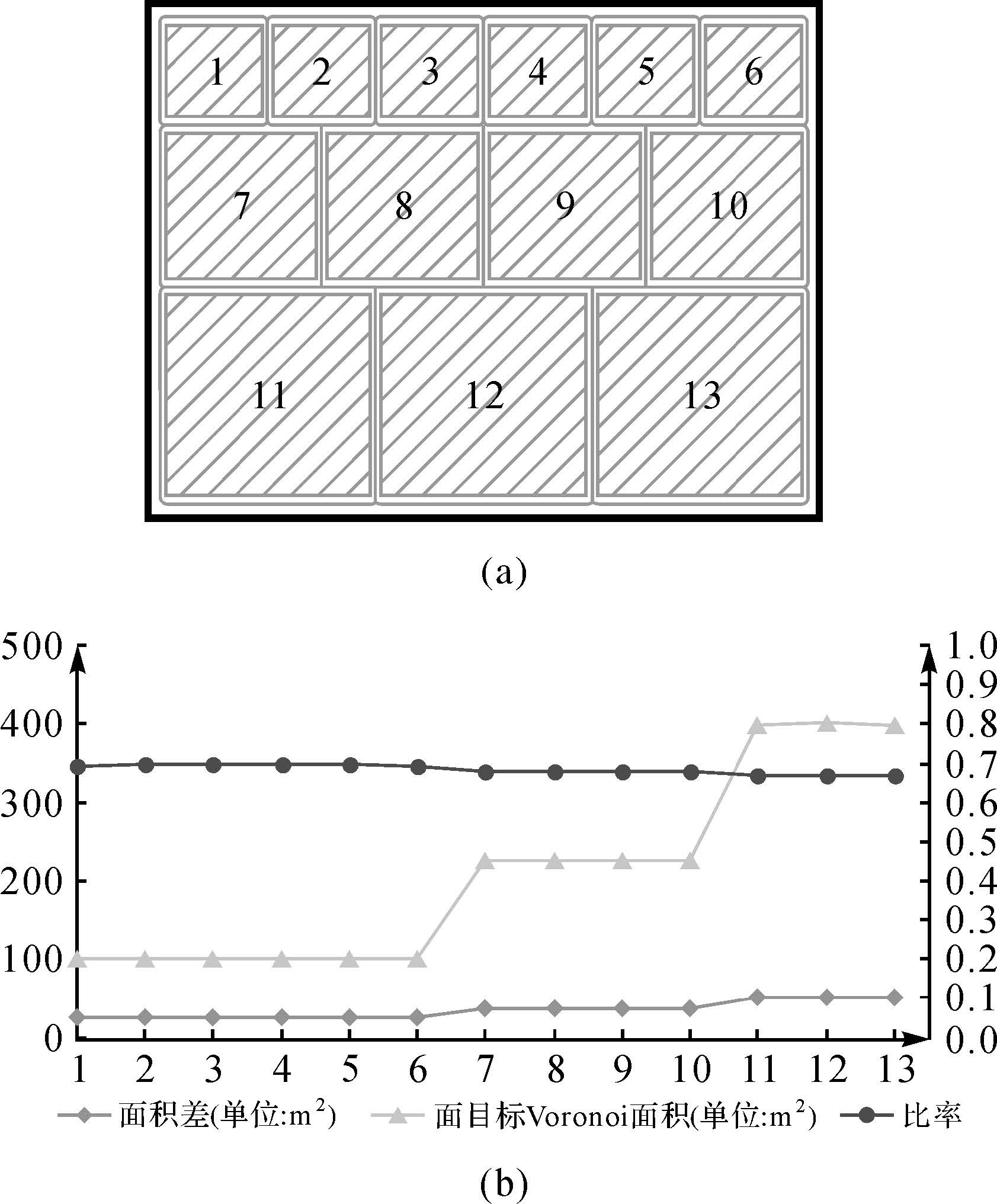
|
| 图 3 相同离散程度下的指标变化 Fig. 3 Changes of indicators under the uniform distribution of objects |
(3) 不同目标尺寸、不同离散程度且带空间障碍约束下的指标变化。图 4(a)中存在不均匀分布的面目标1-39和线状障碍40,经目视判读,面目标1-35属于聚集分布,36-39属于离群分布,也称离群目标。对应于“面目标Voronoi面积”“面积差”和“比率”3项指标值的变化趋势如图 4(b),针对离群目标36-39和空间障碍40而言,因目标的Voronoi面积较大,导致3项指标的值远远大于聚集分布的目标,易于区分和提取。但对于聚集分布的目标1-35而言,研究将位于面簇内部,即其Voronoi一阶邻近目标皆为同类目标的面目标称作类内目标,如目标1-17;将位于面簇边界,即其Voronoi一阶邻近目标中至少包含一个非类内目标(空间障碍、离群目标或其他类目标)的面目标称作类边界目标,如目标18-35。类内目标中,“面目标Voronoi面积”和“面积差”指标的值随面目标面积或延展性的增加而增大,存在波动,如目标3、4、11、14等,而“比率”指标不受面目标尺寸影响,一直保持相对较小且近于稳定的值,能较好地识别类内目标。类边界目标的3个指标变化皆受到类边界目标与非类内目标分布趋势的影响,指标值极不稳定,如目标26和29的指标值相差较大,难以直接通过指标值的大小判断。但值得注意的是,类边界目标的Voronoi一阶邻近目标中至少包含一个类内目标,且与“比率”指标值较小的类内目标存在高度聚集性,可识别为同类,因此,当依据“比率”指标值识别得到类内目标后,可将类边界目标与其Voronoi一阶邻近目标中“比率”指标值最小的类内目标划为同类。
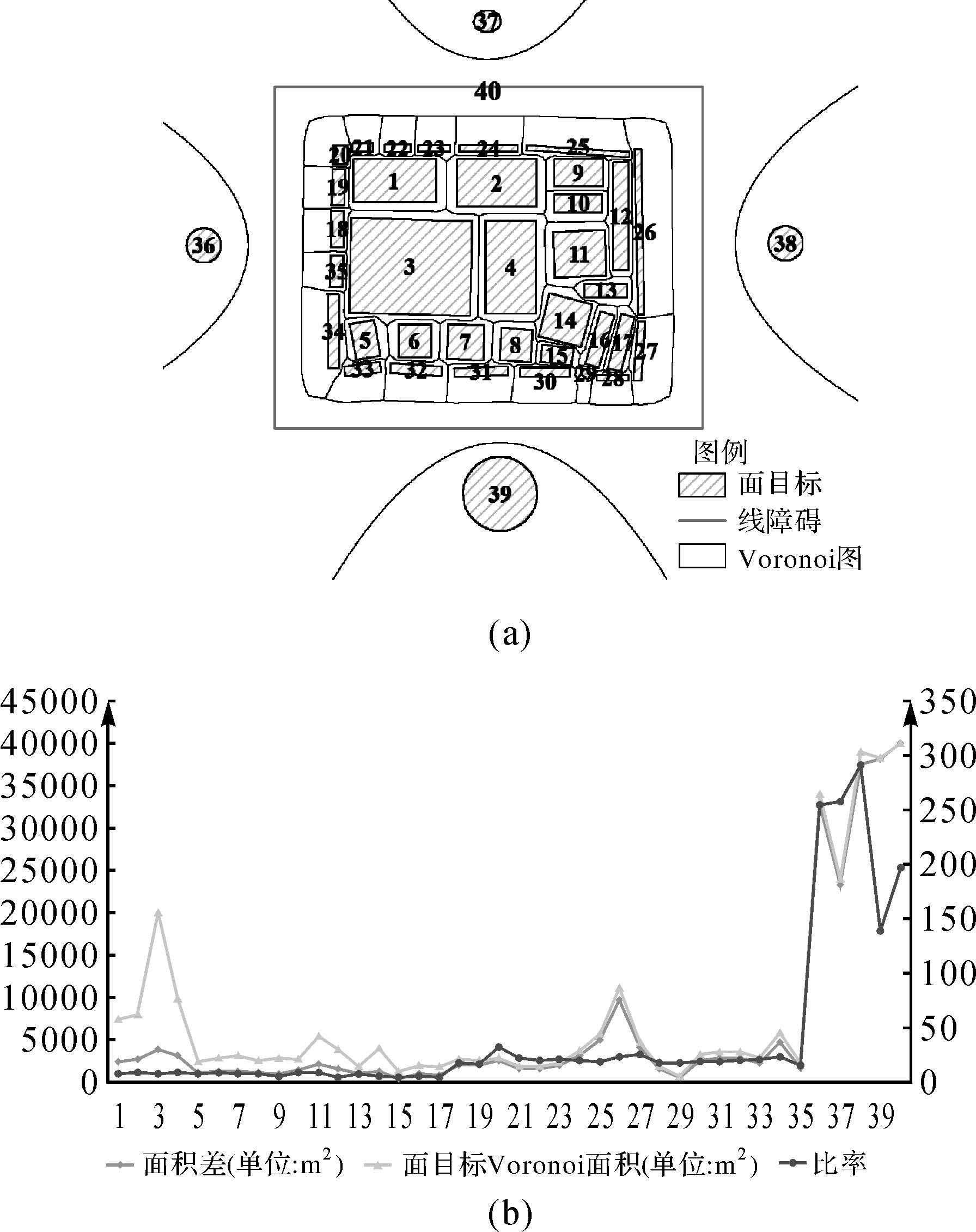
|
| 图 4 障碍约束下的指标变化 Fig. 4 Changes of indicators with obstacles |
2.2 强度函数的定义和值域分析
根据以上3项指标的对比分析,“比率”指标对面目标位置聚集程度的判断准确且稳定,顾以其作为面目标位置相似性计算的方式,称作强度函数。
定义1:面目标的强度函数:面目标集合A= {a1,a2,…,an} ⊂R2,其作为生长元生成的Voronoi图集合记为V(A)= {av1,av2,…,anv}⊂R2,ai∈A,则面目标ai的强度函数f(ai)等于Voronoi多边形面积area(aiv)与面目标面积area(ai)之差和面目标周长perimeter(ai)的比值:
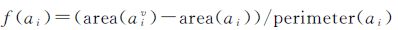 (1)
(1)
面目标的强度函数值越小,表示面目标与周围面目标的聚集性越强;反之,面目标强度函数值越大,表示面目标与周围的面目标越分散。
面目标位置聚类时,常受到空间障碍的阻隔,因而也需要对其与面目标的位置相似性进行计算。空间障碍约束是指以线、面要素表达,且因长度延伸较长、面积覆盖较广而阻碍待聚类目标聚集性的空间目标,如无间断的河流、高速公路等。聚类分析时,空间障碍因具有较大的Voronoi面积,使得其强度函数值远大于聚集目标的强度函数值,易于阻隔并划分面类。就面状障碍而言,可根据公式(1)进行计算,而线状障碍因无面积值,其强度函数可进行简化。
定义2:线目标强度函数:线目标集合L={l1,l2,…,ln}⊂R2,其作为生长元生成的Voronoi多边形集合记为V(L)={l1v,l2v,…,lnv}⊂R2,li∈
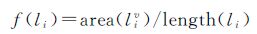 (2)
(2)
强度函数的数值表达了面目标与其邻近目标聚集性的强弱,可作为邻近目标间距离远近的判断标准,随着目标分布的聚集至松散,强度函数的值呈单调递增的趋势,研究设置强度函数阈值Σ提取聚集目标,Σ的取值决定了面目标聚类的粒度,记max(f(A))、min(f(A))分别是面目标集合A中强度函数的最大值和最小值,则Σ的取值范围为[min(f(A)),max(f(A))],Σ值越小,聚类粒度越细,聚类个数越多,类内聚集性越强;反之,亦成立。
3 面目标的多尺度位置聚类方法基于面目标强度函数的构建,本文扩展MSSC方法,提出了面目标的多尺度位置聚类方法(MSSC for polygon,MSSCP),采用Voronoi图剖分空间目标和障碍后,按公式(1)和(2)分别计算面目标和障碍的强度函数值,最终以强度函数阈值的收敛实现面目标聚类。
3.1 聚类预处理MSSCP方法借鉴特征点逼近生成线/面Voronoi图的思想[27-28],以空间目标间最小距离的1/2为间隔,将空间线、面目标边界离散化为特征点,并以特征点为生长元生成Voronoi图,最后合并相同目标的特征点Voronoi图,以生成混合线、面目标的Voronoi图。然而,根据Voronoi图的生成原理可知,Voronoi边界是生长元之间欧氏距离的二等分线,当两个空间目标相交时,平面内的点到交点的距离皆相等,Voronoi边界难以划分,因此,当空间目标存在相交的拓扑关系时,需根据目标在聚类过程中的作用分别处理。具体操作为:当相交目标为待聚类目标时,聚类中属于独立的个体,应在交点或重合边界处稍微收缩线段,使得相交的目标分离后再生成单一目标的Voronoi图;当相交的目标为空间障碍时,对周围面目标具有整体阻隔作用,应将相交障碍的Voronoi图合并成一个完整的Voronoi多边形,改变被阻隔目标的邻近关系。
3.2 面目标的多尺度位置聚类根据MSSC方法思想,如图 3中分析可得,当空间面目标均匀分布时,单一面目标的强度函数值近似等于所有面目标强度函数值的平均值,因此,MSSCP方法以类内面目标强度函数值的平均值作为强度函数阈值,以判断单一尺度下面目标的位置相似性,在初始聚类时,先将所有面目标视为一类,随着尺度的递增,逐层实现面目标聚类的粒度下钻。
定义3:面目标的强度函数阈值:空间存在m个面目标类的集合C={c1,c2,…,cm},ci∈C,对应的强度函数阈值集合Σ={σ1,σ2,…,σm},类ci包含面目标集合A={a1,a2,…,an} ⊂R2,其作为生长元生成的Voronoi多边形集合记为V(A)={a1v,a2v,…,anv}⊂R2,对应类内面目标集合A的强度函数F(A)={f(a1),f(a2),…,f(an)},则类ci的强度函数阈值σi为类内所有面目标的强度函数值的平均值
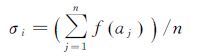 (3)
(3)
相较于MSSC方法,MSSCP方法采用强度函数取代目标的Voronoi面积进行目标位置的相似性计算,并以相邻尺度下,同一面目标类的强度函数阈值相等作为算法的收敛条件,算法流程见图 5。
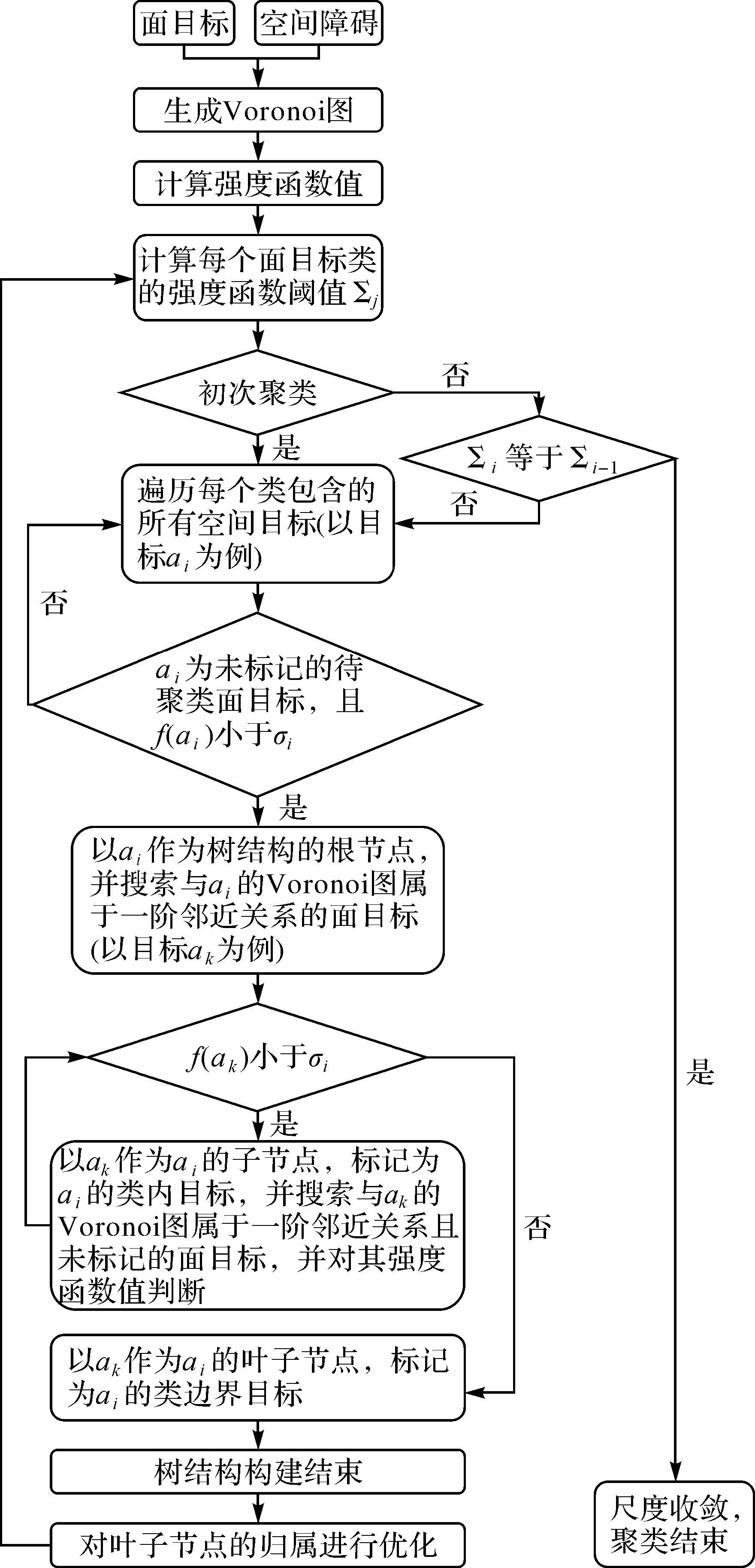
|
| 图 5 MSSCP算法流程图 Fig. 5 The flow chart of MSSCP algorithm |
MSSCP方法在生成空间面目标和障碍的Voronoi图后,根据公式(1)和(2)计算所有目标与障碍的强度函数值,再以公式(3)计算当前聚类尺度下的强度函数阈值,进而通过相邻尺度下的强度函数阈值是否相等,来判断聚类粒度的下钻。单一尺度聚类后,需遍历树结构中的所有非空间障碍的叶子节点进行检查,搜索任一叶子节点及与其属于Voronoi一阶邻近关系的目标集合,将该叶子节点与邻近目标集合中强度函数值最小的目标划为同类。
聚类结束后,每棵完整的树代表了一个面目标类,树的数量即为聚类的个数,树中非空间障碍节点的数量即为该类包含的面目标数量,每棵树的根节点和子节点表示类内目标,非空间障碍的叶子节点代表类边界目标,而未被标记的目标则属于离群目标。
4 聚类结果的有效性评价聚类结果的有效性评价是通过构建有效性指数,对空间簇内部的紧密性和外部的分离性进行量化评估的方法[29]。研究基于相对评价法的思想[9],提出适用于评价MSSCP方法聚类质量的指数AIM(assessment index of MSSCP)。
根据MSSCP方法的聚类结果可知,树的根节点和子节点代表了类内目标,当类内目标的强度函数值与阈值越接近时,表示类内目标分布越均匀;而非空间障碍的叶子节点代表了类边界目标,当类边界目标的强度函数值与阈值相差越大时,表示各面簇间的分离程度越强。根据这一特性,研究采用目标强度函数的方差,分别定义了簇内紧密度指数CI(compactness index)和簇间离散度指数DI(dispersion index)。
设经聚类得到m个面目标类的集合C={c1,c2,…,cm},cj∈C,对应的强度函数阈值集合Σ={σ1,σ2,…,σm},类cj包含类内目标集合AI = {ai1,ai2,…,aip} ⊂R2,对应类内目标AI的强度函数F(AI)={f(ai1),f(ai2),…,f(aip)},另包含类边界目标集合AO={ao1,ao2,…,aoq} ⊂R2,对应类边界目标AO的强度函数F(AO)={f(ao1),f(ao2),…,f(aoq)},则:
定义4:簇内紧密度指数(CI)指簇内目标分布的均匀程度,等于所有面簇各自包含的类内目标的强度函数值与该类强度函数阈值的方差之和的平均值
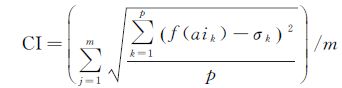 (4)
(4)
定义5:簇间离散度指数(DI)指簇间目标分布的分离程度,等于所有面簇各自包含的类边界目标的强度函数值与该类强度函数阈值的方差之和的平均值
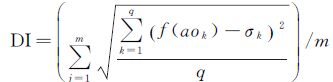 (5)
(5)
簇内紧密度指数CI的数值越小,表示类内目标的强度函数值与该簇的强度函数阈值越接近,即类内目标越趋于均匀而紧密;簇间离散度指数DI的数值越大,则表示类边界目标的强度函数值与该簇的强度函数阈值相差越大,即面簇间的位置越远,因此,可组合CI和DI指数,共同计算AIM指数。
定义6:MSSCP评价指数(AIM)是簇内紧密度指数与簇间离散度指数的综合评价指数
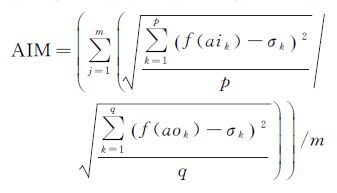 (6)
(6)
AIM指数的数值越小,表示聚类结果的类内紧密度越低,或簇间离散度越高,整体聚类质量越好。
5 试验与讨论 5.1 模拟数据试验为验证MSSCP算法对面目标位置聚类的有效性,试验选取了不同凹凸多边形模拟了5组具有典型位置分布特征的面目标数据集:等密度分离、变密度分离、任意形状分布、桥链接,以及带空间障碍约束的面目标数据集进行聚类,聚类结果在表 1中以虚线框圈出。
| 等密度分离 | 变密度分离 | 任意形状分布 | 桥链接分布 | 空间障碍约束 | |
| 模拟面目标 |  | ||||
| 聚类结果 |  | ||||
试验结果显示,MSSCP方法以强度函数代替Voronoi图面积,并对MSSC方法进行扩展,能够识别不同密度且任意形状的目标簇。同时,通过与现有的面目标位置相似性判断或计算方法进行对比分析,MSSCP方法对面目标位置聚类的有效性,具体表现如下:①相较于以点代面或多边形化简后再计算距离相似度的方法,MSSCP方法充分顾及面目标几何形状信息的约束,在Voronoi图完整剖分目标的前提下,能够准确提取目标间的邻近关系,以判断目标间是否通视或连续;②相较于提取特征点并迭代计算目标间最近距离或平均距离表征目标相似性的计算方法,MSSCP方法既无需考虑特征点选取的不确定性,又通过构建强度函数以直接计算目标与邻近目标聚集程度的强弱,降低了计算的时间复杂度;③MSSCP方法针对“颈”和“链”目标计算的强度函数值远远大于聚集目标,能够准确区分桥链接的面簇。此外,同为识别环状分布的面目标,MSSCP方法能够识别障碍对目标连续性的阻隔作用,将无障碍约束的环状面目标识别为同类,而对空间障碍约束的环状目标簇进行准确划分为4类。
5.2 真实数据试验试验采用MSSC和MSSCP方法对真实的聚落图斑数据进行聚类并对比分析,旨在验证MSSCP算法在面目标几何信息约束和空间障碍约束下的可行性,选取了云南山区部分聚落聚集分布区域作为研究区(图 6(a)),提取研究区内267个面状聚落图斑和7条河流数据进行聚落位置相似性的识别,进而提取聚集分布的聚落群。试验以MSSC和MSSCP方法分别对聚落图斑的质心(点目标)、聚落图斑(面目标)、考虑了河流(线障碍)约束的聚落图斑(面目标)3种形式进行聚落的位置聚类,并以不同符号或颜色区分显示聚类结果,以灰黑色面表示离群目标,如图 6(b)-(d)所示。

|
| 图 6 聚落的位置聚类结果 Fig. 6 The result of position clustering of settlement |
试验结果分析如下:
(1) 几何信息约束的对比。试验采用MSSC算法对聚落质心进行聚类,在未考虑聚落形状的情况下聚类得到4个点目标类(图 6(b)),而采用MSSCP算法对完整的聚落图斑进行聚类,得到9个面目标类(图 6(c))。聚类结果差异原因在于:部分面积较大的图斑被单点代替,改变了聚落的聚集趋势,易将距离较远的图斑识别为同类(如虚线椭圆圈划处),或将距离较近的图斑分为多类(如虚线方框圈划处),存在较大的偏差,特别是在处理覆盖范围较广且形状狭长时,仅以图形质心难以准确判别地物的邻近关系和实际位置的接近程度。
(2) 空间障碍约束的对比。空间障碍对面目标的聚集模式存在阻隔作用,对比图 6(c)和(d)可知,试验加入河流障碍后,MSSCP方法识别得到22个面目标类,将位于河流障碍两侧的面目标进行区分识别,聚类结果与空间认知相符。
(3) 面目标多尺度聚类的结果评价。MSSCP方法将聚落图斑进行多尺度的空间聚类,在空间尺度λ=5时算法收敛,聚类结果如图 6(c)所示,5个空间尺度下分别聚类得到面目标类的数目为:2、3、4、5、9。试验采用CI、DI、AIM 3个指数对不同空间尺度下的面目标聚类结果进行量化分析(表 2),结果显示:随着空间尺度的增加,聚类粒度的下钻,簇内紧密度指数CI下降,表示类内目标越趋于均匀和紧凑;而簇间离散度指数DI的变化虽存在波动,但整体呈下降趋势,原因是聚类粒度的下钻使得部分较为离散的边界目标的聚集性相对减弱,被划分为离群目标;AIM指数呈递减的趋势,表示聚类结果的质量随尺度的增加逐渐优化。
| 空间尺度 | 面类数目 | CI | DI | AIM |
| 1 | 2 | 3869.32 | 31760.94 | 0.12 |
| 2 | 3 | 3071.49 | 37289.06 | 0.10 |
| 3 | 4 | 1884.61 | 20047.41 | 0.10 |
| 4 | 5 | 866.57 | 17764.49 | 0.05 |
| 5 | 9 | 293.81 | 9290.10 | 0.04 |
6 结 论
本文基于MSSC方法进行扩展,在充分考虑面目标几何信息复杂性和空间障碍阻隔双重约束的基础上,提出了MSSCP方法,采用混合线、面目标的Voronoi图提取目标直接或间接的Voronoi邻近关系,并选择不同面目标聚散分布和不同面目标尺寸下,“面目标Voronoi面积”“面积差”和“比率”3项指标变化进行对比分析,构建能够表征面目标位置聚散性的强度函数以定量计算目标间的位置相似性。模拟试验证明,MSSCP方法能够识别不同密度分离、任意形状分布、桥链接以及带障碍约束的面目标类。真实数据试验表明MSSCP方法避免了局部欧氏距离计算所带来的位置相似性的不确定性;适用于空间障碍实体约束下,不规则面目标的位置聚集模式提取;评价指数的分析提现了随空间尺度的下钻,聚类质量逐层优化,面簇的簇内紧密度逐层增加。
MSSCP方法针对面目标的位置进行聚类,适用于空间事物和现象的位置聚集趋势分析,如典型石漠化区的划分、聚落结构扩张变化分析中中心聚落的提取与划分等。后续研究中有两方面问题亟待讨论和解决:考虑到面目标具有的非空间信息和方向、尺寸、形状等空间信息皆具有独立的非连续性、非均匀性与趋势性[30],若将所有信息归一化后进行加权融合,不仅权值难以确定,且易发生信息的互斥,后续研究将于实现面目标的位置相似性识别后,再选择性加入其他信息作为约束,来进行类粒度的细化,以扩展MSSCP方法的应用范畴。该研究主要针对面目标的位置相似性进行聚类,亦可参考式(2)扩展实现线目标的位置相似性聚类。
| [1] | 辜寄蓉, 陈先伟, 杨海龙. 城市功能区划分空间聚类算法研究[J]. 测绘科学 , 2011, 36 (5) : 65–67. GU Jirong, CHEN Xianwei, YANG Hailong. Spatial Clustering Algorithm on Urban Function Oriented Zone[J]. Science of Surveying and Mapping , 2011, 36 (5) : 65 –67. |
| [2] | CAO Zechun, WANG Sujing, FORESTIER G, et al. Analyzing the Composition of Cities Using Spatial Clustering[C]//Proceedings of the 2nd ACM SIGKDD International Workshop on Urban Computing. New York:ACM, 2013:14. |
| [3] | STEINHAUER J H, WIESE T, FREKSA C, et al. Recognition of Abstract Regions in Cartographic Maps[M]//MONTELLO D R. Spatial Information Theory. Berlin Heidelberg:Springer, 2001:306-321. |
| [4] | YAN Haowen, WEIBEL R, YANG Bisheng. A Multi-Parameter Approach to Automated Building Grouping and Generalization[J]. Geoinformatica , 2008, 12 (1) : 73 –89. DOI:10.1007/s10707-007-0020-5 |
| [5] | 邓敏, 孙前虎, 文小岳, 等. 建筑物层次空间聚类方法研究[J]. 计算机工程与应用 , 2011, 47 (28) : 120–123. DENG Min, SUN Qianhu, WEN Xiaoyue, et al. Hierarchical Spatial Clustering of Buildings[J]. Computer Engineering and Applications , 2011, 47 (28) : 120 –123. |
| [6] | 马利邦, 郭晓东, 张启媛. 甘谷县乡村聚落时空布局特征及格局优化[J]. 农业工程学报 , 2012, 28 (13) : 217–225. MA Libang, GUO Xiaodong, ZHANG Qiyuan. Spatio-Temporal Distribution and Optimization of Rural Settlements in Gangu County of Loess Hilly Area[J]. Transactions of the Chinese Society of Agricultural Engineering , 2012, 28 (13) : 217 –225. |
| [7] | 艾廷华, 郭仁忠. 基于格式塔识别原则挖掘空间分布模式[J]. 测绘学报 , 2007, 36 (3) : 302–308. AI Tinghua, GUO Renzhong. Polygon Cluster Pattern Mining based on Gestalt Principles[J]. Acta Geodaetica et Cartographica Sinica , 2007, 36 (3) : 302 –308. DOI:10.3321/j.issn:1001-1595.2007.03.011 |
| [8] | 闫浩文, 应申, 李霖. 多因子影响的地图居民地自动聚群与综合研究[J]. 武汉大学学报(信息科学版) , 2008, 33 (1) : 51–54. YAN Haowen, YING Shen, LI Lin, et al. n Approach for Automated Building Grouping and Generalization Considering Multiple Parameters[J]. Geomatics and Information Science of Wuhan University , 2008, 33 (1) : 51 –54. |
| [9] | 邓敏, 刘启亮, 李光强. Analysis and Application of Spatial Clustering[M]. Beijing: Science Press, 2011 . |
| [10] | BARRAULT M, REGNAULD N, DUCHENE C, et al. Integrating Multi-agent, Object-oriented, and Algorithmic Techniques for Improved Automated Map Generalization[C]//Proceedings of 20th International Cartographic Conference. Beijing:Publishing House of Surveying and Mapping, 2001:2110-2116. |
| [11] | 杨春成, 何列松, 谢鹏, 等. 顾及距离与形状相似性的面状地理实体聚类[J]. 武汉大学学报(信息科学版) , 2009, 34 (3) : 335–338. YANG Chuncheng, HE Liesong, XIE Peng, et al. Clustering Analysis of Geographical Area Entities Considering Distance and Shape Similarity[J]. Geomatics and Information Science of Wuhan University , 2009, 34 (3) : 335 –338. |
| [12] | ZHANG Xiang, AI Tinghua, STOTER J S, et al. Building Pattern Recognition in Topographic Data:Examples on Collinear and Curvilinear Alignments[J]. Geoinformatica , 2013, 17 (1) : 1 –33. DOI:10.1007/s10707-011-0146-3 |
| [13] | ALT H, BEHRENDS B, BLÖMER J. Approximate Matching of Polygonal Shapes[J]. Annals of Mathematics and Artificial Intelligence , 1995, 13 (3-4) : 251 –265. DOI:10.1007/BF01530830 |
| [14] | WANG Sujing, CHEN Chunsheng, RINSURONGKAWONG V, et al. A Polygon-based Methodology for Mining Related Spatial Datasets[C]//Proceedings of the 1st ACM SIGSPATIAL International Workshop on Data Mining for Geoinformatics. New York:ACM, 2010:1-8. |
| [15] | DAVIS E. Representations of Commonsense Knowledge[M]. San Mateo: Morgan Kaufmann, 1990 . |
| [16] | DENG Min, LI Zhilin, CHEN Xiaoyong. Extended Hausdorff Distance for Spatial Objects in GIS[J]. International Journal of Geographical Information Science , 2007, 21 (4) : 459 –475. DOI:10.1080/13658810601073315 |
| [17] | JOSHI D, SAMAL A K, SOH L K. Density-based Clustering of Polygons[C]//Proceedings of the CIDM'09 IEEE Symposium on Computational Intelligence and Data Mining. Nashville, TN:IEEE, 2009:171-178. |
| [18] | HUH Y, KIM J, LEE J, et al. Identification of Multi-Scale Corresponding Object-Set Pairs between Two Polygon Datasets with Hierarchical Co-Clustering[J]. ISPRS Journal of Photogrammetry and Remote Sensing , 2014, 88 : 60 –68. DOI:10.1016/j.isprsjprs.2013.11.017 |
| [19] | 耿协鹏, 杜晓初, 胡鹏. 基于栅格距离变换的扩展对象空间聚类方法[J]. 测绘学报 , 2009, 38 (2) : 162–167. GENG Xiepeng, DU Xiaochu, HU Peng. Spatial Clustering Method Based on Raster Distance Transform for Extended Objects[J]. Acta Geodaetica et Cartographica Sinica , 2009, 38 (2) : 162 –167. DOI:10.3321/j.issn:1001-1595.2009.02.012. |
| [20] | HALKIDI M, VAZIRGIANNIS M. NPClu:An Approach for Clustering Spatially Extended Objects[J]. Intelligent Data Analysis , 2008, 12 (6) : 587 –606. |
| [21] | SANDER J, ESTER M, KRIRGEL H P, et al. Density-based Clustering in Spatial Databases:The Algorithm GDBSCAN and Its Applications[J]. Data Mining and Knowledge Discovery , 1998, 2 (2) : 169 –194. DOI:10.1023/A:1009745219419 |
| [22] | 黎韶光, 周巨锁, 谢玉波, 等. 一种面向扩展空间对象的密度聚类算法[J]. 计算机工程与应用 , 2011, 47 (13) : 166–168. LI Shaoguang, ZHOU Jusuo, XIE Yubo, et al. Density-based Clustering Algorithm for Extended Spatial Objects[J]. Computer Engineering and Applications , 2011, 47 (13) : 166 –168. |
| [23] | 张丽, 吉根林. 基于点面包含关系的GML空间聚类算法[J]. 小型微型计算机系统 , 2010, 31 (4) : 702–705. |
| [24] | 余莉, 甘淑, 袁希平, 等. 综合线面特征分布的点目标多尺度聚类方法[J]. 测绘学报 , 2015, 44 (10) : 1152–1159. YU Li, GAN Shu, YUAN Xiping. Multi-Scale Clustering of Points Synthetically Considering Lines and Polygons Distribution[J]. Acta Geodaetica et Cartographica Sinica , 2015, 44 (10) : 1152 –1159. DOI:10.11947/j.AGCS.2015.20150136 |
| [25] | 王中辉, 闫浩文. 基于方向Voronoi图模型的群组目标空间方向关系计算[J]. 小型微型计算机系统 , 2013, 38 (5) : 584–588. WANG Zhonghui, YAN Haowen. Computation of Direction Relations between Object Groups Based on Direction Voronoi Diagram Model[J]. Geomatics and Information Science of Wuhan University , 2013, 38 (5) : 584 –588. |
| [26] | TOBLER W R. A Computer Movie Simulating Urban Growth in the Detroit Region[J]. Economic Geography , 1970, 46 (S1) : 234 –240. |
| [27] | 王新生, 刘纪远, 庄大方, 等. 基于GIS的任意发生元Voronoi图逼近方法[J]. 地理科学进展 , 2004, 23 (4) : 97–102. WANG Xinsheng, LIU Jiyuan, ZHUANG Dafang, et al. GIS-based Approximation Algorithm for Constructing Voronoi Diagrams with General Generators[J]. Progress in Geography , 2004, 23 (4) : 97 –102. |
| [28] | LIJiatian, YANGQili, LUOFuli, 等. A Decomposition and Combination Algorithm for Voronoi Diagrams of Polylines and Polygons[J]. Geomatics and Information Science of Wuhan University , 2015, 40 (11) : 1545–1550. |
| [29] | BERRY M J A, LINOFF G S. Data Mining Techniques:For Marketing, Sales, and Customer Support[M]. New York: John Wiley &Sons, 1997 . |
| [30] | 刘启亮, 邓敏, 石岩, 等. 一种基于多约束的空间聚类方法[J]. 测绘学报 , 2011, 40 (4) : 509–516. LIU Qiliang, DENG Min, SHI Yan, et al. A Novel Spatial Clustering Method Based on Multi-constraints[J]. Acta Geodaetica et Cartographica Sinica , 2011, 40 (4) : 509 –516. |



