2. 上海电力学院计算机科学与技术学院, 上海 200090
2. College of Computer Science and Technology, Shanghai University of Electric Power, Shanghai 200090, China
随着传感器技术的不断发展,高光谱遥感实现了地表地物波谱信息的精细描述,这使得面向地表特定目标的遥感目标检测与辨识技术成为可能。与此同时,通过光谱特征分析技术挖掘具有特殊光谱变化特征区域的遥感异常检测技术引起了学者们的广泛关注。遥感异常检测技术是一种无须目标光谱先验信息的盲检测技术,旨在通过数据分析的方法挖掘具有特殊光谱变化特性的感兴趣目标,在国防军事安全、精准农业耕作、地质勘测、环境检测等诸多领域具有重要的应用价值[1-3]。
通常,异常目标具备两个特征:①不同于周围背景的特殊波谱变化特性;②出现概率较小,在空间分布特征上表现出稀疏性。基于该假设前提,若周围背景的光谱特征可由统计模型描述,那么不同于背景光谱特征的像素则被判定为异常,这类异常检测算法统称为基于背景建模的异常检测算法。该算法中背景模型描述光谱变化特征的准确性与稳健性决定了异常检测效果。因此,如何获得准确且稳健的背景模型是这类异常检测算法的关键。目前基于背景建模的异常检测算法根据所描述的背景范围,可将其分为局部背景建模与全局背景建模两种。
局部背景建模仅考虑待测像素周围领域的背景,选取待检测像素周围局部区域内的像素作为背景进行建模,不仅实现了局部背景光谱变化的特征描述,同时降低了背景协方差矩阵的计算量。最经典的基于局部背景建模的异常检测算法是在1990年由文献[4]提出的LRX算法,该算法在背景光谱特征平滑且服从高斯分布的假设前提下,通过滑动窗口获得每个待测像素周围的背景区域并进行参数估计,从而实现基于局部背景建模的异常检测。由于该算法无须满足全局背景平滑的假设,可以较好地适应背景在光谱特征与空间特征上的不断变化,因此针对复杂背景下的异常检测,基于局部背景建模的异常检测算法可以获得较理想的检测效果。然而,由于LRX算法缺乏对全局背景的统一描述,容易产生局部异常[5]。
全局背景建模从全局角度描述背景光谱统计特性,试图构建关于背景的全局统一描述用于克服局部异常问题。目前基于全局背景建模的异常检测算法主要有基于多元正态分布模型的异常检测算法[6](multivariate normal,MVN)、基于分类的异常检测算法[7-8](cluster-based anomaly detector,CBAD)和基于子空间变换的异常检测算法[9](sub-space RX,SSRX),这些算法均从不同的角度实现了对全局背景光谱变化特征的统一描述。多元正态分布模型MVN在满足全局背景光谱特征描述要求的同时,其扎实的理论基础和易于处理的数学特性保证了算法较低的计算复杂度。CBAD算法通过分类算法将复杂背景描述问题转换为多个简单背景描述问题获得了较好的检测效果。然而,由于缺乏背景地物种类数量的先验知识,最优分类结果难以确定从而影响异常检测算法的性能。
全局背景建模避免了局部异常问题,但由于模型描述范围较大,尤其是存在复杂光谱变化特性的背景,较难获得合适的统计模型;另外,模型参数估计需涉及全局背景像素,在无任何异常先验信息的前提下,纯背景像素子集较难获得。而当背景像素子集混入异常像素时,检测算法对异常目标的敏感度将大大降低,从而导致漏检率升高[10]。为了降低异常对背景估计的干扰,许多新颖的全局型异常检测算法不断涌现,在背景参数估计稳健性及复杂背景描述等方面取得了较好的效果。
基于块自适应计算的高效异常检测算法(block adaption computationally outlier nominator,BACON)[11]解决了纯背景子集难以获得及遍历时间长等问题,采用迭代估计最大可能地逼近真实背景模型,从而实现异常检测。该算法检测速度快,稳健性好。基于空域相关性滤波器的异常检测算法(whitening special correlation filtering,WSCF)[12]无须背景建模,实现了全局异常检测,特别是对较大尺寸异常目标的检测效果较显著。基于随机子集估计的异常检测算法(random selection anomaly detector,RSAD)[13-14]试图克服BACON对背景子集选择的单一性,采用随机抽取背景像素的方法获得初始估计,并通过多次随机选择与反复迭代消除异常对背景子集的干扰,获得更加准确的全局背景描述。然而,RSAD与BACON类似,同样涉及阈值计算问题。基于核变换的RX算法[15-17]是一种借助子空间变换的全局性异常检测算法,通过核函数的非线性映射将高光谱数据映射到高维特征空间,获得可由高斯模型描述的高维特征信息。然而尺度参数的选择决定了模型描述能力。基于区分测度学习的异常检测算法[18]通过流型理论,分析像素最近邻域的可分解性判定是否存在异常。基于慢变化信号分析的异常检测算法[19]是在假设背景光谱特征具有缓慢变化特性的前提下,提取具有缓慢变化特性的数据实现异常检测。然而,复杂背景下异常检测准确率低的根本原因在于背景的复杂空间结构,导致背景与异常在光谱特征上存在相关性,因此,纯背景像素难以获取,无法准确地描述复杂背景。
昆虫视觉的多孔径系统通过若干独立单个子孔径获得关于整个视场的统一完整的描述,是一种兼顾局部特征与全局特征的综合系统。每个孔径中视场的大小由孔径的直径确定,相邻孔径之间互不干扰,独立成像。孔径内成的像会因孔径角度不同而不同,具有局部区域特性,可以实现对存在局部特征差异的复杂背景的描述。与此同时,昆虫多孔径视觉系统的融合处理机制负责综合各个孔径的观测结果,获得关于场景的全局性整体感知。昆虫的多孔径视觉成像系统对细节描述与全局感知的优势有效地平衡了局部差异性与全局一致性之间的矛盾。
本文借鉴昆虫多孔径视觉系统中并行子孔径分析与融合决策的相关机理,提出一种基于多孔径映射的高光谱异常检测器(multi-aperture anomaly detector,MAAD)。首先,通过构建多孔径映射模型将高光谱数据电磁波谱范围按照光谱亮度变化从高到低拆分为不同的子孔径,并从每个子孔径中获得关于高光谱数据中局部电磁波谱的变化特征。然后,从异常目标光谱特征的相对异常性出发,通过对子孔径的分析判断,获得待测像素在特定子孔径下的属性结果,并通过模糊隶属度值进行编码,实现对适中异常显著性像素的属性分析。最后,将不同孔径下获得的属性判定结果进行融合,获取全局视角下的异常检测结果。为了增强算法的稳健性,本文通过迭代估计获得子孔径映射结果。在迭代过程中采用像素隶属度值作为权重估算背景特征。另外,为了增强算法对低异常显著性目标的敏感性,本文设计的融合规则将最大限度地降低漏检率。本文算法无须背景建模与先验信息,仿真试验采用真实高光谱遥感数据对算法的稳健性及低显著性异常目标的敏感性进行验证。
1 高光谱数据的多孔径映射 1.1 总体框架设计基于多孔径映射的高光谱异常检测算法流程如图 1所示,该算法主要包括3个部分。

|
| 图 1 MAAD信息处理流程 Fig. 1 Flow chart of information process by MAAD |
(1) 借鉴昆虫多孔径视觉系统的映射过程,将高光谱数据进行多孔径映射处理。本文中采用加权迭代估算多孔径映射结果。每个子孔径对应一段电磁波谱变化范围,不同子孔径对应的电磁波谱范围不重叠,所有子孔径的电磁波谱覆盖了整个高光谱数据电磁波谱范围。根据映射结果提取每个子孔径内像素光谱均值向量与协方差向量作为该子孔径的基,因而整个高光谱数据的光谱特征可由所有子孔径基的集合进行表征。子孔径映射的初始估计由欧氏距离的聚类计算获得,迭代过程中将像素的异常显著性作为像素光谱值的权重,采用全局像素计算子孔径基的加权估计值,最后通过比较相邻两次均值变化量作为迭代终止条件。
(2) 参考子孔径基,计算全局范围内所有待测像素的异常显著性,用于衡量待测像素与子孔径基之间的光谱特征相对统计差异。考虑到多孔径映射中各个子孔径互不相同,参考不同子孔径基将获得不同的异常显著性。为了对不同孔径下异常显著性的统一描述及融合处理,本文采用模糊逻辑理论,通过隶属度函数映射将待测像素的异常显著性转化为表示属性概率的隶属度值。与二值化标记相比,这种模糊化的属性标记方法实现了对具有适中异常显著性像素属性的精细描述,弥补了传统检测算法无法对低显著度像素属性进行精细分析的缺点。
(3) 本文借鉴模糊逻辑理论中的去模糊机制,对多孔径下获得的不同检测结果进行融合。首先,将各个子孔径基下获得的检测结果按照属性类别进行叠加;然后,通过比较异常属性与非异常属性概率累计值的大小,将有较大隶属度值的属性作为最终的检测结果。
1.2 多孔径映射模型假设高光谱数据集合定义为RM×K=Ii,M为像素总数,K为波段数,Ii为第i个像素向量(包含了K个波段的光谱亮度值),其大小为1×K。借鉴昆虫多孔径成像系统的成像机理,经过多孔径映射,高光谱遥感数据R可以分解为多个子孔径的集合S={s1,s2,…,sl,…,sL},l=1,2,…,L,sl为第l个子孔径内映射得到的像素集合,L为子孔径总数。每个子孔径sl对应于高光谱数据的一段电磁波谱变化范围,提取子孔径sl的均值与协方差作为该孔径的基Xl,Cl,用于表征子孔径sl对应光谱统计特征。子孔径的统计特征由式(1)和式(2)计算
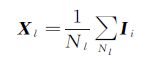 (1)
(1)
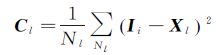 (2)
(2)
式中,Xl与Cl分别为子孔径sl的均值向量与协方差矩阵;Nl为子孔径sl中包含的像素总数。因此整个高光谱数据R的光谱特征可由子孔径基集合{[X1,C1],[X2,C2],…,[Xl,Cl],…,[XL,CL]}表征。考虑到子孔径映射结果的准确性决定了后续属性判断的准确性,本文采用加权迭代估计的方法通过多次筛选与更新获得多孔径映射结果S的稳定估计。
2 基于多孔径映射的异常检测算法 2.1 异常显著性指标马氏距离是较经典的统计差异衡量指标。在异常检测算法中,若背景模型的统计特征已知,那么通过计算马氏距离可以测量待测像素与背景模型之间的统计差异。由于多孔径映射过程不同于背景特征提取过程,无须挑选背景像素,因此,子孔径sl的基[Xl,Cl]是对子孔径内像素集合的表征。参考马氏距离的定义,在已知子孔径sl基[Xl,Cl]的前提下,待测像素Ii与子孔径sl的统计差异d(i,l)可由式(3)表示
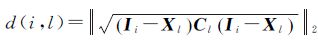 (3)
(3)
式中,i为像素Ii的坐标;l代表了第l个子孔径;d(i,l)的大小反映了待测像素Ii与子孔径sl之间在光谱统计特征上的差异程度;‖·‖2为2范数函数。
考虑到多孔径映射后获得的子孔径映射结果并非纯背景像素集合,因此子孔径sl基Xl,Cl下的马氏距离是一种相对统计差异。根据相对异常的概念,本文将d(i,l)定义为待测像素Ii在子孔径sl基参考下的异常显著性指标。以此类推,对于待测像素Ii,参考多孔径基集合{[X1,C1],[X2,C2],…,[Xl,Cl],…,[XL,CL]}将获得该像素的异常显著性向量[d(i,1),d(i,2),…,d(i,l),…,d(i,L)]。类似于马氏距离,较大的d(i,l)表示待测像素Ii与子孔径sl之间具有明显的光谱特征差异,即像素Ii的异常显著性较强;相反,较小的d(i,l)表示待测像素Ii与子孔径sl之间的不具有明显的光谱特征差异,即像素Ii的异常显著性较弱。异常显著性较强的像素属于异常的可能性较大;异常显著性较弱的像素属于背景的可能性较大;具有这两种特性的像素属性较容易确定。而介于两者之间的像素属性则较难作出明确的判断。而在实际情况中,复杂背景在光谱特征与空域特征上与异常目标的相关性,导致大量像素的异常显著性趋于适中。因此,正确判断具有适中异常显著性像素的属性,是决定检测效果的关键。为了实现对低异常显著性像素属性的进一步分析与判断,本文借鉴模糊逻辑理论,通过属性的模糊化标记实现对像素属性(特别是低显著度像素)的精细描述。
2.2 异常显著性的模糊分析模糊逻辑理论在描述事物的不确定、模糊性等问题上具有不可替代的优势。模糊逻辑理论不同于传统的集合理论,它采用连续型的隶属度值表征变量属性的不确定性,更能满足实际应用的需要。其中Pal和Rosenfeld函数[19]是较经典的模糊隶属度函数,常用于处理图像增强及目标检测中的模糊边界判定问题。
2.2.1 隶属度函数映射基于以上分析,通过隶属度函数映射,可将待测像素Ii的异常显著性向量映射为该像素的隶属度向量。采用隶属度值向量不仅实现了距离的归一化处理,同时还有利于融合计算。隶属度值的大小代表待测像素属于异常的概率值。具体操作如下:根据Pal和Rosenfeld隶属度函数的定义,对于待测像素Ii在子孔径sl基下,其异常显著性d(i,l)可映射为一对隶属度值v0(i,l)和v1(i,l),分别用于表示待测像素Ii属于非异常或异常的概率值
 (4)
(4)
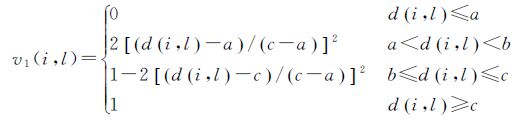 (5)
(5)
式中,参数a、c分别用于界定模糊区间的下限与上限,可根据实际情况调整;[a,c]区间之外的像素属性采用二值化的定性标记方法;[a,c]区间内的像素属性则由其隶属度值v0(i,l)和v1(i,l)进行定量描述;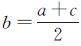
 (6)
(6)
 (7)
(7)
式中,max_dl为子孔径sl基下全局内所有待测像素异常显著性的最大值;min_dl为子孔径sl基下全局内所有待测像素异常显著性的最小值;a和c会随子孔径映射结果自适应地调节大小;参数β1、β2控制异常与非异常之间统计差异(0≤β1,β2<1)。
因此,待测像素Ii 在子孔径sl基 [Xl,Cl]下的属性可由隶属度值[v0(i,l),v1(i,l)]描述.对于任意一个待测像素Ii,其对应两种属性的隶属度值应满足式(8)
 (8)
(8)
考虑到单个子孔径基对整个高光谱数据表征的片面性以及子孔径与子孔径之间的电磁波谱特征的差异性,相同待测像素在不同子孔径基下其属性判定结果可能不同,且每个属性判定结果都具有相同的可信度。因此,应综合考虑所有子孔径基下的属性判定结果,给出待测像素属性的最终检测结果。
对于待测像素Ii在不同子孔径基下获得的不同隶属度值v0(i,l)和v1(i,l),分别组成隶属度向量[v0(i,1),v0(i,2),…,v0(i,l),…,v0(i,L)]与[v1(i,1),v1(i,2),…,v1(i,l),…,v1(i,L)],l=1,2,…,L。[v0(i,1),v0(i,2),…,v0(i,l),…,v0(i,L)]表示待测像素Ii为非异常属性的概率,[v1(i,1),v1(i,2),…,v1(i,l),…,v1(i,L)]表示待测像素Ii为异常属性的概率。不失一般性,具有较大概率的属性具有更高可信度。因此,将不同属性的隶属度值累加获得关于待测像素Ii在不同属性上的累积隶属度值V0(i),V1(i)
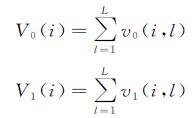 (9)
(9)
式中,V0(i)和V1(i)为像素Ii属于异常或非异常的隶属度值,L为孔径数。通过比较V0(i)和V1(i)的值,将具有较高概率值的属性作为像素Ii的最终检测结果
 (10)
(10)
式中,Iouti是像素Ii的最终检测结果,值为1表示像素Ii属于异常;值为0表示像素Ii属于背景。
2.3 算法设计为了获得稳健的多孔径映射结果,本文采用迭代估计的方法不断逼近最优的映射结果。考虑到迭代过程中初始估计不影响迭代结果,因此采用简单快速的欧氏距离聚类算法获得关于多孔径映射的初始估计。
2.3.1 初始估计统计高光谱遥感各波段光谱亮度的最小值与最大值分别组成向量Ilow及向量Ihig。根据孔径数目L,将高光谱数据的电磁波谱范围[Ilow,Ihig]等分为L个子集。每个子集都对应一个子孔径。按照光谱亮度从低到高定义第一个子孔径为s1,其光谱亮度的最小值为Ib1即整个高光谱数据的最小光谱亮度值。其余子孔径中光谱亮度的最小值Ibl可由Ib1得到
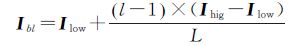 (11)
(11)
式中,Ibl的大小为1×K的响铃,K为高光谱数据的波段总数;Ibl是子孔径sl光谱亮度的最小值或称基本水平。基于子孔径s1初始映射估计,计算全局待测像素Ii与子孔径sl初始亮度值Ibl之间的欧氏距离
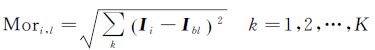 (12)
(12)
式中,较小Mori,l表示待测像素Ii与子孔径sl的光谱特征差异性较小,从而判定像素Ii属于子孔径sl;反之,像素Ii不属于子孔径sl。本文设置阈值ζ对待测像素与子孔径之间的从属关系进行区分,并采用标记变量U(i,l)标记待测像素Ii的归属特性
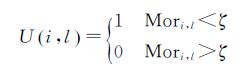 (13)
(13)
式中,U(i,l)=1表示待测像素Ii属于子孔径sl;U(i,l)=0表示待测像素Ii不属于子孔径sl;阈值ζ定义如式(14)所示
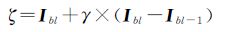 (14)
(14)
式中,[Ibl,Ibl-1]是子孔径sl的光谱亮度变化范围;参数γ(0≤γ≤1)为误差调节参数,用于增强算法对噪声干扰的稳健性。
2.3.2 加权迭代更新考虑到待测像素的隶属度值v0(i,l)的大小反映了该像素属于非异常属性的概率,本文将v0(i,l)作为权重,采用全局像素计算子孔径sl的均值向量与协方差矩阵
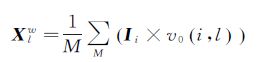 (15)
(15)
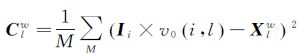 (16)
(16)
式中,M为高光谱数据中包含像素的总数;Xlw与Clw为加权均值向量与加权协方差矩阵;通过比较子孔径光谱均值变化量控制迭代过程的结束。
基于以上分析,多孔径映射下的高光谱遥感异常检测算法流程如下:
(1) 子孔径sl光谱亮度值的初始估计Ibl;
(2) 根据欧氏距离聚类获得子孔径sl映射初始估计;
(3) 基于初始估计计算子孔径sl的基[Xl,Cl];Step1[Xl,Cl]→[Xlw,0,Clw,0];
(4) 计算待测像素Ii的异常显著性d(i,l);
(5) 根据模糊函数计算Ii的隶属度值[v0(i,l),v1(i,l)];
(6) 计算子孔径sl的加权均值Xlw,1和协方差Clw,1;
(7) If:均值变化|Xlw,1-Xlw,0|<ε,End;Else:[Xlw,1,Clw,1]→[Xlw,0,Clw,0];Go to(4)。
3 试 验 3.1 试验数据本文选择不同类型遥感平台获得的真实高光谱遥感数据对本文算法的检测效果进行试验验证。
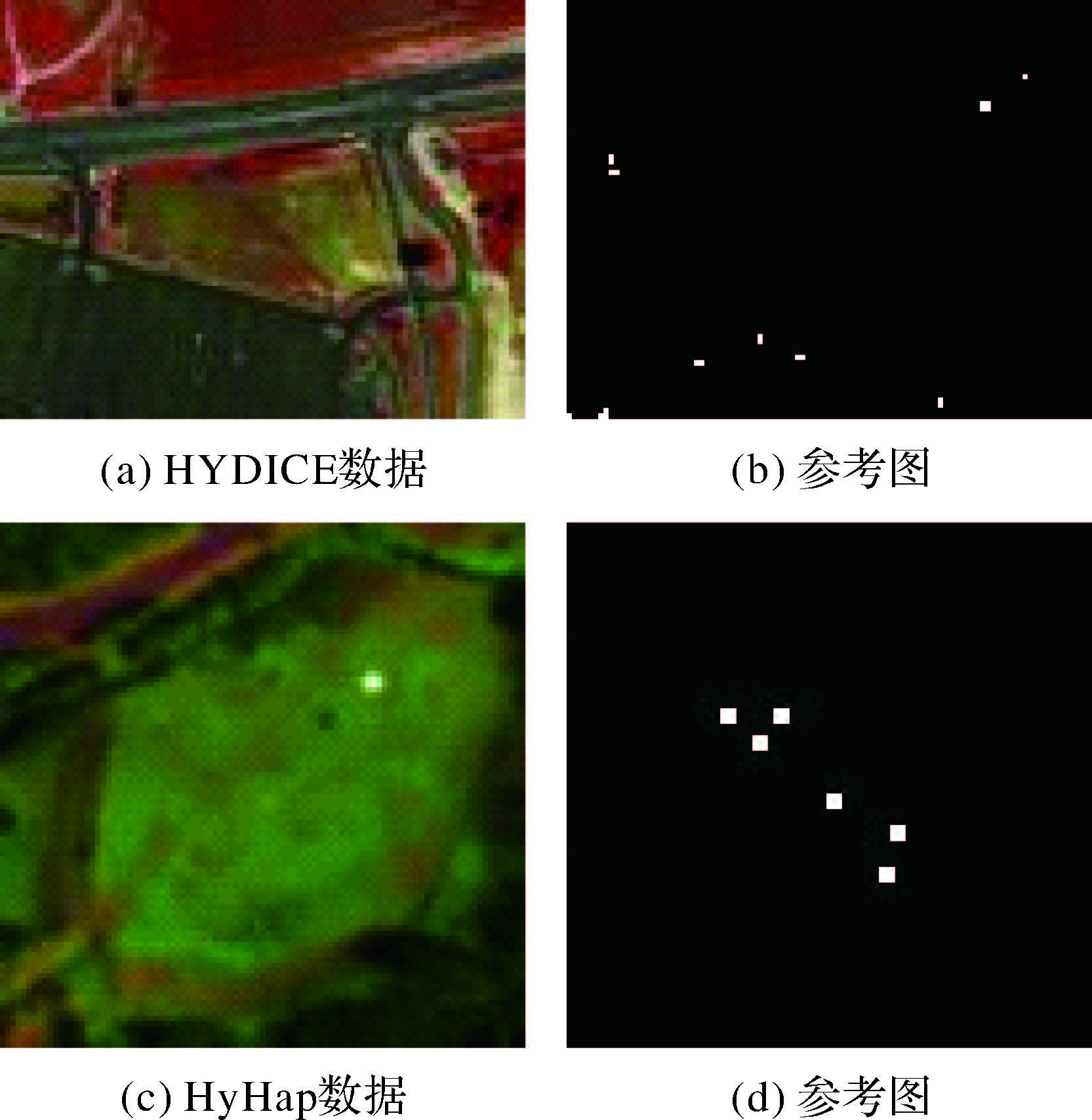
3.1.1 HYDICE数据该数据是通过机载HYDICE传感器获得。HYDICE成像系统的光谱分辨率为10nm,空间分辨率为1m。去掉低信噪比波段及水蒸气吸收波段后,剩余160个波段。整组数据大小为307×307像素,背景包含不同的地物种类,如植被、建筑物、沥青路面和机动车。考虑到异常目标光谱特征及尺寸大小等因素,选取图 2(a)中右上角部分作为试验场景。异常目标为地面机动车与建筑物屋顶,其真实地表参考位置如图 2(b)所示,异常目标尺寸约为1×2~2×2个像素之间。
|
| 图 2 试验数据及地表参考图 Fig. 2 Experiment data and reference map of ground truth |
3.1.2 HyMap数据
该数据是由HyVista提供的HyMap成像光谱仪拍摄,为美国蒙大拿州库克城区域的地表数据。HyMap成像仪的空间分辨率为3m,提供126个波段的光谱数据。本文选择大小为100×100像素的市中心区域作为试验场景如图 2(c)所示,其中包括道路,屋顶和车辆。该区域的地面参考数据由The Target Detection Blind Test data网站提供[21],如图 2(d)所示,其中有包括建筑区和车辆6个真正的目标。不考虑单个像素的异常情况,异常目标包含35个异常像素,异常目标尺寸在2×2~3×3个像素之间。
3.2 试验结果将本文提出的算法与经典的异常检测算法进行比较,如LRX、BACON、RSAD、CBAD和2DCAD。检测结果如图 3所示。LRX是基于高斯分布统计理论的经典异常检测算法,本文中考虑到异常目标的尺寸在4×4像素以内,因此选择局部滑动窗口的尺寸为13×13像素,检测结果的阈值为95%×Max(dis(xi))。RSAD是通过对背景模型数据的多重估计,旨在获得准确的背景模型。在卡方分布的前提假设下,用于计算分割阈值的卡方参数χ2(K)中自由度为波段数K,初始背景子集中像素的个数为c×K,其中c=5;迭代终止条件为子集像素个数增长在10个像素以内。高阶二维交叉滤波器(2-D crossing anomaly detector,2DCAD)[22]根据异常目标因其特殊光谱特性产生高频边缘信息实现异常检测。考虑到异常目标尺寸在4×4像素之内,因此2DCAD的窗口尺寸为内部窗口7×7像素,外部窗口11×11像素。本文算法中的两个参数β1和β2的值为β1=β2=0,均值误差参数ε=10,孔径数为6。两种数据的检测结果如图 3和图 4所示。

|
| 图 3 HYDICE数据的试验验证 Fig. 3 Experiment result of HYDICE data |

|
| 图 4 HyMap数据的试验验证 Fig. 4 Experiment result of HyMap data |
HYDICE数据中目标尺寸较小,周边存在较明显的边缘信息。结合HYDICE数据的地表参考数据,可知本文算法可将图 2(a)中异常目标全部检测到,如图 3(e)所示。RSAD与BACON算法获得检测结果比较相似,2DCAD对具有边缘特征的目标非常敏感,因此图像中的道路边缘也当作目标检测出来,导致虚警。
HyMap数据中异常目标的光谱异常性不显著,而背景中的地物光谱亮度较高,因此异常目标的显著性降低。LRX算法可以检测到部分异常目标,但是虚警率较高。RSAD与BACON可以检测到图像中的一个异常目标。由于背景中存在一个光谱亮度较高的背景物体,边缘特征显著,对该背景地物较敏感2DCAD算法仅仅获得了背景地物的检测结果。CBAD的检测结果中可以观测到3个异常目标,但是虚警率较高。本文算法检测结果如图 4(e)所示。虽然本文算法也将背景中的高亮度目标作为异常检测出来,产生虚警,但是对于真实异常目标,本文算法同样获得较好的命中率,如图 4(f)所示。
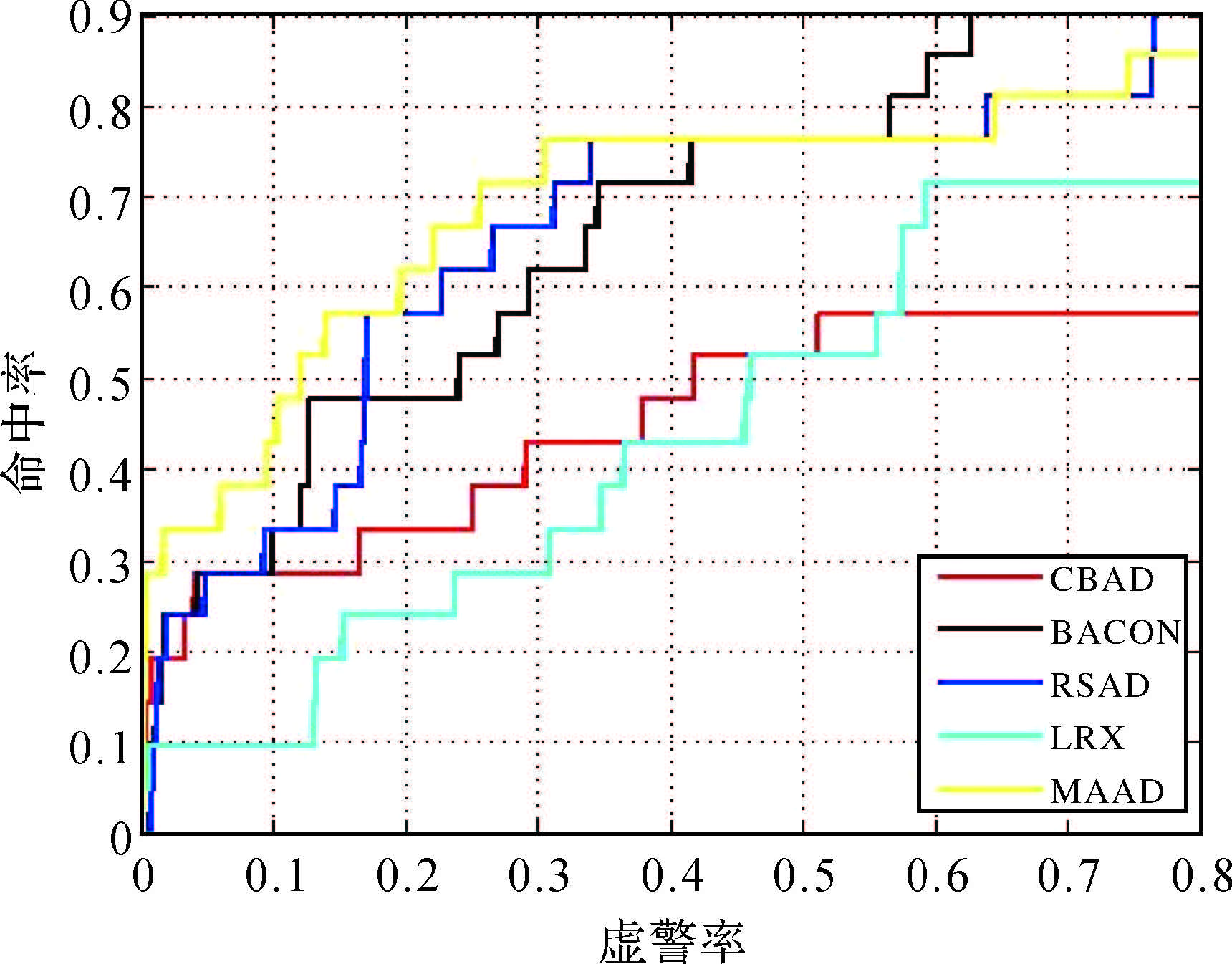
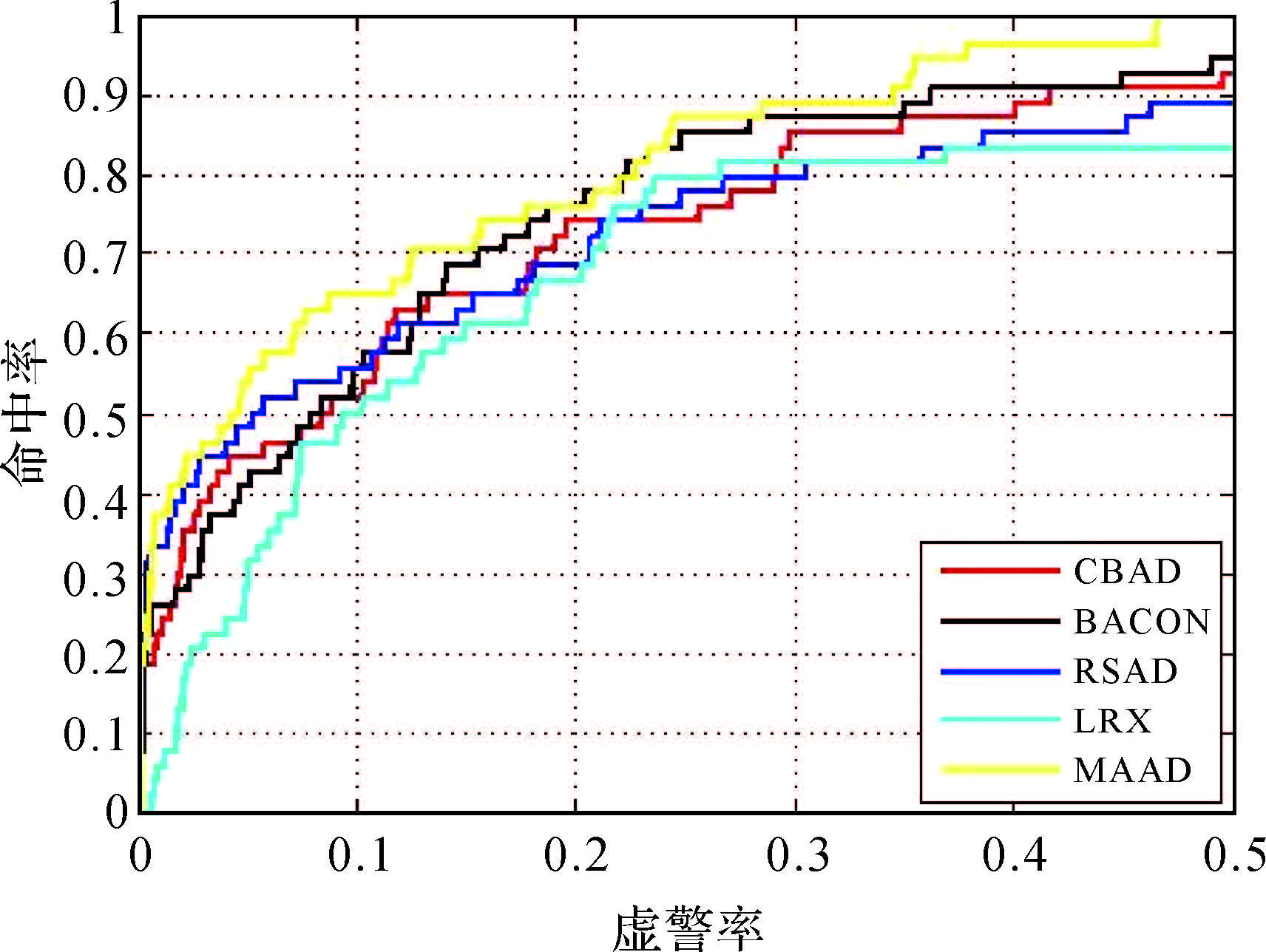
3.3 评价与分析本文采用ROC曲线及AUC对不同检测算法的效果进行定量比较。考虑到2DCAD是通过边缘特征信息进行二值化的分割,因此无法采用ROC曲线进行分析。其余算法例如CBAD、BACON、RSAD、LRX与本文算法(multi-aperture anomaly detector,MAAD)进行虚警率比较。对于HYDICE数据检测结果的ROC曲线如图 5所示,HyMap数据检测结果的ROC曲线如图 6所示。同时将不同检测算法获得结果的AUC值进行比较,如表 1所示。
|
| 图 5 HYDICE数据的ROC曲线 Fig. 5 ROC curve of HYDICE data |
|
| 图 6 HyMap数据的ROC曲线 Fig. 6 ROC curve of HyMap data |
| AUC | CBAD | BACON | RSAD | LRX | MAAD |
| HYDICE | 0.4817 | 0.7269 | 0.7104 | 0.5061 | 0.7386 |
| HyMap | 0.8491 | 0.8668 | 0.8466 | 0.8079 | 0.8963 |
分析各类算法的虚警率指标,可知MAAD算法在虚警率上优于BACON与RSAD算法,且明显优于LRX算法与CBAD算法。但是考虑到MAAD算法无须涉及参数计算问题,相对比BACON与RSAD算法,MAAD算法自适应强。
4 结 论针对复杂背景下异常与背景在光谱特征上的相关性,纯背景像素难以提取以及异常像素的光谱异常显著性下降问题,本文提出了一种基于多孔径映射的异常检测算法。该算法有以下几个优点:首先,该算法避开寻找纯背景像素构建背景模型的方式,采用多孔径映射获得关于高光谱数据的统计特征描述,实现全局视角下对局部光谱变化特征的描述。其次,基于模糊逻辑理论将异常显著性映射为连续的属性概率值,采用定量描述分析具有适中异常显著性像素的属性,从而降低检测虚警率。最后,采用去模糊融合方法对多孔径获得的不同结果进行融合,大大改善了检测算法对微弱异常目标的敏感性。仿真试验证明本文算法对于具有适中异常显著性的目标具有较强的敏感性。同时满足了复杂背景描述的局部差异性与全局一致性的要求。由于对异常目标的尺寸没有特殊要求与限制,不涉及局部窗口选择问题及参数计算问题,本文算法具有较好的自适应性与稳健性。
| [1] | MANOLAKIS D, SHAW G. Detection Algorithms for Hyperspectral Imaging Applications[J]. IEEE Signal Processing Magazine , 2002, 19 (1) : 29 –43. DOI:10.1109/79.974724 |
| [2] | CHANDOLA V, BANERJEE A, KUMAR V. Anomaly Detection:A Survey[J]. ACM Computing Surveys (CSUR) , 2009, 41 (3) : 15 . |
| [3] | MATTEOLI S, DIANI M, CORSINI G. A Tutorial Overview of Anomaly Detection in Hyperspectral Images[J]. IEEE Aerospace and Electronic Systems Magazine , 2010, 25 (7) : 5 –28. DOI:10.1109/MAES.2010.5546306 |
| [4] | REED I S, YU X. Adaptive Multiple-band CFAR Detection of An Optical Pattern with Unknown Spectral Distribution[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing , 1990, 38 (10) : 1760 –1770. DOI:10.1109/29.60107 |
| [5] | MATTEOLI S, VERACINI T, DIANI M, et al. Models and Methods for Automated Background Density Estimation in Hyperspectral Anomaly Detection[J]. IEEE Transactions on Geoscience and Remote Sensing , 2013, 51 (5) : 2837 –2852. DOI:10.1109/TGRS.2012.2214392 |
| [6] | CATTERALL S P. Anomaly Detection Based on the Statistics of Hyperspectral Imagery[C]//Proceedings of the SPIE 5546, Imaging Spectrometry X. Denver, CO:SPIE, 2004:171-178. |
| [7] | CHANG C I, CHIANG S S. Anomaly Detection and Classification for Hyperspectral Imagery[J]. IEEE Transactions on Geoscience and Remote Sensing , 2002, 40 (6) : 1314 –1325. DOI:10.1109/TGRS.2002.800280 |
| [8] | CARLOTTO M J. A Cluster-Based Approach for Detecting Man-Made Objects and Changes in Imagery[J]. IEEE Transactions on Geoscience and Remote Sensing , 2005, 43 (2) : 374 –387. DOI:10.1109/TGRS.2004.841481 |
| [9] | STEIN D W J, BEAVEN S G, Hoff L E, et al. Anomaly Detection from Hyperspectral Imagery[J]. IEEE Signal Processing Magazine , 2002, 19 (1) : 58 –69. DOI:10.1109/79.974730 |
| [10] | FRONTERA-PONS J, VEGANZONES M A, PASCAL F, et al. Hyperspectral Anomaly Detectors Using Robust Estimators[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing , 2016, 9 (2) : 720 –731. DOI:10.1109/JSTARS.2015.2453014 |
| [11] | BILLOR N, HADI A S, VELLEMAN P F. BACON:Blocked Adaptive Computationally Efficient Outlier Nominators[J]. Computational Statistics & Data Analysis , 2000, 34 (3) : 279 –298. |
| [12] | GAUECL J M, GUILLAUME M, BOURENNANE S. Whitening Spatial Correlation Filtering for Hyperspectral Anomaly Detection[C]//Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing. Philadelphia, PA:IEEE, 2005, 5:333-336. |
| [13] | KANAEV A V, ALLMAN E, MURRAY-KREZAN J. Reduction of False Alarms Caused by Background Boundaries in Real Time Subspace RX Anomaly Detection[C]//Proc. SPIE 7334, Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery XV, 733405. Orlando, Florida, USA:SPIE, 2009:733405. |
| [14] | DU Bo, ZHANG Liangpei. Random-Selection-Based Anomaly Detector for Hyperspectral Imagery[J]. IEEE Transactions on Geoscience and Remote Sensing , 2011, 49 (5) : 1578 –1589. DOI:10.1109/TGRS.2010.2081677 |
| [15] | KWON H, NASRABADI N M. Kernel RX-Algorithm:A Nonlinear Anomaly Detector for Hyperspectral Imagery[J]. IEEE Transactions on Geoscience and Remote Sensing , 2005, 43 (2) : 388 –397. DOI:10.1109/TGRS.2004.841487 |
| [16] | MATTEOLI S, DIANI M, THEILER J. An Overview of Background Modeling for Detection of Targets and Anomalies in Hyperspectral Remotely Sensed Imagery[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing , 2014, 7 (6) : 2317 –2336. DOI:10.1109/JSTARS.2014.2315772 |
| [17] | KWON H, NASRABADI N M. Hyperspectral Anomaly Detection Using Kernel RX-Algorithm[C]//Proceedings of the International Conference on Image Processing. Singapore:IEEE, 2004, 5:3331-3334. |
| [18] | DU Bo, ZHANG Liangpei. A Discriminative Metric Learning Based Anomaly Detection Method[J]. IEEE Transactions on Geoscience and Remote Sensing , 2014, 52 (11) : 6844 –6857. DOI:10.1109/TGRS.2014.2303895 |
| [19] | ZHAO Rui, DU Bo, ZHANG Liangpei, et al. Beyond Background Feature Extraction:An Anomaly Detection Algorithm Inspired by Slowly Varying Signal Analysis[J]. IEEE Transactions on Geoscience and Remote Sensing , 2015, 54 (3) : 1757 –1774. |
| [20] | PAL S K, ROSENFELD A. Image Enhancement and Thresholding by Optimization of Fuzzy Compactness[J]. Pattern Recognition Letters , 1988, 7 (2) : 77 –86. DOI:10.1016/0167-8655(88)90122-5 |
| [21] | SNYDER D, KEREKES J, FAIRWEATHER I, et al. Development of A Web-Based Application to Evaluate Target Finding Algorithms[C]Proceedings of the International Geoscience and Remote Sensing Symposium. Boston, MA:IEEE, 2008, 2:915-918. |
| [22] | YUAN Yuan, WANG Qi, ZHU Guokang. Fast Hyperspectral Anomaly Detection via High-Order 2-D Crossing Filter[J]. IEEE Transactions on Geoscience and Remote Sensing , 2015, 53 (2) : 620 –630. DOI:10.1109/TGRS.2014.2326654 |


