目前,合成孔径雷达干涉测量技术(interferometric synthetic aperture radar,InSAR)在获取数字高程模型(digital elevation model,DEM)、监测大面积地表形变和极地冰川运动等方面极具潜力,但仍有许多因素影响其实际应用的精度和范围。受时间、几何、多普勒中心频率和噪声等失相关因素的制约,InSAR干涉图存在随
机噪声,这不同程度地影响了干涉相位质量,在噪声水平严重的情况下,易导致后续相位解缠误差增大,甚至无法进行解缠。基于此,对干涉图进行滤波是保障InSAR产品质量的重要环节[1]。
干涉图滤波一般分为两类:第一类是空域滤波,如圆周期滤波[2]、Lee自适应滤波[3]、堆栈滤波[4]和旋滤波[5]等;第二类为频域滤波,如小波滤波[6-7]、Goldstein滤波及其改进方法[8-9]等。空域滤波继承了传统图像滤波的思想,并结合SAR图像空间特征作了改进。大量试验表明,当SAR图像地表特征比较复杂时,利用该类方法进行干涉图滤波,易造成干涉条纹混叠等失真现象,且常伴随一定的计算复杂度和时间复杂度问题[10]。相比之下,频率域滤波方法中的Goldstein滤波在去噪和保持影像分辨率方面效果更加显著,且计算较为简单,因而广泛用于商业及免费SAR数据处理软件中,已成为当前国际上的主流方法。
随着近年来InSAR数据处理方法的不断发展,在经典Goldstein滤波方法的基础上涌现出许多改进方法[9, 11]。为克服Goldstein滤波参数选取的主观性,Baran滤波[12]利用干涉图相干系数以自适应地计算滤波参数,使滤波效果得到了明显改善。文献[13]借鉴Baran滤波方法,利用伪相关图自动计算滤波参数,提出了一种干涉图迭代滤波方法。该方法充分利用了干涉图自身携带的信息来指导滤波参数的计算,取得了较好的滤波结果。然而,这些自适应方法也存在一些不足之处。如Baran滤波[12]在滤波设计时并未考虑相干系数估计量的有偏性和低精度,造成滤波参数的估值偏低。另外,文献[13]的迭代Goldstein滤波算法中估计量的统计性质尚不明确,且伪相关图的质量易受SAR图像中的地形信息的影响[9, 14],这导致很难评估其滤波参数的优劣。从模拟结果来看,伪相干图的值要明显大于相干系数真值,故滤波参数也是被低估的。为解决以上问题,本文引入第二类统计方法对相干系数进行修正,其主要依据是该统计量能够兼顾系统有偏性和方差,从而精确估计滤波参数以便获得最优的滤波干涉图。
1 基于第二类统计相干性估计量的自适应滤波本节在回顾经典Goldstein滤波方法的基础上,引入第二类统计方法对滤波参数进行稳健估计,并结合待滤波干涉图的干涉视数获得干涉图滤波模型。
1.1 Goldstein滤波Goldstein频域滤波算法[15]的原理是将干涉图分割为相互重叠的滑动窗口(干涉图小块),通过二维傅里叶变换计算每个滑动窗口相位的功率谱,并对该功率谱进行平滑
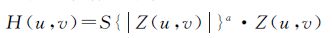 (1)
(1)
式中,α为滤波参数;S{·}为平滑算子;u和v为空间频率;Z(u,v)和H(u,v)分别为滤波前后的干涉图块的傅里叶谱。通过对平滑后的傅里叶谱与原滑动窗口傅里叶谱的乘积进行傅里叶逆变换可以得到滤波后的干涉图。滤波参数α∈[0,1],当α=0时,没有滤波效果,当α=1时,平滑力度最大。由于干涉图噪声分布的非均匀性,因此通常情况下很难确定合适的全局滤波参数α。为解决上述问题,Baran滤波根据相干性是相位噪声水平和评价干涉图质量的指标[8, 12, 17],采用关系式1-${\bar{\hat{r}}}$取代原Goldstein滤波中的固定滤波参数α,其中,${\bar{\hat{r}}}$为滑动窗口中有效像元(滑动窗口减去重叠区域)的平均相干性,以便在相干性低的区域(噪声较强)采用较大的平滑力度,在相干性高的区域(噪声较弱)采用较小的平滑力度,从而在去除噪声的同时减少干涉图信息的丢失。
1.2 基于第二类统计的无偏相干性估计由于SAR传感器不能在同一时刻连续成像,在估计相干性时,通常用SAR信号空间平均来代替汇集平均,求得的相干系数为
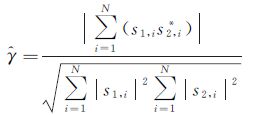 (2)
(2)
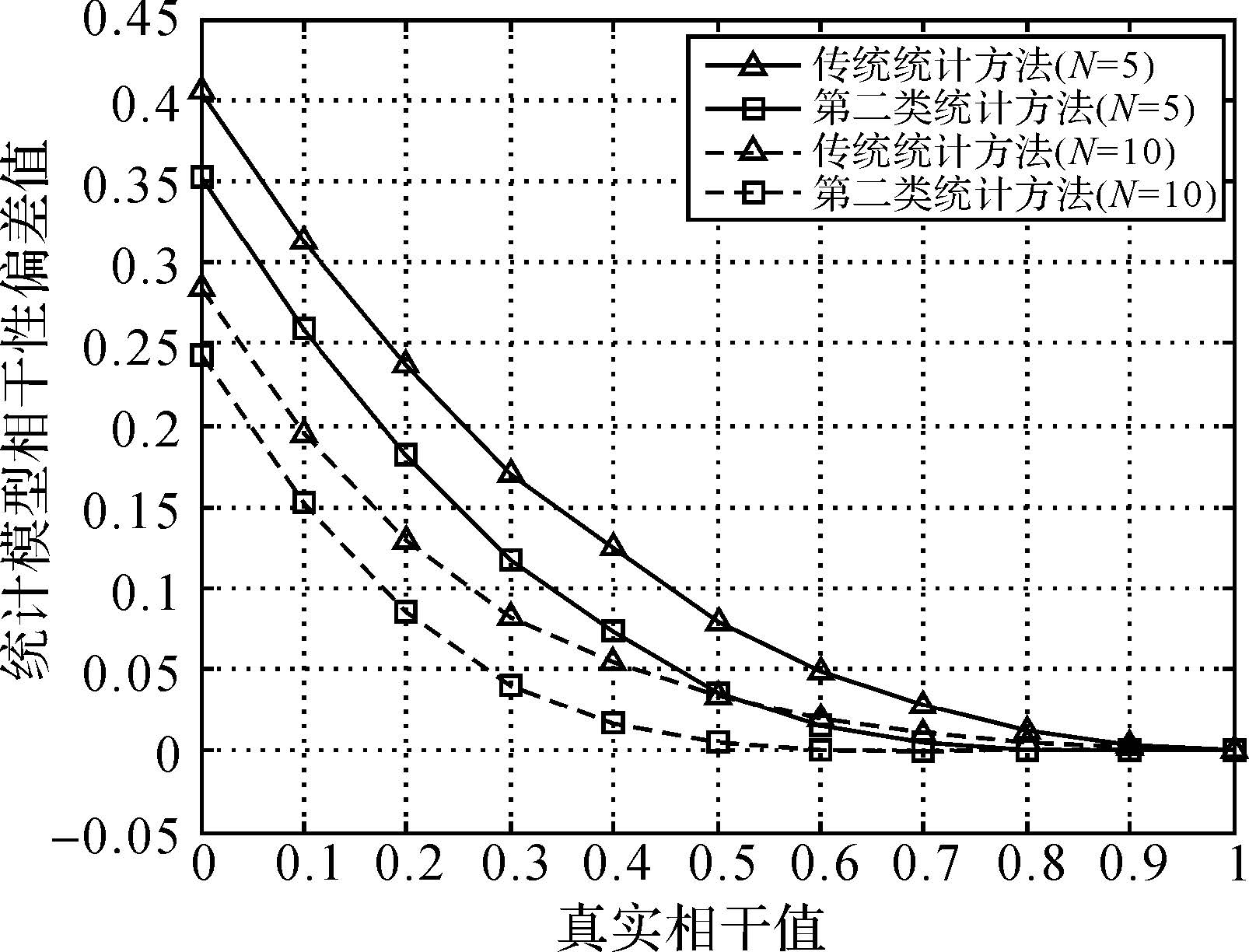
式中,|·|表示对复信号取模操作;s1,is2,i*表示对两个雷达复信号s1和s2取共轭相乘操作;N表示样本数。根据已有文献,估计量是有偏的,其偏差随真实相干性和样本数量的增加而减小[18-19]。针对这一问题,本文引入基于梅林变换的第二类统计估计量。相比传统估计量,第二类统计方法可获得统计偏差和方差更小的估计量[17]。两种估计量的定量描述详见图 1。
|
| 图 1 统计模型相干性统计偏差对比图 Fig. 1 Coherence bias of different estimators |
第二类统计量仅对定义在正半轴上的函数有效,根据定义,概率密度函数p(x)(x∈[0,+∞))的第二类第一特征函数$\phi $(s)和第二类第二特征函数ψ(s)可分别表示为[20]
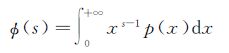 (3)
(3)
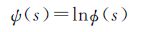 (4)
(4)
第二类统计的第二类矩定义为
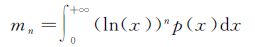 (5)
(5)
根据已知的相干量级的概率密度函数p(d\D,N)[21]
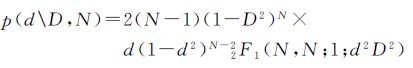 (6)
(6)
可得其一阶log矩为
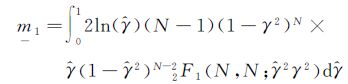 (7)
(7)
式中,γ代表真实相干性;2F1表示超几何函数;N表示样本数。通过计算log矩的指数,可以获得第二类统计相干性量级的等效一阶矩
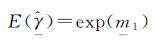 (8)
(8)
式中,E(·)表示期望;${\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\hat{\gamma }}}$表示取对数后的样本相干性量级。根据大数定律,当样本数N足够大,样本估计接近真实值${\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\hat{\gamma }}}$≈m1。因此,通过反方程式(8),可得到第二类统计估计量为
 (9)
(9)
式中,${\bar{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\hat{\gamma }}}}$表示第二类统计相干性样本均值。最后的表述形式为
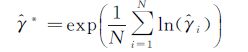 (10)
(10)
图 1展示了蒙特卡罗(Monte Carlo)随机模拟试验的结果。可以看出,在样本N的取值相同时,无论真实相干量级是多少,基于第二类统计的估计量较传统估计量偏差更小。当N=5时,在低相干性区域的偏差大于0.1,暗示了滤波参数差异大于0.1。
1.3 改进的自适应Goldstein滤波在重新定义估计量之后,可以用估计量式(10)代替Baran滤波模型,获得改进的滤波参数。然而在理论上,相位噪声是相干性和干涉视数N的函数,仅考虑相干性的滤波因子不能完全反映当前干涉图噪声的情况[22]。相位标准方差${{\sigma }_{\phi }}$与干涉图相干性γ和干涉视数N之间的关系为[23]
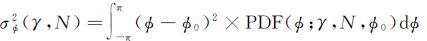 (11)
(11)
式中,$\phi $为干涉图相位;$\phi $0为相位的期望值;PDF为相位概率密度函数
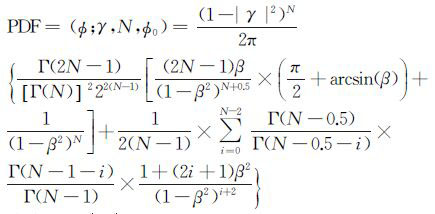 (12)
(12)
式中,β=|γ|cos($\phi $-$\phi $0);Γ为Gamma函数。
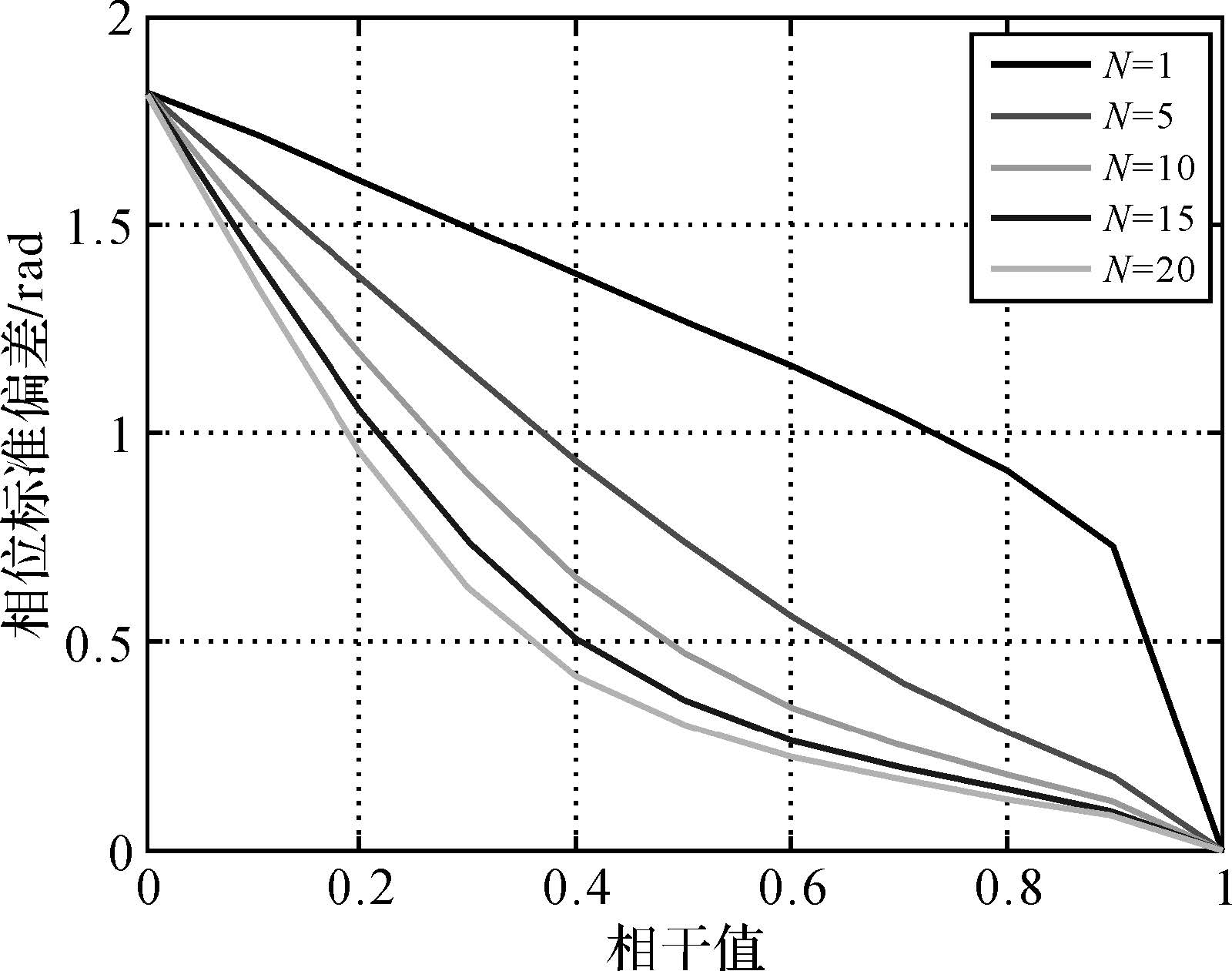
图 2为噪声相位标准方差随干涉图相干性和干涉视数的变化情况。从图中可知,干涉图噪声水平分别随其相干性和干涉视数的增加而减小,故可利用干涉图的相干值和干涉视数重新定义新的滤波参数,从而使其能够更好地适应干涉图噪声的空变特征。
|
| 图 2 噪声相位标准偏差与相干值及样本数关系 Fig. 2 Phase noise standard deviation versus the coherence and samples |
在实际应用中,由于有偏估计和超几何函数的存在,采用方程式(2)、式(11)和式(12)联合估计相位方差会显著增加估计误差和计算复杂度。根据文献[9],相位噪声估计的简易形式以及它与最优滤波参数的函数关系可以近似表述为
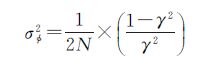 (13)
(13)
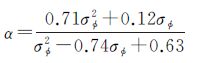 (14)
(14)
联合方程式(10)、式(13)和式(14),得到稳健的滤波参数估计量α
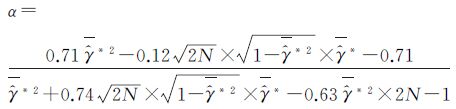 (15)
(15)
其中,${\bar{\hat{\gamma }}}$*为滑动窗口中有效像元(滑动窗口减去重叠区域)内基于第二类统计相干系数的平均值。
综上,新方法的具体步骤如下:
(1) 利用式(2)计算干涉图的原始相干图,再利用式(10)对原始干涉图进行偏差纠正,得到近似无偏的相干系数图。
(2) 把原始干涉图分成若干小块(如32×32像素),为保持小块之间条纹的连续性,每块之间有一定的重叠像素。
(3) 利用式(15)和步骤(1)中的相干系数估算有效区域内(小块像素减去重叠像素)的滤波参数α,再利用式(1)对干涉图进行分块滤波,最后通过逆变换得到滤波后的干涉图。
2 滤波试验对比分析本文采用模拟数据和真实数据对Goldstein滤波、Baran滤波、迭代Goldstein滤波以及本文提出的新滤波方法进行了对比分析。为保证试验公平性,在以下试验中滤波窗口均采用典型滤波窗口,即大小均为32×32,重叠区域为28。传统Goldstein滤波中参数α=0.5,文献[13]的迭代Goldstein滤波为一次迭代滤波的结果。
2.1 模拟数据首先,采用多分形技术和ERS卫星参数(垂直基线30m)模拟500×500像素的无噪声相位图(见图 3(b))。接着,在时空去相关、体散射去相关的影响下,模拟无偏相干系数图(见图 4(a))。然后根据相位标准偏差公式和模拟的相干系数矩阵获得各像素的相位噪声(N=9),最后把模拟的噪声逐点加到无噪声的相位图上进行缠绕,得到含噪干涉图(见图 3(a))。本文将相干性的理论偏差分别加入无偏相干图后得到有偏的相干图(见图 4(b)、图 4(d)),伪相关系数(见图 4(c))采用样本估计公式(参考文献[13]中的式(7))直接获得。

|
| 图 3 含噪声和无噪声干涉图 Fig. 3 Noise added and free interferograms |

|
| 图 4 真实相干图和有偏相干图 Fig. 4 True coherence and bias added coherence maps |
将图 4(b)的相干值代入Baran滤波公式,获得Baran的滤波结果;将图 4(c)的相干图代入文献[13]的迭代Goldstein滤波公式,得到迭代Goldstein滤波结果;最后,将图 4(d)的相干值代入式(15)获得新方法的滤波结果。从图 5可知,所有滤波方法都能得到条纹相对清晰的干涉图,表明能够去除强噪声。但定性地看,新提出的滤波方法滤波效果明显优于其他3种滤波方法,最大限度地还原了原始相位信息。

|
| 图 5 模拟数据的滤波结果对比图 Fig. 5 Filtered interferograms |
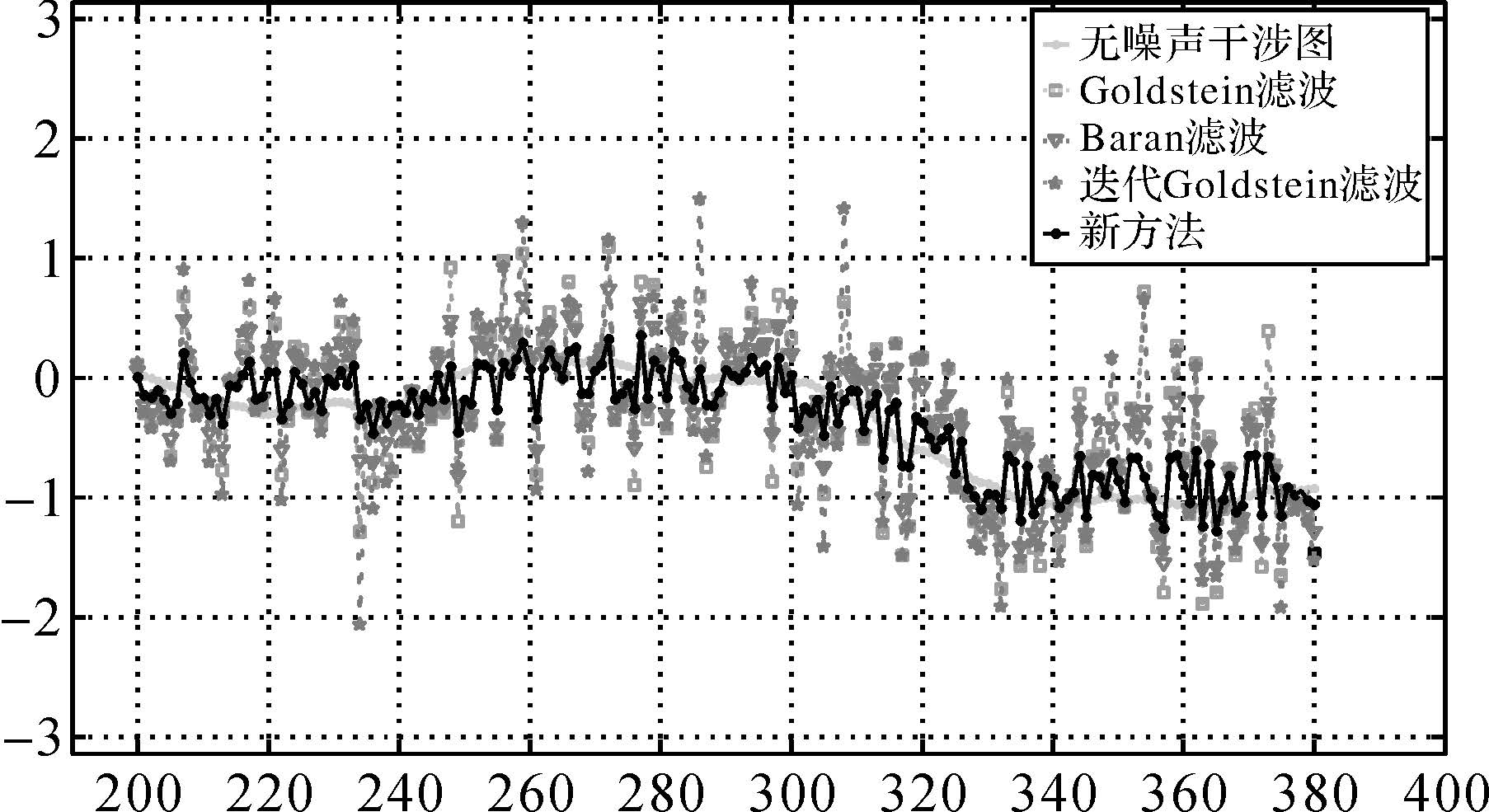
为定量评价滤波结果,本文选取了相位差值和(the sum of phase difference,SPD)[24]及相位均方误差(RMS)作为干涉图质量评价标准,滤波后干涉图的相位梯度值越小,表征干涉图越平滑,滤波效果越好;均方误差越小,代表滤波器的保真性越好。从表 1中可以看出新方法较其他3种滤波具有更好的去噪能力,使模拟噪声干涉图的SPD减少了87.5%。本文还针对每幅干涉图的同一位置(图 5中标记为A黑线所示)作了剖面分析。如图 6所示,从滤波细节上看,相比其他滤波方法,新方法的整体滤波结果更接近原始无噪声相位值,从而说明了新方法在去噪的同时具有更好的信号保真性。
| 滤波方法 | 评价指标 | |||
| SPD | RMS | |||
| 数量(×105) | 减少率/(%) | |||
| 原干涉图 | 3.7793 | 1.2186 | ||
| Goldstein | 1.5890 | 58.0 | 0.5538 | |
| Baran | 1.0356 | 72.6 | 0.3685 | |
| 迭代Goldstein | 1.6459 | 56.4 | 0.5698 | |
| 新方法 | 0.4917 | 87.5 | 0.1950 | |
|
| 图 6 模拟数据滤波结果局部横断面 Fig. 6 Cross-sections of interferograms filtered with different methods 中文注解 |
2.2 真实数据 2.2.1 夏威夷火山区域
为验证上述各种算法在真实数据中干涉条纹稠密区域的滤波效果,本文首先选取了美国夏威夷火山区域的两幅ASAR数据并截取了其中200×200的子区域,其中,图 7(a)为原始干涉图;图 7(b)、图 7(d)分别为基于两类统计模型的相干系数图;图 7(c)为伪相关系数图;图 8为原始干涉图黑色方框区域经过4种滤波方法滤波后的干涉图。

|
| 图 7 夏威夷干涉图和干涉质量图 Fig. 7 Interferogram of Hawaii and estimated coherence maps using different estimators |

|
| 图 8 夏威夷干涉图滤波结果对比图 Fig. 8 Interferogram of Hawaii filtered with different methods |
图 8中4种滤波方法都能滤除一定的干涉图噪声,但是经过迭代Goldstein滤波的干涉图中含有较多噪声,这是因为估计量伪相干值也是有偏的,并产生高估偏差。因此,这一高估现象导致迭代Goldstein滤波的滤波参数被低估,在强噪声处的滤波效果降低。同理,基于传统统计的Baran滤波在低相干区域的滤波效果也较差。而在精确估计相干性后,本文提出的方法较好地抑制了噪声水平,得到了更加清晰的干涉条纹。本文采用国际上通用的滤波评价指标对结果进行评定,即相位奇异点(residue point number)[15]以及SPD。干涉图中的相位奇异点(残差点)越少,表明噪声程度越小,更利于相位解缠处理。如表 2所示,新滤波可以获得最优的结果,使原来噪声干涉图的SPD值降低了36.7%,相位奇异点值则降低了71.7%。这说明在强噪区域,更加精确的相干性估计有益于提高相位质量。
| 滤波方法 | 评价指标 | ||||
| SPD | residues number | ||||
| 数量 (×104) | 减少率 /(%) | 数量 (×103) | 减少率 /(%) | ||
| 原干涉图 | 7.3037 | 7.711 | |||
| Goldstein | 6.1692 | 15.5 | 4.389 | 43.1 | |
| Baran | 5.5614 | 23.9 | 3.114 | 59.6 | |
| 迭代Goldstein | 6.2196 | 14.8 | 4.209 | 45.4 | |
| 新方法 | 4.5149 | 36.7 | 2.164 | 71.7 | |
2.2.2 徐州矿区
本文进一步选取了中国徐州矿区的两幅PALSAR数据验证新方法在干涉条纹稀疏区域的滤波效果。为展现滤波细节,本次试验截取了干涉图中512×512像素的子区域,图 9(a)—(d)分别给出了其中的原始干涉图、基于两类统计模型的相干系数图和伪相关系数图,该图进一步验证了基于第二类统计的相干性估计可获得较传统统计模型偏差更小的估计量。图 10为原始干涉图经过4种滤波方法处理后的滤波结果图。

|
| 图 9 徐州地区干涉图和干涉质量图 Fig. 9 Interferogram of Xuzhou and estimated coherence maps using different estimators |
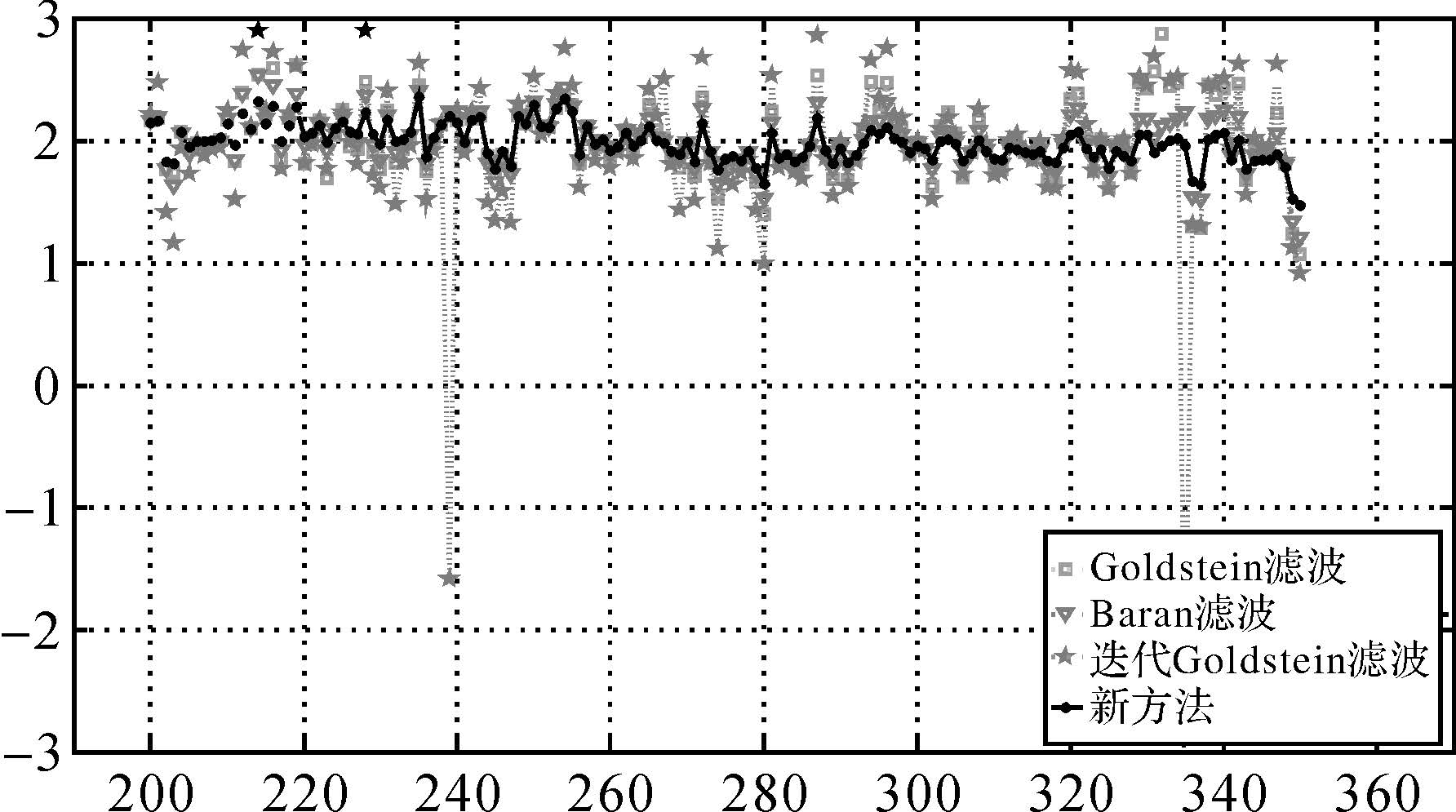
图 10同样给出了笔者期望的滤波结果,与其他3种滤波方法所获滤波结果相比,经过新方法处理的滤波结果图 10(d)再一次展现了较好的平滑效果。此处,本小节仍然采用了相位奇异点和SPD两种滤波评价指标对来自上述4种滤波方法的滤波结果进行定量评定,所得结果已列于表 3,本次试验新的滤波方法使原来噪声干涉图的SPD值和相位奇异点值分别降低了89.7%和99.5%。图 11给出了图 10中4幅干涉图黑色横线位置的剖面图,由于所选区域位于平原区,且为城市区域,地势较平坦,故滤波后的干涉图应该较平滑,而新滤波方法得到的结果比其他3种方法得到的都理想,无明显相位波动。因此,结合图 10和图 11的定量分析结果,不难发现新方法在条纹稀疏的噪声区域,也能得到较好的滤波结果。

|
| 图 10 徐州干涉图滤波结果对比图 Fig. 10 Interferogram of Xuzhou filtered with different methods |
| 滤波方法 | 评价指标 | ||||
| SPD | Residues number | ||||
| 数量 (×105) | 减少率 /(%) | 数量 (×104) | 减少率 /(%) | ||
| 原干涉图 | 4.8515 | - | 3.804 | - | |
| Goldstein | 1.5016 | 69.0 | 0.104 | 97.3 | |
| Baran | 0.9827 | 79.9 | 0.051 | 98.7 | |
| 迭代Goldstein | 2.3057 | 52.5 | 0.144 | 96.2 | |
| 新方法 | 0.4995 | 89.7 | 0.020 | 99.5 | |
|
| 图 11 徐州干涉图滤波结果局部横断面 Fig. 11 Cross-sections of interferograms of Xuzhou filtered with different methods |
3 结 论
本文提出了一种新的Goldstein自适应滤波方法,该方法可以在第二类统计的基础之上获得更加精确的相干性估计量,进而获得更准确的滤波参数。从模拟和真实数据的测试情况来看,相比于现有的自适应方法,该方法能在维护分辨率的同时兼顾滤波效果,降低噪声能力较其他3种滤波方法提高了近一倍。在低相干区域,新方法因纠正了滤波参数的低估偏差而抑制了强噪声,进而解决了现有方法在低相干区域欠滤波的问题。
| [1] | 黄长军, 郭际明, 喻小东, 等. 干涉图EMD-自适应滤波去噪法[J]. 测绘学报 , 2013, 42 (5) : 707–714. HUANG Changjun, GUO Jiming, YU Xiaodong, et al. The Study of Interferogram Denoising Method Based on EMD and Adaptive Filter[J]. Acta Geodaetica et Cartographica Sinica , 2013, 42 (5) : 707 –714. |
| [2] | EICHEL P, GHIGLIA D, JAKOWATZ C, et al. Spotlight SAR Interferometry for Terrain Elevation Mapping and Interferometric Change Detection[R]. Sand:Sandia National Labs Technology, 1993:2539-2546. |
| [3] | LEE J S, PAPATHANASSIOU K P, AINSWORTH T L, et al. A New Technique for Noise Filtering of SAR Interferometric Phase Images[J]. IEEE Transactions on Geoscience and Remote Sensing , 1998, 36 (5) : 1456 –1465. DOI:10.1109/36.718849 |
| [4] | BUEMI M E, JACOBO J, MEJAIL M. SAR Image Processing Using Adaptive Stack Filter[J]. Pattern Recognition Letters , 2010, 31 (4) : 307 –314. DOI:10.1016/j.patrec.2009.02.008 |
| [5] | 于晶涛, 陈鹰. 一种新的INSAR干涉条纹图滤波方法[J]. 测绘学报 , 2004, 33 (2) : 121–126. YU Jingtao, CHEN Ying. A New Filter on InSAR Interferogram Fringe[J]. Acta Geodaetica et Cartographica Sinica , 2004, 33 (2) : 121 –126. DOI:10.3321/j.issn:1001-1595.2004.02.006 |
| [6] | LOPEZ-MARTINEZ C, FABREGAS X. Modeling and Reduction of SAR Interferometric Phase Noise in the Wavelet Domain[J]. IEEE Transactions on Geoscience and Remote Sensing , 2002, 40 (12) : 2553 –2566. DOI:10.1109/TGRS.2002.806997 |
| [7] | 何儒云, 王耀南. 一种基于小波变换的InSAR干涉图滤波方法[J]. 测绘学报 , 2006, 35 (2) : 128–132. HE Ruyun, WANG Yaonan. InSAR Interferogram Filtering Based on Wavelet Transform[J]. Acta Geodaetica et Cartographica Sinica , 2006, 35 (2) : 128 –132. DOI:10.3321/j.issn:1001-1595.2006.02.007 |
| [8] | JIANG Mi, DING Xiaoli, LI Zhiwei, et al. The Improvement for Baran Phase Filter Derived from Unbiased InSAR Coherence[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing , 2014, 7 (7) : 3002 –3010. DOI:10.1109/JSTARS.2013.2296322 |
| [9] | JIANG Mi, DING Xiaoli, TIAN Xin, et al. A Hybrid Method for Optimization of the Adaptive Goldstein Filter[J]. ISPRS Journal of Photogrammetry and Remote Sensing , 2014, 98 : 29 –43. DOI:10.1016/j.isprsjprs.2014.09.012 |
| [10] | 尹宏杰. 基于InSAR的矿区地表形变监测研究[D]. 长沙:中南大学, 2009. YIN Hongjie. Ground Subsidence Monitoring in Mining Area Using InSAR[D]. Changsha:Central South University, 2009. |
| [11] | LI Z W, DING X L, HUANG C, et al. Improved Filtering Parameter Determination for the Goldstein Radar Interferogram Filter[J]. ISPRS Journal of Photogrammetry and Remote Sensing , 2008, 63 (6) : 621 –634. DOI:10.1016/j.isprsjprs.2008.03.001 |
| [12] | BARAN I, STEWART M P, KAMPES B M, et al. A Modification to the Goldstein Radar Interferogram Filter[J]. IEEE Transactions on Geoscience and Remote Sensing , 2003, 41 (9) : 2114 –2118. DOI:10.1109/TGRS.2003.817212 |
| [13] | ZHAO Chaoying, ZHANG Qin, DING Xiaoli, et al. An Iterative Goldstein SAR Interferogram Filter[J]. International Journal of Remote Sensing , 2012, 33 (11) : 3443 –3455. DOI:10.1080/01431161.2010.532171 |
| [14] | GHIGLIA D C, PRITT M D. Two-dimensional Phase Unwrapping:Theory, Algorithms, and Software[M]. New York: Wiley-Interscience, 1998 . |
| [15] | GOLDSTEIN R M, WERNER C L. Radar Interferogram Filtering for Geophysical Applications[J]. Geophysical Research Letters , 1998, 25 (21) : 4035 –4038. DOI:10.1029/1998GL900033 |
| [16] | BARAN I. Advanced Satellite Radar Interferometry for Small-scale Surface Deformation Detection[D]. Perth:Curtin University of Technology, 2004. |
| [17] | 蒋弥, 丁晓利, 李志伟, 等. 基于时间序列的InSAR相干性量级估计[J]. 地球物理学报 , 2013, 56 (3) : 799–811. JIANG Mi, DING Xiaoli, LI Zhiwei, et al. InSAR Coherence Magnitude Estimation Based on Data Stack[J]. Chinese Journal of Geophysics , 2013, 56 (3) : 799 –811. |
| [18] | TOUZI R, LOPES A, BRUNIQUEL J, et al. Coherence Estimation for SAR Imagery[J]. IEEE Transactions on Geoscience and Remote Sensing , 1999, 37 (1) : 135 –149. DOI:10.1109/36.739146 |
| [19] | ABDELFATTAH R, NICOLAS J M. Interferometric SAR Coherence Magnitude Estimation Using Second Kind Statistics[J]. IEEE Transactions on Geoscience and Remote Sensing , 2006, 44 (7) : 1942 –1953. DOI:10.1109/TGRS.2006.870440 |
| [20] | NICOLAS J M, ANFINSEN S N. Introduction to Second Kind Statistics:Application of Log-Moments and Log-Cumulants to the Analysis of Radar Image Distributions[R]. Technical Note, Translation from French, 2012. |
| [21] | TOUZI R, LOPES A. Statistics of the Stokes Parameters and of the Complex Coherence Parameters in One-Look and Multilook Speckle Fields[J]. IEEE Transactions on Geoscience and Remote Sensing , 1996, 34 (2) : 519 –531. DOI:10.1109/36.485128 |
| [22] | SUO Zhiyong, ZHANG Jinqiang, LI Ming, et al. Improved InSAR Phase Noise Filter in Frequency Domain[J]. IEEE Transactions on Geoscience and Remote Sensing , 2016, 54 (2) : 1185 –1195. DOI:10.1109/TGRS.2015.2476355 |
| [23] | HANSSEN R F. Radar Interferometry:Data Interpretation and Error Analysis[M]. Netherlands: Springer, 2001 . |
| [24] | LI Zhilin, ZOU Weibao, DING Xiaoli, et al. A Quantitative Measure for the Quality of InSAR Interferograms Based on Phase Differences[J]. Photogrammetric Engineering & Remote Sensing , 2004, 70 (10) : 1131 –1137. |



