合成孔径雷达差分干涉测量(differential synthetic aperture radar interferometry,DInSAR)技术在地表形变监测、火山监测、地震位移测量等领域具有极大的应用潜力[1]。基于重复轨道的DInSAR技术容易受空间失相干、时间失相干和大气干扰等因素的影响,难以进行常态化的实际应用[2-3]。为了克服传统DInSAR技术的这些限制,自上世纪90年代末,一些新的InSAR处理技术被提出。这些技术的共同特点是:基于时间序列SAR影像进行处理,处理的对象不是整幅影像的全部像元,而是其中具有稳定散射特性从而能在较长时间间隔内保持高相干的像元子集,也就是高相干点目标。主要方法有以永久散射体干涉(permanent scatterer或者persistent scatterer interferometry,或PS-InSAR)为代表的单一主影像时间序列InSAR技术[4-10]和以小基线集 (small baseline subset interferometry,或SBAS InSAR) 技术为代表的多主影像时间序列InSAR技术[11-19]。笔者将其统称为时间序列InSAR技术。
在时间序列InSAR技术中,当提取完点目标后,通常利用Delaunay三角网连接所有的点目标[12],通过相邻点相位差分并建立线性相位模型求解形变参数。但受大气相关距离限制以及模型相干系数阈值影响,Delaunay三角网常常不能完整地连接所有点目标。当点目标质量好且密度较大时,如城区,通过Delaunay建网能够较好地连接各点目标,实现形变参数的解算。但是当点目标质量较差或相隔较远时,如非城区,容易出现大量孤立的子网,这时就无法解算形变信息。
对于这个问题,时间序列InSAR技术的主要提出者Ferretti、Berardino、Mora等人并没有给出解决方案,读者无法从已有文献中得知这方面的技术细节。后来,学者们提出了两种更加稳健的网络连接方式,文献[20]提出了一种点目标自由连接网络方法(freely-connected network,FCN),将一定距离内的所有点两两连接,从而极大地增加了三角网的边数。文献[21]提出了复杂网络与Delaunay三角网相结合的点目标连接方法,首先利用Delaunay三角网对所有点目标快速建网,提取城区密集点目标的形变参数,然后在大气相关距离范围内对没有被估计的点目标建立类似于自由连接的复杂网络,重新计算形变参数。
上述两种方法均能大幅提高点目标之间的连接关系,具有很好的抗噪声能力,但显而易见的是,它们所带来的计算量非常大,容易造成巨大的数据冗余,不适合大区域数据处理。因此,发展一种快速且稳健的Delaunay子网连接技术对于大区域地面沉降监测有重要意义。本文提出了一种多层级、不同步长的子网最近邻点目标快速连接方法,其显著特点是通过逐层连网的方式,可快速减少子网数目,实现子网高效连接。与现有的自由连接网络或复杂网络相比,将大幅提高处理效率。
为了验证该方法的有效性,以华北地区河北省廊坊市为例,利用2003年10月17日至2010年10月15日获取的24景欧洲空间局EnviSat ASAR影像开展地表形变反演试验,并与复杂网络方法进行了耗时与精度方面的对比。自由连接网络方法由于初始就会生成大量的连接边,计算量巨大,因此本文没有与该方法进行对比。
1 不连通子网多层级连接方法 1.1 点目标连接网络分析在时间序列InSAR技术中,当提取稳定点目标后,通常在大气相关距离内利用Delaunay三角网连接相邻点目标。所谓大气相关距离是指大气在空间上存在一个相关距离,当两点间距小于该距离时,可以认为它们的大气相位近似相等,该距离一般为1~3km[22]。通过三角网确定点目标之间关系,进而对每条边上相邻点目标的差分相位进行二次差分。
考察三角网边上两顶点之间的差分相位差,它包括线性地表形变、非线性地表形变、DEM高程误差、大气影响、轨道误差及噪声6个部分贡献。轨道误差由于呈现空间低频特征,可将其视为大气影响的一部分;在大气相关距离内,相邻点的大气影响相位可以相互抵消;非线性形变相位也具有较强的空间相关性,通过相邻点差分可以消除该项贡献。因此可以将差分相位差近似等于线性形变和高程误差二者贡献,并建立包含相对线性形变速率和相对高程误差的线性模型。
为了求解这两个参数,建立如下的目标函数方程,即模型相干系数方程[12],通过最大化方法求解
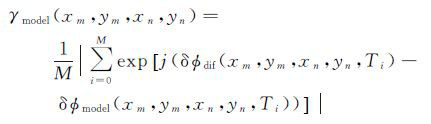 (1)
(1)
式中,(xm,ym)、(xn,yn)为边的两顶点位置坐标;δdif为差分相位差;δmodel为线性模型相位;Ti为第i幅干涉图的时间基线;M为干涉图数目。γ为模型相干系数,反映了两点目标间相对线性形变速率和相对高程误差对差分相位差的拟合程度,该值在[0,1]区间内变化,值越大表示拟合程度越高,求解结果越可靠;值越小表示拟合程度越低,求解结果越不可靠。
当对所有的边完成模型相干系数最大化求解后,需要设置一定的阈值,判断哪些连接边是可靠的(正确解算的边)。在这方面已有学者作了深入研究[5, 12, 23-25],具体阈值的选择应视试验区和数据源情况而定。本文根据所用试验数据,选择0.7作为该阈值经验值。模型相干系数不低于该阈值的边认定为可靠边予以保留[12],不满足此条件的边(不可靠边)将被剔除。
可见,受大气相关距离以及模型相干系数阈值的限制,在点目标分布稀疏的非城镇地区,Delaunay三角网的部分连接边会因为相邻点目标距离过大或模型相干系数较低而被剔除,初始完整的三角网络将被分割为多个孤立的子网,如图 1(a)所示。此时就需要对这些子网间的点目标重新连接,通过计算式(1)查找有效边,以连接这些子网。

|
| 图 1 多层级相邻子网连接示意图 Fig. 1 Sketch map of multi-layer subnetwork connection (MLSC) |
1.2 子网多层级连接算法
为了避免自由连接网络和复杂网络方法带来的巨大计算量,本文提出多层级扩展的相邻子网连接技术,实现不连通子网的快速、稳健闭合。
首先利用邻域搜索方法,查找所有不连通的Delaunay三角网子网及其所属点目标,并对各子网进行编号,1、2、3、…、N。
其次按照子网编号顺序,依次计算每个子网的外接矩形,将位于外接矩形4条边上的点目标作为该子网的边界点,通常情况下,每个子网会有4个边界点,当某条边上有多个点目标时,则仅选择最左边(列坐标最小)或最上边(行坐标最小)的点目标为该条边的边界点;对于某些较小的子网,如三角形或线段形子网,则只有3个或两个边界点。
再以每个子网的各边界点为中心,以给定步长R(可设为500m)为半径,搜索该范围内的所有点目标,并将这些点目标归入相应的子网,如图 1(b)所示,A1为子网A的一个边界点,在设定范围还有A2、B1、B2、B3共4个点目标,这样子网A和子网B之间可连接的共有6条边(A1B1、A1B2、A1B3、A2B1、A2B2、A2B3),将它们按距离由小到大排序,依次计算每条边的模型相干系数,当该系数大于等于给定阈值时即停止,此时相邻子网连接成功;否则继续计算,直至最后一条连接边,若所有边的系数都小于阈值时,子网连接不成功。
理想情况下,A1 B1是子网A和子网B的最短连接路径,但当其模型相干系数小于阈值时,其他5条边均有可能是连接边。若这6条边的模型相干系数都小于阈值,则在该层级(即500m步长)中放弃子网A与子网B的连接。
当遍历完所有的子网后,重新计算新的子网个数并编号,此时子网数目将大大减少,再以每个新子网的各个边界点为中心,将步长扩大为2R(即1000m),搜索该范围内的所有点目标,重复上述流程,直至遍历结束。
同样方法,逐渐扩大搜索步长3R(1500m)、4R(2000m)等,直至大气相关距离最大值3000m,进行子网连接。通过这种多层级扩展方式,逐步减少子网总数,从而实现快速连接。
在扩展过程中,停止计算的条件有两个:一是新的子网数为1,即所有子网已经全部连接,无需扩展;或是第2种情形,即子网数目不变,即通过扩大步长不能连接新的子网,此时不再扩展。
需要注意的是,对于不同分辨率的数据,由于监测点目标的空间密度差异较大,其扩展步长应适当调整。如高分辨率的TerraSAR-X或COSMO-SkyMed数据,点目标数目较多,此时可适当减小扩展步长,以减少搜索耗时。
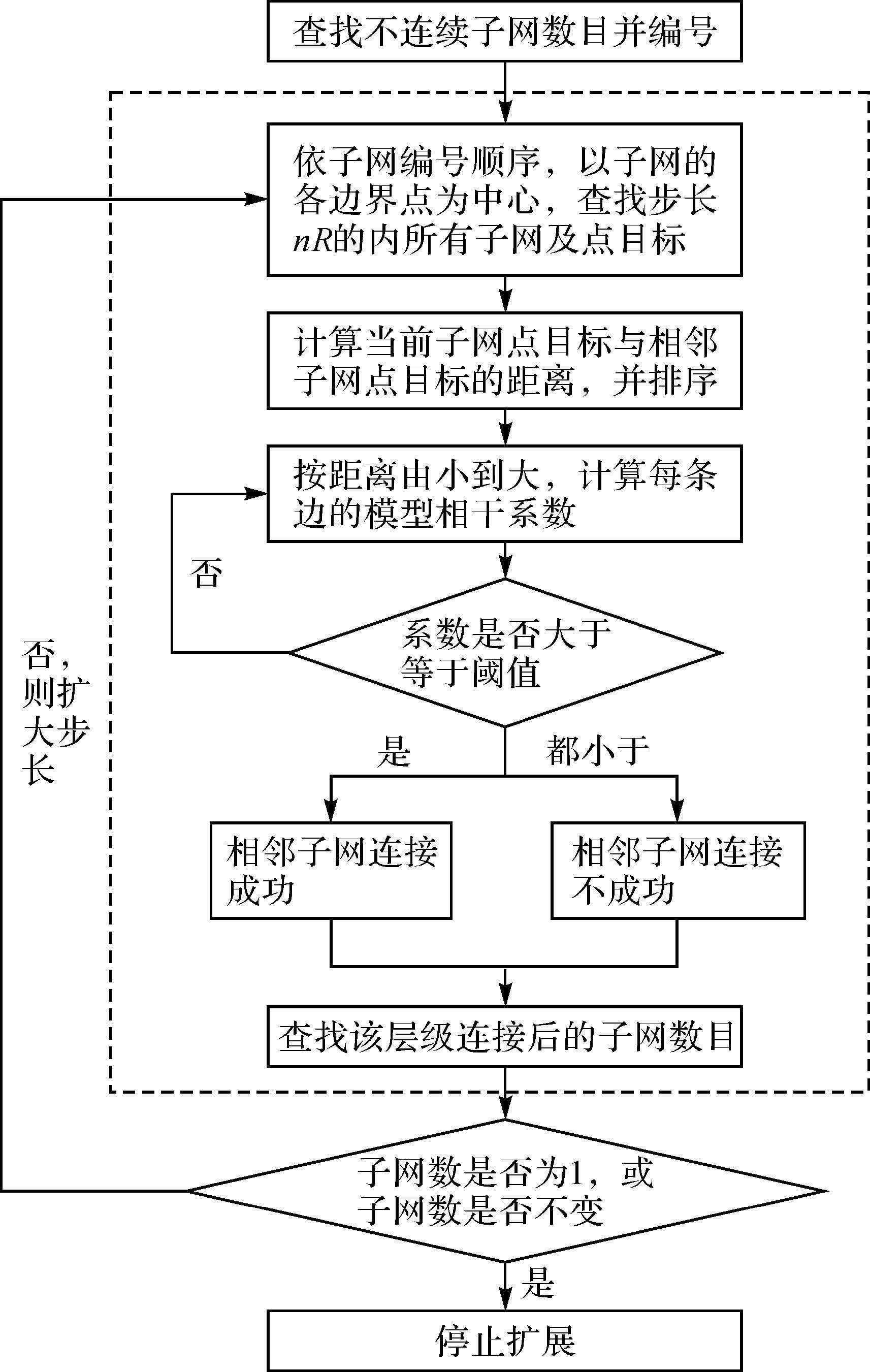
不连通子网多层级连接算法流程如图 2所示。
|
| 图 2 不连通子网多层级连接算法流程 Fig. 2 Flow chart of multi-layer subnetwork connection (MLSC) |
2 试验区与试验数据
试验区为中国华北典型地表沉降区--河北省廊坊市胜芳镇,既有点目标密集分布的城镇地区,也有点目标分布稀疏的农村地区,是验证本文算法的理想区域。试验数据为2003年10月17日-2010年10月15日获取的24景欧洲空间局EnviSat ASAR降轨图像,试验区影像经方位向10视×距离向2视后,分辨率约为40m,影像大小为方位向750像元×距离向600像元,覆盖面积约为720km2。表 1为所用EnviSat ASAR各幅图像相对于第一景图像的垂直基线距和时间基线距参数。图 3(a)为试验区EnviSat ASAR图像的平均幅度图。
| ID | 成像时间 | 垂直 基线距/m | 时间 基线距/d |
| 1 | 2003-10-17 | 0 | 0 |
| 2 | 2003-12-26 | -174.734 | 70 |
| 3 | 2004-03-05 | -902.13 | 140 |
| 4 | 2004-07-23 | -473.047 | 280 |
| 5 | 2004-12-10 | -831.644 | 420 |
| 6 | 2005-03-25 | -1508.06 | 525 |
| 7 | 2005-06-03 | -1046.48 | 595 |
| 8 | 2005-09-16 | -764.074 | 700 |
| 9 | 2005-12-30 | -666.276 | 805 |
| 10 | 2006-03-10 | -784.011 | 875 |
| 11 | 2007-02-23 | -628.441 | 1225 |
| 12 | 2007-06-08 | -790.489 | 1330 |
| 13 | 2007-11-30 | -505.985 | 1505 |
| 14 | 2008-02-08 | -506.497 | 1575 |
| 15 | 2008-05-23 | -773.053 | 1680 |
| 16 | 2008-08-01 | -667.509 | 1750 |
| 17 | 2008-12-19 | -979.962 | 1890 |
| 18 | 2009-02-27 | -559.729 | 1960 |
| 19 | 2009-05-08 | -844.896 | 2030 |
| 20 | 2009-08-21 | -743.935 | 2135 |
| 21 | 2009-12-04 | -627.832 | 2240 |
| 22 | 2010-03-19 | -643.784 | 2345 |
| 23 | 2010-07-02 | -591.557 | 2450 |
| 24 | 2010-10-15 | -310.006 | 2555 |

|
| 图 3 试验区EnviSat ASAR图像的平均幅度图(a)及初始子网分布(b) Fig. 3 EnviSat ASAR average amplitude of the test site (a) and distribution of the initial discontinuous subnetworks (b) |
3 试验结果与分析
利用上述数据,基于Windows 7平台(Intel(R) Xeon(R) CPU 2.0GB,16GB内存)开展干涉处理及子网连接试验,其中干涉处理采用“InSAR地表形变监测系统(GDEMSI)”完成,子网连接试验采用Matlab 7.11.0 完成。基于小基线组合原则,将时间基线距阈值设为2a,垂直基线距阈值设为450m,生成了90个小基线干涉图。考虑到研究区地势平坦(高程范围为3~15m),这里仅去除了平地相位,没有利用外部DEM去除地形相位。为了抑制噪声,采用方位向10视,距离向2视多视处理。
基于平均相干系数方法提取了5260个点目标,通过Delaunay三角网将其连接,最大连接边距离设为3km,经模型相干系数求解后(系数大于或等于0.7的边保留),还剩下5219个点目标,8648条边,共349个子网,如图 3(b)所示。可以看到,城镇地区由于点目标分布密集,连接边相对较多,但其他地区连接边较少,且分布稀疏,无法求解地表形变信息。
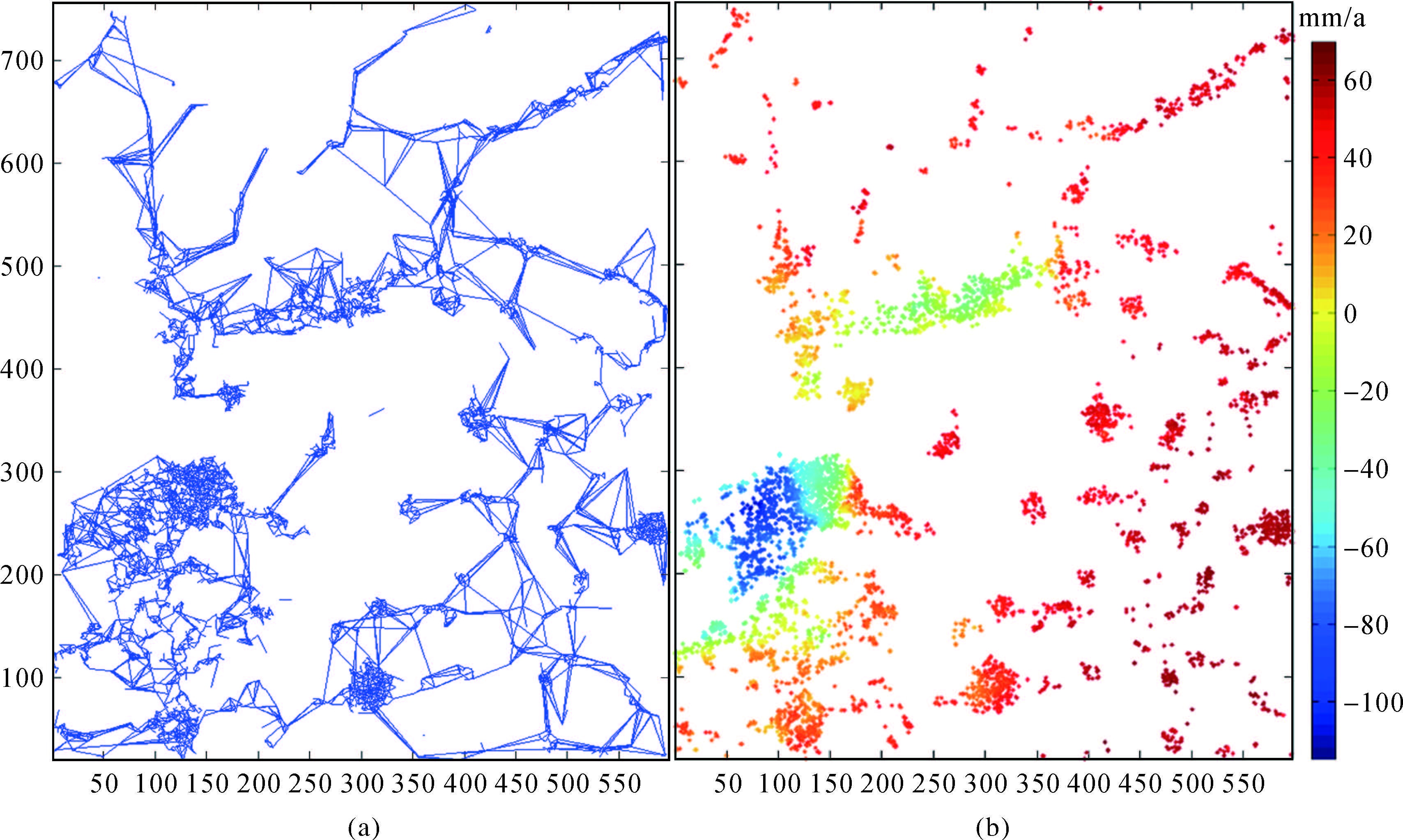
本文以500m为步长,最大搜索距离为3000m,利用上述多层级快速连接算法开展子网连接。通过子网扩展连接,共耗时14min,最终子网数目为9个,边数为10041条(图 4(a)),集成得到了5179个点目标形变信息。图 4(b)为多层级快速连接方法得到的视线向地表形变速率,最大值为69mm/a,最小值为-113mm/a。
|
| 图 4 多层级连接方法得到的最终子网(a)及其形变速率结果(b) Fig. 4 Final networks (a) connected by MLSC and its deformation result (b) |
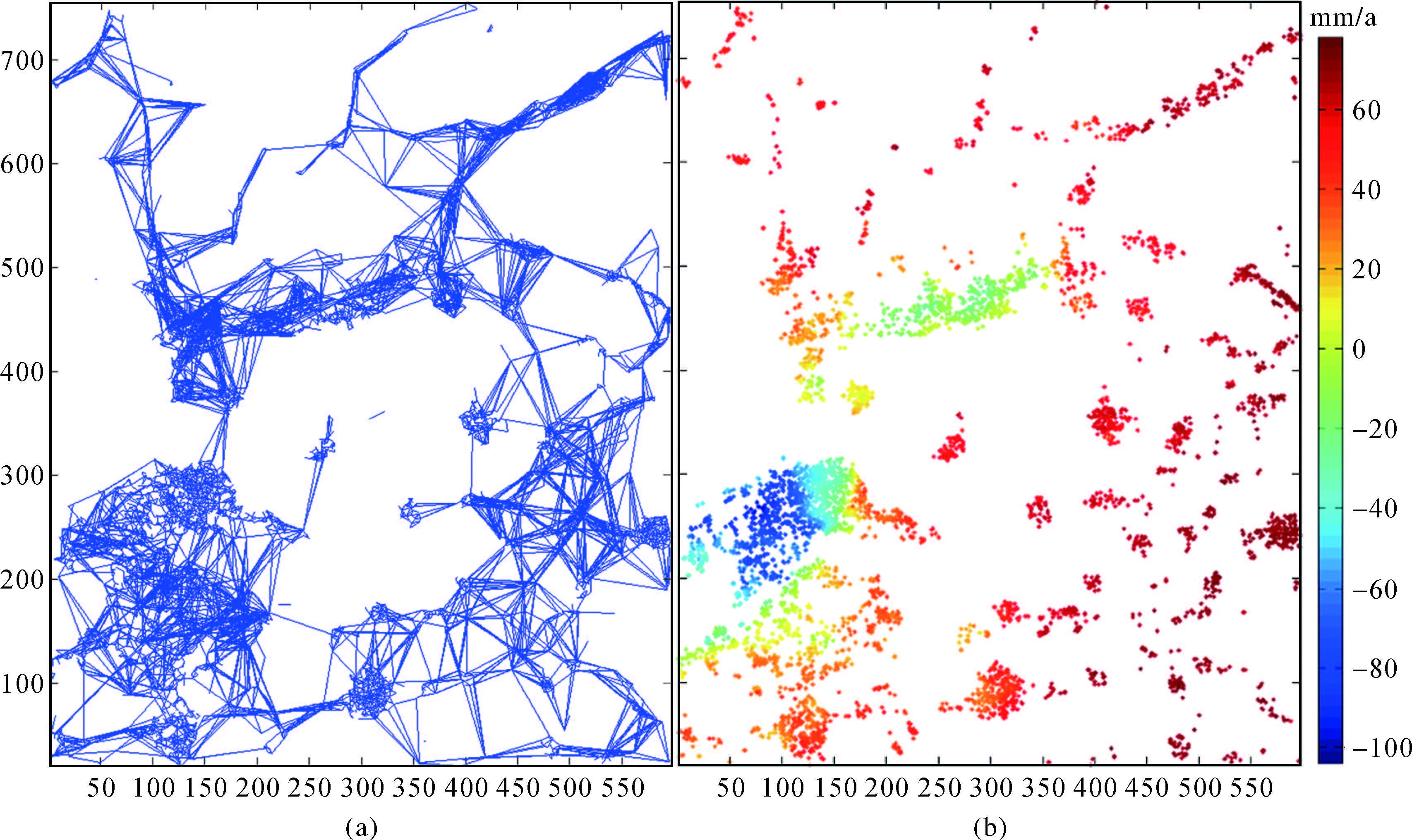
为了对比分析,利用复杂网络方法进行了子网连接试验。在3000m范围内,通过复杂网络连接相邻子网点目标,共耗时43min,最终子网数目也为9个,边数为13000条(图 5(a)),集成得到了5141个点目标形变信息。图 5(b)为复杂网络连接方法得到的视线向地表形变速率,最大值为77mm/a,最小值为-104mm/a,其动态范围与图 4(b)存在一定偏差,这是由于网络集成时二者默认的参考点(即网络中模型相干系数最大边的起点)不一致所致。
|
| 图 5 复杂网络方法得到的最终子网(a)及其形变速率结果(b) Fig. 5 Final networks (a) connected by complex network method and its deformation result (b) |
将图 5(b)和图 4(b)进行叠加分析,共提取了5105个同名点。以图 4(b)为参考,图 5(b)同名点的误差均值为-9.3mm/a,将该值作为整体偏差值标定图 5(b),并与图 4(b)进行相减,得到二者同名点上的形变速率误差及其直方图,如图 6所示。分析图 6(a)可知,二者误差的标准差为2.0mm/a,误差绝对值不超过5mm/a的点共有5037个,占全部同名点的98.67%,可以看到,尽管集成得到的点目标数目不一样,但多层级快速连接方法与复杂网络方法得到的形变速率结果具有高度一致性,这也验证了本文算法的可靠性。同时,从图 6(a)中也可以看到,在部分地区两种方法得到形变结果存在一定差异,这主要是两种方法得到的网络连接边不一致所致,因为点目标的形变速率是通过对所有网络边的相对线性形变速率进行最小二乘平差集成得到的,不同连接边会导致最终集成结果出现较小差异。

|
| 图 6 本文方法与复杂网络方法得到的形变速率误差(a)及其直方图(b) Fig. 6 Difference (a) and its histogram (b) between deformation velocity retrieved by the proposed method and the one by complex network method |
表 2是本文提出的多层级快速连接方法与现有复杂网络连接方法性能对比。可以看到复杂网络由于在3000m范围内,搜索并连接非当前子网的全部点目标,其得到的边数远超过多层级子网连接得到的边数,相应的计算量较大,耗时明显,共占用43min。而多层级子网连接方法,通过逐步向外扩展搜索子网,能够快速减少子网数目,计算耗时较小,占用14min,仅为复杂网络耗时的32.56%。另一方面,复杂网络方法最终得到的点目标数目少于多层级扩展连接方法,这表明尽管前者连接的边数多,但是很多边的质量并不可靠,因为它将3000m范围内所有的点目标都相互连接,而距离越长,错解的几率越大。可见多层级子网连接方法不仅在耗时方面的表现也远远优于复杂网络,其最终集成的点目标数目要多于复杂网络,因此该方法更适合不连通子网的快速连接,有利于大区域的地表形变监测。
| 比较内容 | 多层级子网连接 | 复杂网络连接 |
| 连接的边数 | 10041 | 13000 |
| 最终子网数 | 9 | 9 |
| 集成的点数 | 5179 | 5141 |
| 耗时/min | 14 | 43 |
4 结 论
本文针对时间序列InSAR数据处理中出现的不连通子网问题,提出了一种多层级、不同步长扩展的最近邻点目标子网连接方法(MLSC)。该方法通过逐步扩大搜索步长,连接相邻子网,可快速减少子网数目,从而有利于大区域特别是点目标稀疏的非城镇地区地表形变监测。以河北省廊坊市24景EnviSat ASAR图像为试验数据,开展了网络连接试验,并与现有的复杂网络方法进行了对比。试验结果表明,在保证结果精度的前提下,多层级子网连接方法不仅计算效率远远高于复杂网络,而且最终得到的点目标数目也多于复杂网络方法,验证了该方法的高效性。
致谢: 感谢欧空局提供EnviSat ASAR数据。
| [1] | 王超, 张红, 刘智. 星载合成孔径雷达干涉测量[M]. 北京: 科学出版社, 2002 . WANG Chao, ZHANG Hong, LIU Zhi. Spaceborne Synthetic Aperture Radar Interferometry[M]. Beijing: Science Press, 2002 . |
| [2] | GATELLI F, GUARNIERI A M, PARIZZI F, et al. Wavenumber Shift in SAR Interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing , 1994, 32 (4) : 855 –865. DOI:10.1109/36.298013 |
| [3] | ZEBKER H A, ROSEN P A, HENSLEY S. Atmospheric Effects in Interferometric Synthetic Aperture Radar Surface Deformation and Topographic Maps[J]. Journal of Geophysical Research , 1997, 102 (B4) : 7547 –7563. DOI:10.1029/96JB03804 |
| [4] | FERRETTI A, PRATI C, ROCCA F. Permanent Scatterers in SAR Interferometry[C]//Proceedings of the International Geoscience and Remote Sensing Symposium. Hamburg:IEEE, 1999, 3:1528-1530. |
| [5] | FERRETTI A, PRATI C, ROCCA F. Nonlinear Subsidence Rate Estimation Using Permanent Scatterers in Differential SAR Interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing , 2000, 38 (5) : 2202 –2212. DOI:10.1109/36.868878 |
| [6] | FERRETTI A, PRATI C, ROCCA F. Permanent Scatterers in SAR Interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing , 2001, 39 (1) : 8 –20. DOI:10.1109/36.898661 |
| [7] | VILARDO G, VENTURA G, TERRANOVA C, et al. Ground Deformation Due to Tectonic, Hydrothermal, Gravity, Hydrogeological, and Anthropic Processes in the Campania Region (Southern Italy) from Permanent Scatterers Synthetic Aperture Radar Interferometry[J]. Remote Sensing of Environment , 2009, 113 (1) : 197 –212. DOI:10.1016/j.rse.2008.09.007 |
| [8] | 张永红, 张继贤, 龚文瑜, 等. 基于SAR干涉点目标分析技术的城市地表形变监测[J]. 测绘学报 , 2009, 38 (6) : 482–487. ZHANG Yonghong, ZHANG Jixian, GONG Wenyu, et al. Monitoring Urban Subsidence Based on SAR Interferometric Point Target Analysis[J]. Acta Geodaetica et Cartographica Sinica , 2009, 38 (6) : 482 –487. DOI:10.3321/j.issn:1001-1595.2009.06.003 |
| [9] | 廖明生, 唐婧, 王腾, 等. 高分辨率SAR数据在三峡库区滑坡监测中的应用[J]. 中国科学(地球科学) , 2012, 55 (4) : 590–601. LIAO Mingsheng, TANG Jing, WANG Teng, et al. Landslide Monitoring with High-resolution SAR Data in the Three Gorges Region[J]. Science China Earth Sciences , 2012, 55 (4) : 590 –601. DOI:10.1007/s11430-011-4259-1 |
| [10] | 王洒, 宫辉力, 杜钊峰, 等. 永久散射体干涉测量中最佳主图像选取[J]. 测绘学报 , 2013, 42 (1) : 87–93. WANG Sa, GONG Huili, DU Zhaofeng, et al. Optimal Selection of Master Image in Permanent Scatterer InSAR Technique[J]. Acta Geodaetica et Cartographica Sinica , 2013, 42 (1) : 87 –93. |
| [11] | BERARDINO P, FORNARO G, LANARI R, et al. A New Algorithm for Surface Deformation Monitoring Based on Small Baseline Differential SAR Interferograms[J]. IEEE Transactions on Geoscience and Remote Sensing , 2002, 40 (11) : 2375 –2383. DOI:10.1109/TGRS.2002.803792 |
| [12] | MORA O, MALLORQUI J J, BROQUETAS A. Linear and Nonlinear Terrain Deformation Maps from a Reduced Set of Interferometric SAR Images[J]. IEEE Transactions on Geoscience and Remote Sensing , 2003, 41 (10) : 2243 –2253. DOI:10.1109/TGRS.2003.814657 |
| [13] | HOOPER A, ZEBKER H, SEGALL P, et al. A New Method for Measuring Deformation on Volcanoes and Other Natural Terrains Using InSAR Persistent Scatterers[J]. Geophysical Research Letters , 2004, 31 (23) : L23611 . |
| [14] | HOOPER A, SEGALL P, ZEBKER H. Persistent Scatterer Interferometric Synthetic Aperture Radar for Crustal Deformation Analysis, with Application to Volcán Alcedo, Galápagos[J]. Journal of Geophysical Research , 2007, 112 (B7) : B07407 . |
| [15] | LANARI R, MORA O, MANUNTA M, et al. A Small-baseline Approach for Investigating Deformations on Full-resolution Differential SAR Interferograms[J]. IEEE Transactions on Geoscience and Remote Sensing , 2004, 42 (7) : 1377 –1386. DOI:10.1109/TGRS.2004.828196 |
| [16] | CASU F, MANZO M, PEPE A, et al. SBAS-DInSAR Analysis of Very Extended Areas:First Results on a 60000-km2 Test Site[J]. IEEE Geoscience and Remote Sensing Letters , 2008, 5 (3) : 438 –442. DOI:10.1109/LGRS.2008.916199 |
| [17] | 吴宏安, 张永红, 陈晓勇, 等. 基于小基线DInSAR技术监测太原市2003~2009年地表形变场[J]. 地球物理学报 , 2011, 54 (3) : 673–680. WU Hong'an, ZHANG Yonghong, CHEN Xiaoyong, et al. Ground Deformation Monitoring Using Small Baseline DInSAR Technique:A Case Study in Taiyuan City from 2003 to 2009[J]. Chinese Journal of Geophysics , 2011, 54 (3) : 673 –680. |
| [18] | 张永红, 吴宏安, 孙广通. 时间序列InSAR技术中的形变模型研究[J]. 测绘学报 , 2012, 41 (6) : 864–869. ZHANG Yonghong, WU Hong'an, SUN Guangtong. Deformation Model of Time Series Interferometric SAR Techniques[J]. Acta Geodaetica et Cartographica Sinica , 2012, 41 (6) : 864 –869. |
| [19] | 熊文秀, 冯光财, 李志伟, 等. 顾及时空特性的SBAS高质量点选取算法[J]. 测绘学报 , 2015, 44 (11) : 1246–1254. XIONG Wenxiu, FENG Guangcai, LI Zhiwei, et al. High Quality Targets Selection in SBAS-InSAR Technique by Considering Temporal and Spatial Characteristic[J]. Acta Geodaetica et Cartographica Sinica , 2015, 44 (11) : 1246 –1254. DOI:10.11947/j.AGCS.2015.20140547 |
| [20] | LIU Guoxiang, LUO Xiaojun, CHEN Qiang, et al. Detecting Land Subsidence in Shanghai by PS-networking SAR Interferometry[J]. Sensors , 2008, 8 (8) : 4725 –4741. DOI:10.3390/s8084725 |
| [21] | 吴涛. 多基线距DInSAR技术反演地表缓慢形变研究[D]. 北京:中国科学院研究生院, 2008. WU Tao. Slow Deformation Retrieval of Ground Surface Based on Multibaseline DInSAR Technique[D]. Beijing:Graduate University of Chinese Academy of Sciences, 2008. |
| [22] | HANSSEN R F. Radar Interferometry:Data Interpretation and Error Analysis[M]. Boston, MA, USA: Kluwer, 2001 . |
| [23] | LIU Guoxiang, BUCKLEY S M, DING Xiaoli, et al. Estimating Spatiotemporal Ground Deformation with Improved Persistent-scatterer Radar Interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing , 2009, 47 (9) : 3209 –3219. DOI:10.1109/TGRS.2009.2028797 |
| [24] | LIU Guoxiang, JIA Hongguo, ZHANG Rui, et al. Exploration of Subsidence Estimation by Persistent Scatterer InSAR on Time Series of High Resolution Terra SAR-X Images[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing , 2011, 4 (1) : 159 –170. DOI:10.1109/JSTARS.2010.2067446 |
| [25] | 张瑞. 基于多级网络化的多平台永久散射体雷达干涉建模与形变计算方法[D]. 成都:西南交通大学, 2012. ZHANG Rui. Modeling and Deformation Estimating with Multi-platform Persistent Scatterer Radar Interferometry Based on Multi-level Networking[D]. Chengdu:Southwest Jiaotong University, 2012. http://cdmd.cnki.com.cn/article/cdmd-10613-1014251660.htm |


