2. 国家测绘地理信息局卫星测绘应用中心, 北京 100048
2. Satellite Surveying and Mapping Application Center, National Administration of Surveying, Mapping and Geo-information, Beijing 100048, China
激光雷达与成像光谱技术、合成孔径雷达技术一起被列为对地观测系统最核心的信息获取技术。美国NASA在1994年和1997年两次将航天激光测高仪(shuttle laser altimeter,SLA)安装在航天飞机上,以10Hz的频率、间隔750 m和100 m的脚印光斑采样方式获取并建立全球控制点库[1]。2003年,美国还发射了目前为止唯一的一颗对地观测激光测高卫星ICESat(Ice,Cloud and land Elevation Satellite),该卫星上搭载了地球科学激光测高系统(Geo-science Laser Altimetry System,GLAS),在极地冰盖监测、全球森林生物量估算、陆地高程测量等方面得到广泛应用[2-3],而后续的ICESat-2和LIST(lidar surface topography)卫星也正在研发之中[4-5]。计划中的国产高分七号以及陆地生态系统碳监测卫星上均搭载了激光测高仪。2016年5月30日发射的资源三号02星上搭载了一个激光试验性载荷,文献[6]建立了国产资源三号高分辨率光学测绘卫星的严密成像模型,而针对国产的激光测高卫星的定位模型研究基本处于空白。因此,对激光测高卫星的严密几何定位模型进行系统性的研究非常必要。
在激光测高数据应用方面,文献[2]较系统地对ICESat/GLAS在地学方面的应用作了梳理;文献[7]从ICEsat/GLAS激光测高数据中反演出湖泊的动态水位高程,但前提是所选的激光测高足印点要精度可靠;文献[8-9]采用ICESat/GLAS数据开展南极冰盖高程模型研究;文献[10]采用ICESat/GALS数据提出了一种基于机器学习的实时地形分类算法,并采用北京区域的数据开展了试验,且对数据的精度要求较高;文献[11]对我国的嫦娥一号激光测高数据开展了轨道交叉点分析和平差方法研究;文献[12-13]开展了嫦娥探月的激光测高数据与光学影像联合平差研究,但与对地观测还有一定差异;文献[14-15]结合对地观测的卫星激光测高仪辅助光学立体影像平差和立体测图开展了相关研究,证明了激光测高数据辅助提高光学影像测图精度的可行性。而较高的数据精度是应用的前提。在精度分析方面,文献[16]对激光测高卫星在不同地形条件下的探测能力进行了分析,但没有给出定量的结论;文献[17-18]对ICESat/GLAS脚点定位模型进行了介绍,但对于卫星运行速度引起的光行差改正没有提及,而在600km的轨道高度,激光单向传输约2ms的时间,光行差可达5″,对应地面距离约15m;文献[19]对星载激光测高系统高程误差进行了分析,但采用的是简化的定位模型,对硬件安装误差、测距误差等没有深入涉及;GLAS的ATBD[20](Algorithm Theoretical Basis Document)报告对GLAS脚点定位流程及误差作了较为详细的介绍,但该文档对一些细节并没有涉及。
本文推导了激光测高卫星严密几何定位模型,并对光行差、硬件安装误差作了分析,详细介绍了ICESat/GLAS的激光脚点定位原理和数据处理流程,利用GLAS数据重现了从0级到2级的生产过程,将计算结果与GLAS相应产品作了对比分析,同时利用资源三号02星的首轨激光测高数据的初步处理结果进行了验证。
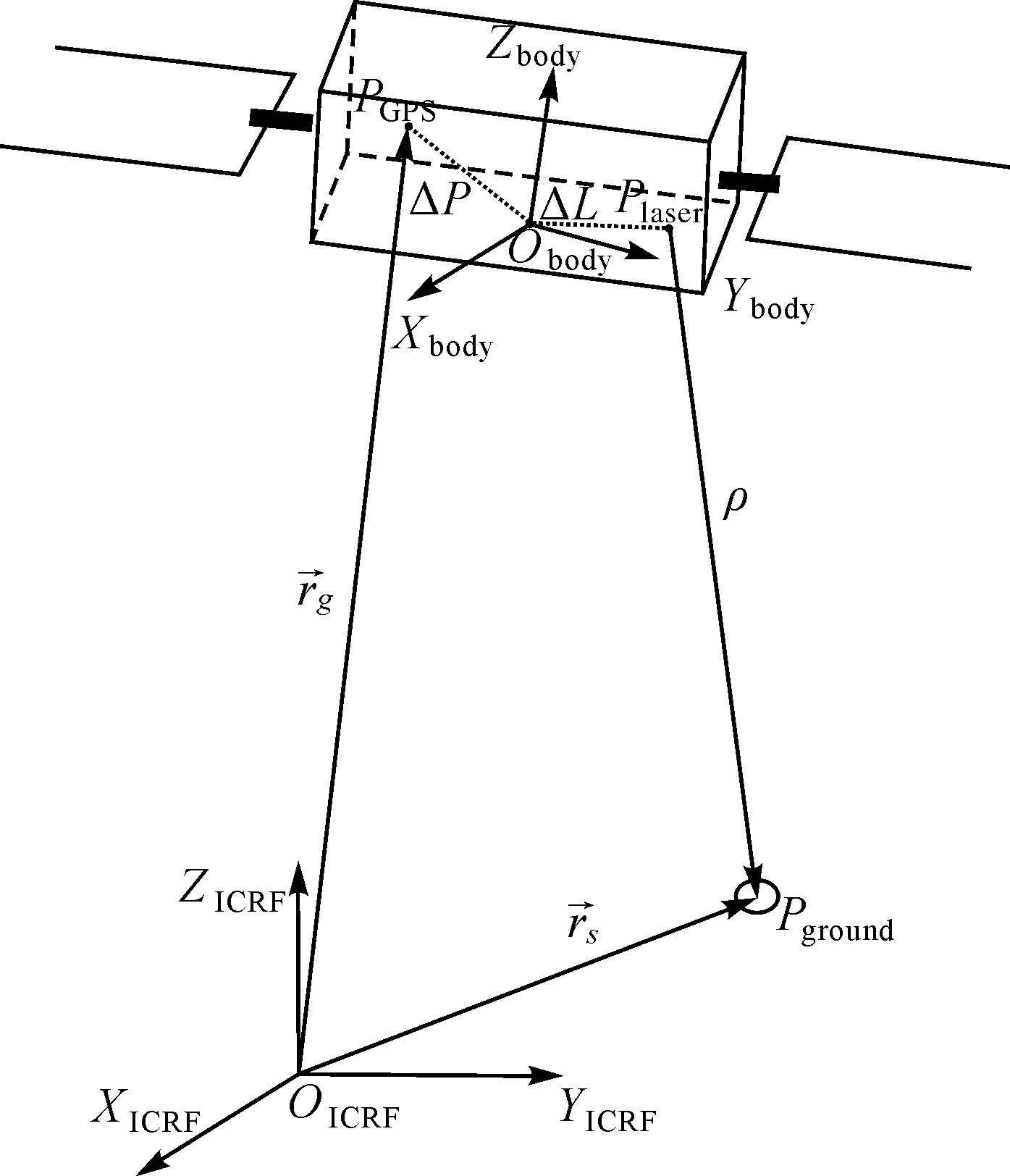
1 严密几何定位模型构建 1.1 严密几何定位模型激光测高卫星的基本原理是:通过卫星发射激光束经地面反射后由卫星接收,计算激光发射和接收的时间间隔t,光的传播速度为c,则激光单程传输距离ρ=ct/2,结合卫星上搭载的GPS定位仪器和星敏感器获得的卫星位置和姿态信息,即可获得激光脚印点的三维坐标。其严密几何模型如图 1所示,其中Plaser为激光发射的参考点,PGPS为GPS天线相位中心,Obody为卫星质心,Pground为激光地面足印点。
|
| 图 1 激光测高卫星严密几何定位模型 Fig. 1 Illustration of rigorous geometric model |
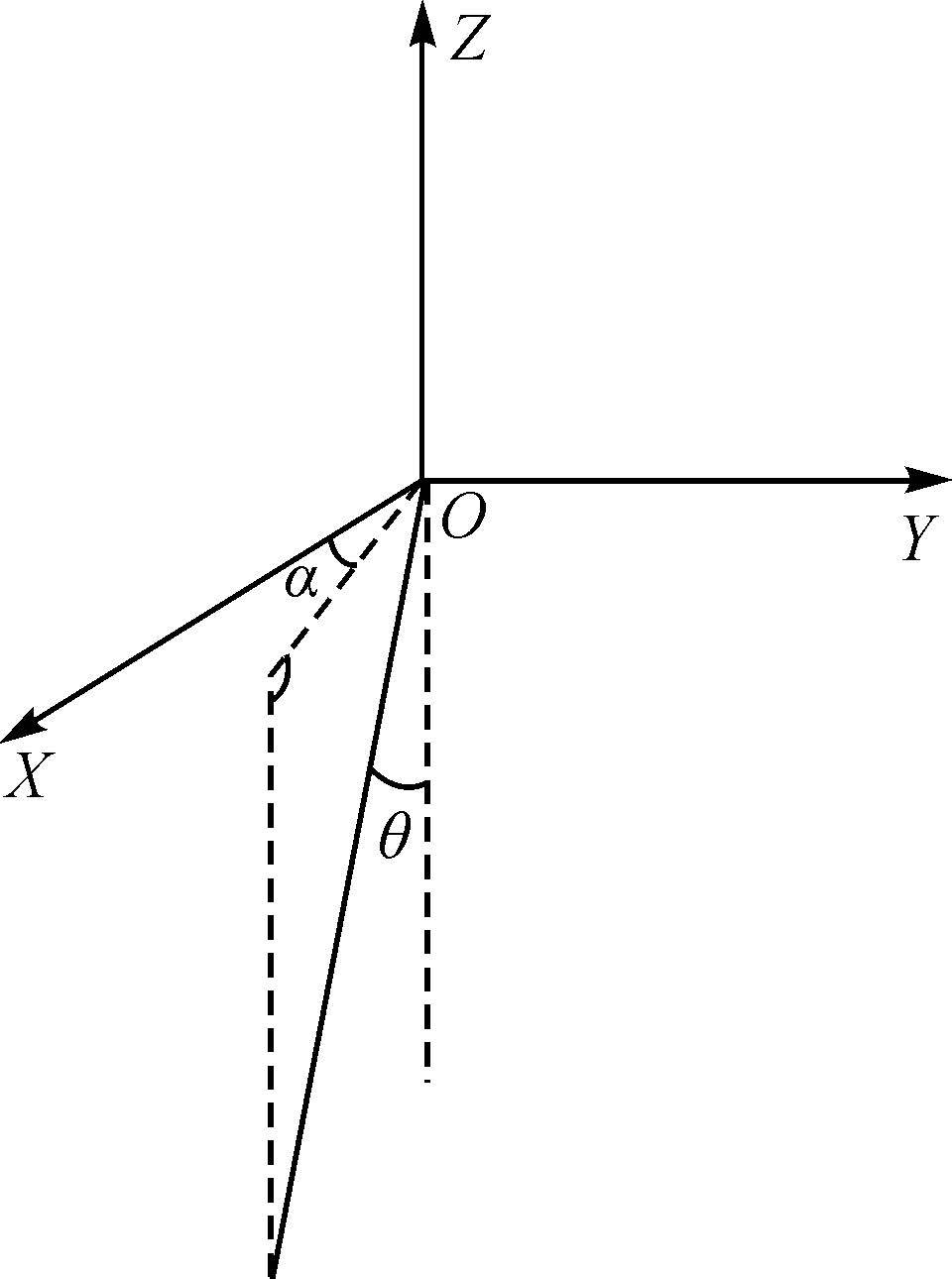
为描述星载激光测高严密几何模型,定义卫星本体坐标系:卫星质心为原点,X轴指向卫星飞行方向,Z轴指向天顶方向,Y轴垂直于卫星轨道平面,与X、Z轴构成右手坐标系。激光发射时指向方向与卫星本体坐标系存在一定的夹角,假设激光指向与本体坐标系Z轴的负向夹角为θ,在XOY平面上的投影与X轴正向夹角为α,如图 2所示。
|
| 图 2 激光发射方向与本体坐标系的夹角示意图 Fig. 2 The laser direction in body coordinate system |
若激光的测距值ρ,激光参考点在本体坐标系中的坐标为:ΔL=[Lx Ly Lz]T,则在激光脚点在卫星本体坐标系下的坐标为
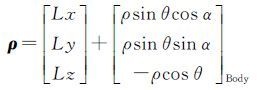 (1)
(1)
卫星搭载的GPS定位系统可以测定卫星的位置[XGPS YGPS ZGPS]T,但GPS的相位中心一般与卫星质心不完全重合,两者之间存在一定的偏差,假定GPS的相位中心在卫星本体坐标系下的坐标为:ΔP=[Dx Dy Dz]T,卫星星敏感器相对于卫星本体坐标的安置矩阵为Rbodystar,而星敏感器测量的是星敏本体系到J2000坐标系下的旋转矩阵RstarJ2000,因此还需要J2000坐标系到ITRF的坐标变换矩阵RJ2000ITRF。因此,在不考虑大气折射影像的条件下,激光测高卫星的严密几何定位公式为
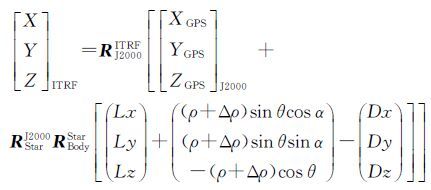 (2)
(2)
式中,Δρ为因大气折射及硬件误差而引起的测距改正值。获得足印点的三维坐标后,可根据需要转换为大地坐标[21]。
1.2 光行差引起的位置误差
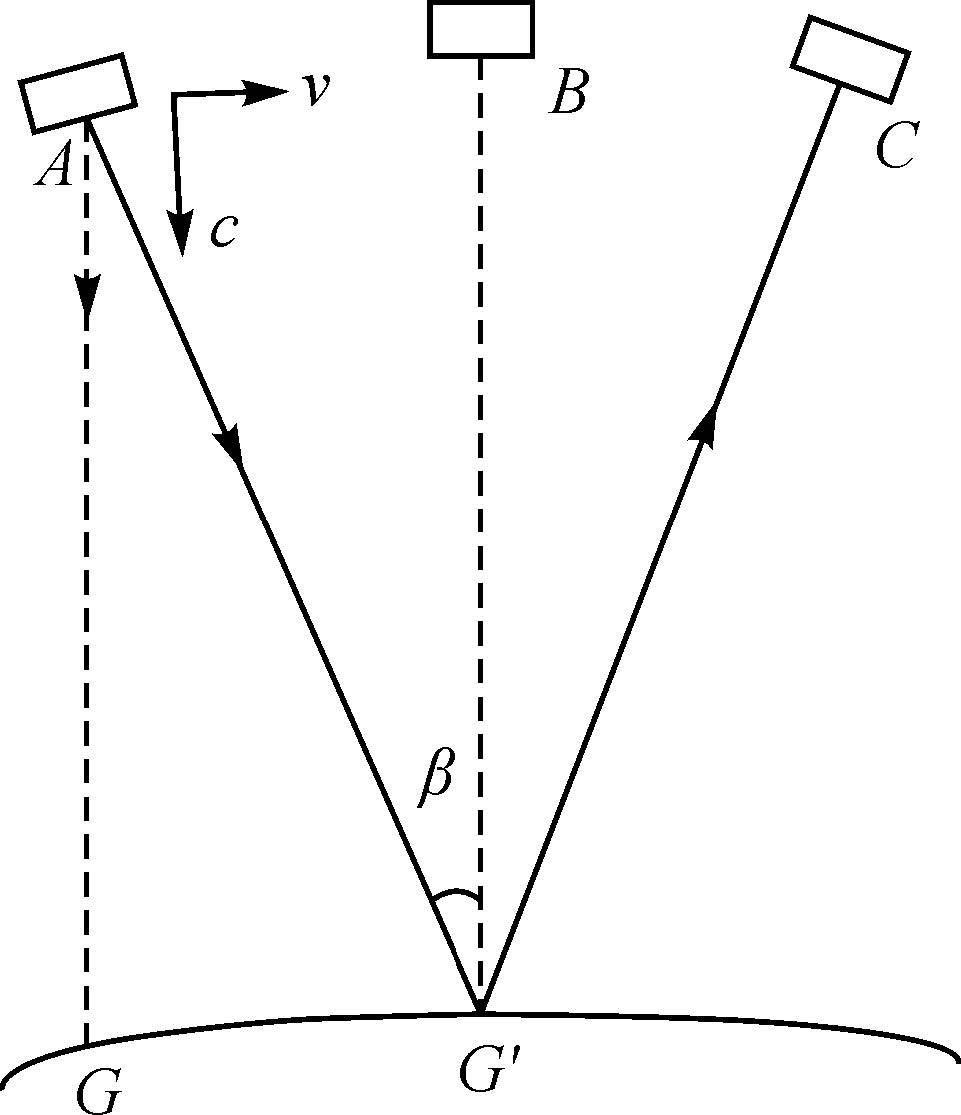
激光测高作为主动遥感方式,其传输路径为卫星到地面距离的两倍,如果卫星高度为600km,则往返一次所需时间约4ms,卫星前进距离约30m。以图 3为例,卫星在A点发射一束激光,激光出射方向为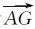

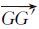
|
| 图 3 光行差引起的位置误差 Fig. 3 The geo-location error induced by laser aberration |
激光发射方向和实际传输方向的夹角为β,由光速和卫星运行速度可得[22]
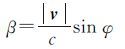 (3)
(3)
式中,φ为卫星运行速度与激光出射方向的夹角。
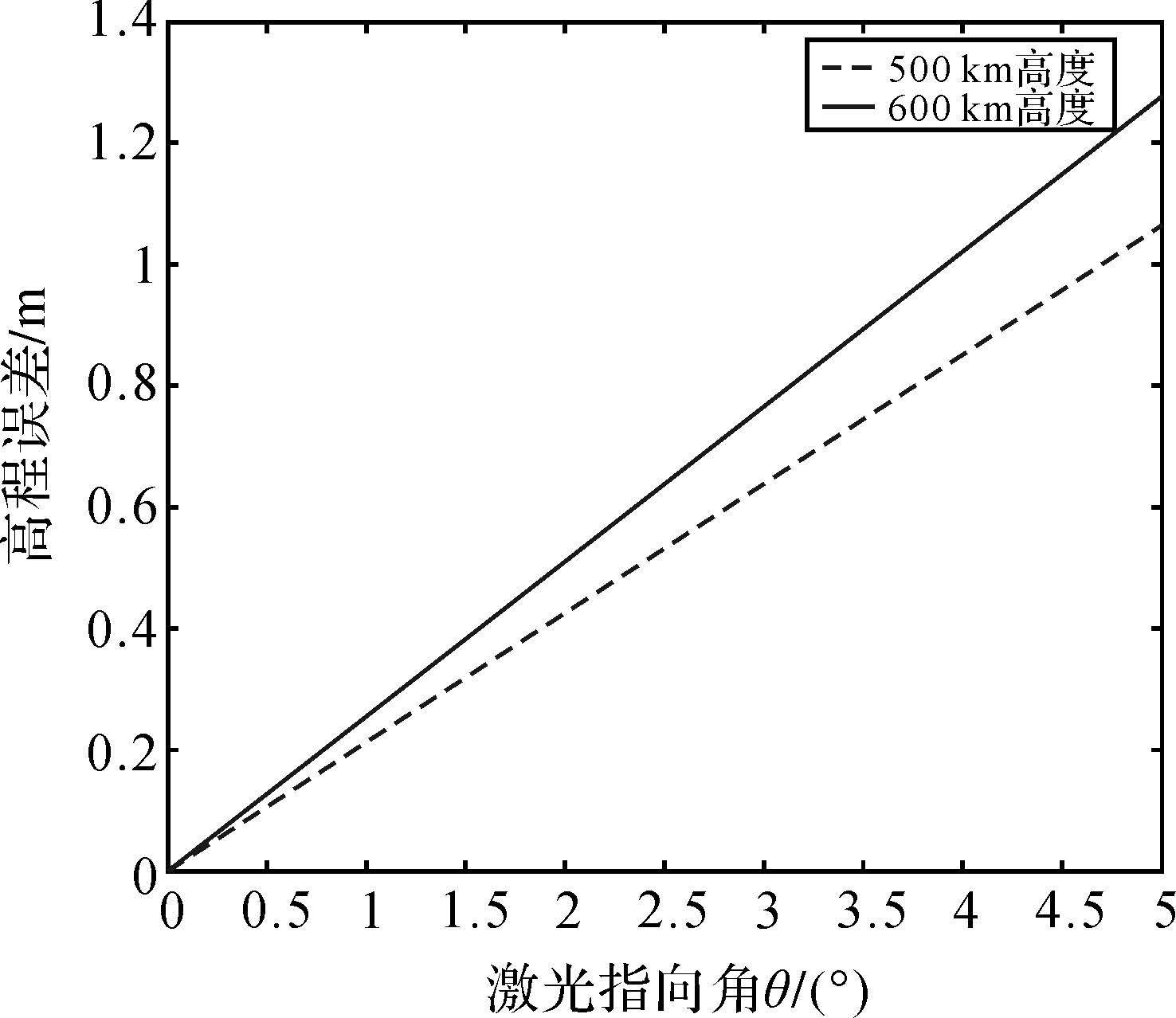
为了尽量减少因激光高度角而引起的大气折射延迟,激光出射方向一般为天底点方向,即φ≈90°。因此,β≈5.2″,GG′≈15m。此时,考虑因光行差对高程测量误差的影响,如图 4所示,当激光指向角θ=1°时,此时因光行差而引起的高程误差为0.212m。当卫星轨道高度降为500km时,因光行差而引起的高程误差虽略有下降,但随着指向角的变大会线性变大。
|
| 图 4 激光指向角与光行差导致的高程测量误差 Fig. 4 The elevation error induced by θ and aberration |
为有效消除光行差引起的位置误差,ICESat卫星采用激光发射时刻的卫星姿态、激光到达地面时卫星的位置,即图 3中卫星在A点的姿态和B的位置,解算激光足印在地面的实际位置G′。
1.3 硬件安装误差引起的位置误差由式(2)可知,硬件安装误差主要包括激光指向与卫星本体系的两个角度测量误差,卫星本体系与星敏本体系的轴向安装误差,以及激光参考点与卫星本体系原点、GPS天线相位中心与卫星本体系原点的偏心量测量误差。偏心量引起的位置误差基本是线性关系,而且目前偏心量的量测误差基本可达毫米级。综合考虑,激光指向与卫星本体系以及卫星本体系与星敏本体系的夹角关系,可简化为激光指向与星敏本体系存在两个夹角(θ,α),对式(2)求两个指向角的偏导
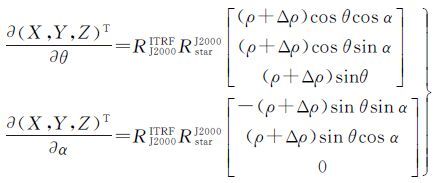 (4)
(4)
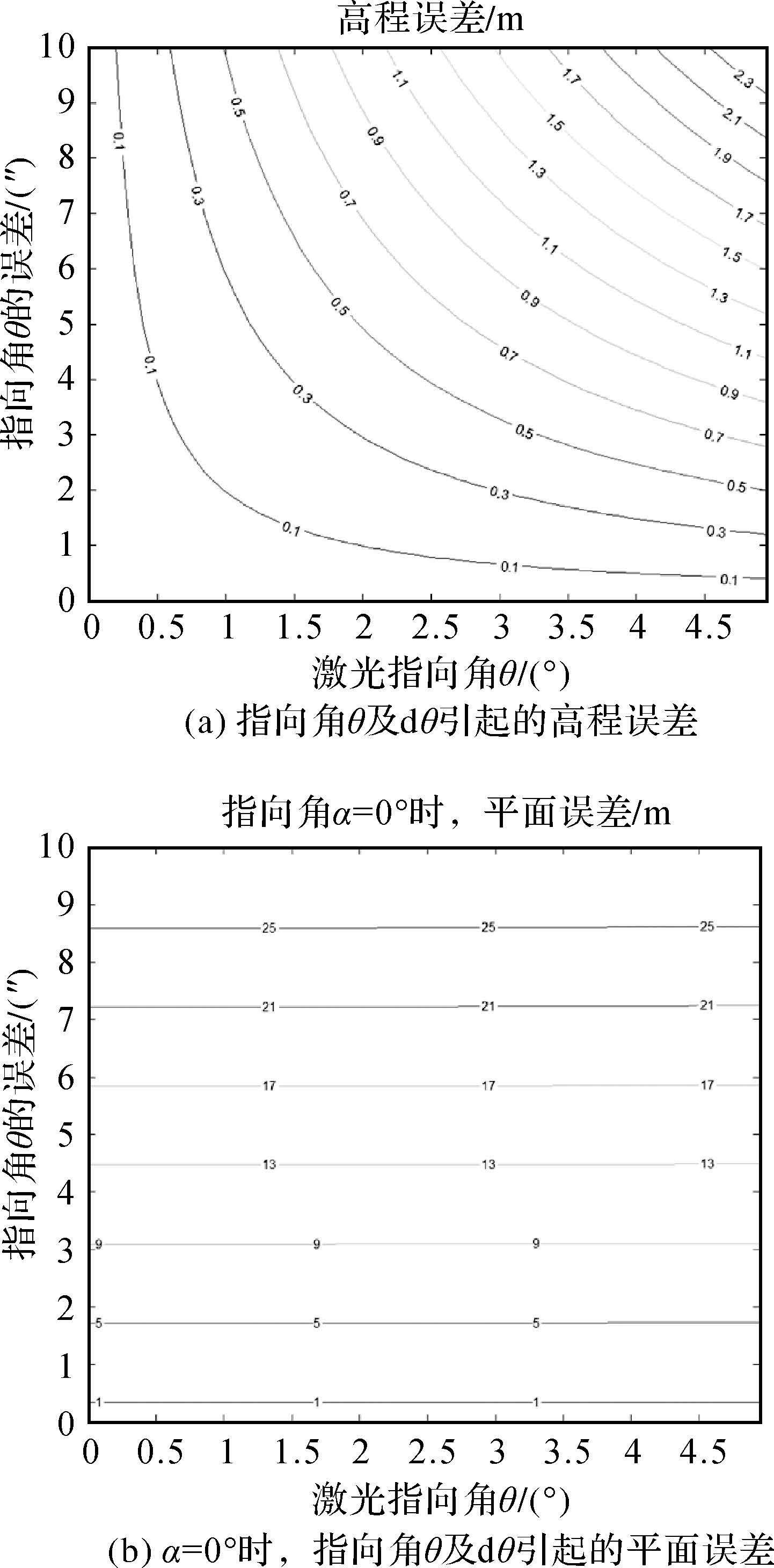
由式(4)可知,激光指向角α对高程误差基本没有影响,对高程有影响的主要是指向角θ。图 5显示了不同指向角θ及其测量误差dθ引起的激光脚印点高程和平面误差大小,图 6显示了不同指向角α及dθ、dα引起的平面误差。
|
| 图 5 θ和dθ引起的高程误差与平面误差 Fig. 5 The elevation and planimetric error induced by different θ and dθ |

|
| 图 6 α、dα和dθ引起的平面误差 Fig. 6 The planimetric error induced by different α,dα and dθ |
2 ICESat/GLAS处理流程介绍
ICESat/GLAS于2003年1月发射成功,2009年10月停止工作,分周期共工作了2465d,采集激光点约20亿个。GLAS数据产品分为0级、1级和2级,其中1级包括1A和1B,1级和2级产品又分为15类,即公开发布的GLA0-GLA15[23-24]。
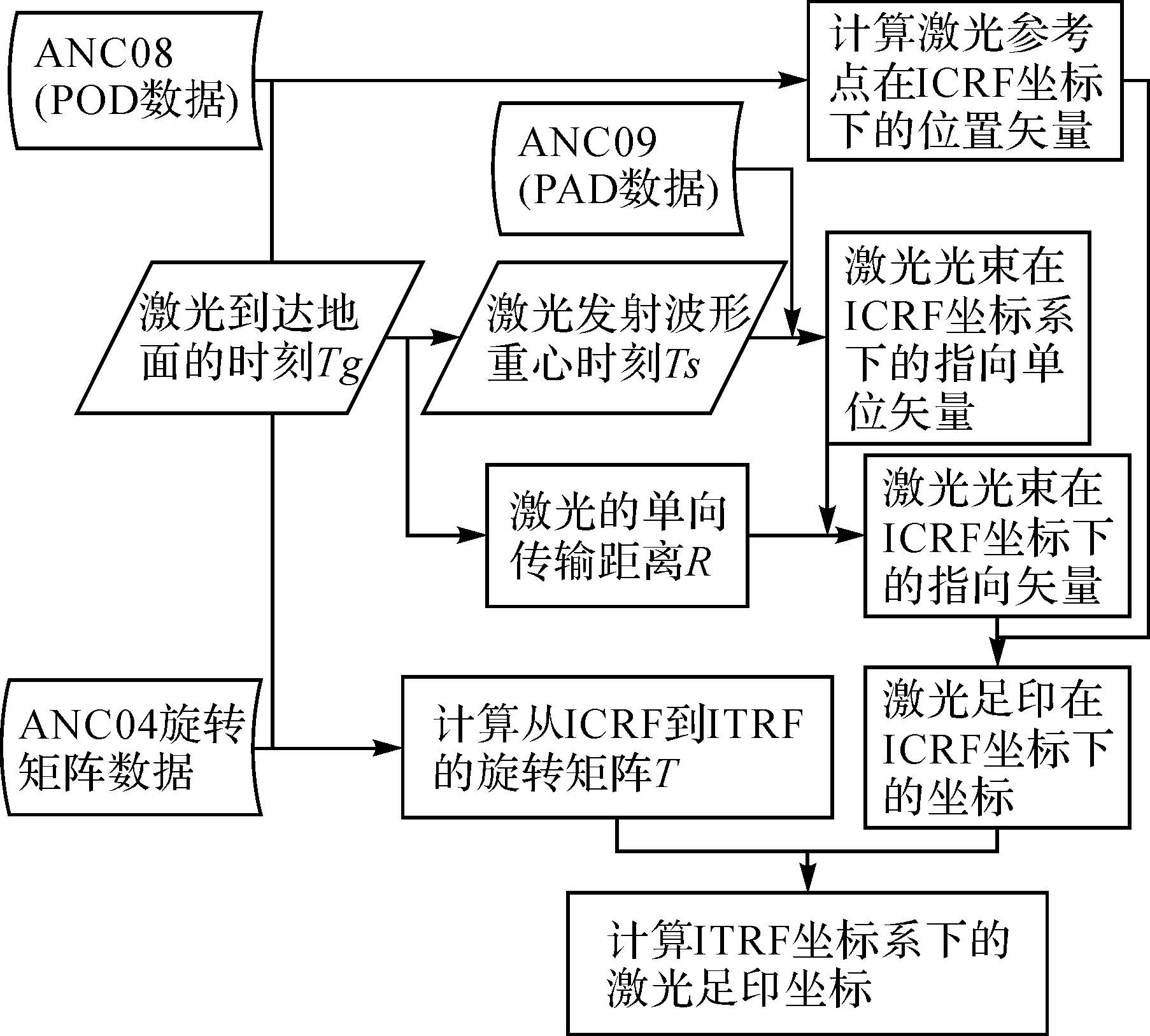
ICESat/GLAS项目组公布了式(2)所建立的严密几何定位模型的简化计算方法[20],即采用ANC04惯性坐标系旋转矩阵、ANC08精密定轨数据(precision orbit determination,POD) [25]、ANC09精密定姿数据(precision attitude determination,PAD)[22]、ANC25时间转换数据以及激光测距值计算脚点三维坐标,其流程如图 7所示。
|
| 图 7 ICESat/GLAS激光足印几何定位流程 Fig. 7 The workflow of ICESat/GLAS geometric location |
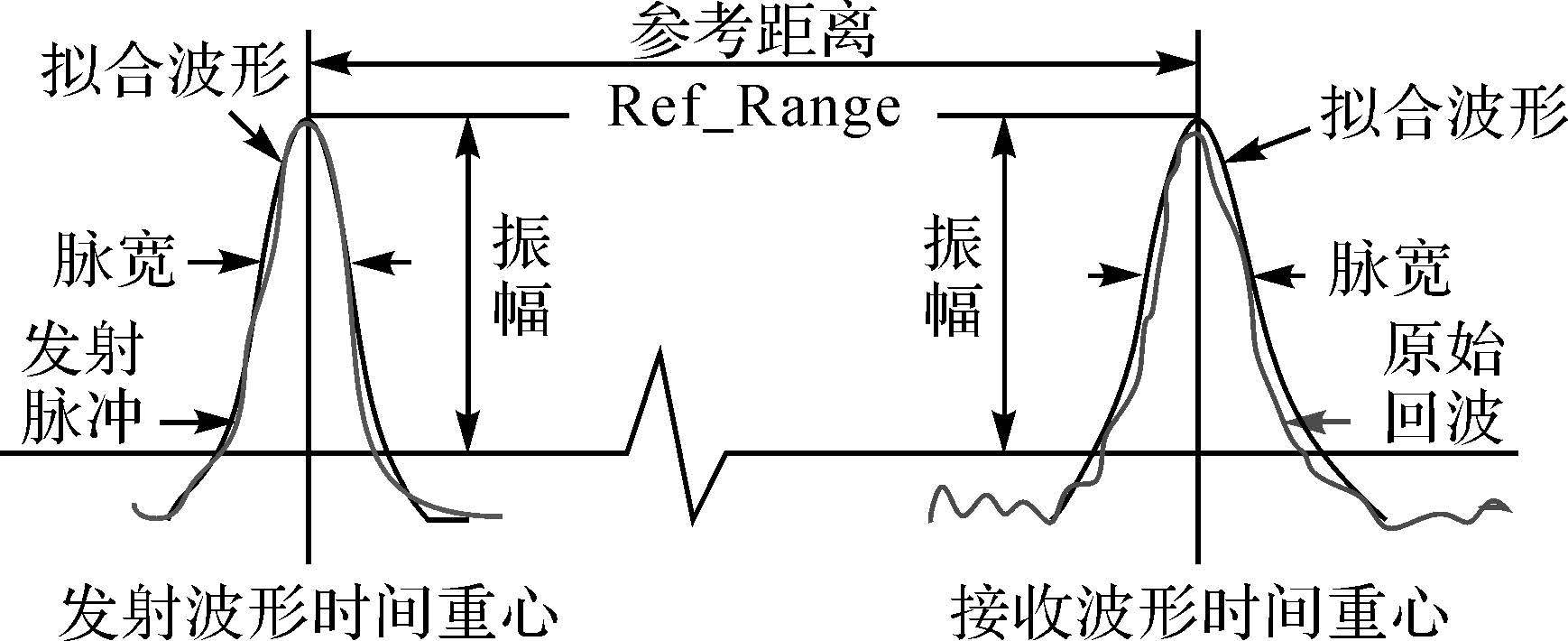
由发射和接收波形计算激光传输距离的原理如图 8所示,图中不规则的曲线表示原始波形,规则曲线表示经最小二乘拟合后的波形,从拟合的波形数据中可以提取出发射与接收波形的时间重心,根据时间重心的间隔与光速即可计算出激光往返的距离[26]。
|
| 图 8 GLAS全波形激光测距 Fig. 8 The illustration of GLAS full waveform ranging |
由于GLAS激光发射波形可近似为高斯脉冲,激光经地表面反射后回波波形可近似看作一次或多次高斯脉冲的叠加。对于多回波波形数据,采用多个高斯函数叠加进行拟合[26]。
结合全波形数据处理、大气延迟改正以及固体潮改正等内容,卫星激光测高数据几何处理流程可描述为:
(1) 对发射和接收波形进行平滑、去噪,提取波形特征参数,确定发射和接收波形重心对应的时刻Ts、Tr;激光传输时间间隔为:Δt=Tr-Ts,激光到达地面时刻Tg=Ts+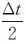
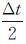
(2) 根据激光发射时刻Ts和PAD数据计算在ICRF坐标系下激光指向的单位向量u。
(3) 根据激光到达地面的时刻Tg和POD数据计算激光参考点在ICRF坐标系下的坐标向量rg。
(4) 根据激光到达地面的时刻Tg,计算ICRF到ITRF的旋转矩阵RICRFITRF。
(5) 利用简化模型rs=RICRFITRF(rg+ρ′u)计算激光脚印点在ITRF下的坐标向量rs。
(6) 利用rs对应的经纬度、高程以及NCEP(National Center for Environmental Prediction)大气参数和大气延迟改正模型计算激光大气延迟改正值Δρatm。
(7) 对测距值ρ′进一步进行修正为ρ′new=ρ′-Δρatm,同时重复步骤(5)计算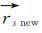
(8) 对新计算的激光脚印点在ITRF下坐标向量rsnew采用潮汐改正模型计算改正量Δrt,最终精确的激光脚印点在ITRF下的坐标向量为:rsnew+Δrt。
在上述步骤中,步骤(5)所对应的为1B级产品GLA05,步骤(7)所对应的为1B级产品GLA06,步骤(8)所对应的为2级产品GLA12-15。
3 精度验证试验本文选取了ICESat/GLAS某一天的辅助数据文件ANC04、ANC08、ANC09、ANC25以及1A级产品GLAS01中的波形参数,采用严密几何模型求解每个激光足印光斑的三维坐标,并与2级产品GLA14中的结果进行对比,其中辅助数据文件及GLAS的1A和2级数据产品从NSIDC网站下载而来。同时对资源三号02星激光试验性载荷的第一轨数据进行了处理与精度验证。
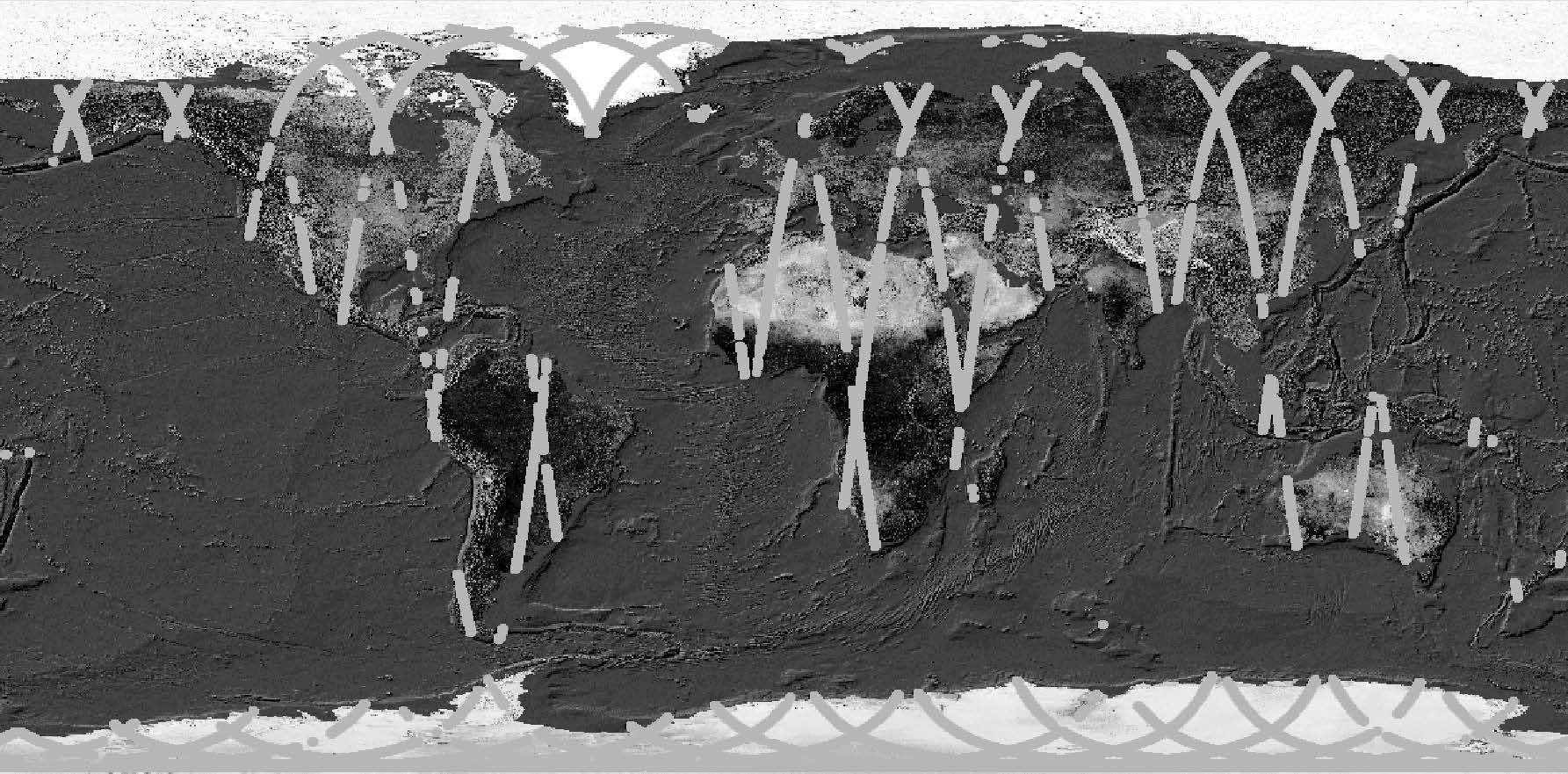
3.1 基于几何模型的精度对比本文选取了2009年3月24日的ICESat/GLAS激光测高数据,其陆地区域的覆盖情况如图 9所示,共约15圈22308个点。采用本文第2部分介绍的数据处理流程,将计算结果与GLA14数据进行对比,统计结果见表 1。在计算过程中,为了与GLA14结果中的Topex/Poseidon椭球保持一致,在ITRF坐标系转成经纬度以及最终投影时均采用T/P椭球参数,其参数为:长轴a=6378136.30m,扁率1/f=298.257。
|
| 图 9 2009年3月24日的GLA14数据覆盖示意图(圆点代表GLAS脚印位置) Fig. 9 The illustration of GLAS data covering on 24th,March 2009 |
从表 1中可以看出,沿轨和垂轨方向的误差与GLAS的结果相比均达到厘米级,其中垂轨方向的多个轨迹数据误差统计的平均值接近于0,这与多次观测的理论平均误差结果是一致的。此外,垂轨和沿轨两者的误差最大值在5~7cm,从误差数量级的角度来说,证明整个基于模型的计算过程是正确的。
| cm | |||
| 垂轨方向dX | 沿轨方向dY | 大地高dh | |
| 最小值 | -5.18 | -7.11 | -19.98 |
| 最大值 | 5.76 | 6.14 | 19.42 |
| 平均值 | 0.06 | -0.25 | -1.70 |
| 中误差 | 2.52 | 3.24 | 11.34 |
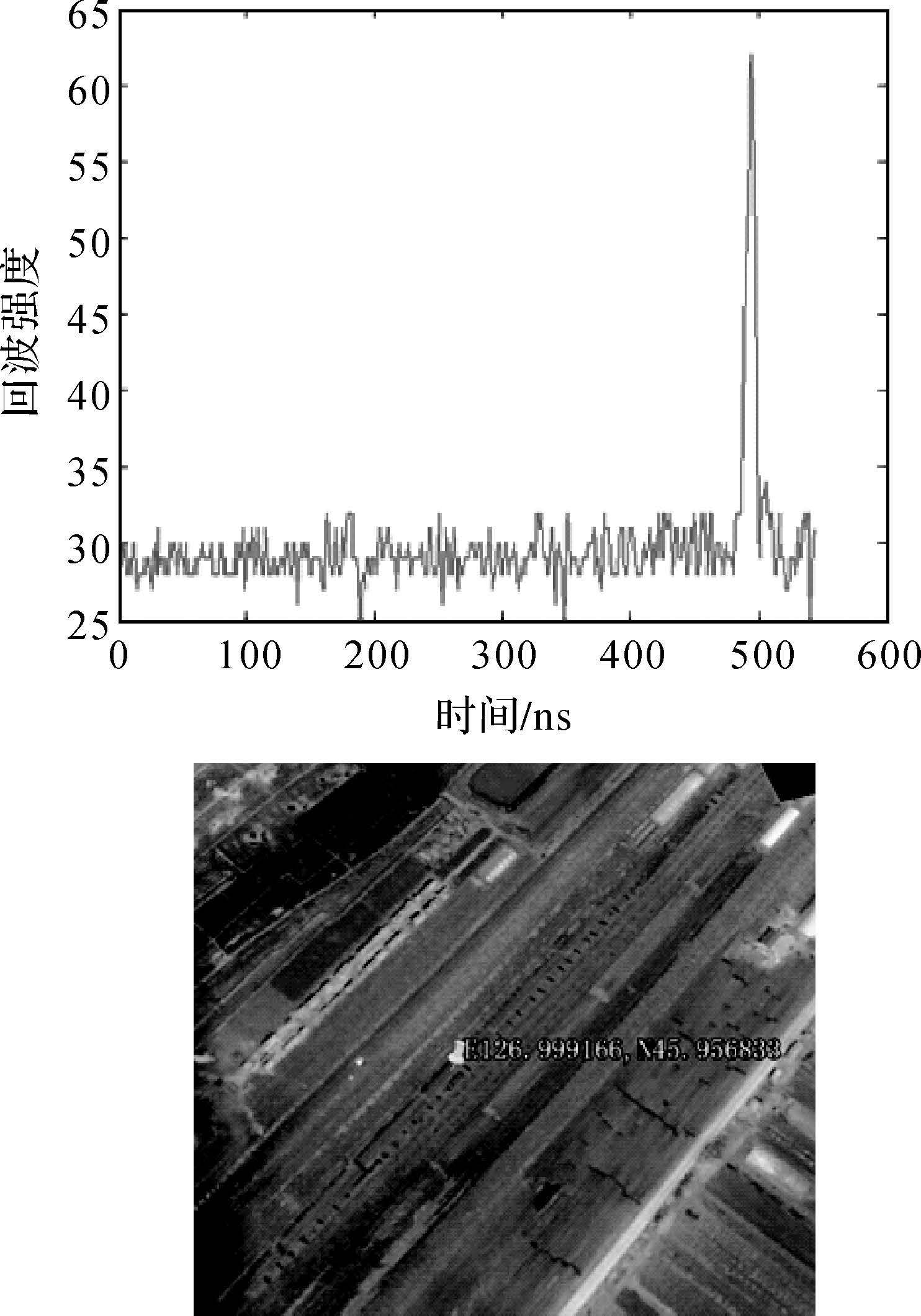
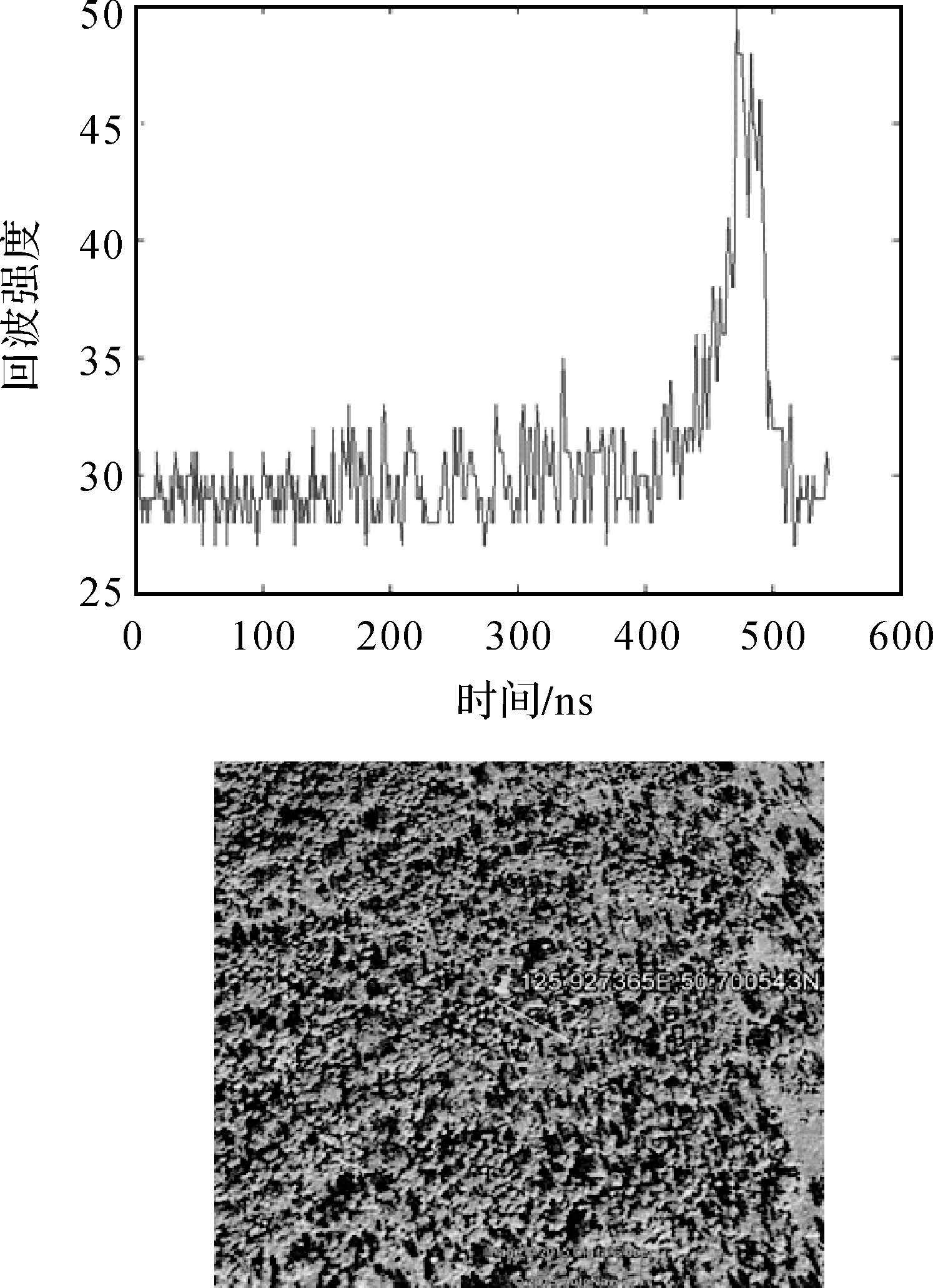
相比GLAS标称的15cm的高程测量误差,本文中基于模型计算的高程相对较差,虽然平均值较小约1.7cm,但最大值超15.0cm。经与GLAS的中间结果对比检查,主要是大气延迟改正和波形拟合时间重心鉴别上存在误差,其中本文计算的大气延迟改正与GLAS给定的改正值差值中误差为1.35cm,但差值最大值为7.64cm。在平坦地形(如图 10)本文提取的波形时间重心与GLAS的基本一致,误差在0.2ns,但在森林或复杂地形区域(如图 11),则与GLAS的时间重心相差较大,误差达1.5ns。
|
| 图 10 平坦地形GLAS激光脚印的回波波形和对应Google影像 Fig. 10 GLAS return waveform of flat terrain and the corresponding image on Google map |
|
| 图 11 复杂波形GLAS激光脚印的回波波形和对应谷歌影像 Fig. 11 GLAS return waveform of rugged terrain and the corresponding image on Google map |
3.2 资源三号02星激光试验载荷初步处理精度验证
资源三号02星于2016年5月30日成功发射,卫星除载有相比01星分辨率略有提升的三线阵相机和多光谱相机外,还额外搭载了试验性的激光测高载荷,该激光测高载荷的有关参数如表 2所示。
| 参数 | 指标 |
| 激光脉冲宽度/ns | 6.5 |
| 重复频率/Hz | 2 |
| 波束数 | 1 |
| 质量/kg | 40 |
| 激光器单脉冲能量/mJ | 175 |
| 有效口径/mm | 210 |
| 激光足印大小/m | 50 |
| 轨道高度/km | 505.984 |
| 测距精度/m | 1(坡度<2°) |
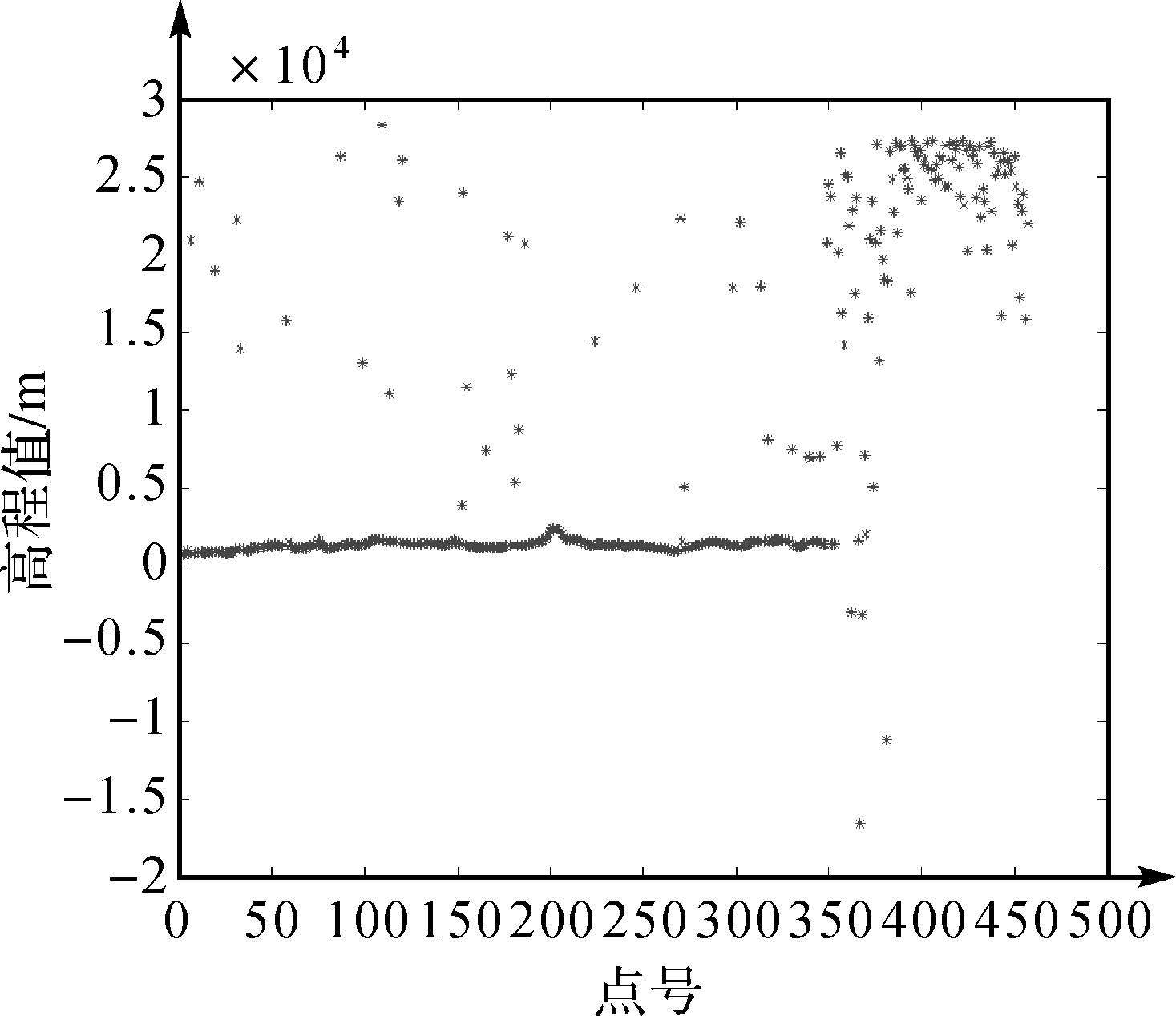
2016年6月24日,资源三号02星激光试验性载荷开机236s,获得了第一轨共472个激光数据,其中14个为无效点。对激光指向角进行初步优化后,按本文的处理方法,计算出每个点的三维大地坐标(经度、纬度和大地高),其地理位置跨蒙古国以及我国的内蒙古、甘肃和青海地区,高程剖面如图 12所示。同时收集了该区域由资源三号和高精度控制数据生产的精度优于3.0m、格网大小为15m的DSM数据作为参考[6],评价激光点的绝对高程精度。
|
| 图 12 资源三号02星第一轨激光数据高程剖面图 Fig. 12 The profile of the first orbit laser altimeter data from ZY3-02 |
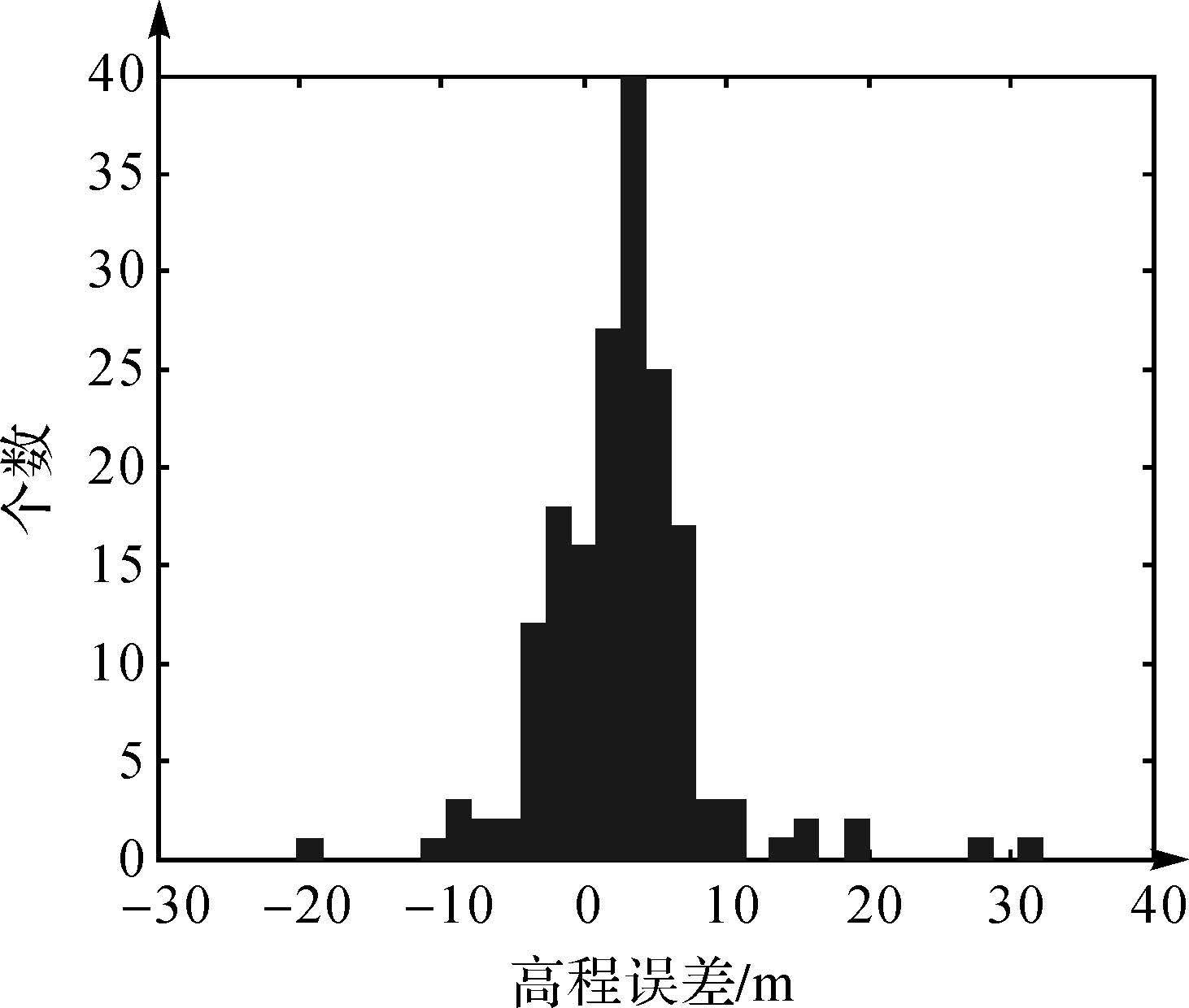
初步分析发现部分激光点因云、霾及地形等原因导致高程值较大,如图 12中最右侧的一些数据点,其高程值达到20000m,存在明显误差,基本能确定是受大气中影响,造成测距值偏小,引起高程偏大。结合试验区的DSM数据的高程范围,试验中以2500m为阈值,将解算出来的激光点高程值大于2500m的去掉不参与计算,对剩下的177个点,利用激光点的经纬度从DSM中内插的高程作为参考值,对激光点的高程误差进行统计分析,高程误差分布直方图见图 13,其统计结果如表 3所示。
|
| 图 13 高程误差的直方图分布 Fig. 13 The histogram of elevation error of laser points |
| 统计类别 | 统计值 |
| 总点数 | 177 |
| 误差绝对值小于5m的点数 | 123 |
| 最小误差/m | -20.09 |
| 最大误差/m | 32.27 |
| 误差均值/m | 2.74 |
| 中误差/m | 5.73 |
4 分 析
本文第2部分对星载激光测高卫星的严密几何定位模型进行系统构建,同时对光行差引起的平面和高程误差进行了分析。在600km轨道高度,因激光光行差而引起的平面位置误差约15m,在定位时必须考虑。而由图 4可知,为了保证激光测高的高程精度,激光指向角必须接近0,若为了使高程误差优于15cm,则激光指向角θ应不大于1°,这在图 5和6中也得到进一步的验证。在让激光指向角θ尽量小的同时,指向角θ的测量误差dθ应优于1.5″,这与ICESat/GLAS的要求是一致的,而另一个指向角α及其测量误差要求则可以相对降低,但为了控制平面误差,α角也应该尽量小,将激光指向尽量控制在卫星本体坐标系的OXZ平面范围内且接近Z轴的负向。
通过采用目前唯一的对地观测激光测高卫星ICESat/GLAS的实际数据对严密几何定位模型的精度进行验证,与GLAS的二级产品GLA14的结果对比,其精度在平面方向与GLAS结果最大偏差在5~7cm,且多轨数据在垂轨方向的均值接近于0。高程方向的偏差中误差为11.3cm,均值约1.7cm,但最大偏差超过19cm,主要由于波形时间重心拟合值与GLAS的值存在一定偏差,且部分区域大气改正值大于GLAS的结果。对资源三号02星第一轨激光数据进行初步处理,同时采用地面DSM数据进行了验证,初步结果表明激光点的高程中误差为5.73m,离激光测距标称的精度还有一定距离。其原因,一方面是由于DSM内插的高程与实际高程有一定的偏差;另一方面是由于激光器的各项硬件参数特别是激光指向角未经过精确在轨检校,与实验室测定的结果有一定的差距,需进一步开展精确标定工作。总体试验结果表明,文中第2部分的模型是正确的,只是在复杂地形及云霾等大气条件下还需进一步的改进和探讨。
5 结 论本文对激光测高卫星严密几何定位模型进行了较为系统地描述,同时对其他文献没有涉及的光行差以及硬件安装误差引起的位置误差进行了分析,相应的分析均建立在严密几何定位模型而非简化模型基础上。分析结果表明,在600km的轨道高度,由于卫星相对运动而产生的激光光行差可引起地面约15m的平面位置偏差,在定位过程中必须加以考虑。此外激光指向角θ和其测量误差dθ需重点关注,为了使高程误差优于15cm,激光指向角θ应不大于1°,dθ应优于1.5″。
本文结合ICESat/GLAS数据以及资源三号02星第一轨激光数据对几何模型进行了分析验证,结果表明该几何模型是正确的,对于ICESat/GLAS基于几何模型的计算精度与官方公布基本一致,能达到ICESat标称的0.15m的测高精度;对于国产的资源三号02星激光试验性载荷的第一轨数据,经该模型初步处理,剔除明显的错误点,采用参考DSM进行评价,其高程中误差为5.73m,与标称的精度还有一定差距,还有待继续深入分析研究。
当前,对地观测卫星发展突飞猛进,搭载了激光测高仪的国产高分七号以及陆地生态系统碳监测卫星也在发射计划中,对激光测高卫星的研究即将进入一个蓬勃发展期,期待本文的研究能对推动国产激光测高卫星的发展作出一点贡献。
| [1] | GARVIN J, BUFTON J, BLAIR J, et al. Observations of the Earth's Topography from the Shuttle Laser Altimeter (SLA):Laser-pulse Echo-recovery Measurements of Terrestrial Surfaces[J]. Physics and Chemistry of the Earth , 1998, 23 (9-10) : 1053 –1068. DOI:10.1016/S0079-1946(98)00145-1 |
| [2] | WANG Xianwei, CHENG Xiao, GONG Peng, et al. Earth Science Applications of ICESat/GLAS:A Review[J]. International Journal of Remote Sensing , 2011, 32 (23) : 8837 –8864. DOI:10.1080/01431161.2010.547533 |
| [3] | SCHUTZ B E, ZWALLY H, SHUMAN C A, et al. Overview of the ICESat Mission[J]. Geophysical Research Letters , 2005, 32 (21) . DOI:10.1029/2005GL024009 |
| [4] | ABDALATI W, ZWALLY H J, BINDSCHADLER R, et al. The ICESat-2 Laser Altimetry Mission[J]. Proceedings of the IEEE , 2010, 98 (5) : 735 –751. DOI:10.1109/JPROC.2009.2034765 |
| [5] | YU A W, HARDING D J, KRAINAK M A, et al. Development of the Airborne Lidar Surface Topography Simulator[C]//Proceedings of SPIE 8286, International Symposium on Lidar and Radar Mapping 2011:Technologies and Applications. Nanjing, China:SPIE, 2011. http://cn.bing.com/academic/profile?id=2003031977&encoded=0&v=paper_preview&mkt=zh-cn |
| [6] | 唐新明, 张过, 祝小勇, 等. 资源三号测绘卫星三线阵成像几何模型构建与精度初步验证[J]. 测绘学报 , 2012, 41 (2) : 191–198. TANG Xinming, ZHANG Guo, ZHU Xiaoyong, et al. Triple Linear-array Imaging Geometry Model of Ziyuan-3 Surveying Satellite and Its Validation[J]. Acta Geodaetica et Cartographica Sinica , 2012, 41 (2) : 191 –198. |
| [7] | 朱长明, 张新, 路明, 等. 湖盆数据未知的湖泊动态库容遥感监测方法[J]. 测绘学报 , 2015, 44 (3) : 309–315. ZHU Changming, ZHANG Xin, LU Ming, et al. Lake Storage Change Automatic Detection by Multi-source Remote Sensing without Underwater Terrain Data[J]. Acta Geodaetica et Cartographica Sinica , 2015, 44 (3) : 309 –315. DOI:10.11947/j.AGCS.2015.20130438 |
| [8] | 李建成, 范春波, 褚永海, 等. ICESAT卫星确定南极冰盖高程模型研究[J]. 武汉大学学报(信息科学版) , 2008, 33 (3) : 226–228. LI Jiancheng, FAN Chunbo, CHU Yonghai, et al. Using ICESAT Altimeter Data to Determine the Antarctic Ice Sheet Elevation Model[J]. Geomatics and Information Science of Wuhan University , 2008, 33 (3) : 226 –228. |
| [9] | 黄海兰, 王正涛, 金涛勇, 等. 利用ICESat激光测高数据确定极地冰盖高程变化[J]. 武汉大学学报(信息科学版) , 2012, 37 (10) : 1221–1223. HUANG Hailan, WANG Zhengtao, JIN Taoyong, et al. Determination of Polar Ice Sheet Height Change from ICESat Altimetry Data[J]. Geomatics and Information Science of Wuhan University , 2012, 37 (10) : 1221 –1223. |
| [10] | LI Xiaolu, MA Lian, XU Lijun. Real-time Terrain Classification Using ICESat/GLAS Data over Beijing Area[J]. Remote Sensing Letters , 2014, 5 (7) : 591 –600. DOI:10.1080/2150704X.2014.942922 |
| [11] | 胡文敏, 邸凯昌, 岳宗玉, 等. 嫦娥一号激光高度计数据交叉点分析与平差处理[J]. 测绘学报 , 2013, 42 (2) : 218–224. HU Wenmin, DI Kaichang, YUE Zongyu, et al. Crossover Analysis and Adjustment for Chang'E-1 Laser Altimeter Data[J]. Acta Geodaetica et Cartographica Sinica , 2013, 42 (2) : 218 –224. |
| [12] | WU Bo, HU Han, GUO Jian. Integration of Chang'E-2 Imagery and LRO Laser Altimeter Data with a Combined Block Adjustment for Precision Lunar Topographic Modeling[J]. Earth and Planetary Science Letters , 2014, 391 : 1 –15. DOI:10.1016/j.epsl.2014.01.023 |
| [13] | 赵双明, 冉晓雅, 付建红, 等. CE-1立体相机与激光高度计数据联合平差[J]. 测绘学报 , 2014, 43 (12) : 1224–1229. ZHAO Shuangming, RAN Xiaoya, FU Jianhong, et al. Combined Adjustment of CE-1 Stereo Camera Image and Laser Altimeter Data[J]. Acta Geodaetica et Cartographica Sinica , 2014, 43 (12) : 1224 –1229. DOI:10.13485/j.cnki.11-2089.2014.0178 |
| [14] | 王任享, 王建荣. 二线阵CCD卫星影像联合激光测距数据光束法平差技术[J]. 测绘科学技术学报 , 2014, 31 (1) : 1–4. WANG Renxiang, WANG Jianrong. Technology of Bundle Adjustment Using Two-Line-Array CCD Satellite Image Combined Laser Ranging Data[J]. Journal of Geomatics Science and Technology , 2014, 31 (1) : 1 –4. |
| [15] | 李国元, 唐新明, 王华斌, 等. GLAS激光测高数据辅助的资源三号三线阵区域网平差研究[C]//第三届高分辨率对地观测学术年会优秀论文集. 北京:中国科学院重大科技任务局, 2015. LI Guoyuan, TANG Xinming, WANG Huabin, et al. ZY-3 Three Line Array Images Block Adjustment Supported by GLAS data[C]//The 3th Annual Conference on High Resolution Earth Observation. Beijing:Major Science and Technology Bureau of the Chinese Academy of Sciences, 2015. |
| [16] | 李鑫, 廖鹤, 赵美玲, 等. 激光测绘卫星对不同地表形貌探测能力分析[J]. 测绘学报 , 2014, 43 (12) : 1238–1244. LI Xin, LIAO He, ZHAO Meiling, et al. Research on LiDAR Surveying Satellite Detection Capacity for Different Terrains[J]. Acta Geodaetica et Cartographica Sinica , 2014, 43 (12) : 1238 –1244. DOI:10.13485/j.cnki.11-2089.2014.0188 |
| [17] | 范春波, 李建成, 王丹, 等. ICESat/GLAS激光脚点定位及误差分析[J]. 大地测量与地球动力学 , 2007, 27 (1) : 104–106. FAN Chunbo, LI Jiancheng, WANG Dan, et al. ICESAT/GLAS Laser Footprint Geolocation and Error Analysis[J]. Journal of Geodesy and Geodynamics , 2007, 27 (1) : 104 –106. |
| [18] | 朱剑锋, 王昱, 胡煜, 等. 星载激光测高的系统误差分析与检校[J]. 测绘通报 , 2014 (S1) : 137–140. ZHU Jianfeng, WANG Yu, HU Yu, et al. Systematic Error Analysis and Calibration of Spaceborne Laser Altimeter[J]. Bulletin of Surveying and Mapping , 2014 (S1) : 137 –140. |
| [19] | 马跃, 阳凡林, 卢秀山, 等. 对地观测星载激光测高系统高程误差分析[J]. 红外与激光工程 , 2015, 44 (3) : 1042–1047. MA Yue, YANG Fanlin, LU Xiushan, et al. Elevation Error Analysis of Spaceborne Laser Altimeter for Earth Observation[J]. Infrared and Laser Engineering , 2015, 44 (3) : 1042 –1047. |
| [20] | SCHUTZ B. Laser Footprint Location (Geolocation) and Surface Profiles[R]. GLAS Algorithm Theoretical Basis Document, Version 3.0, 2002. |
| [21] | 孔祥元, 郭际明, 刘宗泉. 大地测量学基础[M]. 2版 武汉: 武汉大学出版社, 2010 . KONG Xiangyuan, GUO Jiming, LIU Zongquan. Foundation of Geodesy[M]. 2nd ed Wuhan: Wuhan University Press, 2010 . |
| [22] | BAE S, SCHUTZ B E. Precision Attitude Determination(PAD)[R]. Geoscience Laser Altimeter System (GLAS) Algorithm Theoretical Basis Document, Version 2.2.[S.l.]:NASA, 2002. |
| [23] | JESTER P, LEE J. GLAS Standard Data Products Specification Level 1[R]. ICESat (GLAS) Science Processing Software Document Series Version 8.0. 2005. |
| [24] | ZWALLY H J, SCHUTZ BE, HANCOCK D W. GLAS Standard Data Products Specification Level 2[R]. Version 8.0. 2005. |
| [25] | RIM H, SCHUTZ B. Precision Orbit Determination (POD)[R]. GLAS Algorithm Theoretical Basis Document, Version 2.2, 2002. |
| [26] | BRENNER A C, ZWALLY H J, BENTLEY C R, et al. Derivation of Range and Range Distributions from Laser Pulse Waveform Analysis for Surface Elevations, Roughness, Slope, and Vegetation Heights[R]. GLAS Algorithm Theoretical Basis Document, Version 3.0, 2011. |



