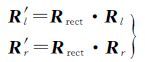随着相机技术的进步和新的匹配算法的提出,在摄影测量和计算机视觉领域诞生了许多基于影像的三维重建商业软件,如Street Factory、Smart3D、PhotoScan、Pixel4d等,而多视密集匹配是自动三维重建的关键步骤之一。多视影像密集匹配一般指在完成测区的光束法区域网平差后,进行逐像素的匹配,获取与原始影像对应地面分辨率同等精度的密集点云和数字表面模型(DSM)。与激光扫描等直接获取三维信息的方式相比,通过影像密集匹配获取三维点云的方式成本较低,同时,影像密集匹配的方式还能获取丰富的纹理信息。另一方面,与激光扫描获取的点云不同的是密集匹配生成的点云通过多余观测的方式获取,因此其每一离散点的精度都可以进行评定。基于影像的三维重建技术由于其轻巧、便捷、成本低等优点,且能够生成与LiDAR相媲美的带纹理点云数据,因此被广泛用于三维建模、制图、导航、机器人、矿产及救援等领域。
多视影像密集匹配算法按照处理单元的不同可以分为基于立体像对的算法[1-4]和基于多视对应的算法[5-11],前者首先对所有立体像对进行匹配生成视差图,再进行多视匹配结果的融合;后者通常在多视影像间利用强约束关系进行匹配,再利用区域生长算法向四周扩散。按照优化策略的不同也可分为基于局部匹配的算法和基于全局匹配的算法,前者使用了一个表面光滑的隐式假设,它们对窗口内的像素计算一个固定视差;相反,所谓的全局算法使用显示的方程来表达光滑性假设,之后通过全局最优问题来求解[12],全局算法的效果要优于局部算法,但是算法复杂度也要高于局部算法。代表算法有动态规划法(Dynamic Programming)、置信传播法(Belief Propagation)及图割法(Graph Cut)等。文献[1-2, 13]提出的半全局匹配(SGM)算法也是应用能量最小化策略,该算法的思想是基于点的匹配代价,利用多个一维方向的计算来逼近二维计算,通过对视差的不同变化加以不同惩罚保证了平滑性约束,因此对噪声具有较好的稳健性。半全局匹配算法顾及了算法的效率和精度,其计算精度优于局部算法,计算时间优于全局算法。文献[14]对目前流行的4款密集匹配软件SURE、MicMac、PMVS、PhotoScan进行了试验,其中SURE[4]属于一种基于立体像对的多视密集匹配方法,首先利用tSGM算法计算每个立体像对的视差影像,接着对视差影像进行融合生成最终点云;MicMac[6, 15]是一种多分辨率多视匹配方法,支持基于像方和物方几何两种匹配策略,在匹配结束后采用能量最小化策略来重建表面;PMVS[9]采用一种基于光照一致性的多视匹配方法,首先进行初始匹配生成种子面元,接着通过区域生长来得到一个准稠密的面元结果,最后通过滤波来剔除局部粗差点;而PhotoScan则采用一种近似SGM的半全局匹配算法。文献[14]研究结果表明采用SGM策略的SURE和PhotoScan在算法精度和效率上要优于PMVS和MicMac。国内对于多视密集匹配的相关研究还比较少,文献[16]提出一种基于对极几何和单应映射双重约束及SIFT特征的宽基线立体匹配算法,文献[17]提出一种像方特征点和物方平面元集成的多视影像匹配方法,但上述算法都是基于特征来进行影像匹配,只能获取稠密或准密集点云。文献[18]提出一种融合SIFT和SGM的倾斜航空影像密集匹配方法,利用匹配的SIFT特征作为SGM优化计算的路径约束条件,减少错误匹配代价的传播并加速最优路径搜索过程。
传统的SGM多视密集匹配算法[2]在进行多视影像视差融合时通常将所有视差影像投影到一个公共投影面上并进行中值滤波获取最终的视差图,这种做法只适用于所有相机的摄站中心近似在同一平面上并且所有相机的方向近似一致的情况。另一方面,由于在生成密集点云的过程中并未充分利用冗余观测值,虽然在视差融合过程中进行了中值滤波,生成的密集点云依然存在大量的粗差点,需要通过滤波进行后处理。本文提出了一种基于网络图的多视影像密集匹配算法,在算法的整体思路上接近SURE方法:首先根据影像间的重叠关系进行立体像对网络图的构建,接着对满足影像重叠率阈值的立体像对执行tSGM算法计算两者间的视差影像,最后依据网络图可生成顾及所有重叠影像的物方密集点云。基于网络图的多视影像密集匹配使用网络图中的所有重叠影像通过多片前方交会来计算物方点云,利用冗余观测值信息可以有效剔除密集匹配中的粗差点,大大减小了后续滤波的难度和耗时。
1 基于网络图的高分辨率多视影像密集匹配基于网络图的多视影像密集匹配主要包括多视影像网络图构建、立体像对视差图计算、基于网络图的单视密集点云生成以及多视密集点云融合4个部分。首先利用影像间的重叠关系构建网络图并确定候选匹配像对列表,接着利用改进的tSGM算法进行立体像对间的双向视差图生成,进而基于网络图进行单视密集点云生成,最后对所有单视点云进行融合处理得到最终的密集匹配结果。
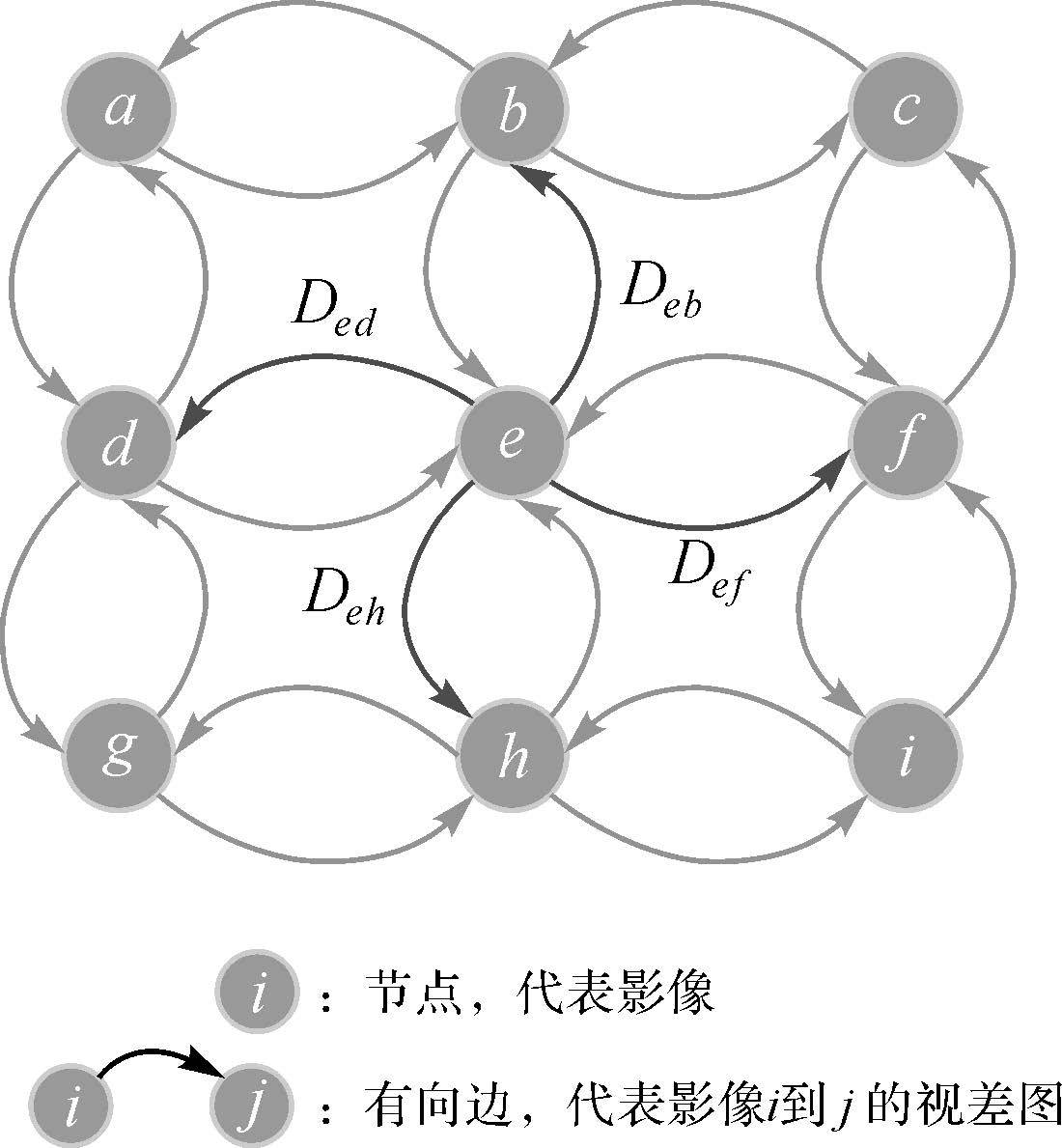
1.1 多视影像网络图构建首先,将整个测区所有已定向的影像作为单一节点加入到网络图中;然后,利用相邻影像间的重叠率约束(默认取0.5)和方向约束从整个测区的影像列表中选取候选匹配像对:当不考虑旁向重叠立体像对时,要求3个姿态角差值Δφ、Δω、Δκ均小于指定阈值(默认取5°);反之,要求φ、ω、min(|Δκ|,π-|Δκ|)小于指定阈值。将满足上述条件的立体像对作为以各影像为起点的有向边加入到图中(图 1),每个有向边代表由起始节点到终止节点的视差图,并定义节点间的距离为两者之间最短路径的有向边数目。以图 1中3条航带为例,影像d和f由于重叠率不满足阈值,未被纳入到图中,但由于网络图的传递性,两幅影像上公共区域的点依然可以通过中间节点e找到对应关系。
|
| 图 1 多视影像网络图结构示意图 Fig. 1 The schematic diagram of multi-view graph network structures |
1.2 立体像对视差图计算 1.2.1 核线影像生成
在对立体像对进行视差计算前,需要首先对两幅影像进行核线矫正[19-21],将二维的匹配搜索降低为一维搜索。假设相机的内参数矩阵为K,已定向的左右影像外方位元素分别为Rl、Cl和Rr、Cr(Rl、Rr为外方位角元素构建的旋转矩阵,Cl、Cr为外方位线元素),基线向量B=Cr-Cl,则原始左右影像变换至核线影像的旋转矩阵Rrect按式(1)计算
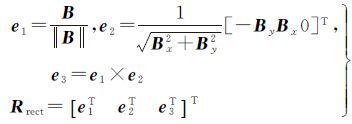 (1)
(1)
可得左右核线影像的旋转矩阵为
则可得原始左右影像到核线影像的单应变换矩阵为
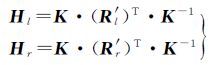 (2)
(2)
在获取上述单应变换矩阵后,原始影像上的像点xo与矫正后核线影像上的对应像点xr满足
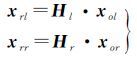 (3)
(3)
即可按照间接微分纠正法获取左右影像对应的核线影像。
1.2.2 半全局匹配SGM[2]立体像对的密集匹配问题是在两幅影像上逐像素寻找同名像点的过程,利用核线影像,传统的二维搜索可以简化为同一扫描行上的一维搜索。令参考影像和匹配影像分别记为Ib和Im,则两幅影像上的同名像点的视差满足:d=xm-xb,SGM算法的目标是估计立体像对的视差使得全局代价函数最小化。全局代价函数E(D)计算公式为
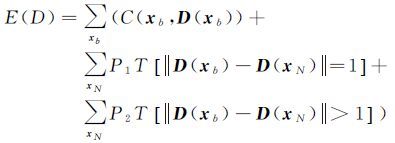 (4)
(4)
式中,D代表参考影像的视差影像,包含了参考影像上所有像素xb的视差估计值;xN代表xb的邻域像素值;T[]代表条件判断操作符,若为真,取1;否则,取0。全局代价函数E(D)由一个数据项和两个光滑项组成,惩罚参数P1和P2用于控制重建表面的光滑程度。SGM算法主要思路如下:首先利用互信息MI作为相似性测度计算参考影像上每个像素xb在候选视差范围dmin,dmax的匹配代价C(xb,D(xb));接着,沿着多个一维方向ri的每个路径进行累计视差的递归计算
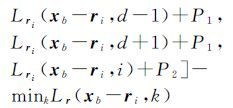 (5)
(5)
式中,最后一项用于保证Lri(xb,d)<Cmax(xb,d)+P2,所有路径的累计代价为
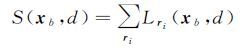 (6)
(6)
最后,取每个像素的累计视差最小值对应视差dfinal=mindS(xb,d)作为视差影像D的视差结果以使得全局代价函数最小化。
1.2.3 改进的金字塔层级匹配策略在对高分辨率影像密集匹配进行处理时,文献[4]提出tSGM 算法:采用由粗到精的金字塔匹配策略,高层级(低分辨率)的金字塔影像的密集匹配视差图作为下一层级金字塔影像密集匹配的视差初值,用于精化MI匹配代价并且减少视差空间的搜索范围.设Dl 作为影像金字塔层级l的视差影像结果,对于每个像素xb 新的搜索范围由视差像素Dl(xb)邻域内的有效视差来确定:如果当前像素匹配成功,则最小dmin和最大dmax视差通过一个邻域7×7的窗口获得并分别存储在影像Rminl和Rmaxl中;如果当前像素匹配失败,在更大的邻域31×31窗口内搜索dmin和dmax,并且当前像素的视差估计d(xb)由搜索邻域窗口内所有视差的中值来代替.限制金字塔层级l的有效、无效匹配点的视差搜索范围分别为16、32像素,Rminl和Rmaxl定义了下一金字塔层级l-1的视差搜索范围.由于采用动态视差空间,使得单个像素的视差搜索范围与邻域像素的视差搜索范围可能部分重叠或无重叠,因此式(5)修改为式(7)
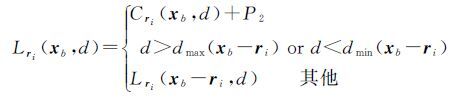 (7)
(7)
在tSGM算法中上一层级密集匹配确定的动态视差搜索范围直接影响到下一层级的密集匹配结果,由于传统的中值滤波算法无法很好地顾及影像的边缘特性,在滤波的过程中会造成边缘部分模糊,本文采用改进的导向中值滤波替代传统的中值滤波算法,即在计算邻域范围内的视差中值时,顾及核线影像上像素的灰度信息,不考虑灰度差大于指定阈值(默认取5)的邻域像素。另外,每一层级金字塔影像进行密集匹配时需要交换参考影像和匹配影像,对估计视差利用左右一致性检验db-dm≤1剔除不满足要求的视差值,并利用OpenCV中的斑块提取算法获取视差突变区域和无效区域,再次利用导向中值滤波对上述区域进行插值。图 2给出了影像局部区域不同阶段的视差结果影像,从左到右依次为原始影像、SGM初始匹配视差影像、中值滤波后的视差影像以及斑块修复后的最终结果影像;同时,还给出了导向中值滤波和传统中值滤波结果对比影像。从局部放大图可以看出,利用改进的导向中值滤波生成的视差图与原始影像上的物体轮廓细节保持了高度的一致性。在本文的算法中,考虑到网络图中边的方向性,需要同时输出参考影像和匹配影像对应的视差影像(图 3)。

|
| 图 2 影像局部区域密集匹配不同阶段视差结果影像和不同中值滤波最终结果 Fig. 2 The dense matching results of different processing stages for local area |

|
| 图 3 核线立体像对及其密集匹配视差影像示例 Fig. 3 Stereo dense matching results of epipolar images |
1.3 基于网络图的单视密集点云生成
基于网络图的影像间的几何对应关系如图 4所示,以影像i和影像j构建的立体像对(索引为m)为例,对于网络图中的有向边
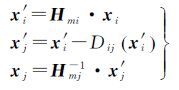 (8)
(8)

|
| 图 4 基于网络图的影像间像素几何对应关系传递 Fig. 4 The geometric correspondence relationship across multi-view images based on graph network |
由于转换后的像点坐标为浮点值,因此在获取对应视差值时需要进行双线性内插。另外,计算过程中视差图需要根据有向图的方向来选择。按照上述思路,在网络图中获取从影像i节点出发的所有有向边,即可获取xi在所有匹配影像上同名像点集合,则根据
 (9)
(9)
式中,xi为同名像点坐标;Pi为像点所在影像的已标定内外方位元素构成的投影矩阵。利用多片前方交会便可计算得到xi对应的物方点坐标Xi以及其对应的平均反投影误差σr,反投影误差按式(10)计算
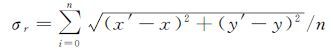 (10)
(10)
式中,(x,y)为原始影像像点坐标;(x′,y′)为利用多片前交物方点反投影到原始影像的像点坐标。
虽然在立体像对视差图生成过程中利用左右一致性检验、斑块剔除和中值滤波处理,依然会存在一些粗差点,通过设置多片前方交会的最少影像数目N(默认取3)和像点平均反投影误差阈值ε(默认取5.0像素)可以有效剔除潜在的粗差点,大大减少后续滤波处理的复杂度和耗时;此外,由于多片前交过程中充分利用了冗余观测值信息,相比于直接利用立体像对生成点云或视差融合的方法,重建的密集点云精度更高。另一方面,由于采样网络图的方式,同一物方点从不同的影像节点出发,其最终搜索到的同名像点列表都是相同的,使得不同的单视影像生成的密集点云坐标系统完全一致,不存在微小的偏移量,降低了后续的多视密集点云融合的难度。
1.4 多视密集点云融合经过上述步骤可以获取每张影像对应的单视密集点云,由于受视角、遮挡、误匹配等因素的影响,不同影像生成的单视点云需要进行融合,以使得重叠区域的点云趋于完整。一方面,由于多视密集点云在视差变化剧烈的建筑物边缘、植被以及遮挡区域依然存在一些误匹配点,需要对融合后的点云进行噪声去除;另一方面,由于多视密集点云之间含有一定的重叠度,导致点云密度很大,需要对融合后的点云进行格网重采样。本文的多视密集点云融合具体思路如下:
(1) 采用开源软件PCL中的点云滤波方法对各单视密集点云进行噪声去除,由于本文的算法在前面步骤中已经剔除了大部分的粗差点,因此该步骤只需要将剩余的一些噪声和离散点剔除。
(2) 根据所有单视密集点云的外包盒求取整个测区的最小外包盒,设定目标格网的采样分辨率,生成等间距的采样格网点。
(3) 逐一遍历格网点,获取覆盖该格网点有效的单视密集点云数据,利用K-d树搜索获取其邻域范围内的M个邻近点,利用单视密集点云生成过程中获取的物方点反投影误差作为优先级测度,保留邻域反投影误差最小的点作为采样点。
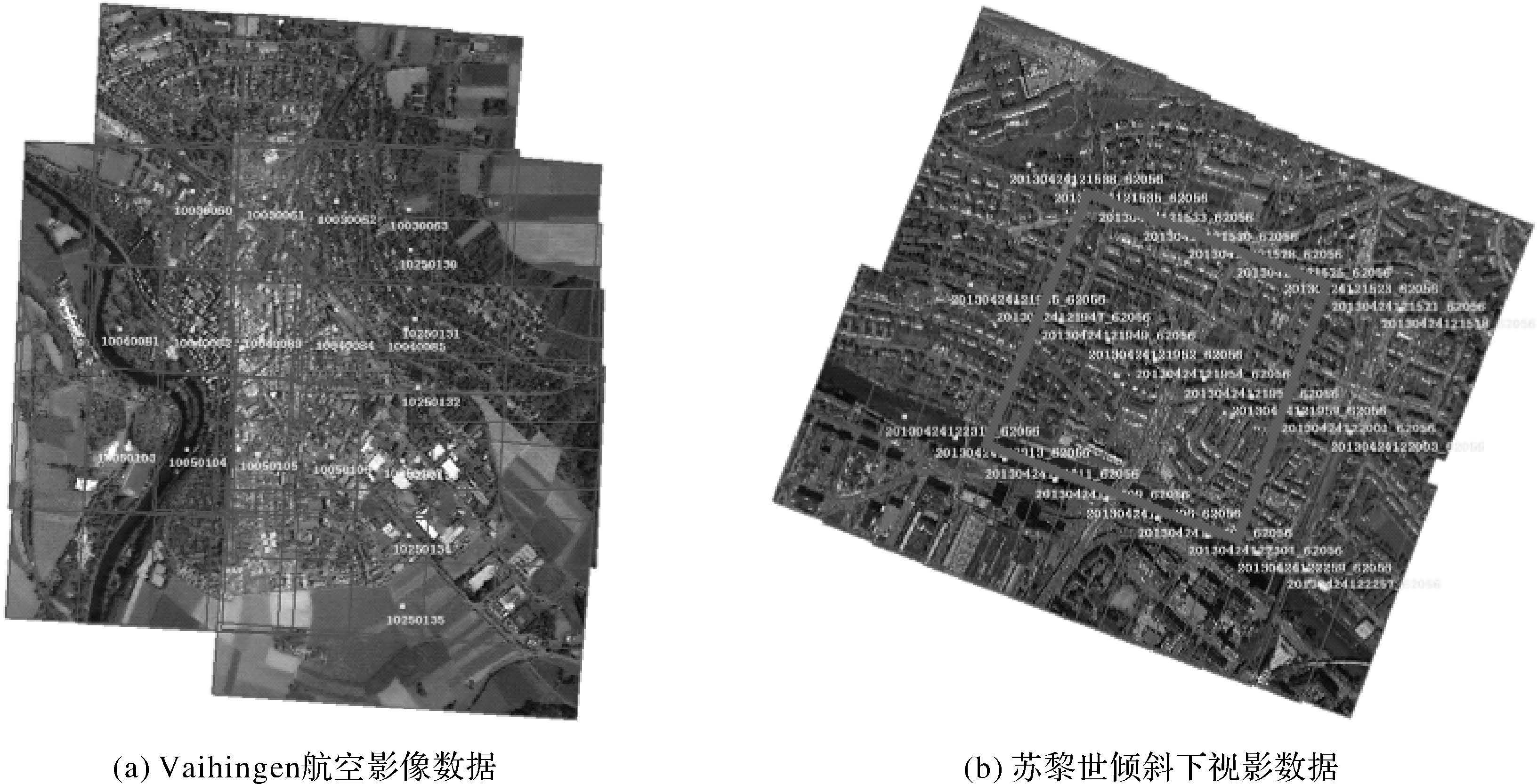
2 试验与分析 2.1 试验数据试验选择ISPRS提供的Vaihingen城市机载航空影像(http://www2.isprs.org/commissions/comm3/wg4/detection-and-reconstruction.html)和ISPRS/EuroSDR项目苏黎世的倾斜下视影像(http://www.ifp.uni-stuttgart.de/ISPRS-EuroSDR/ImageMatching/index.html)作为试验数据,影像集的相关描述见表 1。其中,Vaihingen数据集同时含有机载LiDAR参考点云数据,用于本文算法的实际精度评定。苏黎世数据采用Leica RCD30倾斜相机平台获取,影像数据的测区范围及其重叠关系如图 5所示,研究目标区域为图中红色矩形框范围内的区域,该区域的影像重叠率大部分为8°重叠,冗余观测值信息丰富,有利于获取高精度的密集点云结果。基于Win7 64位系统采用VC++2010、CUDA 6.0开发了多视影像密集匹配软件Mogas-SURF,硬件平台为Dell Precision T7600工作站,处理器为Intel Xeon E5-2650、主频2.0GHz,内存64GB,显卡为16GB NVIDIA GeForce GTX TITAN。考虑到内存占用和处理时间,本文对原始影像均进行一次降采样进行密集匹配试验。
| 组别 | 测试数据 | 影像 分辨率 | 像元大小 /um | 焦距/mm | GSD/cm | 影像 数目 | 航高/m | 重叠度/(%) | 含参考 ALS点云 | |
| 航向 | 旁向 | |||||||||
| 1 | Vaihingen | 7680×13824 | 12.0 | 120.0 | 8.0 | 14 | 900 | 60 | 60 | √ |
| 2 | Zürich | 9000×6732 | 6.0 | 53.0 | 6.0 | 27 | 500 | 70 | 50 | × |
|
| 图 5 试验影像数据集及其重叠关系覆盖图 Fig. 5 The coverage and overlap relationships of test image datasets |
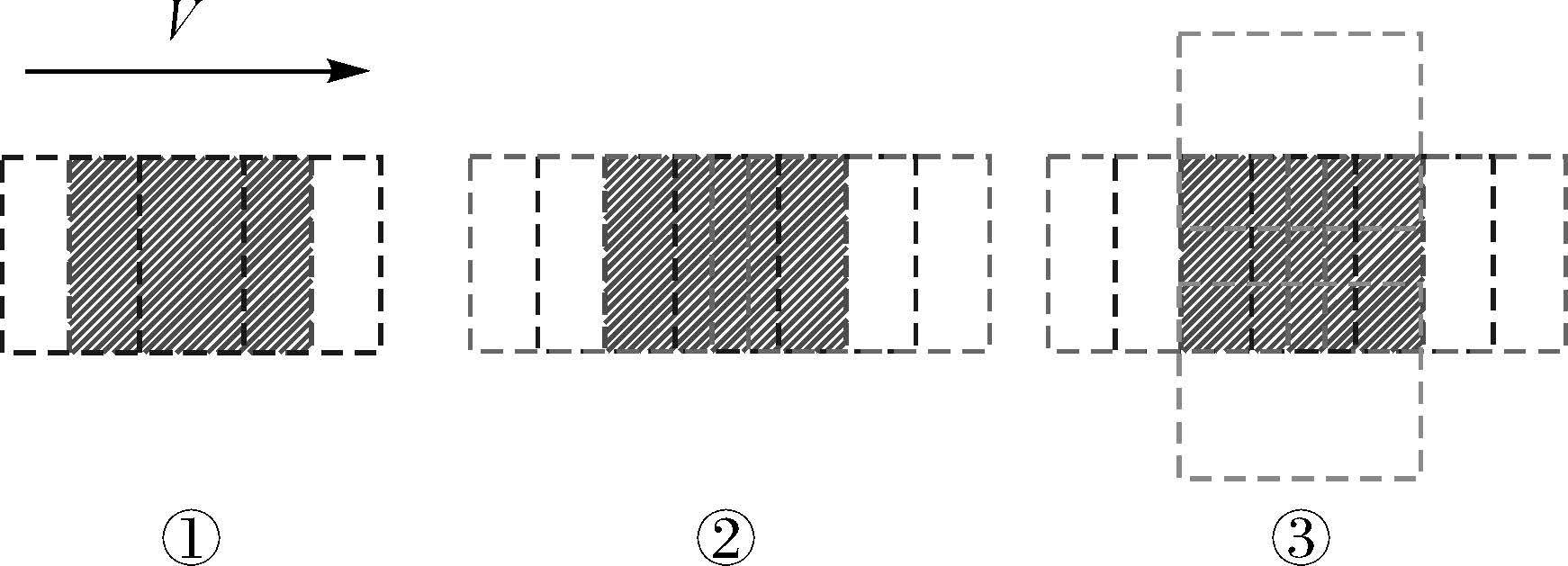
本文通过多视影像网络图构建过程中立体像对重叠度阈值的不同,设计了3种不同配置方案的密集匹配试验(图 6):第1种情形仅考虑航带内的相邻影像构成的立体像对,第2种情形考虑航带内左右各2张影像构建的立体像对,第3种情形在第2种情形基础上增加航带间的旁向重叠立体像对。
|
| 图 6 基于网络图的3种密集匹配配置方案 Fig. 6 Three kind of matching configurations for multi-view dense matching based on graph network |
2.2 密集点云生成及精度分析 2.2.1 苏黎世数据试验
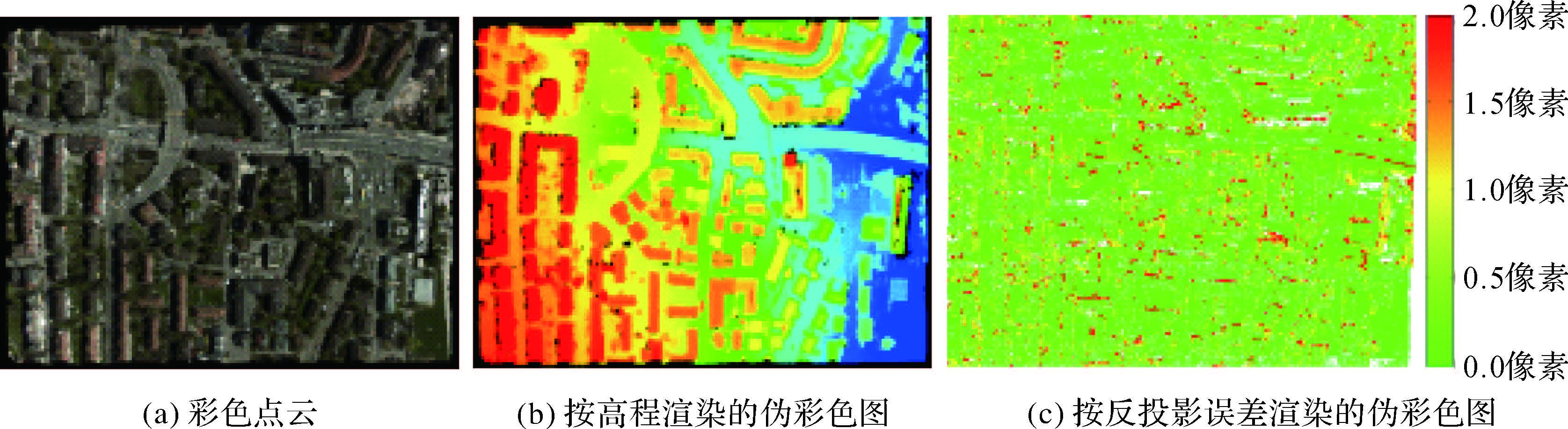
密集匹配点云的内符合精度可以利用多片前方交会过程中的平均反投影误差来反映,以苏黎世的影像-954为例,其对应的单视密集点云结果如图 7所示,从左到右依次为彩色点云、按高程渲染的伪彩色点云、按平均反投影误差渲染的伪彩色图。
|
| 图 7 影像-954密集匹配结果 Fig. 7 The dense matching results of image-954 |
对上述密集匹配点云的平均反投影误差进行统计:整幅影像的平均反投影误差中误差σ0为0.60像素,每个物方点的平均反投影误差分布如图 7(c)所示:从图中结果可以看出,绝大部分点的平均反投影误差在1.0像素以内,误差较大的点一般位于高大建筑物、植被等边缘遮挡区域,与文献[12, 14]得到的结论相一致。这是上述区域在立体像对的视差图生成时容易出现噪声、漏洞等情况,而进行左右一致性检验时粗差点一般也位于该类区域,虽然能够经过中值滤波获取近似视差,但该部分视差的可信度较低,导致最终的平均反投影误差较大,该部分残差较大的物方点可以在多视密集点云融合过程中得以进一步剔除。
为了比较3种不同配置下的密集匹配结果,分别对候选立体像对数目、点云数目、密集匹配耗时、平均反投影误差中误差等因素进行了统计(见表 2),其中点云数目仅取影像-954密集匹配结果为例。
| 方案 | 候选立体 像对数目 | 点云数目 (影像-954) | 密集匹配 耗时/min | 平均反投影 误差中误差 /像素 |
| ① | 24 | 11574821 | ≈58 | 0.60 |
| ② | 45 | 11018062 | ≈101 | 0.70 |
| ③ | 62 | 12136501 | ≈135 | 1.08 |
从上述结果可以看出,增加重叠度较小的航线内立体像对和旁向立体像对对于密集匹配多片前交过程中生成的有效点云数目影响不大,反而使得重建点云的精度下降。通常情况下,交会角越大,重建精度越高,但是在进行密集匹配时,由于重叠度较小的立体像对基高比较大,导致影像间的遮挡区域增多,而遮挡区域的视差精度一般较低,使得这部分点云在多片前交的过程中由于反投影误差超限而被剔除;而由于本文算法利用网络图的传递性,利用高精度的相邻立体像对匹配视差可以获取节点距离大于1的非邻接影像节点的匹配对应关系,优于直接利用小重叠度的立体像对密集匹配精度。将多片前方交会过程中物方点的平均反投影误差作为多视密集点云融合的邻域选择优先级测度,对目标区域的多视密集点云进行融合,结果如图 8所示(方案①结果)。

|
| 图 8 多视密集点云融合结果 Fig. 8 The fused result of multi-view point clouds |
2.2.2 Vaihingen数据试验
由于实际定位精度除了受到匹配精度的影响,同时会受到基高比的影响,仅利用反投影误差不能完全反映密集匹配的实际精度,因此选取Vaihingen数据中包含植被和建筑的目标区域利用参考LiDAR点云对本文算法进行了验证,同时比较了3种方案的实际精度,结果如图 9所示。

|
| 图 9 Vaihingen试验数据目标区域密集匹配结果 Fig. 9 The dense matching results of target area of Vaihingen dataset |
从试验结果可以看出,本文算法获取的密集点云与机载LiDAR参考点云从整体效果来看是一致的,3种方案密集匹配点云的中误差分别为1.50 GSD、1.75 GSD、1.87 GSD,这与上文利用反投影误差来评价得到的结论是一致的。通过比较3种方案下的点位误差分布图可以看出,方案②与方案①相比并未增加用于前方交会的影像数目,由于受宽基线立体像对密集匹配精度较差带来的影响,因此整体精度低于方案①;方案③与方案①相比,增加了旁向影像用于前方交会,从图中可以看出,在一些局部区域点位精度要优于方案①,但旁向立体像对大交会角导致遮挡区域的匹配精度进一步降低,重建密集点云的完整性和整体精度比方案①差。另一方面,考虑到Vaihingen数据的影像航向重叠度仅为60%,而更高的重叠度有利于进一步提高密集点云的点位精度。单个立体像对密集匹配的平均耗时约为2min,总的密集匹配耗时与候选立体像对数目成正比,采用方案①在保证更高精度的同时,可以大大减少密集匹配耗时。在进行航线规划时,建议增加航向重叠度,同时保证一定的旁向重叠,在获取高精度的密集点云的同时提高外业飞行效率。如果是无人机航飞,由于姿态变化较大,需要适当增加旁向重叠度。
2.2.3 与SURE、PhotoScan结果对比为了比较本文算法与当前流行的密集匹配软件精度和效果,利用苏黎世数据分别选取了屋顶平面和房屋横断面两个研究对象(如图 10、图 11所示),图中给出的本文算法和SURE的结果点云是未经过滤波后处理的密集匹配点云,而PhotoScan软件由于无法获取中间数据,直接给出最终的点云数据。密集点云的地面分辨率GSD为0.12m,本文算法采用方案①,SURE和PhotoScan采用默认设置,通过输出日志可知其使用方案③。由于本文方法与SURE整体思路较为接近,首先进行两者的密集匹配结果比较:从图 10、11中结果可以看出,SURE软件生成的点云存在明显的“重影”现象(见图中的红色椭圆区域),而本文算法点云结果很清晰,未出现该现象。究其原因,由于SURE在同一区域的点云生成过程中,使用不同的影像集来前方交会获取,因此生成的点云之间会存在微小偏移量,而本文算法采用了网络图的结构,同一区域的点云无论从哪张主视图影像计算都能获得相同的前方交会影像集,因此生成的点云可以“无缝”融合。

|
| 图 10 屋顶平面研究对象及密集匹配结果 Fig. 10 The test planar roof with its multi-view dense matching results are presented |

|
| 图 11 房屋横断面研究对象及密集匹配结果 Fig. 11 The test profile of roof with its multi-view dense matching results are presented |
研究对象a为一水平屋顶,可认为具有相同的高程值,由于SURE结果包含了多层重复点云,无法直接计算每个点的高程偏差,因此对点云按照1倍GSD进行重采样,取邻域内到平均高程面最小的点最为保留点。分别对本文算法、SURE和PhotoScan 3种方式获取的密集点云进行残差统计,其对应的高程偏差RMSE分别为0.11、0.12、0.10m(如图 10所示)。从结果统计可以看出,虽然本文算法使用了更少的匹配像对,但在匹配精度上与SURE和PhotoScan相当,均在1倍GSD以内。
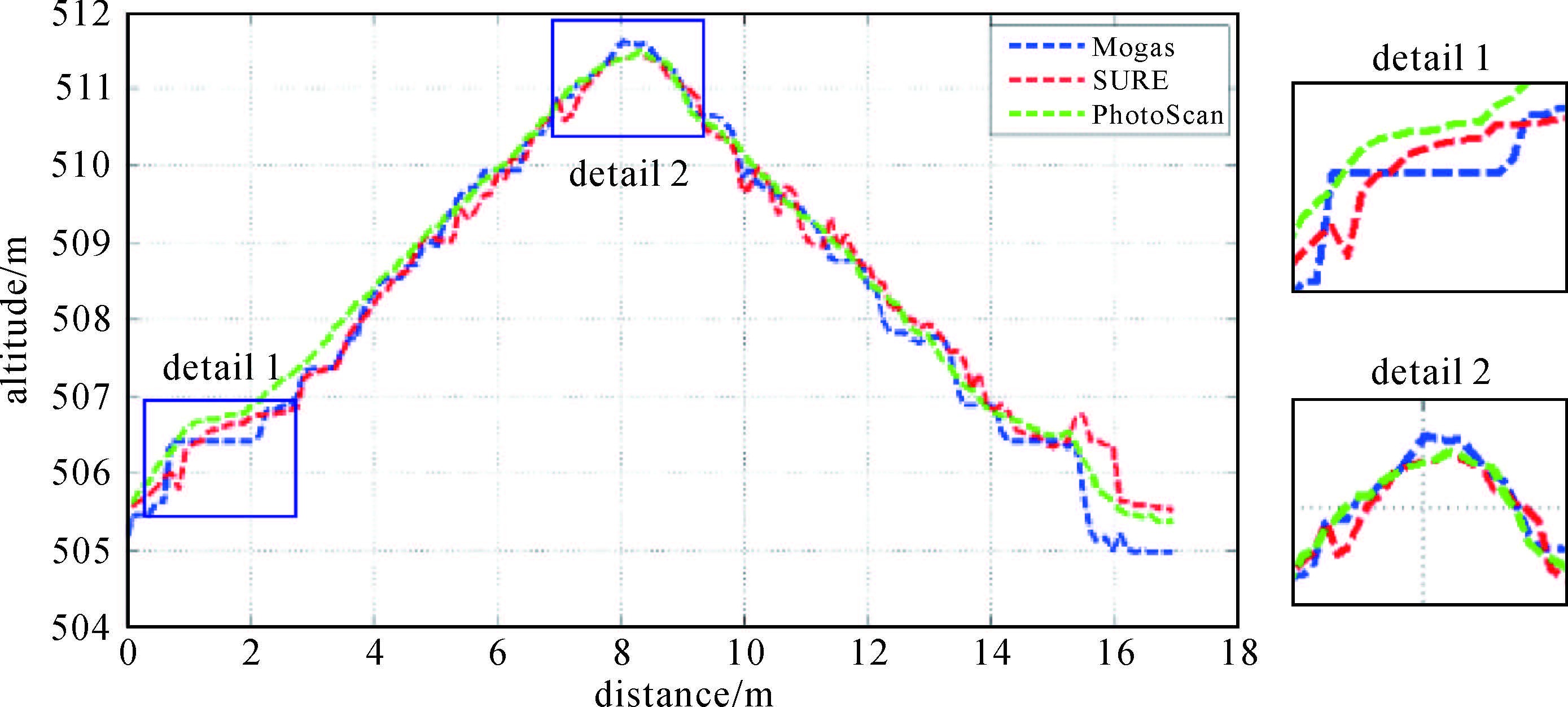
研究对象b为一房屋横断面,可以从另一方面反映匹配的垂直方向精度,分别对3种算法获取的结果点云数据在横断面上进行最邻近采样并叠加显示,其结果如图 12所示。从上述结果可以看出,3种算法均能够很好地反映出屋顶的整体轮廓。Detail1和Detail2分别为屋顶的天窗(平面区域)和屋脊所在区域,从局部细节图上可以看出,本文算法在局部细节上的性能优于SURE和PhotoScan;在屋顶的整体光滑度方面,PhotoScan算法表现最好,本文算法和SURE均出现了细微的 “抖动”。从PhotoScan点云的整体效果上看,推测应该是其对结果点云进行了平滑处理的原因。
|
| 图 12 研究对象b对应3种算法的剖面叠加及局部细节图 Fig. 12 The profiles of roof derived from the proposed method,SURE and PhotoScan are presented as well as the superposition of details |
2.3 特殊区域匹配结果
建筑物边缘、植被、水体等视差不连续、弱纹理或重复纹理区域属于立体匹配中的困难区域[12, 14],本文算法在上述区域也能够获取比较理想的匹配结果(图 13),图中分别给出了按高程渲染的伪彩色图以及不同视角下的三维彩色点云。由于在改进的tSGM算法中引入了导向中值滤波,可以很好地保持目标的边缘特性,同时利用多片前交过程中物方点的平均反投影误差约束密集点云的生成,使得最终的点云具有很高的可信度;另外,对无效视差或噪声区域利用周围有效视差通过导向滤波进行了插值,因此在弱纹理或重复纹理区域也能够获取比较理想的视差结果。

|
| 图 13 特殊区域(建筑、水体、植被等)密集匹配结果 Fig. 13 The multi-view dense matching result in difficult areas with sharp discontinuities,weak textureness or repeat textureness |
3 结论和展望
本文提出了一种基于网络图的高分辨率多视影像密集匹配技术,针对低重叠度宽基线立体像对不直接进行密集匹配而利用网络图的传递性获取影像间的匹配对应关系,不仅减少了密集匹配阶段的立体像对数目提高了效率,同时密集匹配结果点云的完整性和精度更高;另一方面,由于网络图的使用,使得不同主视图影像前方交会生成的密集点云可以无缝“融合”。利用ISPRS提供的Vaihingen和Zürich参考影像数据集进行了试验,结果表明:本文算法对高分辨率多视影像密集匹配是有效可行的,无论在匹配完整性、效率、精度上都能获取较好的结果,重建的密集点云平均反投影误差的中误差可以达到亚像素级精度,实际精度可以达到1.5倍GSD。由于在密集匹配阶段引入导向中值滤波来代替原有的中值滤波,使得密集匹配算法具有更好的边缘保持特性,在建筑物、植被、水体等视差不连续、弱纹理或重复纹理区域也取得了较好的匹配结果。后续将进一步研究如何提高宽基线立体像对的密集匹配精度和高分辨率立体像对密集匹配的效率,本文的相关研究和结论为倾斜多视影像密集匹配提供了良好的基础。
致谢: 感谢ISPRS/EuroSDR项目及斯图加特大学摄影测量研究所提供的倾斜影像试验数据。
| [1] | HIRSCHMULLER H. Accurate and Efficient Stereo Processing by Semi-Global Matching and Mutual Information[C]//Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR'05). San Diego, CA:IEEE, 2005, 2:807-814. |
| [2] | HIRSCHMULLER H. Stereo Processing by Semiglobal Matching and Mutual Information[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence , 2008, 30 (2) : 328 –341. DOI:10.1109/TPAMI.2007.1166 |
| [3] | GEHRKE S, MORIN K, DOWNEY M, et al. Semi-Global Matching:An Alternative to LIDAR for DSM Generation[C]//Proceedings of the 2010 Canadian Geomatics Conference and Symposium of Commission I. Calgary, AB, Canada:[s.n.], 2010, 2:6. |
| [4] | ROTHERMEL M, WENZEL K, FRITSCH D, et al. SURE:Photogrammetric Surface Reconstruction from Imagery[C]//Proceedings LC3D Workshop. Berlin:[s.n.], 2012:8. |
| [5] | ZHANG Li. Automatic Digital Surface Model (DSM) Generation from Linear Array Images[D]. Mitteilungen:Swiss Federal Institute of Technology (ETH) Zürich, 2005. |
| [6] | PIERROT-DESEILLIGNY M, PAPARODITIS N. A Multiresolution and Optimization-based Image Matching Approach:An Application to Surface Reconstruction from SPOT5-HRS Stereo Imagery[C]//IAPRS vol XXXVI-1/W41 in ISPRS Workshop On Topographic Mapping from Space (With Special Emphasis on Small Satellites). Ankara, Turquie:[s.n.], 2006. |
| [7] | GOESELE M, SNAVELY N, CURLESS B, et al. Multi-View Stereo for Community Photo Collections[C]//Proceedings of the 11th International Conference on Computer Vision. Rio de Janeiro:IEEE, 2007:1-8. |
| [8] | REMONDINO F, MENNA F. Image-Based Surface Measurement for Close-Range Heritage Documentation[C]//Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences. Beijing:[s.n.], 2008, 37:199-206. |
| [9] | FURUKAWA Y, PONCE J. Accurate, Dense, and Robust Multiview Stereopsis[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence , 2010, 32 (8) : 1362 –1376. DOI:10.1109/TPAMI.2009.161 |
| [10] | VU H H, LABATUT P, PONS J P, et al. High Accuracy and Visibility-Consistent Dense Multiview Stereo[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence , 2012, 34 (5) : 889 –901. DOI:10.1109/TPAMI.2011.172 |
| [11] | TOLDO R, FANTINI F, GIONA L, et al. Accurate Multiview Stereo Reconstruction with Fast Visibility Integration and Tight Disparity Bounding[C]//Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences. Trento, Italy:[s.n.], 2013:243-249. |
| [12] | HAALA N. The Landscape of Dense Image Matching Algorithms[M]//FRITSCH D. Proceedings of Photogrammetric Week 2013. Stuttgart:[s.n.], 2013. |
| [13] | HIRSCHMÜLLER H. Semi-Global Matching-Motivation, Developments and Applications[C]//Photogrammetric Week 11. Stuttgart, Germany:[s.n.], 2011:173-184. |
| [14] | REMONDINO F, SPERA M G, NOCERINO E, et al. State of the Art in High Density Image Matching[J]. The Photogrammetric Record , 2014, 29 (146) : 144 –166. DOI:10.1111/phor.2014.29.issue-146 |
| [15] | DESEILLIGNY M P, CLERY I. Apero, An Open Source Bundle Adjusment Software for Automatic Calibration and Orientation of Set of Images[C]//Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences. Trento, Italy:[s.n.], 2011:269277. |
| [16] | 杨化超, 姚国标, 王永波. 基于SIFT的宽基线立体影像密集匹配[J]. 测绘学报 , 2011, 40 (5) : 537–543. YANG Huachao, YAO Guobiao, Wang Yongbo. Dense Matching for Wide Base-line Stereo Images Based on SIFT[J]. Acta Geodaetica et Cartographica Sinica , 2011, 40 (5) : 537 –543. |
| [17] | 王竞雪, 朱庆, 王伟玺. 多匹配基元集成的多视影像密集匹配方法[J]. 测绘学报 , 2013, 42 (5) : 691–698. WANG Jingxue, ZHU Qing, WANG Weixi. A Dense Matching Algorithm of Multi-View Image Based on the Integrated Multiple Matching Primitives[J]. Acta Geodaetica et Cartographica Sinica , 2013, 42 (5) : 691 –698. |
| [18] | 吴军, 姚泽鑫, 程门门. 融合SIFT与SGM的倾斜航空影像密集匹配[J]. 遥感学报 , 2015, 19 (3) : 431–442. WU Jun, YAO Zexin, CHENG Menmen. Airborne Oblique Stereo Image Dense Matching by Integrating SIFT and SGM Algorithm[J]. Journal of Remote Sensing , 2015, 19 (3) : 431 –442. |
| [19] | LOOP C, ZHANG Zhengyou. Computing Rectifying Homographies for Stereo Vision[C]//Proceedings of the Computer Society Conference on Computer Vision and Pattern Recognition. Fort Collins, CO:IEEE, 1999:1. |
| [20] | POLLEFEYS M, KOCH R, VAN GOOL L. A Simple and Efficient Rectification Method for General Motion[C]//Proceedings of the 7th IEEE International Conference on Computer Vision. Kerkyra:IEEE, 1999, 1:496-501. |
| [21] | MONASSE P, MOREL J M, TANG Zhongwei. Three-Step Image Rectification[C]//BMVC 2010-British Machine Vision Conference. Aberystwyth, United Kingdom:BMVA Press, 2010:89.1-89.10. |