2. 山东科技大学海洋工程研究院, 山东 青岛 266590 ;
3. 中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室, 湖北 武汉 430077 ;
4. 中国科学院测量与地球物理研究所, 湖北 武汉 430077
2. Institute of Ocean Engineering, Shandong University of Science and Technology, Qingdao 266590, China ;
3. State Key Laboratory of Dynamic Geodesy, Institute of Geodesy and Geophysics, Chinese Academy of Sciences, Wuhan 430077, China ;
4. Institute of Geodesy and Geophysics, Chinese Academy of Sciences, Wuhan 430077, China
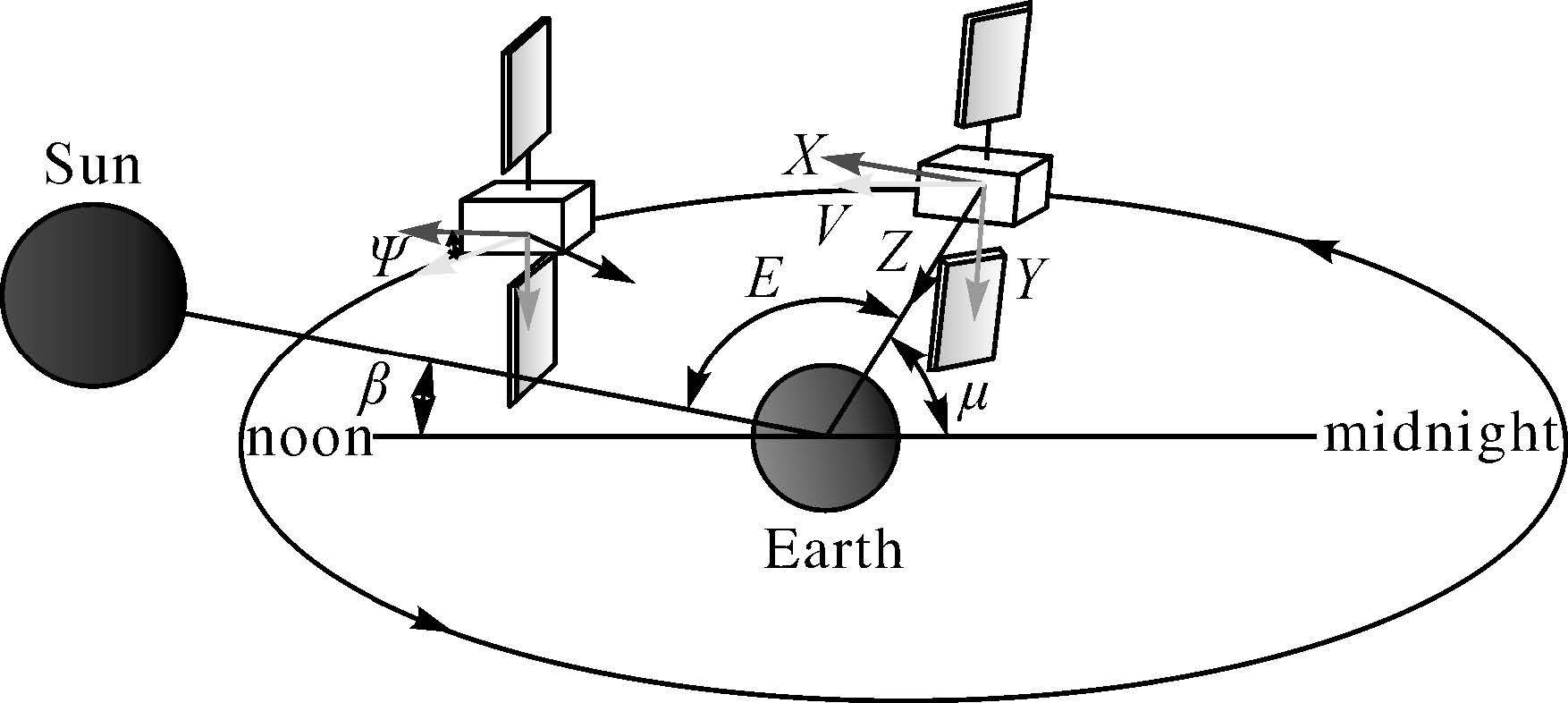
GNSS卫星为了保证地面信号强度,其Z轴指向地心,同时为了保证卫星能够得到更多的太阳能,X轴处于地心、太阳所在平面且朝向太阳,Y轴垂直与X、Z轴构成右手坐标系[1]。如图 1所示,远日点(midnight)、近日点(noon)附近是异常发生的位置。轨道角μ是远日点、地球、卫星三者之间的夹角;太阳角β是太阳向量与轨道面的夹角,在上方为正,下方为负;偏航角ψ为卫星X轴与速度V的夹角,与β符号相反,因此可以通过V绕Z轴旋转ψ得到X;E是太阳、地球、卫星三者之间的夹角。当β角较小时,卫星姿态在远日点和近日点附近就会发生近180°的剧烈翻转,但硬件本身达不到这个翻转速度,就导致姿态异常(正午、子夜机动)。II/IIA/IIF卫星在远日点进入地影就产生异常,与前面两种异常产生原因不同。各分析中心对于姿态异常采取不同的应对策略(ftp.igs.org/pub/center/analysis/)。卫星姿态对于相位缠绕误差具有重要意义,天线质心偏差同样依赖于卫星姿态的确立。在动态PPP中,可观测卫星数较少,考虑到收敛时间和定位精度,姿态异常时期的卫星可采用本文模型改正,不宜剔除。
|
| 图 1 轨道和角度 Fig. 1 Orbit and angles |
1 模型计算 1.1 正常姿态及相位缠绕
根据上面所提的卫星坐标轴指向,可得x、y、z在ITRF(International Terrestrial Reference Frame)下的方向向量
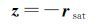 (1)
(1)
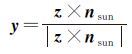 (2)
(2)
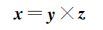 (3)
(3)
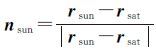 (4)
(4)
式中,rsat、rsun分别表示ITRF下卫星、太阳单位向量。计算相位缠绕时,在卫星和接收机处各定义一个有效偶极D和D′,且分别对应于星固坐标系和测站局部坐标系[3, 4]
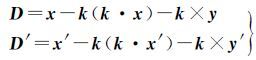 (5)
(5)
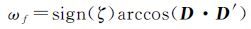 (6)
(6)
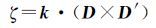 (7)
(7)
式中,k为卫星至接收机方向的单位向量;x′、y′为测站局部坐标系下坐标轴指向;ωf为相位缠绕小数部分。
1.2 GPS姿态改正模型本文的姿态改正模型紧紧围绕着偏航角ψ,而ψ又与太阳角β及轨道角μ有关[5]
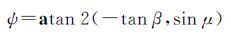 (8)
(8)
atan2(·,·)与arctan(·)类似,均为tan(·)的反函数,不过其周期为2π。β可由ITRF下的卫星单位向量rsat和太阳单位向量rsun以及绝对速度单位向量v得出
 (9)
(9)
v可由ITRF下卫星的相对速度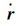
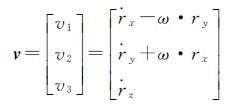 (10)
(10)
β一天之内变化不到1°,可看作常数,因此较短时间内ψ可以看作只是μ的函数,求导得
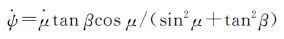 (11)
(11)
式中,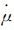
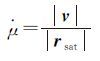 (12)
(12)
当卫星的最大偏航角速度R<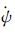
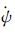
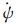
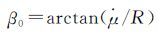 (13)
(13)
根据上述R可得IIR卫星β0为2.4°,II/IIA/IIF卫星β0为3.4°~5.3°。当|β|<β0时,在μ= 0°、180°或附近位置,卫星最大偏航角速度达不到式(11)所要求的偏航角速度,这时就不能用式(8)求偏航角,称此为正午、子夜机动。假设机动开始时刻为ts,μ=0°或180°时刻为tm。将球面直角三角形近似看作平面直角三角形
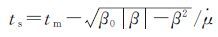 (14)
(14)
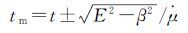 (15)
(15)
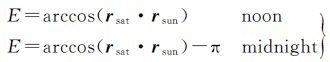 (16)
(16)
对于式(15)的“±”,当卫星在中间位置(轨道角为0°、180°)时v与rsun的夹角θ=arccos(v·rsun)刚好为90°。对于正午机动,θ<90°时,取正,否则取负;对于子夜机动,θ>90°时,取正,否则取负。虽然式(15)中t和E是一对任意时刻的值,但是式(15)是将球面直角三角形近似看作平面直角三角形而得,存在球面角超,且面积越大,球面角超越大。当卫星离机动位置越近时,球面角超越小,计算的ts、tm越准确。
在机动期间,卫星以最大偏航角速度偏转
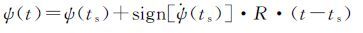 (17)
(17)
其中ψ(ts)、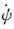
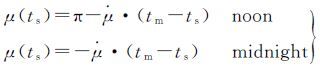 (18)
(18)
II/IIA存在航向角偏差(+0.5°),而IIF的航向角偏差为(-0.5°)。两种反常情况:当0°<β<0.9°时,II/IIA在正午机动时转动方向与理论方向相反;-0.9°<β<0°时,IIF在正午机动时转动方向与理论方向相反[6-7]。
当实际偏航角等于理论偏航角时,机动结束。可以使用迭代的方法计算结束时的偏航角,以II/IIA/IIF为例,假设从开始到结束,偏航角变化了180°,则
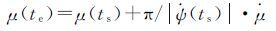 (19)
(19)
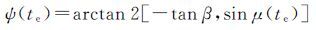 (20)
(20)
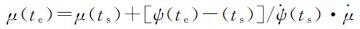 (21)
(21)
对式(20)、式(21)进行迭代计算。
1.3 GPS卫星穿过阴影区域II/IIA/IIF卫星在子夜时不发生子夜机动,一旦进入阴影区域,就产生异常。根据地球半径和卫星轨道半径,可得出阴影角Esh≈13.5°[8],用Esh替换式(14)中的β0可得
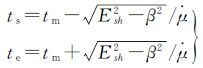 (22)
(22)
II/IIA卫星由于在刚进入阴影区域时,偏航角速度还未达到它的最大偏航角速度R,且偏航角速度方向完全受航向角偏差(+0.5°)控制,所以中途有一个加速过程,假设达到R所需时间ta
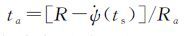 (23)
(23)
其中Ra为偏航角加速度,对于IIA、II卫星分别为0.00165°/s2、0.0018°/s2 [8]。
当ts<t<ts+ta时
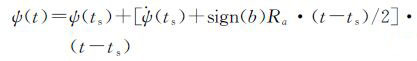 (24)
(24)
当ts+ta<t<te时
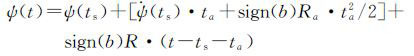 (25)
(25)
对于IIF卫星,为了使出阴影区域时实际偏航角刚好等于名义偏航角,且在阴影区域内偏航角速度保持匀速,其偏航角速度和偏航角可由下式获得[6, 9]
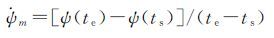 (26)
(26)
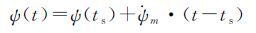 (27)
(27)
式中,ψ(te)为出阴影区域时的名义偏航角,可通过式(8)计算,对应的μ(te)=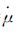
前面已经提到,ψ就是x与v的夹角,故x可通过v绕z轴旋转ψ得到。但是这些向量都是在地固坐标系下,不能直接旋转。可以通过以下步骤完成:①使用旋转矩阵Rx、Ry,使得z轴旋转到与地固系下的Z轴指向一致;②使用旋转矩阵Rz(ψ);③使用RxT、RyT逆旋转使z恢复到原始位置。公式如下
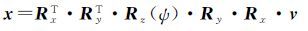 (28)
(28)
北斗GEO卫星采用零偏模式[10],因此主要研究IGSO、MEO卫星的偏航姿态。IGSO、MEO卫星虽然分别在|β|小于8.7°、12.97°时进入阴影期,但是卫星偏航姿态并未产生类似GPS卫星的阴影区域异常,直到|β|≈4°[11]其偏航姿态发生变化,由动偏模式切换为零偏模式[12-14]。零偏模式就是卫星X轴与速度方向一致[15],即x=v。为了在最短时间内由名义偏航角转换为零偏航角,由式(8)可知,当μ=90°时,名义偏航角等于-β,此时与零偏模式最为接近,故此为最合理切换点。由零偏模式切换为动偏模式也类似。
2 数据测试与分析本文采用PPP[16-18]传统无电离层模型,使用IGS站点观测数据(具体站点和日期请看图解)和IGS各分析中心精密产品[19]以及IGMAS(international GNSS Monitoring & Assessment System ) 产品。姿态异常时期分别使用了常规模型和本文改正模型计算相位缠绕变化,并通过观察滤波收敛后观测值的残差变化,分析姿态异常的影响大小。同时对异常时期的卫星采用三步抗差方案进行了适当的降权处理[20]。
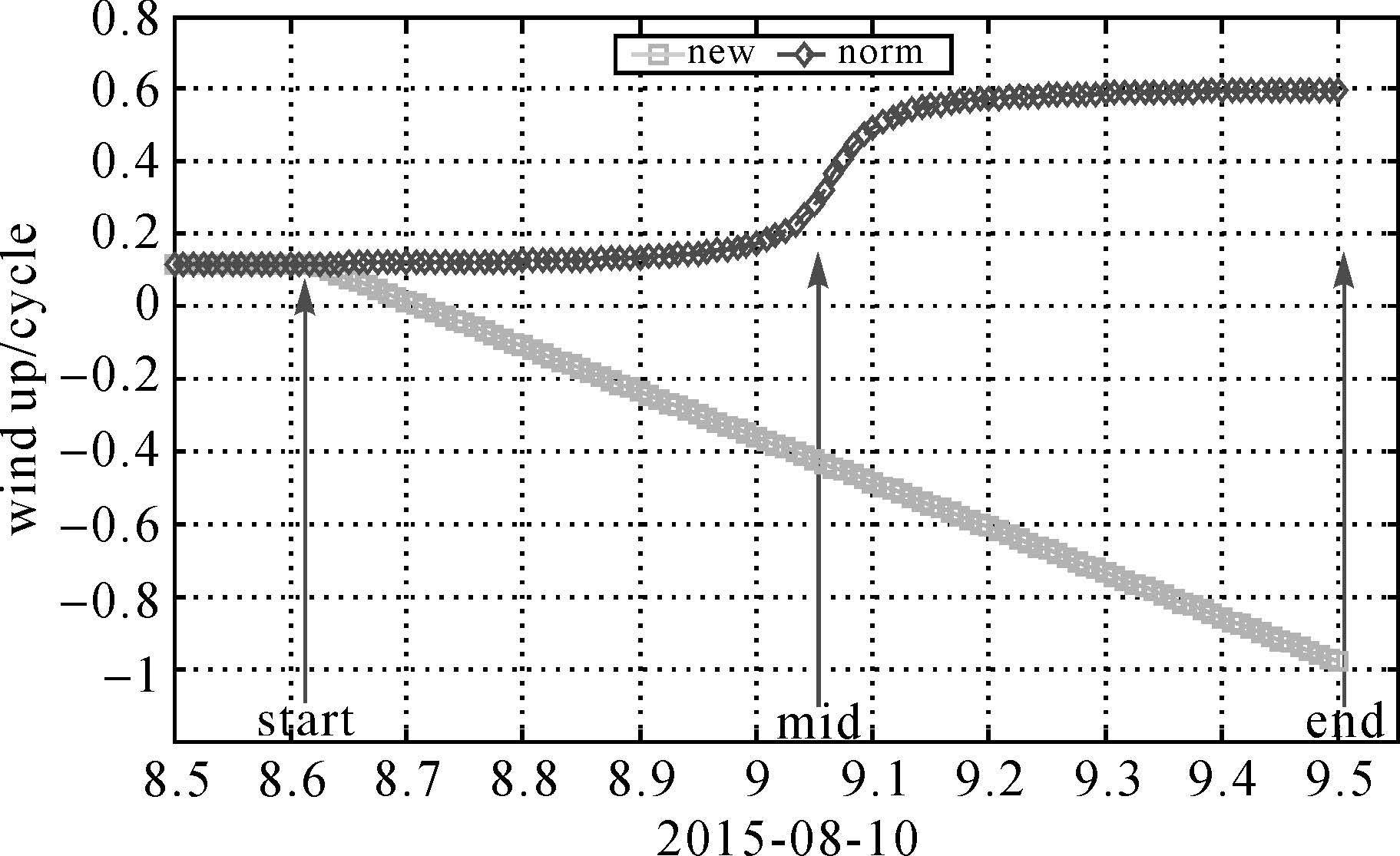
图 2是PRN 4(IIA)分别使用名义偏航角(norm)和本文模型得到偏航角(new)在2015年8月10日的部分相位缠绕变化曲线(IGS站mkea),β=-0.84°。箭头(start,mid,end)分别表示卫星刚进入阴影区域、阴影区域的中间位置出阴影区域。由图可知,穿过阴影区域历时将近1h,由于受航向角偏差控制,实际姿态旋转方向与进入阴影区域时相反,结束时二者相位缠绕相差1.6周左右。
|
| 图 2 PRN 4在阴影区域的相位缠绕 Fig. 2 Wind up of PRN 4 Shadow-crossing |
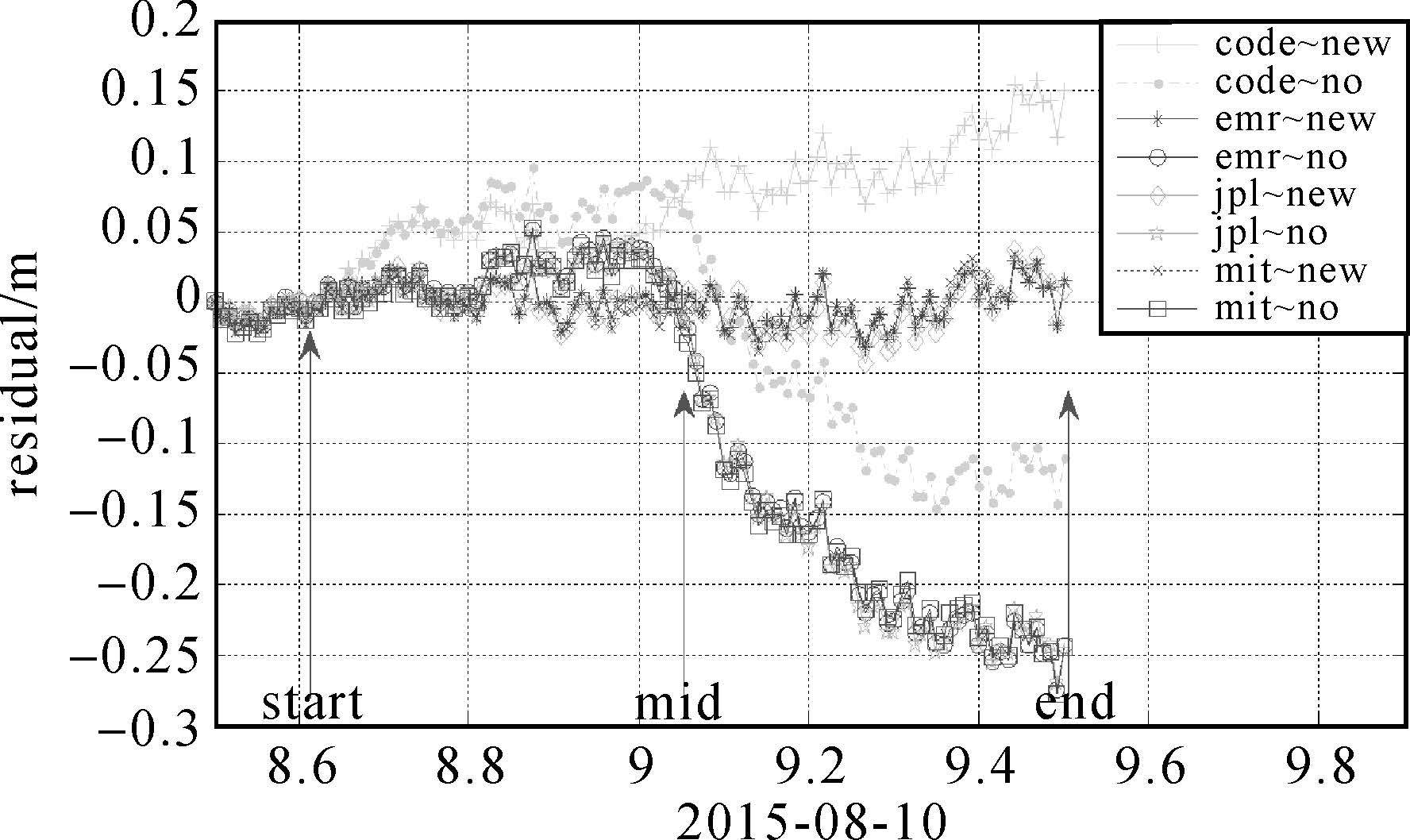
图 3是对应着图 2的残差变化曲线,code~no表示使用的是CODE(Center for Orbit Determination in Europe)提供的精密产品,卫星姿态使用名义偏航角,与此对应,code~new表示使用本文改正模型。ERM(NRCan)、JPL(Jet Propulsion Laboratory)、MIT(Massachusetts Institute of Technology)类似。其中JPL、MIT、EMR曲线表现类似,使用名义偏航角时,最大误差达到了0.25m左右,使用本文模型残差明显变小,都在0.05m以内。而CODE则表现完全不同,不管使用哪种模型,残差都比较大,最大达到0.15m。CODE分析中心指出了其使用的是名义偏航角(ftp://ftp.igs.org/pub/center/analysis/code.acn)。在PPP中,相位缠绕变化率与测站位置无关,因此这项误差可以被卫星钟差所吸收,但是天线质心偏差与测站位置有关,无法被卫星钟差吸收,因此可能是这种原因造成了上述矛盾现象。
|
| 图 3 PRN 4在阴影区域的残差 Fig. 3 Residual of PRN 4 Shadow-crossing |
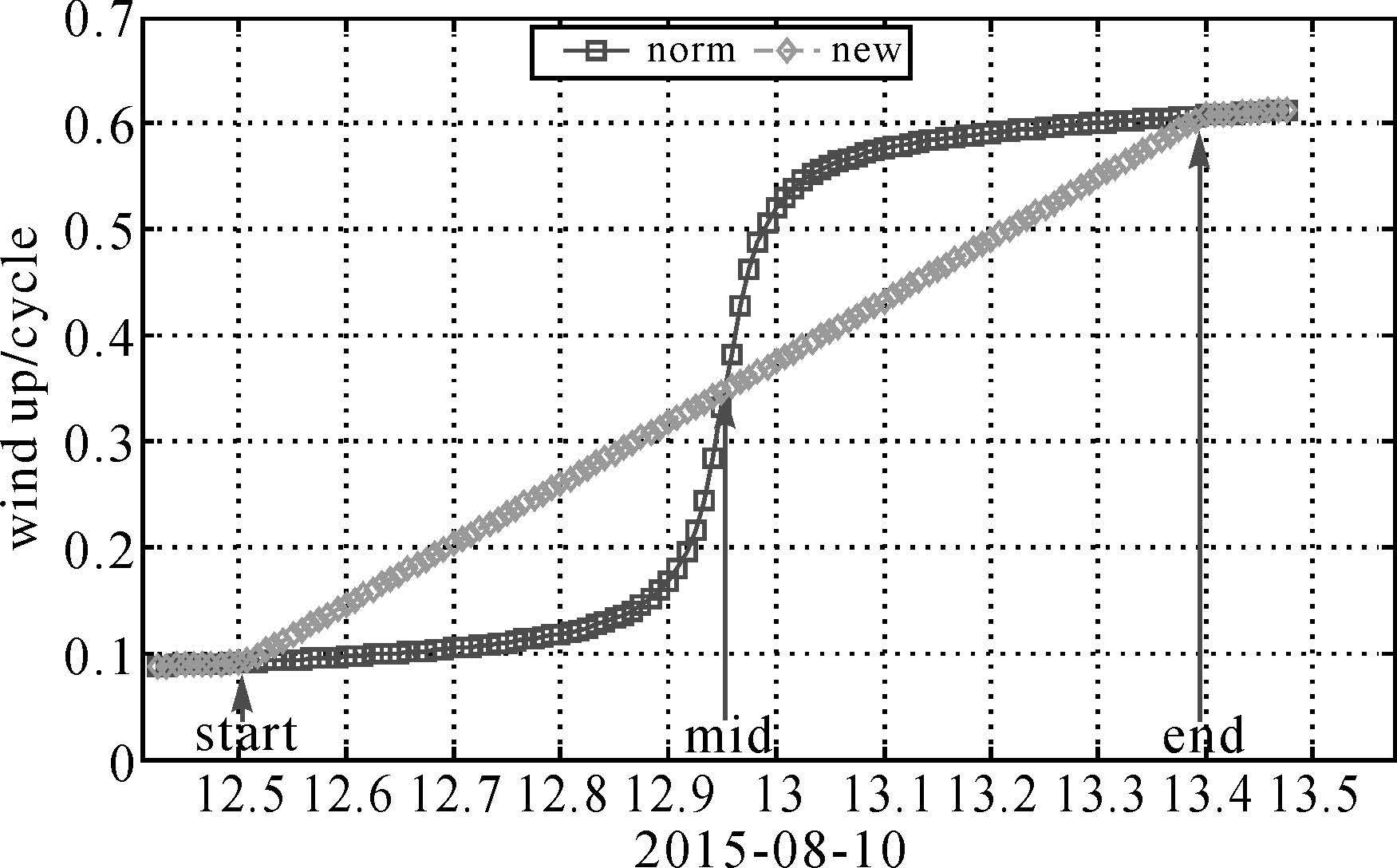
图 4是PRN 6(IIF)分别使用名义偏航角(norm)和本文模型得到偏航角(new)在2015年8月10日的部分相位缠绕变化曲线(IGS站mkea),β=-0.75°。是一个中心对称图形,出阴影区域时,实际偏航角与名义偏航角相等,因此相位缠绕相等,其实相位缠绕变化趋势与偏航角变化趋势基本一致的。异常时间将近1h。
|
| 图 4 PRN 6在阴影区域的相位缠绕 Fig. 4 Wind up of PRN 6 Shadow-crossing |
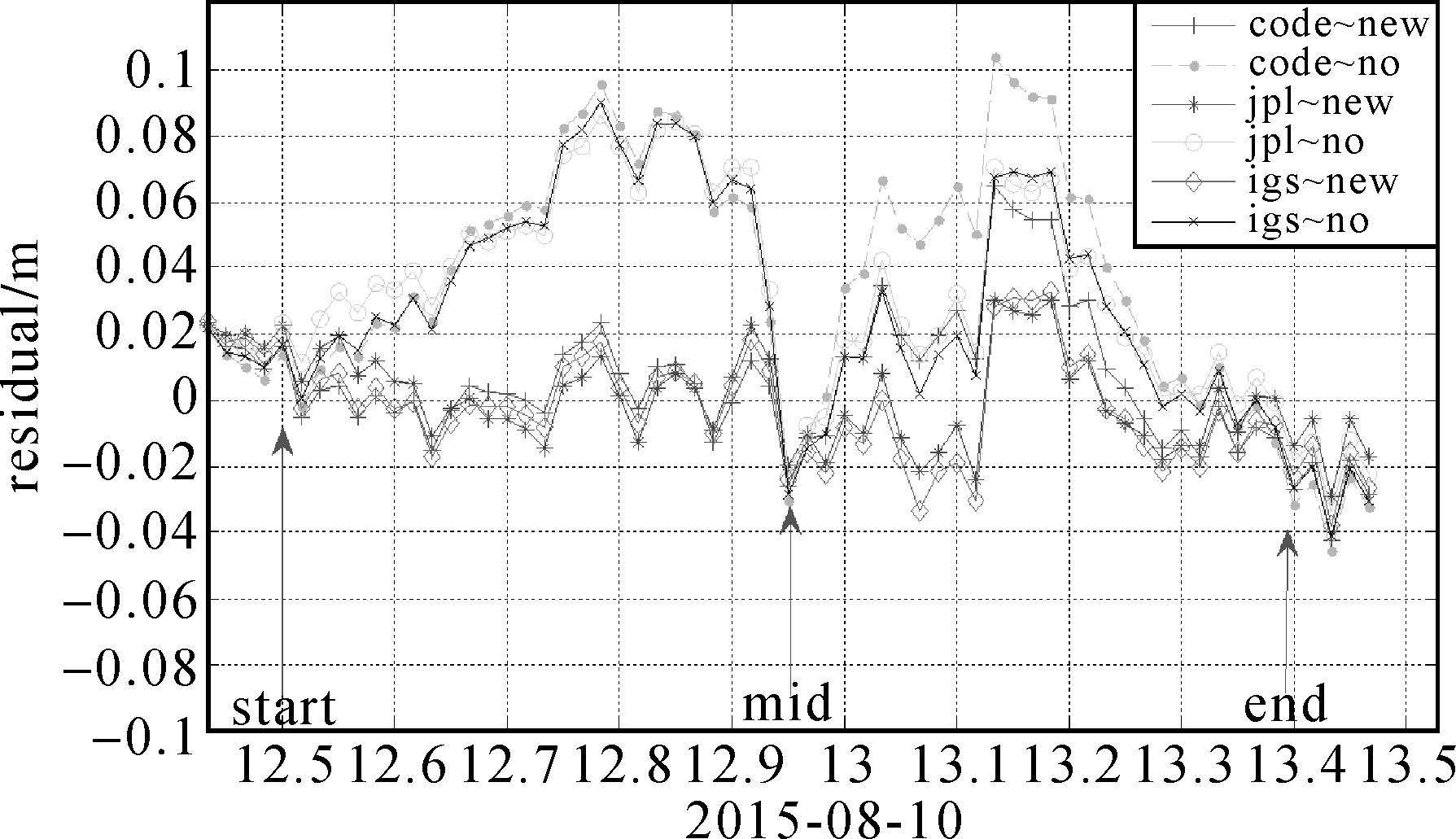
图 5为对应图 4的残差曲线,各曲线的意义同前面类似,不再赘述。JPL、EMR、MIT曲线基本一致,为了显示清楚只画出其中一个。在mid(箭头)之前,使用各机构的精密产品其观测值的残差类似,但是之后CODE残差相比IGS、JPL大了一点。
|
| 图 5 PRN 6在阴影区域的残差 Fig. 5 Residual of PRN 6 Shadow-crossing |
图 6是PRN 2(IIR)分别使用名义偏航角(norm)和本文模型得到偏航角(new)在2015年8月9日的部分相位缠绕变化曲线(IGS站sey1),β=-0.58°。二者相位缠绕差别最大为0.2周左右。

|
| 图 6 PRN 2在正午时的相位缠绕 Fig. 6 Wind up of PRN 2 Noon |
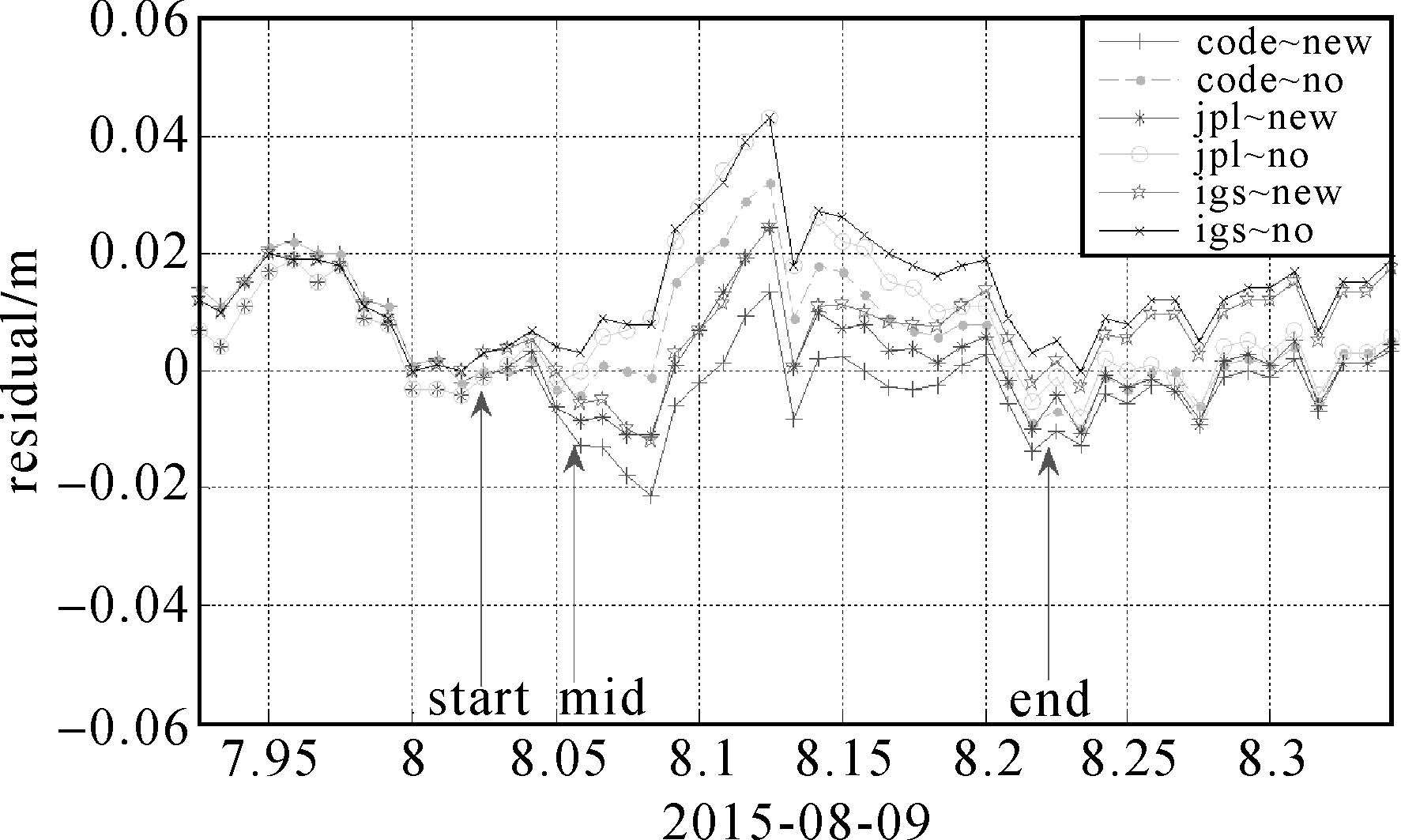
图 7为对应图 6的残差曲线,IIR卫星的正午、子夜机动所造成的误差较小,一般不超过0.1m。当β≈0°时,在正午、子夜时刻会发生180°剧烈翻转,这时候造成的误差相位缠绕误差将近0.5周。根据精密产品来看,如果β在当天发生符号变化(β存在等于0°的时刻,如前一天数据),JPL、EMR就没有提供这颗卫星当天产品。
|
| 图 7 PRN 2在正午机动时的残差 Fig. 7 Residual of PRN 2 Noon |
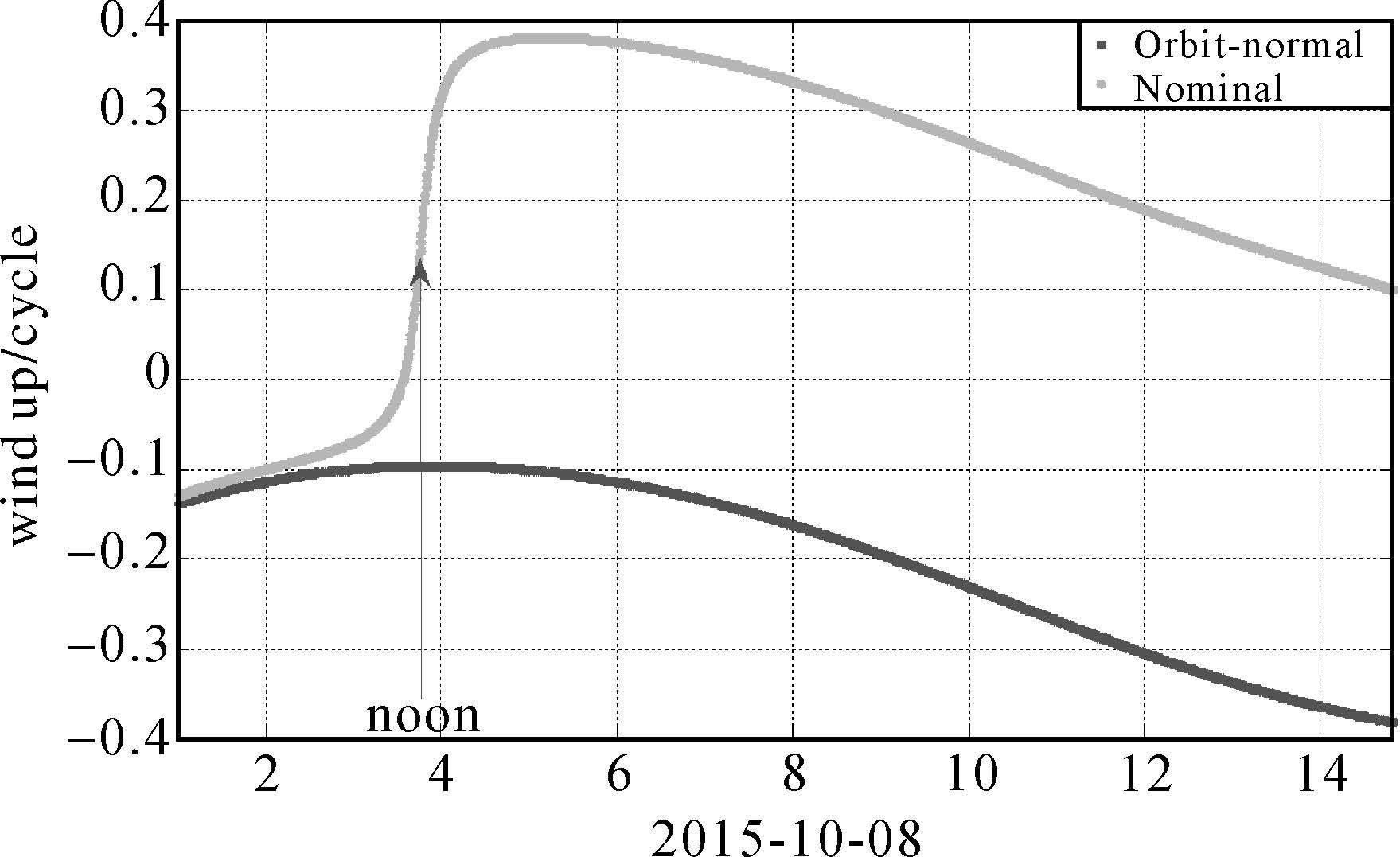
图 8是BDS卫星C06(IGSO)分别使用动偏模式名义偏航角(Nominal)和零偏模式(Orbit-normal)在2015年10月8日的部分相位缠绕曲线(IGS站jfng),β=2.17°。在正午之前,动偏模式的偏航角比β略大一点而已,因此跟零偏模式相位缠绕差别很小。当快要到正午时,差异就显现出来,在正午之后,基本上都差别半周。这项误差持续时间长,10天左右,尤其是在正午之后误差比较大。
|
| 图 8 C06相位缠绕 Fig. 8 Wind up of C06 |
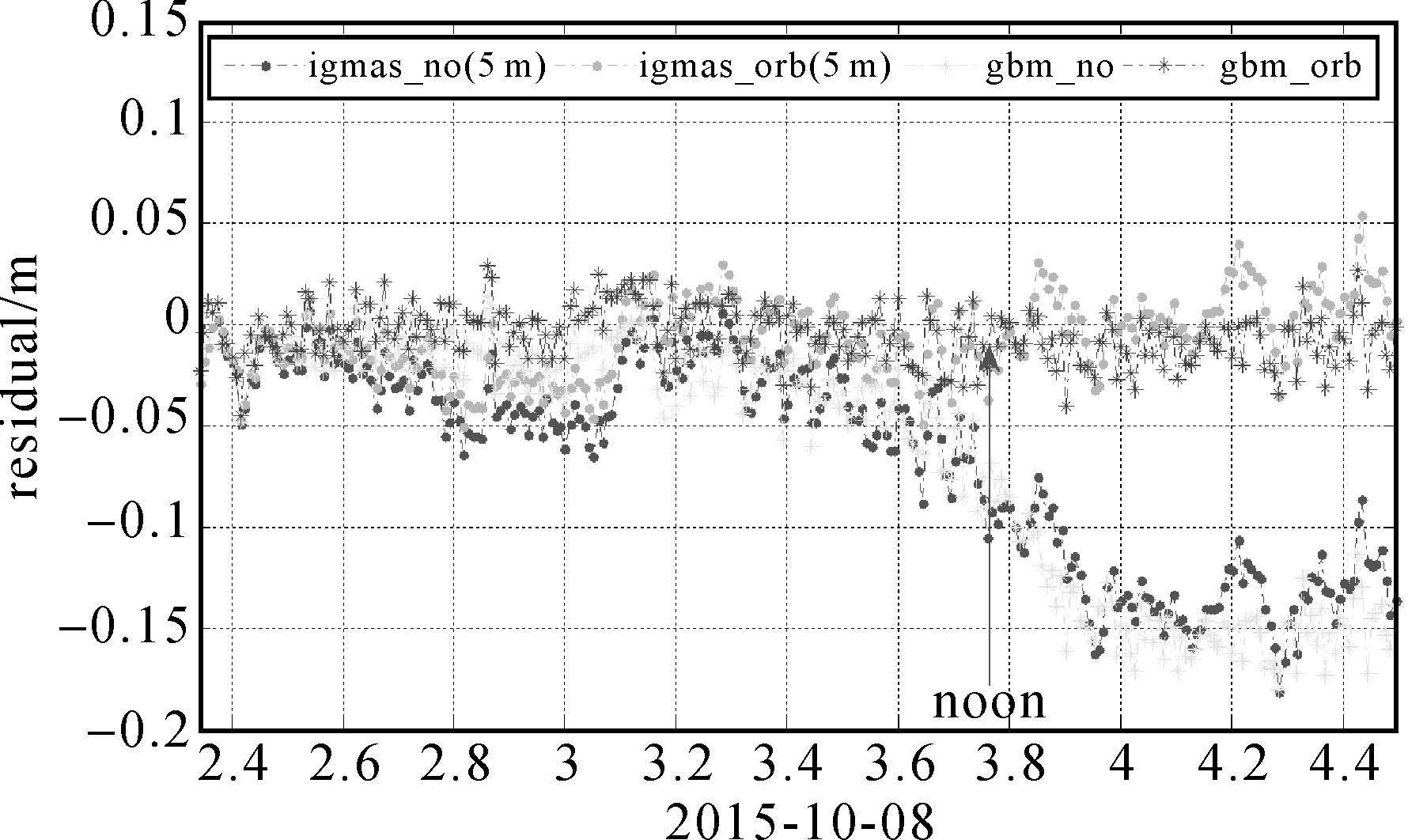
图 9为对应图 8的残差曲线,使用igmas提供的精密产品(钟差产品5min)和GFZ(GeoForschungsZentrum)提供的精密产品gbm(钟差产品30s)。分别使用动偏模式名义偏航角(~no)和零偏模式(~orb)计算结果比较。由图可以看出,igmas和gbm表现类似,最大误差达到0.15m,且误差还将持续,对定位产生较大影响。北斗卫星质心偏差存在于X方向上(约60cm),因此这部分残差不仅由相位缠绕这一项误差造成,还由天线质心偏差造成。
|
| 图 9 C06在正午前后的残差 Fig. 9 Residual of C06 |
3 结 论
各分析中心的姿态模型可能会不同,如CODE在任何时期都采用名义偏航角,其卫星钟差可以吸收姿态异常导致的相位缠绕误差,但是天线质心偏差不能被吸收(如果偏差存在于X轴上),这就导致了图 3所示的矛盾现象;使用IGS、JPL、EMR、MIT的精密产品,配合本文模型,可以使异常时期的误差显著减小,但是误差波动仍然比正常时期的大,有时达到几厘米。可能有以下原因:①本文模型不是特别精确,进行了部分简化;②理论上卫星最大偏航角速度R不可能完全符合实际;③钟差产品精度也是一个原因。
| [1] | LICHTEN S M, BORDER J S. Strategies for High-precision Global Positioning System Orbit Determination[J]. Journal of Geophysical Research:Solid Earth , 1987, 92 (B12) : 12751 –12762. DOI:10.1029/JB092iB12p12751 |
| [2] | XU Guochang. GPS:Theory, Algorithms and Applications[M]. 2nd ed Berlin Heidelberg: Springer, 2007 : 82 -85. |
| [3] | WU J T, WU S C, HAJJ G A, et al. Effects of Antenna Orientation on GPS Carrier Phase[J]. Manuscripta Geodetica , 1993, 18 (2) : 91 –91. |
| [4] | ZHANG Baocheng, OU Jikun, YUAN Yunbin, et al. Yaw Attitude of Eclipsing GPS Satellites and Its Impact on Solutions from Precise Point Positioning[J]. Chinese Science Bulletin , 2010, 55 (32) : 3687 –3693. DOI:10.1007/s11434-010-4130-3 |
| [5] | KOUBA J. A Simplified Yaw-attitude Model for Eclipsing GPS Satellites[J]. GPS Solutions , 2009, 13 (1) : 1 –12. DOI:10.1007/s10291-008-0092-1 |
| [6] | DILSSNER F, SPRINGER T, ENDERLE W. GPS ⅡF Yaw Attitude Control during Eclipse Season[C]//AGU Fall Meeting. San Francisco:American Geophysical Union, 2011:9. |
| [7] | KOUBA J. A Note on the December 2013 Version of the Eclips.f Subroutine[EB/OL]. (2013-12-23). http://acc.igs.org/orbits/eclipsDec2013note.pdf. |
| [8] | BAR-SEVER Y E. A New Model for GPS Yaw Attitude[J]. Journal of Geodesy , 1996, 70 (11) : 714 –723. DOI:10.1007/BF00867149 |
| [9] | DILSSNER F. GPS ⅡF-1 Satellite Antenna Phase Center and Attitude Modeling[J]. Inside GNSS , 2010, 5 (6) : 59 –64. |
| [10] | GUO Jing, ZHAO Qile. Analysis of Precise Orbit Determination for BeiDou Satellites during Yaw Maneuvers[C]//China Satellite Navigation Conference 2014. Nanjing:CSNC, 2014. |
| [11] | LOU Yidong, LIU Yang, SHI Chuang, et al. Precise Orbit Determination of BeiDou Constellation Based on BETS and MGEX Network[J]. Scientific Reports , 2014, 4 : 4692 . |
| [12] | DAI Xiaolei, GE Maorong, LOU Yidong, et al. Estimating the Yaw-attitude of BDS IGSO and MEO Satellites[J]. Journal of Geodesy , 2015, 89 (10) : 1005 –1018. DOI:10.1007/s00190-015-0829-x |
| [13] | 李敏, 施闯, 赵齐乐, 等. 多模全球导航卫星系统融合精密定轨[J]. 测绘学报 , 2011, 40 (S0) : 26–30. LI Min, SHI Chuang, ZHAO Qile, et al. Multi-GNSS Precision Orbit Determination[J]. Acta Geodaetica et Cartographica Sinica , 2011, 40 (S0) : 26 –30. |
| [14] | 毛悦, 宋小勇, 王维, 等. IGSO姿态控制模式切换期间定轨策略研究[J]. 武汉大学学报(信息科学版) , 2014, 39 (11) : 1352–1356. MAO Yue, SONG Xiaoyong, WANG Wei, et al. IGSO Satellite Orbit Determining Strategy Analysis with the Yaw-steering and Orbit-normal Attitude Control Mode Switching[J]. Geomatics and Information Science of Wuhan University , 2014, 39 (11) : 1352 –1356. |
| [15] | WANG Wei, CHEN Gucang, GUO Shuren, et al. A study on the Beidou IGSO/MEO Satellite Orbit Determination and Prediction of the Different Yaw Control Mode[C]//Proceedings of China Satellite Navigation Conference (CSNC) 2013. Berlin Heidelberg:Springer, 2013:31-40. |
| [16] | LIBofeng, GEHaibo, SHENYunzhong. Comparison of Ionosphere-free, Uofc and Uncombined PPP Observation Models[J]. Acta Geodaetica et Cartographica Sinica , 2015, 44 (7) : 734–740. 李 博峰, 葛 海波, 沈 云中. 无电离层组合、Uofc和非组合精密单点定位观测模型比较[J]. 测绘学报 , 2015, 44 (7) : 734 –740. DOI:10.11947/j.AGCS.2015.20140161 |
| [17] | 张宝成. GNSS非差非组合精密单点定位的理论方法与应用研究[D]. 武汉:中国科学院测量与地球物理研究所, 2012. ZHANG Baocheng.Study on the Theoretical Methodology and Applications of Precise Point Positioning Using Un-differenced and Uncombined GNSS Data[D].Wuhan:Institute of Geodesy and Geophysics Chinese Academy of Sciences,2012. http://www.cnki.com.cn/article/cjfdtotal-chxb201410019.htm |
| [18] | 刘冬, 张清华. 基于高斯过程的精密卫星钟差加密[J]. 测绘学报 , 2011, 40 (S) : 59–62. LIU Dong, ZHANG Qinghua. Densification of Precise Satellite Clock Errors Based on Gaussian Processes[J]. Acta Geodaetica et Cartographica Sinica , 2011, 40 (S) : 59 –62. |
| [19] | DOW J M, NEILAN R E, GENDT G. The International GPS Service:Celebrating the 10th Anniversary and Looking to the Next Decade[J]. Advances in Space Research , 2005, 36 (3) : 320 –326. DOI:10.1016/j.asr.2005.05.125 |
| [20] | 欧吉坤. 一种三步抗差方案的设计[J]. 测绘学报 , 1996, 25 (3) : 173–179. OU Jikun. Design of a New Scheme of Robust Estimation by Three Steps[J]. Acta Geodaetica et Cartographica Sinica , 1996, 25 (3) : 173 –179. |



