北斗卫星导航系统是我国自主建设、独立运行的全球卫星导航系统[1-2],其轨道精度水平直接影响到系统的拓展应用[3-4]。在导航卫星精密定轨中,通常以一天为一个时段进行处理,然而由于单天解轨道存在末端效应,即时段两端的轨道误差相对较大,因此,需要将单天解轨道合成为多天解轨道[5-6]。
以往的处理是将几个单天时段的数据集合到一起,而后统一处理得到多天解轨道,计算耗时耗力,并随着跟踪站数目及处理天数的增多,对计算机性能的要求越来越苛刻。而后发展起来的法方程叠加方法通过并行处理单天观测数据,再在法方程层面进行轨道合成,极大地提高了处理效率[7-8]。国外关于法方程叠加方法的研究起步较早,早在20世纪90年代中后期,文献[5]就研究了应用法方程叠加合成多天轨道的方法;随后,文献[7]系统探讨了法方程叠加原理及其在大地测量与地球动力学中的应用;文献[9]将法方程叠加原理应用到了区域形变估计中。国内,文献[10]在深入研究了法方程叠加原理的基础上,探讨了基于法方程叠加的多时段轨道合成方法;文献[11]利用法方程叠加原理,分析了多个子网解轨道合成整网解轨道的处理效果。然而,以上研究大多是针对GPS和GLONASS卫星,目前北斗卫星采用的多天解轨道主要是依靠传统的多天数据累积解算获得[12-17]。这种处理模式在精度上与基于法方程叠加的结果是一致的,但是计算过程复杂,无法并行处理各天数据,计算效率较低。此外,在轨道合成中,涉及的主要轨道参数包括密切元素、力学参数和伪随机脉冲参数,已有研究主要集中于密切元素(参考时刻的6个开普勒根数)和力学参数(如光压模型参数等)的合成处理,而对另一类重要参数--伪随机脉冲的处理方法虽有所涉及,但相关研究还不够深入。伪随机脉冲具有弥补力学模型精度不足的作用[18],对当前数据累积有限、部分摄动力难以精确建模的北斗卫星精密定轨具有重要意义。
针对以上问题,本文首先给出了法方程叠加的基本原理,并重点推导了轨道合成中主要应用的参数转换方法。而后,在给出密切元素和力学参数合成方法的基础上,着重研究了伪随机脉冲的处理方法。据此,提出了附加伪随机脉冲的北斗卫星多天轨道合成方法。最后,利用北斗卫星实测数据,设计相应算例,验证了本文方法的应用效果。
1 法方程叠加基本原理在基于法方程叠加的轨道合成中,首先处理单天数据,形成单天解法方程并保存,再在法方程水平进行参数转换、叠加等处理,得到多天解轨道。参数转换的本质是对法方程进行重新参数化,其基本思想是通过建立新参数与原参数的线性关系,并利用这一关系对原法方程系统进行转换,形成新的法方程系统,在进行法方程叠加之前,通常需要进行参数转换。这里首先推导了法方程转换方法,而后给出了法方程叠加的基本原理。
1.1 参数转换设有误差方程
 (1)
(1)
其对应的法方程为
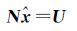 (2)
(2)
式中,N=BTPB;U=BTPL;P为观测值的权阵。
假定要将法方程中的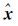

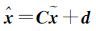 (3)
(3)
将式(3)代入式(1),得
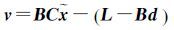 (4)
(4)
则新的法方程系统可表示为
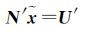 (5)
(5)
式中
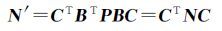 (6)
(6)
 (7)
(7)
式(6)和式(7)即为对应的参数转换公式。实际应用中,首先建立新参数与原参数的线性关系(如式(3)),即给定C和d的具体形式,而后直接由参数转换公式获得新法方程的系数矩阵,即可建立新的法方程系统。
1.2 法方程叠加假设有两组观测量,相互之间独立,且有观测方程如下
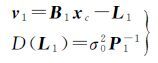 (8)
(8)
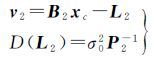 (9)
(9)
式中,xc表示待估参数;σ02表示单位权方差;D(·)表示协方差矩阵;L1、L2表示两组独立观测量;B1、B2表示对应的设计矩阵;v1、v2表示残差向量;P1、P2表示观测权阵。
按照最小二乘原理,式(8)和式(9)对应的法方程可分别表示为
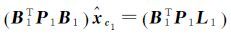 (10)
(10)
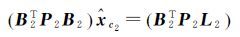 (11)
(11)
式中,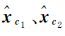
两组法方程叠加得到如下新的法方程系统
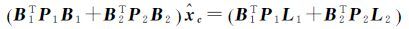 (12)
(12)
式中,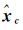
通过法方程叠加进行多天轨道合成时,可将对应的单天解法方程中包含的参数分为两大类:一类为“感兴趣”的轨道参数;另一类为暂时“不感兴趣”的参数,如对流层延迟参数、钟差参数等。对于后者,可以在叠加之前首先将其预消除,待到叠加完成并解得轨道参数后,再通过回代的方法进行解算。关于参数的预消除与回代方法,相关文献多有论及[7, 10-11],不再赘述。这里主要关注轨道参数,通常包括密切元素和力学参数。结合北斗卫星目前数据累积有限、部分力学模型有待进一步精化的特点,这里还考虑在轨道合成时于单天边界处附加伪随机脉冲参数,以吸收力学模型误差。下面首先给出密切元素和力学参数的合成方法,而后重点推导伪随机脉冲的具体处理方法。
2.1 密切元素和力学参数的合成假定有n天轨道需要合成,那么只要能够建立第1天的密切元素和力学参数与其后n-1天相关参数的线性关系,并利用这一关系对n-1个单天解法方程进行参数变换,以统一所有单天解法方程的待估参数集,最后,根据法方程叠加原理,即可完成相关参数的合成。
如果要将n-1天的轨道通过第1天的轨道参数表示,就要求相邻两天边界处卫星位置与速度具有连续性,同时可要求各天的力学参数相等。有如下关系
 (13)
(13)
式中,r、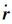
利用密切元素与卫星位置、速度的对应关系以及式(13),经过推导,可以得到如下线性关系
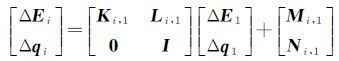 (14)
(14)
式中,ΔEi、Δqi分别表示第i天(i=2,3,…,n)的密切元素和力学参数;ΔE1、Δq1分别表示第1天的密切元素和力学参数;Ki,1、Li,1、Mi,1、Ni,1分别表示对应的关系矩阵,具体形式可参阅文献[7];I表示单位阵。
利用式(14)建立的线性关系,参照1.1节给出的参数转换方法,对n-1天的法方程系统进行参数转换,统一各天的待估参数集,而后利用1.2节给出的法方程叠加方法,即可完成相应的合成处理。
2.2 伪随机脉冲参数的合成为了减弱北斗卫星力学模型精度不足的不利影响,考虑在单天边界处附加伪随机脉冲参数,其可定义为在给定历元的瞬间速度增量[19-20],通过下式表示
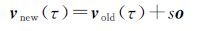 (15)
(15)
式中,s表示伪随机脉冲的大小,o表示伪随机脉冲的方向,两者共同定义了伪随机脉冲;τ表示伪随机脉冲发生的时刻;vold、vnew分别表示伪随机脉冲发生前后的卫星速度。
在进行轨道合成时,需要考虑当前时刻之前所有伪随机脉冲对卫星轨道的影响。为便于讨论,假定τ为附加伪随机脉冲对应的参考历元,ti为第i天法方程对应的参考历元,分两步处理以上问题:
2.2.1 τ历元伪随机脉冲对τ历元密切元素的影响将τ历元伪随机脉冲so在径向、横向和轨道面法向的分量分别记为sR、sT、sN。根据牛顿受摄运动方程[21],引起的密切元素变化量可表示为
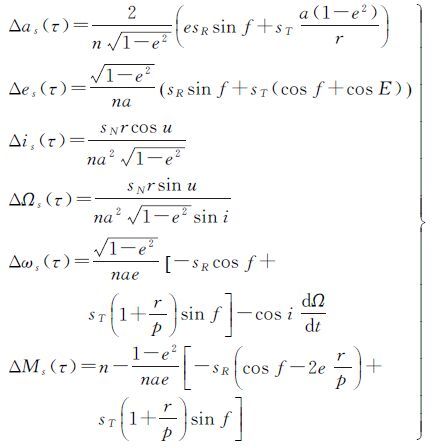 (16)
(16)
式中,a为轨道半长轴;e为轨道偏心率;i为轨道倾角;Ω为升交点赤经;n为卫星运动的平均角速度;u为升交角距;f为真近点角;E为偏近点角;r为卫星位置矢量的模;p=a(1-e2)为半通径。
将τ历元伪随机脉冲对τ历元密切元素的影响以矩阵形式表示,有
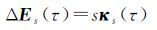 (17)
(17)
式中,ΔEs(τ)表示伪随机脉冲引起的密切元素的变化量;κs(τ)是由式(16)给定的系数矩阵;s含义与以上相同。
2.2.2 τ历元密切元素对ti历元密切元素的影响根据卫星变分方程,可得状态转移矩阵Ms(ti,τ),其元素为
 (18)
(18)
则τ历元密切元素对ti历元密切元素的影响,可表示为
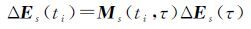 (19)
(19)
综合式(17)和式(19),可得τ历元伪随机脉冲对ti历元密切元素的影响为
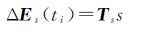 (20)
(20)
并有
 (21)
(21)
综上,当前时刻之前所有伪随机脉冲对ti历元密切元素的影响可通过式(20)获得,表示如下
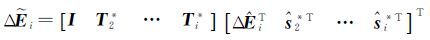 (22)
(22)
式中,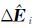
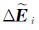

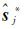
对第i天的法方程系统进行参数转换,对照式(3),有
 (23)
(23)
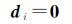 (24)
(24)
利用参数转换公式(6)和式(7),可得
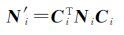 (25)
(25)
 (26)
(26)
式中,Ni、Ui为第i天原法方程系统的法矩阵和自由项;N′i、U
利用以上方法,对各单天解法方程进行参数转换,得到新的法方程系统,而后基于法方程叠加原理,即可完成伪随机脉冲参数的合成。
方便推导起见,以上分别讨论了密切元素、力学参数和伪随机脉冲的合成方法。实际处理中,3类参数同时出现在法方程中,需首先按照处理伪随机脉冲的方法对各单天解法方程进行参数转换,而后进行密切元素和力学参数的参数转换,最后再进行法方程叠加,即可完成多天轨道的合成处理。
3 算例分析为了验证本文方法的正确性及其在北斗卫星精密定轨中的实际应用效果,结合北斗卫星实测数据,首先探讨单天边界附加伪随机脉冲对北斗卫星轨道精度的改善作用,而后,分析北斗卫星多天轨道合成的实际效果。
3.1 伪随机脉冲的作用采用全球24个测站2013年6月3日到2013年6月24日共22d的北斗观测数据进行试验分析,其中,12个测站来自IGS组织的多系统实验网(multi-GNSS experiment,M-GEX),12个测站来自武汉大学建立的北斗卫星观测实验网(BeiDou experimental tracking stations,BETS),测站分布见图 1。
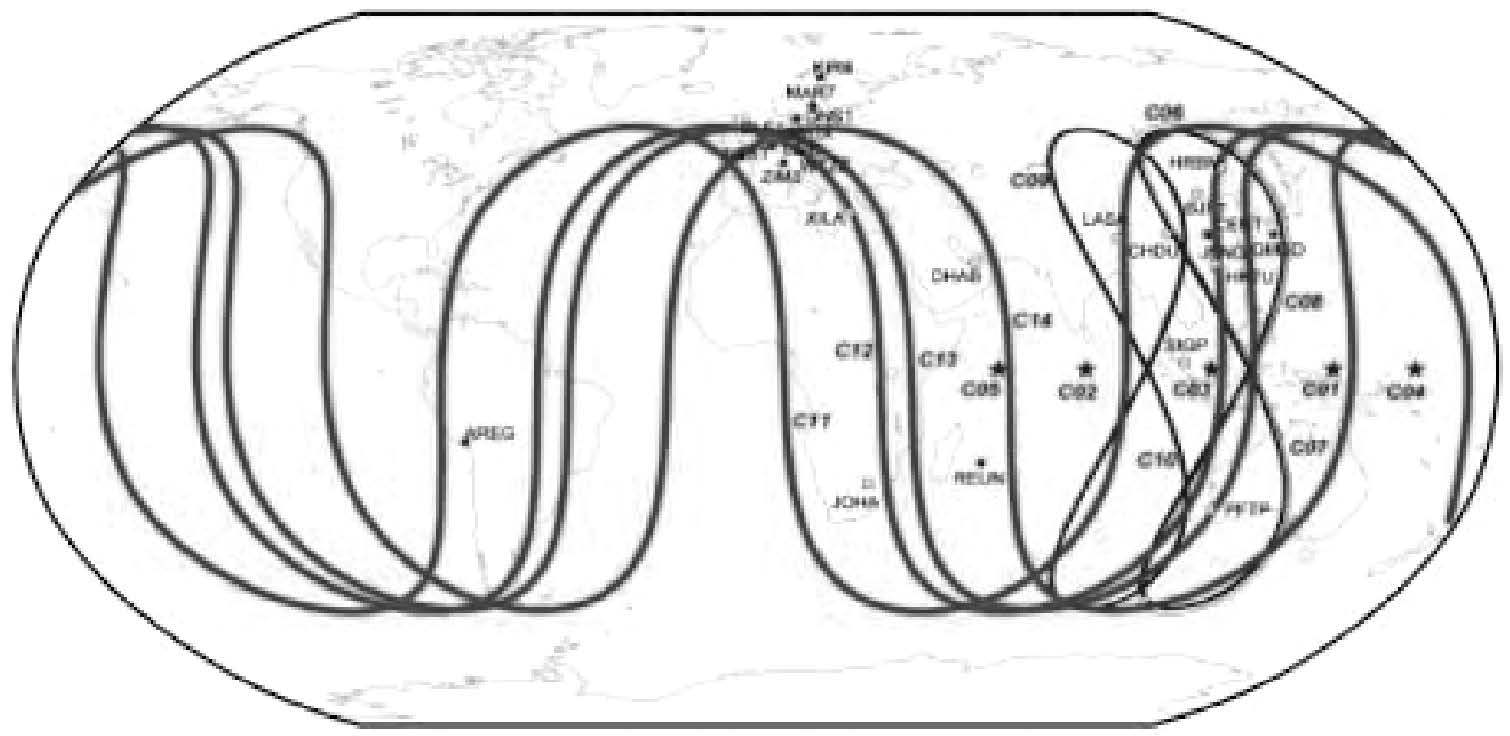
|
| 图 1 测站分布图 Fig. 1 Station layout |
处理中,首先利用单天数据以非差动力法进行北斗卫星单系统精密定轨,并保存单天解法方程,而后,利用本文给出的方法进行3d轨道合成。为了方便对比,轨道合成时采用如下两种方案,两种处理方案仅在伪随机脉冲的处理上有所区别,其他处理策略(见表 1)相同。
| 类别 | 模型与参数 |
| 观测量 | 非差消电离层组合相位和相位平滑伪距 |
| 高度截止角 | 3° |
| 采样间隔 | 180s |
| 地球重力场 | JGM3 12×12阶 |
| N体引力 | JPL DE200(日、月) |
| 固体潮 | TIDE2000 |
| 海潮 | CSR30 |
| 相对论效应 | IERS 2003 |
| 太阳光压 | ECOM模型 |
| 测站坐标 | IGS08先验坐标,紧约束 |
| 对流层误差 | SAAS+NIELL干分量改正;每4h估计一组天顶湿分量 |
| 电离层误差 | 消电离组合消除 |
| 潮汐改正 | IERS2003;FES2004 |
| 接收机钟差 | 历元参数估计 |
| 卫星钟差 | 历元参数估计 |
| 模糊度参数 | 浮点解 |
| 轨道参数 | 6个卫星状态参数+5个光压参数 |
方案1(S1):3d轨道合成,单天边界处不附加伪随机脉冲。
方案2(S2):3d轨道合成,单天边界处附加伪随机脉冲。
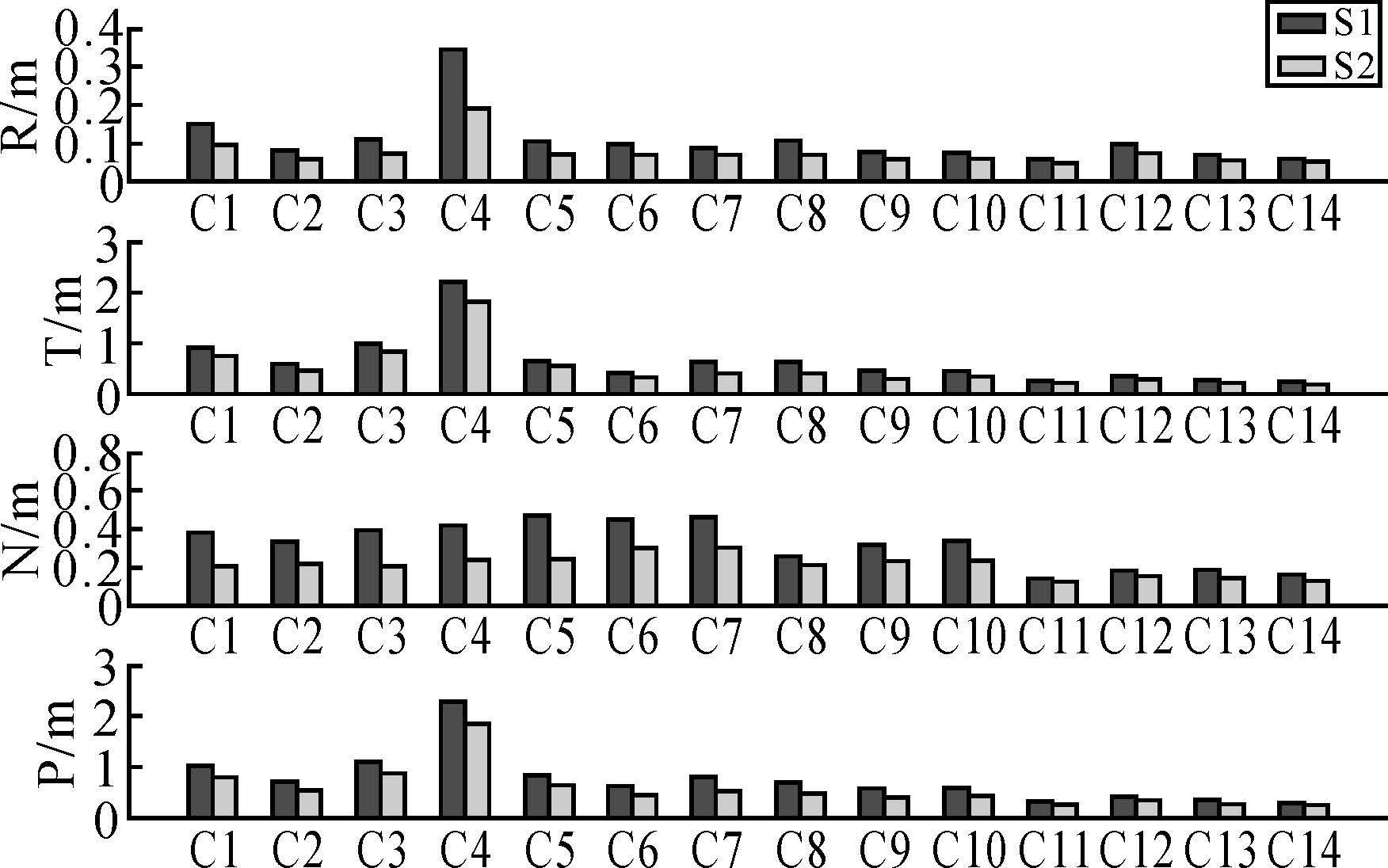
以3d轨道的重叠弧段轨道差值考察两种方案的定轨精度,方法如图 2。表 2和图 3给出了两种方案下各卫星在所有重叠弧段上径向(R)、切向(T)、法向(N)和三维(P)的平均RMS情况。
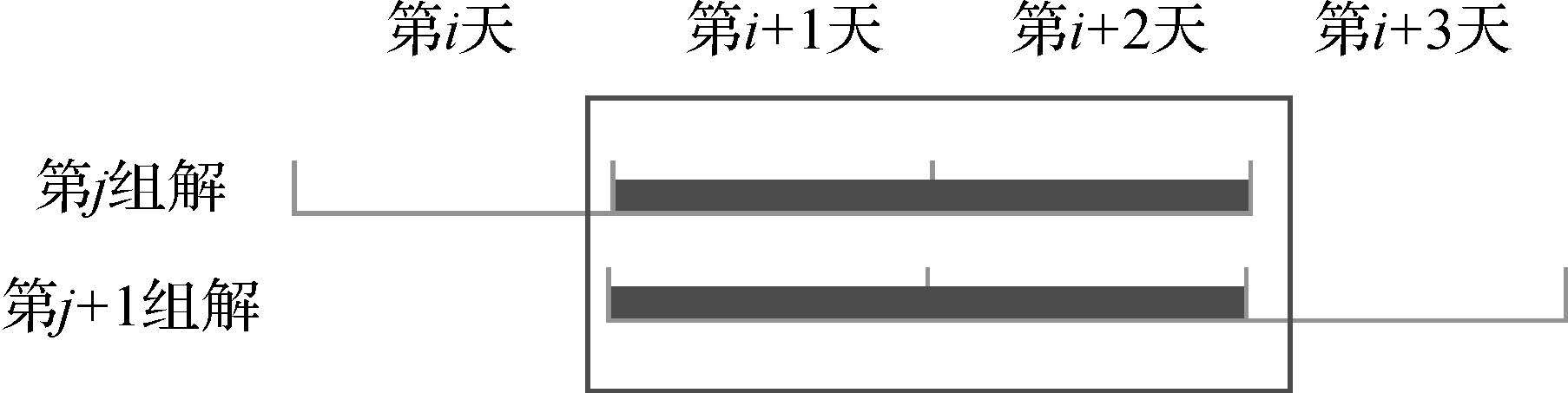
|
| 图 2 重叠弧段轨道差值比较方法 Fig. 2 Method of overlapped-arc comparison |
|
| 图 3 北斗卫星精密定轨精度对比图 Fig. 3 Comparison of BeiDou satellites orbit precision |
| m | ||||||||||||
| type | PRN | R | T | N | P | |||||||
| S1 | S2 | S1 | S2 | S1 | S2 | S1 | S2 | |||||
| GEO | C1 | 0.151 | 0.095 | 0.910 | 0.731 | 0.379 | 0.203 | 1.019 | 0.785 | |||
| C2 | 0.082 | 0.058 | 0.584 | 0.456 | 0.334 | 0.215 | 0.705 | 0.533 | ||||
| C3 | 0.111 | 0.072 | 0.980 | 0.825 | 0.394 | 0.205 | 1.099 | 0.875 | ||||
| C4 | 0.347 | 0.191 | 2.207 | 1.813 | 0.420 | 0.235 | 2.286 | 1.850 | ||||
| C5 | 0.106 | 0.071 | 0.640 | 0.542 | 0.470 | 0.242 | 0.830 | 0.618 | ||||
| mean | 0.159 | 0.097 | 1.064 | 0.873 | 0.399 | 0.220 | 1.188 | 0.932 | ||||
| IGSO | C6 | 0.096 | 0.068 | 0.398 | 0.300 | 0.449 | 0.294 | 0.624 | 0.437 | |||
| C7 | 0.087 | 0.068 | 0.624 | 0.398 | 0.462 | 0.301 | 0.789 | 0.512 | ||||
| C8 | 0.107 | 0.069 | 0.624 | 0.392 | 0.254 | 0.206 | 0.695 | 0.454 | ||||
| C9 | 0.079 | 0.060 | 0.459 | 0.295 | 0.312 | 0.232 | 0.578 | 0.393 | ||||
| C10 | 0.076 | 0.060 | 0.456 | 0.327 | 0.337 | 0.235 | 0.588 | 0.418 | ||||
| mean | 0.089 | 0.065 | 0.512 | 0.342 | 0.363 | 0.254 | 0.655 | 0.443 | ||||
| MEO | C11 | 0.061 | 0.047 | 0.258 | 0.208 | 0.141 | 0.122 | 0.309 | 0.251 | |||
| C12 | 0.098 | 0.072 | 0.358 | 0.288 | 0.181 | 0.149 | 0.421 | 0.334 | ||||
| C13 | 0.070 | 0.056 | 0.268 | 0.215 | 0.187 | 0.141 | 0.343 | 0.270 | ||||
| C14 | 0.059 | 0.051 | 0.235 | 0.184 | 0.160 | 0.128 | 0.298 | 0.234 | ||||
| mean | 0.072 | 0.057 | 0.280 | 0.224 | 0.167 | 0.135 | 0.343 | 0.272 | ||||
由图 3和表 2的结果可见,多天轨道合成时在单天边界处附加伪随机脉冲,所有北斗卫星的精密定轨精度都获得了明显改善。平均来讲,GEO卫星轨道精度在R、T、N方向分别提高了0.062、0.191和0.179m;IGSO卫星分别提高了0.024、0.170和0.109m;MEO卫星分别提高了0.015、0.056和0.032m。相比R方向,伪随机脉冲的引入对3类卫星T、N方向轨道精度的改善更为明显。从三维定轨精度来看,GEO、IGSO和MEO卫星分别提高了0.256、0.212和0.071m,GEO和IGSO卫星轨道精度的提高幅度明显大于MEO卫星。伪随机脉冲的主要作用是弥补力学模型精度的不足,以上结果在一定程度上表明,北斗系统3类卫星的力学模型在T、N方向具有较大的残余误差影响,相比MEO卫星,GEO和IGSO卫星的力学模型精度具有更大的改进空间。
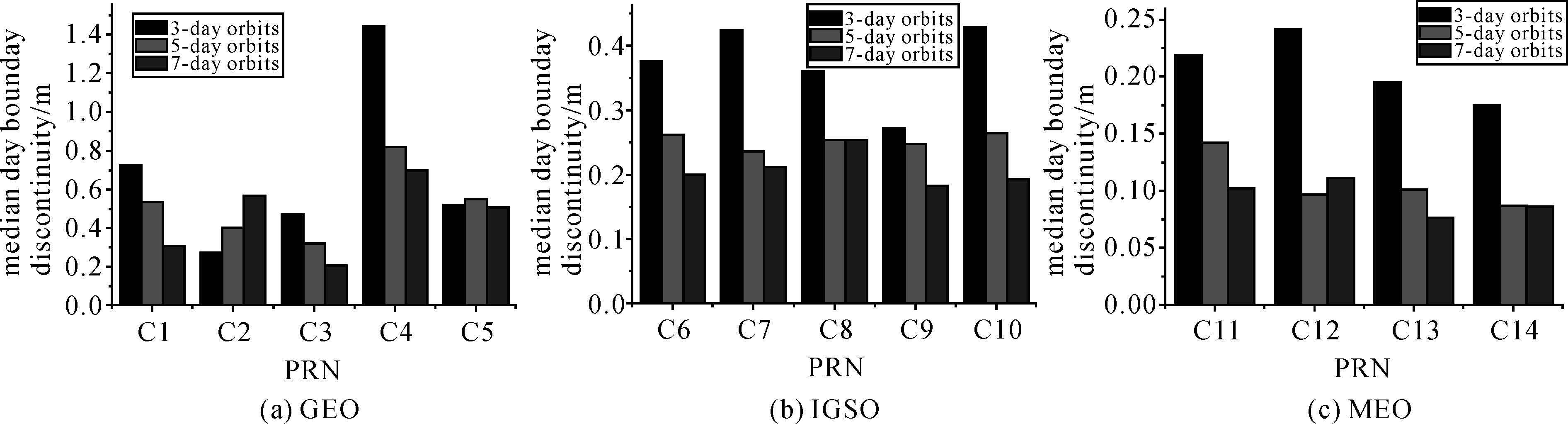
3.2 多天轨道合成效果为了进一步验证北斗卫星多天轨道合成的效果,采用2013年6月1日到2013年6月26日共26d的北斗卫星实测数据,所用测站及处理策略与上一算例方案2相同。在附加伪随机脉冲的条件下,分别计算了北斗卫星3d(S1)、5d(S2)和7d(S3)解轨道。便于对比起见,仅取多天解轨道的中间一天作为当天最终轨道,采用文献[17]给出的方法,通过统计连续两天最终轨道在00:00:00(或24:00:00)的轨道差异值中位数,来评定定轨精度。图 4以图示的形式对比了GEO、IGSO和MEO卫星3d 、5d和7d解轨道的三维轨道差异值中位数,表 3则对3种解算方案中各卫星径向(R)、切向(T)、法向(N)和三维(P)的轨道差异值中位数进行了统计。
|
| 图 4 多天轨道合成试验各星轨道精度对比图 Fig. 4 Comparison of BeiDou satellites orbit precision in orbit combination |
| m | ||||||||||||||||
| type | PRN | R | T | N | P | |||||||||||
| S1 | S2 | S3 | S1 | S2 | S3 | S1 | S2 | S3 | S1 | S2 | S3 | |||||
| GEO | C1 | 0.092 | 0.058 | 0.047 | 0.720 | 0.520 | 0.270 | 0.116 | 0.066 | 0.045 | 0.725 | 0.534 | 0.307 | |||
| C2 | 0.030 | 0.034 | 0.020 | 0.195 | 0.382 | 0.566 | 0.050 | 0.040 | 0.041 | 0.274 | 0.399 | 0.566 | ||||
| C3 | 0.090 | 0.054 | 0.041 | 0.465 | 0.310 | 0.181 | 0.063 | 0.041 | 0.040 | 0.469 | 0.319 | 0.204 | ||||
| C4 | 0.185 | 0.127 | 0.073 | 1.410 | 0.817 | 0.694 | 0.119 | 0.072 | 0.045 | 1.443 | 0.819 | 0.697 | ||||
| C5 | 0.032 | 0.020 | 0.022 | 0.499 | 0.547 | 0.505 | 0.126 | 0.067 | 0.053 | 0.518 | 0.549 | 0.507 | ||||
| mean | 0.086 | 0.059 | 0.041 | 0.658 | 0.515 | 0.440 | 0.095 | 0.057 | 0.045 | 0.686 | 0.524 | 0.456 | ||||
| IGSO | C6 | 0.046 | 0.046 | 0.048 | 0.235 | 0.159 | 0.125 | 0.256 | 0.195 | 0.175 | 0.376 | 0.262 | 0.200 | |||
| C7 | 0.047 | 0.028 | 0.023 | 0.278 | 0.151 | 0.174 | 0.226 | 0.203 | 0.105 | 0.424 | 0.236 | 0.212 | ||||
| C8 | 0.051 | 0.022 | 0.017 | 0.318 | 0.229 | 0.253 | 0.110 | 0.098 | 0.114 | 0.361 | 0.253 | 0.253 | ||||
| C9 | 0.046 | 0.041 | 0.040 | 0.199 | 0.176 | 0.103 | 0.197 | 0.126 | 0.128 | 0.272 | 0.248 | 0.183 | ||||
| C10 | 0.038 | 0.032 | 0.036 | 0.345 | 0.200 | 0.124 | 0.244 | 0.150 | 0.093 | 0.429 | 0.265 | 0.192 | ||||
| mean | 0.046 | 0.034 | 0.033 | 0.275 | 0.183 | 0.156 | 0.207 | 0.154 | 0.123 | 0.372 | 0.253 | 0.208 | ||||
| MEO | C11 | 0.029 | 0.024 | 0.012 | 0.175 | 0.093 | 0.074 | 0.086 | 0.075 | 0.052 | 0.219 | 0.142 | 0.102 | |||
| C12 | 0.020 | 0.019 | 0.010 | 0.143 | 0.067 | 0.082 | 0.069 | 0.072 | 0.046 | 0.241 | 0.097 | 0.111 | ||||
| C13 | 0.041 | 0.021 | 0.013 | 0.137 | 0.057 | 0.044 | 0.083 | 0.053 | 0.043 | 0.195 | 0.101 | 0.076 | ||||
| C14 | 0.035 | 0.019 | 0.011 | 0.093 | 0.056 | 0.035 | 0.109 | 0.051 | 0.029 | 0.175 | 0.087 | 0.086 | ||||
| mean | 0.031 | 0.021 | 0.012 | 0.137 | 0.068 | 0.059 | 0.087 | 0.063 | 0.043 | 0.208 | 0.107 | 0.094 | ||||
(1) 随着定轨弧段的增长,大部分卫星的定轨精度都获得了不同程度的改善。但是,应该引起注意的是,C02星轨道精度随定轨弧段的增长反而有明显的降低趋势,具体原因尚待进一步分析。
(2) 从三维轨道精度来看,由3d定轨弧段增长到5d时,GEO、IGSO、MEO平均定轨精度分别提高了23.6%、32.0%和48.6%;由5d增长到7d时,3类卫星分别提高了13.0%、17.8%和12.1%。由此可见,定轨弧段由3d增长到5d对轨道精度的改善作用更为明显。这一点在图 4中也有直观反映,这是由于定轨弧段增长到一定限度对观测构形的改善作用就不再显著,力学模型的精度也在一定程度上限制了定轨弧段的长度。此外,定轨弧段由3d增长到5d时,GEO、IGSO和MEO的轨道精度提高幅度依次增大,主要是由于多天数据的累积对“运动”中的IGSO和MEO(特别是MEO)卫星观测结构改善作用更大,而对“静止”的GEO卫星改善作用稍弱。但是,这种改善对观测几何结构较差的GEO卫星却具有重要意义,表现在其轨道精度改进的绝对量要明显大于IGSO和MEO卫星。当定轨弧段由5d增长到7d时,3类卫星轨道精度改善幅度的差异性已经不甚明显。
(3) 以3d定轨弧长与7d定轨弧长作对比,在R方向上,GEO、IGSO、MEO卫星平均定轨精度分别提高了0.045、0.013和0.019m,在T方向上,3类卫星分别提高了0.215、0.119和0.078m,在N方向上,3类卫星分别提高了0.050、0.084和0.044m。随着定轨弧段的增长,3类卫星T方向轨道精度改善最为明显。这主要是由于导航卫星的距离观测量对轨道T方向几何约束不足,通过多天数据累积,有助于改善T方向的观测几何约束。
在使用相同的轨道精度评定方法并采用相同长度的定轨弧长的条件下,以上结果与文献[17]的定轨精度基本相当,本文结果略优。除了附加伪随机脉冲对力学模型缺陷的弥补作用之外,还得益于文中使用了更多的测站数据。需要说明的是,以上轨道精度评定方法实质上是以单天边界处轨道的不连续性来统计定轨精度,由于动力法定轨的末端效应,定轨弧段两端轨道精度较低,因此以弧段中间一天边界处轨道的不连续性统计获得的轨道精度要略优于重叠弧段的结果。此外,随着定轨弧段的增长,相邻两个定轨弧段公用的观测数据会不断增多,这在一定程度上也会引起轨道内符合精度升高。因此,算例中轨道精度随定轨弧段增长而不断提高,除得益于观测数据的累积效应之外,以上两个因素也具有一定的影响作用。
4 结 论针对目前北斗卫星多天解轨道计算依靠常规方法效率低下的问题,本文深入研究了基于法方程叠加的多天轨道合成方法,同时,结合北斗卫星部分摄动力模型精度尚待进一步精化的现实情况,在研究了密切元素和力学参数处理方法的基础上,重点推导了伪随机脉冲参数的合成方法,提出了附加伪随机脉冲的北斗卫星多天轨道合成方法。结合北斗实测数据,对相关方法进行了分析验证,结果表明:在轨道多天合成中,单天边界附加伪随机脉冲对北斗卫星轨道精度有明显改进作用,其中,3类卫星T、N方向轨道精度的改善程度大于R方向,GEO和IGSO卫星轨道精度的提高幅度大于MEO卫星。伪随机脉冲的主要作用是弥补力学模型精度的不足,以上试验结果在一定程度上也说明:北斗系统3类卫星的力学模型在T、N方向具有较大的残余误差影响;相比MEO卫星,GEO和IGSO卫星的力学模型精度具有更大的改进空间。此外,利用文中方法进行北斗卫星多天轨道合成,一定范围内,随着定轨弧段的增长,北斗星定轨精度能够得到不同程度的改善。定轨弧长由3d增长到5d对定轨精度的改善作用要明显大于由5d增长到7d的情况,定轨弧长的增长对北斗3类卫星T方向的轨道精度改善作用更大,但是C02星轨道精度随定轨弧段的增长反而有明显的降低趋势,具体原因有待进一步分析。
需要指出的是,利用本文方法在附加伪随机脉冲条件下获得的高精度轨道反过来可以用于精化北斗卫星力学模型,其具体方法有待进一步深入研究。
致谢: 感谢全球连续监测评估系统(iGMAS)信息工程大学分析中心对本文工作的帮助和支持。
| [1] | 杨元喜. 北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报 , 2010, 39 (1) : 1–6. YANG Yuanxi. Progress, Contribution and Challenges of Compass/BeiDou Satellite Navigation System[J]. Acta Geodaetica et Cartographica Sinica , 2010, 39 (1) : 1 –6. |
| [2] | 冉承其. 北斗卫星导航系统的发展[R]. 武汉:第四届中国卫星导航学术年会, 2013. RAN Chengqi. Development of BeiDou Navigation Satellite System[R]. Wuhan:CSNC 2013. |
| [3] | 中国卫星导航系统管理办公室. 北斗卫星导航系统发展报告2.2[S]. 北京:中国卫星导航系统管理办公室, 2013:1-10. China Satellite Navigation Office. Report on the Development of BeiDou Navigation Satellite System V2.2[S]. Beijing:China Satellite Navigation Office, 2013. |
| [4] | 郝金明, 刘伟平, 杨力, 等. 北斗卫星导航系统精密定轨技术研究现状[J]. 测绘科学技术学报 , 2015, 32 (3) : 221–225. HAO Jinming, LIU Weiping, YANG Li, et al. Status of Precise Orbit Determination of BeiDou Navigation Satellite System[J]. Journal of Geomatics Science and Technology , 2015, 32 (3) : 221 –225. |
| [5] | BEUTLER G, BROCKMANN E, HUGENTOBLER U, et al. Combining Consecutive Short Arcs into Long Arcs for Precise and Efficient GPS Orbit Determination Combining n Consecutive One-Day-Arcs into One n-days-arc[J]. Journal of Geodesy , 1996, 70 (5) : 287 –299. DOI:10.1007/BF00867349 |
| [6] | 姚宜斌. GPS轨道合成原理及其实现[J]. 武汉大学学报(信息科学版) , 2007, 32 (11) : 1487–1492. YAO Yibin. Theory and Realization of GPS Orbit Integration[J]. Geomatics and Information Science of Wuhan University , 2007, 32 (11) : 1487 –1492. |
| [7] | BROCKMANN E. Combination of Solutions for Geodetic and Geodynamic Applications of the Global Positioning System (GPS)[D]. Berne:University of Bern, 1996:1-7. |
| [8] | 刘伟平. 北斗卫星导航系统精密轨道确定方法研究[D]. 郑州:信息工程大学, 2014:70-90. LIU Weiping. Research on Precise Orbit Determination of BeiDou Navigation Satellite System[D]. Zhengzhou:Information Engineering University, 2014:70-90. |
| [9] | DONG D, HERRING T A, KING R W. Estimating Regional Deformation from a Combination of Space and Terrestrial Geodetic Data[J]. Journal of Geodesy , 1998, 72 (4) : 200 –214. DOI:10.1007/s001900050161 |
| [10] | 姚宜斌. GPS精密定位定轨后处理算法与实现[D]. 武汉:武汉大学, 2004:1-7. YAO Yibin. Research on the Algorithm and Realization of Post-processing for GPS Precise Positioning and Orbit Determination[D]. Wuhan:Wuhan University, 2004:1-7. http://cdmd.cnki.com.cn/article/cdmd-10486-2006035432.htm |
| [11] | 刘伟平, 郝金明, 钱龙, 等. 卫星轨道的法方程叠加合成方法[J]. 测绘科学技术学报 , 2014, 31 (1) : 23–27. LIU Weiping, HAO Jinming, QIAN Long, et al. Method of Satellite Orbit Combination Based on Normal Equation Stacking[J]. Journal of Geomatics Science and Technology , 2014, 31 (1) : 23 –27. |
| [12] | 施闯, 赵齐乐, 李敏, 等. 北斗卫星导航系统的精密定轨与定位研究[J]. 中国科学:地球科学 , 2012, 42 (6) : 854–861. SHI Chuang, ZHAO Qile, LI Min, et al. Precise Orbit Determination of BeiDou Satellites with Precise Positioning[J]. Science China Earth Sciences , 2012, 42 (6) : 854 –861. |
| [13] | ZHAO Qile, GUO Jing, LI Min, et al. Initial Results of Precise Orbit and Clock Determination for COMPASS Navigation Satellite System[J]. Journal of Geodesy , 2013, 87 (5) : 475 –486. DOI:10.1007/s00190-013-0622-7 |
| [14] | 刘伟平, 郝金明, 李建文, 等. 多GNSS融合的北斗卫星精密定轨[J]. 测绘学报 , 2014, 43 (11) : 1132–1138. LIU Weiping, HAO Jinming, LI Jianwen, et al. Multi-GNSS Joint Precise Orbit Determination of BeiDou Navigation Satellite System[J]. Acta Geodaetica et Cartographica Sinica , 2014, 43 (11) : 1132 –1138. DOI:10.13485/j.cnki.11-2089.2014.0186 |
| [15] | HE Lina, GE Maorong, WANG Jiexian, et al. Experimental Study on the Precise Orbit Determination of the BeiDou Navigation Satellite System[J]. Sensors , 2013, 13 (3) : 2911 –2928. DOI:10.3390/s130302911 |
| [16] | LIU Yang, LOU Yidong, SHI Chuang, et al. BeiDou Regional Navigation System Network Solution and Precision Analysis[C]//China Satellite Navigation Conference (CSNC) 2013 Proceedings. Guangzhou:CSNC, 2013:173-186. |
| [17] | STEIGENBERGER P, HUGENTOBLER U, MONTENBRUCK O, et al. Precise Orbit Determination of GIOVE-B Based on the CONGO Network[J]. Journal of Geodesy , 2011, 85 (6) : 357 –365. DOI:10.1007/s00190-011-0443-5 |
| [18] | BEUTLER G, BROCKMANN E, GURTNER W, et al. Extended Orbit Modeling Techniques at the CODE Processing Center of the International GPS Service for Geodynamics (IGS):Theory and Initial Results[J]. Manuscripta Geodaetica , 1994, 19 : 367 –386. |
| [19] | 刘伟平, 郝金明, 田英国, 等. 一种伪随机脉冲的快速参数估计方法[J]. 武汉大学学报(信息科学版) , 2015, 40 (11) : 1487–1492. LIU Weiping, HAO Jinming, TIAN Yingguo, et al. Fast Parameter Estimation for Pseudo-stochastic Pulse[J]. Geomatics and Information Science of Wuhan University , 2015, 40 (11) : 1487 –1492. |
| [20] | BEUTLER G, JÄGGI A, HUGENTOBLER U, et al. Efficient Satellite Orbit Modelling Using Pseudo-stochastic Parameters[J]. Journal of Geodesy , 2006, 80 (7) : 353 –372. DOI:10.1007/s00190-006-0072-6 |
| [21] | 刘林. 天体力学方法[M]. 南京: 南京大学出版社, 1998 : 45 -47. LIU Lin. Method of Celestial Mechanics[M]. Nanjing: Nanjing University Press, 1998 : 45 -47. |


