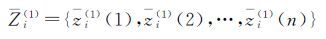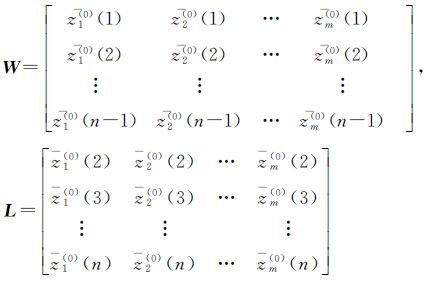2. 地球空间信息技术协同创新中心, 湖北 武汉 430079
2. Collaborative Innovation Center for Geospatial Technology, Wuhan 430079, China
采用空间多点的立体布网模式监测工程建筑物的安全状态,用变形观测序列的潜在信息进行定量预测是当前变形监测分析与预报的有效方法。由于受工程现状、观测条件及突发因素等影响,变形观测所获得的数据不一定是大样本的长期观测序列,而是小样本、非等间距的观测数据,因此,针对小样本数据处理的灰色系统理论就具有优越性[1-2]。由于传统GM(1,1)建模要求数据序列是等间距的,不少学者就非等间距GM(1,1)建模方法进行了研究[3-11],但仍局限在单点或单方向时间序列的研究上,事实上监测工程建筑物的变形状态都布设有大量的变形监测点,监测点间是相互影响、彼此关联的,单点的处理没有利用监测点间相互关系的信息,不足以反映变形体的整体变形趋势和变形规律[12-14]。而事实上,同一变形块体上的变形点,其各向变形规律应具有相似性,通过变形观测序列进行关联分析与描述,在结合工程地质综合考虑的基础上,将彼此关联的多个变形点视为同一块体上的点,从而建立空间多点的整体变形预测模型。
针对变形体的整体变形分析与模型研究,文献[12]首次提出了将单点GM(1,1)模型扩展为多点灰色预测模型的新方法,建立了多点变形预测模型。文献[13]利用多点动态预测模型描述了建筑物整体变形的趋势和规律。近年来,不少学者也进行了相关研究[15-21],并在系统工程、岩土工程等领域得到了应用,但上述研究均是基于等间距序列所建立的预测模型,对于实际工程可能存在非等间距观测或某几期缺测的实际状况,如何建立非等间距观测的多点变形模型却鲜有报道。本文基于非等间距的变形观测序列,首先提出了一种非等间距等距化处理的改进方法,在此基础上,将单点的GM(1,1)模型扩展为空间多点的变形预测模型,最后再处理为非等间距多点变形预测模型。为验证非等间距多点变形预测模型的可行性和有效性,首先以实例给出了建模的具体步骤及模型拟合和预测结果,并与单点GM(1,1)模型进行了对比分析;再利用文献[12]和文献[13]的实例与等间距多点预测模型进行了对比分析;最后利用文献[14]的实例,采用人为删去部分观测数据,使原等间距序列变为缺测某几期数据的不等间距序列进行了建模与对比,结果表明非等间距多点变形预测模型既适用于观测时间超前或滞后、以及因缺测某几期观测数据导致的非等间距序列的建模,也适用于等间距序列的建模,且具有较高的模型拟合精度与预测精度,是一种非线性时空整体变形分析与预测的新方法。相比单点GM(1,1)建模,利用彼此关联的变形监测点所建立的空间多点整体变形预测模型的拟合及预测精度更高。
1 非等间距多点变形预测模型 1.1 模型建立设对某工程建筑物的沉降监测有m个彼此关联的变形观测点,获得了n期变形观测资料,其原始观测序列为Xi(0)={xi(0)(t1),xi(0)(t2),…,xi(0)(tn)},i=1,2,…,m,对应的观测时序为T=(t1,t2,…,tn),若tk-tk-1≠const(k=2,3,…,n),则称原始观测序列Xi(0)为非等间距序列[9]。建模的m个变形观测点彼此关联的特征分析,其基本思路是:同一变形块体上的变形点,其各向变形规律应具有相似性。可采用灰关联与模糊聚类方法,通过变形观测序列进行描述和分析,并结合工程地质综合考虑,具体方法参考文献[14]。
与现有非等间距序列等距化处理方法不同[5-7],考虑到非等间距序列在时间轴上相对等间距而言,可能出现超前或滞后的现象,本文提出一种非等间距序列等距化处理的改进方法,具体步骤如下:
(1) 求平均时间间隔
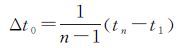 (1)
(1)
(2) 求等距处理后的时间序列
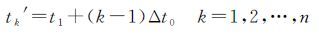 (2)
(2)
(3) 求等距处理前后各期的时间差
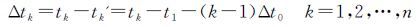 (3)
(3)
(4) 计算各序列值的修正系数
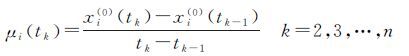 (4)
(4)
(5) 计算各序列值的修正值
Δxi(0)(tk)=μiΔtk(5) 式中,Δtk≥0时,μi取μi(tk);Δtk<0时,μi取μi(tk+1)。
(6) 求得处理后的等间距序列值
 (6)
(6)
通过式(1)-式(6)的处理,便可得到重新构造的等间距序列Zi(0)={zi(0)(1),zi(0)(2),…,zi(0)(n)} ,i=1,2,…,m。上述等距处理的实质是将非等间距原始序列Xi(0)在时间区间t1,tn上通过插值法处理为以平均时间间隔Δt0的等间距序列Zi(0)。
对Zi(0)进行均值化处理,得到均值序列Zi(0)={zi(0)(1),zi(0)(2),…,zi(0)(n)}。其中
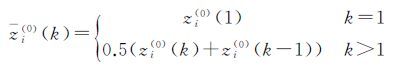 (7)
(7)
其一阶累加生成序列为
其中,zi(1)(k)=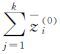
考虑m个点相互关联,将GM(1,1)模型扩展到空间多点的变形预测模型,其一阶白化微分方程为
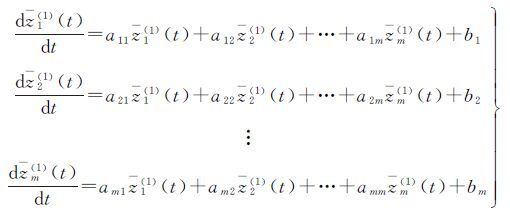 (8)
(8)
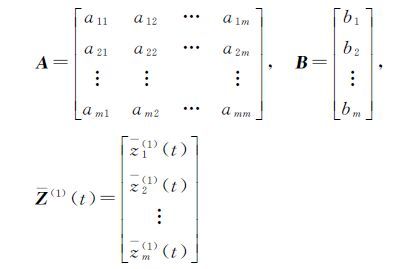
用矩阵表示为
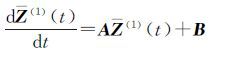 (9)
(9)
式中
按照灰色系统理论以Z(1)(1)为初始条件求得等间距的多点变形模型响应函数式
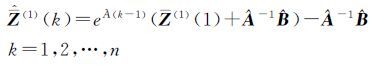 (10)
(10)
式中,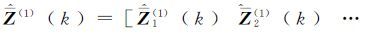
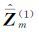
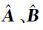
对式(10)进行一阶累减还原处理,可得到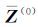
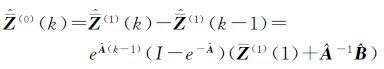 (11)
(11)
式中,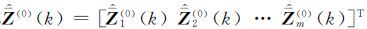
由式(11)可得
 (12)
(12)
为求解式(12)中的参数,按照平差原理,得到相应的残差方程为
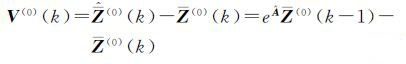 (13)
(13)
对式(13)作转置处理,并将k=2,3,…,n代入,得
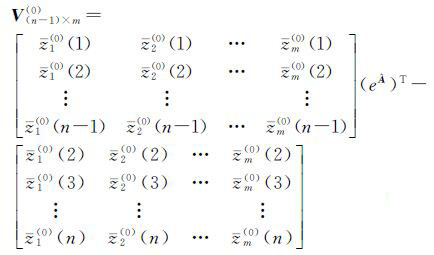 (14)
(14)
按最小二乘准则求得
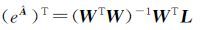 (15)
(15)
根据式(15)求得模型参数A的最小二乘解
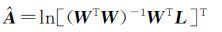 (16)
(16)
式中
设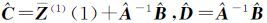
 (17)
(17)
式(11)整理为
 (18)
(18)
由式(18)可知,只需求得模型参数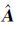
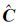
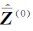
将k=1,2,…,n代入式(17),整理得
 (19)
(19)
其相应的残差方程为
 (20)
(20)
同理,可根据最小二乘准则求得
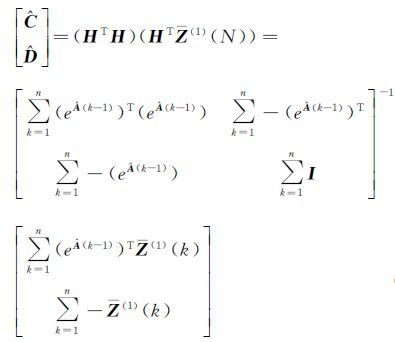 (21)
(21)
式中
根据假设可得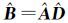
由式(18)并顾及均值化处理式(7),可得等间距序列的预测模型为
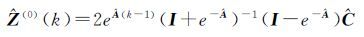 (22)
(22)
式(22)中的时序k=1,2,…,n,其时间间隔为1;考虑实际观测序列为非等间距序列tk-tk-1≠const(k=2,3,…,n),则可以得到非等间距多点预测模型在任一时刻tk的预测式为
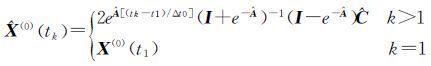 (23)
(23)
式中,当k≤n时,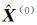
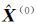
为了检验非等间距多点变形灰色模型预测结果的可靠性,需要对其进行检验。一般采用模型的拟合精度和模型预测的平均相对误差来检验[12, 19]。
模型的拟合精度
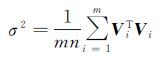 (24)
(24)
式中,Vi=[vi(t1)vi(t2)…vi(tn)]T,vi(tk)=xi(0)(tk)-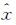
记ρtk为tk时预测值的平均相对误差,则
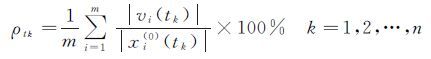 (25)
(25)
通过关联性分析,选取位于某基坑北侧边坡上相互关联的4个沉降观测点的监测数据进行整体变形分析与建模,表 1给出了A点非等间距的累积沉降观测数据及其等距化处理计算结果。本文取前9期序列用于建模,后5期数据作为模型预测结果的对比分析。下面给出建模的具体步骤及模型拟合预测结果。
| k | tk | x(0)(tk) | tk′ | Δtk | μ(tk) | Δx(0)(tk) | z(0)(k) |
| 1 | 1 | 8.45 | 1 | 0 | 0 | 8.45 | |
| 2 | 14 | 13.70 | 14.875 | -0.875 | 0.4038 | -0.50 | 14.20 |
| 3 | 28 | 21.70 | 28.75 | -0.75 | 0.5714 | -0.01 | 21.71 |
| 4 | 43 | 21.90 | 42.625 | 0.375 | 0.0133 | 0.01 | 21.89 |
| 5 | 56 | 26.40 | 56.5 | -0.5 | 0.3462 | -0.02 | 26.42 |
| 6 | 70 | 26.95 | 70.375 | -0.375 | 0.0393 | -0.03 | 26.98 |
| 7 | 79 | 27.73 | 84.25 | -5.25 | 0.0867 | 0.06 | 27.66 |
| 8 | 98 | 27.51 | 98.125 | -0.125 | -0.0116 | -0.01 | 27.52 |
| 9 | 112 | 28.35 | 112 | 0 | 0.06 | 0 | 28.35 |
| Δt0=13.875 | |||||||
2.1.1 原始序列等距化处理
根据上面的计算公式,首先对4个监测点前9期非等间距序列进行等间距化处理,表 1给出了A点的等距化处理计算结果。
2.1.2 计算模型参数由预测式(23)知,预测式只需要模型参数A、C,求解结果为
2.1.3 计算模型拟合值与预测值经过计算,所建立的多点模型的拟合精度为σ2=0.80,模型的拟合与预测结果如表 2所示。
| 期数 | 观测 时间 | 时序 | 累积沉降量实测值 | 模型拟合及预测值 | 残差v | ρtk /(%) | |||||||||||
| A点 | B点 | C点 | D点 | A点 | B点 | C点 | D点 | A点 | B点 | C点 | D点 | ||||||
| 1 | 2013.11.10 | 1 | 8.45 | 15.05 | 9.00 | 11.45 | 8.45 | 15.05 | 9.00 | 11.45 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ||
| 2 | 2013.11.23 | 14 | 13.70 | 22.75 | 13.55 | 13.80 | 14.36 | 21.90 | 13.58 | 13.53 | 0.66 | -0.85 | 0.03 | -0.27 | 2.68 | ||
| 3 | 2013.12.07 | 28 | 21.70 | 25.80 | 18.80 | 18.95 | 19.39 | 26.40 | 17.66 | 17.12 | -2.31 | 0.60 | -1.14 | -1.83 | 7.17 | ||
| 4 | 2013.12.22 | 43 | 21.90 | 28.80 | 20.70 | 19.10 | 23.40 | 29.75 | 21.17 | 20.56 | 1.50 | 0.95 | 0.47 | 1.46 | 5.02 | ||
| 5 | 2014.01.04 | 56 | 26.40 | 33.50 | 24.00 | 22.20 | 25.66 | 31.50 | 23.22 | 22.65 | -0.74 | -2.00 | -0.78 | 0.45 | 3.51 | ||
| 6 | 2014.01.18 | 70 | 26.95 | 32.25 | 23.71 | 22.65 | 27.08 | 32.45 | 24.54 | 24.02 | 0.13 | 0.20 | 0.83 | 1.37 | 2.66 | ||
| 7 | 2014.01.27 | 79 | 27.73 | 32.30 | 24.88 | 25.11 | 27.57 | 32.69 | 24.99 | 24.51 | -0.16 | 0.39 | 0.11 | -0.60 | 1.15 | ||
| 8 | 2014.02.15 | 98 | 27.51 | 32.55 | 25.38 | 26.20 | 27.82 | 32.49 | 25.25 | 24.82 | 0.31 | -0.06 | -0.13 | -1.38 | 1.77 | ||
| 9 | 2014.03.01 | 112 | 28.35 | 31.39 | 25.43 | 24.25 | 27.54 | 31.95 | 25.01 | 24.62 | -0.81 | 0.56 | -0.42 | 0.37 | 1.95 | ||
| 10 | 2014.03.05 | 116 | 28.43 | 31.93 | 25.59 | 24.16 | 27.42 | 31.75 | 24.90 | 24.52 | -1.01 | -0.18 | -0.69 | 0.36 | 2.08 | ||
| 11 | 2014.03.08 | 119 | 28.23 | 32.41 | 25.69 | 25.10 | 27.31 | 31.60 | 24.81 | 24.43 | -0.92 | -0.81 | -0.88 | -0.67 | 2.96 | ||
| 12 | 2014.03.15 | 126 | 28.91 | 32.33 | 25.80 | 23.70 | 27.03 | 31.20 | 24.55 | 24.19 | -1.88 | -1.13 | -1.25 | 0.49 | 4.23 | ||
| 13 | 2014.03.23 | 134 | 29.09 | 32.48 | 26.06 | 24.25 | 26.66 | 30.71 | 24.22 | 23.87 | -2.43 | -1.77 | -1.84 | -0.38 | 5.61 | ||
| 14 | 2014.04.06 | 148 | 29.11 | 32.72 | 26.04 | 24.18 | 25.92 | 29.78 | 23.56 | 23.22 | -3.19 | -2.94 | -2.48 | -0.96 | 8.36 | ||
| 均值 | -0.78 | -0.50 | -0.58 | -0.11 | 3.51 | ||||||||||||
2.2 与单点预测模型的比较
为了比较非等间距多点模型与单点模型的模拟和预测结果,对4个监测点分别建立了非等间距单点GM(1,1)模型,各监测点的拟合和预测结果如表 3所示。由表 2和表 3可知,无论是残差均值还是模型的模拟和预测精度,多点整体变形模型的拟合和预测结果均优于单点模型,说明了空间多点模型由于利用了具有相似变形性质、彼此关联和相互影响的多个变形监测点建模,可以获得更好的模型拟合和预测效果。图 1给出了非等间距的单点与多点模型的拟合与预测结果的对比。
| 期数 | 模型拟合及预测值 | 残差v | ρtk/(%) | |||||||
| A点 | B点 | C点 | D点 | A点 | B点 | C点 | D点 | |||
| 1 | 8.45 | 15.05 | 9.00 | 11.45 | 0 | 0 | 0 | 0 | 0.00 | |
| 2 | 18.41 | 24.65 | 16.86 | 16.94 | 4.71 | 1.90 | 3.31 | 3.14 | 19.50 | |
| 3 | 19.95 | 26.14 | 18.21 | 18.18 | -1.75 | 0.34 | -0.59 | -0.77 | 3.17 | |
| 4 | 21.74 | 27.82 | 19.78 | 19.60 | -0.16 | -0.98 | -0.92 | 0.50 | 3.32 | |
| 5 | 23.42 | 29.37 | 21.25 | 20.92 | -2.98 | -4.13 | -2.75 | -1.28 | 9.94 | |
| 6 | 25.38 | 31.14 | 22.95 | 22.44 | -1.57 | -1.11 | -0.76 | -0.21 | 2.73 | |
| 7 | 26.72 | 32.33 | 24.11 | 23.48 | -1.01 | 0.03 | -0.77 | -1.63 | 3.25 | |
| 8 | 29.80 | 35.00 | 26.77 | 25.83 | 2.29 | 2.45 | 1.39 | -0.37 | 5.03 | |
| 9 | 32.29 | 37.10 | 28.92 | 27.71 | 3.94 | 5.71 | 3.49 | 3.46 | 15.30 | |
| 10 | 33.03 | 37.73 | 29.56 | 28.27 | 4.60 | 5.80 | 3.97 | 4.11 | 16.85 | |
| 11 | 33.61 | 38.20 | 30.06 | 28.70 | 5.38 | 5.79 | 4.37 | 3.60 | 16.57 | |
| 12 | 34.98 | 39.33 | 31.24 | 29.72 | 6.07 | 7.00 | 5.44 | 6.02 | 22.61 | |
| 13 | 36.62 | 40.67 | 32.65 | 30.94 | 7.53 | 8.19 | 6.59 | 6.69 | 26.02 | |
| 14 | 39.68 | 43.11 | 35.26 | 33.19 | 10.57 | 10.39 | 9.22 | 9.01 | 34.90 | |
| 均值 | 2.69 | 2.96 | 2.29 | 2.31 | 12.80 | |||||
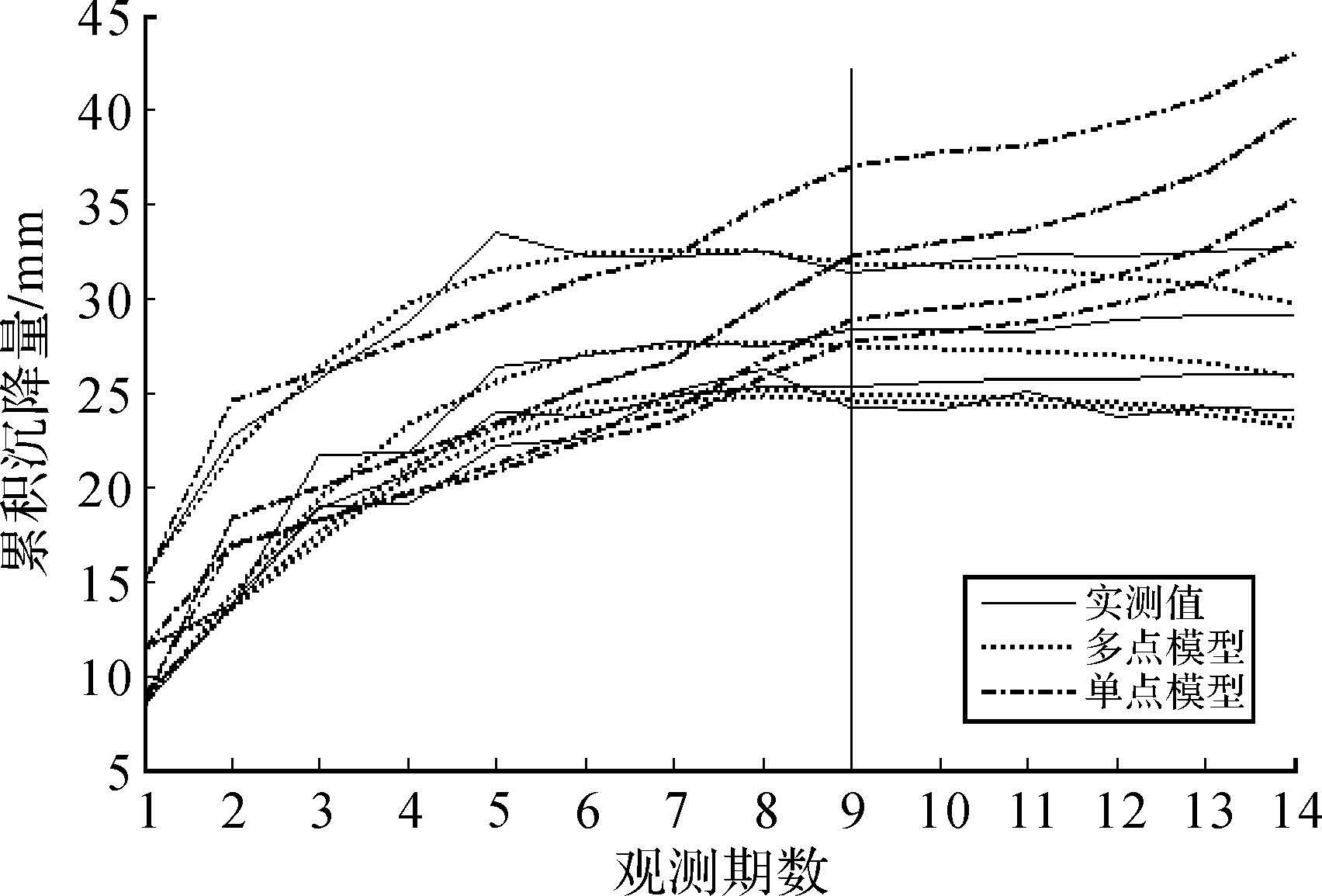
|
| 图 1 单点与多点模型的对比图 Fig. 1 Comparison between single point and multi-points modeling |
2.3 与等间距多点预测模型比较
为验证非等间距多点变形预测模型的有效性和适用性,本文对等间距多点变形预测模型也进行了对比分析,数据来源分别为文献[12]和文献[13]的等间距多点变形监测实例。由解算结果可知:①本文计算的模型参数与文献[12]基本一致,但由于文献[12]给出的是图形结果,因此可以量化比较的差异在于本文模型的模拟精度为0.22,文献[12]为0.28,其差异在于预测模型式(23)的细微差别;②本文提出的建模思路因与文献[13]在模型参数求解方式及模型预测公式上完全不同,两者对比结果略有差异,但都具有很好的预测效果。表 4给出了取自文献[13]的实测值和残差(实测值减拟合或预测值)以及本文计算的对比结果,前8期为模拟结果,后两期为预测结果,两种模型的相对误差和残差绝对值的均值由本文计算给出。
| 序号K | 实测值 | 文献[13]的残差 | ρtk /(%) | 本文计算的残差 | ρtk /(%) | |||||||||
| x1(0)(k) | x2(0)(k) | x3(0)(k) | x4(0)(k) | v1(k) | v2(k) | v3(k) | v4(k) | v1(k) | v2(k) | v3(k) | v4(k) | |||
| 1 | 4 | 6 | 6 | 4 | 0 | 0 | 0 | 0 | 0.00 | 0 | 0 | 0 | 0 | 0.00 |
| 2 | 7 | 9 | 11 | 6 | -0.18 | -0.03 | -0.30 | 0.46 | 3.32 | 0.35 | -0.01 | -0.24 | 0.38 | 3.41 |
| 3 | 10 | 14 | 21 | 11 | 0.16 | -0.41 | -0.60 | -1.49 | 5.23 | 0.49 | -0.21 | 0.42 | -0.98 | 4.32 |
| 4 | 12 | 20 | 30 | 21 | -0.44 | -1.08 | -2.00 | -0.39 | 4.40 | -0.35 | -0.04 | -0.10 | 1.65 | 2.83 |
| 5 | 15 | 25 | 37 | 25 | -0.12 | -0.65 | -0.68 | -1.07 | 2.38 | -0.14 | -0.21 | -0.50 | -0.41 | 1.19 |
| 6 | 18 | 30 | 43 | 29 | -0.30 | 0.64 | 1.02 | 0.25 | 1.76 | -0.11 | 0.47 | 0.25 | -0.69 | 1.29 |
| 7 | 22 | 33 | 47 | 33 | -0.02 | -0.87 | -0.82 | 0.34 | 1.38 | 0.52 | -0.44 | -0.01 | 0.03 | 0.95 |
| 8 | 25 | 38 | 52 | 37 | -1.03 | -0.99 | -2.32 | -0.74 | 3.30 | -0.32 | 0.59 | 0.64 | 0.78 | 1.54 |
| 9 | 30 | 43 | 58 | 41 | 0.03 | -0.35 | -0.86 | -1.06 | 1.25 | 0.46 | 1.47 | 2.06 | 1.15 | 2.82 |
| 10 | 35 | 46 | 60 | 43 | 1.61 | 0.51 | 0.91 | -0.89 | 2.32 | 1.13 | 0.62 | 0.06 | -0.52 | 1.47 |
| 均值 | 0.389 | 0.553 | 0.951 | 0.669 | 2.53 | 0.387 | 0.406 | 0.428 | 0.659 | 1.98 | ||||
2.4 缺测数据的建模与比较
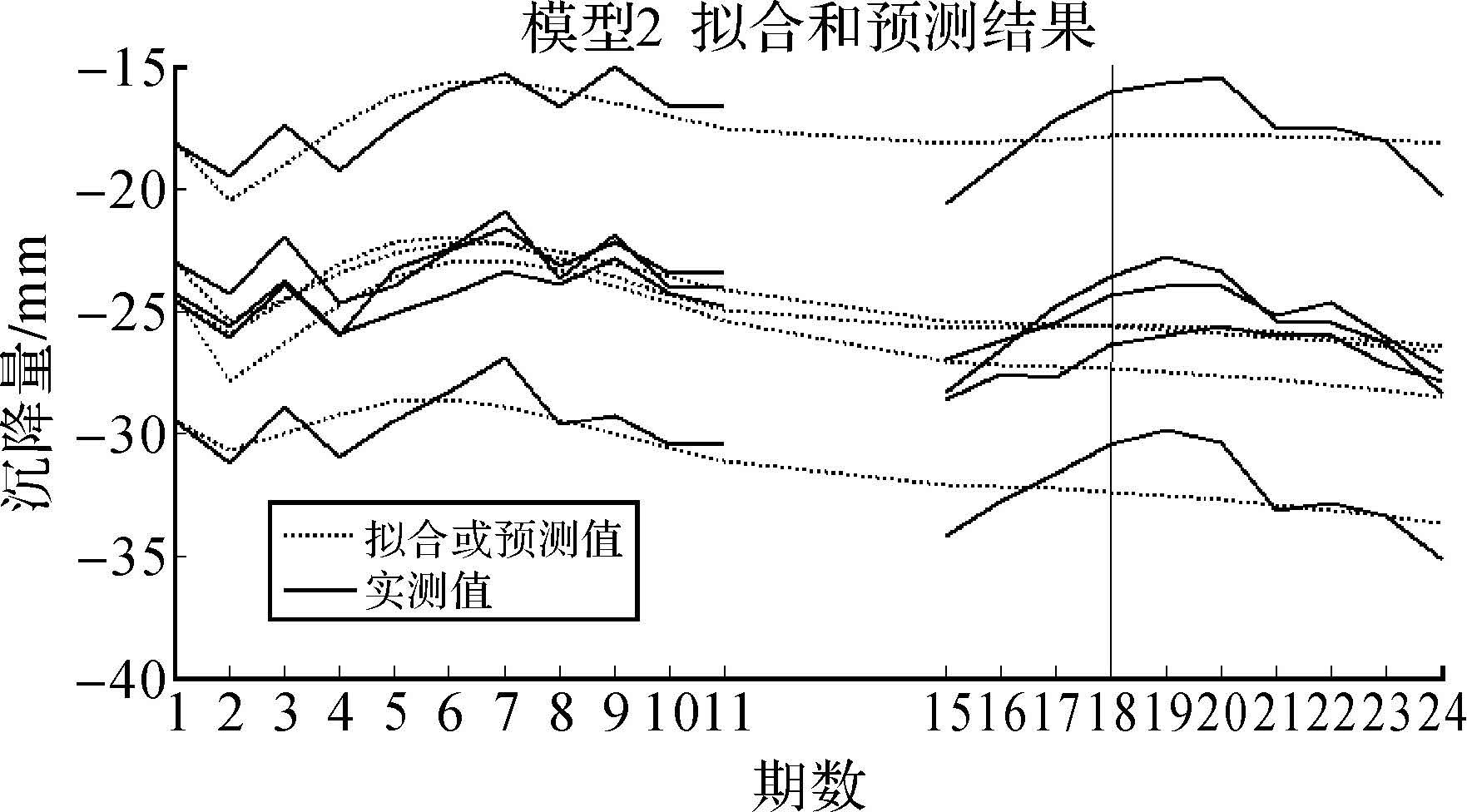
对工程建筑物进行周期性的重复观测是变形监测的基本要求,但由于多种原因可能会出现漏测或缺测的情况,导致变形观测数据为非等间距序列,对此,本文利用文献[14]所给的5个监测点共计24期等间距沉降观测资料,人为假设第9、10期缺测及第12、13、14期缺测的两种情况,如图 2、图 3实线所示为两组不同的非等间距观测序列,其中断链为数据缺测处。

|
| 图 2 模型1的拟合与预测结果 Fig. 2 Simulation and prediction results of model 1 |
|
| 图 3 模型2的拟合与预测结果 Fig. 3 Simulation and prediction results of model 2 |
利用上述非等间距多点变形模型分别对两组数据进行建模,并对后6期进行预测,图 2、图 3给出了模型的拟合和预测结果。表 5给出了取自文献[14]与利用图 2、图 3缺测数据序列计算得到的预测精度的对比结果,再次验证了非等间距多点变形预测模型的有效性和适用性。
3 结 论
由以上理论分析与实例计算可以得到以下结论。
(1) 借鉴单变量非等间距等距化的数据处理方法并加以改进,可以将等间距的多点变形预测模型拓展到非等间距的多点变形预测模型,这是一种解决非等间距观测序列多点整体建模与预测问题的有效方法。
(2) 通过实例计算与对比分析,验证了本文所提出的利用彼此关联和相互影响的多个变形监测点,所建立的非等间距多点变形预测模型不仅适用于非等间距序列的建模与预测,也适用于等间距序列的建模与预测,且优于单个点的GM(1,1)建模,是一种通用的多点整体变形预测模型。
(3) 非等间距多点变形预测模型既可针对观测时间与原定观测周期出现超前或滞后而产生的非等间距序列建模,也可直接针对缺测或漏测部分观测周期数据的非等间距序列建模,不需要对缺测数据作内插等数据预处理,具有工程实用性。
(4) 将单点单变量的变形分析拓展到空间多点的整体分析与建模,是时空变形监测分析与预测更为科学和合理的模式和方法,但需要顾及变形监测中多点观测序列的时空关联性,具有时空关联的变形监测点才能纳入整体模型建模,这将是本文后续研究探讨的内容之一。
| [1] | DENG Julong. Control Problems of Grey Systems[J]. Systems & Control Letters , 1982, 1 (5) : 288 –294. |
| [2] | 尹晖. 时空变形分析与预报的理论和方法[M]. 北京: 测绘出版社, 2002 . YIN Hui. Theory and Methodology for Temporal-spatial Deformation Analysis and Forecasting[M]. Beijing: Surveying and Mapping Press, 2002 . |
| [3] | SHEN Chunguang. Grey Models for Non-equidistant Sequence Based on Trapezoid Formula and Central Difference Quotient[J]. Journal of Grey System , 2010, 22 (1) : 17 –24. |
| [4] | WANG Qin, WEI Yong. A Kind of New Strengthening Buffer Operator Suitable for Non-equigap GM(1, 1) Model[J]. Journal of Grey System , 2009, 21 (1) : 105 –112. |
| [5] | LI Qiufeng, DANG Yaoguo, WANG Zhengxin, et al. An Extended GM(1, 1) Power Model for Non-equidistant Series[J]. Journal of Grey System , 2012, 24 (3) : 269 –274. |
| [6] | 孙虎元, 魏绪钧. 非等间隔灰色模型及应用[J]. 应用基础与工程科学学报 , 1996, 4 (4) : 407–411. SUN Huyuan, WEI Xujun. Non-equal Time-interval Grey Model and Its Application[J]. Journal of Basic Science and Engineering , 1996, 4 (4) : 407 –411. |
| [7] | 黄声享, 李志成. 工程建筑沉降预测的非等间距灰色建模[J]. 地理空间信息 , 2004, 2 (1) : 41–43. HUANG Shengxiang, LI Zhicheng. Grey Modeling of Non-equidistant Data Sepuent for Forecasting Subsidence of the Engineering Buildings[J]. Geospatial Information , 2004, 2 (1) : 41 –43. |
| [8] | 李斌, 朱健. 非等间隔灰色GM(1, 1)模型在沉降数据分析中的应用[J]. 测绘科学 , 2007, 32 (4) : 52–55. LI Bin, ZHU Jian. Application of Unequal Interval Grey Model in Analysis of Settlement Data[J]. Science of Surveying and Mapping , 2007, 32 (4) : 52 –55. |
| [9] | 戴文战, 李俊峰. 非等间距GM(1, 1)模型建模研究[J]. 系统工程理论与实践 , 2005, 26 (9) : 89–93. DAI Wenzhan, LI Junfeng. Modeling Research on Non-equidistance GM(1, 1) Model[J]. Systems Engineering-Theory & Practice , 2005, 26 (9) : 89 –93. |
| [10] | 史雪荣, 王作雷, 张正娣. 变参数非等间距GM(1, 1)模型及应用[J]. 数学的实践与认识 , 2006, 36 (6) : 216–220. SHI Xuerong, WANG Zuolei, ZHANG Zhengdi. GM(1, 1) Model with Variational Parameter for Non-equidistant Sequence and Its Application[J]. Mathematics in Practice and Theory , 2006, 36 (6) : 216 –220. |
| [11] | 姜爱平, 张启敏. 非等间距近似非齐次指数序列的灰色建模方法及其优化[J]. 系统工程理论与实践 , 2014, 34 (12) : 3199–3203. JIANG Aiping, ZHANG Qimin. Methods and Optimum of Grey Modeling for Approximation Non-homogenous and Non-equidistant Series[J]. Systems Engineering-Theory & Practice , 2014, 34 (12) : 3199 –3203. |
| [12] | 尹晖, 陈永奇, 张琰. 贫信息条件下的多点变形预测模型及其应用[J]. 测绘学报 , 1997, 26 (4) : 365–372. YIN Hui, CHEN Yongqi, ZHANG Yan. Multi-point Deformation Prediction Model with Poor Data Information and Its Application[J]. Acta Geodaetica et Cartographica Sinica , 1997, 26 (4) : 365 –372. |
| [13] | 潘国荣, 王穂辉. 多点变形动态灰色模型辨识及预测[J]. 测绘学报 , 2002, 31 (S1) : 66–69. PAN Guorong, WANG Suihui. Dynamic Grey Modelling Identification and Predication of Multi-point Deformation[J]. Acta Geodaetica et Cartographica Sinica , 2002, 31 (S1) : 66 –69. DOI:10.3321/j.issn:1001-1595.2002.z1.014 |
| [14] | 尹晖, 王尚庆. 基于灰关联聚类分析的多点时空非线性模型及其应用[J]. 武汉测绘科技大学学报 , 1998, 23 (2) : 100–104. YIN Hui, WANG Shangqing. Multi-point Spatial Nonlinear Model Based on Grey Correlation Clustering and Its Application[J]. Journal of Wuhan Technical University of Surveying and Mapping , 1998, 23 (2) : 100 –104. |
| [15] | 崔立志, 刘思峰, 吴正朋. 基于向量连分式理论的MGM(1, n)模型[J]. 系统工程 , 2008, 26 (10) : 47–51. CUI Lizhi, LIU Sifeng, WU Zhengpeng. MGM(1, n) Based on Vector Continued Fractions Theory[J]. Systems Engineering , 2008, 26 (10) : 47 –51. |
| [16] | 熊萍萍, 党耀国, 王正新. MGM(1, m)模型背景值的优化[J]. 控制与决策 , 2011, 26 (6) : 806–810. XIONG Pingping, DANG Yaoguo, WANG Zhengxin. Optimization of Background Value in MGM(1, m) Model[J]. Control and Decision , 2011, 26 (6) : 806 –810. |
| [17] | 刘寒冰, 向一鸣, 阮有兴. 背景值优化的多变量灰色模型在路基沉降预测中的应用[J]. 岩土力学 , 2013, 34 (1) : 173–181. LIU Hanbing, XIANG Yiming, RUAN Youxing. A Multivariable Grey Model Based on Background Value Optimization and Its Application to Subgrade Settlement Prediction[J]. Rock and Soil Mechanics , 2013, 34 (1) : 173 –181. |
| [18] | 夏卫国, 米传民, 刘思峰, 等. 基于初值改进的多变量MGM(1, m)模型研究[J]. 中国管理科学 , 2013, 21 (S1) : 81–85. XIA Weiguo, MI Chuanmin, LIU Sifeng, et al. The Study on the Improved Multiple Variable MGM(1, m) Model Based on Improving the Initial Value[J]. Chinese Journal of Management Science , 2013, 21 (S1) : 81 –85. |
| [19] | WANG Qijie, WANG Changcheng, XIE Rong'an, et al. An Improved SCGM(1,m) Model for Multi-point Deformation Analysis[J]. Geosciences Journal , 2014, 18 (4) : 477 –484. DOI:10.1007/s12303-014-0012-z |
| [20] | GUO Xiaojun, LIU Sifeng, WU Lifeng, et al. A Multi-variable Grey Model with A Self-memory Component and Its Application on Engineering Prediction[J]. Engineering Applications of Artificial Intelligence , 2015, 42 : 82 –93. DOI:10.1016/j.engappai.2015.03.014 |
| [21] | 李晓蕾, 刘睿, 田永瑞, 等. 基于灰色预测的空间多点残差修正模型研究[J]. 大地测量与地球动力学 , 2010, 30 (5) : 125–128. LI Xiaolei, LIU Rui, TIAN Yongrui, et al. Study on Spatial Multi-point Residual Model Based on Grey Prediction[J]. Journal of Geodesy and Geodynamics , 2010, 30 (5) : 125 –128. |