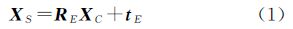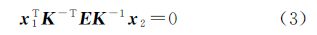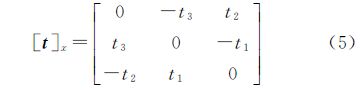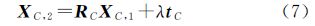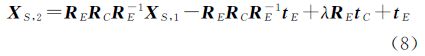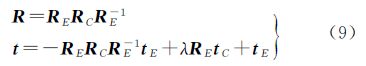近年来随着地面激光扫描技术的日益进步,获取任意物体或区域的空间数据即三维点云变得越来越容易。为了获得一个物体或区域的完整覆盖,必须用激光扫描设备从不同扫描站点对其进行扫描。然而不同站点的点云数据都处于各自独立的坐标系,因此还需将它们进一步整合到同一坐标系,也就是进行三维点云的拼接。点云拼接是点云处理流程中的重要步骤,拼接的精度与速度也会直接影响整个点云处理的效果与效率[1]。
点云拼接算法是通过寻找不同点云间的同名特征来计算它们之间的变换矩阵,然后将点云拼接在同一坐标系下的。目前普遍使用的点云拼接算法为文献[2]提出的ICP(iterated closest point)算法,它选取最近点作为同名点来估计变换矩阵,并用同名点间的距离建立目标函数,然后通过迭代方式使建立的目标函数收敛到最小值,完成点云的精细拼接。对于包含海量数据的扫描点云数据,ICP算法计算复杂度通常较高以致运算时间较长。此外在很多情况下它总会收敛到局部最优值从而得到错误拼接结果。为了提高ICP算法的收敛速度与稳健性,很多学者对其进行了改进,如设计不同的策略选取最近点[3, 4],或构建不同的目标函数[5],但是这些改进算法仍不能处理两个点云变换过大,尤其是旋转变换很大的情况。因此ICP算法通常需要其他寻找同名点的方法提供一个粗略的拼接结果,如4PCS[6],RANSAC-Based DARCES[7],基于特定标靶的方法[8]等,这些粗拼接算法在对大数据点云处理时也需耗费较长时间。
现有的地面激光扫描仪通常会配有同轴的红外或可见光相机,其拍摄的扫描场景图像可为点云拼接提供辅助信息。文献[9—10]即利用扫描设备形成的反射强度柱状全景图像对点云进行拼接,其中使用了SIFT算子[11, 12]检测图像特征点,但由于柱状全景图改变了图像结构,使用SIFT算子并不能得到很好的拼接效果。文献[13]提出了一种基于共线方程的改进丹麦法选权迭代法,可实现任意角度光学影像和点云的精确配准。文献[14]先由已知的控制点获得可见光图像中二维点与点云中三维点的对应关系,然后通过检测图像中对应特征点直接找到三维点云中的同名点从而完成点云拼接。文献[15]也是通过图像信息获得相机的相对旋转变换,但它仍旧需要先对相机和激光扫描设备坐标系之间的关系进行标定,才能获得点云间的旋转平移变换从而将点云进行拼接。
本文针对带有同轴相机的激光扫描设备,在ICP算法的基础上,提出了一种结合图像信息的快速点云拼接算法。不同于以往拼接算法需要同时计算点云间的旋转和平移变换,本文对这两种变换分别进行求解:即首先对同轴相机在不同扫描站点拍摄的图像进行特征提取和匹配,然后利用视觉几何中的本质矩阵计算出相机在不同扫描站点间的相对旋转变换。由于同轴相机坐标系与扫描仪坐标系之间的变换是已知的,所以从相机的相对旋转变换可以直接得到扫描仪的相对旋转变换,即扫描点云间的旋转变换。对于点云间平移变换的求解,本文提出一种改进的ICP算法。该算法在迭代过程中仅需更新平移变换中的3个变量,而不是如传统ICP算法同时更新迭代旋转和平移6个变量,所以此算法降低了迭代过程中的计算复杂度,加快了收敛速度,同时也减小了收敛到错误局部最优值的可能性。
1 地面激光扫描仪与同轴相机现有的地面激光扫描仪通常都配备有一个同轴的可见光相机,它可以在扫描仪采集三维点云的同时对该场景进行拍摄。一般情况下,同轴相机与激光扫描仪坐标系之间存在固定的变换关系,而同轴相机在不同扫描站点拍摄的图像之间也包含着相机在不同扫描站点之间的变换关系。
1.1 激光扫描仪坐标系与同轴相机坐标系激光扫描仪坐标系可记为OS-xSySzS,相机坐标系可记为OC-xCyCzC。当相机固定于扫描仪之上时,这两个坐标系之间存在固定的刚性变换关系,可以表示为旋转变换RE和平移变换tE,这个刚性变换可通过基于标定物的标定方法[15]求解。对于空间中任一点,它在两个坐标系下的坐标分别用XS和XC表示,则
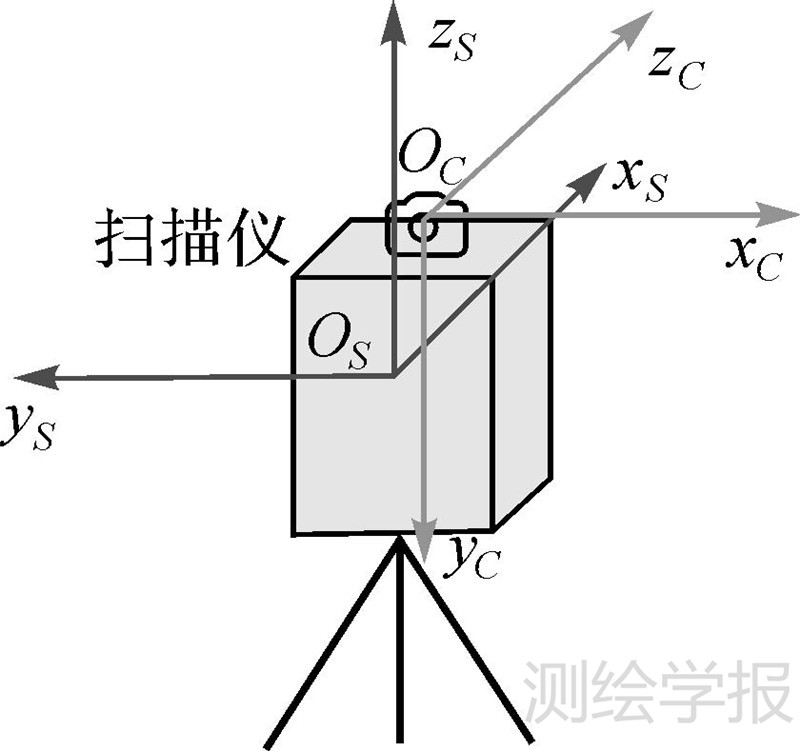
现有地面激光扫描仪配备的相机都与激光扫描仪同轴放置,如图 1所示,此时扫描仪坐标系与其同轴相机坐标系中的 xS轴与zC轴,yS轴与xC轴,zS轴与yC轴分别互相平行。针对这种情况,无须通过标定就能推导出同轴相机坐标系到扫描仪坐标系的旋转变换RE为
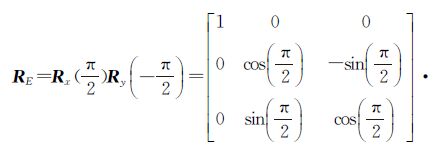
|
| 图 1 扫描仪坐标系与相机坐标系相互关系 Fig. 1 Relationship between the coordinates systems of the scanner and the camera |
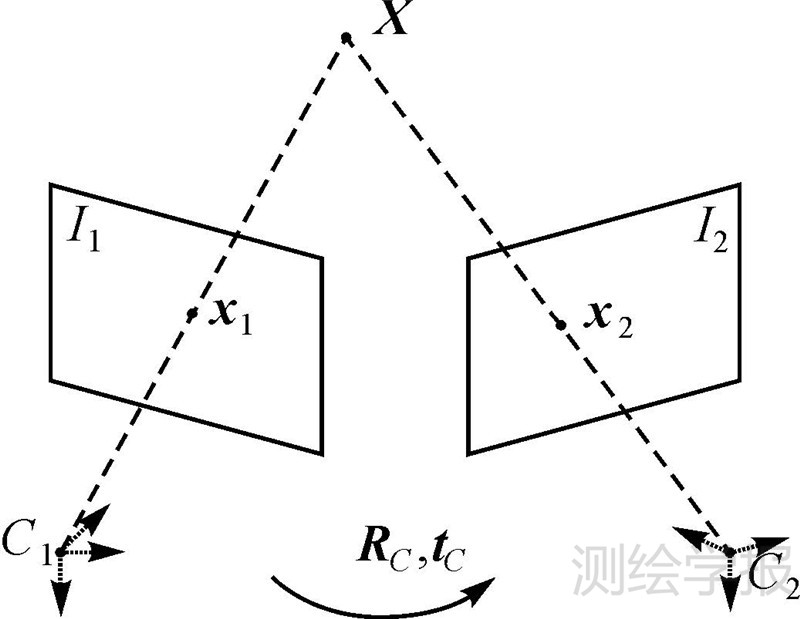
如图 2所示,图像I1与I2为同一相机在C1、C2两个位置对同一场景拍摄得到的图像,x1、x2分别为空间点X在I1与I2上的投影,被称为一对对应点。假设相机由C1位置运动到C2位置的相对旋转、平移变换分别为RC、tC,则由对极几何[16]可知
式中,K为相机内参数矩阵,其表达形式为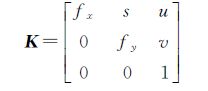
|
| 图 2 图像恢复运动 Fig. 2 Motion from images |
因此,在事先对相机进行标定获得相机的内参数矩阵K后,图像间的本质矩阵E[17, 18]可以通过图像间的若干对应点由式(3)计算出,而E被分解为如式(4)的形式[16]后,即得到相机在两个位置间的相对变换RC、tC。但是由于E具有齐次性,从它分解得到的平移向量tC与真实的平移向量存在着尺度变换,所以本质矩阵只能提供两个位置的准确相对旋转变换RC。
2 快速点云拼接算法ICP算法是使用非常广泛的点云拼接算法,计算复杂度高,运算时间长,并且在很多情况下都不能收敛到正确的拼接结果。考虑到扫描仪配有的同轴相机所拍摄的图像可以提供关于扫描点云之间的辅助信息,本文在ICP算法的基础上,提出一种结合图像信息的快速点云配准方法。
2.1 图像信息获取旋转变换R设XS,1和XS,2为扫描仪在两个位置获得两个点云中的对应点坐标,XC,1和XC,2分别为XS,1和XS,2在相应同轴相机坐标系下的坐标,则
由2.2节可知,通过同轴相机拍摄图像间的本质矩阵,可以获得同轴相机在两个不同位置的相对旋转和平移变换RC、λtC,即
由式(6)、(7)可得
因此扫描仪在两个扫描站点获得的点云间旋转平移变换分别为 式中,RE为已知;RC可由图像信息计算得到,所以通过式(9)可以计算出在两个扫描站点获得的点云间旋转变换R。然而对于点云间的平移向量t,由于λ和tE无法确定,所以它并不能从图像信息中得到。一般情况下,若图像之间含有较大的对应部分,则现有的图像特征点检测匹配算法,如SIFT算法[11, 12],可以自动且快速地获得它们之间的匹配特征点,并可达到亚像素精度。此外,由文献[18]可知在宽基线及大景深的情况下,从图像信息获得相机的相对旋转变换误差仅在0.02°左右。因此,由图像信息获取旋转变换的准确度十分高且可以自动处理。 2.2 改进ICP算法由2.1节可知,从同轴相机拍摄的图像可以直接获得相应待拼接点云间的旋转变换,将其代入待拼接的点云,即可获得去除旋转变换后的两个点云,此时只需使用ICP算法对这两个点云间的平移变换进行求解。在本文中,为了快速获得点云间平移向量,本文对传统ICP算法进行了改进,即对迭代过程进行约束,使其仅对平移向量进行计算并更新。
已知源点云数据集为P,目标点云数据集为Q,它们之间只包含平移变换。k表示迭代次数,Pk为P经过第k次更新后的数据集,Dk为第k次迭代时Pk中的每一点在Q中寻找到的对应最近点所形成的点集,tk为第k次迭代计算出的平移向量,dk代表第k次迭代的估计误差。改进ICP算法的具体步骤描述如下:
(1) 初始化。令P0=RP,R=I,t0=0,k =0。I为3×3的单位阵,这是认为两个待拼接点云之间无旋转变换;0为3×1的零向量。
(2) 计算最近点集。计算数据点集Pk在Q中对应的最近点集Dk,其中Pk={Pk,1,Pk,2,…,Pk,N},Dk={Dk,1,Dk,2,…,Dk,N}。
(3) 计算平移向量tk和估计误差dk
式中,Pk和Dk分别为点集Pk和Dk的质心,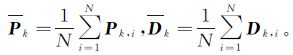
(4) 更新源数据集。使用tk对数据集Pk进行更新,有
(5) 重复迭代。当两次迭代间的估计误差变化小于某一阈值δ,即dk-dk+1<δ时,停止迭代过程。
在传统ICP算法中,进行迭代更新的变量为旋转矩阵和平移向量含有的6个未知量,计算复杂度相对较高,且其中主要的运算量都集中于旋转矩阵的计算[19, 20]。而上述的改进ICP算法只对平移向量t的3个变量进行迭代计算,因此算法计算复杂度降低且运算量大量减少,从而减少了运算时间并加快了收敛速度。此外由于所求未知量的减少,也降低了算法收敛到错误局部最优值的可能性。
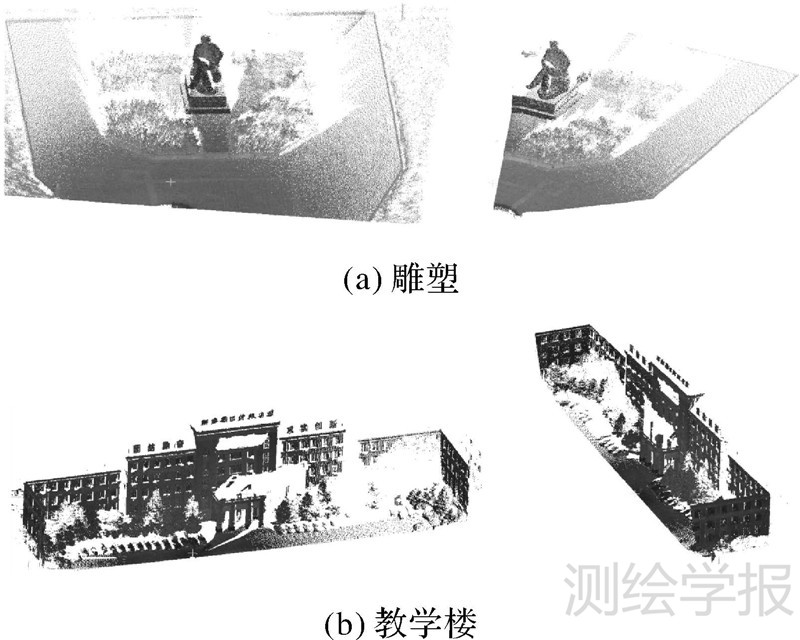
3 试验结果与分析使用真实点云数据对本文拼接算法进行了试验。真实点云数据如图 3所示,其中图 3(a)为用激光扫描仪在两个扫描站点对某雕塑采集的数据,图中点云分别包含10.6万和4.8万个点;图 3(b)为在某教学楼前两个扫描对教学楼采集的数据,图中点云分别包含254.6万和176.2万个点。在每个扫描站点,相机都会在整个扫描设备处于稳定状态时对扫描场景进行拍摄。本试验用相机单幅图像分辨率为3588×2368像素,水平视场角为73°,垂直视场角为53°。因此其水平及垂直角度分辨率分别可达0.020 3°及0.022 4°。该相机已事先进行了标定,其内参数矩阵为

|
| 图 3 点云数据 Fig. 3 Original point clouds |
在实际情况下,相机拍摄的图像都存在一定的畸变,畸变图像中对应点之间并不严格满足式(3)的关系。但是在对相机标定时,相机的畸变参数已经测得,所以拍摄图像首先按照畸变参数进行了去畸变处理,然后再在图中寻找特征点并匹配。图 4和图 5分别为扫描仪在采集图 3(a)和(b)中数据时相机拍摄的图像,并且已去除了图像畸变,图中检测到的匹配点已由黑线所连接。其中,图 4雕塑图片由SIFT算法进行特征点提取匹配,对图片的处理时间为5.3 s,并得到144对匹配特征点。由于两幅图视角相差太大,所以匹配点对中有一定的错误率。图 5教学楼图片由于拍摄照片的视角旋转角度过大且图像对应部分较小,SIFT算法不能有效地检测出匹配点,所以试验中采用Harris算法检测角点并手动配准,共获得10对匹配特征点,这两幅图片的处理有人工参与,但耗时也不超过10 s。

|
| 图 4 雕塑图像的匹配特征点 Fig. 4 Matched correspondences between the statue images |

|
| 图 5 教学楼图像的匹配特征点 Fig. 5 Matched correspondences between the teaching building images |
图 6(a)和图 7(a)分别显示了两组点云数据用计算得到的旋转矩阵对点云进行变换后的顶视图及前视图。从图中可以看出,两个点云之间几乎不再存在旋转变换。这说明本文提出的通过图像信息获得点云旋转变换的方法稳健性很强,即使在提取匹配点对有一定错误率或匹配点对很少的情况下,依然可以获得准确的旋转变换。然后使用本文改进的ICP算法分别对图 6(a)和图 7(a)中的两个点云数据进行迭代配准,最终拼接结果如图 6(b)、图 7(b)所示,其相应的拼接中误差分别为5.01 cm与5.26 cm。为了更加清楚地显示本文算法的拼接结果,图 6(c)和图 7(c)分别显示了图 6(b)和图 7(b)拼接结果的局部放大图,从图中可以看出两个点云很好地拼接在一起,验证了本文算法的可行性。

|
| 图 6 雕塑数据拼接结果 Fig. 6 Registration results of the statue |

|
| 图 7 教学楼数据拼接结果 Fig. 7 Registration results of the teaching building |
为了对比本文拼接算法与传统ICP算法的性能,本文也将两组点云用传统ICP算法进行拼接。图 8(a)、(b)中分别显示了用传统ICP算法将原始雕塑点云(图 3(a))以及去除旋转变换后的两个雕塑点云(图 6(a))进行拼接的结果。可以看到,对于这两组待拼接点云,传统ICP算法都没有把它们很好地拼接。这是由于这两个点云重叠部分较小,且重叠部分的数据点大多位于一个平面上,所以很容易落入局部的最优值。

|
| 图 8 雕塑数据的传统ICP算法拼接结果 Fig. 8 Registration results of the statue by traditional ICP algorithm |
对于教学楼点云数据,它们的重叠部分很大,但是每个点云中都有部分由于树木的遮挡以及建筑物的自遮挡产生了数据缺失。因此为了获得教学楼的完整三维点云数据,这两个点云的拼接也是十分必要的。同样,传统ICP算法也对原始主楼点云数据(图 3(b)),以及去除旋转变换后的两个主楼点云数据(图 7(a))进行拼接,它们几乎都收敛到图 7(b)的拼接结果。这证明了当配准点云重叠部分较大时,本文提出的拼接算法和传统ICP算法都能收敛到全局最优值。
表 1分别列举了传统ICP算法对教学楼原始点云数据、去除旋转变换后点云数据,以及改进ICP算法对去除旋转变换后点云数据进行拼接时算法迭代次数、运算时间及拼接中误差。从拼接精度上来看,3组拼接结果的中误差相差无几,都在5 cm左右,这证明了本文算法的精度可以达到ICP 算法的精度。由算法分析可知,从图像中获取点云相对旋转变换具有相当高的精度,因此可以认为本文算法系统误差主要存在于改进的ICP算法中。在迭代次数及运算时间上,本文改进的ICP算法是最少的,其次是传统ICP算法对去除旋转变换后点云数据的处理。这一方面证明了由图像信息获得的旋转变换给传统ICP算法提供了很好的初值以致其收敛速度及运算时间都有所降低,另一方面也证明了本文改进的ICP算法可以大幅提高算法的收敛速度并降低运算时间。考虑到当同轴相机拍摄的图像之间有较大对应部分时,利用图像信息计算扫描点云间的旋转变换仅需5 s左右时间,与后续改进ICP算法迭代过程相比可忽略不计,因此本文提出的结合图像信息ICP点云拼接算法可以有效地提高点云拼接效率。在实际应用中,三维场景是多种多样的,尚需要加大试验量,以验证该方法的应用有效性。
| 点云拼接算法 | 迭代次数 | 运算时间/s | 拼接结果 | 中误差/m |
| 传统ICP(图 2点云) | 255 | 519.89 | 正确 | 0.052 2 |
| 传统ICP(图 6(a)点云) | 205 | 342.46 | 正确 | 0.051 0 |
| 改进ICP(图 6(a)点云) | 168 | 256.04 | 正确 | 0.052 6 |
本文针对带有同轴相机的三维激光扫描设备,提出了一种结合图像信息的快速点云拼接算法。本算法适用于可以拍到清晰可见光图像的情景下,并且要求两个站点拍摄的可见光图像必须有对应重叠部分。在图像信息有一半以上重叠时,此方法可以自动进行;否则,图像的视角差异大会导致特征点匹配算法无法自动提供准确匹配点,此时该方法还需人工干预。与传统ICP拼接算法相比,本文算法减少了迭代过程求解的未知量个数,降低了迭代算法的计算复杂度以及收敛到局部最优解的可能性,从而使得拼接效率大幅提高。最后文中两组地面激光点云数据的拼接试验表明本方法可以更稳健且更快速地对点云进行拼接。
| [1] | 浦石, 李京伟, 郭四清. 融合语义特征与GPS位置的地面激光点云拼接方法[J]. 测绘学报, 2014, 43(5): 545-550. PU Shi, LI Jingwei, GUO Siqing. Registration of Terrestrial Laser Point Clouds by Fusing Semantic Features and GPS Positions[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(5): 545-550. |
| [2] | BESL P J, MCKAY N D.A Method for Registration of 3-D Shapes[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1992, 14(2): 239-256. |
| [3] | BLAIS G, LEVINE M D. Registering Multiview Range Data to Create 3D Computer Objects[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1995, 17(8): 820-824. |
| [4] | RUSINKIEWICZ S, LEVOY M. Efficient Variants of the ICP Algorithm[C]//Proceedings of the 3rd International Conference on 3-D Digital Imaging and Modeling. Quebec City: IEEE, 2001: 145-152. |
| [5] | BAE K H, LICHT D D. A Method for Automated Registration of Unorganised Point Clouds[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2008, 63(1): 36-54. |
| [6] | AIGER D, MITRA N J, COHEN-OR D. 4-Points Congruent Sets for Robust Pairwise Surface Registration[J]. ACM Transactions on Graphics, 2008, 27(3): 85. |
| [7] | CHEN C S, HUNG Y P, CHENG J B. RANSAC-based DARCES: A New Approach to Fast Automatic Registration of Partially Overlapping Range Images[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1999, 21(11): 1229-1234. |
| [8] | 姚吉利, 马宁, 贾象阳, 等. 光束法区域网平差的地面激光扫描多站点云自动定向方法[J]. 测绘学报, 2014, 43(7): 711-716, 723. YAO Jili, MA Ning, JIA Xiangyang, et al. Auto-registration for Terrestrial Laser Scanning Multi-stations Point Clouds with Bundle Block Adjustment Method[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(7): 711-716, 723. |
| [9] | KANG Zhizhong, LI J, ZHANG Liqiang, et al. Automatic Registration of Terrestrial Laser Scanning Point Clouds Using Panoramic Reflectance Images[J]. Sensors, 2009, 9(4): 2621-2646. |
| [10] | WEINMANN M, JUTZI B. Fully Automatic Image-based Registration of Unorganized TLS Data[J]. International Archives Photogrammetry, Remote Sensing and Spatial Information Sciences, 2011, 38(5/W12): 55-60. |
| [11] | LOWE D G. Distinctive Image Features from Scale-invariant Keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91-110. |
| [12] | 杨化超, 姚国标, 王永波. 基于SIFT的宽基线立体影像密集匹配[J]. 测绘学报, 2011, 40(5): 537-543. YANG Huachao, YAO Guobiao, WANG Yongbo. Dense Matching for Wide Base-line Stereo Images Based on SIFT[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(5): 537-543. |
| [13] | 王晏民, 胡春梅. 一种地面激光雷达点云与纹理影像稳健配准方法[J]. 测绘学报, 2012, 41(2): 266-272. WANG Yanmin, HU Chunmei. A Robust Registration Method for Terrestrial LiDAR Point Clouds and Texture Image[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(2): 266-272. |
| [14] | HAN J Y, PERNG N H, CHEN Huangjie. LIDAR Point Cloud Registration by Image Detection Technique[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(4): 746-750. |
| [15] | AL-MANASIR K, FRASER C S. Registration of Terrestrial Laser Scanner Data Using Imagery[J]. The Photogrammetric Record, 2006, 21(115): 255-268. |
| [16] | HARTLEY R, ZISSERMAN A. Multiple View Geometry in Computer Vision[M]. Cambridge: Cambridge University Press, 2003. |
| [17] | HARTLEY R. In Defense of the Eight-point Algorithm[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1997, 19(6): 580-593. |
| [18] | NISTER D. An Efficient Solution to the Five-point Relative Pose Problem[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2004, 26(6): 756-770. |
| [19] | HORN B K P. Closed-form Solution of Absolute Orientation Using Unit Quaternions[J]. Journal of the Optical Society of America A, 1987, 4(4): 629-642. |
| [20] | ARUN K S, HUANG T S, BLOSTEIN S D. Least-squares Fitting of Two 3-D Point Sets[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1987, 9(5): 698-700. |