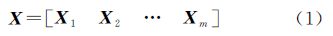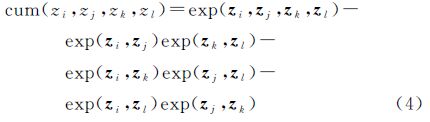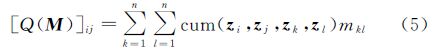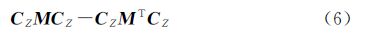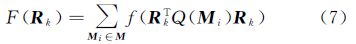2. 武汉大学测绘学院, 湖北 武汉 430079;
3. 国家测绘地理信息局卫星测绘应用中心, 北京 101300
2. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China;
3. Satellite Surveying and Mapping Application Center, NASG, Beijing 101300, China
提取大尺度范围的水储量变化信息,对于了解区域水循环和提高水资源的利用效率是非常有用的。通过GRACE卫星提供的数据可以监测全球范围陆地水储量的变化,而对GRACE得到的陆地水储量变化信息进行准确的估计和分析,还需要一个合适的信号分离过程[1]。
目前,有多种方法可以从多维数据中提取特征模式,其中大多数是通过选择几个方差较大的成分来降低数据的维数。在这些方法中,经验正交函数(empirical orthogonal function,EOF)及其扩展方法,如旋转EOF(REOF)和复合EOF(CEOF)等特征空间法,应用已经非常广泛[2, 3, 4, 5]。但是,上述方法只用到了协方差矩阵或相关系数矩阵的二阶矩,而忽略了观测数据概率分布函数的高阶矩中所包含的信息。另外,由于EOF分析过程中的不相关和正交性假设,其给出的信号成分解释不一定很合理[6]。
为了从概率分布函数中获取更多信息,文献[7]建议在EOF方法中加入高阶统计矩,这就是独立成分分析(independent component analysis,ICA)方法的由来。ICA最初是为解决盲源分离问题而提出的一种信号处理方法,该方法在没有源信号先验信息的条件下,利用信号的高阶统计信息,按照统计独立的原则将观测信号分解成多个独立成分,或表示为独立成分的线性组合。ICA是一种非常有效的统计方法,它在生物医学领域、语音信号处理、图像特征提取和无线电通信等领域已经得到了广泛应用[8, 9]。近年来,ICA在地学领域也取得了很好的成果,如地震数据的分离识别、GPS多路径误差的消除和GRACE卫星数据的处理等[10, 11, 12]。
本文以青藏高原及其周边地区(20 °N—40 °N,70 °E—100 °E)为例,说明在源信号及其混合方式未知的情况下,假设各个源信号成分相互独立且满足非高斯分布,采用ICA方法能够解决较为复杂的信号分离问题,即从GRACE反演得到的水储量变化中获取有意义的物理信息。为验证结果的可靠性,分别对该区域的GRACE水储量变化和水文模型数据进行分解,结果表明从GRACE水储量变化和水文模型数据中分离的信号具有高度的一致性,而且ICA分解得到的各个成分具有统计意义上的独立性。
1 数 据 1.1 GRACE卫星数据2002年3月欧空局(European Space Agency,ESA)发射的GRACE卫星,是首颗可直接应用于地表质量变化研究的重力卫星。由两颗卫星之间的距离变化可以确定地球重力场的变化,进而反演得到相应的陆地水储量变化信息。在这方面已经有了许多研究成果,如利用GRACE卫星重力测量确认格陵兰冰盖在加速融化和探测南极冰盖的质量变化[13],利用GRACE位模型研究全球陆地水储量变化以及利用GRACE卫星监测长江流域和黑河流域的水储量变化等[14, 15, 16]。
采用美国空间研究中心(Center for Space Research,CSR)提供的2003年1月到2013年12月间的GRACE RL05月重力场模型数据,最大阶数为60。因为GRACE重力位模型在处理的过程中已经扣除了潮汐、大气和海洋的影响,所以除了计算误差和模型误差外,GRACE时变重力场在陆地区域反映的主要是水储量变化信息。在计算过程中,首先从月重力场模型中扣除了132个月的平均值,GRACE重力场模型中的项用卫星激光测距(satellite laser ranging,SLR)观测得到的数据进行了替换。经过冰川均衡调整改正(glacial isostatic adjustment correction,GIA)、去相关和高斯滤波(滤波半径350km)[17, 18, 19, 20],得到GRACE反演的陆地水储量变化时间序列信息。为确定合理的空间采样,利用残差系数解算成1°×1°的水储量变化格网值。
1.2 水文模型数据全球陆面数据同化系统(Global Land Data Assimilation System,GLDAS)由美国宇航局哥达德地球科学数据和信息服务中心(Goddard Earth Sciences Data and Information Services Center,GESDISC)和美国国家环境预报中心(National Centers for Environmental Prediction,NCEP)共同建立,采用了NOAH、VIC和CLM等多种地表模型,以空间观测系统提供的全球降雨观测值和太阳辐射等多种水文气象数据作为输入参数,获取了不同地表模型下的各项参数。本文采用基于NOAH地面模型的GLDAS水文模型,通过该模型中的土壤湿度和积雪变化等参数综合描述的陆地水储量变化可用于GRACE反演水储量变化信息的验证等[21]。采用与GRACE相同滤波方法处理后的NOAH 1°×1°空间分辨率的格网数据,时间范围从2003年1月至2013年12月。
WGHM水文模型(water GAP global hydrology model,WGHM)采用重要的水文过程概念公式来模拟大陆水循环,其最初是在Dll等研究大陆水资源的可利用性基础上发展起来的。该模型对包含土壤湿度、积雪变化和地下水等水质量变化进行了估计,它对认识全球水储量变化及其动态的水文分析过程有着非常重要的意义[22],WGHM水文模型已经多次用于陆地水储量变化与GRACE反演水储量变化的比较[23]。采用与GRACE相同滤波方法处理后的WGHM 1°×1°格网数据,由于数据获取有限,故在本文中,收集到的数据时间范围为2003年1月至2012年4月。
2 ICA方法简介假设利用n个月的重力场模型获取了m个水储量变化的格网值,则可以将格网值的时间序列表示成矩阵X,使X中的一行对应于某个月的所有水储量变化值
式中,Xi为第i列,表示第i个格网点上对应于不同时间的观测值,即Xi=[x1i…xni]T(i=1,…,m)。矩阵X的EOF分解可以表示成 式中,P由X的主要成分组成;E由X的特征向量组成(EET=I)。由于特征值和特征向量表示时间序列的重要特征,在求解的过程中将特征向量归一化为单位向量,然后再对特征值进行排序,并与特征向量相对应。ICA方法能够将上述EOF分解得到的主要成分或特征向量变换成尽可能独立的部分,其表达式为
式中,A称为混合矩阵;S为源信号;R表示正交旋转矩阵(RRT=I),k是选取的主要成分或特征向量的数量。旋转矩阵R采用文献[24]提出的特征矩阵联合近似对角化(joint approximate diagonalization of eigenmatrices,JADE)方法求出,具体的计算过程如下文。假设用Z表示EOF分解得到的矩阵P或E,其列向量zi、zj、zk、zl(1≤i,j,k,l≤n)的均值都为零,那么Z的四阶累积量可以表示成
设M为任一n×n阶矩阵,可以定义一个n×n阶的四阶累积量矩阵Q(M),其第(i,j)个元素为
式中,mkl为矩阵M的第(k,l)个元素。由于Z是中心化的,因此可以得到 式中,CZ是Z的协方差矩阵,tr表示矩阵的迹。根据Cardoso(1999)所述,能够找到这样一个正交归一化矩阵R,其可以使得所有的四阶累积量矩阵Q(M)进行近似对角化。用式(6)可以估计出EOF分解得到的Pk或Ek的累积量矩阵Q(M)。定义如下函数
式中,函数f表示求矩阵非对角元素的平方和。通过Rk约束下的平面旋转对累积量矩阵Q(M)进行优化,当式(7)中的非对角元素平方和最小时,即得到了最优解。最后,采用旋转主要时间成分的ICA方法计算出独立成分(Sk=PkRk),然后将数据投影得到相应的空间模式(Ak=XTSk)。本文中,采用ICA方法分析水储量变化主要分为两步。首先,用EOF分解水储量变化数据获取主要正交模式,按降序排列;然后根据相关准则,求出式(3)中的旋转矩阵Rk,并对主要时间成分进行旋转。观测数据可以分解成独立的时间序列和空间序列的混合,通过旋转的时间成分就可以求出对应的空间模式。
3 水储量变化分析结果 3.1 GRACE反演得到的水储量变化信息以青藏高原及其周边地区作为研究区域,对GRACE反演的水储量变化数据进行分析。首先,将数据按要求进行排列,然后计算其峰度exp(X4)/exp(X2)2-3(exp是期望算子)。计算结果显示,峰度绝对值大于0.5的数据有62.7%,因此认为采用的数据符合非高斯分布。
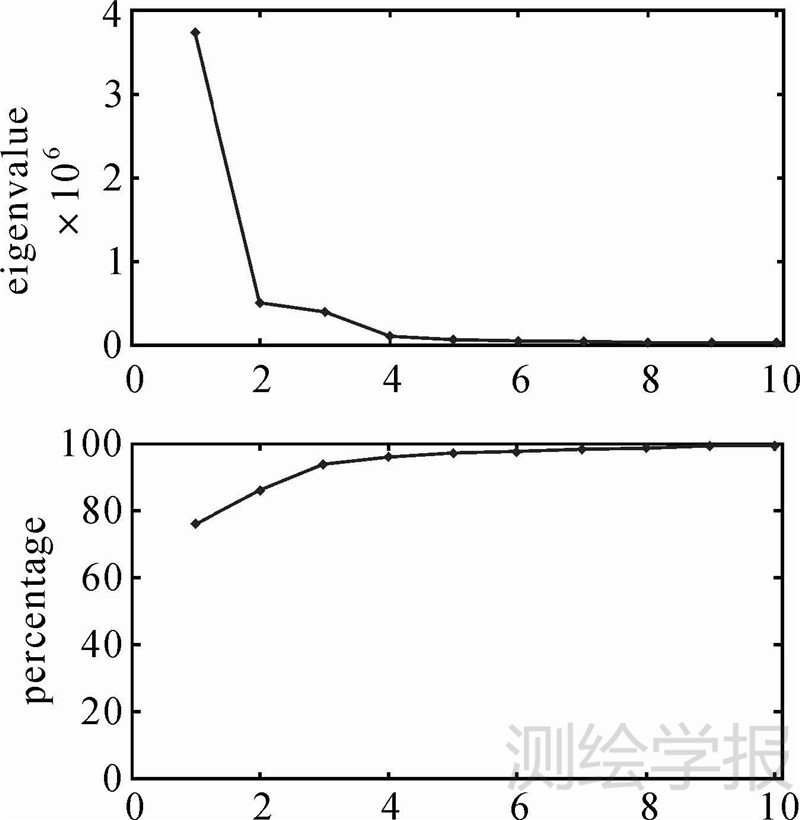
从中心化的数据计算自协方差矩阵,再用特征值分解法将自协方差矩阵对角化,计算的前10个特征值如图 1所示(由大到小排列)。结果显示,第1特征值占总能量的75.9%,远大于其他的特征值;第2、第3和第4特征值分别占总能量的10.0%、7.8%和2.1%。前4个特征分量含有水储量变化95.8%左右的能量,因此可以不考虑后面的特征值。
|
| 图 1 GRACE反演水储量变化的特征值频谱分布 Fig. 1 Spectrum distribution of eigenvalues from GRACE-derived water storage changes |
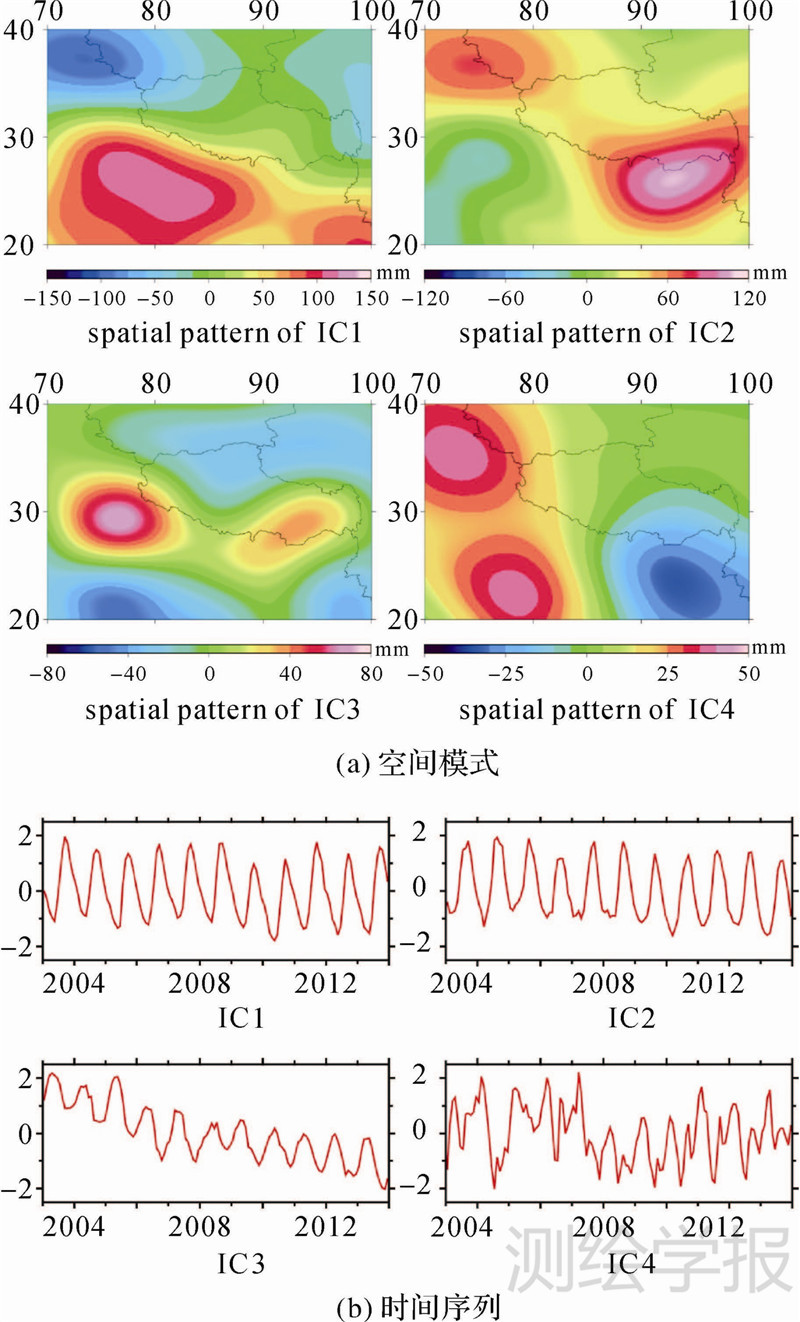
假设GRACE反演水储量变化的信号成分之间是相互独立的,对青藏高原地区GRACE反演的陆地水储量变化进行ICA分析,结果如图 2所示,各个时间序列按方差由大到小排列。
|
| 图 2 ICA分解GRACE反演132个月水储量变化得到的(a)空间模式和(b)时间序列 Fig. 2 Spatial pattern (a) and time series (b) by ICA analysis using 132 months GRACE-derived water storage changes |
图 2中的时间成分采用标准差进行归一化处理,其对应的空间模式也进行了相应调整,单位为毫米。在空间模式图中,颜色为正的区域表示该区域的水储量变化与时间序列的变化一致,而颜色为负的区域表示该区域的水储量变化与时间序列的变化相反。用空间模式乘以对应的时间序列,可以得到该区域水储量变化的具体值。
由图 2可以看出,第1、第2成分(IC1、IC2)都显示了较强的年周期信号,第3成分(IC3)显示的是年周期信号和长期趋势信号的混合,而第4成分(IC4)中则含有年周期和半年周期信号。此外,IC1和IC2表示的年周期信号在喜马拉雅山以南的地区较为明显,而在喜马拉雅山以北的地区年周期信号则相对较弱,这可能与降水量的周年变化有关。从IC3中的长期变化趋势可以看出,在2003年1月至2013年12月期间,青藏高原西部和南部地区的水储量在减少,可能与冰川消退和积雪融化有关;而青藏高原中部地区的水储量有所增加,这应该与高原湖泊的面积增大有关。文献[25]等利用GRACE和ICESat的卫星数据研究发现,自2003年以来,青藏高原中部的青海湖和纳木错等主要湖泊的面积在增加,这与近十年该区域降雨量增多、湖泊蒸发量减少以及积雪融化加快等因素有关[25]。
4 与水文模型的比较由于水文过程的复杂性、水文资料误差和水文模型结构误差等因素的存在,水文模型具有明显的非高斯性,通过计算得出,68.7%的NOAH数据的峰度绝对值大于0.5,71.4%的WGHM数据的峰度绝对值大于0.5,因此水文模型具有明显的非高斯分布特征。GRACE反演的水储量变化信息、NOAH和WGHM水文模型每个格网点时间序列的均方根如图 3(a)—(c)所示,采用12点加权滑动平均该区域格网点数值(去除季节性变化的影响)的结果如图 3(d)—(f)所示。由图 3可以看出,该地区的水储量变化呈现明显的年周期性。GRACE反演的水储量变化周期与水文模型数据非常相似,但是GRACE反演水储量变化信号的强度比水文模型大一些,这可能与GRACE反演的水储量变化还包括地下水的变化情况等有关。

|
| 图 3 GRACE反演水储量变化与水文模型的信号强度(上)及滑动平均值(下) Fig. 3 Signal strength(up) and moving average results(down) of GRACE-derived water storage changes and hydrological models |
用ICA方法分析NOAH和WGHM水文模型的数据,结果如图 4和图 5,各个时间序列按方差由大到小排列。由图 4可以看出,NOAH水文模型得到的第1、第3和第4成分都表现出明显的年周期性,并且第3成分含有长期趋势信号,而第2成分主要是半年周期信号。在图 5中,WGHM的4个成分都含有明显的年周期信号。

|
| 图 4 ICA分解132个月NOAH水文模型数据得到的(a)空间模式和(b)时间序列 Fig. 4 Spatial pattern(a) and time series(b) by ICA analysis using 132 months NOAH |

|
| 图 5 ICA分解112个月WGHM水文模型数据得到的(a)空间模式和(b)时间序列 Fig. 5 Spatial pattern(a) and time series(b) by ICA analysis using 112 months WGHM |
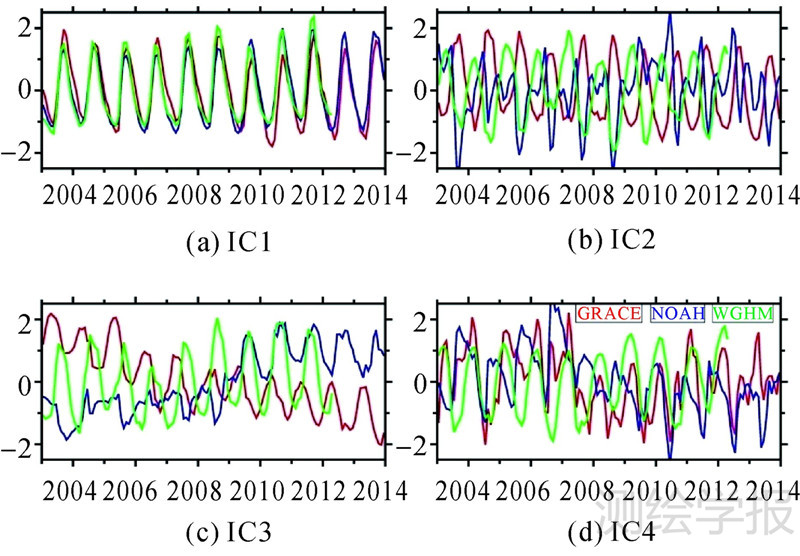
为验证分析结果的可靠性,采用相关系数对主要成分的时间序列进行比较,如图 6所示,各个成分间的相关系数列于表 1。
|
| 图 6 GRACE反演水储量变化与水文模型的ICA分解结果比较 Fig. 6 Comparison of time series results of GRACE and hydrological models by ICA analysis |
| 相关系数 | IC1 | IC2 | IC3 | IC4 |
| GRACE和NOAH | 0.884 | -0.500 | -0.662 | 0.404 |
| GRACE和WGHM | 0.877 | -0.874 | 0.256 | 0.454 |
GRACE反演的水储量变化和水文模型的周期性信号IC1具有高度的一致性,这可以从表 1中的相关系数体现出来,GRACE与NOAH和WGHM的相关系数分别是0.884和0.877。IC1主要表现的是年周期变化的信号,而IC3主要为长期趋势信号,GRACE水储量变化与水文模型给出的IC3结果存在较大差异的原因可能在于:①水文模型在青藏高原地区较少的观测与全覆盖的GRACE卫星数据之间的差异导致;②由于水文模型反映的主要是地表水的变化(包括降水、冰雪融化和湿地变化等),而GRACE反演的水储量变化还包括地下水的变化情况等,水文模型忽略地下水的变化,可能会导致数据的部分误差;③不同的模型采用不同的计算方法,其结果难免会引入一些误差,这可以从NOAH和WGHM水文模型的分析结果看出。
5 结 论近几十年来,由于气候变化的影响,青藏高原地区的冰川消融程度在增大。因此,需要一种方法来分析青藏高原地区的水循环变化,以进一步了解该区域的水资源和冰川变化情况等。在源信号及其混合方式未知的情况下,独立的各个源信号可能会交叉结合到观测结果中。本文利用ICA方法研究了青藏高原及周边地区的水储量在大尺度范围的变化情况。在分析水储量的时空变化中,可以研究自然和人为因素等对区域气候的影响。用ICA方法将GRACE反演的水储量变化分离成各个相互独立的成分,再从各个成分中提取有关特征,得到的各个独立成分与水文模型的结果符合较好,这从表 1中IC1的相关性上可以看出。在空间模式上,GRACE反演水储量变化信号的强度比水文模型信号要大,这与GRACE反演的水储量变化还包括地下水的变化情况等有关。近10年青藏高原西南部地区的水储量一直在下降,这可能是受气候变暖的影响,使该区域的冰川和积雪在加速融化减少。
ICA只需要少量的先验信息(即各个成分相互独立且符合非高斯分布)就可以分离出相互独立的信号成分,因此该方法在GRACE重力数据和水文模型资料的信息提取中具有很好的应用前景。
| [1] | FOROOTAN E, RIETBROEK R, KUSCHE J, et al. Separation of Large Scale Water Storage Patterns over Iran Using GRACE, Altimetry and Hydrological Data[J]. Remote Sensing of Environment, 2014, 140: 580-595. |
| [2] | JEFFERS J N R. Two Case Studies in the Application of Principal Component Analysis[J]. Applied Statistics, 1967, 16(3): 225-236. |
| [3] | PRICE A L, PATTERSON N J, PLENGE R M, et al. Principal Components Analysis Corrects for Stratification in Genome-Wide Association Studies[J]. Nature Genetics, 2006, 38(8): 904-909. |
| [4] | OROPEZA V, SACCHI M. Simultaneous Seismic Data Denoising and reconstruction via Multichannel Singular Spectrum Analysis[J]. Geophysics, 2011, 76(3): 25-32. |
| [5] | 牛涛, 陈隆勋, 王文. 青藏高原冬季平均温度、湿度气候特征的REOF分析[J]. 应用气象学报, 2002, 13(5): 560-570. NIU Tao, CHEN Longxun, WANG Wen. REOF Analysis of Climatic Characteristics of Winter Temperature and Humidity on Xizang-Qinghai Plateau[J]. Journal of Applied Meteorological Science, 2002, 13(5): 560-570. |
| [6] | JOLLIFFE I T. A Cautionary Note on Artificial Examples of EOFs[J]. Journal of Climate, 2003, 16(7): 1084-1086. |
| [7] | CARDOSO J. Fourth-order Cumulant Structure Forcing: Application to Blind Array Processing[C]//Proceedings of the IEEE 6th SP Workshop on Statistical Signal and Array Processing. Victoria, BC: IEEE, 1992: 136-139. |
| [8] | MAKEIG S, BELL A J, JUNG T P, et al. Independent Component Analysis of Electroencephalographic Data[J]. Advances in Neural Information Processing Systems, 1996: 145-151. |
| [9] | 郭科, 陈聆, 陈辉, 等. 基于JADE算法的地震资料随机噪声盲分离方法研究[J]. 地学前缘, 2011, 18(3): 302-309. GUO Ke, CHEN Ling, CHEN Hui, et al. The Method of Seismic Random Noise Blind Separation Based on JADE[J]. Earth Science Frontiers, 2011, 18(3): 302-309. |
| [10] | 吕文彪, 尹成, 张白林, 等. 利用独立分量分析法去除地震噪声[J]. 石油地球物理勘探, 2007, 42(2): 132-136. LV Wenbiao, YIN Cheng, ZHANG Bailin, et al. Using Independent Component Analysis to Eliminate Seismic Noises[J]. Oil Geophysical Prospecting, 2007, 42(2): 132-136. |
| [11] | GUO Jinyun, MU Dapeng, LIU Xin, et al. Equivalent Water Height Extracted from GRACE Gravity Field Model with Robust Independent Component Analysis[J]. Acta Geophysica, 2014, 62(4): 953-972. |
| [12] | FRAPPART F, RAMILLIEN G, MAISONGRANDE P, et al. Denoising Satellite Gravity Signals by Independent Component Analysis[J]. IEEE Geoscience and Remote Sensing Letters, 2010, 7(3): 421-425. |
| [13] | CHEN J L, WILSON C R, BLANKENSHIP D D, et al. Antarctic Mass Rates from GRACE[J]. Geophysical Research Letters, 2006, 33(11): L11502. |
| [14] | 朱广彬, 李建成, 文汉江, 等. 利用GRACE时变重力位模型研究全球陆地水储量变化[J]. 大地测量与地球动力学, 2008, 28(5): 39-44. ZHU Guangbin, LI Jiancheng, WEN Hanjiang, et al. Study on Variations of Global Continental Water Storage with GRACE Gravity Field Models[J]. Journal of Geodesy and Geodynamics, 2008, 28(5): 39-44. |
| [15] | HU Xiaogong, CHEN Jianli, ZHOU Yonghong, et al. Seasonal Water Storage Change of the Yangtze River Basin Detected by GRACE[J]. Science in China(Series D), 2006, 49(5): 483-491. |
| [16] | 罗志才, 李琼, 钟波. 利用GRACE时变重力场反演黑河流域水储量变化[J]. 测绘学报, 2012, 41(5): 676-681. LUO Zhicai, LI Qiong, ZHONG Bo. Water Storage Variations in Heihe River Basin Recovered from GRACE Temporal Gravity Field[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 676-681. |
| [17] | CHEN J L, RODELL M, WILSON C R, et al. Low Degree Spherical Harmonic Influences on Gravity Recovery and Climate Experiment (GRACE) Water Storage Estimates[J]. Geophysical Research Letters, 2005, 32(14): L14405. |
| [18] | WEN Hanjiang, ZHU Guangbin, CHENG Pengfei, et al. The Ice Sheet Height Changes and Mass Variations in Antarctica by Using ICESat and GRACE Data[J]. International Journal of Image and Data Fusion, 2011, 2(3): 255-265. |
| [19] | PAULSON A, ZHONG Shijie, WAHR J. Modelling Post-glacial Rebound with Lateral Viscosity Variations[J]. Geophysical Journal International, 2005, 163(1): 357-371. |
| [20] | DUAN Xiaojuan, GUO Junyi, SHUM C K, et al. On the Postprocessing Removal of Correlated Errors in GRACE Temporal Gravity Field Solutions[J]. Journal of Geodesy, 2009, 83(11): 1095-1106. |
| [21] | RODELL M, HOUSER P R, JAMBOR U, et al. The Global Land Data Assimilation System[J]. Bulletin of the American Meteorological Society, 2004, 85(3): 381-394. |
| [22] | WERTH S, GVNTNER A. Calibration Analysis for Water Storage Variability of the Global Hydrological Model WGHM[J]. Hydrology and Earth System Sciences, 2010, 14(1): 59-78. |
| [23] | SCHMIDT R, PETROVIC S, GVNTNER A, et al. Periodic Components of Water Storage Changes from GRACE and Global Hydrology Models[J]. Journal of Geophysical Research: Solid Earth (1978-2012), 2008, 113(B8): B08419. |
| [24] | CARDOSO J F, SOULOUMIAC A. Blind Beamforming for Non-Gaussian Signals[J]. IEE Proceedings F Radar and Signal Processing, 1993, 140(6): 362-370. |
| [25] | ZHANG Guoqing, YAO Tandong, XIE Hongjie, et al. Increased Mass over the Tibetan Plateau: From Lakes or Glaciers?[J]. Geophysical Research Letters, 2013, 40(10): 2125-2130. |