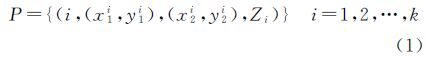2. 深圳市数字城市工程研究中心,广东 深圳 518040
2. Shenzhen Research Center of Digital City Engineering, Shenzhen 518040, China
影像匹配是摄影测量和计算机视觉领域研究的关键问题,是实现影像三维重建的基础。常用的匹配基元有点(像方特征点[1, 2, 3, 4]、规则格网点[5]、物方面元[6]等)、线(单直线[5, 6]、组直线[7, 8]、边缘线[9]等)两种。与点匹配相比,线匹配更具有挑战性,主要原因在于:①受噪声、光照、遮挡及直线提取算法的影响,同一地物的直线特征在不同影像上不能被同时提取出来,或者提取结果差异较大,如提取过程中产生的直线断裂,使得同一条直线在不同影像上提取结果存在数目不等、长度不同、端点不一致等问题。这些都将增加匹配的难度,造成匹配结果存在“一配零”、“一配多”、“多配一”、“多配多”的现象;②单一的核线约束不能给予直线匹配提供强有力的搜索范围约束。
而直线匹配过程中主要问题是匹配约束问题,可归为3个方面:①约束匹配的搜索范围,确定候选直线。常用的约束条件有核线约束[9]、同名三角形约束[10, 11, 12, 13]、同名点约束等[14, 15, 16]。其中同名点约束包括直接利用同名点与直线间的相对位置关系约束或者利用同名点计算左、右影像间的仿射变换矩阵或者单位矩阵。该约束需要一定数量可靠的同名点作为前提,文献[16]中也提及这类方法对特征点匹配具有一定的要求。②在候选直线中,利用相似性约束确定同名直线。该方面是匹配的关键,常用的约束有属性相似性测度函数约束[17]、灰度窗口相似性约束及自适应窗口相似性约束[18]。其中灰度相似性约束首先需要利用核线约束确定直线同名端点,建立相关窗口,然后在候选直线中选择灰度相似性系数最大的直线作为同名直线。该过程没有考虑由于直线提取结果的断裂,候选直线中存在多条与目标直线对应的同名直线的情况。③匹配结果检核。经典的约束是双向一致性约束,该约束受限于两张影像之间,同时由于左、右影像上同名直线提取结果差异,在保证正确匹配的前提下,从左到右的匹配与从右到左的直线匹配结果并非一一对应,因此该过程会导致一些正确的匹配结果被剔除。同时,上述所有约束条件大多停留在像方,而忽略物方这一核心基础。
针对上述直线匹配的难点问题及匹配约束的有效性,本文提出同名点及高程平面约束的航空影像直线匹配算法,该算法结合像方和物方相似性约束代替传统单一的像方相似性约束,保证了直线匹配的可靠性。
1 算法原理本文算法整体流程如图 1所示。匹配过程中首先利用同名点约束候选直线搜索范围,与现有同名点获取方法不同,本文利用文献[19—20]中移动高程平面约束特征点匹配算法对影像上的边缘像素点进行匹配。将边缘点作为匹配基元可以更好地保证待匹配直线上或其邻域内同名点的分布,因此本文首先利用Canny算子对左、右影像进行边缘检测,得到左、右影像上的边缘像素点。同时对左、右影像进行直线提取。为了约束边缘点及后续直线匹配,根据影像覆盖范围及影像分辨率大小,构建物方栅格化金字塔平面。下层金字塔平面格网单元大小(即分辨率大小)与试验影像分辨率大小相同,为0.045m;上层金字塔平面格网单元大小为0.315m,即上层平面一个面元对应下层7×7个平面元。上层平面用于约束边缘点匹配,并将匹配结果传递到下层金字塔平面,下层金字塔平面用于约束直线匹配。直线匹配主要包括4个步骤:①确定候选直线;②确定同名直线;③直线合并;④直线同名端点确定。

|
| 图 1 直线匹配流程图 Fig. 1 Flowchart of line matching |
移动高程平面约束匹配后,得到的同名点可表示为
式中,i为同名点索引号;(x1i,y1i)、(x2i,y2i)分别为左、右影像同名点坐标;Zi为该点所在物方平面高程值。左、右影像直线提取结果分别表示为L1={l11,l12,…,l1M},L2={l21,l22,…,l2N}。对左影像上任一条直线l1m,在右影像L2中寻找其同名直线。首先利用初始匹配得到的同名点约束候选直线,减少匹配搜索范围。具体原理如图 2所示,左影像上以l1m为中心建立邻域窗口,窗口宽度为2w+1,文中取w=6。判断左影像上P中哪些点位于该窗口内,鉴于初始边缘点匹配结果中可能存在误匹配,因此进一步利用高程连续性约束对窗口内的点进行检核,剔除错误匹配并记录窗口内保留点的索引号。然后在右影像上,再根据直线斜率和索引号对应的右影像上的同名点确定候选直线集合Cm。即在保证直线斜率相似情况下,判断右影像L2中哪些直线邻域窗口内(窗口宽度同为2w+1)存在这些点。当其邻域内存在同名点数目≥1时,认为该直线为目标直线的候选直线。最后l1m在右影像上候选直线集合可表示为Cm(l2n1,l2n2,l2n3,…)。
|
| 图 2 左、右影像直线邻域窗口 Fig. 2 Neighborhoods of lines on the left and right images |
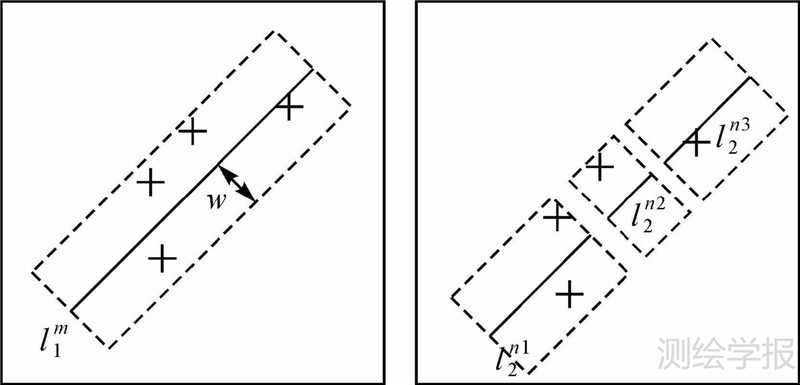
在上述条件约束下得到目标直线对应的候选直线的情况大致可以归为以下6种情况:“一对零”、“一对一”正确、“一对一”错误、“一对多”正确、“一对多”错误、“一对多”正确同错误。如图 3所示,为了更好地区分候选直线正确与否(即是否为目标直线的同名直线),图中将直线邻域内的同名点同时显示出来。其中,如图 3(a)所示“一对零”:即左影像上的目标直线,在右影像上没有对应的候选直线;如图 3(b)所示,“一对一”正确:即左影像上的目标直线,在右影像上仅有一条候选直线,且该直线为同名直线;如图 3(c)所示,“一对一”错误:即左影像上的目标直线,在右影像上仅有一条候选直线,该直线不是同名直线;其他3种“一对多”情况表达含义依此类推。
|
| 图 3 目标直线对应候选直线情况 Fig. 3 Situation of straight line and the matching candidates |
针对每条目标直线得到的候选集合Cm,进一步利用相似性约束确定同名直线。即在Cm(l2n1,l2n2,l2n3,…)中确定l1m的同名直线,该过程分为物方约束和像方约束两个步骤。
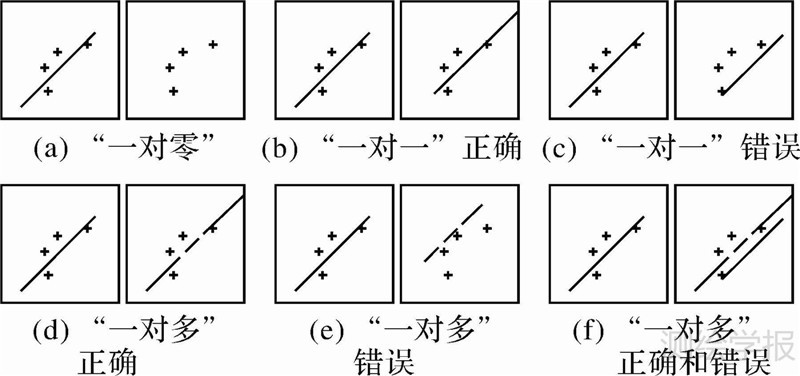
(1) 物方约束。计算直线l1m邻域内所有同名点高程值的均值,将其作为物方投影平面的高程值。利用共线方程将左影像上目标直线l1m和其对应的右影像上的候选直线集合Cm(l2n1,l2n2,l2n3,…)中的所有直线分别投影到高程平面,得到平面上对应直线l1m′和候选直线集合C′m(l2n1′,l2n2′,l2n3′,…)。分别比较l1m′与C′m中每条候选直线间的垂直距离和重叠距离[17]。如图 4所示,以l1m′和l2n1′为例,以l1m′作为基准,D(l1m′,l2n1′)表示候选直线l2n1′的中点到目标直线l1m′的垂直距离,O(l1m′,l2n1′)表示候选直线l2n1′在目标直线l1m′上的投影与直线l1m′的重叠距离。当同时满足D(l1m′,l2n1)<TD,O(l1m′,l2n1′)>TO两个条件时,再利用像方同名点与直线相对位置关系和点到直线最短距离进一步确定同名直线。其中TD和TO分别为垂直距离和重叠距离阈值,文中分别取TD=3,TO=5。
|
| 图 4 直线间垂直距离和重叠距离 Fig. 4 Vertical distance and overlap distance between lines |
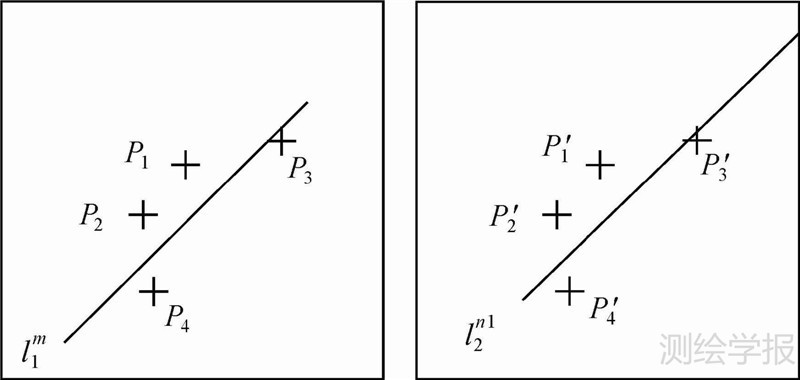
(2) 像方约束。如图 5所示,在左影像上,直线l1m邻域内存在4个点,其中,点P1、P2位于l1m上方,点P3、P4位于l1m下方。以左影像上和4个点的相对位置关系为基准,判断右影像上l2n1(假设l2n1符合上述物方约束条件)与同名点的位置关系是否与左影像相一致。同时,根据点到直线距离进行判断,即左影像上点P3到l1m的距离最小,记为DP3,同样,计算右影像上P3′点到l2n1的距离D′P3′,如果abs(DP3-D′P3′)<TC,则确定候选直线l2n1为l1m同名直线,试验过程中取TC=1。
|
| 图 5 同名点与直线相对位置关系 Fig. 5 Relative positions from corresponding points to lines |
鉴于直线提取过程中存在断裂,本文算法匹配过程中充分考虑了同一直线提取结果在左影像上连续、右影像上断裂的情况,即匹配结果中左影像上一条直线对应右影像上多条直线的情况,简称左影像上直线“一配多”的结果。如图 6匹配结果中第3组同名直线所示,左影像上的索引号为3的直线同时对应右影像上索引号为443和784两条直线。但匹配过程中没有对直线提取结果中右影像上连续、左影像上断裂的情况进行考虑。如图 6中第1、2、4组同名直线所示,右影像上索引号为343的直线分别对应左影像上1、2、5这3条直线,得到3组同名直线,即匹配结果中右影像上直线还存在“一配多”的结果没有整合。因此还需进一步利用索引对应关系对其进行整合,具体原理如下。

|
| 图 6 右影像上“一配多”结果整合 Fig. 6 Integrated results of “one-to-many” on the right image |
假设初始匹配共得到n组同名直线,Si={Mi,Ni}记录第i组同名直线索引号,i≤n,其中Mi为左影像上的直线索引号,Ni为右影像上的直线索引号。初始情况下,每个Mi记录单个索引号,每个Ni记录单个或者多个直线索引号。初始i=1,m=n,m为后续合并产生新的同名直线组索引,直线合并具体步骤如下。
(1) 令m=m+1,定义变量Ze、Mm、Nm、Sm为空。取Si={Mi,Ni}中Ni记录的右影像直线索引号,并将其赋值给Ze。
(2) 将Ze中第一个索引值作为基准,置为当前,将该值记为v,并将其从Ze中删除。
(3) 依次判断第Ni+1到Nn中,是否存在于与v相同的索引号。如果存在,进行步骤(4),如果不存在,进行步骤(5)。
(4) 假设Nk中存在索引号v,分别合并Mi和Mk到Mm中,合并Ni和Nk到Nm中,记为Mm={Mm;[Mi,Mk,…]},Nm={Nm;[Ni,Nk,…]},并将其记录到Sm中,即Sm=[Mm,Nm],令Si和Sk为空,同时更新Ze,增加Nk中新的索引值到Ze中,转到步骤(5)。
(5) 判断Ze是否为空,如果不为空,转到步骤(2),如果为空,取i=i+1;如果i<n,转到步骤(1),如果i=n,转到步骤(6)。
(6) “一配多”结果整合结束,清除其中所有为空的元素。
通过上述处理后,右影像上“一配多”的情况得到合并,该过程使得右影像直线提取过程中断裂的直线得到合并。最终得到左、右影像上同名单直线间、同名组直线间的一一对应关系。进一步将匹配结果全部转化为“一对一”的同名直线关系,对Mi和Ni中记录的多条直线进行合并,使其构成一条直线。该过程是对Mi或者Ni中包含的所有直线端点坐标按照x坐标(或y坐标)从小到大进行排序,连接最大、最小值点构成新的直线,并将其作为直线端点坐标进行存储。
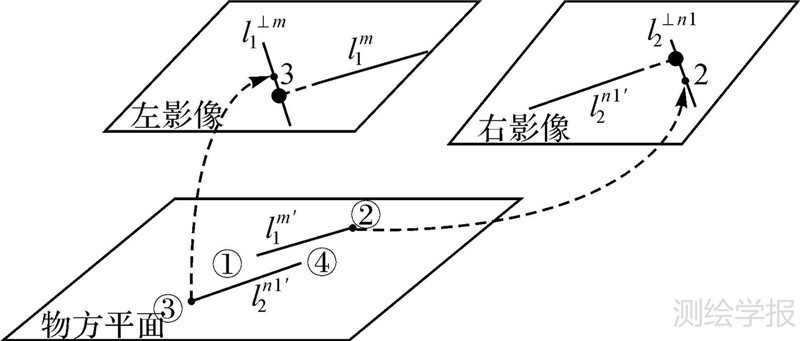
1.4 直线同名端点确定经过上述匹配和直线合并后,得到“一对一”的同名直线。但是左、右影像上同名直线长度不等、端点不一,因此还需进一步确定直线的同名端点。现有算法均在像方利用核线约束进行同名直线重叠部分截取或者延伸直线与核线相交,尽量得到长度较长的直线,该过程可能会对同名直线对的4个端点都进行判断,增加了计算量。本文通过“像方-物方-像方”模式确定直线的同名端点。如图 7所示,首先分别将左、右影像上的同名直线l1m、l2n1投影到其对应的物方高程平面,得到直线l1m′、l2n1′。对两条直线4个端点坐标按照x坐标(或y坐标)从小到大进行排序,本文以x坐标进行排序结果为③、①、④、②。选择最小和最大值对应的端点,即③和②,分别将其投影到像方。以端点③为例,该点来自右影像直线l2n1的投影点,因此,将其反投影到左影像上,得到点3,在左影像上,过点3作垂直于直线l1m的直线,记为l1⊥m,延长l1m与l1⊥m的交点即为最终的同名端点。
|
| 图 7 直线同名端点确定 Fig. 7 Determination of corresponding endpoints for corresponding lines |
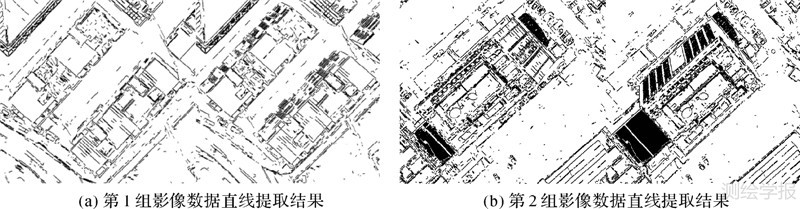
为了验证本文算法的有效性,本文采用两组UCX数字航空影像的子影像数据进行直线匹配试验。第1组影像数据如图 8(a)所示,左、右影像大小分别为1319×1411像素、1389×1330像素。影像集中在城市建筑物密集区域,包含建筑物立面信息及屋顶边缘,存在纹理断裂。第2组影像数据如图 8(b)所示,左、右影像大小分别为1772×1985像素、1735×1827像素。图中包含高大建筑物,不同视角拍摄使其在两张影像上成像差异较大,对周围地物产生不同程度的遮挡,增加了匹配的难度。试验过程中,首先对图 8所示每组影像进行边缘点匹配及直线提取,然后在此基础上实现直线匹配。对于第1组试验影像,边缘点匹配后共得到5220对同名点,左、右影像直线提取数目分别为1861条、2162条。第2组试验影像,边缘点匹配后共得到7781对同名点,左、右影像直线提取数目分别为4068条、3819条。两组数据的直线提取结果如图 9所示。

|
| 图 8 航空影像 Fig. 8Aerial images |
|
| 图 9 直线提取结果 Fig. 9 Results of line extraction |
本文算法在确定同名直线过程中主要涉及TD、TO、TC 3个阈值的设定,因此本文针对第1组影像数据,在TD、TO、TC取不同值的情况下进行匹配试验,并对结果进行对比分析。
(1) 阈值TD的设定。TD是用于限定物方平面上目标直线与候选直线间的垂直距离。理论上,不同影像上的同名直线(水平直线)投影到其对应的物方平面上应重合,因此,TD取值不宜过大。首先,固定TO=11,TC=1,对TD值为1~6时的匹配结果进行分析,结果如表 1所示。通过比较,TD值为1~3时,匹配得到同名直线的数目及其包含左、右上直线的数目具有较大幅度的增加。而当TD>3时,同名直线数目变化较小。同时随着TD值的增加,匹配正确率降低。因此,综合同名直线数目和正确率来看,本文设定TD值为3。
| TD值 | 1 | 2 | 3 | 4 | 5 | 6 |
| 同名直线数目 | 258 | 371 | 416 | 422 | 424 | 426 |
| 左/右影像直线数目 | 267/281 | 402/411 | 459/466 | 471/474 | 473/476 | 476/478 |
| 正确直线数目 | 257 | 369 | 413 | 417 | 417 | 418 |
| 正确率/(%) | 99.6 | 99.4 | 99.2 | 98.8 | 98.3 | 98.1 |
(2) 阈值TO的设定。TO是限定物方平面上目标直线与候选直线间的重叠距离。理想状态下,两条直线应100%重叠,即重叠距离等于直线的长度。但是由于左、右影像上直线提取结果的不连续,同名直线投影到物方平面可能存在很小的重叠范围或者完全不重叠。因此,阈值分析过程中对与目标直线存在重叠的候选直线都进行考虑。固定TD=3,TC=1,分别对TO在1~11范围内取值进行分析,结果如表 2所示。可以看出,匹配结果在TO取不同值的情况下变动较小。最终,为了最大程度减小直线提取结果不连续对匹配造成的影响,本文设定TO值为5。
| TO值 | 1 | 3 | 5 | 7 | 9 | 11 |
| 同名直线数目 | 436 | 437 | 432 | 427 | 421 | 416 |
| 左/右影像直线数目 | 487/506 | 487/504 | 482/497 | 476/488 | 464/477 | 459/466 |
| 正确直线数目 | 430 | 431 | 427 | 422 | 418 | 413 |
| 正确率/(%) | 98.6 | 98.6 | 98.8 | 98.8 | 99.2 | 99.2 |
(3) 阈值TC的设定。TC是用于约束不同影像上同名点与同名直线的相对位置关系。该约束的主要作用是避免同一影像上邻近直线引起的错误匹配。在连续表面情况下,不同影像上同名点到同名直线的距离应近似相等。因此,TC设定不宜过大。固定TD=3,TO=5,对TC值为1~4的匹配结果进行分析。从表 3可知,随着TC值变大,匹配结果中包含的左、右影像上直线的数目逐渐增多,但同时匹配的正确率也在减小。从匹配的正确率考虑,设定TC值为1。
| TC值 | 1 | 2 | 3 | 4 |
| 同名直线数目 | 432 | 445 | 438 | 433 |
| 左/右影像直线数目 | 482/497 | 504/535 | 517/551 | 520/557 |
| 正确直线数目 | 427 | 437 | 425 | 418 |
| 正确率/(%) | 98.8 | 98.2 | 97.0 | 96.5 |
此外,从匹配结果中可以看出,同名直线中包含左、右影像上直线的数目随着参数的变化依次增加或者减小,但同名直线的数目呈现无规律现象,没有随着参数的变化或者直线数目的变化递增或者递减,如表 2中TO=3,表 3中TC=3、TC=4的结果。这是由于直线合并产生的,即匹配结果中由于新直线的出现引起原有一些同名直线组的合并产生的结果。
2.2 本文算法匹配结果采用本文算法对图 8所示的两组影像进行匹配试验。第1组影像数据初始匹配共得到同名直线组数为432,结果如图 10(a)所示。其中包含左影像上的直线482条,右影像上的直线497条。再对上述结果中“一对多”、“多对一”及“多对多”的同名直线组进行合并,并确定同名端点,使其变为“一对一”同名直线关系的同时并保证最长的直线效果。最终得到的同名直线如图 10(b)所示。第2组影像数据初始匹配共得到同名直线组数为527,结果如图 11(a)所示。其中包含左影像上的直线576条,右影像上的直线598条。经直线合并及同名端点确定后得到的同名直线如图 11(b)所示。从结果图中可以看出,本文算法在建筑物屋顶主要边缘处均能获得较好的匹配结果。两组影像匹配结果正确率分别为98.8%、97.9%。为了更好地观察后续的处理效果,分别将图 10和图 11中每组结果的对应区域(如图中黄色方框所示)进行局部放大,如图 12所示。对比图中椭圆形区域内的直线效果,可以看出,直线合并及同名端点确定在一定程度上改善了直线提取结果的断裂及不完整。此外,从图 12(b)中还可以看出,影像上由于遮挡未被提取完整的直线也得到延长,尽管延长的直线与影像上灰度信息不吻合,但从直线本身而言,它是真实存在的,因此该匹配结果也是正确的。

|
| 图 10 第1组影像数据直线匹配结果 Fig. 10 Matching results of lines on the first group images by algorithm in this paper |

|
| 图 11 第2组影像数据直线匹配结果 Fig. 11 Matching results of lines on the second group images by algorithm in this paper |

|
| 图 12 部分结果放大 Fig. 12 Parts of zooming results |
为了分析不同约束条件对匹配的影响,本文实现了文献[9]中以核线约束为主的直线匹配算法及文献[16]中以同名点约束为主的直线匹配算法,结果分别如图 13、图 14所示。同时为了验证边缘点匹配结果在直线匹配过程中的优势,在文献[16]及本文算法实现过程中分别采用SIFT匹配和边缘点匹配得到的同名点约束直线匹配。对于两组试验影像,SIFT匹配得到同名点数目分别为2043和5811。不同算法的直线匹配结果统计如表 4所示。下面将从约束条件及同名点获取方式两个方面对结果进行分析。
| 试验影像 | 提取直线数目(左/右) | 算法 | 约束条件 | 同名直线数目 | 左/右影像直线数目 | 正确直线数目 | 正确率/(%) |
| 图 8(a) | 1861 / 2162 | 文献[9]算法 | 核线约束 | 496 | 496/ 496 | 403 | 81.2 |
| 文献[16]算法 | SIFT同名点约束 | 53 | 53 / 53 | 52 | 98.1 | ||
| 边缘同名点约束 | 272 | 272 / 272 | 268 | 98.5 | |||
| 本文算法 | SIFT同名点约束 | 52 | 53 / 56 | 52 | 100 | ||
| 边缘同名点约束 | 432 | 482 / 497 | 427 | 98.8 | |||
| 图 8(b) | 4068 / 3819 | 文献[9]算法 | 核线约束 | 735 | 735 / 735 | 538 | 73.1 |
| 文献[16]算法 | SIFT同名点约束 | 124 | 124 / 124 | 124 | 100 | ||
| 边缘同名点约束 | 433 | 433 / 433 | 421 | 97.2 | |||
| 本文算法 | SIFT同名点约束 | 113 | 115 / 121 | 113 | 100 | ||
| 边缘同名点约束 | 527 | 576 / 598 | 516 | 97.9 |
与同名点约束匹配相比较,文献[9]中采用核线约束得到同名直线数目较多,但是正确率也相对较低。这是由于该算法不受同名点分布限制,每条直线均参与匹配。但航空影像上重复纹理较多,且单一的核线约束搜索范围较大,从而导致较多的错误匹配。
2.3.2从采用不同方式获取同名点约束匹配的角度分析对文献[16]及本文算法,对其分析如下:
(1) 对于单一算法中,采用不同方式获取同名点约束直线匹配而言,边缘点约束匹配得到同名直线数目多于SIFT同名点约束匹配的数目,但后者正确率相对较高。这是由于SIFT匹配得到的同名点少,可靠性高,且同名点多分布在地面和屋顶,而对于匹配难度较大的区域,如建筑物边缘,影像上纹理断裂处分布较少,几乎没有同名点,这也导致后续该区域无直线参与匹配,降低了该区域产生错误匹配的概率。
(2) 对于同一组影像数据而言,采用SIFT同名点约束匹配,两种算法得到的同名直线数目相当;而采用边缘点约束匹配,本文算法匹配得到同名直线数目多于文献[16]算法,且本文算法正确率高于文献[16]算法。这是由于本文算法采用直线邻域内所有同名点同时约束匹配,且对初始匹配获取的同名点具有一定的容错能力。
(3) 就两种算法本身而言,与文献[16]算法相比,本文算法得到的同名直线数目相对较多,这是由于边缘点匹配得到的同名点数目多于SIFT匹配得到的同名点的数目,且分布均匀,均位于影像边缘线上或其邻域内,这对确定候选直线具有较好的约束效果。而文献[16]算法的弊端是只选取直线两侧距离直线最近的点,而最近的点并非是确定候选直线最优的点,这将导致一些候选直线漏选从而没有匹配到同名直线。
综上所述,同名点约束能有效避免重复纹理引起的错误匹配。此外,与传统同名点约束直线匹配相比较,本文算法能获取较多数目的同名直线,且保证了匹配的可靠性,具有较高的正确率。
3 结 论本文提出了一种同名点及高程平面约束的航空影像直线匹配算法,该算法具有以下特点:①利用边缘点匹配结果代替传统特征点匹配结果约束后续直线匹配,更有利于保证直线邻域内存在较多同名点,有效约束了候选直线范围;②采用像方和物方相结合的匹配模式,提高了直线匹配结果的可靠性;③匹配过程中有效地考虑了左、右影像直线提取过程中产生的断裂,并对“一配多”、“多配一”、“多配多”的匹配结果进行合并,最终得到“一配一”的同名直线,提高了边缘的连续性;④利用物方平面作为中介确定直线同名端点,有效地避免了与核线平行的直线端点难以确定的问题。
鉴于本文较严格的直线约束条件,相对于影像本身直线提取数目而言,匹配得到同名直线的数目相对较少,同时,算法没有对垂直线和倾斜直线进行针对性研究,这两方面有待进一步深入研究。
| [1] | 戴激光, 宋伟东, 贾永红, 等. 一种新的异源高分辨率光学卫星遥感影像自动匹配算法[J]. 测绘学报, 2013, 42(1): 80-86. DAI Jiguang, SONG Weidong, JIA Yonghong, et al. A New Automatically Matching Algorithm for Multi-source High Resolution Optical Satellite Images[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(1): 80-86. |
| [2] | 戴激光, 宋伟东, 李玉. 渐进式异源光学卫星影像SIFT匹配方法[J]. 测绘学报, 2014, 43(7): 746-752. DAI Jiguang, SONG Weidong, LI Yu. Progressive SIFT Matching Algorithm for Multi-source Optical Satellite Images[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(7): 746-752. |
| [3] | 袁修孝, 明洋. 一种综合利用像方和物方信息的多影像匹配方法[J]. 测绘学报, 2009, 38(3): 216-222. YUAN Xiuxiao, MING Yang. A Novel Method of Multi-image Matching Using Image and Space Synthesis Information[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(3): 216-222. |
| [4] | 姚国标, 邓喀中, 张力, 等. 融合互补仿射不变特征的倾斜立体影像高精度自动配准方法[J]. 测绘学报, 2013, 42(6): 869-876, 883. YAO Guobiao, DENG Kazhong, ZHANG Li, et al. An Automated Registration Method with High Accuracy for Oblique Stereo Images Based on Complementary Affine Invariant Features[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(6): 869-876, 883. |
| [5] | ZHANG Li. Automatic Digital Surface Model (DSM) Generation from Linear Array Images[D]. Wuhan: Wuhan University, 2005. |
| [6] | 纪松. 线阵影像多视匹配自动提取DSM的理论与方法[D]. 郑州: 解放军信息工程大学, 2008. JI Song. Multi-View Matching Theories and Methods for Automatic DSM Extraction from Linear Array Images[D]. Zhengzhou: PLA Information Engineering University, 2008. |
| [7] | KIM H,LEE S. Simultaneous Line Matching and Epipolar Geometry Estimation Based on the Intersection Context of Coplanar Line Pairs[J]. Pattern Recognition Letters, 2012, 33(10): 1349-1363. |
| [8] | 文贡坚. 一种基于特征编组的直线立体匹配全局算法[J]. 软件学报, 2006, 17(12): 2471-2484. WEN Gongjian. A Global Algorithm for Straight Line Stereo Matching Based on Feature Grouping[J]. Journal of Software, 2006, 17(12): 2471-2484. |
| [9] | SCHMID C,ZISSERMAN A.The Geometry and Matching of Lines and Curves over Multiple Views[J]. International Journal of Computer Vision, 2000, 40(3): 199-233. |
| [10] | 江万寿. 航空影像多视匹配与规则建筑物自动提取方法研究[D]. 武汉: 武汉大学, 2004. JIANG Wanshou. Multiple Aerial Image Matching and Automatic Building Detection[D]. Wuhan: Wuhan University, 2004. |
| [11] | 刘亚文. 基于TIN的半自动多影像同名线段匹配算法研究[J]. 武汉大学学报(信息科学版), 2004, 29(4): 342-345. LIU Yawen.A Semi-automatic Algorithm for Line Matching Based on Delaunay Triangulation[J]. Geomatics and Information Science of Wuhan University, 2004, 29(4): 342-345. |
| [12] | WU Bo, ZHANG Yunsheng, ZHU Qing. Integrated Point and Edge Matching on Poor Textural Images Constrained by Self-adaptive Triangulations[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2012, 68: 40-55. |
| [13] | 张云生. 自适应三角形约束的多基元多视影像匹配方法[D]. 武汉: 武汉大学, 2011. ZHANG Yunsheng. A Multi-primitive and Multi-view Image Matching Method Based on Self-adaptive Triangle Constraint[D]. Wuhan: Wuhan University, 2011. |
| [14] | FAN Bin, WU Fuchao, HU Zhanyi. Line Matching Leveraged By Point Correspondences[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition. San Francisco, CA: IEEE, 2010: 390-397. |
| [15] | TIAN Yixiang, GERKE M, VOSSELMAN G, et al. Automatic Edge Matching Across an Image Sequence Based on Reliable Points[C]//Proceedings of the XXI Congress: Silk Road for Information from Imagery. Beijing: The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2008, 37: 657-662. |
| [16] | 梁艳, 盛业华, 张卡, 等. 利用局部仿射不变及核线约束的近景影像直线特征匹配[J]. 武汉大学学报(信息科学版), 2014, 39(2): 229-233. LIANG Yan, SHENG Yehua, ZHANG Ka, et al. Linear Feature Matching Method based on Local Affine Invariant and Epipolar Constraint for Close-Range Images[J]. Geomatics and Information Science of Wuhan University, 2014, 39(2): 229-233. |
| [17] | 李芳芳, 贾永红, 肖本林, 等. 利用线特征和SIFT点特征进行多源遥感影像配准[J]. 武汉大学学报(信息科学版), 2010, 35(2): 233-236. LI Fangfang, JIA Yonghong, XIAO Benlin,et al.A Multi-sensor Image Registration Algorithm Based on Line Features and SIFT Points[J]. Geomatics and Information Science of Wuhan University, 2010, 35(2): 233-236. |
| [18] | 张云生, 朱庆, 吴波, 等. 一种基于三角网约束的立体影像线特征多级匹配方法[J]. 武汉大学学报(信息科学版), 2013, 38(5): 522-527. ZHANG Yunsheng, ZHU Qing, WU Bo, et al. A Hierarchical Stereo Line Matching Method Based on a Triangle Constraint[J]. Geomatics and Information Science of Wuhan University, 2013, 38(5): 522-527. |
| [19] | 王竞雪, 宋伟东, 王伟玺. 移动高程平面约束的多视影像特征点匹配[J]. 遥感学报, 2012, 16(4): 691-704. WANG Jingxue, SONG Weidong,WANG Weixi.A Multi-view Image Matching Algorithm for Feature Point under the Moving Z-Plane Constraint[J]. Journal of Remote Sensing, 2012, 16(4): 691-704. |
| [20] | 王竞雪, 朱庆, 王伟玺. 多匹配基元集成的多视影像密集匹配方法[J]. 测绘学报, 2013, 42(5): 691-698. WANG Jingxue, ZHU Qing, WANG Weixi. A Dense Matching Algorithm of Multi-View Image Based on the Integrated Multiple Matching Primitives[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(5): 691-698. |