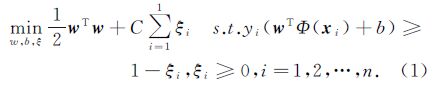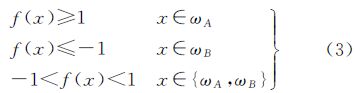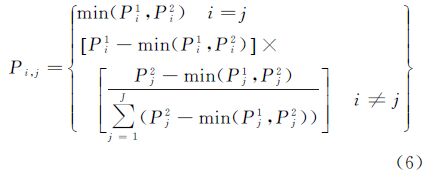由于传感器的空间分辨率以及地面的复杂多样性,混合像元问题在遥感影像中普遍存在[1]。混合像元的存在不仅影响地物识别和分类的精度,而且也是遥感定向、定量化发展的瓶颈之一[2],严重影响了计算机处理的效果和计算机技术在遥感领域的应用[3]。处理好混合像元问题,将显著提升遥感图像质量和边界的清晰度,提高遥感信息的精度和可用性,扩大其应用范围,带来较好的社会效益和经济效益。
光谱分解(special mixture analysis,SMA)是解决混合像元问题的有效途径[4]。多光谱影像由于不同地物间光谱信息的相似性,其混合像元分解研究极具挑战[2]。传统混合像元分解中固定端元光谱应用于影像所有像元组分提取,很难高精度地识别影像地物。像元分解精度的关键点在于改善端元光谱矩阵的结构[5]。因此,基于端元光谱变化的SMA研究正在逐步开展[6]。其中多端元光谱分解法(multiple endmember spectral mixture analysis,MESMA)利用不同端元组合方式线性分解混合像元,被广泛应用[7, 8]。但光谱库较大时,MESMA为寻找所有可能端元组合会造成极低的运算效率。同时,由于大气的多重散射和仪器的校准等因素,光谱混合是高度非线性的[9],非线性混合模型具有较高的分解精度和普适性[10]。为了避免复杂的物理模型,学者们提出基于核函数进行非线性光谱分解的方法[11, 12]。由于实现的灵活性,机器学习策略运用到非线性分解中[13, 14, 15]。多项式非线性混合模型具有足够的通用性,可涵盖广泛的非线性混合情况[16],也运用到非线性光谱分解中。但非线性混合分解研究与线性混合相比还很不成熟。
支持向量机(support vector machines,SVM)方法是具有良好的泛化能力、可并行处理、降低运算时间等特性的统计学习方法[17, 18],通过核函数计算非线性变换,可有效地实现非线性混合[19]。本文提出基于SVM的端元可变非线性混合像元分解方法(nonlinear changeable SVM,NCSVM),为每个像元构造优化的端元集,进行非线性分解,提高分解精度。
1 NCSVM混合像元分解遥感影像的端元集合,通过端元提取算法确定。NCSVM算法首先对影像中每一个像元获取优化的端元集合,并最终生成组分值。
1.1 优化端元集 1.1.1 SVM分类SVM分类算法通过构造最优超平面解决两类的分类问题。假设样本集为(xi,yi),i=1,2,…,n,x∈Rd,y∈{+1,-1}是类别标号,分别代表类ωA和ωB,分类的目的就是找到一个超平面将ωA和ωB两类样本完全分开[20]。对于线性不可分空间,SVM可通过核函数映射到高维特征空间来解决。这里,采用C-SVC方法来解决问题,即
式中,xi是支持向量;Φ为核函数。判别函数为
判别规则为
1.1.2 构造优化端元集影像地物有k种类型时,需构造k个SVM模型。第i个SVM模型训练时第i类样本为正样本,其他类样本为负样本。对于像元x,生成fi(x)i=1,2,…,k,根据判定规则(式(3))进行判断,当fi(x)≤-1,可知像元x中完全不包含类型i,将第i类样本从端元集中去掉。依次判定,将所有像元组分为负的类型样本去掉,最终生成像元x的优化端元集。
1.2 组分提取基于每个像元的优化端元集,构造多类SVM模型。通过SVM最优分类函数可得到对象所属类别,为了求得混合像元中各个端元的组成成分,引入后验概率,通过两类配对(pairwise coupling,PWC)方法有效地提取混合像元组分信息[19, 21]。SVM-PWC方法获取的组分值满足和为1和非负的约束。
1.3 精度验证由于像元中存在多个组成类型,传统的混淆矩阵不适用于混合像元分解精度评价。本文采用两种方法进行评价[22]。平均绝对误差法(mean absolute error,MAE) [23, 24]定义如下
式中,Pij 1是本文方法求得的像元j中i类地物的组分;Pij 2是从参考数据分类影像中求得的“实际”地物组成;N是像元个数;J是地物类型数目。文献[25]提出的交叉举证适合于进一步分析算法组分结果与实际参考数据间的差异
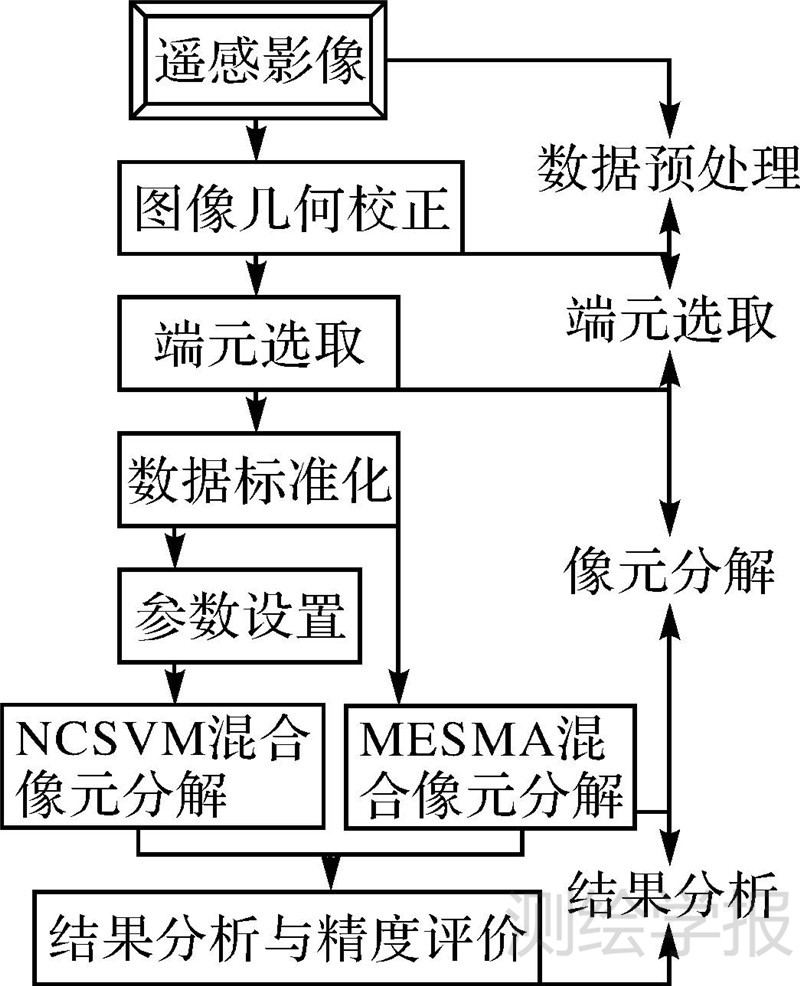
式中,Pi,j是交叉表中类i和类j交叉处的值。Pi1代表本文算法得到的类i的百分含量,Pi2代表类i在参考数据中的组成量。一旦所有Pi,j值求得,可计算出总体精度和Kappa值。 2 NCSVM混合像元分解试验本文试验基本流程如图 1所示,处理步骤主要包括相关预处理、训练样本的选取、数据标准化、参数设置、NCSVM和MESMA方法混合像元分解以及精度评价。
|
| 图 1 混合像元分解试验流程图 Fig. 1 Procedure of unmixing image based on NCSVM and MESMA |
研究区位于广东南部(21°48′N —22°27′N,113°03′E—114°19′E),遥感影像为经过几何精度校正的2004年30 m分辨率Landsat ETM+影像大小为179×111像素。运用最小噪声分离法(minimum noise fraction,MNF)去除6个波段间光谱的相关性(由于热红外波段6空间分辨率不同,因此已去除)。选取覆盖同一区域的经过几何精度校正的2005年5 m分辨率SPOT HRG影像(影像大小为1074×666像素)作为精度验证的参考数据。根据影像的光谱属性和应用实践,影像分为5类:植被、水、阴影、居民用地、工业用地。Landsat ETM+遥感影像选取第7、4、1波段的图像,作RGB彩色合成得到伪彩色图像,如图 2所示。SPOTHRG遥感影像选取第1、2、3波段的图像,作RGB彩色合成得到伪彩色图像,见图 2。

|
| 图 2 试验数据 Fig. 2 Image data used in this paper |
运用最大似然分类法(maximum likelihood classification,MLC)得到SPOT HRG分类影像(图 3)。直接从遥感影像上获取每类地物25个采样点,然后采用目视解译的方法进行精度分析,总体精度为0.81,Kappa系数为0.78。由于没有更高精度的分类影像和地面真实数据,SPOT HRG分类影像作为参考数据指导端元样本选取和算法分解精度验证。

|
| 图 3 SPOT HRG分类图 Fig. 3 SPOT HRG classification image |
研究区Landsat ETM+影像中,上述5类地物分别选取72、23、9、31、18个端元样本。由于MESMA方法每个地物类型支持一个样本,因此选取每类端元样本的均值作为类型的端元值。为消除不同属性数据数值差别很大造成对组分结果的影响,进行混合像元分解前需对数据标准化。本研究中,端元样本数据和试验数据都标准化到0~1区间。
2.3 参数设置高斯径向基核函数(radial basis function,RBF)是一个普适的核函数,通过选择合适的参数,可以适用于任意分布的样本,在SVM模型中广泛采用[26, 27],因此,本文选择高斯径向基核函数,其中惩罚系数参数C和高斯函数参数g在每次构建SVM模型时,采用LibSVM软件中基于交叉验证的“网格搜寻”方法实时获取。
2.4 分解结果NCSVM算法首先构建5个SVM两类分类模型,通过运算为每个像元获取其优化端元集,在此基础上进行SVM+PWC混合像元分解,得到各个像元的组分值,如图 4所示。MESMA算法构建所有的端元组合模型,基于每个端元组合模型求解各个像元的组分值,选取均方根值最小的组分值作为此像元最终的组分值,结果见图 5。组分图中灰度越亮代表对应端元在混合像元的面积比(丰度)越大,灰度越暗表示端元在对应混合像元中丰度越小。对比相同地物的组分图像发现,NCSVM方法的组分图像视觉效果优于MESMA分解结果。图 4中,不同地物的区分特别明显,与SPOT HRG分类影像相比无明显错分状况。图 5中阴影和工业用地两类地物存在明显错分情况。原因如下:①由于影像分辨率及坡度、方向等地物分布原因,单一的端元样本很难完全代表本地物的光谱变化,NCSVM因支持地物类型拥有多个端元样本,可将光谱相近的地物进行分类,而MESMA每个地物类型只有一个端元样本;②由于存在不属于混合类型的端元样本加入会产生小的均方根值,MESMA中易产生过适应现象;③NCSVM方法运用核函数将非线性混合映射到高维特征空间使其线性可分,能揭示混合像元中各组分间的非线性特性,改善了混合像元分解效果。

|
| 图 4 NCSVM算法组分图 Fig. 4 Fractional images generated by the NCSVM method |

|
| 图 5 MESMA算法组分图 Fig. 5 Fractional images generated by the MESMA method |
计算NCSVM算法和MESMA算法分解得到的各像元地物组分值与SPOT HRG影像地物组分间的均方根误差(root mean squared error,RMSE),RMSE值越小代表分解精度越高,结果如图 6所示。图像中灰度越暗表示RMSE值越小。从图 6中可以发现NCSVM方法所获得的均方根误差图像包含的信息量比MESMA方法所获得的均方根误差图像要小,混合像元分解精度高。对两种方法得到的RMSE图做统计分析,结果见表 1。表 1中NCSVM方法所获得的组分结果具有较小的均方根误差,像元分解精度高。

|
| 图 6 混合像元分解均方跟误差图 Fig. 6 RMSE image |
| 方法 | RMSE最小值 | RMSE最大值 | RMSE均值 |
| NCSVM | 0 | 0.632 5 | 0.210 1 |
| MESMA | 0 | 0.632 6 | 0.230 3 |
表 2是算法NCSVM和MESMA的MAE精度值。MAE值越小像元分解精度越高。NCSVM算法的总体精度值为0.35,算法的精度高于MESMA。地物水的MAE值最小(0.06),具有最优的分解精度,阴影次之。居民用地和植被的分解精度较差,其原因可能是居民用地和植被表面光谱类型丰富,分解难度大。表 3中是算法NCSVM和MESMA的交叉表,NCSVM具有最高的总体精度(0.93)和Kappa值(0.90),显示了NCSVM算法较好的混合像元分解性能。
| MAE | 植被 | 水 | 阴影 | 居民用地 | 工业用地 | 总体 |
| NCSVM | 0.19 | 0.06 | 0.07 | 0.27 | 0.11 | 0.35 |
| MESMA | 0.20 | 0.13 | 0.13 | 0.26 | 0.15 | 0.44 |
| 算法 | 地物 | 参考数据 | ||||
| 植被 | 水 | 阴影 | 居民用地 | 工业用地 | ||
| NCSVM | 植被 | 33.12 | 0 | 0 | 0 | 0 |
| 水 | 0.19 | 14.49 | 0 | 0.78 | 0 | |
| 阴影 | 0.07 | 0 | 4.31 | 0.27 | 0 | |
| 居民用地 | 0 | 0 | 0 | 34.34 | 0 | |
| 工业用地 | 1.07 | 0 | 0 | 4.5 | 6.87 | |
| 总体精度 | 0.93 | Kappa | 0.90 | |||
| MESMA | 植被 | 24.79 | 3.07 | 2.71 | 0 | 2.56 |
| 水 | 0 | 15.45 | 0 | 0 | 0 | |
| 阴影 | 0 | 0 | 4.65 | 0 | 0 | |
| 居民用地 | 0 | 5.43 | 4.8 | 19.58 | 4.53 | |
| 工业用地 | 0 | 0 | 0 | 0 | 12.44 | |
| 总体精度 | 0.77 | Kappa | 0.71 | |||
为了进一步分析混合像元算法的分解精度,在Landsat ETM+影像数据上任意选取30个数据点[21],运用NCSVM和MESMA算法求得数据点的组分值。数据点的组分值与SPOT HRG参考数据实际组分值之间的关系如图 7和图 8所示。图中DTotal表示各样本组分值与SPOT HRG参考数据实际组分差值之和,DTotal越小代表组分值越接近SPOT HRG参考数据所代表的实际地物组成。与MESMA算法相比,NCSVM方法在各类型中得到的DTotal值均较小,混合像元分解精度高。

|
| 图 7 NCSVM算法组分值与SPOT HRG参考数据间关系(Landsat ETM+影像任意采样30个点) Fig. 7 Relationships for the 30 test samples between the estimated fraction using NCSVM and the “actual” fraction digitized from the SPOT HRG image |

|
| 图 8 MESMA算法组分值与SPOT HRG参考数据间关系(LandsatETM+影像任意采样30个点) Fig. 8 Relationships for the 30 test samples between the estimated fraction using MESMA and the “actual” fraction digitized from the SPOT HRG image |
由于混合像元的存在,传统的基于像素的分类方法存在明显误差。混合像元分解中固定端元光谱应用于影像所有像元组分提取,也很难高精度地识别多光谱影像地物。因此,文中提出了基于SVM的端元可变非线性混合像元分解算法,并与经典MESMA算法分解结果进行比较,结果表明本文方法在分解准确性方面有明显优势。
研究还发现,虽然NCSVM算法进行遥感影像混合像元分解提高了分解精度,但还有错分情况。为了提高分解精度,在光谱信息的基础上可以融合坡度、纹理等影像信息。另外,参数的优化设置也是NCSVM混合像元精确分解的关键因素之一,参数优化方法仍可加以改善。
| [1] | 刘正春, 曾永年, 何丽丽, 等. 基于光谱归一化的变组分光谱混合分析(NMESMA)方法及其应用[J]. 遥感技术与应用, 2012, 27(2): 159-167. LIU Zhengchun, ZENG Yongnian, HE Lili, et al. Method of Normalized Multiple Endmember Spectral Mixture Analysis and Its Application[J]. Remote Sensing Technology and Application, 2012, 27(2): 159-167. |
| [2] | 陈述彭, 童庆禧, 郭华东. 遥感信息机理研究[M]. 北京: 科学出版社, 1998. CHEN Shupeng, TONG Qinxi, GUO Huadong. Research on Mechanism of Remote Sensing Information[M]. Beijing: Science Press, 1998. |
| [3] | 王旭红, 郭建明, 贾百俊, 等. 元胞自动机的遥感影像混合像元分类[J]. 测绘学报, 2008, 37(1): 42-48. WANG Xuhong, GUO Jianming,JIA Baijun, et al. Mixed Pixels Classification of Remote Sensing Images Based on Cellular Automata[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(1): 42-48. |
| [4] | SOMERS B, ASNER G P, TITS L, et al. Endmember Variability in Spectral Mixture Analysis: A Review[J]. Remote Sensing of Environment, 2011, 115(7): 1603-1616. |
| [5] | 吴波, 熊助国. 基于光谱最佳尺度分割特征的高光谱混合像元分解[J]. 测绘学报, 2012, 41(2): 205-212. WU Bo,XIONG Zhuguo.Unmixing of Hyperspectral Mixture Pixels Based on Spectral Multiscale Segemented Features[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(2): 205-212. |
| [6] | ZARE A, HO K C. Endmember Variability in Hyperspectral Analysis: Addressing Spectral Variability during Spectral Unmixing[J]. IEEE Signal Processing Magazine, 2014, 31(1): 95-104. |
| [7] | BEDINI E.Mapping Lithology of the Sarfartoq Carbonatite Complex,Southern West Greenland, Using HyMap Imaging Spectrometer Data[J]. Remote Sensing of Environment, 2009, 113(6): 1208-1219. |
| [8] | 丁建丽, 姚远. 干旱区绿洲典型地物MESMA模拟分解与验证[J]. 地球信息科学学报, 2013, 15(3): 452-460. DING Jianli, YAO Yuan. Research on Pixel Unmixing of Typical Surface Features in Oasis Based on the MESMA Model[J]. Journal of Geo-Information Science, 2013, 15(3): 452-460. |
| [9] | BACHMANN C M, AINSWORTH T L, FUSINA R A. Improved Manifold Coordinate Representations of Large-Scale Hyperspectral Scenes[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(10): 2786-2803. |
| [10] | 吴波, 袁春. 非线性混合像元分解的可视化分析与评价[J]. 中国图象图形学报, 2010, 15(1): 167-173. WU Bo, YUAN Chun. Visualized Analysis and Evaluation of Nonlinear Unmixing the Mixed Pixels[J]. Journal of Image and Graphics, 2010, 15(1): 167-173. |
| [11] | BROADWATER J, BANERJEE A. A Generalized Kernel for Areal and Intimate Mixtures[C]//Proceedings of the 2nd Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing. Reykjavik: IEEE, 2010: 1-4. |
| [12] | BROADWATER J, BANERJEE A. Mapping Intimate Mixtures Using An Adaptive Kernel-based Technique[C]//Proceedings of the 3rd Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing. Lisbon: IEEE, 2011: 1-4. |
| [13] | PLAZA J, PLAZA A. Spectral Mixture Analysis of Hyperspectral Scenes using Intelligently Selected Training Samples[J]. IEEE Geoscience and Remote Sensing Letters, 2010, 7(2): 371-375. |
| [14] | ALTMANN Y, DOBIGEON N, TOURNERET J Y, et al. Nonlinear Unmixing of Hyperspectral Images using Radial Basis Functions and Orthogonal Least Squares[C]//Proceedings of IEEE International Conference Geoscience and Remote Sensing Symposium. Vancouver: IEEE, 2011: 1151-1154. |
| [15] | LICCIARDI G A, DEL F F. Pixel Unmixing in Hyperspectral Data by Means of Neural Networks[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(11): 4163-4172. |
| [16] | ALTMANN Y, HALIMI A, DOBIGEON N, et al. Supervised Nonlinear Spectral Unmixing Using a Postnonlinear Mixing Model for Hyperspectral Imagery[J]. IEEE Transactions on Image Processing, 2012, 21(6): 3017-3025. |
| [17] | VLADIMIR N V. The Nature of Statistical Learning Theory[M]. New York: Springer, 1998. |
| [18] | BOVOLO F,BRUZZONE L,CARLIN L.A Novel Technique for Subpixel Image Classification Based on Support Vector Machine[J]. IEEE Transactions on Image Processing, 2010, 19(11): 2983-2999. |
| [19] | 李慧, 王云鹏, 李岩, 等. 基于SVM和PWC的遥感影像混合像元分解[J]. 测绘学报, 2009, 38(4): 318-323. LI Hui, WANG Yunpeng, LI Yan, et al. Unmixing of Remote Sensing Images Based on Support Vector Machines and Pairwise Coupling[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(4): 318-323. |
| [20] | HSU C W, LIN C J. A Comparison of Methods for Multiclass Support Vector Machines[J]. IEEE Transactions on Neural Networks, 2002, 13(2): 415-425. |
| [21] | 李慧, 王云鹏, 李岩, 等. 基于形态学和支持向量的遥感图像混合像元分解[J]. 遥感技术与应用, 2009, 24(1): 114-119. LI Hui, WANG Yunpeng, LI Yan, et al. Unmixing Remote Sensing Imagery Based on Morphology and Support Vector Machines[J]. Remote Sensing Technology and Application, 2009, 24(1): 114-119. |
| [22] | TANG J, WANG L, MYINT S W. Improving Urban Classification Through Fuzzy Supervised Classification and Spectral Mixture Analysis[J]. International Journal of Remote Sensing, 2007, 28(18): 4047-4063. |
| [23] | PONTIUS Jr R G, SHUSAS E, MCEACHERN M. Detecting Important Categorical Land Changes While Accounting for Persistence[J]. Agriculture, Ecosystems & Environment, 2004, 101(2-3): 251-268. |
| [24] | WILLMOTT C J, MATSUURA K. On the Use of Dimensioned Measures of Error to Evaluate the Performance of Spatial Interpolators[J]. International Journal of Geographical Information Science, 2006, 20(1): 89-102. |
| [25] | PONTIUS Jr R G, CHEUK M L. A Generalized Cross-tabulation Matrix to Compare Soft-classified Maps at Multiple Resolutions[J]. International Journal of Geographical Information Science, 2006, 20(1): 1-30. |
| [26] | CHAPELLE O, VAPNIK V, BOUSQUET O, et al. Choosing Multiple Parameters for Support Vector Machines[J]. Machine Learning, 2002, 46(1-3): 131-159. |
| [27] | 吴涛. 核函数的性质、方法及其在障碍检测中的应用[D]. 长沙: 国防科学技术大学, 2003. WU Tao. Kernels' Properties, Tricks and Its Applications on Obstacle Detection[D]. Changsha: National University of Defense Technology, 2003. |