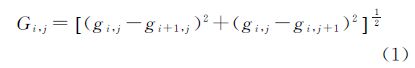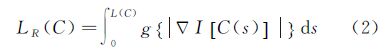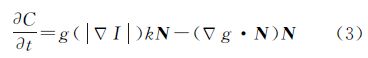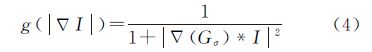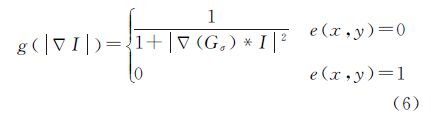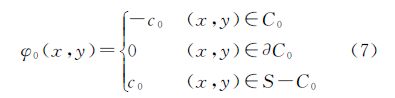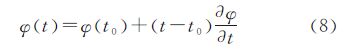2. 海军海洋测绘研究所,天津 300061
2. Navey Institute of Hydrographic Surveying and Charting, Tianjin 300061, China
海陆影像分割,即海岸带及岛(礁)影像水边线提取,对后续的海岸线提取[1, 2, 3, 4, 5, 6, 7]、潮间带地形反演[8]、海岸演化分析[9, 10]、潮间带性质和分布信息提取[10, 11]、航行方位物提取[12]等都具有十分重要的意义。海陆影像分割的方法较多,除了传统的基于边界检测和基于区域提取的图像分割方法[1, 2]以外,还有基于小波变换[3]、神经网络[4]、数学形态学[13]、分形理论和模糊集理论等数学工具的新型分割方法。一般来说,现有方法进行海陆影像自动分割主要存在以下3个问题[6, 7]:①潮湿的潮滩以及近岸水体的高含沙量使得遥感影像上水、陆交界处灰度和色度变化不明显,即表现为“弱边缘”,在这类“弱边缘”难以实现准确分割;②潮滩表面复杂的微地形及大量潮沟的存在,造成海陆交界线形状复杂,特别是会出现严重凹陷的情况,即表现为“严重凹陷边缘”,这类“严重凹陷边缘”容易提前收敛,造成分割错误;③需要人机交互,自动化程度低,分割时间长。
近年来随着活动轮廓模型在图像分割领域得到广泛应用[14, 15, 16, 17, 18, 19, 20],一些学者[19, 20]也将其应用于海陆影像分割中来解决上述问题。特别是测地线活动轮廓(geodesic active contour,GAC)模型用于影像分割的诸多优势引起了国内外学者的广泛关注,并在一系列图像中验证了其有效性[6, 7, 15, 16, 17, 18],逐渐成为最有生机和最成功的图像分割技术之一。学者们针对上述海陆影像自动分割方面存在的问题进行了积极的探索。文献[20]将光谱特性引进偏微分方程活动轮廓模型,保证了水、陆区域分割的精度,但自动化程度低,并且高光谱自身数据量大,算法运算时间长;文献[2]提出了一种基于四叉树和几何活动轮廓模型的海陆影像分割方法,实现海陆影像的自动快速分割,但分割的准确度不够高,特别是在上述“弱边缘”处不能准确分割;文献[6—7]研究了基于测地线活动轮廓模型的影像水边线提取方法,提高了海陆影像分割的可靠性,但仍然需要人工在影像上选择种子区域,自动化程度较低,提取时间较长,还不能很好地满足后续研究或者自动测图的需求。
综合考虑上述各方法的优势和不足,在对四叉树影像分割、Canny边缘检测和GAC模型影像分割原理进行分析的基础上,本文提出了一种基于四叉树、Canny算子和GAC模型相结合的海陆影像分割方法,既实现了包括“弱边缘”和“严重凹陷边缘”在内的水边线准确提取,又无须人工确定初始边界。
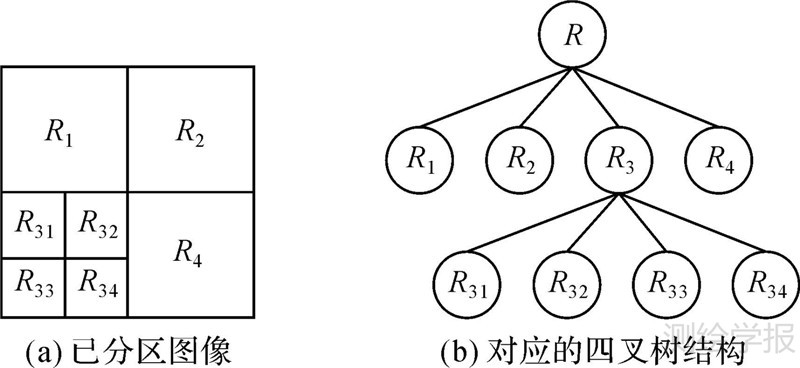
1 四叉树和GAC模型相结合的海陆影像分割原理 1.1 基于四叉树的海陆影像分割四叉树分割的基本思想是将方形的原始影像分成4个相同大小的方块,如图 1所示,判断每个方块是否满足一致性测度,如灰度是否均匀;如果满足就不再继续分裂,如果不满足就再分成4个方块,并对得到的方块继续应用一致性检验;迭代直到所有的方块都满足一致性测度;最后还要对相同性质的邻近区域进行合并,同时在合并的过程中完成对像素的标记。基于四叉树的图像分割方法,实质是区域的分裂与合并技术采用四叉树的结构进行图像分割,其分割速度较快,且分割过程是全自动的[21],这是基于四叉树的图像分割的明显优势。
|
| 图 1 四叉树分割 Fig. 1 Quadtree Segmentation |
海岸带、海岛(礁)影像的海域部分像素的灰度值具有一定的均匀特性,采用四叉树的方法进行海岛礁分割比较适合。由于海域部分的梯度相对较小,而海陆分界处的梯度相对较大,构建梯度图后更有利于分割。为提高运算效率,采用简单的梯度算子,如式(1)进行梯度图构建
海岸带、海岛(礁)区域在整体上呈现出灰度分布的不均匀性,但在区域内部可能存在一些灰度值比较均匀的局部区域,这样基于四叉树方法分割结束并进行二值化处理后可能会产生孔洞,这时需要对孔洞进行填充。具体的填充方法是根据图像的连通性确定陆地边界,对陆地边界内的背景像素进行填充操作,如图 2所示。

|
| 图 2 孔洞填充结果 Fig. 2 The result of holes filled |
基于四叉树海陆影像分割的缺陷是当海域和陆地的界限不明显时,往往导致分割错误或分割精度不高,特别是对于上述“弱边缘”和“严重凹陷边缘”不能准确地完成分割。但该分割方法的优势可以考虑在海陆影像分割中加以利用,提高分割的效率,实现全自动海陆影像分割。
1.2 Canny算子边缘检测边缘检测是影像分割常用的一类方法,Canny提出了优良的边缘检测算子应满足的3个准则:信噪比好、定位性能好、单边缘响应。Canny算子[22]就是基于3个最优准则提出的,能在噪声抑制和边缘检测之间取得较好的平衡,且对受白噪声影响的阶跃型边缘的响应是最优的,特别是检测的精度很高,因此适合于海陆影像的分割。
但是包括Canny算子在内的边缘检测算子存在着一些不足,主要表现在检测的边缘往往是不连续的,边缘点之间出现断裂,如图 3所示,不利于后续边缘跟踪和精化处理,这样利用Canny算子进行海陆影像分割就难以得到一条完整、理想的水陆交界线。但Canny算子边缘检测精度高,对弱边缘也有响应的优点,可以在海陆影像分割中加以利用。

|
| 图 3 Canny算子检测结果 Fig. 3 Edge detection results of Canny operator |
GAC模型的基本思想是使用连续曲线来表达目标边缘,并定义一个能量泛函使其自变量包括边缘曲线,因此分割过程就转变为求解能量泛函最小值的过程,一般通过求解函数对应的欧拉方程来实现,能量达到最小时的曲线位置就是目标的轮廓所在。GAC模型的基础是水平集方法,即把n维描述视为有n维变量的水平集函数f的水平集,避免了对闭合曲线演化过程的跟踪,将曲线的演化转化成一个纯粹的偏微分方程求解问题。
GAC模型的能量泛函为
式中,L(C)表示闭合演化曲线C的弧长;g(|▽I|)为边界停止函数;▽I[C(s)]为图像I[C(s)]的梯度;▽|I[C(s)]|为图像I[C(s)]梯度的模;C(s)函数指闭合曲线C;s表示闭合曲线的弧长参数;LR(C)则表示“加权弧长”。则式(2)的梯度下降流表示为 式中,k为曲线的曲率;N为曲线上点的单位法向量;边界停止函数g(|▽I|)定义为 式中,Gσ指标准差为σ的高斯核;*表示卷积;g(|▽I|)是关于图像梯度模|▽I|的递减函数,在图像边缘附近,该函数值将变得很小致使闭合曲线“停止”演化。公式(3)中的▽为梯度算子,▽g是由图像I产生的,其作用就是使曲线C向着图像中目标的边缘靠近,并稳定在边缘上。基于曲线演化理论和水平集方法的GAC模型不仅能够自适应地处理拓扑结构变化、提供高精度的闭合分割曲线,而且对初始条件不敏感、数值实现简单,这些优点都有利于海陆影像分割。但基于GAC模型的影像分割方法也存在一些缺点,主要表现为需要人工选取初始轮廓、水平集方程演化速度较慢、对严重凹陷边缘的提取容易陷入局部极小值而提前停止演变、弱边缘分割可靠性差等问题。
经过距离正则化,得到的梯度流演化方程为[17]
式中,φ为高维超曲面函数;t为时间;▽为梯度算子;div为散度算子;g(|▽I|)为边界停止函数;δε(φ)为正则化的狄拉克函数;μ、λ和α为常系数,通常μ取1.0、λ取5.0、α取2.0;φ(·,0)表示初始演化时函数φ的取值,φ0为初始化嵌入函数。dp(▽φ)计算公式为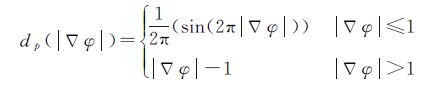
式(5)第1项是为了保持水平集函数为距离符号函数;第2项保证演变的轮廓曲线的平滑性;第3项的常系数α是为了增加轮廓法方向上的演变速度,提高演变效率。GAC模型主要依靠边界停止函数实现图像分割,实际影像边界处梯度值有界,根据式(4)可知边界停止函数在边界处的值并不为零,由式(3)可知此时轮廓法方向上的演变速度不为零,这会造成分割越界,尤其是在水陆界限不明显的“弱边缘”处。针对“严重凹陷边缘”局部极小值问题加入常系数α,虽然这能够使得能量函数收敛于深度凹陷的边界,而且提高了轮廓演化的效率,但是也带来了一些问题:α过小时,分割曲线未到达凹陷边缘处便提前停止演变,如图 4所示;但α过大时,轮廓法方向上的演变速度线性放大,轮廓越过非“严重凹陷边缘”以及“弱边缘”的可能性又会增加。因此,即使改进后的GAC模型也难以实现“弱边缘”和“严重凹陷边缘”的同时提取。

|
| 图 4 GAC模型的局部极小值问题 Fig. 4 Local minimum value problem of GAC model |
由以上分析可以看出,如果边界停止函数在边界处的值为零,轮廓法方向上的演变速度则为零,这样即使α较大,轮廓法方向上的演变速度线性放大,也不可能发生演化轮廓越过非凹陷边缘以及弱边缘的问题,同时凹陷边缘也能准确提取。考虑到Canny算子能准确地检测出包括海陆界限不明显的“弱边缘”在内的目标边界,因此对边界停止函数进行如下重构:e为Canny算子边缘检测结果,e(x,y)=1表示该点为边缘点,e(x,y)=0表示该点为非边缘点,则
这样就既可以实现对包括海陆界限不明显的“弱边缘”的准确提取,不至于越过弱边缘;又可以实现对“严重凹陷边缘”的准确提取,不至于提前停止演变。
但这样改进后的方法仍然需要人工确定种子区域,自动化程度低、速度慢。考虑到上述基于四叉树的海陆影像分割方法在这些方面具有的优势,这里将基于四叉树的海陆影像分割方法和上述改进后的海陆影像分割方法进行结合:首先利用Canny算子进行海陆影像边缘检测,检测得到水边线上的边缘点,接着利用四叉树方法实现海陆影像初分割,然后利用此初分割获取的轮廓作为GAC模型海陆影像分割的初始轮廓,最后将Canny边缘检测结果作为判别条件融入到GAC模型重构的边界停止函数中,演化水平集方程,最终实现海陆影像的自动、快速和精确分割。
为了给海陆影像分割提供良好的初始轮廓,并考虑到提高后续算法的计算效率,要求基于四叉树方法获取的初始轮廓与真正边界越接近越好,但必须要求初始轮廓边界不能越过真正边界,否则会造成最终分割错误。因此在利用四叉树进行影像初分割时,一致性测度阈值的选取非常关键。在完成梯度图的构建以后,在梯度图上完成四叉树初分割。本文选取基于区域灰度差的一致性测度。即用m(x)表示像素x的灰度值,对于某一图像方块区域的任意x1、x2,若||m(x1)-m(x2)||≤T,则停止分裂,否则继续分裂为4等分。T为预先设置的阈值,由经验确定,以256个灰度级的图像为例,当影像中水域与陆地交界处的灰度变化明显时,T取较大的值,一般取30为宜;否则,T取较小的值,为防止越过真正边界,一般取20为宜。为了防止初始轮廓边界越过真正边界,从客观上降低T阈值的不当选取对最后分割结果的影响,Canny算子的边缘检测结果也得到了应用。若初始轮廓边界越过了Canny算子检测到的边缘,则需要适当增大阈值T的取值,确保初始轮廓边界不会越过真正边界,防止造成最后的分割错误。
初始轮廓对比如图 5所示,图 5(a)为人工选取初始轮廓,图 5(c)为基于四叉树初分割自动获取的初始轮廓,孔洞的填充使得初始轮廓均位于海域,其与目标边界又比较接近,为全自动进行海陆影像分割,减少后续轮廓演化的迭代次数、缩短影像分割时间提供了条件。

|
| 图 5 初始轮廓对比 Fig. 5 Comparison of initial contours |
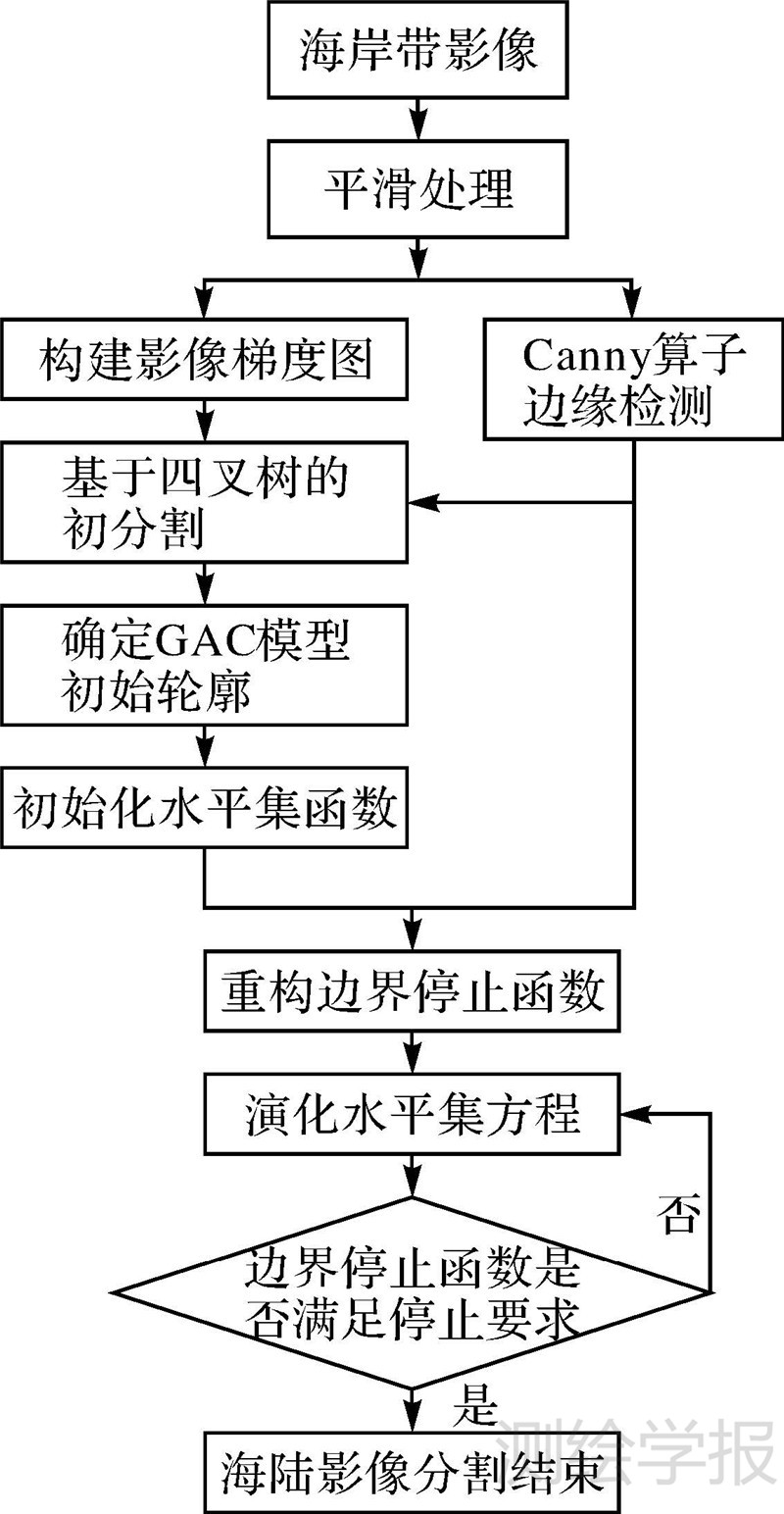
基于四叉树和GAC模型的海陆影像分割算法流程如图 6所示,过程如下。
|
| 图 6 海陆影像分割流程图 Fig. 6 Flowchart for image segmentation of island and coastal |
(1) 对海岸带遥感影像进行平滑处理,全色影像以亮度为处理域,彩色影像以HSV空间的色度空间为处理域,色度空间能够减小由于波浪的镜面反射对提取结果的影响。
(2) 利用Canny算子进行影像边缘检测。
(3) 利用四叉树对原始影像进行初分割,利用Canny算子的边缘检测结果防止初始轮廓边界越过真正边界,孔洞填充,得到初始轮廓C0,影像定义为S,边界为∂C0。对水平集函数进行如下初始化
式中,c0为大于0的常数。(4) 利用Canny算子边缘检测结果重构边界停止函数(利用式(6))。
(5) 演化水平集方程。每次迭代在前一次t0的基础上进行,在当前t时刻处计算新的梯度和散度等数值,利用式(5)计算得到$\frac{\partial \varphi }{\partial t}$,新的轮廓曲线由式(8)计算得到
(6) 当轮廓不再发生变化时停止演变,否则返回步骤(5)继续迭代,进行演化。
3 试验及结果分析对上述算法进行了多组试验验证,下面列出3组试验结果,硬件环境为Inter(R) Core(TM) i5-3570 3.40 GHz,4.00 GB RAM。试验1是本文提出的海陆影像分割方法与文献[2]、文献[7]方法分别进行海陆影像分割,并进行试验结果对比;试验2和3分别是针对“弱边缘”和“严重凹陷边缘”水边线的海陆影像分割。
试验1结果如图 7所示:(a)为天绘一号卫星影像(部分影像),分辨率2 m,影像尺寸为498×427像素;(b)为Canny算子边缘检测结果;(c)为基于四叉树初分割获取的初始轮廓;(d)为文献[2]方法分割结果;(e)为文献[7]方法分割结果;(f)为本文提出方法分割结果。

|
| 图 7 试验1结果 Fig. 7 Results of experiment 1 |
从图 7可以看出,Canny算子边缘检测的精度很高,为后续水边线精确提取打下了基础;基于四叉树分割获取的初始轮廓均位于海域,与实际水边线比较接近,为减少后续算法迭代次数、提高计算效率提供了条件;文献[2]方法海陆影像分割结果不够准确,有较多地方越过水边线(如选区中的影像);本文提出的方法和文献[7]方法在本试验中的分割结果一致,与真实海陆交界线吻合较好。试验过程中,为了定量分析3种方法水边线提取的效率,从迭代次数和运行时间两方面进行说明,结果见表 1。
通过图 7和表 1可以看出,本文提出的方法继承了基于四叉树的海陆影像分割(文献[2])方法的优势,并且精度和可靠性更高,其较基于GAC模型的水边线提取方法(文献[7]),效率有明显提高,并且实现了分割过程的全自动。
试验2结果如图 8所示,为针对“弱边缘”水边线的海陆影像分割试验结果。原始影像为天绘卫星影像(部分影像),分辨率2 m,如图 8(a),影像尺寸为859×710像素,退潮后露出的滩涂、礁石区域由于之前在水下,使得影像选区存在水陆界限很不明显的弱边缘水边线,如图 8(d)。从图 8(b)、(e)可以看出,文献[2]算法分割时越过了弱边界;从图 8(c)、(f)可以看出,本文提出的算法分割精细,能够实现对水陆界限不明显的“弱边缘”水边线的准确提取。各算法迭代次数及运行时间见表 2。

|
| 图 8 “弱边缘”水边线提取试验结果 Fig. 8 Experimental results of waterline extraction for weak edges |
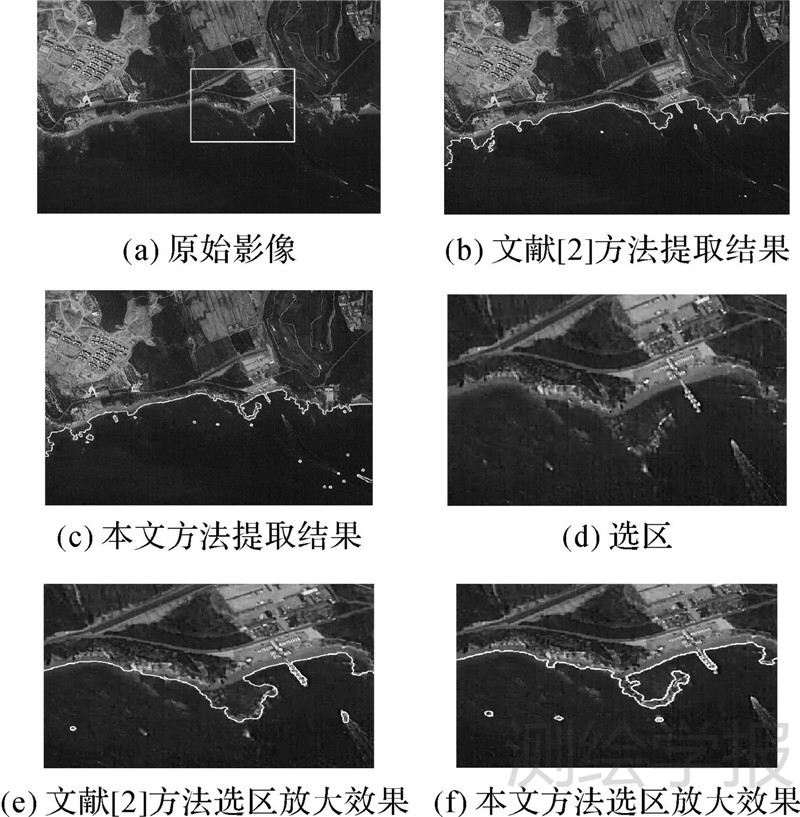
试验3结果如图 9所示,为“严重凹陷边缘”水边线提取结果。原始影像为天绘卫星影像(部分影像),分辨率2 m,如图 9(a),影像尺寸为811×639像素,影像中存在着“严重凹陷边缘”(图 9(a)中的选区内)。从图 9(b)、(e)可以看出,文献[2]算法不能实现“严重凹陷边缘”的提取,分割效果较差;从图 9(c)、(f)可以看出,本文提出的算法演化轮廓能够较好地收敛于凹陷边界处,实现对“严重凹陷边缘”的准确提取。各算法迭代次数及运行时间见表 3。
|
| 图 9 “严重凹陷边缘”水边线提取试验结果 Fig. 9 Experimental results of waterline extraction for serious concave edges |
试验2和试验3中,文献[7]算法也能实现“弱边缘”和“严重凹陷边缘”水边线的准确提取(结果与本文方法相似,未列出),但从表 2和表 3可以看出,迭代次数明显比本文提出的算法多,提取时间长,由于还需要人工选取初始轮廓,自动化程度低。从试验2和试验3可以看出,本文方法很好地解决了“弱边缘”和“严重凹陷边缘”水边线提取的技术难题,海陆影像分割可靠性强,精度高,速度快。
4 结 论针对海陆影像自动分割,特别是“弱边缘”和“严重凹陷边缘”水边线的提取问题,本文提出了一种四叉树、Canny算子和GAC模型相结合的海陆影像分割方法。试验结果表明,该方法具有以下特点:①自动化程度高,不需要人机交互选取初始轮廓,为后续自动化测图打下基础;②海陆影像分割速度快,迭代次数少,效率高;③精度高,利用Canny算子的边缘检测结果重构边界停止函数,继承了Canny算子高精度的优点;④能够提供闭合的分割边界且可靠性强,对于水陆界限不明显的“弱边缘”和“严重凹陷边缘”的水边线都能得到较好地提取。
| [1] | LIU H, JEZEK K C. Automated Extraction of Coastline from Satellite Imagery by Integrating Canny Edge Detection and Locally Adaptive Thresholding Methods[J]. International Journal of Remote Sensing, 2004, 25(5): 937-958. |
| [2] | ZHANG Hongwei,ZHANG Baoming,GUO Haitao,et al. An Automatic Coastline Extraction Method Based on Active Contour Model[C]//Proceedings of the 21st International Conference on Geoinformatics. Kaifeng: IEEE, 2013: 111-115. |
| [3] | NIEDERMEIER A, ROMANEESSEN E, LEHNER S. Detection of Coastlines in SAR Images Using Wavelet Methods[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(5): 2270-2281. |
| [4] | RYU J H, WON J S. Application of Neural Networks to Waterline Extraction in Tidal Flat from Optic Satellite Images[C]//Proceedings of IEEE International Geoscience and Remote Sensing Symposium (IGARSS). Toronto: IEEE, 2002, 4: 2026-2028. |
| [5] | DING Xianwen, NUNZIATA F, LI Xiaofeng, et al. Performance Analysis and Validation of Waterline Extraction Approaches Using Single-and Dual-polarimetric SAR Data[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(3): 1019-1027. |
| [6] | 沈琦, 汪承义, 赵斌. 几何活动轮廓模型用于高分辨率遥感影像海岸线自动提取. 复旦学报(自然科学版), 2012, 51(1): 77-82, 104. SHEN Qi, WANG Chengyi, ZHAO Bin. Automatic Waterline Extraction in VHR Imagery Using Geometric Active Contour Model[J]. Journal of Fudan University (Natural Science),2012, 51(1): 77-82, 104. |
| [7] | 申家双, 郭海涛, 李海滨, 等. 基于Canny算子和GAC模型相结合的影像水边线提取方法[J]. 测绘科学技术学报, 2013, 30(3): 264-268. SHEN Jiashuang, GUO Haitao, LI Haibin, et al. A Water Edge Extraction Method from Images Based on Canny Operator and GAC Model[J]. Journal of Geomatics Science and Technology, 2013, 30(3): 264-268. |
| [8] | 沈芳, 郜昂, 吴建平, 等. 淤泥质潮滩水边线提取的遥感研究及DEM构建——以长江口九段沙为例[J]. 测绘学报, 2008, 37(1): 102-107. SHEN Fang, GAO Ang, WU Jianping, et al.A Remotely Sensed Approach on Waterline Extraction of Silty Tidal Flat for DEM Construction: A Case Study in Jiuduansha Shoal of Yangtze River[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(1): 102-107. |
| [9] | NOAA, Shoreline Mapping. Silver Spring, MD, USA: NOAA, 1997[EB/OL]. [2015-05-03]http://anchor.ncd.noaa.gov/psn/shoreline.html. |
| [10] | ZHANG Suoping, ZHANG Chuntian. Image Analysis for Wave Swash Using Color Feature Extraction[C]//Proceedings of the 2nd International Congress on Image and Signal Processing (CISP). Tianjin: IEEE, 2009: 1-4. |
| [11] | QIN Ping. Waterline Information Extraction from Radial Sand Ridge of South Yellow Sea[C]//Proceedings of the 6th International Congress on Image and Signal Processing (CISP). Hangzhou: IEEE, 2013: 459-463. |
| [12] | LI Heng, WANG Xinyu. Automatic Recognition of Ship Types from Infrared Images Using Support Vector Machines[C]//Proceedings of International Conference on Computer Science and Software Engineering. Wuhan: IEEE, 2008, 6: 483-486. |
| [13] | BAGLI S, SOILE P. Morphological Automatic Extraction of Pan-European Coastline from Landsat ETM+ Images[C]//Proceedings of the 5th International Symposim on GIS and Computer Cartography for Coastal Zone Management. Genova: [s.n.], 2003. |
| [14] | 孔丁科. 几何活动轮廓图像分割模型的研究[D]. 杭州: 浙江大学, 2010. KONG Dingke. Research on Geometric Active Contour Models for Image Segmentation[D]. Hangzhou: Zhejiang University, 2010. |
| [15] | 孙颖, 张新长, 康停军, 等. 改进GAC模型在点云和影像自动提取建筑物边界中的应用[J]. 测绘学报, 2013, 42(3): 337-340, 350. SUN Ying, ZHANG Xinchang, KANG Tingjun,et al. Improved GAC Model for Automatic Building Extraction from LiDAR Point Clouds and Aerial Image[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(3): 337-343, 350. |
| [16] | 戚世乐, 王美清. 自适应分割弱边缘的活动轮廓模型[J]. 山东大学学报(工学版), 2013, 43(6): 17-20. QI Shile,WANG Meiqing. Adaptive Active Contour Model for Weak Boundary Extraction[J]. Journal of Shandong University (Engineering Science), 2013, 43(6): 17-20. |
| [17] | LI Chunming, XU Chenyang, GUI Changfeng, et al. Distance Regularized Level Set Evolution and Its Application to Image Segmentation[J]. IEEE Transactions on Image Processing, 2010, 19(12): 3243-3254. |
| [18] | CASELLES V, CATTÉF, COLL T et al. A Geometric Model for Active Contours in Image Processing[J]. Numerische Mathematik, 1993, 66(1): 1-31. |
| [19] | 欧阳越, 种劲松. 基于改进水平集算法的SAR图像海岸线检测[J]. 遥感技术与应用, 2004, 19(6): 456-460. OUYANG Yue, CHONG Jinsong. Coastline Detection Method in SAR Images Based on an Improved Level Set Algorithm[J]. Remote Sensing Technology and Application, 2004, 19(6): 456-460. |
| [20] | 王相海, 金弋博. 高光谱海岸带区域分割的活动轮廓模型[J]. 中国图象图形学报, 2013, 18(8): 1031-1037. WANG Xianghai, JIN Yibo. The Active Contour Model for Segmentation of Coastal Hyperspectral Remote Sensing Image[J]. Journal of Image and Graphics, 2013, 18(8): 1031-1037. |
| [21] | 朱述龙. 四叉树结构在数字图像分割中的应用[J]. 测绘学院学报, 1994, 11(1): 21-24. ZHU Shulong. The Application of Quadtree to Digital Picture Segmentation[J]. Journal of Institute of Surveying and Mapping, 1994, 11(1): 21-24. |
| [22] | CANNY J. A Computational Approach to Edge Detection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1986, 8(6): 679-698. |