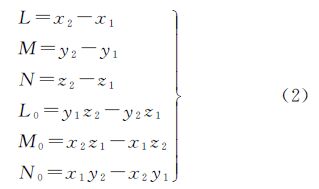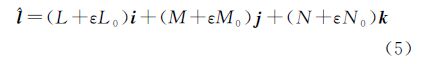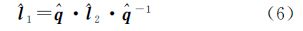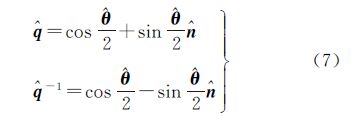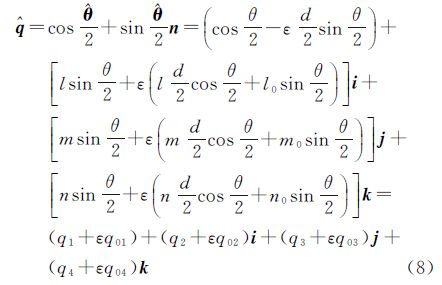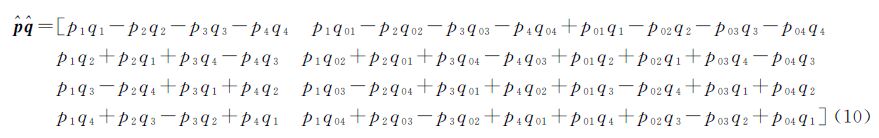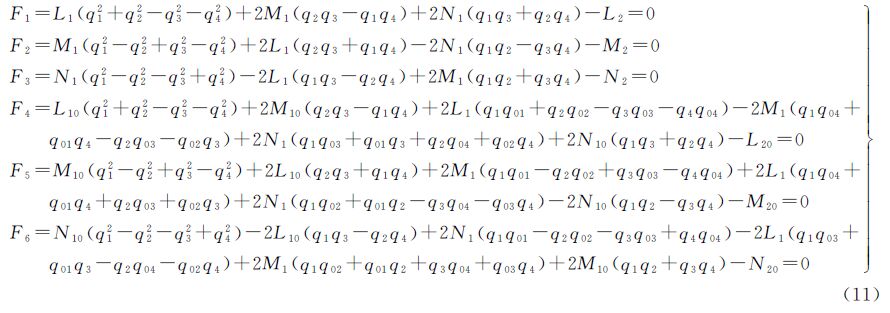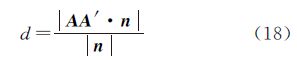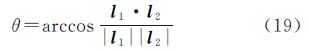LiDAR是城市空间信息获取的重要手段[1, 2, 3],由于城市空间目标复杂度较高,LiDAR系统数据采集通常需要从不同视角对空间目标进行扫描,再利用配准算法将相邻测站数据进行拼接,从而实现对空间目标的完整表达。根据配准基元的不同,配准算法主要是利用LiDAR点云之间的同名点、同名线和同名面特征。基于点特征的点云配准算法[4, 5, 6, 7, 8, 9],其主要为迭代最近点算法,实际上待配准的点云间不存在完全对应的同名点特征,这使得同名点特征配准算法的精度难以得到保证。选择平面作为特征则具有更好的准确性和稳健性[10, 11],基于面特征的点云配准算法便于确定同名平面特征,但是匹配算法对平面的拓扑关系以及数量有限制。一般情况,直线是遥感数据中高级的几何特征描述符号,相对于点,直线具有更强的几何拓扑性和几何约束性,可获得更高的配准精度。根据配准模型的不同,配准算法主要分为旋转矩阵与四元数,前者可用直线的单位向量代替直线求解旋转矩阵,然后采用两条相交直线的交点坐标求解平移矩阵[12];后者用四元数法来表达旋转矩阵,用两条相交直线来求解平移矩阵,角度的配准精度可以达到0.025°[13]。
然而,上述方法没有充分考虑空间直线的几何拓扑关系,配准模型的几何约束强度弱。唯一确定一条空间直线所需的最少参数是4个,然而这4维参数空间是一个4维流形,它不是4维欧几里德空间[14],因此采用何种数学方法描述和表达三维空间中的任意直线,才能充分发挥直线的几何拓扑性和几何约束性,增加配准模型区域网的几何强度,是提高LiDAR点云配准精度的关键。
Plücker直线坐标由直线相对于空间坐标系原点的矩矢量和直线方向矢量组成,其几何意义更加明确,形式上更加简洁,利用螺旋的Plücker坐标进行空间直线变换表示更加有效、快捷[15, 16, 17, 18, 19]。本文研究利用Plücker直线构建的点云配准模型,实现LiDAR点云的高精度配准。
1 Plücker直线 1.1 Plücker直线概念设一空间直线上的两个点分别为P1(x1,y1,z1)T与P2(x2,y2,z2)T,那么这条直线的方向矢量w和矩矢量v分别为
如果将w和v的分量表示成5维射影空间上的6个齐次坐标,那么用非零标量乘以所有的齐次坐标后仍然表示同一个点,因此每条直线确定了该空间上的唯一点,这6个齐次坐标被称作直线的Plücker坐标[20],即
若对w进行归一化处理,则Plücker坐标满足条件
根据式(1),可知w×v=0,因此可得到Plücker坐标满足的另外一个条件为
1.2 Plücker直线空间螺旋运动根据Charles定理,任何一个刚体的一般运动都可以通过绕某个轴的转动和沿该轴的平移实现,这种转动和平动的组合就像是螺旋式运动,因此可用螺旋运动来表示Plücker直线的一般运动变换[21]。文献[22]仿照描述空间点的螺旋运动,用对偶角和对偶方向余弦实现了Plücker直线的三维空间连续螺旋运动,方法包括对偶正交3×3矩阵、对偶特殊酉2×2矩阵、对偶泡利自旋矩阵以及对偶四元数法,通过比较,对偶四元数法是最好的Plücker直线螺旋运动表示方法,能统一处理Plücker直线的旋转和平移,克服螺旋运动时所产生的双值性的缺点[22],用单位对偶矢量$\hat{l}$表示的Plücker直线为
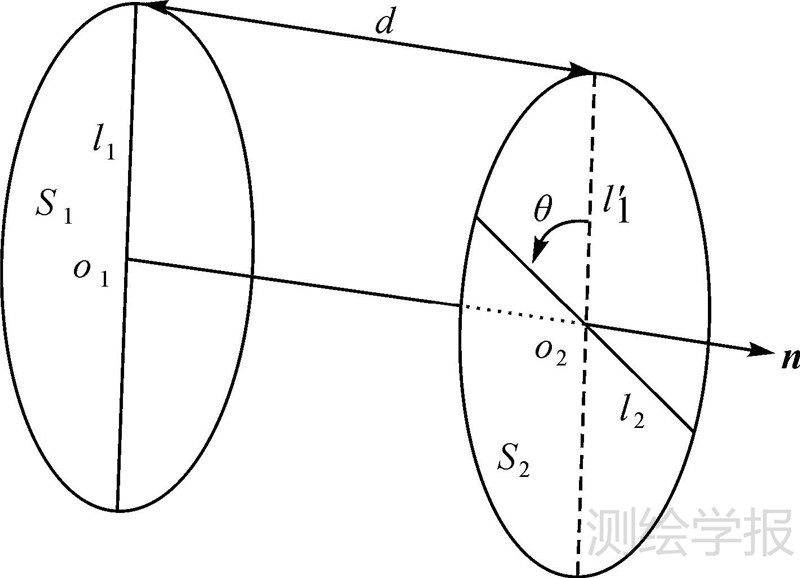
式中,ε为对偶单位,满足ε2=0,ε≠0;i、j、k为虚数单位,满足i2=j2=k2=ijk=-1。如图 1所示,Plücker直线空间坐标变换的几何意义为:l1沿着矢量n的方向平移距离d得到l′1,l′1绕着n旋转角度θ得到l2。其中,矢量n是l1与l2的公垂线,方向由o1指向o2,S1与S2是分别包含了l1与l2的相互平行的平面,从图 1中可以看出l′1与l1相互平行,l′1与l2在图 1所示的平面S2内共面。表达此空间变换的Plücker直线运动方程为
式中,$\hat{l}$1和$\hat{l}$2为直线l1和l2的单位对偶向量;$\hat{q}$为单位对偶四元数,$\hat{q}$-1为$\hat{q}$的逆。其中,$\hat{q}$与$\hat{q}$-1定义为 式中,$\hat{n}$为矢量n的单位对偶矢量,记为$\hat{n}$=(l+εl0)i+(m+εm0)j+(n+εn0)k;$\hat{\theta }$表示旋转的角度和平移的距离,$\hat{\theta }$=θ+εd。$\hat{q}$可展开为为便于计算,将$\hat{q}$、$\hat{q}$-1、$\hat{l}$1、$\hat{l}$2写成矩阵形式,根据式(3)和式(4)可知,$\hat{l}$1和$\hat{l}$2是标量部分为零的单位对偶四元数,则
|
| 图 1 Plücker直线表示的空间螺旋运动 Fig. 1 Plücker linear spiral movement of space |
对偶四元数矩阵形式的乘法运算法则如式(10)所示[20]。由于对偶四元数乘法不满足乘法的交换律和结合律,因此式(6)在进行计算时,要按照从左到右的顺序依次相乘
2 Plücker直线LiDAR点云配准模型 2.1 Plücker直线共线条件方程令l1表示待配准点云上的一条直线,l2表示基准点云上l1的同名直线,则相邻测站点云配准的几何条件为l1与l2完全重合,即在同一坐标系中两条直线共线。根据Plücker直线坐标的理论[20],两条直线共线的充要条件为两条直线的Plücker坐标对应成比例,又由于Plücker直线坐标经过式(3)的归一化处理,因此两条直线共线的条件是其各个坐标对应相等,即为式(6)的展开形式。
根据式(10)对偶四元数乘法运算法则,将式(6)展开可以得到6个方程
式(11)就是Plücker直线共线条件方程。将Plücker直线共线条件方程线性化,对$\hat{q}$按照泰勒公式展开至一次项
式中,a11=2L1q1+2N1q3-2M1q4;a12=2L1q2+2M1q3+2N1q4;a13=2N1q1+2M1q2-2L1q3;a14=-2M1q1+2N1q2-2L1q4; a21=2M1q1-2N1q2+2L1q4;a22=-2M1q2-2N1q1+2L1q3;a23=2M1q3+2N1q4+2L1q2;a24=-2M1q4+2N1q3+2L1q1 a31=2N1q1+2M1q2-2L1q3;a32=-2N1q2+2M1q1+2L1q4;a33=2M1q4-2N1q3-2L1q1; a34=2N1q4+2M1q3+2L1q2; a41=2L1q01+2L10q1-2M1q04-2M10q4+2N1q03+2N10q3; a42=-2L1q02+2L10q2-2M1q03-2M10q3+2N1q04+2N10q4; a43=-2L1q03+2L10q3+2M1q02+2M10q2+2N1q01+2N10q1; a44=-2L1q04-2L10q4-2M1q01-2M10q1+2N1q02+2N10q2; a51=2L1q04+2L10q4+2M1q01+2M10q1-2N1q02-2N10q2; a52=2L1q03+2L10q3-2M1q02-2M10q2-2N1q01-2N10q1; a53=2L1q02+2L10q2+2M1q03+2M10q3+2N1q04+2N10q4; a54=2L1q01+2L10q1-2M1q04-2M10q4+2N1q03+2N10q3; a61=-2L1q03-2L10q3+2M1q02+2M10q2+2N1q01+2N10q1; a62=2L1q04+2L10q4+2M1q01+2M10q1-2N1q02-2N10q2; a63=-2L1q01-2L10q1+2M1q04+2M10q4-2N1q03-2N10q3; a64=2L1q02+2L10q2+2M1q03+2M10q3+2N1q04+2N10q4; a15=a16=a17=a18=0;a25=a26=a27=a28=0;a35=a36=a37=a38=0;a45=a11;a46=a12;a47=a13; a48=a14a55=a21,a56=a22,a57=a23,a58=a24a65=a31,a66=a32,a67=a33,a68=a34; F10、F20、F30、F40、F50、F60分别为$\hat{q}$的近似值带入式(11)得到的F1—F6的近似值;dq1、dq2、dq3、dq4、dq01、dq02、dq03、dq04分别为待求的对偶四元数各元素的改正数。 2.2 平差解算将式(12)写成误差方程式的矩阵形式
式中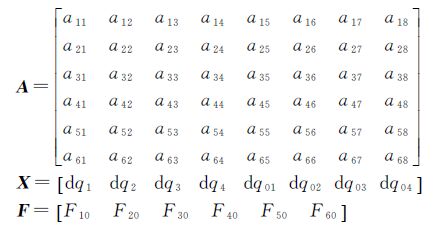
由于$\hat{q}$是单位对偶四元数,因此还存在两个约束条件
对式(14)进行线性化,可得约束条件方程的矩阵形式为
式中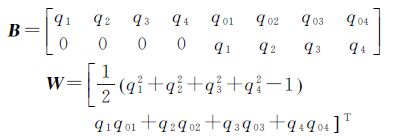
假设有n对同名直线,对每对直线可列一个式(13)的误差方程,联合式(15),得到Plücker直线LiDAR点云配准方程的整体平差公式为
式(16)中,V和F是6n维矩阵;A是6n×8维矩阵。根据最小二乘原理,得 式中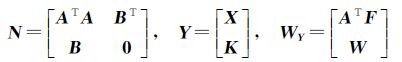
两条直线配准后,两条重合直线间的距离与夹角均为0。为评价两条直线的配准精度,可利用配准后的两条直线之间的距离与夹角指标。
n为l1和l2的公共法向量,在直线l1和l2上各取任意一点,记为A和A′,则向量AA′在n上的投影d即为两条直线间距离
两条直线l1和l2的夹角θ计算公式为
d和θ的几何意义为:当待配准点云与基准点云完成配准时,d=0 m,θ=0°;若没有完成配准,则d≠0 m或者θ≠0°,其数值大小反映出同名直线的匹配程度。
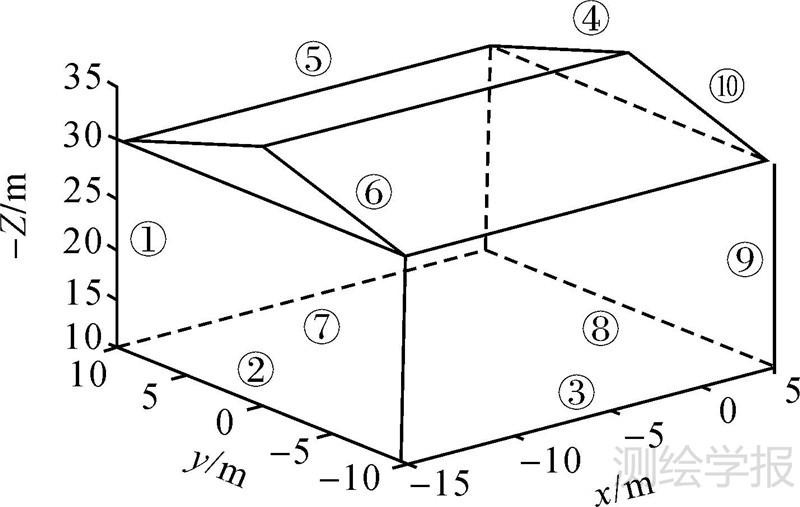
3 试验结果分析 3.1 模拟数据试验利用文献[23]的建筑物数据作为基准点云,将基准点云绕z轴旋转30°,各坐标轴方向上平移距离1 m,将所得到的数据作为待配准点云,直线分布如图 2所示。图 2中编号为①—④的直线用于配准,共4条;编号为⑤—⑩的直线为检查直线,共6条,试验结果见表 1和表 2。由表 1看出,配准结果与理论值基本一致,说明本文采用的方法是正确可行的。从表 2看出,直线配准后的距离精度均值为0.090 4 mm,角度均值为0.000 02°,说明算法对模拟数据具有较高的精度。
|
| 图 2 建筑物点云直线分布 Fig. 2 Lines distribution of building LiDAR point cloud |
| 参数 | 结果 |
| XS/m | 1.000 1 |
| YS/m | 0.999 94 |
| ZS/m | 0.999 96 |
| φ/(°) | -0.000 04 |
| ω/(°) | 0.000 005 |
| κ/(°) | 30.000 7 |
| 序号 | d/mm | θ/(°) |
| l1 | 0.105 6 | 0.000 039 |
| l2 | 0.088 3 | 0.000 007 |
| l3 | 0.109 2 | 0.000 039 |
| l4 | 0.058 6 | 0.000 008 |
| l5 | 0.106 4 | 0.000 004 |
| l6 | 0.092 7 | 0.000 007 |
| 均值 | 0.090 4 | 0.000 02 |
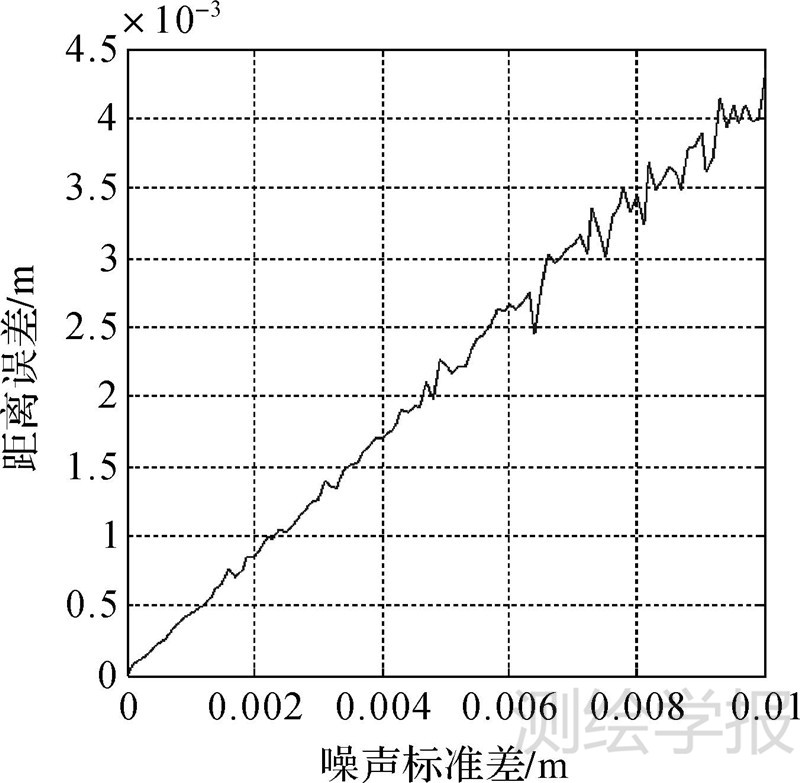
由于试验待配准数据是由基准数据整体旋转平移后得到的,未考虑同名直线匹配误差。为此,模拟实际测量中匹配误差,在待配准数据直线的2个端点(6个坐标值)加入高斯白噪声,且加入的白噪声互不相关。考虑实际数据LiDAR点云精度为10 mm,噪声标准差设定在0~0.01 m之间变化,为了保证结果的稳定性,在每一个噪声水平上,程序运行100次,得到的噪声标准差对配准精度的影响结果如图 3和图 4所示。由图 3和图 4可以看出,当噪声标准差在0~0.01 m之间变化过程中,直线配准的距离误差和角度误差都呈现线性增大的趋势,但是距离误差均值在0~4.5 mm之间,角度误差均值在0°~0.055°之间,由此可见距离误差小于噪声标准差变化,距离误差和角度误差均可以满足LiDAR点云配准精度要求。
|
| 图 3 不同噪声水平下配准距离误差曲线图 Fig. 3 Distance error under different noise levels |

|
| 图 4 不同噪声水平下配准角度误差曲线图 Fig. 4 Angle error under different noise levels |
为了验证算法在实际LiDAR点云配准中的实用性,利用文献[13]中的直线特征作为试验数据,数据为奥地利Riegl公司的LMS-Z420系列地面LiDAR设备采集得到的某建筑物立面点云,采样精度为10 mm。基于点云的线状特征提取,采用的方法是首先通过人机交互的方式选择相应的LiDAR点云实现平面的拟合,在此基础上,通过平面相交的方法来实现线状特征的精确提取。选取编号2和4两条直线进行试验,配准结果见表 3。选取编号1和3的直线作为检查直线,按照式(18)和式(19)计算实际精度,得到的结果见表 4。
| 方法 | XS/m | YS/m | ZS/m | φ/(°) | ω/(°) | κ/(°) | t/s |
| 欧拉角法 | -22.998 | 29.286 | -2.227 | 12.602 | 1.069 | 28.897 | 0.102 |
| 四元数法 | -22.999 | 29.292 | -2.230 | 12.601 | 1.073 | 28.900 | 0.084 |
| Plücker直线 | -22.993 | 29.397 | -2.314 | 12.551 | 1.081 | 28.902 | 0.078 |
| 方法 | d/m | θ/(°) | |||||
| l1 | l3 | 均值 | l1 | l3 | 均值 | ||
| 欧拉角法 | 0.008 2 | 0.009 6 | 0.008 9 | 0.016 7 | 0.045 5 | 0.031 1 | |
| 四元数法 | 0.008 1 | 0.009 3 | 0.008 7 | 0.015 8 | 0.044 6 | 0.030 2 | |
| Plücker直线 | 0.005 6 | 0.005 8 | 0.005 7 | 0.010 6 | 0.037 2 | 0.023 9 | |
从表 3看出,3种方法结果基本相同。在计算效率方面,Plücker直线法与四元数法基本相同,由于两种方法都避免了繁琐的三角函数运算,因此相比欧拉角法效率更高。
从表 4看出,Plücker直线法配准后的距离精度均值为5.7 mm,角度精度均值为0.023 9°,均高于四元数法和欧拉角法。这是因为欧拉角法的外方位元素之间存在相关性,如Xs与φ、Ys与ω等,导致最小二乘估计存在复共线性,不再是最优估计。四元数法虽然采用两个端点描述直线,但基元本质上仍是点的三维坐标。而本文方法用方向矢量与矩矢量将直线描述为5维空间中的6个齐次坐标,将6个齐次坐标描述的直线作为基元,并且直接利用同名直线重合的空间拓扑关系建立共线条件方程,是真正的基于直线的点云配准方法。
4 结 论本文提出了一种基于Plücker直线的LiDAR点云共线条件配准方法,首先通过Plücker坐标描述同名直线,然后利用单位对偶四元数表示Plücker直线的空间螺旋运动,根据同名Plücker直线的共线条件建立LiDAR点云配准模型。分别进行了模拟数据试验和实际数据试验,试验结果表明,本文方法充分利用了待配准点云与基准点云同名直线间的空间拓扑关系,增强了配准模型的几何约束性。然而本文配准方法未考虑存在比例缩放的点云数据,这是下一步需要解决的问题。
| [1] | 张东, 黄腾, 李桂华. 地面LiDAR点云数据先局部后整体配准方法[J]. 测绘工程, 2012, 21(2): 6-8. ZHANG Dong, HUANG Teng, LI Guihua. Registration Method of Terrestrial LiDAR Data from Parts to Whole[J]. Engineering of Surveying Mapping, 2012, 21(2): 6-8. |
| [2] | 陈卓, 马洪超. 基于机载LiDAR数据的大型立交桥三维建模方法[J]. 测绘学报, 2012, 41(2): 252-258. CHEN Zhuo, MA Hongchao. Automatic Extracting and Modeling Approach of City Cloverleaf from Airborne LiDAR Data[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(2): 252-258. |
| [3] | 方莉娜,杨必胜. 车载激光扫描的三维道路自动提取方法[J]. 测绘学报, 2013, 42(2): 260-267. FANG Lina, YANG Bisheng. Automated Extracting Structural Roads from Moblie Laser Scanning Point Clouds[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(2): 260-267. |
| [4] | BESL P J, MCKAY N D. A Method for Registration of 3-D Shapes[J]. IEEE Transactions on Pattern Analysis and Machines Intelligence, 1992, 14(2): 239-256. |
| [5] | ROBERT J M P. Theory and Application of Weighted Least Squares Surface Matching for Accurate Spatial Data Registration[D]. Australia: The University of Newcastle, 2004. |
| [6] | ROSENHOLM D, TORLEGARD K. Three-dimensional Absolute Orientation of Stereo Models Using Digital Elevation Models[J]. Photogrammetric Engineering and Remote Sensing, 1988, 54(10): 1385-1389. |
| [7] | 张剑清, 翟瑞芳, 郑顺义. 激光扫描多三维视图的全自动无缝镶嵌[J]. 武汉大学学报(信息科学版), 2007, 32(2): 100-103. ZHANG Jianqing, ZHAI Ruifang, ZHENG Shunyi. Automatic Seamless Registration of 3D Multiple Range Views[J]. Geomatics and Information Science of Wuhan University, 2007, 32(2): 100-103. |
| [8] | 童礼华,程亮,李满春,等. 基于建筑轮廓的车载和航空LiDAR数据配准[J].测绘学报, 2013, 42(5): 699-706, 714. TONG Lihua, CHENG Liang, LI Manchun, et al. Registration of Vehicle and Airborne LiDAR with Building Contours[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(5): 699-706, 714. |
| [9] | 戴静兰, 陈志杨, 叶修梓. ICP算法在点云配准中的应用[J]. 中国图象图形学报, 2007, 12(3): 517-521. DAI Jinglan, CHEN Zhiyang, YE Xiuzi. The Application of ICP Algorithm in Point Cloud Alignment[J]. Journal of Image and Graphics, 2007, 12(3): 517-521. |
| [10] | 何文峰, 查红彬. 基于平面特征的深度图像配准[C]//中国人工智能进展-中国人工智能学会第10届全国学术年会论文集.北京: 北京邮电大学出版社, 2003:643-648. HE Wengfeng, ZHA Hongbin. Registration of Range Data Based on Planar Features[C]//Advances in Chinese Artificial Intelligence.Beijing: Beijing University of Posts and Telecommunications press, 2003, 643-648. |
| [11] | PARK S Y, SUBBARAO M. An Accurate and Fast Point-to-Plane Registration Technique[J]. Pattern Recognition Letters, 2003, 24(16): 2967-2976. |
| [12] | GUAN Yunlan, ZHANG Hongjun. Initial Registration for Point Clouds Based on Linear Features[C]//Proceedings of 2011 4th International Symposium on Knowledge Acquisition and Modeling.Sanya: IEEE, 2011: 474-477. |
| [13] | 王永波, 杨化超, 刘燕华, 等. 线状特征约束下基于四元数描述的LiDAR点云配准方法[J]. 武汉大学学报(信息科学版), 2013, 38(9): 1057-1062. WANG Yongbo, YANG Huachao, LIU Yanhua, et al. Linear-Feature-Constrained Registration of LiDAR Point Cloud via Quaternion[J]. Geomatics and Information Science of Wuhan University, 2013, 38(9): 1057-1062. |
| [14] | AYACHE N, FAUGERAS O D. Maintaining Representations of the Environment of a Mobile Robot[J]. IEEE Transactions on Robotics and Automation, 1989, 5(6): 804-819. |
| [15] | FUNDA J, TAYLOR R H, PAUL R P. On Homogeneous Transforms, Quaternions, and Computational Efficiency[J]. IEEE Transactions on Robotics and Automation, 1990, 6(3): 382-388. |
| [16] | ZHANG Wenxiang. Plücker Coordinates of Screws and Their Applications in Gear Studies[J]. Journal of Huainan Mining Institute, 1991, 11(1-2): 86-97, 56. |
| [17] | RONDA J I, VALDES A, GALLEGO G. Camera Autocalibration Using Plücker Coordinates[C]//IEEE International Conference on Image Processing 2005. Genova: IEEE, 2005: 3125-3128. |
| [18] | SARIYILDIZ E, TEMELTAS H. Solution of Inverse Kinematic Problem for Serial Robot Using Dual Quaterninons and Plücker Coordinates[C]//Proceedings ofIEEE/ASME International Conference on Advanced Intelligent Mechatronics. Singapore: IEEE, 2009: 338-343. |
| [19] | 李静, 王惠南, 刘海颖. 基于普吕克直线的交会对接相对位姿确定算法[J]. 中国空间科学技术, 2013, 33(1): 69-74. LI Jing, WANG Huinan, LIU Haiying. Plucker Line Based Relative Position and Attitude Determination Algorithm for RVD[J]. Chinese Space Science and Technology, 2013, 33(1): 69-74. |
| [20] | SELIG J M. 机器人学的几何基础[M].杨向东, 译.北京: 清华大学出版社, 2008. SELIG J M. Robotics Foundations of Geometry[M]. YANG Xiangdong, trans.Beijing: Tsinghua University Press, 2008. |
| [21] | CHASLES M. Note sur les Proprietes Generales du Systeme de Deux Corps Semblables Entreux et Places Dune Maniere Quelconque Dans Lespace; et sur le Deplancement Fini ou Infiniment Petit dun Corps Solide Libre[J]. Bulletin des Science Mathematiques, Astronomiques, Physiques et Chimiques, 1830, 14: 321-326. |
| [22] | ROONEY J. A Comparison of Representations of General Spatial Screw Displacement[J]. Environment and Planning B Planning and Design, 1978, 5(1): 45-88. |
| [23] | LASENBY J, FITZGERALD W J, LASENBY A N, et al. New Geometric Methods for Computer Vision: An Application to Structure and Motion Estimation[J]. International Journal of Computer Vision, 1998, 26(3): 191-213. |