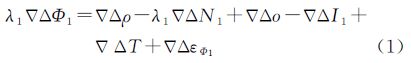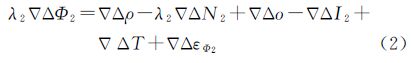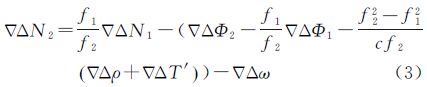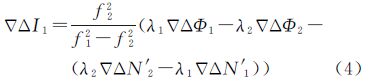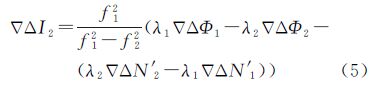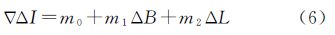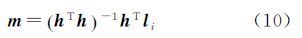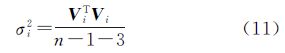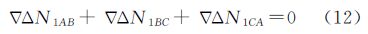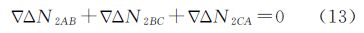北斗导航卫星系统(BeiDou navigation satellite system，BDS)是我国具有独立自主产权、自主研发的卫星导航定位系统[1]。目前，北斗导航卫星系统空间星座由5颗地球同步轨道(geo-synchronous orbit，GEO)卫星、5颗倾斜地球同步轨道(inclined geo-synchronous orbits，IGSO)卫星、4颗中高度轨道(medium earth orbit，MEO)卫星组成[2]。2012年12月27日，北斗系统空间信号接口控制文件(ICD)正式版公布，北斗导航卫星系统正式对亚太地区提供无源定位、导航、授时服务。BDS提供的标准服务定位精度为10 m，测速精度为0.2 m/s，授时精度为20 ns[3]。BDS网络RTK方法是提高BDS标准定位精度的重要手段之一。
实现BDS高精度定位都是采用载波相位观测数据[4]。而利用BDS网络RTK方法进行高精度动态定位的首要条件是参考站间载波相位整周模糊度的准确确定，只有正确固定了参考站模糊度才能得到高精度的综合误差或是建立高精度的误差模型。由于网络RTK参考站间距离较长，一般在几十千米以上，采用简单双差组合的方法单历元确定BDS载波相位整周模糊度非常困难，主要是由于电离层延迟和对流层延迟等误差对双差观测值的影响大于模糊度的半个波长。即使在使用双频观测数据和参考站坐标已知的情况下，整周模糊度也难以与误差分离。
目前，国内外学者对GPS网络RTK参考站双差模糊度解算作了大量研究，并取得了很多成果[5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16]。文献[5]研究了GPS长距离静态定位模糊度解算算法；文献[6]使用卡尔曼滤波方法实现了参考站间模糊度的快速解算；文献[7]研究了纳伪概率可控的四舍五入方法进行GPS参考站间的模糊度固定，可提高模糊度整数解的可靠性。由于GPS系统发展比较成熟，研究者们研究和实现了GPS网络RTK参考站整周模糊度的单历元确定[8, 9]，文献[8]提出了GPS网络RTK参考站间单历元模糊度搜索方法。但BDS刚刚建立，其信号质量、接收设备等相对于GPS不够完善，同时，BDS星座中包含GEO卫星和IGSO卫星，广播星历的卫星轨道精度相对于GPS较低。所以，利用GPS网络RTK参考站整周模糊度解算方法不能很好地实现BDS参考站的整周模糊度单历元解算。
因此，本文针对B1、B2双频载波相位观测数据，提出一种BDS网络RTK参考站间的双频载波相位整周模糊度单历元解算方法。该方法利用B1、B2载波相位整周模糊度间的线性关系选择载波相位整周模糊度备选值，然后通过参考站间双差电离层延迟误差线性计算模型的建立搜索和确定B1、B2载波相位的整周模糊度。
1 参考站B1、B2载波相位整周模糊度间的线性关系BDS系统B1、B2的频率分别为1 561.098 Mhz、1 207.140 Mhz，B1频率与GPS的L1频率接近，B2频率与Galileo E5b频率相同。因为双差组合观测值具有可消除接收机钟差和卫星钟差，大大削弱卫星星历误差、电离层延迟误差、对流层延迟误差等误差影响的优点，双差载波相位模糊度可保持整周特性，所以，本文对BDS载波相位双差模糊度进行单历元解算。通常情况下，BDS网络RTK的参考站都设在比较开阔的地方，卫星的多路径效应较小，可忽略多路径的影响，则参考站的双差B1、B2载波相位观测方程可表示为
式中，Δ▽是双差操作符；Φ为载波相位观测值；o为卫星轨道误差；I是电离层延迟误差；T是对流层延迟误差；εΦ为载波相位观测噪声；N为载波相位观测值的模糊度；ρ为卫星到接收机的几何距离；λ=c/f为载波相位的波长，c为真空中的光速，f为频率；下标分别表示B1、B2载波相位频率。
对流层延迟误差T可以通过模型改正或其他方法进行消除或削弱[17, 18, 19, 20, 21]。由于B1频率和B2频率上的载波相位电离层延迟误差关系为Δ▽I1=f22Δ▽I2/f12，根据这一关系可消除式(1)和式(2)中的电离层延迟误差(一阶项)，得到
式中，Δ▽T′为通过对流层延迟误差模型得到的双差对流层延迟误差计算值；因为参考站的坐标已知，Δ▽ρ可以精确计算；Δ▽ω为对流层延迟误差模型改正后的双差残差、双差卫星轨道误差的残差及观测噪声的综合影响。
式(3)是表示B2载波相位整周模糊度Δ▽N2与B1载波相位整周模糊度Δ▽N1间线性关系的直线形式，设：k=f1/f2=1 561.098/1 207.14=763/590≈1.293 22。式(3)表示的线性关系不受电离层延迟误差一阶项的影响，主要是对流层延迟误差残差和BDS卫星轨道误差残差等非弥散误差的影响。对于式(3)，由于存在BDS广播星历卫星轨道的误差以及对流层模型改正后的模型误差，双差组合后仍然受残余误差以及观测噪声的影响。如果各种误差完全消除，则在该线性关系的整数约束下，满足式(3)的Δ▽N1备选值变化590周，Δ▽N2备选值将变化763周。显然，这种情况只能在理想条件下存在，如果出现这种情况则B1、B2载波相位整周模糊度可以很容易实现单历元确定。由于误差并不能完全消除，所以，实际上满足这一线性关系的模糊度整数备选值的变化率是由比值与1.293 22近似的两个整数表示的。例如13/10=1.3，即Δ▽N1变化10周，Δ▽N2变化13周。判断模糊度备选值的依据是双频模糊度整数值带入式(3)之后能够满足式(3)的约束。式(3)中的误差残余越大，则线性关系的约束能力越小，模糊度整数备选值之间的变化间隔越短，反之，模糊度整数备选值之间的变化间隔越大。
2 参考站B1、B2载波相位整周模糊度的单历元确定 2.1 利用模糊度备选值计算双差电离层延迟误差根据参考站各BDS卫星电离层延迟误差的空间相关关系，可以建立双差电离层延迟误差的空间计算模型，通过构建双差电离层延迟误差的空间计算模型搜索和确定B1、B2载波相位的整周模糊度。正确的B1、B2载波相位整周模糊度备选值组合可以计算出正确的电离层延迟误差，而错误的B1、B2载波相位整周模糊度组合计算出的电离层延迟误差存在偏差。可利用双频载波相位模糊度备选值组合得到对应的双差电离层延迟误差，然后利用这些双差电离层延迟误差构建多个双差电离层延迟误差模型，其中只有正确的双差电离层延迟误差建立的误差模型才是准确的，即可实现对B1、B2载波相位整周模糊度的搜索。
利用式(1)计算出Δ▽N1的初值，然后在模糊度初值左右一定范围内，使用式(3)选择出的Δ▽N2备选值与Δ▽N1备选值，不受电离层延迟误差(主要是一阶项)的影响。忽略载波相位的观测噪声，根据式(1)、式(2)可得由B1、B2载波相位整周模糊度备选值计算相应频率双差电离层延迟误差的公式
式中，Δ▽N′1、Δ▽N′2分别为B1载波相位整周模糊度和B2载波相位整周模糊度的备选值。B1、B2双频波相位模糊度的备选值由式(3)选择出，每组整周模糊度备选值包括一对Δ▽N′1、Δ▽N′2。 2.2 利用双差电离层延迟误差模型搜索模糊度
根据两个参考站电离层延迟误差的空间相关性，可以建立BDS双差电离层延迟误差的空间线性模型如式(6)所示
式中，Δ▽I是参考站间的双差电离层延迟误差；m0、m1、m2为双差电离层延迟误差的线性拟合计算模型的系数，m0是常数项，m1和m2是水平双差电离层延迟误差拟合系数；ΔB为卫星与基准卫星的穿刺点纬度差值；ΔL为卫星与基准卫星的穿刺点经度差值。因为两个网络RTK参考站上同一对双差卫星穿刺点的经纬度差值非常接近，所以，式(6)中卫星穿刺点的经纬度差值可在两个参考站中任取其一。
如果当前参考站的共视卫星有n颗(n-1>3)，则对于参考站BDS系统B1载波相位的电离层延迟误差，其计算双差电离层延迟误差的线性计算模型有
以矩阵的形式表示为< 式中，ιli=Δ▽I1iΔ▽I2i…Δ▽In－1i、m=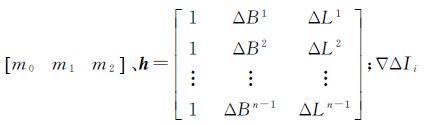
为载波相位的双差电离层延迟误差；上标表示卫星编号，下标i表示频率，1表示B1载波相位的双差电离层延迟误差，2表示B2载波相位的双差电离层延迟误差；向量m为双差电离层延迟误差拟合系数。
利用2.1节中得到的各双差卫星整周模糊度备选值对应的双差电离层延迟误差，计算参考站双差电离层延迟误差线性计算模型的系数，根据最小二乘解算模型系数的计算确定正确的模糊度备选值。将参考站每颗双差卫星模糊度备选值对应的B1、B2载波相位双差电离层延迟误差作为待检测对象。对各颗BDS双差卫星相同频率的待检测电离层延迟误差数值进行组合，组成多组n-1维的双差电离层延迟误差向量，利用各组待检测双差电离层延迟误差向量计算双差电离层延迟误差的线性计算模型系数。根据式(8)，li即为n-1维的双差电离层延迟误差向量，则计算载波相位双差电离层延迟误差模型系数m的误差方程为<
根据最小二乘计算原理，如果进行等权计算，则有
对于式(10)，也可根据卫星高度角定权，进行加权计算。将式(10)平差计算出的双差电离层延迟误差线性计算模型的系数代入式(9)，可得
式中，下标i表示频率。一个n-1维载波相位双差电离层延迟误差向量计算出一个σi2，将各个σi2进行比较，取最小的σi2对应的双差电离层延迟误差组合为正确的双差电离层延迟误差，其对应的B1、B2载波相位整周模糊度备选值则为正确的模糊度备选值。同时，将σi2的最小值与次小值进行Ratio检验，增加搜索的准确性。由于，B1、B2载波相位模糊度整数备选值之间有间隔变化，所以，每对B1、B2载波相位模糊度整数备选值组合对应的电离层延迟误差值之间有一定的差别，有利于区分出正确的模糊度备选组合。
分别对B1、B2载波相位双差电离层延迟误差组合进行上述计算和搜索，确定出满足要求的双差电离层延迟误差，其对应的B1、B2载波相位整周模糊度备选值则为正确的模糊度备选值。
2.3 B1、B2载波相位整周模糊度的检验将根据B1载波相位双差电离层延迟误差模型搜索出的B1、B2载波相位整周模糊度备选值，与根据B2载波相位双差电离层延迟误差模型搜索出的B1、B2载波相位整周模糊度备选值进行比较，如果二者一致则说明搜索出的B1、B2载波相位整周模糊度为正确的整周模糊度组合。
此外，对于任意两个以上的参考站所组成的闭合基线，双差整周模糊度的代数和在理论上为零。以参考站A、B和C为例，则
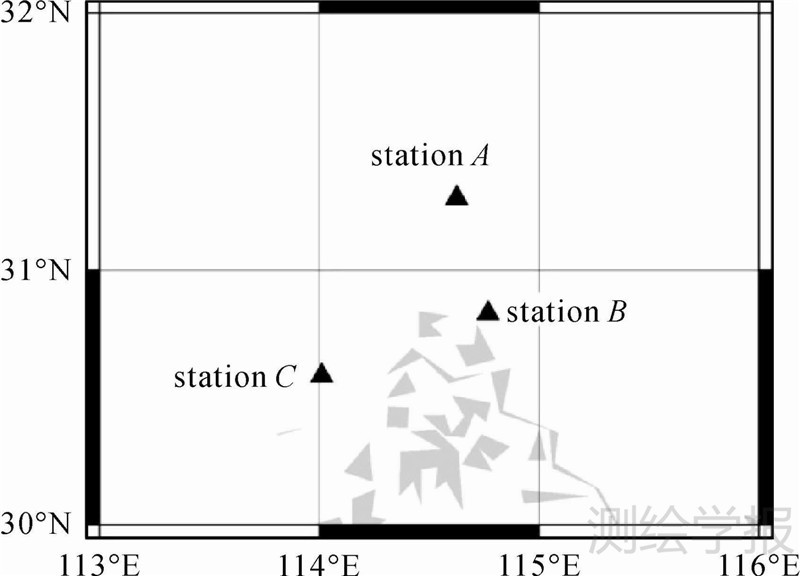
式中，下标表示参考站。将闭合基线的双差B1、B2载波相位整周模糊度代入式(12)、式(13)进行检验，如果满足该闭合条件则认为被检验的双差B1、B2载波相位整周模糊度是正确的。同时，3条基线同一双差卫星的3个双差电离层延迟误差的代数和也为零，此条件也可用来对解算出的载波相位整周模糊度进行检验。 3 算例与分析
本文使用2013年4月29日(BDS时382周，起始时刻周内秒为86 400)华中地区CORS网一天的BDS实测数据进行算法检验，采样间隔为1 s。该试验数据共有3个参考站，测站分布如图 1所示，station A到station B距离53 km，station A到station C距离102 km，station B到station C距离81 km。
|
| 图 1 测站分布 Fig. 1 Location of stations |
按照本文的方法对该试验数据的B1、B2载波相位模糊度进行单历元解算，使用Saastamoinen模型计算式(3)中的Δ▽T′。以基线station A—station B的第一个历元为例，基准卫星选取C07。使用式(3)选取B1、B2载波相位整周模糊度的备选值，如表 1所示。各整周模糊度备选组合中第1项、第2项为B1、B2载波相位整周模糊度数值，第3项为该模糊度备选组合求得的B1载波相位电离层延迟误差，对应的B2载波相位电离层延迟误差为B1载波相位电离层延迟误差的f12/f22倍，这里不具体给出。式(3)的线性约束关系对模糊度备选值选择能力的强弱体现在模糊度备选值的变化。各卫星线性关系的约束能力随对流层延迟误差和卫星轨道误差等误差的双差残差不同而变化，因此，各卫星模糊度备选值的数值变化大小并不一致。式(3)主要受卫星广播星历的轨道误差和对流层延迟误差的双差残差影响，GEO卫星的广播星历轨道精度较差，所以，大部分GEO卫星的线性关系约束能力稍弱(同时也与卫星高度角相关)，即模糊度备选值的变化周期短。
| PRN | 双频整周模糊度备选组合 | 高度角/(°) |
| C03 | -548/-424/0.023-541/-415/-1.301 -538/-411/-1.922 | 52.9 |
| C02 | -110 857/-85 727/1.97 -110 854/-85 723/ 1.35 -110 847/-85 714/ 0.025 -110 844/-85 710/-0.595 | 39.1 |
| C10 | -5645/-4367/0.712 -5642/-4363/0.091 -5635/-4354/-1.233 -5632/-4350/-1.854 | 38.9 |
| C01 | 80 067/61 911/0.695 80 070/61 915/0.075 80 077/61 924/-1.249 80 080/61 928/-1.869 | 44.3 |
| C04 | 109 265/84 487/1.34 109 268/84 491/0.719 109 271/84 495/0.099109 275/84 500/-0.605 | 29.2 |
| C05 | -171 882/-132 914/1.453 -171 879/-132 910/0.832 -171 875/-132 905/0.128 -171 872/-132 901/-0.492-171 869/-132 897/-1.112 | 20.7 |
| C09 | 160 167/-123 855/1.402 -160 160/-123 846/0.077-160 157/ -123 842/-0.543 | 61.3 |
| C13 | 77 474/59 903/1.776 77 477/59 907/1.156 77 483/59 915/-0.08477 489/59 923/-1.324 | 20.7 |
| C06 | -56 280/-43 523/1.379 -56 273/-43 514/0.054 -56 266/-43 505/-1.271 | 67.7 |
由于B1、B2载波相位模糊度整数备选值之间有间隔变化，所以各B1、B2载波相位模糊度整数备选值组合对应的电离层延迟误差值之间有较大的差别，有利于利用式(11)确定出正确的模糊度备选组合。根据式(11)搜索出方差σ12最小的各双差卫星B1载波相位整周模糊度备选值为：-548、-110 847、-5642、80 070、109 271、-171 875、-160 160、77 483、-56 273，σ12=0.005 47。搜索出方差σ22最小的各双差卫星B2载波相位整周模糊度备选值为：-424、-85 714、-4363、61 915、84 495、-132 905、-123 846、59 915、-43 514，σ22=0.015 37。从表 1中可知，B1、B2载波相位整周模糊度搜索的结果分别是各卫星对应的一对B1、B2载波相位整周模糊度备选值。采用所有数据准确确定该试验数据中的双差整周模糊度作为参考值，各双差卫星B1载波相位整周模糊度的准确参考值为：-548、-110 847、-5642、80 070、109 271、-171 875、-160 160、77 483、-56 273。本文方法的搜索结果与B1载波相位整周模糊度的准确参考值相同。同时，使用相同的方法对station B—station C、station C—station A各双差卫星的整周模糊度备选值进行搜索和确定，并利用式(12)、式(13)对station A—station B、station B—station C、station C—station A的模糊度搜索结果进行闭合关系检验，可将第1个历元3个参考站的双差整周模糊度确准确确定。
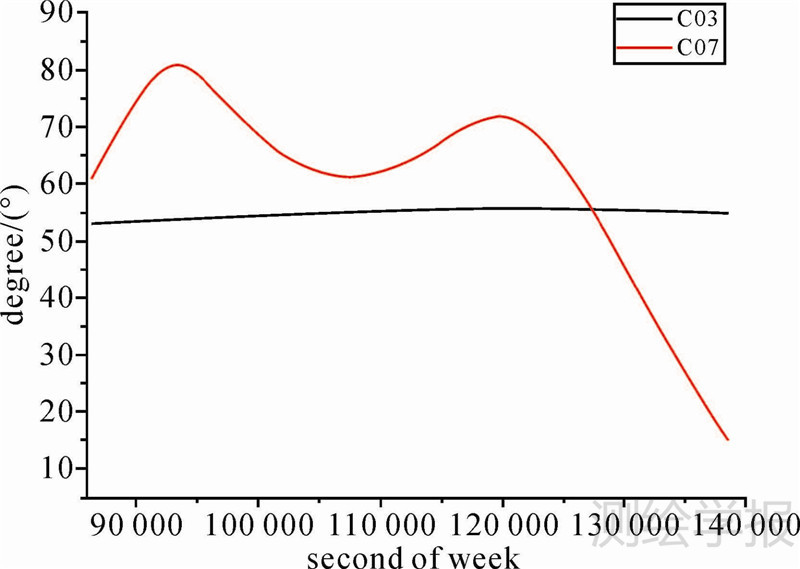
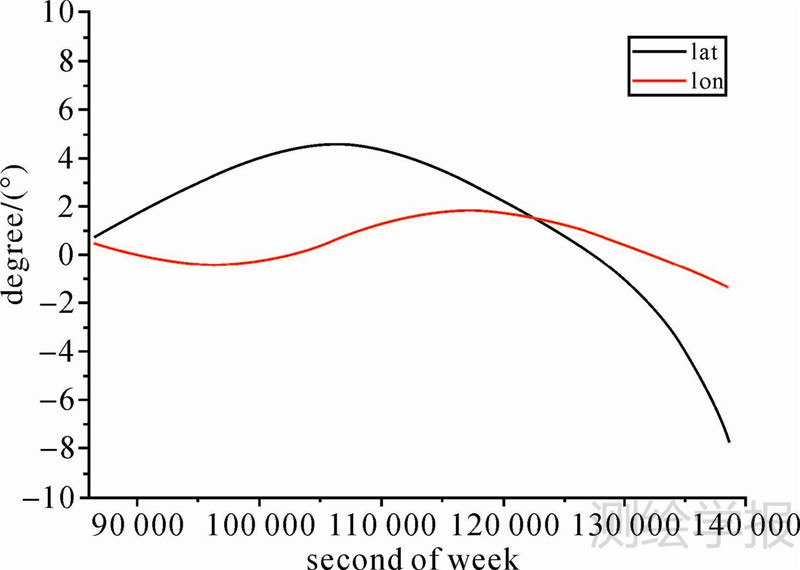
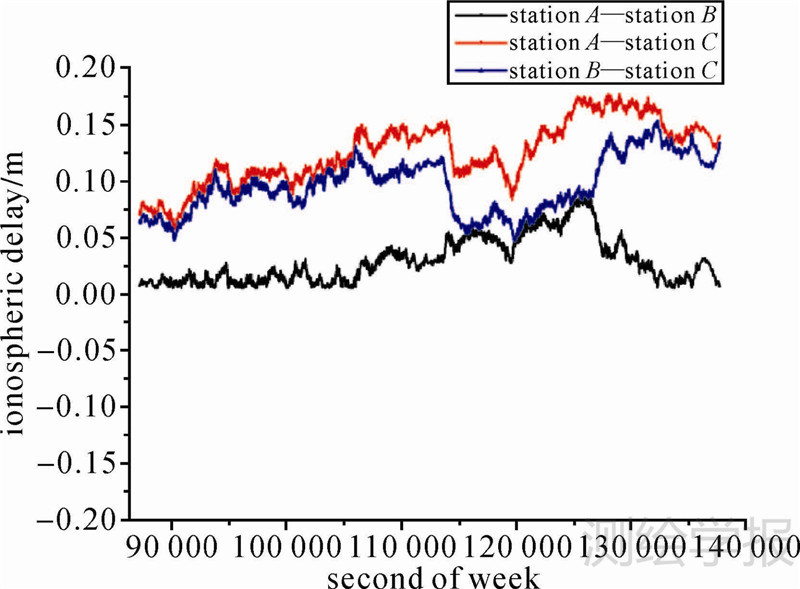
本文一天的试验数据算法验证中，分别以卫星C03-C07、C09-C07双差卫星为例。卫星C03-C07高度角变化如图 2所示，卫星C03-C07电离层穿刺点的经纬度差值如图 3所示。C03为GEO卫星，其高度角变化很小，C07为IGSO卫星运动周期约为24 h。在截止高度角选择为15°的情况下，该组一天的试验数据中参考站连续观测卫星的时间达到约14.5 h。由于参考站观测到的GEO卫星电离层穿刺点变化较小，所以，电离层穿刺点的经纬度差值的变化，是C07的穿刺点经纬度变化决定的。IGSO卫星的运行轨道星下点轨迹以子午线为中心，参考站观测到的C07电离层穿刺点经度变化较小，纬度变化较大。所以，卫星C03-C07电离层穿刺点的经纬度差值中，经度方向的差值变化较慢，纬度方向的差值变化稍大。利用本文的方法将B1、B2载波相位整周模糊度准确确定后，卫星C03-C07的B1载波相位观测值双差电离层延迟误差值如图 4所示。
|
| 图 2 C03-C07高度角 Fig. 2 The elevations of C03-C07 |
|
| 图 3 卫星C03-C07穿刺点经纬度差值 Fig. 3 The longitude and latitude difference of C03-C07 IPP |
|
| 图 4 卫星C03-C07双差电离层延迟误差 Fig. 4 Double difference ionosphere delay error of C03-C07 |
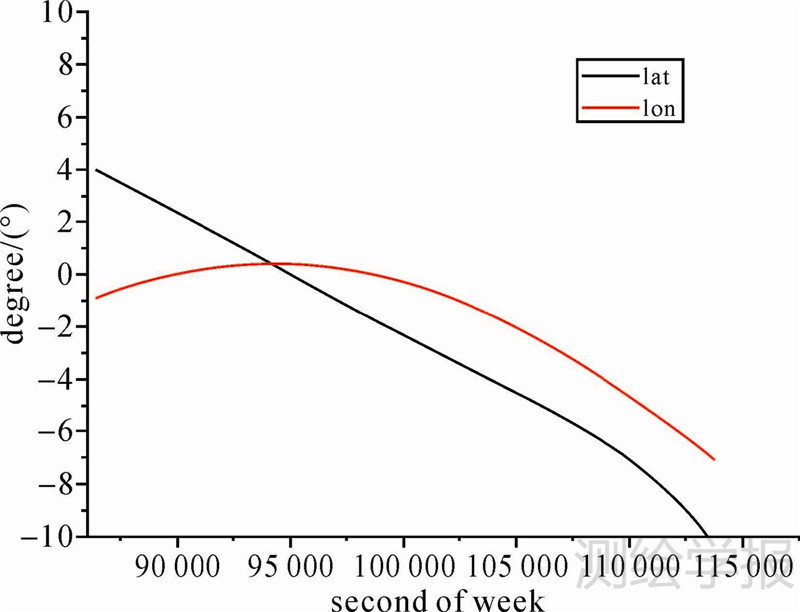
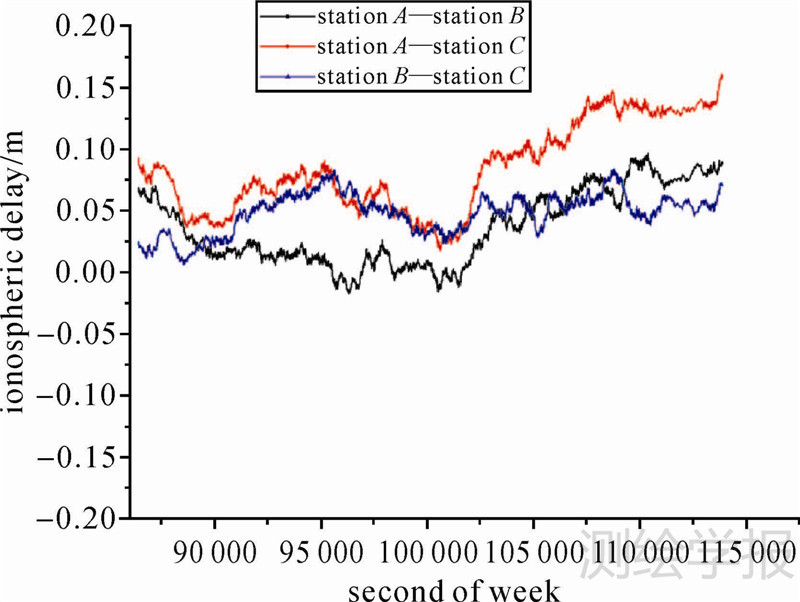
卫星C09-C07高度角变化如图 5所示，卫星C09-C07电离层穿刺点的经纬度差值如图 6所示。C09-C07均为IGSO卫星，运动周期约24 h，截止高度角选择为15°，该组一天的参考站试验数据中第1个连续观测到卫星C09的时段长约8 h。从图 6中可知，卫星C09-C07电离层穿刺点的经纬度差值的变化相对于卫星C03-C07较快。卫星C09-C07电离层穿刺点的经纬度差值中，经度方向的差值变化较慢，纬度方向的差值变化稍大。利用本文的方法将B1、B2载波相位整周模糊度准确确定后，卫星C09-C07连续8 h的B1载波相位观测值双差电离层延迟误差值如图 7所示。
|
| 图 5 卫星C09-C07的高度角 Fig. 5 The elevations of C09-C07 |
|
| 图 6 卫星C09-C07穿刺点经纬度差值 Fig. 6 The longitude and latitude difference of C09-C07 IPP |
|
| 图 7 卫星C09-C07双差电离层延迟误差 Fig. 7 Double difference ionosphere delay error of C09-C07 |
本文算例的观测时间从凌晨开始，随着观测值时间的推移，越接近中午，图 4、图 7中3条基线双差电离层延迟误差的整体数值呈逐渐增大的趋势。同时，双差的电离层延迟误差与卫星高度角以及两颗求双差卫星的电离层穿刺点的空间位置关系有关，即卫星高度角越大，电离层延迟误差越小，双差卫星穿刺点经纬度的差值绝对值越小(电离层穿刺点的空间位置越接近)，双差电离层延迟误差越小。因此，图 4、图 7中的B1载波相位观测值双差电离层延迟误差除了随观测时间变化外，还受卫星高度角和双差卫星电离层穿刺点经纬度差值的影响，双差电离层延迟误差有数值增减的抖动，即双差电离层延迟误差会出现小范围内减小或增大的情况。
图 4、图 7中的双差电离层延迟误差，满足闭合基线电离层延迟误差和等于零，即station A—station B、station B—station C、station C—station A上同一颗双差卫星的电离层延迟误差之和为零，station C—station A的电离层延迟误差由station A—station C的电离层延迟误差取相反数得到。表 2为该算例3个参考站间双差载波相位整周模糊度固定的成功率(卫星截止高度角15°)。方法1为本文的方法，从表 2中可以看出该算例利用本文方法的模糊度固定成功率较高。方法2为文献[8]中的单历元模糊度确定方法。由于BDS与GPS的波长不同，且BDS广播星历的轨道精度和伪距观测值的精度较GPS差，所以，利用方法2进行该算例BDS整周模糊度的单历元解算效率和成功率较低。方法3是利用MW组合计算宽巷模糊度，然后计算确定当前历元原始载波相位模糊度。MW组合计算宽巷模糊度的收敛过程需要一段观测时间，表 2中的统计信息为宽巷模糊度固定之后单历元确定载波相位模糊度的数目。由于BDS伪距观测值的噪声较大，精度较低，所以，消耗了较多的观测时间用于确定宽巷模糊度，导致很多单历元模糊度不能在当前历元固定。同时，由于BDS系统的广播星历轨道精度较低，即使宽巷模糊度固定之后，原始载波相位模糊度的确定效率和成功率也较低。从表 2中可以看出，本文的方法相比方法2、方法3具有较高的BDS载波相位整周模糊度单历元固定成功率。根据算法试验结果可知，本文的方法能够实现BDS中距离参考站载波相位整周模糊度的单历元准确解算，且具有较高成功率和效率。
| 类别 | 方法 | C03-C07 | C09-C07 | 所有双差卫星 |
| 3个参考站单历元双差模糊度总数 | 156 348 | 82 002 | 956 790 | |
| 3个参考站单历元双差模糊度固定个数 | ||||
| 方法1 | 154 071 | 81 891 | 947 124 | |
| 方法2 | 63 036 | 42 236 | 486 452 | |
| 方法3 | 56 710 | 40 560 | 468 243 | |
| 模糊度固定成功率/(%) | ||||
| 方法1 | 98.54 | 99.86 | 98.98 | |
| 方法2 | 40.91 | 51.50 | 50.84 | |
| 方法3 | 36.80 | 49.46 | 48.93 |
本文方法通过消除电离层延迟误差选取载波相位模糊度的备选组合，并构建双差电离层延迟误差模型进行模糊度搜索，可降低电离层延迟误差对参考站间整周模糊度解算的影响。利用该方法参考站网只需一个历元即可启动，实用性强，可靠性好。同时，本文利用当前历元电离层延迟误差的空间关系建立双差电离层延迟误差改正模型，并且是进行参考站整周模糊度的单历元解算，因此，电离层延迟误差历元间的变化对本文的方法影响较小。由于GEO卫星相对于地球静止、IGSO卫星运动周期长，卫星的电离层穿刺点变化缓慢，历元之间的电离层延迟误差的相关性较强。因此，随着观测时间的延长，在没有电离层剧烈突变的情况下，可以根据电离层延迟误差的变化，对解算出的B1、B2载波相位整周模糊度进行可靠性判断。本文的方法是针对中距离BDS网络RTK参考站整周模糊度的单历元解算，对于长距离BDS网络RTK参考站整周模糊度的单历元解算方法还需进一步研究。
| [1] | 杨元喜. 北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报, 2010, 39(1): 1-6. YANG Yuanxi. Progress, Contribution and Challenges of Compass-BeiDou Satellite Navigation System[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 1-6. |
| [2] | 杨元喜, 李金龙, 徐君毅, 等. 中国北斗卫星导航系统对全球PNT用户的贡献[J]. 科学通报, 2011, 56(21): 1734-1740. YANG Yuanxi, LI Jinlong, XU Junyi, et al. Contribution of the Compass Satellite Navigation System to Global PNT Users[J]. Chinese Science Bulletin, 2011, 56(26): 2813-2819. |
| [3] | SHI Chuang, ZHAO Qile, LI Min, et al. Precise Orbit Determination of BeiDou Satellites with Precise Positioning[J]. Science China Earth Sciences, 2012, 55(7): 1079-1086. |
| [4] | 高星伟, 过静珺, 程鹏飞, 等. 基于时空系统统一的北斗与GPS融合定位[J]. 测绘学报, 2012, 41(5): 743-748, 755. GAO Xingwei, GUO Jingjun, CHENG Pengfei, et al. Fusion Positioning of BeiDou-GPS Based on Spatio Temporal System Unification[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 743-748, 755. |
| [5] | VOLLATH U, LANDAU H, CHEN Xiaoming. Network RTK——Concept and Performance[C]//Proceedings of the GNSS Symposium. Wuhan: [s.n.], 2002. |
| [6] | 周乐韬, 黄丁发, 袁林果, 等. 网络RTK参考站间模糊度动态解算的卡尔曼滤波算法研究[J]. 测绘学报, 2007, 36(1): 37-42. ZHOU Letao, HUANG Dingfa, YUAN Linguo, et al. A Kalman Filtering Algorithm for Online Integer Ambiguity Resolution in Reference Station Network[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(1): 37-42. |
| [7] | 李博峰, 沈云中, 张兴福. 纳伪概率可控的四舍五入法及其在RTK模糊度固定中的应用[J]. 测绘学报, 2012, 41(4): 483-489, 495. LI Bofeng, SHEN Yunzhong, ZHANG Xingfu. Error Probability Controllable Integer Rounding Method and Its Application to RTK Ambiguity Resolution[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(4): 483-489, 495. |
| [8] | 高星伟, 刘经南, 葛茂荣. 网络RTK基准站间基线单历元模糊度搜索方法[J]. 测绘学报, 2002, 31(4): 305-309. GAO Xingwei,LIU Jingnan,GE Maorong.An Ambiguity Searching Method for Network RTK Baselines between Base Stations at Single Epoch[J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(4): 305-309. |
| [9] | 祝会忠, 刘经南, 唐卫明, 等. 长距离网络RTK基准站间整周模糊度单历元确定方法[J]. 测绘学报, 2012, 41(3): 359-365. ZHU Huizhong, LIU Jingnan, TANG Weiming, et al. The Algorithm of Single-epoch Integer Ambiguity Resolution between Long-range Network RTK Base Stations[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 359-365. |
| [10] | 高星伟, 陈锐志, 赵春梅. 网络RTK算法研究与实验[J]. 武汉大学学报(信息科学版), 2009, 34(11): 1350-1353. GAO Xingwei, CHEN Ruizhi, ZHAO Chunmei. A Network RTK Algorithm and Its Test[J]. Geomatics and Information Science of Wuhan University, 2009, 34(11): 1350-1353. |
| [11] | BLEWITT G. Carrier Phase Ambiguity Resolution for the Global Positioning System Applied to Geodetic Baselines up to 2000 km[J]. Journal of Geophysical Research, 1989, 94(B8): 10187-10203. |
| [12] | DONG Danan, BOCK Y. Global Positioning System Network Analysis with Phase Ambiguity Resolution Applied to Crustal Deformation Studies in California[J]. Journal of Geophysical Research, 1989, 94(B4): 3949-3966. |
| [13] | BLEWITT G. An Automatic Editing Algorithm for GPS Data[J]. Geophysical Research Letters, 1990, 17(3): 199-202. |
| [14] | SUN Huangqi, CANNON M E, MELGARD T E. Real-time GPS Reference Network Carrier Phase Ambiguity Resolution[C]//Proceedings of the National Technical Meeting of the Institute of Navigation. San Diego: Institute of Navigation, 1999: 193-199. |
| [15] | HAN Shaowei. Carrier Phase-based Long-range GPS Kinematic Positioning[D]. Sydney: University of New South Wales, 1997. |
| [16] | DAI Liwen, WANG Jinling, RIZOS C, et al. Predicting Atmospheric Biases for Real-time Ambiguity Resolution in GPS-GLONASS Reference Station Networks[J]. Journal of Geodesy, 2003, 76(11-12): 617-628. |
| [17] | 葛茂荣, 刘经南. GPS定位中对流层折射估计研究[J]. 测绘学报, 1996, 25(4): 285-291. GE Maorong, LIU Jingnan. The Estimation Methods for Tropospheric Delays in Global Positioning System[J]. Acta Geodaetica et Cartographica Sinica, 1996, 25(4): 285-291. |
| [18] | 高星伟, 陈锐志, 李夕银. 中性大气对非差伪距定位的影响及其模型改正分析[J]. 测绘学报, 2007, 36(2): 134-140. GAO Xingwei, CHEN Ruizhi, LI Xiyin. A Study of the Neutral Atmospheric Effects on Pseudorange Positioning with Non-difference Models[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(2): 134-140. |
| [19] | HOPFIELD H S. Two-quartic Tropospheric Refractivity Profile for Correcting Satellite Data[J]. Journal of Geophysical Research, 1969, 74(18): 4487-4499. |
| [20] | SAASTAMOINEN J. Contributions to the Theory of Atmospheric Refraction[J]. Bulletin Géodésique, 1973, 107(1): 13-34. |
| [21] | BLACK H D. An Easily Implemented Algorithm for the Tropospheric Range Correction[J]. Journal of Geophysical Research, 1978, 83(B4): 1825-1828. |